六年级数学正比例与反比例的奥数题
【精品】比例和反比例 (奥数)
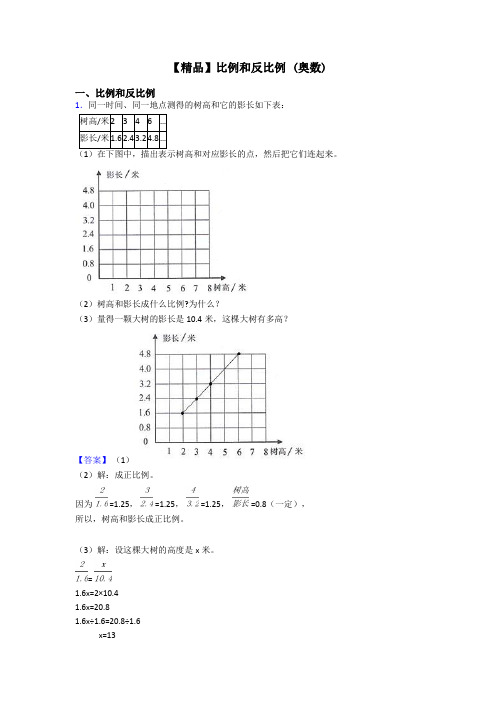
【精品】比例和反比例 (奥数)一、比例和反比例1．同一时间、同一地点测得的树高和它的影长如下表：树高/米2346…影长/米1.62.43.24.8…（2）树高和影长成什么比例?为什么？（3）量得一颗大树的影长是10.4米，这棵大树有多高？【答案】（1）（2）解：成正比例。
因为 =1.25， =1.25， =1.25， =0.8（一定），所以，树高和影长成正比例。
（3）解：设这棵大树的高度是x米。
=1.6x=2×10.41.6x=20.81.6x÷1.6=20.8÷1.6x=13答：这棵大树的高度是13米。
【解析】【分析】（1）观察统计图可知，横轴表示树高，竖轴表示影长，据此先描点，再连线，据此作图；（2）分别用树高：影长，求出比值，当比值一定时，成正比例，据此判断；（3）根据题意可知，设这棵大树的高度是x米，用树高：影长=树高：影长，据此列正比例解答.2．一辆货车从甲地去相距315千米的乙地送货。
已知前3时行了135千米，如果用同样的速度行完剩下的路程，还要行几时？（用比例解）【答案】解：设还要行x时。
=x =4答：还要行4时。
【解析】【分析】因为速度相同即一定，故路程与时间成正比例，所以，前3小时行的路程：3=剩下的路程：需要的时间，设所需时间为x小时，则可以用这个等量关系列出比例式。
3．某工程队要铺设一条公路，前20天已铺设了2.8千米，照这样计算，剩下的4.2千米，还要多少天才能铺完?(用比例解)【答案】解：设还要x天才能铺完。
2.8∶20=4.2∶xx=30答：还要30天才能铺完。
【解析】【分析】照这样计算的意思就是每天铺的长度不变，铺的长度与天数成正比例，先设出未知数，根据每天铺的长度不变列出比例解答即可。
4．表中x和y是两个成比例的量，观察表格并填完整。
X36181210y51020X361812109y510151820空位中x和y的值。
5．小兰看一本故事书，每天看10页，12天看完，若每天看15页，几天可以看完?【答案】解：设x天可以看完。
比例和反比例 (奥数)
比例和反比例 (奥数)一、比例和反比例1．如果10千克菜籽可以榨6.5千克菜油，那么有这种菜籽360千克，可以榨多少千克油?（用比例解）【答案】解：设可以榨x千克油。
10：6.5=360：x10x=6.5×360x=2340÷10x=234答：可以榨油234千克。
【解析】【分析】菜籽的重量和榨油的质量的比值是不变的，二者成正比例，设出未知数，根据正比例关系列出比例，解比例求出可以榨油的重量即可。
2．王叔叔开车从甲地到乙地，一共用了3小时，每小时行80km，原路返回每小时行100km。
返回时用了多长时间？【答案】解：设返回时用了x小时，100x=80×3100x=240100x÷100=240÷100x=2.4答：返回时用了2.4小时.【解析】【分析】根据题意可知，从甲地到乙地的路程是一定的，速度与时间成反比例，据此列比例解答.3．服装厂要加工一批服装，一共有4500套，头5天加工了750套，照这样计算，一共要多少天才能加工完这批报装？（用比例解）【答案】解：设一共要x天才能加工完这批服装。
750：5=4500：x750x=5×4500x=22500÷750x=30答：一共要30天才能加工完这批服装。
【解析】【分析】每天加工服装的套数不变，加工的总数与天数成正比例关系；设出未知数，根据每天加工的套数不变列出比例，解比例即可解决问题。
4．给一间房子铺地，如果用边长6分米的方砖，需要80块。
如果改用边长8分米的方砖，需要多少块？【答案】解：设需要x块。
（8×8）x=6×6×8064x=2880x=2880÷64x=45答：需要45块。
【解析】【分析】每块方砖的面积×方砖的块数=房间的面积，每块方砖的面积与方砖的块数成反比例；设出未知数，根据总面积不变列出比例，解比例求出需要方砖的块数即可。
六年级奥数《正反比例的应用》练习题
第六讲正反比例的应用（必做与选做）1.分别判断下面两种情况分别属于哪种关系：工作效率一定，工作总量和工作时间的关系；长方形的长一定，面积和宽的关系。
A. 正比例正比例B. 正比例反比例C. 反比例正比例D. 反比例反比例解析：工作效率＝工作总量÷工作时间，当工作效率一定时，工作总量和工作时间的比值一定，因此工作总量和工作时间是正比例关系；长方形的面积＝长×宽，长＝面积÷宽，当长一定，面积与宽的比值一定，因此面积和宽是正比例关系。
所以选A。
2.分别判断下面两种情况分别属于哪种关系：百米赛跑，速度和时间的关系；分子一定，分母和分数值的关系。
A. 正比例正比例B. 正比例反比例C. 反比例正比例D. 反比例反比例解析：百米赛跑，路程一定，路程＝速度×时间，速度和时间的乘积一定，因此速度和时间是反比例关系；分子一定，分子＝分母×分数值，分母和分数值的乘积一定，因此分母和分数值是反比例关系。
所以选D。
3.分别判断下面两种情况分别属于哪种关系：单价一定，总价和数量的关系；长方体的体积一定，底面积和高的关系。
A. 正比例正比例B. 正比例反比例C. 反比例正比例D. 反比例反比例解析：总价＝单价×数量，单价＝总价÷数量，单价一定，总价和数量比值一定，因此总价和数量是正比例关系；长方体的体积＝底面积×高，体积一定，底面积和高的积也一定，所以底面积和高是反比例关系。
所以选B。
4.下列各项哪个属于反比例关系？A. 速度一定，路程和时间B. 工作时间一定，工作总量和效率C. 数量一定，总价和单价D. 总人数一定，排队的行数和列数解析：速度一定，路程和时间的比值一定，所以是正比例关系；工作时间一定，工作总量和工作效率的比值一定，所以是正比例关系；数量一定，总价和单价的比值一定，所以是正比例关系；总人数一定，排队的行数和列数的乘积一定，因此是反比例关系。
【数学】比例和反比例 (奥数)
【数学】比例和反比例 (奥数)一、比例和反比例1．小兰看一本故事书，每天看10页，12天看完，若每天看15页，几天可以看完?【答案】解：设x天可以看完。
10×12=15x解得x=8答：8天可以看完。
【解析】【分析】已知每天看的页数×对应看完的天数=预计每天看的页数×对应预计看完的天数。
等式的性质2：等式两边同时乘（或除以）一个相同的数或式子，两边依然相等。
2．化肥厂生产一批化肥，每天生产35吨，40天完成任务。
如果要28天完成任务，那么每天应生产多少吨?(用比例知识解答)【答案】解：设每天应生产x吨.28x=35×40x=1400÷28x=50答：每天应生产50吨.【解析】【分析】这批化肥的总质量不变，每天生产的质量和天数成反比例，设出未知数，根据总质量不变列出比例解答即可.3．给一间卧室铺地砖，每块砖的面积和砖的块数成________比例；同一个圆的半径和周长成________比例。
【答案】反；正【解析】【解答】因为每块砖的面积×砖的块数=这间卧室的面积（一定），一间卧室的面积是不变的，每块砖的面积和砖的块数成反比例；因为圆的周长：半径=2π（一定），所以同一个圆的半径和周长成正比例。
故答案为：反；正。
【分析】如果用字母x和y表示两种相关联的量，用k表示它们的比值，正比例关系可以用以下关系式表示：y：x=k（一定）；如果用字母x和y表示两种相关联的量，用k表示它们的积，反比例关系可以用下面关系式表示：xy=k（一定），据此判断。
4．a÷b=35，那么a与b成________比例关系，如果 = ，那么a与b成________比例关系．【答案】正；反【解析】【解答】解：a÷b=35，a与b的商一定，a与b成正比例关系；，则ab=35，所以a与b从反比例关系。
故答案为：正；反。
【分析】两个相关联的量，一个量变化，另一个量也随着变化。
正反比例奥数题
正反比例奥数题《有趣又烧脑的正反比例奥数题》嘿！同学们，你们知道吗？奥数题里的正反比例问题，那可真是太有趣啦！就像是一个神秘的宝藏，等着我们去挖掘。
有一次上奥数课，老师在黑板上出了一道题：“小明骑自行车从A 地到B 地，如果速度提高20%，那么所用时间就会减少百分之几？” 哎呀，这可把我难住了，我抓耳挠腮，脑袋里就像一团乱麻。
我心想：这到底该从哪儿下手呀？我看看同桌，他也皱着眉头，一脸苦相。
我忍不住问他：“喂，你有思路没？”他摇摇头，嘟囔着：“这题也太难了，就像个迷宫，我都找不到出口！”这时候，学霸小李举起了手，老师让他回答。
他站起来，不慌不忙地说：“假设原来的速度是1，时间是t，路程就是1×t = t。
速度提高20%，现在的速度就是1.2，路程不变，现在的时间就是t÷1.2 = 5t/6 。
原来的时间是t，现在的时间是5t/6 ，时间减少了（t - 5t/6）÷ t = 1/6 ，也就是16.7%。
” 哇，他说得头头是道，我和同桌听得一愣一愣的，忍不住感叹：“学霸就是学霸，这脑子咋长的呀！”还有一次，老师又出了一道题：“一辆汽车从甲地开往乙地，如果速度是每小时60 千米，那么8 小时可以到达。
如果速度变为每小时80 千米，几小时可以到达？”我赶紧拿起笔在本子上算起来。
我先算出甲地到乙地的路程：60×8 = 480（千米），再用路程除以新的速度：480÷80 = 6（小时）。
我高兴地喊起来：“我算出来啦！”老师笑着点点头，说：“不错不错，继续加油！”你说这正反比例的奥数题，是不是像一场刺激的冒险？有时候让我们绞尽脑汁，有时候又让我们兴奋不已。
就好像在攀登一座高山，过程中充满了挑战，但当我们登上山顶，看到那美丽的风景时，一切的努力都值了！反正我觉得，虽然这些奥数题有时候真的很难，会让我觉得头疼，甚至想放弃。
但是只要坚持思考，多练习，就能找到解题的窍门，那种成就感简直无与伦比！这不就是学习的乐趣所在吗？同学们，你们是不是也这么觉得呢？。
【数学】比例和反比例 (奥数)
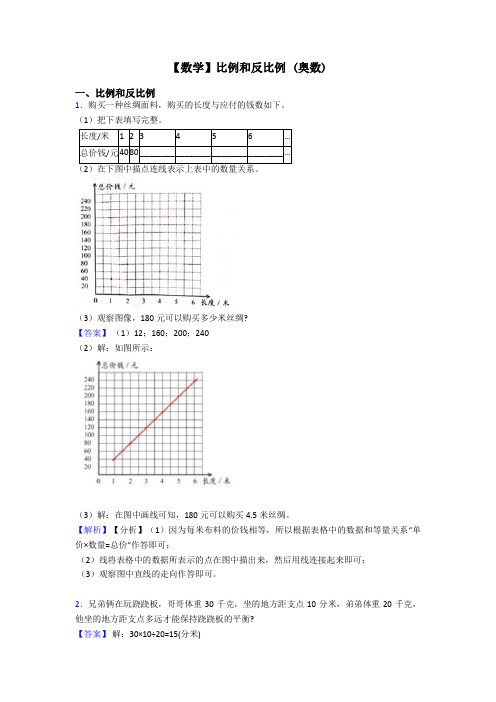
【数学】比例和反比例 (奥数)一、比例和反比例1．购买一种丝绸面料，购买的长度与应付的钱数如下。
（1）把下表填写完整。
长度/米123456…总价钱/元4080________________________________…（3）观察图像，180元可以购买多少米丝绸?【答案】（1）12；160；200；240（2）解：如图所示：（3）解：在图中画线可知，180元可以购买4.5米丝绸。
【解析】【分析】（1）因为每米布料的价钱相等，所以根据表格中的数据和等量关系“单价×数量=总价”作答即可；（2）线将表格中的数据所表示的点在图中描出来，然后用线连接起来即可；（3）观察图中直线的走向作答即可。
2．兄弟俩在玩跷跷板，哥哥体重30千克，坐的地方距支点10分米，弟弟体重20千克，他坐的地方距支点多远才能保持跷跷板的平衡?【答案】解：30×10÷20=15(分米)答：他坐的地方距支点15分米才能保持跷跷板的平衡。
【解析】【分析】根据题意可知：哥哥的体重×坐的地方距支点的长度=弟弟的体重×他坐的地方距支点的长度，用哥哥的体重×坐的地方距支点的长度÷弟弟的体重=他坐的地方距支点的长度，据此解答.3．甲乙两地相距440千米，一辆汽车从甲地开往乙地，3时行了240千米，照这样计算，几小时可以到达乙地？（用比例解）【答案】解：设小时可以到达乙地，答：5.5小时可以到达乙地。
【解析】【分析】“照这样计算”的意思就是汽车的速度不变，路程与时间成正比例；设出未知数，根据速度不变列出比例，解比例求出到达乙地的速度即可。
4．从甲地到乙地，小华用了5小时，小红用了3小时。
小华和小红所用的时间的比是________，他们的速度比是________。
【答案】 5∶3；3∶5【解析】【解答】解：小华和小红所用的时间的比是5：3，他们的速度比是3：5。
故答案为：5：3；3：5。
【精品】比例和反比例 (奥数)
【精品】比例和反比例 (奥数)一、比例和反比例1．同一时间、同一地点测得的树高和它的影长如下表：树高/米2346…影长/米1.62.43.24.8…（2）树高和影长成什么比例?为什么？（3）量得一颗大树的影长是10.4米，这棵大树有多高？【答案】（1）（2）解：成正比例。
因为 =1.25， =1.25， =1.25， =0.8（一定），所以，树高和影长成正比例。
（3）解：设这棵大树的高度是x米。
=1.6x=2×10.41.6x=20.81.6x÷1.6=20.8÷1.6x=13答：这棵大树的高度是13米。
【解析】【分析】（1）观察统计图可知，横轴表示树高，竖轴表示影长，据此先描点，再连线，据此作图；（2）分别用树高：影长，求出比值，当比值一定时，成正比例，据此判断；（3）根据题意可知，设这棵大树的高度是x米，用树高：影长=树高：影长，据此列正比例解答.2．铁路工人铺一条铁轨，计划每天铺400米，18天完成，实际每天比计划多铺50米，实际多少天完成?【答案】解：400×18÷（400+50）=16（天）答：实际16天完成。
【解析】【解答】解：设实际x天完成。
（400+50）x=400×18x=7200÷450x=16答：实际16天完成。
【分析】铁轨的总长度不变，每天铺的长度与铺的天数成反比例，设出未知数，根据铁轨的总长度不变列出比例，解比例求出未知数的值即可。
3．小明打算12天看完一本故事书，平均每天看15页。
如果要提前2天看完，平均每天应看多少页?(用比例知识解)【答案】解：设平均每天应看x页，则（12-2）x=12×15x=18答：平均每天应看15页。
【解析】【分析】根据故事书的总页数不变可得等量关系式：实际看的天数×实际平均每天应看多少页=计划看的天数×计划平均每天看多少页，据此代入数据列方程解答即可。
六年级数学正比例与反比例的奥数题
正比例与反比例的认识19、被减数一定，减数和差。
20、总人数一定，每行人数和行数。
奥数常识判断题21、长方体的底面积一定，体积和高。
一、判断下面各题中的两个量成什么比例，并说明理由。
22、路程一定，已走的路程和剩下的路程。
、订《少先队员》的份数和总钱数。
123、百米赛跑中，跑步速度和所用时间。
、三角形的面积一定，底和高。
224、车轮的转数一定时，车轮的直径和行驶的路程。
、总人数一定，行数和每行人数。
3 4、总价一定，单价和数量。
1x=2y，（x、y不为025、）那么x和y.、购买同一种钢笔的数量和总价。
5 、正方形的周长与它的边长。
626、大豆的出油率一定，大豆的数量和出油的数量。
、圆的面积与它的半径。
727、圆的面积和圆的半径。
、圆的周长与它的半径。
2、圆的面积和圆的半径的平方9、长方形的长一定，它的面积与宽3、正方形的面积和边长10、分数值一定，分子和分母3、正方形的周长和边长、一个加数一定，另一个加数与和。
13、长方形的面积一定时，长和宽12、路程一定，速度和时间3、长方形的周长一定时，长和宽、圆柱的底面积一定，它的体积与高。
13、三角形的面积一定时，底和高每天看的页数和所剩下、14看一本故事书，的页数3梯形的面积一定时上底和下底的和高15、圆锥的体积一定，它的底面积与高3、圆的周长和圆的半径购买苹果的千克、16购买苹果的总价一定，数和单价3、路程一定，速度和时间它的底面积周长与圆柱的侧面积一定，173一堆煤的总量不变烧去的煤与剩下的高煤。
、正方体的棱长与表面积。
18．59、订《少先队员》的份数和总钱数。
花生的重量与榨出39、花生的出油率一定，花生油的重量。
60、三角形的面积一定，底和高。
40、平行四边形的面积不变，它的底与高。
61、总人数一定，行数和每行人数。
41、比例尺一定，图上距离与实际距离。
62、总价一定，单价和数量。
、圆的面积一定，直径与圆周率。
4263、购买同一种钢笔的数量和总价。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
奥数常识判断题
一、判断下面各题中的两个量成什么比例，并说明理由。
1、订《少先队员》的份数和总钱数。
2、三角形的面积一定，底和高。
3、总人数一定，行数和每行人数。
4、总价一定，单价和数量。
5、购买同一种钢笔的数量和总价。
6、正方形的周长与它的边长。
7、圆的面积与它的半径。
8、圆的周长与它的半径。
9、长方形的长一定，它的面积与宽。
10、分数值一定，分子和分母。
11、一个加数一定，另一个加数与和。
12、路程一定，速度和时间。
13、圆柱的底面积一定，它的体积与高。
14、看一本故事书，每天看的页数和所剩下的页数。
15、圆锥的体积一定，它的底面积与高。
16、购买苹果的总价一定，购买苹果的千克数和单价。
17、圆柱的侧面积一定，它的底面积周长与高。
18、正方体的棱长与表面积。
39、花生的出油率一定，花生的重量与榨出花生油的重量。
40、平行四边形的面积不变，它的底与高。
41、比例尺一定，图上距离与实际距离。
42、圆的面积一定，直径与圆周率。
43、比的前项一定，比的后项与比值。
44、时间一定，速度与路程。
45、被减数一定，减数与差。
46、圆锥体体积一定，底面积与高。
47、买相同的电脑，购买的电脑台数与总价
48、每捆练习本的本数相同，练习本的总本数与捆数
49、总路程一定，已行的路程与未行的路程
50、分数值一定，分数的分子与分母
51、长方形的长一定，它的面积和宽
52、长方体的体积一定，底面积和高
53、一本书的总页数一定，看的天数与平均每天看的页数
54、圆的周长和直径
55、订阅《扬子晚报》，订的份数与总价
56、图上距离一定，实际距离与比例尺
57、小麦的出粉率一定，小麦的质量与面粉的质量
58、六（1）班同学做操，每排站的人数与排数59、订《少先队员》的份数和总钱数。
60、三角形的面积一定，底和高。
61、总人数一定，行数和每行人数。
62、总价一定，单价和数量。
63、购买同一种钢笔的数量和总价。
64、正方形的周长与它的边长。
65、圆的面积与它的半径。
66、圆的周长与它的半径。
67、长方形的长一定，它的面积与宽。
68、分数值一定，分子和分母。
69、一个加数一定，另一个加数与和。
70、路程一定，速度和时间。
71、圆柱的底面积一定，它的体积与高。
72、看一本故事书，每天看的页数和所剩下的页数。
73、圆锥的体积一定，它的底面积与高。
74、购买苹果的总价一定，购买苹果的千克数和单价。
75、圆柱的侧面积一定，它的底面积周长与高。
76、正方体的棱长与表面积。
77、被减数一定，减数和差。
78、总人数一定，每行人数和行数。
79、长方体的底面积一定，体积和高。
80、路程一定，已走的路程和剩下的路程。
81、百米赛跑中，跑步速度和所用时间。
82、车轮的转数一定时，车轮的直径和行驶的路程。
83、x=2y，（x、y不为0）那么x和y.
84、大豆的出油率一定，大豆的数量和出油的数量。
二、判断下列变化的量成什么比例。
1、比例尺一定，图上距离与实际距离。
2、被除数一定，除数和商。
3、工效一定，工作量与工作时间。
4、和一定，一个加数与另一个加数。
5、长方体体积一定，底面积与高。
6、全校学生人数一定,每排人数和所站的排数。
7、平行四边形的高一定,底和高。
8、7x=8y,x和y。
9、圆的周长和半径。
10、圆的面积和半径。
三、根据圆柱的体积、底面积、高在个量之间的关系，完成关系式：
（）（一定），（）和（）成（）比例；
（）（一定），（）和（）成（）比例；
（）（一定），（）和（）成（）比例。
一、填空。
1、a÷b=c，当c一定时a和b（）；当a一定时b和c（）；当b一定时a 和c（）。
2、长方形的（）一定，它的长和面积成正比例。
3、圆柱体体积一定，（）和高成反比例。
4、每块砖的面积一定，铺地面积与块数成（）比例。
5、年级总人数一定，每班人数与班数成（）比例。
6、被除数一定，商和除数成（）比例。
7、糖水的含糖率一定，糖和水成（）比例。
8、三角形的面积一定，它的底和高（）比例。
9、如果=y，（x不为0），那么x和y成（）比例。
10、如果x= y÷1.5，那么x和y成（）比例。
11、每块砖的面积一定，铺地面积与块数成（）比例。
12、年级总人数一定，每班人数与班数成（）比例。
13、被除数一定，商和除数成（）比例。
14、糖水的含糖率一定，糖和水成（）比例。
15、三角形的面积一定，它的底和高（）比例。
16、如果
x
8
=y，（x不为0），那么x和y成（）比例。
17、如果x= y÷1.5，那么x和y成（）比例。