运筹王坤

合集下载

成品油配送多车舱车辆指派及路径优化问题研究

Ｍｕｌｔｉ — ｃｏｍｐａｒｔｍｅｎｔＶｅｈｉｃｌｅＤｉｓｐａｔｃｈｉｎｇａｎｄＲｏｕｔｉｎｇｆｏｒＰｒｏｄｕｃｔＯｉｌＤｉｓｔｒｉｂｕｔｉｏｎ ‘
Ａｂｓｔｒａｃｔ：Ｔｈｉｓｐａｐｅｒｉｎｖｅｓｔｉｇａｔｅｓｔｈｅｄｉｓｐａｔｃｈｉｎｇａｎｄｒｏｕｔｉｎｇｐｒｏｂｌｅｍｏｆｈｅｔｅｒｏｇｏｎｏｕｓａｎｄｍｕｌｔｉ — ｃｏｍｐａｒｔｍｅｎｔ
ｉｎｇｃｏｓｔｗｈｉｃｈｃｏｎｓｉｓｔｓｏｆｖｅｈｉｃｌｅｄｉｓｐａｔｃｈｉｎｇｃｏｓｔａｎｄｆｕｅｌｃｏｓｔ．Ｔｏｒｅｄｕｃｅｔｈｅｃｏｍｐｌｅｘｉｔｙｏｆｍｏｄｅｌｓｏｌｕｔｉｏｎ，ｂａｓｅｄｏｎＣ－Ｗａｌｇｏｒｉｔｈｍ，ａｖｅｈｉｃｌｅｌｏａｄｉｎｇｐｏｌｉｃｙｃａｌｌｅｄ “ｓｐｌｉｔｔｉｎｇｄｅｍａｎｄｃｏｍｂｉｎｉｎｇｌｏａｄ” ｉｓｐｒｅｓｅｎｔｅｄ，ａｎｄｔｈｅｏｐｔｉｍｉｚｅｄｒｏｕｔｉｎｇｓｃｈｅｍｅｏｆｖｅｈｉｃｌｅｓｉｓｏｂｔａｉｎｅｄｔｈｒｏｕｇｈｔｗｏｐａｒａｌｌｅｌｎｅｉｇｈｂｏｒｈｏｏｄｓｅａｒｃｈｉｎｇｏｐｅｒａｔｏｒｓｏｆＲｅｌｏ —

智能化作战条件下的无人机系统应用及其关键技术

甘肃科技Gansu Science and Technology第37卷第4期2021年2月Vol.37 No.4Feb. 2021智能化作战条件下的无人机系统应用及其关键技术张明杰1,盛耀威2（1.解放军69250部队，新疆乌鲁木齐830000；2.郑州日产汽车有限公司，河南郑州451191）摘要:本文指出未来战争是智能化战争的发展趋势，分析了智能化作战的主要特征，对无人机系统在智能化作战中的应用进行浅析，指出智能化作战条件下的无人机系统关键技术主要包括:智能态势感知技术、智能自主控制技术和智能协同交互技术。

关键词：智能化作战;无人机;态势感知；自主控制；协同交互中图分类号:TN959.1近年来，以移动互联网、云计算、大数据、仿生技术、机器学习、计算机视觉技术等新兴技术,正加速推进战争形态由机械化、信息化向智能化方向演进，传统以人为主的战法逐步被AI 的模型和算法所替代，战争即将进入无人系统自主对抗的智能作战阶段。

无人机系统的智能化发展,使无人机系统作战的实战化程度不断提高，并逐步走上战场，拉开智能化作战的序幕。

1智能化作战的主要特征智能化作战运用智能化的武器装备平台，利用智能化的网络支撑，进行智能化的分析决策，在作战指挥、战术运用等领域呈现出与机械化、信息化战争不同的鲜明特征。

吴明曦认为智能化战争呈现出分布式部署、网络化链接、扁平化结构、模块化结合、自适应重构、平行化交互、聚焦式释能、非线性效应等特征,制胜机理颠覆传统。

王鹏认为智能化战争有以下特征：目标重心是“制智权”、武器装备“自主化”、作战空间“全维化”、交互方式“无人化”、指挥决策“超脑化”、战场支撑“云计算”。

赵荣春等认为智能化作战主要有四个显著特征：指挥高效化、操作自动化、打击精确化、操作自动化。

智能化作战与信息化作战相比，制胜机理已经发生了显著变化，主要表现为智能自主。

1）智能感知战场态势。

随着物联网、遥感与地理信息技术、计算机视觉技术、卫星实时通信、大数据等技术的应用，侦察装备发生质的变化，基于人工智能技术的侦察装备能够处理智能分析判断战场态势，通过智能化情报处理平台，自主获取敌、我、友兵力兵器部署和战场环境等情报信息，实时生成融合态势，并能预测下一步态势。

华东交通大学2011年硕士研究生录取名单+保送名单

华东交通大学2011年硕士研究生录取名单（不含保送）姓名学院名称专业名称胡盼安电气学院电力电子与电力传动黎冰电气学院电力电子与电力传动李洋电气学院电力电子与电力传动李云丰电气学院电力电子与电力传动舒婕妤电气学院电力电子与电力传动王光余电气学院电力电子与电力传动王锴电气学院电力电子与电力传动周军电气学院电力电子与电力传动蔡双电气学院电力系统及其自动化陈首昆电气学院电力系统及其自动化李冲电气学院电力系统及其自动化李玉庆电气学院电力系统及其自动化刘雨欣电气学院电力系统及其自动化齐彦伟电气学院电力系统及其自动化王立娜电气学院电力系统及其自动化严金花电气学院电力系统及其自动化袁琳电气学院电力系统及其自动化张景景电气学院电力系统及其自动化朱二中电气学院电力系统及其自动化陈健亨电气学院电气工程胡强电气学院电气工程贾豪威电气学院电气工程康淦明电气学院电气工程李澄电气学院电气工程于天剑电气学院电气工程周纬亮电气学院电气工程杜汉亭电气学院检测技术与自动化装置金小龙电气学院检测技术与自动化装置李图之电气学院检测技术与自动化装置陈广鑫电气学院交通信息工程及控制陈振华电气学院交通信息工程及控制冯莹电气学院交通信息工程及控制龚正电气学院交通信息工程及控制郭亮电气学院交通信息工程及控制侯新星电气学院交通信息工程及控制李惠浈电气学院交通信息工程及控制申杰电气学院交通信息工程及控制唐宏建电气学院交通信息工程及控制汪媛电气学院交通信息工程及控制陈立勇电气学院控制工程郭文文电气学院控制工程丁贤达电气学院控制理论与控制工程罗文志电气学院控制理论与控制工程欧阳超明电气学院控制理论与控制工程沈友进电气学院控制理论与控制工程伍迎节电气学院控制理论与控制工程谢斌斌电气学院控制理论与控制工程袁军锋电气学院控制理论与控制工程张芳电气学院控制理论与控制工程张鹏电气学院控制理论与控制工程张琼洁电气学院控制理论与控制工程仲昆电气学院控制理论与控制工程洪龙龙机电学院材料加工工程江民华机电学院材料加工工程江新焱机电学院材料加工工程焦宇机电学院材料加工工程宋燕机电学院材料加工工程谢斌机电学院材料加工工程李克诚机电学院车辆工程李易燃机电学院车辆工程秦豫江机电学院车辆工程徐小翔机电学院车辆工程赵辽翔机电学院车辆工程郑冰冰机电学院车辆工程罗珊珊机电学院工业工程熊非易机电学院工业工程丁茹机电学院管理科学与工程许彩鸽机电学院管理科学与工程黄敏机电学院机械电子工程贾慧芳机电学院机械电子工程李海东机电学院机械电子工程施宇机电学院机械电子工程田青青机电学院机械电子工程谢小强机电学院机械电子工程张光伟机电学院机械电子工程周延睿机电学院机械电子工程董钦机电学院机械工程刘烁机电学院机械工程王红机电学院机械工程杨建国机电学院机械工程黄玮机电学院机械设计及理论兰光英机电学院机械设计及理论廖小东机电学院机械设计及理论王铨机电学院机械设计及理论成佐明机电学院机械制造及其自动化邓文强机电学院机械制造及其自动化胡维东机电学院机械制造及其自动化黄金城机电学院机械制造及其自动化黄林昕机电学院机械制造及其自动化廖芳蓉机电学院机械制造及其自动化阮航机电学院机械制造及其自动化赵进机电学院机械制造及其自动化蔡颖机电学院交通运输工程蒋铁钢机电学院交通运输工程蔡莉机电学院精密仪器及机械符正晴机电学院精密仪器及机械胡林海机电学院精密仪器及机械叶冰机电学院精密仪器及机械程凯皆机电学院物流工程王坤机电学院物流工程周烁机电学院物流工程陈伟达机电学院载运工具运用工程程雯玉机电学院载运工具运用工程邓洋机电学院载运工具运用工程李清华机电学院载运工具运用工程王若飞机电学院载运工具运用工程薛曙光机电学院载运工具运用工程陈波基础学院材料物理与化学甘维基础学院材料物理与化学田璐槐基础学院材料物理与化学董泽民基础学院分析化学纪忆基础学院分析化学王淑怡基础学院分析化学杨献从基础学院分析化学高新瑶基础学院化学工程黄丹灵基础学院应用化学邱鳞军基础学院应用化学孙清基础学院应用化学唐静基础学院应用化学王威基础学院应用化学徐娜娜基础学院应用化学张雅琴基础学院应用化学蔡飞基础学院应用数学丘赟立基础学院应用数学王蒙基础学院应用数学王腾飞基础学院应用数学熊娟基础学院应用数学胡媛媛基础学院运筹学与控制论喻卫基础学院运筹学与控制论陈彦竹经管学院产业经济学程高卫经管学院产业经济学高研经管学院产业经济学李俊经管学院产业经济学沈鑫伟经管学院产业经济学王曼曼经管学院产业经济学祝伟萍经管学院产业经济学尚婷经管学院管理科学与工程王海军经管学院管理科学与工程徐义政经管学院管理科学与工程余乐经管学院管理科学与工程张威经管学院管理科学与工程陈亚男经管学院会计硕士何龙经管学院会计硕士刘佩经管学院会计硕士陆珊经管学院会计硕士孟丹丹经管学院会计硕士彭文竞经管学院会计硕士沈毅经管学院会计硕士陶文静经管学院会计硕士王红霞经管学院会计硕士吴菲菲经管学院会计硕士吴真经管学院会计硕士夏阳经管学院会计硕士杨彬彬经管学院会计硕士杨园经管学院会计硕士赵亮经管学院会计硕士陈其圣经管学院会计学陈伟丹经管学院会计学凌艺菁经管学院会计学龙立惠经管学院会计学楼佳佳经管学院会计学牟琪经管学院会计学孙乐超经管学院会计学汤文经管学院会计学魏培培经管学院会计学张瑞经管学院会计学李为博经管学院交通运输规划与管理王良琴经管学院交通运输规划与管理陈冉经管学院劳动经济学邓黎芳经管学院劳动经济学赖小妹经管学院劳动经济学刘玉卿经管学院劳动经济学娄小云经管学院劳动经济学潘国锋经管学院劳动经济学余靓经管学院劳动经济学周欢情经管学院劳动经济学方莹莹经管学院企业管理高阳经管学院企业管理李冰洁经管学院企业管理李盟经管学院企业管理刘良经管学院企业管理孙滦峰经管学院企业管理孙新经管学院企业管理王晓宁经管学院企业管理吴蕾经管学院企业管理杨雅岚经管学院企业管理赵晔经管学院企业管理阙俊峰经管学院统计学王小晨经管学院物流工程朱晨晨经管学院应用统计硕士康亮人文学院科学社会主义与国际共产主义运动牛向宇人文学院科学社会主义与国际共产主义运动闫迎春人文学院科学社会主义与国际共产主义运动周志远人文学院科学社会主义与国际共产主义运动栾天人文学院马克思主义基本原理黎隆人文学院民商法学李琳俐人文学院民商法学杨莹人文学院民商法学张婧人文学院民商法学李欢人文学院思想政治教育马帅人文学院思想政治教育任倩人文学院思想政治教育王瑞人文学院思想政治教育温春勇人文学院思想政治教育徐欢人文学院思想政治教育喻涵人文学院思想政治教育左层山人文学院思想政治教育蔡燕琦人文学院政治经济学胡姗姗人文学院政治经济学黄徐玲人文学院中国古代文学刘莉莉人文学院中国古代文学刘婷婷人文学院中国古代文学王杰人文学院中国古代文学薛少阳人文学院中国古代文学李凯软件学院计算机软件与理论薛海英软件学院计算机软件与理论冯斌软件学院软件工程姜龙软件学院软件工程刘乔软件学院软件工程赵磊软件学院软件工程钟涛软件学院软件工程周长雨软件学院软件工程王磊体育学院体育教育训练学王跃飞体育学院体育教育训练学艾成刚土建学院道路与铁道工程陈养强土建学院道路与铁道工程赖建英土建学院道路与铁道工程涂勤明土建学院道路与铁道工程张永伟土建学院道路与铁道工程邹永祥土建学院道路与铁道工程柏俊土建学院供热、供燃气、通风及空调工程黄辰勰土建学院供热、供燃气、通风及空调工程戴宏赟土建学院管理科学与工程龚小虎土建学院管理科学与工程李龙龙土建学院管理科学与工程李伟朋土建学院管理科学与工程刘可敬土建学院管理科学与工程彭雁南土建学院管理科学与工程党晓芳土建学院环境工程简美鹏土建学院环境工程舒建辉土建学院环境工程宋嘉骏土建学院环境工程吴杰土建学院环境工程朱平土建学院环境工程蔡少杰土建学院建筑与土木工程黄纲领土建学院建筑与土木工程李孟廷土建学院建筑与土木工程李曦土建学院建筑与土木工程刘增军土建学院建筑与土木工程钱琴珍土建学院建筑与土木工程唐晓飞土建学院建筑与土木工程涂平平土建学院建筑与土木工程王凯土建学院建筑与土木工程徐向春土建学院建筑与土木工程徐勇土建学院建筑与土木工程杨猛猛土建学院建筑与土木工程朱道文土建学院建筑与土木工程朱沛土建学院建筑与土木工程叶知骁土建学院交通运输工程程丽敏土建学院交通运输规划与管理丁仲凡土建学院结构工程胡智圆土建学院结构工程李军土建学院结构工程罗晶土建学院结构工程温群昊土建学院结构工程吴章勇土建学院结构工程夏峰土建学院结构工程余洛凝土建学院结构工程衷政杰土建学院结构工程周叶威土建学院结构工程陈志兴土建学院桥梁与隧道工程黄鹏土建学院桥梁与隧道工程黎峰土建学院桥梁与隧道工程李玉华土建学院桥梁与隧道工程梁力土建学院桥梁与隧道工程乔振土建学院桥梁与隧道工程胡贵州土建学院市政工程李珏钰土建学院项目管理郭俊土建学院岩土工程黄宗强土建学院岩土工程刘林土建学院岩土工程刘秋宇土建学院岩土工程陈翔信息学院计算机技术郭建伟信息学院计算机技术胡锐锋信息学院计算机技术金思新信息学院计算机技术李林信息学院计算机技术刘颖婷信息学院计算机技术祁美丽信息学院计算机技术王世昌信息学院计算机技术吴小元信息学院计算机技术肖天儒信息学院计算机技术张权信息学院计算机技术黄志强信息学院计算机软件与理论李健信息学院计算机软件与理论石菲信息学院计算机软件与理论尤慧信息学院计算机软件与理论陈建军信息学院计算机应用技术郭岩信息学院计算机应用技术江健健信息学院计算机应用技术李志平信息学院计算机应用技术林华清信息学院计算机应用技术沈陈镱信息学院计算机应用技术谭龙信息学院计算机应用技术谢丽娟信息学院计算机应用技术徐海洲信息学院计算机应用技术杨丽信息学院计算机应用技术褚红亮信息学院通信与信息系统方玲信息学院通信与信息系统何姗信息学院通信与信息系统雷久淮信息学院通信与信息系统雷明东信息学院通信与信息系统李申信息学院通信与信息系统林雁华信息学院通信与信息系统刘洁丽信息学院通信与信息系统路春信息学院通信与信息系统任宝平信息学院通信与信息系统王会芹信息学院通信与信息系统王小妹信息学院通信与信息系统袁野信息学院通信与信息系统张阳信息学院通信与信息系统朱明信息学院通信与信息系统华东交通大学2011年研究生推免名单公示。

运筹学在军事后勤保障中的应用

运筹学在军事后勤保障中的应用运筹学是一门应用数学学科，通过建立数学模型来解决实际问题。

军事后勤保障是指在军事行动中，为军队的运输、补给、维修、医疗等提供有效支持的一系列活动。

运筹学的应用可以帮助军事后勤保障更加高效和精确地完成任务。

本文将探讨运筹学在军事后勤保障中的具体应用。

一、军事物资采购与储备运筹学在军事物资采购和储备方面有着广泛的应用。

通过建立数学模型，可以确定物资采购的最佳时间、数量和交付方式。

同时考虑到需求的不确定性和供给的限制，运筹学可以帮助军队在不同战术阶段和任务需求下，合理安排物资的储备量和补给计划，以减少资源浪费和保证战斗的连贯性。

二、军事运输路线规划军事行动中的物资运输是军事后勤保障的重要组成部分。

通过运筹学方法，可以对运输路线进行规划和优化，确保物资的快速、安全到达目的地。

例如，可以利用网络规划算法来确定最短路径和最优运输方式，考虑到不同地形、气候和交通条件的影响。

三、军队维修和保障军队的装备维修和保障是军事后勤保障中的一项重要任务。

通过建立维修队伍和装备资源的数学模型，可以帮助军队确定维修站点的最佳位置、维修人员的调配方案，以及装备维修和保养的时间安排。

运筹学方法还可以用来优化装备的维修调度，提高装备的可用率和使用寿命。

四、医疗救护和人员调度在战场上，伤病员的及时医疗救护至关重要。

运筹学在医疗资源的分配和人员调度方面有着重要作用。

通过建立数学模型，可以将医疗资源合理分配到各个前线医疗营地，以及规划伤病员的疏散和转运。

同时，运筹学的方法可以帮助军队合理安排医疗人员的调度和分工，确保伤病员得到及时且有效的救治。

五、军事后勤系统优化运筹学还可以用来优化整个军事后勤系统的运作效率和效益。

通过建立系统模型和仿真分析，可以评估不同军事后勤方案的优劣，并提出改进措施。

例如，可以利用线性规划方法来确定物资储备的最佳配置方案，以减少战争损失和提高军事行动的成功率。

在现代战争中，军事后勤保障的重要性不言而喻。

大学生创新创业训练计划实验室开放项目的通知-湖州师范学院教务处

湖师院教字〔2012〕23号
关于公布2011－2012学年“大学生创新创业训练计划”实验室开放项目的通知
各下属学院、实验中心：
根据《于做好2011—2012学年“大学生创新创业训练计划”实验室开放项目申报、评审工作的通知》（湖师院教〔2012〕19号）文件精神，各下属学院(实验中心)对各自申报的2011—2012学年实验室开放项目进行了评审,经教务处认定，现予以公布。

湖州师范学院2011—2012学年实验室开放项目汇总表
湖州师范学院2011—2012学年实验室开放项目一览表
二○一二年七月二日主题词：教育学生项目通知
湖州师范学院教务处2012年7月2日印发。

运筹学1至6章习题参考答案

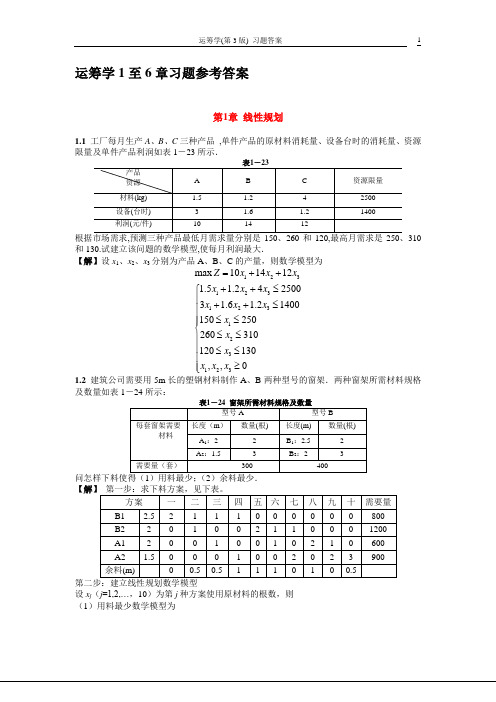
运筹学1至6章习题参考答案第1章线性规划1.1 工厂每月生产A 、B 、C 三种产品 ,单件产品的原材料消耗量、设备台时的消耗量、资源限量及单件产品利润如表1－23所示．310和130.试建立该问题的数学模型,使每月利润最大．【解】设x 1、x 2、x 3分别为产品A 、B 、C 的产量，则数学模型为123123123123123max 1014121.5 1.2425003 1.6 1.21400150250260310120130,,0Z x x x x x x x x x x x x x x x =++++≤⎧⎪++≤⎪⎪≤≤⎪⎨≤≤⎪⎪≤≤⎪≥⎪⎩ 1.2 建筑公司需要用5m 长的塑钢材料制作A 、B 两种型号的窗架．两种窗架所需材料规格及数量如表1－24所示：【解设x j （j =1,2,…，10）为第j 种方案使用原材料的根数，则（1）用料最少数学模型为10112342567368947910min 28002120026002239000,1,2,,10jj j Z x x x x x x x x x x x x x x x x x x j ==⎧+++≥⎪+++≥⎪⎪+++≥⎨⎪+++≥⎪⎪≥=⎩∑ （2）余料最少数学模型为2345681012342567368947910min 0.50.50.52800212002*********0,1,2,,10j Z x x x x x x x x x x x x x x x x x x x x x x x x j =++++++⎧+++≥⎪+++≥⎪⎪+++≥⎨⎪+++≥⎪⎪≥=⎩1.3某企业需要制定1～6月份产品A 的生产与销售计划。

已知产品A 每月底交货，市场需求没有限制，由于仓库容量有限，仓库最多库存产品A1000件，1月初仓库库存200件。

1～6月份产品A 的单件成本与售价如表1－25所示。

（2）当1月初库存量为零并且要求6月底需要库存200件时，模型如何变化。

基于数据挖掘的大学生综合素质评定系统

素质情况，使学生的综合素质评价具有科学性、系
统性和完整性。
１数据挖掘技术和学生评价模型设计
数据挖掘是从大量的数据中提取或挖掘有用
的信息或知识。获取的信息和知识可以广泛应用。数据挖掘是信息技术自然发展的结果，数据收集和数据库创建机制的早期开发，已成为稍后数据存储和检索、询和事务处理有效机制开发的必查备基础。随着提供查询处理和事务管理的大量数据库系统广泛付诸实践，数据分析和理解自然成为数据处理的一个目标。数据挖掘被称为数据库中的知识发现，数据清理和集成主要是清除不一致的数据并把多种数据源组合在一起；数据选择
第ｌ卷０
学生综合素质水平
２学生层次模型和系统建立
２１学生数据的层次模型．
利用萨蒂层次模型层次决策方法从三个方面对学生的综合素质进行考察。ｌ［Ｚ
２１１知识水平方面．．学生在校学习一定的理论课程、础知识，基因
ｐ２Ｘｐｌ２ｘｐ＋ ’ｎｐ１２ｎｌ２２２ …‘ ２＋ｐ１１－ｐ
学生综合素质评价：
ＩＸ２ … … … … … …
／／１＼
＼
其中：Ｗ表示综合素质得分，（１２．表示Ｐｉ，…．）＝ｎ因素獗的权系数，表示因素ｘ的权系数。ｐｊ
第１卷第４期Ｏ
２０年ｌ０８２月
河北软件职业技术学院学报

南京农业大学2003年SRT计划学校资助项目表

固体超强酸催化合成吡啶及烷基吡啶
自筹
2007B006
自筹经费
宋霄
袁昌坤
楚琳
徐淑飞
赵斌
固体超强碱催化羟醛综合反应的研究
自筹
化学科学学院
2007B007
自筹经费
张国敏
石慧
袁通
赵育磊
田来进
分子磁体的合成、结构表征及性质研究
自筹
化学科学学院
2007B008
自筹经费
樊良子
郭建
崔明海
徐菲菲
张翠平
王增华
张洪林
微量量热法对酸奶发酵条件的研究
学校资助
陈兴旺
李峰
王兆杰
薛立山
刘自龙
秦文华
无线数据通信网络与组网分析
1000
2007B004
自筹经费
方惠
李基中
王春香
王星
黄勇坚
螺旋状低功耗立体声扩音系统
自筹
化学科学学院
2007A020
学校资助
毕璇璇
王镇
高荣科
郭晓辉
毕思玮
甲基钌金属有机体系与炔类换位反应的理论研究
1000
2007A021
学校资助
付蓉
张莉莉
自筹
生命科学
学院
2007A024
学校资助
栾鹤翔
王军军
崔方圆
包颖
山东省桃树品种的资源调查和遗传多样性分析
1000
2007A025
学校资助
庄立琨
周诺贝
李文娇
刘华波
邱念伟
绿色蔬菜常温保鲜剂的研制
1000
2007A026
学校资助
高晓琳
王化敦
呼庆勋

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

运筹上机实验报告专业：市场营销班级：营销C121学号： 127903姓名：王坤指导教师：孔造杰河北工业大学城市学院经济管理系2014 年 6 月 13 日目录一、线性规划问题 (2)二、整数规划问题 (6)三、目标规划问题 (8)四、运输规划问题 (11)五、指派问题 (15)六、图与网络分析 (18)七、网络计划 (22)一、线性规划问题:1、①原问题的最优解（包括决策变量和松弛变量）、最优值；②对偶问题的最优解；③目标函数价值系数的变化范围；④右端常数的变化范围。

运算结果报告表目标单元格 (最大值)单元格名字初值终值$B$10 最优解14 14可变单元格单元格名字初值终值$B$8 变量 2 2$C$8 变量 4 4约束单元格名字单元格值公式状态型数值$B$12 50 $B$12<=$D$12 到达限制值$B$13 6 $B$13>=$D$13 未到限制值5$B$14 4 $B$14<=$D$14 到达限制值灵敏性报告表可变单元格终递减目标式允许的允许的单元格名字值成本系数增量减量$B$8 变量 2 0 1 0.5 1 $C$8 变量 4 0 3 1E+30 1 约束终阴影约束允许的允许的单元格名字值价格限制值增量减量$B$12 50 0.2 50 1E+30 10$B$13 6 0 1 5 1E+30$B$14 4 1 4 1 4答案:①最优解为X*=（4，2）T，最优值为14②对偶问题最优解即为影子价格，X*=（0.2,0,1）T③目标函数价值系数变化范围为X1(0,1.5),X2(2,33+1E)④第一约束(40,80+1E)。

第二约束（-29+1E，6）。

第三约束（0，5）2、（1）求解：①原问题的最优解（包括决策变量和松弛变量）、最优值；②对偶问题的最优解；③目标函数价值系数的变化范围；④右端常数的变化范围运算结果报告表目标单元格 (最大值)单元格名字初值终值$B$9 最优135.2666667 135.2666667可变单元格单元格名字初值终值$I$7 变量22.79411765 0$J$7 变量25.29411765 0$K$7 变量0 0约束单元格名字单元格值公式状态型数值$I$11 <= 0 $I$11<=$K$11 未到限制值300$I$12 <= 0 $I$12<=$K$12 未到限制值400$I$13 <= 0 $I$13<=$K$13 未到限制值420灵敏度报告表终递减目标式允许的允许的名字值成本系数增量减量变量22.53333333 0 3 0.333333333 1.454545455变量23.2 0 2 0.214285714 0.777777778变量7.333333333 0 2.9 1.6 0.15终阴影约束允许的允许的名字值价格限制值增量减量300 0.03 300 165.7142857 36.66666667400 0.266666667 400 44 122.9090909420 0.046666667 420 397.6470588 220答案：①最优解为X*=（22.5，23.2，7.3）T，最优值为135.3②对偶问题最优解即为影子价格，X*=（0.03，0.27,0.05）T③目标函数价值系数变化范围为X1(1.5，3.3),X2(1.2,2.2)，X3（2.75，4.5）④第一约束(270+1E,330+1E)。

第二约束（370+1E，430+1E）。

第三约束（390+1E，450+1E）（2）对产品I进行改进，改进后系数列向量为（9，12，4）T价值系数为 4.5①原问题的最优解（包括决策变量和松弛变量）、最优值；②对偶问题的最优解；③目标函数价值系数的变化范围；④右端常数的变化范围；⑤对原问题的最优解有什么影响。

运算结果报告表目标单元格 (最大值)单元格名字初值终值$I$9 最优153.1617647 153.1617647可变单元格单元格名字初值终值$I$7 变量22.79411765 22.79411765$J$7 变量25.29411765 25.29411765$K$7 变量0 0约束单元格名字单元格值公式状态型数值$I$11 <= 255.7352941 $I$11<=$K$11 未到限制值44.26470588$I$12 <= 400 $I$12<=$K$12 到达限制值$I$13 <= 420 $I$13<=$K$13 到达限制值灵敏度报告表可变单元格终递减目标式允许的允许的单元格名字值成本系数增量减量$I$7 变量22.79411765 0 4.5 0.3 0.455555556 $J$7 变量25.29411765 0 2 12.625 0.125 $K$7 变量0 -0.180882353 2.9 0.180882353 1E+30 约束终阴影约束允许的允许的单元格名字值价格限制值增量减量$I$11 <= 255.7352941 0 300 1E+30 44.26470588 $I$12 <= 400 0.371323529 400 55.2293578 238.4615385 $I$13 <= 420 0.011029412 420 620 286.6666667 答案：①最优解为X*=（22.8，25.3，0）T，最优值为153.2②对偶问题最优解即为影子价格，X*=（0,0.37,0.01）T③目标函数价值系数变化范围为X1(4.05，4.8)，X2(1.725,14.625)，X3（-27+1E，3.1）④第一约束(256，330+1E)。

第二约束（161.5，445）。

第三约束（133.3，1040）二、整数规划：写出下面问题的最优解和最优值（1）运算结果报告表目标单元格 (最大值)单元格名字初值终值$B$10 最优0 26可变单元格单元格名字初值终值$B$8 变量0 2$C$8 变量0 1$D$8 变量0 6约束单元格名字单元格值公式状态型数值$B$12 4 $B$12<=$D$12 未到限制值1$B$13 4 $B$13<=$D$13 未到限制值1$B$14 5 $B$14<=$D$14 到达限制值$B$8 变量 2 $B$8=整数到达限制值$C$8 变量 1 $C$8=整数到达限制值$D$8 变量 6 $D$8=整数到达限制值答案：最优解为X*=（2,1,6）T，最优值为26 （2）运算结果报告表目标单元格 (最小值)单元格名字初值终值$B$9 最优0 2可变单元格单元格名字初值终值$B$7 变量0 0$C$7 变量0 0$D$7 变量0 1约束单元格名字单元格值公式状态型数值$B$11 3 $B$11<=$E$11 未到限制值1$B$12 3 $B$12>=$E$12 到达限制值$B$13 1 $B$13>=$E$13 到达限制值$B$7 变量0 $B$7=二进制到达限制值$C$7 变量0 $C$7=二进制到达限制值$D$7 变量 1 $D$7=二进制到达限制值答案：最优解为X*=（0,0,1）T，最优值为2 三、目标规划（1）求解：①问题的解，并判断是满意解还是最优解；运算结果报告表目标单元格 (最小值)单元格名字初值终值$C$12 第一次优化目标函数变量2 0 0可变单元格单元格名字初值终值$C$10 决策变量变量2 0 35$D$10 决策变量实际值0 45$E$5 目标约束1 正偏差0 0$F$5 目标约束1 负偏差0 0$E$6 目标约束2 正偏差0 0$F$6 目标约束2 负偏差0 35$E$7 目标约束3 正偏差0 0$F$7 目标约束3 负偏差0 0$E$8 目标约束4 正偏差0 25$F$8 目标约束4 负偏差0 0约束单元格名字单元格值公式状态型数值$G$5 目标约束1 合计80 $G$5=$H$5 未到限制值$G$6 目标约束2 合计70 $G$6=$H$6 未到限制值$G$7 目标约束3 合计45 $G$7=$H$7 未到限制值$G$8 目标约束4 合计10 $G$8=$H$8 未到限制值答案：本题所求解为满意解。

②若目标函数变为，问原解有什么变化；运算结果报告表目标单元格 (最小值)单元格名字初值终值$C$10 第一次优化目标函数变量2 0 0可变单元格单元格名字初值终值$C$8 决策变量变量2 0 70$D$8 决策变量实际值0 50$E$3 目标约束1 正偏差0 0$F$3 目标约束1 负偏差0 0$E$4 目标约束2 正偏差0 0$F$4 目标约束2 负偏差0 0$E$5 目标约束3 正偏差0 5$F$5 目标约束3 负偏差0 0$E$6 目标约束4 正偏差0 60$F$6 目标约束4 负偏差0 0约束单元格名字单元格值公式状态型数值$G$3 目标约束1 合计120 $G$3=$H$3 未到限制值$G$4 目标约束2 合计70 $G$4=$H$4 未到限制值$G$5 目标约束3 合计45 $G$5=$H$5 未到限制值$G$6 目标约束4 合计10 $G$6=$H$6 未到限制值答案：本题解无变化③若第一个约束条件的右端项改为 120，原解有什么变化。

运算结果报告表目标单元格 (最小值)单元格名字初值终值$C$10 第一次优化目标函数变量2 0 0可变单元格单元格名字初值终值$C$8 决策变量变量2 70 75$D$8 决策变量实际值50 45$E$3 目标约束1 正偏差0 0$F$3 目标约束1 负偏差0 0$E$4 目标约束2 正偏差0 5$F$4 目标约束2 负偏差0 0$E$5 目标约束3 正偏差 5 0$F$5 目标约束3 负偏差0 0$E$6 目标约束4 正偏差60 65$F$6 目标约束4 负偏差0 0约束单元格名字单元格值公式状态型数值$G$3 目标约束1 合计120 $G$3=$H$3 未到限制值$G$4 目标约束2 合计70 $G$4=$H$4 未到限制值$G$5 目标约束3 合计45 $G$5=$H$5 未到限制值$G$6 目标约束4 合计10 $G$6=$H$6 未到限制值答案：第三次目标实际值变为15四、运输问题（1）求解下面运输问题，并求出最优解和最优值运算结果报告目标单元格 (最小值)单元格名字初值终值$I$10 1加班总成本0 820可变单元格单元格名字初值终值$C$19 期初需求节点0 0$D$19 期初 M 0 0$E$19 期初0 2$C$20 1正常需求节点0 0$D$20 1正常 M 0 0$E$20 1正常0 1$C$21 1加班需求节点0 0$D$21 1加班 M 0 0$E$21 1加班0 0$C$22 2正常需求节点0 3$D$22 2正常 M 0 0$E$22 2正常0 0$C$23 2加班需求节点0 0$D$23 2加班 M 0 0$E$23 2加班0 0$C$24 3正常需求节点0 0$D$24 3正常 M 0 1$E$24 3正常0 2.62046E-11$C$25 3加班需求节点0 0$D$25 3加班 M 0 3$E$25 3加班0 0约束单元格名字单元格值公式状态型数值$F$19 期初总运出量 2 $F$19<=$H$19 到达限制值$F$20 1正常总运出量 1 $F$20<=$H$20 未到限制值1$F$21 1加班总运出量0 $F$21<=$H$21 未到限制值3$F$22 2正常总运出量 3 $F$22<=$H$22 未到限制值1$F$23 2加班总运出量0 $F$23<=$H$23 未到限制值2$F$24 3正常总运出量 1 $F$24<=$H$24 到达限制0值$F$25 3加班总运出量 3 $F$25<=$H$25 到达限制值$C$28 总需求量 = 3 $C$28<=$C$26 到达限制值$D$28 总需求量 = 4 $D$28<=$D$26 到达限制值$E$28 总需求量 = 3 $E$28<=$E$26 到达限制值答案：因为产量大于销量，所以加入一个松弛变量销地4 期初向销地2运输21正常向销地2运输4.44089E-16，向销地4运输2 1加班向销地4运输32正常向销地1运输3，向销地4运输了12加班向销地2运输1，向销地3运输13正常向销地2运输1,3加班向销地3运输3（2 ）求解下面运输问题，并求出最优解和最优值运算结果报告表目标单元格 (最小值)单元格名字初值终值$J$11 总成本0 235 可变单元格单元格名字初值终值$C$15 工厂A 用户1 0 0$D$15 工厂A 用户2 0 0$E$15 工厂A 用户3 0 20$F$15 工厂A 用户4 0 0$G$15 工厂A 用户5 0 0$C$16 工厂B 用户1 0 0$D$16 工厂B 用户2 0 25$E$16 工厂B 用户3 0 0$F$16 工厂B 用户4 0 5$G$16 工厂B 用户5 0 0$C$17 工厂C 用户1 0 25$D$17 工厂C 用户2 0 0$E$17 工厂C 用户3 0 0$F$17 工厂C 用户4 0 5$G$17 工厂C 用户5 0 3.9443E-31$C$18 工厂D 用户1 0 0$D$18 工厂D 用户2 0 0$E$18 工厂D 用户3 0 0$F$18 工厂D 用户4 0 0$G$18 工厂D 用户5 0 20约束单元格名字单元格值公式状态型数值$C$19 总收货量用户1 25 $C$19>=$C$21 到达限制值0$D$19 总收货量用户2 25 $D$19>=$D$21 到达限制值0$E$19 总收货量用户3 20 $E$19>=$E$21 到达限制值0$F$19 总收货量用户4 10 $F$19>=$F$21 到达限制值0$G$19 总收货量用户5 20 $G$19>=$G$21 到达限制值0$H$15 工厂A 总运出量20 $H$15<=$J$15 到达限制值0$H$16 工厂B 总运出量30 $H$16<=$J$16 到达限制值0$H$17 工厂C 总运出量30 $H$17<=$J$17 到达限制值0$H$18 工厂D 总运出量20 $H$18<=$J$18 到达限制值0答案：因为销量大于产量，所以加入一个松弛变量产地4产地1向丙运输30产地2向乙运输25，丁运输5产地3向甲运输25，丁运输5产地4向戊运输20五、指派问题分配甲乙丙丁四人去完成五项任务，每人完成各项任务时间如下表，由于任务数多于人数，故规定其中有一个人可兼完成两项任务，其余三人每人完成一项，试确定花费时间最少的指派方案。