人教中考数学专题训练---圆的综合的综合题分类附答案

合集下载

中考数学压轴题专题圆的综合的经典综合题附详细答案

中考数学压轴题专题圆的综合的经典综合题附详细答案中考数学压轴题专题：圆的综合一、圆的综合1.如图，⊙O的半径为6cm，经过⊙O上一点C作⊙O的切线交半径OA的延长于点B，作∠ACO的平分线交⊙O于点D，交OA于点F，延长DA交BC于点E。

1) 求证：AC∥OD；2) 如果DE⊥BC，求AC的长度。

答案】(1) 证明见解析；(2) 2π。

解析】试题分析：(1) 由OC=OD，CD平分∠ACO，易证得∠ACD=∠ODC，即可证得AC∥OD；(2) BC切⊙O于点C，DE⊥BC，易证得平行四边形ADOC是菱形，继而可证得△AOC是等边三角形，则可得：∠AOC=60°，继而求得弧AC的长度。

试题解析：1) 证明：因为OC=OD，所以∠OCD=∠XXX。

因为CD平分∠ACO，所以∠XXX∠ACD。

因此，∠ACD=∠ODC，即可证得AC∥OD。

2) 因为BC切⊙XXXC，所以XXX。

因为DE⊥BC，所以OC∥DE。

因为AC∥OD，所以四边形ADOC是平行四边形。

因为OC=OD，所以平行四边形ADOC是菱形，所以OC=AC=OA。

因为△AOC是等边三角形，所以∠AOC=60°，因此弧AC的长度为2π。

点睛：本题考查了切线的性质、等腰三角形的判定与性质、菱形的判定与性质以及弧长公式。

此题难度适中，注意掌握数形结合思想的应用。

2.(类比概念) 三角形的内切圆是以三个内角的平分线的交点为圆心，以这点到三边的距离为半径的圆，则三角形可以称为圆的外切三角形，可以得出三角形的三边与该圆相切。

以此类推，如图1，各边都和圆相切的四边形称为圆外切四边形。

性质探究) 如图1，试探究圆外切四边形的ABCD两组对边AB，CD与BC，AD之间的数量关系。

猜想结论：(要求用文字语言叙述)写出证明过程（利用图1，写出已知、求证、证明）性质应用)①初中学过的下列四边形中哪些是圆外切四边形(填序号)：A：平行四边形；B：菱形；C：矩形；D：正方形。

中考数学圆的综合综合试题附答案

一、圆的综合真题与模拟题分类汇编（难题易错题）1．如图，⊙M交x轴于B、C两点，交y轴于A，点M的纵坐标为2．B（﹣33，O），C（3，O）．（1）求⊙M的半径；（2）若CE⊥AB于H，交y轴于F，求证：EH=FH．（3）在（2）的条件下求AF的长．【答案】（1）4；（2）见解析;（3）4．【解析】【分析】（1）过M作MT⊥BC于T连BM，由垂径定理可求出BT的长，再由勾股定理即可求出BM的长；（2）连接AE，由圆周角定理可得出∠AEC=∠ABC，再由AAS定理得出△AEH≌△AFH，进而可得出结论；（3）先由（1）中△BMT的边长确定出∠BMT的度数，再由直角三角形的性质可求出CG 的长，由平行四边形的判定定理判断出四边形AFCG为平行四边形，进而可求出答案．【详解】（1）如图（一），过M作MT⊥BC于T连BM，∵BC是⊙O的一条弦，MT是垂直于BC的直径，∴BT=TC=123∴124；（2）如图（二），连接AE，则∠AEC=∠ABC，∵CE⊥AB，∴∠HBC+∠BCH=90°在△COF中，∵∠OFC+∠OCF=90°，∴∠HBC=∠OFC=∠AFH，在△AEH和△AFH中，∵AFH AEHAHF AHE AH AH∠=∠⎧⎪∠=∠⎨⎪=⎩，∴△AEH≌△AFH（AAS），∴EH=FH；（3）由（1）易知，∠BMT=∠BAC=60°，作直径BG，连CG，则∠BGC=∠BAC=60°，∵⊙O的半径为4，∴CG=4，连AG，∵∠BCG=90°，∴CG⊥x轴，∴CG∥AF，∵∠BAG=90°，∴AG⊥AB，∵CE⊥AB，∴AG∥CE，∴四边形AFCG为平行四边形，∴AF=CG=4．【点睛】本题考查的是垂径定理、圆周角定理、直角三角形的性质及平行四边形的判定与性质，根据题意作出辅助线是解答此题的关键．2．如图1，直角梯形OABC中，BC∥OA，OA=6，BC=2，∠BAO=45°．（1）OC的长为；（2）D是OA上一点，以BD为直径作⊙M，⊙M交AB于点Q．当⊙M与y轴相切时，sin∠BOQ=；（3）如图2，动点P以每秒1个单位长度的速度，从点O沿线段OA向点A运动；同时动点D以相同的速度，从点B沿折线B﹣C﹣O向点O运动．当点P到达点A时，两点同时停止运动．过点P作直线PE∥OC，与折线O﹣B﹣A交于点E．设点P运动的时间为t （秒）．求当以B、D、E为顶点的三角形是直角三角形时点E的坐标．【答案】（1）4；（2）35；（3）点E的坐标为（1，2）、（53，103）、（4，2）．【解析】分析：（1）过点B作BH⊥OA于H，如图1（1），易证四边形OCBH是矩形，从而有OC=BH，只需在△AHB中运用三角函数求出BH即可．（2）过点B作BH⊥OA于H，过点G作GF⊥OA于F，过点B作BR⊥OG于R，连接MN、DG，如图1（2），则有OH=2，BH=4，MN⊥OC．设圆的半径为r，则MN=MB=MD=r．在Rt△BHD中运用勾股定理可求出r=2，从而得到点D与点H重合．易证△AFG∽△ADB，从而可求出AF、GF、OF、OG、OB、AB、BG．设OR=x，利用BR2=OB2﹣OR2=BG2﹣RG2可求出x，进而可求出BR．在Rt△ORB中运用三角函数就可解决问题．（3）由于△BDE的直角不确定，故需分情况讨论，可分三种情况（①∠BDE=90°，②∠BED=90°，③∠DBE=90°）讨论，然后运用相似三角形的性质及三角函数等知识建立关于t的方程就可解决问题．详解：（1）过点B作BH⊥OA于H，如图1（1），则有∠BHA=90°=∠COA，∴OC∥BH．∵BC∥OA，∴四边形OCBH是矩形，∴OC=BH，BC=OH．∵OA=6，BC=2，∴AH=0A﹣OH=OA﹣BC=6﹣2=4．∵∠BHA=90°，∠BAO=45°，∴tan∠BAH=BHHA=1，∴BH=HA=4，∴OC=BH=4．故答案为4．（2）过点B作BH⊥OA于H，过点G作GF⊥OA于F，过点B作BR⊥OG于R，连接MN、DG，如图1（2）．由（1）得：OH=2，BH=4．∵OC与⊙M相切于N，∴MN⊥OC．设圆的半径为r，则MN=MB=MD=r．∵BC ⊥OC ，OA ⊥OC ，∴BC ∥MN ∥OA ． ∵BM =DM ，∴CN =ON ，∴MN =12（BC +OD ），∴OD =2r ﹣2，∴DH =OD OH -=24r -．在Rt △BHD 中，∵∠BHD =90°，∴BD 2=BH 2+DH 2，∴（2r ）2=42+（2r ﹣4）2．解得：r =2，∴DH =0，即点D 与点H 重合，∴BD ⊥0A ，BD =AD ． ∵BD 是⊙M 的直径，∴∠BGD =90°，即DG ⊥AB ，∴BG =AG ． ∵GF ⊥OA ，BD ⊥OA ，∴GF ∥BD ，∴△AFG ∽△ADB ， ∴AF AD =GF BD =AG AB =12，∴AF =12AD =2，GF =12BD =2，∴OF =4，∴OG同理可得：OB AB ，∴BG =12AB ．设OR =x ，则RG x ．∵BR ⊥OG ，∴∠BRO =∠BRG =90°，∴BR 2=OB 2﹣OR 2=BG 2﹣RG 2， ∴（2﹣x 2=（）2﹣（x ）2．解得：x ，∴BR 2=OB 2﹣OR 2=（2）2=365，∴BR在Rt △ORB 中，sin ∠BOR =BR OB35．故答案为35．（3）①当∠BDE =90°时，点D 在直线PE 上，如图2．此时DP =OC =4，BD +OP =BD +CD =BC =2，BD =t ，OP =t ．则有2t =2．解得：t =1．则OP =CD =DB =1． ∵DE ∥OC ，∴△BDE ∽△BCO ，∴DE OC =BD BC =12，∴DE =2，∴EP =2， ∴点E 的坐标为（1，2）． ②当∠BED =90°时，如图3．∵∠DBE =OBC ，∠DEB =∠BCO =90°，∴△DBE ∽△OBC ，∴BEBC =2DB BE OB ∴，∴BE ． ∵PE ∥OC ，∴∠OEP =∠BOC ．∵∠OPE =∠BCO =90°，∴△OPE ∽△BCO ， ∴OEOB =OPBC，2t ，∴OE ．∵OE+BE=OB=255，∴t+55t=25．解得：t=53，∴OP=53，OE=55，∴PE=22OE OP-=103，∴点E的坐标为（51033，）．③当∠DBE=90°时，如图4．此时PE=PA=6﹣t，OD=OC+BC﹣t=6﹣t．则有OD=PE，EA=22PE PA+=2（6﹣t）=62﹣2?t，∴BE=BA﹣EA=42﹣（62﹣2t）=2t﹣22．∵PE∥OD，OD=PE，∠DOP=90°，∴四边形ODEP是矩形，∴DE=OP=t，DE∥OP，∴∠BED=∠BAO=45°．在Rt△DBE中，cos∠BED=BEDE=22，∴DE=2BE，∴t=22（t﹣22）=2t﹣4．解得：t=4，∴OP=4，PE=6﹣4=2，∴点E的坐标为（4，2）．综上所述：当以B、D、E为顶点的三角形是直角三角形时点E的坐标为（1，2）、（51033，）、（4，2）．点睛：本题考查了圆周角定理、切线的性质、相似三角形的判定与性质、三角函数的定义、平行线分线段成比例、矩形的判定与性质、勾股定理等知识，还考查了分类讨论的数学思想，有一定的综合性．3．如图，AB是半圆O的直径，C是的中点，D是的中点，AC与BD相交于点E.（1）求证：BD平分∠ABC；（2）求证：BE=2AD；（3）求DEBE的值.【答案】（1）答案见解析（2）BE=AF=2AD（3）21 2 -【解析】试题分析：（1）根据中点弧的性质，可得弦AD=CD，然后根据弦、弧、圆周角、圆心角的性质求解即可；（2）延长BC与AD相交于点F, 证明△BCE≌△ACF, 根据全等三角形的性质可得BE=AF=2AD；（3）连接OD,交AC于H.简要思路如下：设OH为1，则BC为2，OB=OD=2，DH=21-, 然后根据相似三角形的性质可求解.试题解析：（1）∵D是的中点∴AD=DC∴∠CBD=∠ABD∴BD平分∠ABC（2）提示：延长BC与AD相交于点F,证明△BCE≌△ACF,BE=AF=2AD（3）连接OD,交AC于H.简要思路如下：设OH为1，则BC为2，2，21, DEBE=DHBCDE BE =2124．如图，△ABC内接于⊙O，弦AD⊥BC垂足为H，∠ABC＝2∠CAD．（1）如图1，求证：AB＝BC；（2）如图2，过点B作BM⊥CD垂足为M，BM交⊙O于E,连接AE、HM，求证：AE∥HM;（3）如图3，在（2）的条件下，连接BD交AE于N，AE与BC交于点F，若NH＝25，AD＝11，求线段AB的长.【答案】（1）证明见解析；（2）证明见解析；（3）AB的长为10.【解析】分析：（1）根据题意，设∠CAD=a，然后根据直角三角形的两锐角互余的关系，推导出∠BAC=∠ACB，再根据等角对等边得证结论；（2）延长AD、BM交于点N，连接ED.根据圆周角定理得出∠N=∠DEN=∠BAN，进而根据等角对等边，得到DE=DN,BA=BN，再根据等腰三角形和直角三角形的性质，求得MH∥AE；（3）连接CE，根据（2）的结论，由三角形全等的判定与性质证得HF=HC，然后结合勾股定理求出AC2-AH2=CD2-DH2，解得CD=5,CH=4,AH=8，最后根据锐角三角函数的性质得到AB.详解：（1）证明：设∠CAD=a,则∠ABC=2a,∠C=90°-a,∠BAD=90°-2a,∴∠BAC=90°-2a+a=90°-a∴∠BAC=∠ACB.∴AB=BC(2）证明：延长AD、BM交于点N，连接ED.∵∠DEN=∠DAB,∠N=∠BCD,∠BCD=∠BAN∴∠N=∠DEN=∠BAN∴DE=DN,BA=BN又∵BH ⊥AN,DM ⊥EN ∴EM=NM,HN=HA,∴MH ∥AE （3）连接CE.∠BDA=∠BCA,∠BDM=∠BAC,由（1）知∠BCA=∠BAC ∴∠BDA=∠BDM,∴△BDM ≌△BDH, ∴DH=MH,∠MBD=∠HBD,∴BD ⊥MH 又∵MH ∥AE,∴BD ⊥EF,∴△FNB ≌△ENB, 同理可证△AFH ≌△ACH,∴HF=HC,又∵FN=NE∴NH ∥EC,EC=2NH,又∵NH=25∴EC=45∠EAC=2∠AEC=2a=∠ABC,可证弧AC=弧EC, ∴AC=EC=5 设HD=x ，AH=11-x ，∵∠ADC=2∠CAD,翻折△CHD 至△CHG,可证CG=CD=AG AH=CD+DH,CD=AH-DH=11-x-x=11-2x又∵AC 2-AH 2=CD 2-DH 2,∴(52-(11-x)2=(11-2x)2-x 2 ∴x 1=3,x 2=272(舍去)∴CD=5,CH=4,AH=8. 又∵tan2AH CHa BH DH==,∴BH=6 ∴22226810BM AH +=+= 点睛：此题主要考查了圆的综合，结合圆周角定理，勾股定理，全等三角形的判定与性质，解直角三角形的性质，综合性比较强，灵活添加辅助线，构造方程求解是解题关键.5．如图，在RtΔABC 中，∠ABC=90°，AB=CB ，以AB 为直径的⊙O 交AC 于点D ，点E 是AB 边上一点（点E 不与点A 、B 重合），DE 的延长线交⊙O 于点G ，DF ⊥DG ，且交BC 于点F.（1）求证：AE=BF ；（2）连接EF ，求证：∠FEB=∠GDA ；（3）连接GF,若AE=2，EB=4，求ΔGFD 的面积.【答案】（1）（2）见解析；（3）9【解析】分析：（1）连接BD，由三角形ABC为等腰直角三角形，求出∠A与∠C的度数，根据AB 为圆的直径，利用圆周角定理得到∠ADB为直角，即BD垂直于AC，利用直角三角形斜边上的中线等于斜边的一半，得到AD=DC=BD=12AC，进而确定出∠A=∠FBD，再利用同角的余角相等得到一对角相等，利用ASA得到三角形AED与三角形BFD全等，利用全等三角形对应边相等即可得证；（2）连接EF，BG，由三角形AED与三角形BFD全等，得到ED=FD，进而得到三角形DEF为等腰直角三角形，利用圆周角定理及等腰直角三角形性质得到一对同位角相等，利用同位角相等两直线平行，再根据平行线的性质和同弧所对的圆周角相等，即可得出结论；（3）由全等三角形对应边相等得到AE=BF=1，在直角三角形BEF中，利用勾股定理求出EF的长，利用锐角三角形函数定义求出DE的长，利用两对角相等的三角形相似得到三角形AED与三角形GEB相似，由相似得比例，求出GE的长，由GE+ED求出GD的长，根据三角形的面积公式计算即可．详解：（1）连接BD．在Rt△ABC中，∠ABC=90°，AB=BC，∴∠A=∠C=45°．∵AB为圆O的直径，∴∠ADB=90°，即BD⊥AC，∴AD=DC=BD=12AC，∠CBD=∠C=45°，∴∠A=∠FBD．∵DF⊥DG，∴∠FDG=90°，∴∠FDB+∠BDG=90°．∵∠EDA+∠BDG=90°，∴∠EDA=∠FDB．在△AED和△BFD中，A FBDAD BDEDA FDB∠=∠⎧⎪=⎨⎪∠=∠⎩，∴△AED≌△BFD（ASA），∴AE=BF；（2）连接EF，BG．∵△AED≌△BFD，∴DE=DF．∵∠EDF=90°，∴△EDF是等腰直角三角形，∴∠DEF=45°．∵∠G=∠A=45°，∴∠G=∠DEF，∴GB∥EF，∴∠FEB=∠GBA．∵∠GBA=∠GDA，∴∠FEB=∠GDA；（3）∵AE=BF，AE=2，∴BF=2．在Rt△EBF中，∠EBF=90°，∴根据勾股定理得：EF 2=EB 2+BF 2．∵EB =4，BF =2，∴EF =2242+=25．∵△DEF 为等腰直角三角形，∠EDF =90°，∴cos ∠DEF =DEEF． ∵EF =25，∴DE =25×22=10． ∵∠G =∠A ，∠GEB =∠AED ，∴△GEB ∽△AED ，∴GE AE =EBED，即GE •ED =AE •EB ，∴10•GE =8，即GE =4105，则GD =GE +ED =9105． ∴119101109222S GD DF GD DE =⨯⨯=⨯⨯=⨯⨯=．点睛：本题属于圆综合题，涉及的知识有：全等三角形的判定与性质，相似三角形的判定与性质，勾股定理，圆周角定理，以及平行线的判定与性质，熟练掌握判定与性质是解答本题的关键．6．等腰Rt △ABC 和⊙O 如图放置，已知AB=BC=1，∠ABC=90°，⊙O 的半径为1，圆心O 与直线AB 的距离为5．（1）若△ABC 以每秒2个单位的速度向右移动，⊙O 不动，则经过多少时间△ABC 的边与圆第一次相切？（2）若两个图形同时向右移动，△ABC 的速度为每秒2个单位，⊙O 的速度为每秒1个单位，则经过多少时间△ABC 的边与圆第一次相切？（3）若两个图形同时向右移动，△ABC 的速度为每秒2个单位，⊙O 的速度为每秒1个单位，同时△ABC 的边长AB 、BC 都以每秒0.5个单位沿BA 、BC 方向增大．△ABC 的边与圆第一次相切时，点B 运动了多少距离？【答案】（1）522-；（2）52-；（3）20423-【解析】分析：（1）分析易得，第一次相切时，与斜边相切，假设此时，△ABC移至△A′B′C′处，A′C′与⊙O切于点E，连OE并延长，交B′C′于F．由切线长定理易得CC′的长，进而由三角形运动的速度可得答案；（2）设运动的时间为t秒，根据题意得：CC′=2t，DD′=t，则C′D′=CD+DD′-CC′=4+t-2t=4-t，由第（1）的结论列式得出结果；（3）求出相切的时间，进而得出B点移动的距离．详解：（1）假设第一次相切时，△ABC移至△A′B′C′处，如图1，A′C′与⊙O切于点E，连接OE并延长，交B′C′于F，设⊙O与直线l切于点D，连接OD，则OE⊥A′C′，OD⊥直线l，由切线长定理可知C′E=C′D，设C′D=x，则C′E=x，∵△ABC是等腰直角三角形，∴∠A=∠ACB=45°，∴∠A′C′B′=∠ACB=45°，∴△EFC′是等腰直角三角形，∴2x，∠OFD=45°，∴△OFD也是等腰直角三角形，∴OD=DF，∴2x+x=1，则2-1，∴CC′=BD-BC-C′D=5-1-2-1）2，∴点C运动的时间为522；则经过522秒，△ABC的边与圆第一次相切；（2）如图2，设经过t秒△ABC的边与圆第一次相切，△ABC移至△A′B′C′处，⊙O与BC 所在直线的切点D移至D′处，A′C′与⊙O 切于点E ，连OE 并延长，交B′C′于F ， ∵CC′=2t ，DD′=t ，∴C′D′=CD+DD′-CC′=4+t -2t=4-t ，由切线长定理得C′E=C′D′=4-t ，由（1）得：4-t=2-1，解得：t=5-2，答：经过5-2秒△ABC 的边与圆第一次相切；（3）由（2）得CC′=（2+0.5）t=2.5t ，DD′=t ，则C′D′=CD+DD′-CC′=4+t -2.5t=4-1.5t ，由切线长定理得C′E=C′D′=4-1.5t ，由（1）得：4-1.5t=2-1，解得：t=10223-， ∴点B 运动的距离为2×10223-=20423-．点睛：本题要求学生熟练掌握圆与直线的位置关系，并结合动点问题进行综合分析，比较复杂，难度较大，考查了学生数形结合的分析能力．7．已知P 是O 的直径BA 延长线上的一个动点，∠P 的另一边交O 于点C 、D ，两点位于AB 的上方，AB ＝6，OP=m ，1sin 3P ＝，如图所示．另一个半径为6的1O 经过点C 、D ，圆心距1OO n ＝．（1）当m=6时，求线段CD 的长；（2）设圆心O 1在直线AB 上方，试用n 的代数式表示m ；（3）△POO 1在点P 的运动过程中，是否能成为以OO 1为腰的等腰三角形，如果能，试求出此时n 的值；如果不能，请说明理由．【答案】(1)CD=25;(2)m=23812n n- ;(3) n 的值为955或9155 【解析】分析：（1）过点O 作OH ⊥CD ，垂足为点H ，连接OC ．解Rt △POH ，得到OH 的长．由勾股定理得CH 的长，再由垂径定理即可得到结论；（2）解Rt △POH ，得到Rt 3mOH OCH ＝．在和Rt △1O CH 中，由勾股定理即可得到结论；（3）△1POO 成为等腰三角形可分以下几种情况讨论：① 当圆心1O 、O 在弦CD 异侧时，分1OP OO ＝和11O P OO ＝．②当圆心1O 、O 在弦CD 同侧时，同理可得结论．详解：（1）过点O 作OH ⊥CD ，垂足为点H ，连接OC ．在Rt △1sin 63POH P PO =中，＝，，∴2OH =． ∵AB ＝6，∴3OC ＝．由勾股定理得： 5CH = ∵OH ⊥DC ，∴225CD CH ==．（2）在Rt △1sin 3POH P PO m 中，＝，＝，∴3m OH ＝．在Rt △OCH 中，2293m CH ⎛⎫- ⎪⎝⎭＝．在Rt △1O CH 中，22363m CH n ⎛⎫-- ⎪⎝⎭＝．可得： 2236933m m n ⎛⎫⎛⎫--- ⎪ ⎪⎝⎭⎝⎭＝，解得23812n m n -：＝．（3）△1POO 成为等腰三角形可分以下几种情况： ① 当圆心1O 、O 在弦CD 异侧时i ）1OP OO ＝，即m n ＝，由23812n n n-＝，解得9n ：＝．即圆心距等于O 、1O 的半径的和，就有O 、1O 外切不合题意舍去．ii ）11O P OO ＝，由22233m m n m -+-（）（） n ＝，解得：23m n ＝，即23n 23812n n-＝，解得9155n ：＝． ②当圆心1O 、O 在弦CD 同侧时，同理可得： 28132n m n-＝．∵1POO ∠是钝角，∴只能是m n =，即28132nn n-＝，解得955n ：＝．综上所述：n 的值为955或9155．点睛：本题是圆的综合题．考查了圆的有关性质和两圆的位置关系以及解直径三角形．解答（3）的关键是要分类讨论．8．在O 中，AB 为直径，C 为O 上一点.（Ⅰ）如图①，过点C 作O 的切线，与AB 的延长线相交于点P ，若28CAB ∠=︒，求P ∠的大小；（Ⅱ）如图②，D 为弧AC 的中点，连接OD 交AC 于点E ，连接DC 并延长，与AB 的延长线相交于点P ，若12CAB ∠=︒，求P ∠的大小. 【答案】（1）∠P ＝34°；（2）∠P ＝27° 【解析】【分析】（1）首先连接OC ，由OA=OC ，即可求得∠A 的度数，然后由圆周角定理，求得∠POC 的度数，继而求得答案；（2）因为D 为弧AC 的中点，OD 为半径，所以OD ⊥AC ，继而求得答案．【详解】（1）连接OC，∵OA＝OC，∴∠A＝∠OCA＝28°，∴∠POC＝56°，∵CP是⊙O的切线，∴∠OCP＝90°，∴∠P＝34°；（2）∵D为弧AC的中点，OD为半径，∴OD⊥AC，∵∠CAB＝12°，∴∠AOE＝78°，∴∠DCA＝39°，∵∠P＝∠DCA﹣∠CAB，∴∠P＝27°．【点睛】本题考查切线的性质以及等腰三角形的性质．注意准确作出辅助线是解此题的关键．9．如图，△ABC中，AC＝BC＝10，cosC＝35，点P是AC边上一动点（不与点A、C重合），以PA长为半径的⊙P与边AB的另一个交点为D，过点D作DE⊥CB于点E．（1）当⊙P与边BC相切时，求⊙P的半径．（2）连接BP交DE于点F，设AP的长为x，PF的长为y，求y关于x的函数解析式，并直接写出x的取值范围．（3）在（2）的条件下，当以PE长为直径的⊙Q与⊙P相交于AC边上的点G时，求相交所得的公共弦的长.【答案】（1）409R=;（2）25880320xy x xx=-++;（3）50105-.【解析】【分析】（1）设⊙P与边BC相切的切点为H，圆的半径为R，连接HP，则HP⊥BC，cosC＝35，则sinC＝45，sinC＝HPCP＝10RR-＝45，即可求解；（2）首先证明PD∥BE，则EB BFPD PF=，即：2024588x yxxxy-+--=，即可求解；（3）证明四边形PDBE为平行四边形，则AG＝EP＝BD，即：AB＝DB+AD＝AG+AD＝45，即可求解．【详解】（1）设⊙P与边BC相切的切点为H，圆的半径为R，连接HP，则HP⊥BC，cosC＝35，则sinC＝45，sinC＝HPCP＝10RR-＝45，解得：R＝409；（2）在△ABC中，AC＝BC＝10，cosC＝35，设AP＝PD＝x，∠A＝∠ABC＝β，过点B作BH⊥AC，则BH ＝ACsinC ＝8，同理可得：CH ＝6，HA ＝4，AB ＝45，则：tan ∠CAB ＝2， BP ＝228+(4)x -＝2880x x -+，DA ＝25x ，则BD ＝45﹣25x ，如下图所示，PA ＝PD ，∴∠PAD ＝∠CAB ＝∠CBA ＝β，tanβ＝2，则cosβ5，sinβ5， EB ＝BDcosβ＝（525x ）5＝4﹣25x ，∴PD ∥BE ，∴EB BFPD PF=，即：2024588x y x xx -+--=，整理得：y 25xx 8x 803x 20-++（3）以EP 为直径作圆Q 如下图所示，两个圆交于点G ，则PG ＝PQ ，即两个圆的半径相等，则两圆另外一个交点为D ， GD 为相交所得的公共弦， ∵点Q 是弧GD 的中点， ∴DG ⊥EP ， ∵AG 是圆P 的直径， ∴∠GDA ＝90°， ∴EP ∥BD ，由（2）知，PD ∥BC ，∴四边形PDBE 为平行四边形， ∴AG ＝EP ＝BD ，∴AB ＝DB+AD ＝AG+AD ＝5 设圆的半径为r ，在△ADG 中，AD ＝2rcosβ5DG 5AG ＝2r ，5＝52r 51+，则：DG 550﹣5相交所得的公共弦的长为50﹣5 【点睛】本题考查的是圆知识的综合运用，涉及到解直角三角形、勾股定理等知识，其中（3），要关键是根据题意正确画图，此题用大量的解直角三角形的内容，综合难度很大．10．如图所示，ABC ∆内接于圆O ，CD AB ⊥于D ；（1）如图1，当AB 为直径，求证：OBC ACD ∠=∠；（2）如图2，当AB 为非直径的弦，连接OB ，则（1）的结论是否成立？若成立请证明，不成立说明由；（3）如图3，在（2）的条件下，作AE BC ⊥于E ，交CD 于点F ，连接ED ，且2AD BD ED =+，若3DE =，5OB =，求CF 的长度．【答案】（1）见解析；（2）成立；（3）145【解析】【分析】（1）根据圆周角定理求出∠ACB=90°，求出∠ADC=90°，再根据三角形内角和定理求出即可；（2）根据圆周角定理求出∠BOC=2∠A ，求出∠OBC=90°-∠A 和∠ACD=90°-∠A 即可；（3）分别延长AE 、CD 交⊙O 于H 、K ，连接HK 、CH 、AK ，在AD 上取DG=BD ，延长CG 交AK 于M ，延长KO 交⊙O 于N ，连接CN 、AN ，求出关于a 的方程，再求出a 即可．【详解】（1）证明：∵AB 为直径， ∴ACB 90∠=︒，∵CD AB ⊥于D ，∴ADC 90∠=︒，∴OBC A 90∠∠+=︒，A ACD 90∠∠+=︒， ∴OBC ACD ∠∠=；（2）成立，证明：连接OC ，由圆周角定理得：BOC 2A ∠∠=， ∵OC OB =， ∴()()11OBC 180BOC 1802A 90A 22∠∠∠∠=︒-=︒-=︒-， ∵ADC 90∠=︒，∴ACD 90A ∠∠=︒-，∴OBC ACD ∠∠=；（3）分别延长AE 、CD 交⊙O 于H 、K ，连接HK 、CH 、AK ，∵AE BC ⊥，CD BA ⊥，∴AEC ADC 90∠∠==︒，∴BCD CFE 90∠∠+=︒，BAH DFA 90∠∠+=︒， ∵CFE DFA ∠∠=， ∴BCD BAH ∠∠=，∵根据圆周角定理得：BAH BCH ∠∠=， ∴BCD BAH BCH ∠∠∠==，∴由三角形内角和定理得：CHE CFE ∠∠=，∴CH CF =， ∴EH EF =，同理DF DK =， ∵DE 3=， ∴HK 2DE 6==，在AD 上取DG BD =，延长CG 交AK 于M ，则AG AD BD 2DE 6=-==，BC GC =，∴MCK BCK BAK ∠∠∠==， ∴CMK 90∠=︒，延长KO 交⊙O 于N ，连接CN 、AN ，则NAK 90CMK ∠∠=︒=， ∴CM //AN ， ∵NCK ADK 90∠∠==︒，∴CN //AG ，∴四边形CGAN 是平行四边形， ∴AG CN 6==，作OT CK ⊥于T ，则T 为CK 的中点， ∵O 为KN 的中点， ∴1OT CN 32==，∵OTC 90∠=︒，OC 5=，∴由勾股定理得：CT 4=，∴CK 2CT 8==，作直径HS ，连接KS ，∵HK 6=，HS 10=，∴由勾股定理得：KS 8=， ∴3tan HSK tan HAK 4∠∠==， ∴1tan EAB tan BCD 3∠∠==，设BD a =，CD 3a =， ∴AD BD 2ED a 6=+=+，11DK AD a 233==+， ∵CD DK CK +=， ∴13a a 283++=，解得：9a 5=， ∴113DK a 235=+=， ∴2614CF CK 2DK 855=-=-=．【点睛】本题考查了垂径定理、解直角三角形、等腰三角形的性质、圆周角定理、勾股定理等知识点，能综合运用知识点进行推理是解此题的关键，综合性比较强，难度偏大．。

中考数学《圆》专项复习综合练习题-附带答案

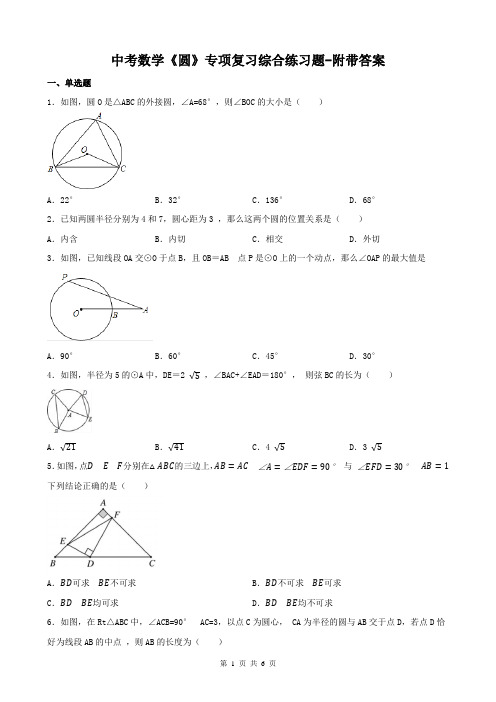
中考数学《圆》专项复习综合练习题-附带答案一、单选题1．如图，圆O是△ABC的外接圆，∠A=68°，则∠BOC的大小是（）A．22°B．32°C．136°D．68°2．已知两圆半径分别为4和7，圆心距为3 ，那么这两个圆的位置关系是（）A．内含B．内切C．相交D．外切3．如图，已知线段OA交⊙O于点B，且OB＝AB 点P是⊙O上的一个动点，那么∠OAP的最大值是A．90°B．60°C．45°D．30°4．如图，半径为5的⊙A中，DE＝2 √5，∠BAC+∠EAD＝180°，则弦BC的长为（）A．√21B．√41C．4 √5D．3 √55．如图，点D E F分别在△ABC的三边上，AB=AC∠A=∠EDF=90°与∠EFD=30°AB=1下列结论正确的是（）A．BD可求BE不可求B．BD不可求BE可求C．BD BE均可求D．BD BE均不可求6．如图，在Rt△ABC中，∠ACB=90° AC=3，以点C为圆心， CA为半径的圆与AB交于点D，若点D恰好为线段AB的中点，则AB的长度为（）B．3 C．9 D．6A．327．如图，⊙O是△ABC的外接圆，弦BD交AC于点E，AE=DE， BC=CE，过点O作OF⊥AC于点F，延长FO 交BE于点G ，若DE=6，EG=4，则AB的长为（）A．4√5B．8√3C．13 D．148．如图，把正六边形各边按同一方向延长，使延长的线段与原正六边形的边长相等，顺次连接这六条线段外端点可以得到一个新的正六边形…，重复上述过程，经过2018次后所得到的正六边形边长是原正六边形边长的（）A．（√2）2016倍B．（√3）2017倍C．（√3）2018倍D．（√2）2019倍二、填空题9．如图，PA、PB切⊙O于点A、B ，已知⊙O半径为2 且∠APB=60°，则AB= ．10．如图，矩形ABCD中，BC＝4 CD＝2 以AD为直径的半圆O与BC相切于点E，连接BD，则阴影部分的面积为.（结果保留π）11．如图，两边平行的刻度尺在圆上移动当刻度尺的一边与直径为6.5cm的圆相切时另一边与圆两个交点处的读数恰好为“2”和“8”（单位：cm）则刻度尺的宽为 cm．12．如图，两圆相交于A、B两点小圆经过大圆的圆心O 点C D分别在两圆上若∠ADB＝100°则∠ACB的度数为。

人教中考数学专题训练---圆的综合的综合题分类含详细答案

一、圆的综合真题与模拟题分类汇编（难题易错题）1．如图，△ABC是⊙O的内接三角形，点D在BC上，点E在弦AB上（E不与A重合），且四边形BDCE为菱形．（1）求证：AC=CE；（2）求证：BC2﹣AC2=AB•AC；（3）已知⊙O的半径为3．①若ABAC=53，求BC的长；②当ABAC为何值时，AB•AC的值最大？【答案】（1）证明见解析；（2）证明见解析；（3）2；②3 2【解析】分析：（1）由菱形知∠D=∠BEC，由∠A+∠D=∠BEC+∠AEC=180°可得∠A=∠AEC，据此得证；（2）以点C为圆心，CE长为半径作⊙C，与BC交于点F，于BC延长线交于点G，则CF=CG=AC=CE=CD，证△BEF∽△BGA得BE BGBF BA=，即BF•BG=BE•A B，将BF=BC-CF=BC-AC、BG=BC+CG=BC+AC代入可得；（3）①设AB=5k、AC=3k，由BC2-AC2=AB•AC知6k，连接ED交BC于点M，Rt△DMC中由DC=AC=3k、MC=126k求得22CD CM-3，可知OM=OD-3，在Rt△COM中，由OM2+MC2=OC2可得答案．②设OM=d，则MD=3-d，MC2=OC2-OM2=9-d2，继而知BC2=（2MC）2=36-4d2、AC2=DC2=DM2+CM2=（3-d）2+9-d2，由（2）得AB•AC=BC2-AC2，据此得出关于d的二次函数，利用二次函数的性质可得答案．详解：（1）∵四边形EBDC为菱形，∴∠D=∠BEC，∵四边形ABDC是圆的内接四边形，∴∠A+∠D=180°，又∠BEC+∠AEC=180°，∴∠A=∠AEC，∴AC=CE；（2）以点C为圆心，CE长为半径作⊙C，与BC交于点F，于BC延长线交于点G，则CF=CG，由（1）知AC=CE=CD，∴CF=CG=AC，∵四边形AEFG是⊙C的内接四边形，∴∠G+∠AEF=180°，又∵∠AEF+∠BEF=180°，∴∠G=∠BEF，∵∠EBF=∠GBA，∴△BEF∽△BGA，∴BE BGBF BA=，即BF•BG=BE•AB，∵BF=BC﹣CF=BC﹣AC、BG=BC+CG=BC+AC，BE=CE=AC，∴（BC﹣AC）（BC+AC）=AB•AC，即BC2﹣AC2=AB•AC；（3）设AB=5k、AC=3k，∵BC2﹣AC2=AB•AC，∴6k，连接ED交BC于点M，∵四边形BDCE是菱形，∴DE垂直平分BC，则点E、O、M、D共线，在Rt△DMC中，DC=AC=3k，MC=126k，∴223CD CM k-=，∴OM=OD﹣DM=33k，在Rt△COM中，由OM2+MC2=OC2得（33）2+6k）2=32，解得：k=33或k=0（舍），∴62；②设OM=d，则MD=3﹣d，MC2=OC2﹣OM2=9﹣d2，∴BC2=（2MC）2=36﹣4d2，AC2=DC2=DM2+CM2=（3﹣d）2+9﹣d2，由（2）得AB•AC=BC2﹣AC2=﹣4d2+6d+18=﹣4（d﹣34）2+814，∴当d=34，即OM=34时，AB•AC最大，最大值为814，∴DC2=272，∴AC=DC=362，∴AB=964，此时32ABAC．点睛：本题主要考查圆的综合问题，解题的关键是掌握圆的有关性质、圆内接四边形的性质及菱形的性质、相似三角形的判定与性质、二次函数的性质等知识点．2．如图，AB是⊙O的直径，PA是⊙O的切线，点C在⊙O上，CB∥PO．（1）判断PC与⊙O的位置关系，并说明理由；（2）若AB=6，CB=4，求PC的长．【答案】（1）PC是⊙O的切线，理由见解析；（235 2【解析】试题分析：（1）要证PC是⊙O的切线，只要连接OC，再证∠PCO=90°即可．（2）可以连接AC，根据已知先证明△ACB∽△PCO，再根据勾股定理和相似三角形的性质求出PC的长．试题解析：（1）结论：PC是⊙O的切线．证明：连接OC∵CB∥PO∴∠POA=∠B，∠POC=∠OCB∵OC=OB∴∠OCB=∠B∴∠POA=∠POC又∵OA=OC，OP=OP∴△APO≌△CPO∴∠OAP=∠OCP∵PA是⊙O的切线∴∠OAP=90°∴∠OCP=90°∴PC是⊙O的切线．（2）连接AC∵AB是⊙O的直径∴∠ACB=90°（6分）由（1）知∠PCO=90°，∠B=∠OCB=∠POC∵∠ACB=∠PCO∴△ACB∽△PCO∴∴．点睛：本题考查了切线的判定．要证某线是圆的切线，已知此线过圆上某点，连接圆心与这点（即为半径），再证垂直即可．同时考查了勾股定理和相似三角形的性质．3．如图，在RtΔABC中，∠ABC=90°，AB=CB，以AB为直径的⊙O交AC于点D，点E是AB边上一点（点E不与点A、B重合），DE的延长线交⊙O于点G，DF⊥DG，且交BC于点F.（1）求证：AE=BF；（2）连接EF，求证：∠FEB=∠GDA；（3）连接GF,若AE=2，EB=4，求ΔGFD的面积.【答案】（1）（2）见解析；（3）9【解析】分析：（1）连接BD，由三角形ABC为等腰直角三角形，求出∠A与∠C的度数，根据AB 为圆的直径，利用圆周角定理得到∠ADB为直角，即BD垂直于AC，利用直角三角形斜边上的中线等于斜边的一半，得到AD=DC=BD=12AC，进而确定出∠A=∠FBD，再利用同角的余角相等得到一对角相等，利用ASA得到三角形AED与三角形BFD全等，利用全等三角形对应边相等即可得证；（2）连接EF，BG，由三角形AED与三角形BFD全等，得到ED=FD，进而得到三角形DEF为等腰直角三角形，利用圆周角定理及等腰直角三角形性质得到一对同位角相等，利用同位角相等两直线平行，再根据平行线的性质和同弧所对的圆周角相等，即可得出结论；（3）由全等三角形对应边相等得到AE=BF=1，在直角三角形BEF中，利用勾股定理求出EF的长，利用锐角三角形函数定义求出DE的长，利用两对角相等的三角形相似得到三角形AED与三角形GEB相似，由相似得比例，求出GE的长，由GE+ED求出GD的长，根据三角形的面积公式计算即可．详解：（1）连接BD．在Rt△ABC中，∠ABC=90°，AB=BC，∴∠A=∠C=45°．∵AB为圆O的直径，∴∠ADB=90°，即BD⊥AC，∴AD=DC=BD=12AC，∠CBD=∠C=45°，∴∠A=∠FBD．∵DF⊥DG，∴∠FDG=90°，∴∠FDB+∠BDG=90°．∵∠EDA+∠BDG=90°，∴∠EDA=∠FDB．在△AED和△BFD中，A FBDAD BDEDA FDB∠=∠⎧⎪=⎨⎪∠=∠⎩，∴△AED≌△BFD（ASA），∴AE=BF；（2）连接EF，BG．∵△AED≌△BFD，∴DE=DF．∵∠EDF=90°，∴△EDF是等腰直角三角形，∴∠DEF=45°．∵∠G=∠A=45°，∴∠G=∠DEF，∴GB∥EF，∴∠FEB=∠GBA．∵∠GBA=∠GDA，∴∠FEB=∠GDA；（3）∵AE=BF，AE=2，∴BF=2．在Rt△EBF中，∠EBF=90°，∴根据勾股定理得：EF2=EB2+BF2．∵EB=4，BF=2，∴EF∵△DEF为等腰直角三角形，∠EDF=90°，∴cos∠DEF=DE EF．∵EF=∴DE=2．∵∠G =∠A ，∠GEB =∠AED ，∴△GEB ∽△AED ，∴GE AE =EB ED ，即GE •ED =AE •EB ，∴10•GE =8，即GE =4105，则GD =GE +ED =9105． ∴1191011092252S GD DF GD DE =⨯⨯=⨯⨯=⨯⨯=．点睛：本题属于圆综合题，涉及的知识有：全等三角形的判定与性质，相似三角形的判定与性质，勾股定理，圆周角定理，以及平行线的判定与性质，熟练掌握判定与性质是解答本题的关键．4．如图，OB 是以（O ，a ）为圆心，a 为半径的⊙O 1的弦，过B 点作⊙O 1的切线，P 为劣弧OB 上的任一点，且过P 作OB 、AB 、OA 的垂线，垂足分别是D 、E 、F ．（1）求证：PD 2=PE•PF ；（2）当∠BOP=30°，P 点为OB 的中点时，求D 、E 、F 、P 四个点的坐标及S △DEF ．【答案】（1）详见解析；（2）D 3，34a ），E 33a ，34a ），F 3，0），P （﹣32a ，2a ）；S △DEF =3316a 2．【解析】试题分析：（1）连接PB ，OP ，利用AB 切⊙O 1于B 求证△PBE ∽△POD ，得出 PB PE OP PD = ，同理，△OPF ∽△BPD ，得出PB PD OP PF= ，然后利用等量代换即可．（2）连接O 1B ，O 1P ，得出△O 1BP 和△O 1PO 为等边三角形，根据直角三角形的性质即可解得D 、E 、F 、P 四个点的坐标．再利用三角形的面积公式可直接求出三角形DEF 的面积．试题解析：（1）证明：连接PB ，OP ，∵PE⊥AB，PD⊥OB，∴∠BEP=∠PDO=90°，∵AB切⊙O1于B，∠ABP=∠BOP，∴△PBE∽△POD，∴=，同理，△OPF∽△BPD∴=，∴=，∴PD2=PE•PF；（2）连接O1B，O1P，∵AB切⊙O1于B，∠POB=30°，∴∠ABP=30°，∴∠O1BP=90°﹣30°=60°，∵O1B=O1P，∴△O1BP为等边三角形，∴O1B=BP，∵P为弧BO的中点，∴BP=OP，即△O1PO为等边三角形，∴O1P=OP=a，∴∠O1OP=60°，又∵P为弧BO的中点，∴O1P⊥OB，在△O1DO中，∵∠O1OP=60°O1O=a，∴O1D=a，OD=a，过D作DM⊥OO1于M，∴DM=OD=a，OM=DM=a，∴D（﹣a， a），∵∠O1OF=90°，∠O1OP=60°∴∠POF=30°，∵PE⊥OA，∴PF=OP=a，OF=a，∴P（﹣a，），F（﹣a，0），∵AB切⊙O1于B，∠POB=30°，∴∠ABP=∠BOP=30°，∵PE⊥AB，PB=a，∴∠EPB=60°∴PE=a，BE=a，∵P为弧BO的中点，∴BP=PO，∴∠PBO=∠BOP=30°，∴∠BPO=120°，∴∠BPE+∠BPO=120°+60°=180°，即OPE三点共线，∵OE=a+a=a，过E作EM⊥x轴于M，∵AO切⊙O1于O，∴∠EOA=30°，∴EM=OE=a，OM=a，∴E（﹣a， a），∵E（﹣a， a），D（﹣a， a），∴DE=﹣a﹣（﹣a）=a，DE边上的高为： a，∴S△DEF=×a×a=a2．故答案为：D（﹣a， a），E（﹣a， a），F（﹣a，0），P（﹣a，）；S△DEF=a2．5．已知：如图1，∠ACG=90°，AC=2，点B为CG边上的一个动点，连接AB，将△ACB沿AB边所在的直线翻折得到△ADB，过点D作DF⊥CG于点F．（1）当BC=233时，判断直线FD与以AB为直径的⊙O的位置关系，并加以证明；（2）如图2，点B在CG上向点C运动，直线FD与以AB为直径的⊙O交于D、H两点，连接AH，当∠CAB=∠BAD=∠DAH时，求BC的长．【答案】（1）直线FD与以AB为直径的⊙O相切，理由见解析；（2）222.【解析】试题分析：（1）根据已知及切线的判定证明得，直线FD与以AB为直径的⊙O相切；（2）根据圆内接四边形的性质及直角三角形的性质进行分析，从而求得BC的长．试题解析：（1）判断：直线FD与以AB为直径的⊙O相切．证明：如图，作以AB为直径的⊙O；∵△ADB是将△ACB沿AB边所在的直线翻折得到的，∴△ADB≌△ACB，∴∠ADB=∠ACB=90°．∵O为AB的中点，连接DO，∴OD=OB=AB，∴点D在⊙O上．在Rt△ACB中，BC=，AC=2；∴tan∠CAB==，∴∠CAB=∠BAD=30°，∴∠ABC=∠ABD=60°，∴△BOD是等边三角形．∴∠BOD=60°．∴∠ABC=∠BOD，∴FC∥DO．∵DF⊥CG，∴∠ODF=∠BFD=90°，∴OD⊥FD，∴FD为⊙O的切线．（2）延长AD交CG于点E，同（1）中的方法，可证点C在⊙O上；∴四边形ADBC是圆内接四边形．∴∠FBD=∠1+∠2．同理∠FDB=∠2+∠3．∵∠1=∠2=∠3，∴∠FBD=∠FDB，又∠DFB=90°．∴EC=AC=2．设BC=x，则BD=BC=x，∵∠EDB=90°，∴EB=x．∵EB+BC=EC，∴x+x=2，解得x=2﹣2，∴BC=2﹣2．6．（1）问题背景如图①，BC是⊙O的直径，点A在⊙O上，AB=AC，P为BmC上一动点（不与B，C重2PA=PB+PC．小明同学观察到图中自点A出发有三条线段AB，AP，AC，且AB=AC，这就为旋转作了铺垫．于是，小明同学有如下思考过程：第一步：将△PAC绕着点A顺时针旋转90°至△QAB（如图①）；第二步：证明Q，B，P三点共线，进而原题得证．请你根据小明同学的思考过程完成证明过程．（2）类比迁移如图②，⊙O的半径为3，点A，B在⊙O上，C为⊙O内一点，AB=AC，AB⊥AC，垂足为A，求OC的最小值．（3）拓展延伸如图③，⊙O的半径为3，点A，B在⊙O上，C为⊙O内一点，AB=43AC，AB⊥AC，垂足为A，则OC的最小值为．【答案】（1）证明见解析；（2）OC最小值是32﹣3；（3）32．【解析】试题分析：（1）将△PAC绕着点A顺时针旋转90°至△QAB（如图①），只要证明△APQ 是等腰直角三角形即可解决问题；（2）如图②中，连接OA，将△OAC绕点O顺时针旋转90°至△QAB，连接OB，OQ，在△BOQ中，利用三边关系定理即可解决问题；（3）如图③构造相似三角形即可解决问题．作AQ⊥OA，使得AQ=43OA，连接OQ，BQ，OB．由△QAB∽OAC，推出BQ=43OC，当BQ最小时，OC最小；试题解析：（1）将△PAC绕着点A顺时针旋转90°至△QAB（如图①）；∵BC是直径，∴∠BAC=90°，∵AB=AC，∴∠ACB=∠ABC=45°，由旋转可得∠QBA=∠PCA，∠ACB=∠APB=45°，PC=QB，∵∠PCA+∠PBA=180°，∴∠QBA+∠PBA=180°，∴Q，B，P三点共线，∴∠QAB+∠BAP=∠BAP+∠PAC=90°，∴QP 2=AP 2+AQ 2=2AP 2， ∴QP=2AP=QB+BP=PC+PB ，∴2AP=PC+PB ．（2）如图②中，连接OA ，将△OAC 绕点A 顺时针旋转90°至△QAB ，连接OB ，OQ ，∵AB ⊥AC,∴∠BAC=90°,由旋转可得 QB=OC ，AQ=OA ，∠QAB=∠OAC ，∴∠QAB+∠BAO=∠BAO+∠OAC=90°， ∴在Rt △OAQ 中，OQ=32，AO=3 ，∴在△OQB 中，BQ≥OQ ﹣OB=32﹣3 ，即OC 最小值是32﹣3；（3）如图③中，作AQ ⊥OA ，使得AQ=43OA ，连接OQ ，BQ ，OB ．∵∠QAO=∠BAC=90°，∠QAB=∠OAC ，∵QA AB OA AC =43， ∴△QAB ∽OAC ，∴BQ=43OC ，当BQ 最小时，OC 最小，易知OA=3，AQ=4，OQ=5，BQ≥OQ ﹣OB ，∴OQ≥2，] ∴BQ 的最小值为2， ∴OC 的最小值为34×2=32，故答案为32．【点睛】本题主要考查的圆、旋转、相似等知识，能根据题意正确的添加辅助线是解题的关键.7．在O 中，AB 为直径，C 为O 上一点.（Ⅰ）如图①，过点C 作O 的切线，与AB 的延长线相交于点P ，若28CAB ∠=︒，求P ∠的大小；（Ⅱ）如图②，D 为弧AC 的中点，连接OD 交AC 于点E ，连接DC 并延长，与AB 的延长线相交于点P ，若12CAB ∠=︒，求P ∠的大小. 【答案】（1）∠P ＝34°；（2）∠P ＝27° 【解析】【分析】（1）首先连接OC ，由OA=OC ，即可求得∠A 的度数，然后由圆周角定理，求得∠POC 的度数，继而求得答案；（2）因为D 为弧AC 的中点，OD 为半径，所以OD ⊥AC ，继而求得答案．【详解】（1）连接OC ， ∵OA ＝OC ， ∴∠A ＝∠OCA ＝28°， ∴∠POC ＝56°， ∵CP 是⊙O 的切线， ∴∠OCP ＝90°， ∴∠P ＝34°；（2）∵D 为弧AC 的中点，OD 为半径， ∴OD ⊥AC ， ∵∠CAB ＝12°， ∴∠AOE ＝78°， ∴∠DCA ＝39°， ∵∠P ＝∠DCA ﹣∠CAB ， ∴∠P ＝27°．【点睛】本题考查切线的性质以及等腰三角形的性质．注意准确作出辅助线是解此题的关键．8．（问题情境）如图1，点E是平行四边形ABCD的边AD上一点，连接BE、CE．求证：BCE 1S2=S平行四边形ABCD．（说明：S表示面积）请以“问题情境”为基础，继续下面的探究（探究应用1）如图2，以平行四边形ABCD的边AD为直径作⊙O，⊙O与BC边相切于点H，与BD相交于点M．若AD＝6，BD＝y，AM＝x，试求y与x之间的函数关系式．（探究应用2）如图3，在图1的基础上，点F在CD上，连接AF、BF，AF与CE相交于点G，若AF＝CE，求证：BG平分∠AGC．（迁移拓展）如图4，平行四边形ABCD中，AB：BC＝4：3，∠ABC＝120°，E是AB的中点，F在BC上，且BF：FC＝2：1，过D分别作DG⊥AF于G，DH⊥CE于H，请直接写出DG：DH的值．【答案】【问题情境】见解析；【探究应用1】18yx=；【探究应用2】见解析；【迁移1927【解析】【分析】（1）作EF⊥BC于F，则S△BCE＝12BC×EF，S平行四边形ABCD＝BC×EF，即可得出结论；（2）连接OH，由切线的性质得出OH⊥BC，OH＝12AD＝3，求出平行四边形ABCD的面积＝AD×OH＝18，由圆周角定理得出AM⊥BD，得出△ABD的面积＝12BD×AM＝12平行四边形的面积＝9，即可得出结果；（3）作BM⊥AF于M，BN⊥CE于N，同图1得：△ABF的面积＝△BCE的面积＝12平行四边形ABCD的面积，得出12AF×BM＝12CE×BN，证出BM＝BN，即可得出BG平分∠AGC．（4）作AP⊥BC于P，EQ⊥BC于Q，由平行四边形的性质得出∠ABP＝60°，得出∠BAP＝30°，设AB ＝4x ，则BC ＝3x ，由直角三角形的性质得出BP ＝12AB ＝2x ，BQ ＝12BE ，AP ＝BP ＝，由已知得出BE ＝2x ，BF ＝2x ，得出BQ ＝x ，EQ x ，PF ＝4x ，QF ＝3x ，QC ＝4x ，由勾股定理求出AF ＝x ，CE，连接DF 、DE ，由三角形的面积关系得出AF×DG ＝CE×DH ，即可得出结果．【详解】（1）证明：作EF ⊥BC 于F ，如图1所示：则S △BCE ＝12BC×EF ，S 平行四边形ABCD ＝BC×EF ， ∴12BCEABCDSS =．（2）解：连接OH ，如图2所示： ∵⊙O 与BC 边相切于点H ， ∴OH ⊥BC ，OH ＝12AD ＝3， ∴平行四边形ABCD 的面积＝AD×OH ＝6×3＝18， ∵AD 是⊙O 的直径， ∴∠AMD ＝90°， ∴AM ⊥BD ， ∴△ABD 的面积＝12BD×AM ＝12平行四边形的面积＝9，即12xy ＝9， ∴y 与x 之间的函数关系式y ＝18x；（3）证明：作BM ⊥AF 于M ，BN ⊥CE 于N ，如图3所示：同图1得：△ABF 的面积＝△BCE 的面积＝12平行四边形ABCD 的面积， ∴12AF×BM ＝12CE×BN ， ∵AF ＝CE ， ∴BM ＝BN ，∴BG 平分∠AGC ．（4）解：作AP ⊥BC 于P ，EQ ⊥BC 于Q ，如图4所示： ∵平行四边形ABCD 中，AB ：BC ＝4：3，∠ABC ＝120°， ∴∠ABP ＝60°，∴∠BAP ＝30°，设AB ＝4x ，则BC ＝3x ，∴BP ＝12AB ＝2x ，BQ ＝12BE ，AP ＝3BP ＝23x ， ∵E 是AB 的中点，F 在BC 上，且BF ：FC ＝2：1， ∴BE ＝2x ，BF ＝2x ， ∴BQ ＝x ，∴EQ ＝3x ，PF ＝4x ，QF ＝3x ，QC ＝4x ，由勾股定理得：AF ＝22AP PF +＝27x ，CE ＝22EQ QC +＝19x ，连接DF 、DE ，则△CDE 的面积＝△ADF 的面积＝12平行四边形ABCD 的面积， ∴AF×DG ＝CE×DH ，∴DG ：DH ＝CE ：AF ＝19x :27x 19:27=．【点睛】本题是圆的综合题目，考查了圆周角定理、平行四边形的性质、三角形面积公式、含30°角的直角三角形的性质、勾股定理、角平分线的判定等知识；本题综合性强，需要添加辅助线，熟练掌握平行四边形的性质和勾股定理是解题的关键．9．如图，在中，，以为直径作，交边于点，交边于点，过点作的切线，交的延长线于点，交于点．（1）求证：；（2）若，，求的半径．【答案】（1）证明见解析；（2）4．【解析】试题分析：（1）连接AD，根据等腰三角形三线合一即可证明．（2）设⊙O的半径为R，则FO=4+R，FA=4+2R，OD=R，连接OD，由△FOD∽△FAE，得列出方程即可解决问题．试题解析：（1）连接AD，∵AB是直径，∴∠ADB=90°，∵AB=AC，AD⊥BC，∴BD=DC．（2）设⊙O的半径为R，则FO=4+R，FA=4+2R，OD=R，连接OD、∵AB=AC，∴∠ABC=∠C，∵OB=OD，∴∠ABC=∠ODB，∴∠ODB=∠C，∴OD∥AC，∴△FOD∽△FAE，∴，∴，整理得R2﹣R﹣12=0，∴R=4或（﹣3舍弃）．∴⊙O的半径为4．考点：切线的性质、等腰三角形的性质等知识．10．已知AB 是半圆O 的直径，点C 在半圆O 上.(1)如图1，若AC＝3，∠CAB＝30°，求半圆O 的半径；(2)如图2，M 是BC的中点，E 是直径AB 上一点，AM 分别交CE，BC 于点F，D. 过点F 作FG∥AB 交边BC 于点G，若△ACE 与△CEB 相似，请探究以点D 为圆心，GB 长为半径的⊙D 与直线AC 的位置关系，并说明理由.【答案】（1）半圆O的半径为3；（2）⊙D与直线AC相切，理由见解析【解析】试题分析：(1)依据直径所对的圆周角是直角可得∠C＝90°,2再依据三角函数即可求解;(2) 依据△ACE与△CEB相似证出∠AEC＝∠CEB＝90°, 再依据M是BC的中点,证明CF＝CD, 过点F作FP∥GB交于AB于点P, 证出△ACF≌△APF,得出CF=FP,再证四边形FPBG是平行四边形,得到 FP＝GB从而CD＝GB,点D到直线AC的距离为线段CD的长.试题解析：（1）∵ AB是半圆O的直径，∴∠C＝90°．在Rt△ACB中，AB＝cos AC CAB ∠＝3 cos30︒＝3．∴ OA＝3（2）⊙D与直线AC相切.理由如下：由（1）得∠ACB＝90°．∵∠AEC＝∠ECB＋∠6，∴∠AEC＞∠ECB，∠AEC＞∠6．∵△ACE与△CEB相似，∴∠AEC＝∠CEB＝90°．在Rt△ACD，Rt△AEF中分别有∠1＋∠3＝90°，∠2＋∠4＝90°．∵ M是BC的中点，∴∠COM＝∠BOM．∴∠1＝∠2，∴∠3＝∠4．∵∠4＝∠5，∴∠3＝∠5．∴ CF＝CD．过点F作FP∥GB交于AB于点P，则∠FPE＝∠6．在Rt△AEC，Rt△ACB中分别有∠CAE＋∠ACE＝90°，∠CAE＋∠6＝90°．∴∠ACE＝∠6＝∠FPE．又∵∠1＝∠2，AF＝AF，∴△ACF≌△APF．∴ CF＝FP．∵ FP∥GB，FG∥AB，∴四边形FPBG是平行四边形．∴ FP＝GB．∴ CD＝GB．∵ CD⊥AC，∴点D到直线AC的距离为线段CD的长∴⊙D与直线AC相切.。

人教备战中考数学压轴题专题圆的综合的经典综合题含答案

一、圆的综合真题与模拟题分类汇编（难题易错题）1．如图，在平面直角坐标系xoy中，E（8,0），F(0 , 6)．（1）当G(4，8)时，则∠FGE= °（2）在图中的网格区域内找一点P，使∠FPE=90°且四边形OEPF被过P点的一条直线分割成两部分后，可以拼成一个正方形．要求：写出点P点坐标，画出过P点的分割线并指出分割线（不必说明理由，不写画法）．【答案】（1）90；（2）作图见解析，P（7，7），PH是分割线．【解析】试题分析：（1）根据勾股定理求出△FEG的三边长，根据勾股定理逆定理可判定△FEG是直角三角形，且∠FGE="90" °．（2）一方面，由于∠FPE=90°，从而根据直径所对圆周角直角的性质，点P在以EF为直径的圆上；另一方面，由于四边形OEPF被过P点的一条直线分割成两部分后，可以拼成一个正方形，从而OP是正方形的对角线，即点P在∠FOE的角平分线上，因此可得P（7，7），PH是分割线．试题解析：（1）连接FE，∵E（8,0），F(0 , 6)，G(4，8)，∴根据勾股定理，得FG=，EG=，FE=10．∵，即．∴△FEG是直角三角形，且∠FGE=90 °．（2）作图如下：P（7，7），PH是分割线．考点：1．网格问题；2．勾股定理和逆定理；3．作图（设计）；4．圆周角定理．2．如图，AB是⊙O的直径，PA是⊙O的切线，点C在⊙O上，CB∥PO．（1）判断PC与⊙O的位置关系，并说明理由；（2）若AB=6，CB=4，求PC的长．【答案】（1）PC是⊙O的切线，理由见解析；（235 2【解析】试题分析：（1）要证PC是⊙O的切线，只要连接OC，再证∠PCO=90°即可．（2）可以连接AC，根据已知先证明△ACB∽△PCO，再根据勾股定理和相似三角形的性质求出PC的长．试题解析：（1）结论：PC是⊙O的切线．证明：连接OC∵CB∥PO∴∠POA=∠B，∠POC=∠OCB∵OC=OB∴∠OCB=∠B∴∠POA=∠POC又∵OA=OC，OP=OP∴△APO≌△CPO∴∠OAP=∠OCP∵PA是⊙O的切线∴∠OAP=90°∴∠OCP=90°∴PC是⊙O的切线．（2）连接AC∵AB是⊙O的直径∴∠ACB=90°（6分）由（1）知∠PCO=90°，∠B=∠OCB=∠POC∵∠ACB=∠PCO∴△ACB∽△PCO∴∴．点睛：本题考查了切线的判定．要证某线是圆的切线，已知此线过圆上某点，连接圆心与这点（即为半径），再证垂直即可．同时考查了勾股定理和相似三角形的性质．3．如图，AB是圆O的直径，射线AM⊥AB，点D在AM上，连接OD交圆O于点E，过点D作DC=DA交圆O于点C（A、C不重合），连接O C、BC、CE．（1）求证：CD是⊙O的切线；（2）若圆O的直径等于2，填空：①当AD=时，四边形OADC是正方形；②当AD=时，四边形OECB是菱形．【答案】(1)见解析；（2）①1；②3．【解析】试题分析：（1）依据SSS证明△OAD≌△OCD，从而得到∠OCD=∠OAD=90°；（2）①依据正方形的四条边都相等可知AD=OA；②依据菱形的性质得到OE=CE，则△EOC为等边三角形，则∠CEO=60°，依据平行线的性质可知∠DOA=60°，利用特殊锐角三角函数可求得AD的长．试题解析：解：∵AM⊥AB，∴∠OAD=90°．∵OA=OC，OD=OD，AD=DC，∴△OAD≌△OCD，∴∠OCD=∠OAD=90°．∴OC⊥CD，∴CD是⊙O的切线．（2）①∵当四边形OADC是正方形，∴AO=AD=1．故答案为：1．②∵四边形OECB是菱形，∴OE=CE．又∵OC=OE，∴OC=OE=CE．∴∠CEO=60°．∵CE∥AB，∴∠AOD=60°．在Rt△OAD中，∠AOD=60°，AO=1，∴AD=．故答案为：．点睛：本题主要考查的是切线的性质和判定、全等三角形的性质和判定、菱形的性质、等边三角形的性质和判定，特殊锐角三角函数值的应用，熟练掌握相关知识是解题的关键．4．如图，在直角坐标系中，⊙M经过原点O(0，0)，点A(6，0)与点B(0，－2)，点D 在劣弧OA上，连结BD交x轴于点C，且∠COD＝∠CBO.(1)求⊙M的半径；(2)求证：BD平分∠ABO；(3)在线段BD的延长线上找一点E，使得直线AE恰为⊙M的切线，求此时点E的坐标．【答案】（1）M的半径r2；（2）证明见解析；（3）点E的坐标为(2632)．【解析】试题分析：根据点A和点B的坐标得出OA和OB的长度，根据Rt△AOB的勾股定理得出AB的长度，然后得出半径；根据同弧所对的圆周角得出∠ABD=∠COD，然后结合已知条件得出角平分线；根据角平分线得出△ABE≌△HBE，从而得出2，从而求出OH 的长度，即点E的纵坐标，根据Rt△AOB的三角函数得出∠ABO的度数，从而得出∠CBO 的度数，然后根据Rt△HBE得出HE的长度，即点E的横坐标.试题解析：（1）∵点A6，0），点B为（02）∴62∴根据Rt△AOB的勾股定理可得：2∴M的半径r=122.（2）根据同弧所对的圆周角相等可得：∠ABD=∠COD ∵∠COD=∠CBO ∴∠ABD=∠CBO ∴BD 平分∠ABO（3）如图，由（2）中的角平分线可得△ABE ≌△HBE ∴BH=BA=22∴OH=22－2=2在Rt △AOB 中，3OA OB=∴∠ABO=60° ∴∠CBO=30° 在Rt △HBE 中，HE=263=∴点E 的坐标为（26，2）考点：勾股定理、角平分线的性质、圆的基本性质、三角函数.5．如图，已知AB 是⊙O 的直径，P 是BA 延长线上一点，PC 切⊙O 于点C ，CD ⊥AB ，垂足为D ．（1）求证：∠PCA ＝∠ABC ；（2）过点A 作AE ∥PC 交⊙O 于点E ，交CD 于点F ，交BC 于点M ，若∠CAB ＝2∠B ，CF 3【答案】（1）详见解析；（2633π-. 【解析】【分析】（1）如图，连接OC ，利用圆的切线的性质和直径对应的圆周角是直角可得∠PCA=∠OCB ，利用等量代换可得∠PCA=∠ABC.（2）先求出△OCA 是等边三角形，在利用三角形的等边对等角定理求出FA=FC 和CF=FM,然后分别求出AM 、AC 、MO 、CD 的值，分别求出0A E S ∆、BOE S 扇形、ABM S ∆ 的值，利用0A E ABM BOE S S S S ∆∆=+-阴影部分扇形，然后通过计算即可解答.【详解】解：（1）证明：连接OC，如图，∵PC切⊙O于点C，∴OC⊥PC,∴∠PCA+∠ACO=90º,∵AB是⊙O的直径，∴∠ACB=∠ACO+OCB=90º∴∠PCA=∠OCB,∵OC=OB,∴∠OBC=∠OCB,∴∠PCA=∠ABC；（2）连接OE，如图，∵△ACB中，∠ACB＝90º,∠CAB＝2∠B,∴∠B＝30º,∠CAB＝60º,∴△OCA是等边三角形，∵CD⊥AB,∴∠ACD+∠CAD＝∠CAD＋∠ABC＝90º,∴∠ACD＝∠B＝30º,∵PC∥AE,∴∠PCA＝∠CAE＝30º,∴FC=FA,同理，CF＝FM,∴AM＝2CF=23,Rt△ACM中，易得AC=23×3=3＝OC,∵∠B＝∠CAE＝30º,∴∠AOC=∠COE=60º,∴∠EOB=60º,∴∠EAB=∠ABC=30º,∴MA=MB,连接OM,EG⊥AB交AB于G点，如图所示，∵OA=OB,∴MO⊥AB,∴MO＝3∵△CDO≌△EDO(AAS)，∴332∴1332ABM S AB MO ∆=⨯=, 同样，易求934AOE S ∆=， 260333602BOE S ππ⨯==扇形 ∴0A E ABM BOE S S S S ∆∆=+-阴影部分扇形=93363333424ππ-+-=. 【点睛】本题考查了切线的性质、解直角三角形、扇形面积和识图的能力，综合性较强，有一定难度，熟练掌握定理并准确识图是解题的关键.6．如图，在Rt △ABC 中，点O 在斜边AB 上，以O 为圆心，OB 为半径作圆，分别与BC ，AB 相交于点D ，E ，连接AD ．已知∠CAD ＝∠B ．（1）求证：AD 是⊙O 的切线；（2）若CD ＝2，AC ＝4，BD ＝6，求⊙O 的半径．【答案】（1）详见解析；（2）35. 【解析】【分析】 (1)解答时先根据角的大小关系得到∠1＝∠3，根据直角三角形中角的大小关系得出OD ⊥AD ，从而证明AD 为圆O 的切线；(2)根据直角三角形勾股定理和两三角形相似可以得出结果【详解】（1）证明：连接OD ，∵OB ＝OD ，∴∠3＝∠B ，∵∠B ＝∠1，∴∠1＝∠3，在Rt△ACD中，∠1+∠2＝90°，∴∠4＝180°﹣（∠2+∠3）＝90°，∴OD⊥AD，则AD为圆O的切线；（2）过点O作OF⊥BC，垂足为F，∵OF⊥BD∴DF＝BF＝12BD＝3∵AC＝4，CD＝2，∠ACD＝90°∴AD＝22AC CD＝25∵∠CAD＝∠B，∠OFB＝∠ACD＝90°∴△BFO∽△ACD∴BFAC = OB AD即34=25∴OB＝352∴⊙O的半径为352．【点睛】此题重点考查学生对直线与圆的位置关系，圆的半径的求解，掌握勾股定理，两三角形相似的判定条件是解题的关键7．（问题情境）如图1，点E是平行四边形ABCD的边AD上一点，连接BE、CE．求证：BCE 1S2=S平行四边形ABCD．（说明：S表示面积）请以“问题情境”为基础，继续下面的探究（探究应用1）如图2，以平行四边形ABCD的边AD为直径作⊙O，⊙O与BC边相切于点H，与BD相交于点M．若AD＝6，BD＝y，AM＝x，试求y与x之间的函数关系式．（探究应用2）如图3，在图1的基础上，点F在CD上，连接AF、BF，AF与CE相交于点G，若AF＝CE，求证：BG平分∠AGC．（迁移拓展）如图4，平行四边形ABCD中，AB：BC＝4：3，∠ABC＝120°，E是AB的中点，F在BC上，且BF：FC＝2：1，过D分别作DG⊥AF于G，DH⊥CE于H，请直接写出DG：DH的值．【答案】【问题情境】见解析；【探究应用1】18yx=；【探究应用2】见解析；【迁移【解析】【分析】（1）作EF⊥BC于F，则S△BCE＝12BC×EF，S平行四边形ABCD＝BC×EF，即可得出结论；（2）连接OH，由切线的性质得出OH⊥BC，OH＝12AD＝3，求出平行四边形ABCD的面积＝AD×OH＝18，由圆周角定理得出AM⊥BD，得出△ABD的面积＝12BD×AM＝12平行四边形的面积＝9，即可得出结果；（3）作BM⊥AF于M，BN⊥CE于N，同图1得：△ABF的面积＝△BCE的面积＝12平行四边形ABCD的面积，得出12AF×BM＝12CE×BN，证出BM＝BN，即可得出BG平分∠AGC．（4）作AP⊥BC于P，EQ⊥BC于Q，由平行四边形的性质得出∠ABP＝60°，得出∠BAP＝30°，设AB＝4x，则BC＝3x，由直角三角形的性质得出BP＝12AB＝2x，BQ＝12BE，AP＝BP＝，由已知得出BE＝2x，BF＝2x，得出BQ＝x，EQ x，PF＝4x，QF＝3x，QC＝4x，由勾股定理求出AF＝x，CE，连接DF、DE，由三角形的面积关系得出AF×DG＝CE×DH，即可得出结果．【详解】（1）证明：作EF⊥BC于F，如图1所示：则S△BCE＝12BC×EF，S平行四边形ABCD＝BC×EF，∴12BCE ABCD S S =．（2）解：连接OH ，如图2所示：∵⊙O 与BC 边相切于点H ， ∴OH ⊥BC ，OH ＝12AD ＝3， ∴平行四边形ABCD 的面积＝AD×OH ＝6×3＝18，∵AD 是⊙O 的直径，∴∠AMD ＝90°，∴AM ⊥BD ，∴△ABD 的面积＝12BD×AM ＝12平行四边形的面积＝9，即12xy ＝9， ∴y 与x 之间的函数关系式y ＝18x ；（3）证明：作BM ⊥AF 于M ，BN ⊥CE 于N ，如图3所示：同图1得：△ABF 的面积＝△BCE 的面积＝12平行四边形ABCD 的面积， ∴12AF×BM ＝12CE×BN ， ∵AF ＝CE ，∴BM ＝BN ，∴BG 平分∠AGC ．（4）解：作AP ⊥BC 于P ，EQ ⊥BC 于Q ，如图4所示：∵平行四边形ABCD 中，AB ：BC ＝4：3，∠ABC ＝120°，∴∠ABP ＝60°，∴∠BAP ＝30°，设AB ＝4x ，则BC ＝3x ，∴BP ＝12AB ＝2x ，BQ ＝12BE ，AP BP ＝， ∵E 是AB 的中点，F 在BC 上，且BF ：FC ＝2：1，∴BE ＝2x ，BF ＝2x ，∴BQ ＝x ， ∴EQ，PF ＝4x ，QF ＝3x ，QC ＝4x ，由勾股定理得：AF ＝x ，CE ，连接DF 、DE ，则△CDE 的面积＝△ADF 的面积＝12平行四边形ABCD 的面积，∴AF×DG ＝CE×DH ，∴DG ：DH ＝CE ：AF ＝19x :27x 19:27=．【点睛】本题是圆的综合题目，考查了圆周角定理、平行四边形的性质、三角形面积公式、含30°角的直角三角形的性质、勾股定理、角平分线的判定等知识；本题综合性强，需要添加辅助线，熟练掌握平行四边形的性质和勾股定理是解题的关键．8．对于平面直角坐标系xoy 中的图形P ，Q ，给出如下定义：M 为图形P 上任意一点，N 为图形Q 上任意一点，如果M ，N 两点间的距离有最小值，那么称这个最小值为图形P ，Q 间的“非常距离”，记作d （P ,Q ）．已知点A （4,0），B （0,4），连接AB ．（1）d （点O ，AB ）= ；（2）⊙O 半径为r ，若d （⊙O ，AB ）=0，求r 的取值范围；（3）点C （－3，－2），连接AC ，BC ，⊙T 的圆心为T （t ，0），半径为2，d （⊙T ，△ABC ），且0<d <2，求t 的取值范围．【答案】（1）222）224r ≤≤；（3）25252t -<<-或6<r <8．【解析】【分析】（1）如下图所示，由题意得：过点O 作AB 的垂线，则垂线段即为所求；（2）如下图所示，当d （⊙O ，AB ）=0时，过点O 作OE ⊥AB ，交AB 于点E ，则：OB=2， OE=22，即可求解；（3）分⊙T 在△ABC 左侧、⊙T 在△ABC 右侧两种情况，求解即可．【详解】（1）过点O 作OD ⊥AB 交AB 于点D ，根据“非常距离”的定义可知，d （点O ，AB ）=OD=2AB =22442+=22; （2）如图，当d （⊙O ，AB ）=0时，过点O 作OE ⊥AB,则OE=22,OB=OA=4，∵⊙O 与线段AB 的“非常距离”为0，∴224r ≤≤；（3）当⊙T 在△ABC 左侧时，如图，当⊙T 与BC 相切时，d=0,BC=2236+=35,过点C 作CE ⊥y 轴，过点T 作TF ⊥BC,则△TFH ∽△BEC,∴TF TH BE BC=, 即2=635TH , ∴TH=5,∵HO ∥CE,∴△BHO ∽△BEC,∴HO=2，此时T(-5-2，0);当d=2时，如图，同理可得，此时T （252--）；∵0<d <2，∴25252t --<<--；当⊙T 在△ABC 右侧时，如图，当p=0时，t=6，当p=2时，t=8.∵0<d <2，∴6<r <8；综上，25252t --<<--或6<r <8．【点睛】本题主要考查圆的综合问题，解题的关键是理解并掌握“非常距离”的定义与直线与圆的位置关系和分类讨论思想的运用．9．如图，AB 是半圆⊙O 的直径，点C 是半圆⊙O 上的点，连接AC ，BC ，点E 是AC 的中点，点F 是射线OE 上一点．（1）如图1，连接FA ，FC ，若∠AFC ＝2∠BAC ，求证：FA ⊥AB ；（2）如图2，过点C 作CD ⊥AB 于点D ，点G 是线段CD 上一点（不与点C 重合），连接FA ，FG ，FG 与AC 相交于点P ，且AF ＝FG ．①试猜想∠AFG 和∠B 的数量关系，并证明；②连接OG ，若OE ＝BD ，∠GOE ＝90°，⊙O 的半径为2，求EP 的长．【答案】（1）见解析；（2）①结论：∠GFA ＝2∠ABC ．理由见解析；②PE 3．【解析】【分析】（1）证明∠OFA ＝∠BAC ，由∠EAO +∠EOA ＝90°，推出∠OFA +∠AOE ＝90°，推出∠FAO ＝90°即可解决问题．（2）①结论：∠GFA ＝2∠ABC ．连接FC ．由FC ＝FG ＝FA ，以F 为圆心FC 为半径作⊙F ．因为AG AG =，推出∠GFA ＝2∠ACG ，再证明∠ACG ＝∠ABC ．②图2﹣1中，连接AG ，作FH ⊥AG 于H ．想办法证明∠GFA ＝120°，求出EF ，OF ，OG 即可解决问题．【详解】（1）证明：连接OC ．∵OA＝OC，EC＝EA，∴OF⊥AC，∴FC＝FA，∴∠OFA＝∠OFC，∵∠CFA＝2∠BAC，∴∠OFA＝∠BAC，∵∠OEA＝90°，∴∠EAO+∠EOA＝90°，∴∠OFA+∠AOE＝90°，∴∠FAO＝90°，∴AF⊥AB．（2）①解：结论：∠GFA＝2∠ABC．理由：连接FC．∵OF垂直平分线段AC，∴FG＝FA，∵FG＝FA，∴FC＝FG＝FA，以F为圆心FC为半径作⊙F．∵AG AG，∴∠GFA＝2∠ACG，∵AB是⊙O的直径，∴∠ACB＝90°，∵CD⊥AB，∴∠ABC+∠BCA＝90°，∵∠BCD+∠ACD＝90°，∴∠ABC＝∠ACG，∴∠GFA＝2∠ABC．②如图2﹣1中，连接AG，作FH⊥AG于H．∵BD ＝OE ，∠CDB ＝∠AEO ＝90°，∠B ＝∠AOE ，∴△CDB ≌△AEO （AAS ），∴CD ＝AE ，∵EC ＝EA ，∴AC ＝2CD ．∴∠BAC ＝30°，∠ABC ＝60°，∴∠GFA ＝120°，∵OA ＝OB ＝2，∴OE ＝1，AE ＝，BA ＝4，BD ＝OD ＝1， ∵∠GOE ＝∠AEO ＝90°，∴OG ∥AC ， 323DG OG ∴==, 222213AG DG AD ∴=+=， ∵FG ＝FA ，FH ⊥AG ，∴AH ＝HG 21∠AFH ＝60°， ∴AF ＝27sin 603AH ︒=，在Rt △AEF 中，EF 2213AF AE -=， ∴OF ＝OE +EF ＝43 ， ∵PE ∥OG ， ∴PE EF OG 0F=， ∴134233=， ∴PE 3．【点睛】圆综合题，考查了垂径定理，勾股定理，圆周角定理，全等三角形的判定和性质，锐角三角函数，解直角三角形等知识，解题的关键是学会添加常用辅助线，构造直角三角形解决问题.10．如图，已知在△ABC中，AB=15，AC=20，tanA=12，点P在AB边上，⊙P的半径为定长.当点P与点B重合时，⊙P恰好与AC边相切；当点P与点B不重合时，⊙P与AC边相交于点M和点N．（1）求⊙P的半径；（2）当AP=65时，试探究△APM与△PCN是否相似，并说明理由．【答案】（1）半径为35；（2）相似，理由见解析.【解析】【分析】（1）如图，作BD⊥AC，垂足为点D，⊙P与边AC相切，则BD就是⊙P的半径，利用解直角三角形得出BD与AD的关系，再利用勾股定理可求得BD的长；（2）如图，过点P作PH⊥AC于点H，作BD⊥AC，垂足为点D，根据垂径定理得出MN=2MH，PM=PN，再利用勾股定理求出PH、AH、MH、MN的长，从而求出AM、NC的长，然后求出AMMP、PNNC的值，得出AMMP=PNNC，利用两边对应成比例且夹角相等的两三角形相似即可证明.【详解】（1）如图，作BD⊥AC，垂足为点D，∵⊙P与边AC相切，∴BD就是⊙P的半径，在Rt△ABD中，tanA= 1BD2AD ，设BD=x，则AD=2x，∴x2+(2x)2=152，解得：5∴半径为35；（2）相似，理由见解析，如图，过点P 作PH ⊥AC 于点H ，作BD ⊥AC ，垂足为点D ，∴PH 垂直平分MN ，∴PM=PN ，在Rt △AHP 中，tanA=12PH AH =，设PH=y ，AH=2y ，y 2+（2y ）2=（65）2解得：y=6（取正数），∴PH=6，AH=12，在Rt △MPH 中，MH=()22356-=3，∴MN=2MH=6，∴AM=AH-MH=12-3=9，NC=AC-MN-AM=20-6-9=5，∴3535AM MP ==，35PN NC =， ∴AM MP =PN NC，又∵PM=PN ，∴∠PMN=∠PNM ，∴∠AMP=∠PNC ，∴△AMP ∽△PNC.【点睛】本题考查了解直角三角形、垂径定理、相似三角形的判定与性质等，综合性较强，有一定的难度，正确添加辅助线、灵活应用相关的性质与定理是解题的关键.。

人教中考数学压轴题专题复习——圆的综合的综合及详细答案

人教全国中考数学圆的综合的综合中考真题分类汇总附答案

一、圆的综合真题与模拟题分类汇编（难题易错题）1．（1）如图1，在矩形ABCD 中，点O 在边AB 上，∠AOC =∠BOD ，求证：AO =OB ；（2）如图2，AB 是⊙O 的直径，PA 与⊙O 相切于点A ，OP 与⊙O 相交于点C ，连接CB ，∠OPA =40°，求∠ABC 的度数．【答案】（1）证明见解析；（2）25°.【解析】试题分析：（1）根据等量代换可求得∠AOD=∠BOC ，根据矩形的对边相等，每个角都是直角，可知∠A=∠B=90°，AD=BC ，根据三角形全等的判定AAS 证得△AOD ≌△BOC ，从而得证结论．（2）利用切线的性质和直角三角形的两个锐角互余的性质得到圆心角∠POA 的度数，然后利用圆周角定理来求∠ABC 的度数．试题解析：（1）∵∠AOC=∠BOD∴∠AOC -∠COD=∠BOD-∠COD即∠AOD=∠BOC∵四边形ABCD 是矩形∴∠A=∠B=90°，AD=BC∴AOD BOC ∆≅∆∴AO=OB（2）解：∵AB 是O 的直径，PA 与O 相切于点A ， ∴PA ⊥AB ，∴∠A=90°.又∵∠OPA=40°，∴∠AOP=50°，∵OB=OC ，∴∠B=∠OCB.又∵∠AOP=∠B+∠OCB ， ∴1252B OCB AOP ∠=∠=∠=︒.2．如图1，将长为10的线段OA 绕点O 旋转90°得到OB ，点A 的运动轨迹为AB ，P 是半径OB 上一动点，Q 是AB 上的一动点，连接PQ.发现：∠POQ ＝________时，PQ 有最大值，最大值为________；思考：（1）如图2，若P是OB中点，且QP⊥OB于点P，求BQ的长；（2）如图3，将扇形AOB沿折痕AP折叠，使点B的对应点B′恰好落在OA的延长线上，求阴影部分面积；探究：如图4，将扇形OAB沿PQ折叠，使折叠后的弧QB′恰好与半径OA相切，切点为C，若OP＝6，求点O到折痕PQ的距离．【答案】发现： 90°，102；思考：（1）103π=；（2）25π−1002+100；（3）点O到折痕PQ的距离为30.【解析】分析：发现：先判断出当PQ取最大时，点Q与点A重合，点P与点B重合，即可得出结论；思考：（1）先判断出∠POQ=60°，最后用弧长用弧长公式即可得出结论；（2）先在Rt△B'OP中，OP2+(102−10)2=（10-OP）2，解得OP=102−10，最后用面积的和差即可得出结论．探究：先找点O关于PQ的对称点O′，连接OO′、O′B、O′C、O′P，证明四边形OCO′B是矩形，由勾股定理求O′B，从而求出OO′的长，则OM=12OO′=30．详解：发现：∵P是半径OB上一动点，Q是AB上的一动点，∴当PQ取最大时，点Q与点A重合，点P与点B重合，此时，∠POQ=90°，PQ=22OA OB+=102；思考：（1）如图，连接OQ，∵点P是OB的中点，∴OP=12OB=12OQ．∵QP⊥OB，∴∠OPQ=90°在Rt△OPQ中，cos∠QOP=12 OPOQ=，∴∠QOP=60°，∴l BQ =6010101803ππ⨯=；（2）由折叠的性质可得，BP ＝B ′P ，AB ′＝AB ＝102，在Rt △B'OP 中，OP 2+(102−10)2=（10-OP ）2解得OP=102−10，S 阴影=S 扇形AOB -2S △AOP =290101210(10210)3602π⨯-⨯⨯⨯- ＝25π−1002+100；探究：如图2，找点O 关于PQ 的对称点O′，连接OO′、O′B 、O′C 、O′P ，则OM=O′M ，OO′⊥PQ ，O′P=OP=3，点O′是B Q '所在圆的圆心，∴O′C=OB=10，∵折叠后的弧QB′恰好与半径OA 相切于C 点，∴O′C ⊥AO ， ∴O′C ∥OB ，∴四边形OCO′B 是矩形，在Rt △O′BP 中，226425-=在Rt △OBO′K ，2210(25)=230-，∴OM=12OO′=12×23030 即O 到折痕PQ 30点睛：本题考查了折叠问题和圆的切线的性质、矩形的性质和判定，熟练掌握弧长公式l=180n R π（n 为圆心角度数，R 为圆半径），明确过圆的切线垂直于过切点的半径，这是常考的性质；对称点的连线被对称轴垂直平分．3．如图1，以边长为4的正方形纸片ABCD 的边AB 为直径作⊙O ，交对角线AC 于点E ．（1）图1中，线段AE= ；（2）如图2，在图1的基础上，以点A 为端点作∠DAM=30°，交CD 于点M ，沿AM 将四边形ABCM 剪掉，使Rt △ADM 绕点A 逆时针旋转（如图3），设旋转角为α（0°＜α＜150°），在旋转过程中AD 与⊙O 交于点F ．①当α=30°时，请求出线段AF的长；②当α=60°时，求出线段AF的长；判断此时DM与⊙O的位置关系，并说明理由；③当α=°时，DM与⊙O相切．【答案】（1）2（2）①2②2，相离③当α=90°时，DM与⊙O相切【解析】（1）连接BE，∵AC是正方形ABCD的对角线，∴∠BAC=45°，∴△AEB是等腰直角三角形，又∵AB=8，∴AE=4；（2）①连接OA、OF，由题意得，∠NAD=30°，∠DAM=30°，故可得∠OAM=30°，∠DAM=30°，则∠OAF=60°，又∵OA=OF，∴△OAF是等边三角形，∵OA=4，∴AF=OA=4；②连接B'F，此时∠NAD=60°，∵AB'=8，∠DAM=30°，∴AF=AB'cos∠DAM=8×=4；此时DM与⊙O的位置关系是相离；③∵AD=8，直径的长度相等，∴当DM与⊙O相切时，点D在⊙O上，故此时可得α=∠NAD=90°．点睛：此题属于圆的综合题，主要是仔细观察每一次旋转后的图形，根据含30°角的直角三角形进行计算，另外在解答最后一问时，关键是判断出点D的位置，有一定难度．4．如图1，在Rt△ABC中，AC=8cm，BC=6cm，D、E分别为边AB、BC的中点，连结DE，点P从点A出发，沿折线AD﹣DE运动，到点E停止，点P在AD上以5cm/s的速度运动，在DE上以1cm/s的速度运动，过点P作PQ⊥AC于点Q，以PQ为边作正方形PQMN．设点P的运动时间为t（s）．（1）当点P在线段DE上运动时，线段DP的长为_____cm．（用含t的代数式表示）（2）当正方形PQMN与△ABC重叠部分图形为五边形时，设五边形的面积为S（cm2），求S与t的函数关系式，并写出t的取值范围．（3）如图2，若点O在线段BC上，且CO=1，以点O为圆心，1cm长为半径作圆，当点P 开始运动时，⊙O的半径以0.2cm/s的速度开始不断增大，当⊙O与正方形PQMN的边所在直线相切时，求此时的t值．【答案】（1）t﹣1；（2）S=﹣38t2+3t+3（1＜t＜4）；（3）t=103s．【解析】分析：（1）根据勾股定理求出AB ，根据D 为AB 中点，求出AD ，根据点P 在AD 上的速度，即可求出点P 在AD 段的运动时间，再求出点P 在DP 段的运动时间，最后根据DE 段运动速度为1c m/s ，即可求出DP ；（2）由正方形PQMN 与△ABC 重叠部分图形为五边形，可知点P 在DE 上，求出DP =t ﹣1，PQ =3，根据MN ∥BC ，求出FN 的长，从而得到FM 的长，再根据S =S 梯形FMHD +S 矩形DHQP ，列出S 与t 的函数关系式即可；（3）当圆与边PQ 相切时，可求得r =PE =5﹣t ，然后由r 以0.2c m/s 的速度不断增大，r =1+0.2t ，然后列方程求解即可；当圆与MN 相切时，r =CM =8﹣t =1+0.2t ，从而可求得t 的值．详解：（1）由勾股定理可知：AB =22AC BC +=10． ∵D 、E 分别为AB 和BC 的中点，∴DE =12AC =4，AD =12AB =5， ∴点P 在AD 上的运动时间=55=1s ，当点P 在线段DE 上运动时，DP 段的运动时间为（t ﹣1）s ． ∵DE 段运动速度为1c m/s ，∴DP =（t ﹣1）cm ．故答案为t ﹣1．（2）当正方形PQMN 与△ABC 重叠部分图形为五边形时，有一种情况，如下图所示．当正方形的边长大于DP 时，重叠部分为五边形，∴3＞t ﹣1，t ＜4，DP ＞0，∴t ﹣1＞0，解得：t ＞1，∴1＜t ＜4．∵△DFN ∽△ABC ，∴DN FN =AC BC =86=43． ∵DN =PN ﹣PD ，∴DN =3﹣（t ﹣1）=4﹣t ， ∴4t FN -=43，∴FN =344t -（）， ∴FM =3﹣344t -（）=34t ， S =S 梯形FMHD +S 矩形DHQP ，∴S=12×（34t+3）×（4﹣t）+3（t﹣1）=﹣38t2+3t+3（1＜t＜4）．（3）①当圆与边PQ相切时，如图：当圆与PQ相切时，r=PE，由（1）可知，PD=（t﹣1）cm，∴PE=DE﹣DP=4﹣（t﹣1）=（5﹣t）cm．∵r以0.2c m/s的速度不断增大，∴r=1+0.2t，∴1+0.2t=5﹣t，解得：t=103s．②当圆与MN相切时，r=CM．由（1）可知，DP=（t﹣1）cm，则PE=CQ=（5﹣t）cm，MQ=3cm，∴MC=MQ+CQ=5﹣t+3=（8﹣t）cm，∴1+0.2t=8﹣t，解得：t=356s．∵P到E点停止，∴t﹣1≤4，即t≤5，∴t=356s（舍）．综上所述：当t=103s时，⊙O与正方形PQMN的边所在直线相切．点睛：本题主要考查的是圆的综合应用，解答本题主要应用了勾股定理、相似三角形的性质和判定、正方形的性质，直线和圆的位置关系，依据题意列出方程是解题的关键．5．如图，正三角形ABC内接于⊙O，P是BC上的一点，且PB＜PC，PA交BC于E，点F 是PC延长线上的点，CF=PB，13PA=4．（1）求证：△ABP≌△ACF；（2）求证：AC 2=PA•AE ；（3）求PB 和PC 的长．【答案】（1）证明见解析；（2）证明见解析；（3）PB=1，PC=3．【解析】试题分析：（1）先根据等边三角形的性质得到AB=AC ，再利用圆的内接四边形的性质得∠ACF=∠ABP ，于是可根据“SAS”判断△ABP ≌△ACF ；（2）先根据等边三角形的性质得到∠ABC=∠ACB=60°，再根据圆周角定理得∠APC=∠ABB=60°，加上∠CAE=∠PAC ，于是可判断△ACE ∽△APC ，然后利用相似比即可得到结论；（3）先利用AC 2=PA•AE 计算出AE=134 ，则PE=AP-AE=34，再证△APF 为等边三角形，得到PF=PA=4，则有PC+PB=4，接着证明△ABP ∽△CEP ，得到PB•PC=PE•A=3，然后根据根与系数的关系，可把PB 和PC 看作方程x 2-4x+3=0的两实数解，再解此方程即可得到PB 和PC 的长．试题解析：（1）∵∠ACP+∠ABP=180°，又∠ACP+∠ACF=180°，∴∠ABP=∠ACF在ABP ∆和ACF ∆中，∵AB=AC ，∠ABP=∠ACF ， CF PB =∴ABP ∆≌ACF ∆．(2)在AEC ∆和ACP ∆中，∵∠APC=∠ABC ，而ABC ∆是等边三角形，故∠ACB=∠ABC=60º，∴∠ACE =∠APC .又∠CAE =∠PAC ，∴AEC ∆∽ACP ∆ ∴AC AE AP AC=,即2AC PA AE =⋅. 由（1）知ABP ∆≌ACF ∆，∴∠BAP=∠CAF ， CF PB =∴∠BAP+∠PAC=∠CAF+∠PAC∴∠PAF=∠BAC=60°，又∠APC ＝∠ABC ＝60°.∴APF ∆是等边三角形∴AP=PF∴4PB PC PC CF PF PA +=+===在PAB ∆与CEP ∆中，∵∠BAP=∠ECP ，又∠APB=∠EPC=60°，∴PAB ∆∽CEP ∆ ∴PB PA PE PC=,即PB PC PA PE ⋅=⋅ 由（2）2AC PA AE =⋅， ∴()22AC PB PC PA AE PA PE PA AE PE PA +⋅=⋅+⋅=+= ∴()22AC PB PC PA AE PA PE PA AE PE PA +⋅=⋅+⋅=+=∴()2222224133PB PC PA AC PA AB ⋅=-=-=-=因此PB 和PC 的长是方程2430x x --=的解．解这个方程，得11x =， 23x =．∵PB<PB ，∴PB=11x =，PC=23x =，∴PB 和PC 的长分别是1和3。

中考数学圆的综合综合题含答案解析

一、圆的综合真题与模拟题分类汇编（难题易错题）1．如图1，已知扇形MON 的半径为2，∠MON=90°，点B 在弧MN 上移动，联结BM ，作OD ⊥BM ，垂足为点D ，C 为线段OD 上一点，且OC=BM ，联结BC 并延长交半径OM 于点A ，设OA=x ，∠COM 的正切值为y.（1）如图2，当AB ⊥OM 时，求证：AM=AC ；（2）求y 关于x 的函数关系式，并写出定义域；（3）当△OAC 为等腰三角形时，求x 的值.【答案】 (1)证明见解析;(2) 2=+y x 02<≤x 1422=x . 【解析】分析：（1）先判断出∠ABM =∠DOM ，进而判断出△OAC ≌△BAM ，即可得出结论；（2）先判断出BD =DM ，进而得出DM ME BD AE =，进而得出AE =122x （），再判断出2OA OC DM OE OD OD==，即可得出结论；（3）分三种情况利用勾股定理或判断出不存在，即可得出结论．详解：（1）∵OD ⊥BM ，AB ⊥OM ，∴∠ODM =∠BAM =90°．∵∠ABM +∠M =∠DOM +∠M ，∴∠ABM =∠DOM ．∵∠OAC =∠BAM ，OC =BM ，∴△OAC ≌△BAM ，∴AC =AM ．（2）如图2，过点D 作DE ∥AB ，交OM 于点E ．∵OB =OM ，OD ⊥BM ，∴BD =DM ．∵DE ∥AB ，∴DM ME BD AE =，∴AE =EM ．∵OM 2，∴AE =122x （）． ∵DE ∥AB ，∴2OA OC DM OE OD OD==， ∴22DM OA y OD OE x =∴=+，02x ≤＜（3）（i）当OA=OC时．∵111222DM BM OC x===．在Rt△ODM中，222124OD OM DM x=-=-．∵2121224xDMyOD xx=∴=+-，．解得1422x-=，或1422x--=（舍）．（ii）当AO=AC时，则∠AOC=∠ACO．∵∠ACO＞∠COB，∠COB=∠AOC，∴∠ACO＞∠AOC，∴此种情况不存在．（ⅲ）当CO=CA时，则∠COA=∠CAO=α．∵∠CAO＞∠M，∠M=90°﹣α，∴α＞90°﹣α，∴α＞45°，∴∠BOA=2α＞90°．∵∠BOA≤90°，∴此种情况不存在．即：当△OAC为等腰三角形时，x的值为1422-．点睛：本题是圆的综合题，主要考查了相似三角形的判定和性质，圆的有关性质，勾股定理，等腰三角形的性质，建立y关于x的函数关系式是解答本题的关键．2．四边形ABCD 的对角线交于点E，且AE＝EC，BE＝ED，以AD 为直径的半圆过点E，圆心为O．（1）如图①，求证：四边形ABCD 为菱形；（2）如图②，若BC 的延长线与半圆相切于点F，且直径AD＝6，求弧AE 的长．【答案】（1）见解析；（2）π2【解析】试题分析：（1）先判断出四边形ABCD是平行四边形，再判断出AC⊥BD即可得出结论；（2）先判断出AD=DC且DE⊥AC，∠ADE=∠CDE，进而得出∠CDA=30°，最后用弧长公式即可得出结论．试题解析：证明：（1）∵四边形ABCD的对角线交于点E，且AE=EC，BE=ED，∴四边形ABCD 是平行四边形．∵以AD 为直径的半圆过点E ，∴∠AED =90°，即有AC ⊥BD ，∴四边形ABCD 是菱形；（2）由（1）知，四边形ABCD 是菱形，∴△ADC 为等腰三角形，∴AD =DC 且DE ⊥AC ，∠ADE =∠CDE ．如图2，过点C 作CG ⊥AD ，垂足为G ，连接FO ．∵BF 切圆O 于点F ，∴OF ⊥AD ，且132OF AD ==，易知，四边形CGOF 为矩形，∴CG =OF =3．在Rt △CDG 中，CD =AD =6，sin ∠ADC =CG CD =12，∴∠CDA =30°，∴∠ADE =15°．连接OE ，则∠AOE =2×∠ADE =30°，∴3031802AE ππ⋅⨯==．点睛：本题主要考查菱形的判定即矩形的判定与性质、切线的性质，熟练掌握其判定与性质并结合题意加以灵活运用是解题的关键．3．等腰Rt △ABC 和⊙O 如图放置，已知AB=BC=1，∠ABC=90°，⊙O 的半径为1，圆心O 与直线AB 的距离为5．（1）若△ABC 以每秒2个单位的速度向右移动，⊙O 不动，则经过多少时间△ABC 的边与圆第一次相切？（2）若两个图形同时向右移动，△ABC 的速度为每秒2个单位，⊙O 的速度为每秒1个单位，则经过多少时间△ABC 的边与圆第一次相切？（3）若两个图形同时向右移动，△ABC 的速度为每秒2个单位，⊙O 的速度为每秒1个单位，同时△ABC 的边长AB 、BC 都以每秒0.5个单位沿BA 、BC 方向增大．△ABC 的边与圆第一次相切时，点B 运动了多少距离？【答案】（152-；（2） 52；（32042- 【解析】分析：（1）分析易得，第一次相切时，与斜边相切，假设此时，△ABC 移至△A′B′C′处，A′C′与⊙O 切于点E ，连OE 并延长，交B′C′于F ．由切线长定理易得CC′的长，进而由三角形运动的速度可得答案；（2）设运动的时间为t 秒，根据题意得：CC′=2t ，DD′=t ，则C′D′=CD+DD′-CC′=4+t -2t=4-t ，由第（1）的结论列式得出结果；（3）求出相切的时间，进而得出B 点移动的距离．详解：（1）假设第一次相切时，△ABC 移至△A′B′C′处，如图1，A′C′与⊙O 切于点E ，连接OE 并延长，交B′C′于F ，设⊙O 与直线l 切于点D ，连接OD ，则OE ⊥A′C′，OD ⊥直线l ，由切线长定理可知C′E=C′D ，设C′D=x ，则C′E=x ，∵△ABC 是等腰直角三角形，∴∠A=∠ACB=45°，∴∠A′C′B′=∠ACB=45°，∴△EFC′是等腰直角三角形，∴C′F=2x ，∠OFD=45°， ∴△OFD 也是等腰直角三角形，∴OD=DF ，∴2x+x=1，则x=2-1，∴CC′=BD -BC-C′D=5-1-（2-1）=5-2，∴点C 运动的时间为522-；则经过52-秒，△ABC 的边与圆第一次相切；（2）如图2，设经过t 秒△ABC 的边与圆第一次相切，△ABC 移至△A′B′C′处，⊙O 与BC 所在直线的切点D 移至D′处，A′C′与⊙O 切于点E ，连OE 并延长，交B′C′于F ，∵CC′=2t ，DD′=t ，∴C′D′=CD+DD′-CC′=4+t -2t=4-t ，由切线长定理得C′E=C′D′=4-t ，由（1）得：4-t=2-1，解得：t=5-2，答：经过5-2秒△ABC 的边与圆第一次相切；（3）由（2）得CC′=（2+0.5）t=2.5t ，DD′=t ，则C′D′=CD+DD′-CC′=4+t -2.5t=4-1.5t ，由切线长定理得C′E=C′D′=4-1.5t ，由（1）得：4-1.5t=2-1，解得：t=10223-， ∴点B 运动的距离为2×10223-=20423-．点睛：本题要求学生熟练掌握圆与直线的位置关系，并结合动点问题进行综合分析，比较复杂，难度较大，考查了学生数形结合的分析能力．4．如图，AB 是⊙O 的直径，弦BC ＝OB ，点D 是AC 上一动点，点E 是CD 中点，连接BD 分别交OC ，OE 于点F ，G ．（1）求∠DGE 的度数；（2）若CF OF ＝12，求BF GF的值；（3）记△CFB ，△DGO 的面积分别为S 1，S 2，若CF OF＝k ，求12S S 的值．（用含k 的式子表示）【答案】(1)∠DGE ＝60°；(2)72；(3)12S S =211k k k +++.【解析】【分析】（1）根据等边三角形的性质，同弧所对的圆心角和圆周角的关系，可以求得∠DGE 的度数；（2）过点F 作FH ⊥AB 于点H 设CF ＝1，则OF ＝2，OC ＝OB ＝3,根据勾股定理求出BF 的长度，再证得△FGO ∽△FCB ，进而求得BF GF的值；（3）根据题意，作出合适的辅助线，然后根据三角形相似、勾股定理可以用含k 的式子表示出12S S 的值．【详解】解：(1)∵BC ＝OB ＝OC ，∴∠COB ＝60°，∴∠CDB ＝12∠COB ＝30°， ∵OC ＝OD ，点E 为CD 中点，∴OE ⊥CD ，∴∠GED ＝90°，∴∠DGE ＝60°；(2)过点F 作FH ⊥AB 于点H设CF ＝1，则OF ＝2，OC ＝OB ＝3∵∠COB ＝60°∴OH ＝12OF ＝1， ∴HFHB ＝OB ﹣OH ＝2，在Rt △BHF 中，BF ==由OC ＝OB ，∠COB ＝60°得：∠OCB ＝60°，又∵∠OGB ＝∠DGE ＝60°，∴∠OGB ＝∠OCB ，∵∠OFG ＝∠CFB ，∴△FGO ∽△FCB ， ∴OF GF BF CF=， ∴， ∴BF GF =72. (3)过点F 作FH ⊥AB 于点H ，设OF ＝1，则CF ＝k ，OB ＝OC ＝k+1，∵∠COB ＝60°，∴OH ＝12OF=12， ∴HF＝330H =，HB ＝OB ﹣OH ＝k+12，在Rt △BHF 中， BF ＝222HB HF k k 1+=++，由(2)得：△FGO ∽△FCB ，∴GO OF CB BF=，即211GO k k k =+++， ∴GO 21k k =++，过点C 作CP ⊥BD 于点P∵∠CDB ＝30°∴PC ＝12CD ， ∵点E 是CD 中点，∴DE ＝12CD ， ∴PC ＝DE ，∵DE ⊥OE ， ∴12S S =BF GO =22111k k k k k +++++=211k k k +++【点睛】圆的综合题，解答本题的关键是明确题意，找出所求问题需要的条件，利用三角形相似和勾股定理、数形结合的思想解答．5．已知P 是O 的直径BA 延长线上的一个动点，∠P 的另一边交O 于点C 、D ，两点位于AB 的上方，AB ＝6，OP=m ，1sin 3P ＝，如图所示．另一个半径为6的1O 经过点C 、D ，圆心距1OO n ＝．（1）当m=6时，求线段CD 的长；（2）设圆心O 1在直线AB 上方，试用n 的代数式表示m ；（3）△POO 1在点P 的运动过程中，是否能成为以OO 1为腰的等腰三角形，如果能，试求出此时n 的值；如果不能，请说明理由．【答案】(1)CD=25;(2)m=23812n n- ;(3) n 的值为955或9155 【解析】分析：（1）过点O 作OH ⊥CD ，垂足为点H ，连接OC ．解Rt △POH ，得到OH 的长．由勾股定理得CH 的长，再由垂径定理即可得到结论；（2）解Rt △POH ，得到Rt 3m OH OCH ＝．在和Rt △1O CH 中，由勾股定理即可得到结论；（3）△1POO 成为等腰三角形可分以下几种情况讨论：① 当圆心1O 、O 在弦CD 异侧时，分1OP OO ＝和11O P OO ＝．②当圆心1O 、O 在弦CD 同侧时，同理可得结论．详解：（1）过点O 作OH ⊥CD ，垂足为点H ，连接OC ．在Rt △1sin 63POH P PO =中，＝，，∴2OH =．∵AB ＝6，∴3OC ＝．由勾股定理得： 5CH =∵OH ⊥DC ，∴225CD CH ==．（2）在Rt △1sin 3POH P PO m 中，＝，＝，∴3m OH ＝．在Rt △OCH 中，2293m CH ⎛⎫- ⎪⎝⎭＝．在Rt △1O CH 中，22363m CH n ⎛⎫-- ⎪⎝⎭＝．可得： 2236933m m n ⎛⎫⎛⎫--- ⎪ ⎪⎝⎭⎝⎭＝，解得23812n m n -：＝．（3）△1POO 成为等腰三角形可分以下几种情况：① 当圆心1O 、O 在弦CD 异侧时i ）1OP OO ＝，即m n ＝，由23812n n n -＝，解得9n ：＝．即圆心距等于O 、1O 的半径的和，就有O 、1O 外切不合题意舍去．ii ）11O P OO ＝ n ＝，解得：23m n ＝，即23n 23812n n-＝，解得n ： ②当圆心1O 、O 在弦CD 同侧时，同理可得： 28132n m n-＝．∵1POO ∠是钝角，∴只能是m n =，即28132n n n-＝，解得n ：综上所述：n 点睛：本题是圆的综合题．考查了圆的有关性质和两圆的位置关系以及解直径三角形．解答（3）的关键是要分类讨论．6．如图1，是用量角器一个角的操作示意图，量角器的读数从M 点开始（即M 点的读数为0），如图2，把这个量角器与一块30°（∠CAB ＝30°）角的三角板拼在一起，三角板的斜边AB 与量角器所在圆的直径MN 重合，现有射线C 绕点C 从CA 开始沿顺时针方向以每秒2°的速度旋转到与CB ，在旋转过程中，射线CP 与量角器的半圆弧交于E ．连接BE ．（1）当射线CP 经过AB 的中点时，点E 处的读数是，此时△BCE 的形状是；（2）设旋转x 秒后，点E 处的读数为y ，求y 与x 的函数关系式；（3）当CP 旋转多少秒时，△BCE 是等腰三角形？【答案】（1）60°，直角三角形；（2）y＝4x（0≤x≤45）；（3）7.5秒或30秒【解析】【分析】（1）根据圆周角定理即可解决问题；（2）如图2﹣2中，由题意∠ACE＝2x，∠AOE＝y，根据圆周角定理可知∠AOE＝2∠ACE，可得y＝2x（0≤x≤45）；（3）分两种情形分别讨论求解即可；【详解】解：（1）如图2﹣1中，∵∠ACB＝90°，OA＝OB，∴OA＝OB＝OC，∴∠OCA＝∠OAC＝30°，∴∠AOE＝60°，∴点E处的读数是60°，∵∠E＝∠BAC＝30°，OE＝OB，∴∠OBE＝∠E＝30°，∴∠EBC＝∠OBE+∠ABC＝90°，∴△EBC是直角三角形；故答案为60°，直角三角形；（2）如图2﹣2中，∵∠ACE＝2x，∠AOE＝y，∵∠AOE＝2∠ACE，∴y＝4x（0≤x≤45）．（3）①如图2﹣3中，当EB＝EC时，EO垂直平分线段BC，∵AC⊥BC，∵EO∥AC，∴∠AOE＝∠BAC＝30°，∠AOE＝15°，∴∠ECA＝12∴x＝7.5．②若2﹣4中，当BE＝BC时，易知∠BEC＝∠BAC＝∠BCE＝30°，∴∠OBE＝∠OBC＝60°，∵OE＝OB，∴△OBE是等边三角形，∴∠BOE＝60°，∴∠AOB＝120°，∴∠ACE＝12∠ACB＝60°，∴x＝30，综上所述，当CP旋转7.5秒或30秒时，△BCE是等腰三角形；【点睛】本题考查几何变换综合题、创新题目、圆周角定理、等腰三角形的判定和性质等知识，解题的关键是理解题意，学会用分类讨论的思想思考问题，属于中考压轴题．7．如图，线段BC所在的直线是以AB为直径的圆的切线，点D为圆上一点，满足BD＝BC，且点C、D位于直径AB的两侧，连接CD交圆于点E. 点F是BD上一点，连接EF，分别交AB、BD于点G、H，且EF＝BD.(1)求证：EF∥BC；(2)若EH＝4，HF＝2，求BE的长.【答案】(1)见解析；(2) 233【解析】【分析】（1）根据EF＝BD可得EF＝BD，进而得到BE DF，根据“在同圆或等圆中，同弧或等弧所对的圆周角相等”即可得出角相等进而可证.（2）连接DF，根据切线的性质及垂径定理求出GF、GE的长，根据“在同圆或等圆中，同弧或等弧所对的圆周角相等”及平行线求出相等的角，利用锐角三角函数求出∠BHG，进而求出∠BDE的度数，确定BE所对的圆心角的度数，根据∠DFH＝90°确定DE为直径，代入弧长公式即可求解.【详解】(1)∵EF＝BD，∴EF＝BD∴BE DF∴∠D＝∠DEF又BD＝BC，∴∠D＝∠C，∴∠DEF=∠CEF∥BC(2)∵AB是直径，BC为切线，∴AB⊥BC又EF∥BC，∴AB⊥EF，弧BF=弧BE,GF＝GE＝12(HF+EH)=3，HG=1DB平分∠EDF，又BF∥CD，∴∠FBD＝∠FDB＝∠BDE＝∠BFH ∴HB＝HF＝2∴cos∠BHG＝HGHB ＝12，∠BHG＝60°.∴∠FDB＝∠BDE＝30°∴∠DFH＝90°，DE为直径，DE＝3BE所对圆心角＝60°.∴弧BE＝163π＝233π【点睛】本题是圆的综合题，主要考查圆周角、切线、垂径定理、弧长公式等相关知识，掌握圆周角的有关定理，切线的性质，垂径定理及弧长公式是解题关键.8．如图，已知△ABC，23BC=，∠B=45°，点D在边BC上，联结AD，以点A 为圆心，AD为半径画圆，与边AC交于点E，点F在圆A上，且AF⊥AD．（1）设BD为x，点D、F之间的距离为y，求y关于x的函数解析式，并写出定义域；（2）如果E是DF的中点，求:BD CD的值；（3）联结CF，如果四边形ADCF是梯形，求BD的长．【答案】(1) 2442y x x (0≤x≤3); (2) 45; (3) BD 的长是1或1+5. 【解析】【分析】（1）过点A 作AH ⊥BC ，垂足为点H ．构造直角三角形，利用解直角三角形和勾股定理求得AD 的长度．联结DF ，点D 、F 之间的距离y 即为DF 的长度，在Rt △ADF 中，利用锐角三角形函数的定义求得DF 的长度，易得函数关系式．（2）由勾股定理求得：AC=22AH DH +．设DF 与AE 相交于点Q ，通过解Rt △DCQ 和Rt △AHC 推知12DQ CQ =．故设DQ=k ，CQ=2k ，AQ=DQ=k ，所以再次利用勾股定理推知DC 的长度，结合图形求得线段BD 的长度，易得答案．（3）如果四边形ADCF 是梯形，则需要分类讨论：①当AF ∥DC 、②当AD ∥FC ．根据相似三角形的判定与性质，结合图形解答．【详解】（1）过点A 作AH ⊥BC ，垂足为点H ．∵∠B =45°，AB 2∴·cos 1BH AH AB B ===．∵BD 为x ，∴1DH x =-．在Rt △ADH 中，90AHD ∠=︒，∴22222AD AH DH x x =+=-+．联结DF ，点D 、F 之间的距离y 即为DF 的长度．∵点F 在圆A 上，且AF ⊥AD ，∴AD AF =，45ADF ∠=︒．在Rt △ADF 中，90DAF ∠=︒，∴2442cos AD DF x x ADF==-+∠ ∴2442y x x =-+．()03x ≤≤ ;（2）∵E 是DF 的中点，∴AE DF ⊥，AE 平分DF ．∵BC=3，∴312HC =-=．∴225AC AH HC =+=．设DF 与AE 相交于点Q ，在Rt △DCQ 中，90DQC ∠=︒，tan DQ DCQ CQ ∠=．在Rt △AHC 中，90AHC ∠=︒，1tan 2AH ACH HC ∠==． ∵DCQ ACH ∠=∠，∴12DQ CQ =．设,2DQ k CQ k ==，AQ DQ k ==，∵35k =，5k =，∴2253DC DQ CQ =+=． ∵43BD BC DC =-=，∴4:5BD CD =．（3）如果四边形ADCF 是梯形则①当AF ∥DC 时，45AFD FDC ∠=∠=︒．∵45ADF ∠=︒，∴AD BC ⊥，即点D 与点H 重合． ∴1BD =．②当AD ∥FC 时，45ADF CFD ∠=∠=︒．∵45B ∠=︒，∴B CFD ∠=∠．∵B BAD ADF FDC ∠+∠=∠+∠，∴BAD FDC ∠=∠．∴ABD ∆∽DFC ∆．∴AB AD DF DC =． ∵2DF AD =，DC BC BD =-． ∴2AD BC BD =-．即()222-23x x x +=-,整理得 210x x --=，解得 15x ±=（负数舍去）．综上所述，如果四边形ADCF 是梯形，BD 的长是1或1+52．【点睛】此题属于圆的综合题，涉及了平行四边形的性质、相似三角形的判定与性质、三角函数值以及勾股定理等知识，综合性较强，解答本题需要我们熟练各部分的内容，对学生的综合能力要求较高，一定要注意将所学知识贯穿起来．9．如图，是大半圆的直径，是小半圆的直径，点是大半圆上一点，与小半圆交于点，过点作于点. （1）求证：是小半圆的切线；（2）若，点在上运动（点不与两点重合），设，. ①求与之间的函数关系式，并写出自变量的取值范围； ②当时，求两点之间的距离.【答案】（1）见解析；（2）①，，②两点之间的距离为或.【解析】【分析】（1）连接CO、CM，只需证到CD⊥CM．由于CD⊥OP，只需证到CM∥OP，只需证到CM 是△AOP的中位线即可．（2）①易证△ODC∽△CDP，从而得到CD2=DP•OD，进而得到y与x之间的函数关系式．由于当点P与点A重合时x=0，当点P与点B重合时x=4，点P在大半圆O上运动（点P不与A，B两点重合），因此自变量x的取值范围为0＜x＜4．②当y=3时，得到-x2+4x=3，求出x．根据x的值可求出CD、PD的值，从而求出∠CPD，运用勾股定理等知识就可求出P，M两点之间的距离．【详解】（1）连接，如图1所示∵是小半圆的直径，∴即∵∴∵∴∴，∵∴，∴∴.，即∵经过半径的外端，且∴直线是小半圆的切线.（2）①∵，，∴∴∴∽∴∴∵,,，∴当点与点重合时，；当点与点重合时，∵点在大半圆上运动（点不与两点重合），∴∴与之间的函数关系式为，自变量的取值范围是.②当时，解得,Ⅰ当时，如图2所示在中，∵，∴，∴∵，∴是等边三角形∵∴∴.Ⅱ当时，如图3所示，同理可得∵∴∴过点作，垂足为，连接，如图3所示∵，∴同理在中，∵，∴综上所述，当时，两点之间的距离为或.【点睛】考查了切线的判定、平行线的判定与性质、等边三角形的判定与性质、相似三角形的判定与性质、特殊角的三角函数值、勾股定理等知识，综合性比较强．10．如图，AN是⊙M的直径，NB∥x轴，AB交⊙M于点C．（1）若点A（0，6），N（0，2），∠ABN=30°，求点B的坐标；（2）若D为线段NB的中点，求证：直线CD是⊙M的切线．【答案】(1) B（，2）．(2)证明见解析.【解析】试题分析：（1）在Rt△ABN中，求出AN、AB即可解决问题；（2）连接MC，NC．只要证明∠MCD=90°即可试题解析：（1）∵A的坐标为（0，6），N（0，2），∴AN=4，∵∠ABN=30°，∠ANB=90°，∴AB=2AN=8，∴由勾股定理可知：NB=，∴B（，2）．（2）连接MC，NC∵AN是⊙M的直径，∴∠ACN=90°，∴∠NCB=90°，在Rt△NCB中，D为NB的中点，∴CD=NB=ND，∴∠CND=∠NCD，∵MC=MN，∴∠MCN=∠MNC，∵∠MNC+∠CND=90°，∴∠MCN+∠NCD=90°，即MC⊥CD．∴直线CD是⊙M的切线．考点：切线的判定；坐标与图形性质．。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

一、圆的综合真题与模拟题分类汇编（难题易错题）1．如图1，直角梯形OABC中，BC∥OA，OA=6，BC=2，∠BAO=45°．（1）OC的长为；（2）D是OA上一点，以BD为直径作⊙M，⊙M交AB于点Q．当⊙M与y轴相切时，sin∠BOQ=；（3）如图2，动点P以每秒1个单位长度的速度，从点O沿线段OA向点A运动；同时动点D以相同的速度，从点B沿折线B﹣C﹣O向点O运动．当点P到达点A时，两点同时停止运动．过点P作直线PE∥OC，与折线O﹣B﹣A交于点E．设点P运动的时间为t （秒）．求当以B、D、E为顶点的三角形是直角三角形时点E的坐标．【答案】（1）4；（2）35；（3）点E的坐标为（1，2）、（53，103）、（4，2）．【解析】分析：（1）过点B作BH⊥OA于H，如图1（1），易证四边形OCBH是矩形，从而有OC=BH，只需在△AHB中运用三角函数求出BH即可．（2）过点B作BH⊥OA于H，过点G作GF⊥OA于F，过点B作BR⊥OG于R，连接MN、DG，如图1（2），则有OH=2，BH=4，MN⊥OC．设圆的半径为r，则MN=MB=MD=r．在Rt△BHD中运用勾股定理可求出r=2，从而得到点D与点H重合．易证△AFG∽△ADB，从而可求出AF、GF、OF、OG、OB、AB、BG．设OR=x，利用BR2=OB2﹣OR2=BG2﹣RG2可求出x，进而可求出BR．在Rt△ORB中运用三角函数就可解决问题．（3）由于△BDE的直角不确定，故需分情况讨论，可分三种情况（①∠BDE=90°，②∠BED=90°，③∠DBE=90°）讨论，然后运用相似三角形的性质及三角函数等知识建立关于t的方程就可解决问题．详解：（1）过点B作BH⊥OA于H，如图1（1），则有∠BHA=90°=∠COA，∴OC∥BH．∵BC∥OA，∴四边形OCBH是矩形，∴OC=BH，BC=OH．∵OA=6，BC=2，∴AH=0A﹣OH=OA﹣BC=6﹣2=4．∵∠BHA=90°，∠BAO=45°，∴tan∠BAH=BHHA=1，∴BH=HA=4，∴OC=BH=4．故答案为4．（2）过点B作BH⊥OA于H，过点G作GF⊥OA于F，过点B作BR⊥OG于R，连接MN、DG，如图1（2）．由（1）得：OH =2，BH =4．∵OC 与⊙M 相切于N ，∴MN ⊥OC ．设圆的半径为r ，则MN =MB =MD =r ．∵BC ⊥OC ，OA ⊥OC ，∴BC ∥MN ∥OA ．∵BM =DM ，∴CN =ON ，∴MN =12（BC +OD ），∴OD =2r ﹣2，∴DH =OD OH -=24r -．在Rt △BHD 中，∵∠BHD =90°，∴BD 2=BH 2+DH 2，∴（2r ）2=42+（2r ﹣4）2．解得：r =2，∴DH =0，即点D 与点H 重合，∴BD ⊥0A ，BD =AD ．∵BD 是⊙M 的直径，∴∠BGD =90°，即DG ⊥AB ，∴BG =AG ．∵GF ⊥OA ，BD ⊥OA ，∴GF ∥BD ，∴△AFG ∽△ADB ， ∴AF AD =GF BD =AG AB =12，∴AF =12AD =2，GF =12BD =2，∴OF =4，∴OG同理可得：OB AB ，∴BG =12AB ．设OR =x ，则RG x ．∵BR ⊥OG ，∴∠BRO =∠BRG =90°，∴BR 2=OB 2﹣OR 2=BG 2﹣RG 2，∴（2﹣x 2=（）2﹣（x ）2．解得：x =5，∴BR 2=OB 2﹣OR 2=（2﹣（5）2=365，∴BR =5．在Rt △ORB 中，sin ∠BOR =BR OB35．故答案为35．（3）①当∠BDE =90°时，点D 在直线PE 上，如图2．此时DP =OC =4，BD +OP =BD +CD =BC =2，BD =t ，OP =t ．则有2t =2．解得：t =1．则OP =CD =DB =1．∵DE ∥OC ，∴△BDE ∽△BCO ，∴DE OC =BD BC =12，∴DE =2，∴EP =2， ∴点E 的坐标为（1，2）．②当∠BED =90°时，如图3．∵∠DBE =OBC ，∠DEB =∠BCO =90°，∴△DBE ∽△OBC ，∴BEBC =2DB BE OB ∴，∴BE =5t ． ∵PE ∥OC ，∴∠OEP =∠BOC ．∵∠OPE =∠BCO =90°，∴△OPE ∽△BCO ，∴OEOB =25OPBC∴，=2t，∴OE=5t．∵OE+BE=OB=255，∴t+5t=25．解得：t=53，∴OP=53，OE=55，∴PE=22OE OP-=103，∴点E的坐标为（51033，）．③当∠DBE=90°时，如图4．此时PE=PA=6﹣t，OD=OC+BC﹣t=6﹣t．则有OD=PE，EA=22PE PA+=2（6﹣t）=62﹣2?t，∴BE=BA﹣EA=42﹣（62﹣2t）=2t﹣22．∵PE∥OD，OD=PE，∠DOP=90°，∴四边形ODEP是矩形，∴DE=OP=t，DE∥OP，∴∠BED=∠BAO=45°．在Rt△DBE中，cos∠BED=BEDE=2，∴DE=2BE，∴t=22（t﹣22）=2t﹣4．解得：t=4，∴OP=4，PE=6﹣4=2，∴点E的坐标为（4，2）．综上所述：当以B、D、E为顶点的三角形是直角三角形时点E的坐标为（1，2）、（51033，）、（4，2）．点睛：本题考查了圆周角定理、切线的性质、相似三角形的判定与性质、三角函数的定义、平行线分线段成比例、矩形的判定与性质、勾股定理等知识，还考查了分类讨论的数学思想，有一定的综合性．2．如图，AB是⊙O的直径，弦CD⊥AB，垂足为H，连结AC，过BD上一点E作EG∥AC 交CD的延长线于点G，连结AE交CD于点F，且EG=FG，连结CE．（1）求证：∠G=∠CEF；（2）求证：EG是⊙O的切线；（3）延长AB交GE的延长线于点M，若tanG =34，AH=33，求EM的值．【答案】（1）证明见解析；（2）证明见解析；（3）253 8.【解析】试题分析：（1）由AC∥EG，推出∠G=∠ACG，由AB⊥CD推出AD AC=，推出∠CEF=∠ACD，推出∠G=∠CEF，由此即可证明；（2）欲证明EG是⊙O的切线只要证明EG⊥OE即可；（3）连接OC．设⊙O的半径为r．在Rt△OCH中，利用勾股定理求出r，证明△AHC∽△MEO，可得AH HCEM OE=，由此即可解决问题；试题解析：（1）证明：如图1．∵AC∥EG，∴∠G=∠ACG，∵AB⊥CD，∴AD AC=，∴∠CEF=∠ACD，∴∠G=∠CEF，∵∠ECF=∠ECG，∴△ECF∽△GCE．（2）证明：如图2中，连接OE．∵GF=GE，∴∠GFE=∠GEF=∠AFH，∵OA=OE，∴∠OAE=∠OEA，∵∠AFH+∠FAH=90°，∴∠GEF+∠AEO=90°，∴∠GEO=90°，∴GE⊥OE，∴EG是⊙O的切线．（3）解：如图3中，连接OC．设⊙O的半径为r．在Rt△AHC中，tan∠ACH=tan∠G=AHHC=34，∵AH=33∴HC=3Rt△HOC中，∵OC=r，OH=r﹣33HC=43∴222(33)(43)r r-+=，∴r=2536，∵GM∥AC，∴∠CAH=∠M，∵∠OEM=∠AHC，∴△AHC∽△MEO，∴AH HCEM OE=，∴33432536=，∴EM253．点睛：本题考查圆综合题、垂径定理、相似三角形的判定和性质、锐角三角函数、勾股定理等知识，解题的关键是学会添加常用辅助线，灵活运用所学知识解决问题，正确寻找相似三角形，构建方程解决问题吗，属于中考压轴题．3．已知▱ABCD的周长为26，∠ABC=120°，BD为一条对角线，⊙O内切于△ABD，E，F，G 为切点，已知⊙O的半径为3▱ABCD的面积．【答案】3【解析】【分析】首先利用三边及⊙O的半径表示出平行四边形的面积，再根据题意求出AB+AD=13，然后利用切线的性质求出BD的长即可解答.【详解】设⊙O分别切△ABD的边AD、AB、BD于点G、E、F；平行四边形ABCD的面积为S；则S=2S△ABD=2×12(AB·OE+BD·OF+AD·3（AB+AD+BD）；∵平行四边形ABCD的周长为26，∴AB+AD=13，∴S=3(13+BD)；连接OA；由题意得：∠OAE=30°，∴AG=AE=3；同理可证DF=DG，BF=BE；∴DF+BF=DG+BE=13﹣3﹣3=7，即BD=7，∴S=3（13+7）=203．即平行四边形ABCD的面积为203．4．如图，已知Rt△ABC中，C=90°，O在AC上，以OC为半径作⊙O，切AB于D点，且BC=BD．（1）求证：AB为⊙O的切线；（2）若BC=6，sinA=35，求⊙O的半径；（3）在（2）的条件下，P点在⊙O上为一动点，求BP的最大值与最小值.【答案】（1）连OD，证明略；（2）半径为3；（3）最大值35+3 ，35-3.【解析】分析：（1）连接OD，OB，证明△ODB≌△OCB即可.（2）由sinA=35且BC=6可知，AB=10且cosA=45，然后求出OD的长度即可.（3）由三角形的三边关系，可知当连接OB交⊙O于点E、F，当点P分别于点E、F重合时，BP分别取最小值和最大值.详解：（1）如图：连接OD、OB.在△ODB和△OCB中：OD=OC,OB=OB,BC=BD;∴△ODB≌△OCB（SSS）.∴∠ODB=∠C=90°.∴AB为⊙O的切线.（2）如图：∵sinA=35，∴CB3AB5=,∵BC=6，∴AB=10,∵BD=BC=6,∴AD=AB-BD=4,∵sinA=35，∴cosA=45，∴OA=5，∴OD=3，即⊙O的半径为：3.（3）如图：连接OB，交⊙O为点E、F，由三角形的三边关系可知：当P点与E点重合时，PB取最小值.由（2）可知：OD=3，DB=6,∴223635+=∴PB=OB-OE=353.当P点与F点重合时，PB去最大值，PB=OP+OB=3+35点睛：本题属于综合类型题，主要考查了圆的综合知识.关键是对三角函数值、勾股定理、全等三角形判定与性质的理解.5．如图所示，以Rt △ABC 的直角边AB 为直径作圆O ，与斜边交于点D ，E 为BC 边上的中点，连接DE ．（1）求证：DE 是⊙O 的切线；（2）连接OE ，AE ，当∠CAB 为何值时，四边形AOED 是平行四边形？并在此条件下求sin ∠CAE 的值．【答案】(1)见解析;(2)1010. 【解析】分析：（1）要证DE 是⊙O 的切线，必须证ED ⊥OD ，即∠EDB+∠ODB=90°（2）要证AOED 是平行四边形，则DE ∥AB ，D 为AC 中点，又BD ⊥AC ，所以△ABC 为等腰直角三角形，所以∠CAB=45°，再由正弦的概念求解即可．详解：（1）证明：连接O 、D 与B 、D 两点，∵△BDC 是Rt △，且E 为BC 中点，∴∠EDB=∠EBD ．（2分）又∵OD=OB 且∠EBD+∠DBO=90°，∴∠EDB+∠ODB=90°．∴DE 是⊙O 的切线．（2）解：∵∠EDO=∠B=90°，若要四边形AOED 是平行四边形，则DE ∥AB ，D 为AC 中点，又∵BD ⊥AC ，∴△ABC 为等腰直角三角形．∴∠C AB=45°．过E 作EH ⊥AC 于H ，设BC=2k ，则EH=22k ，AE=5k ， ∴sin ∠CAE=10EH AE ．点睛：本题考查的是切线的判定，要证某线是圆的切线，已知此线过圆上某点，连接圆心和这点（即为半径），再证垂直即可．6．在平面直角坐标系中，已知点A（2，0），点B（0，），点O（0，0）．△AOB绕着O顺时针旋转，得△A'OB'，点A、B旋转后的对应点为A'，B'，记旋转角为α．（Ⅰ）如图1，A'B'恰好经过点A时，求此时旋转角α的度数，并求出点B'的坐标；（Ⅱ）如图2，若0°＜α＜90°，设直线AA'和直线BB'交于点P，求证：AA'⊥BB'；（Ⅲ）若0°＜α＜360°，求（Ⅱ）中的点P纵坐标的最小值（直接写出结果即可）．【答案】（Ⅰ）α＝60°，B'（3，）；（Ⅱ）见解析；（Ⅲ）点P纵坐标的最小值为﹣2．【解析】【分析】（Ⅰ）作辅助线,先根据点A（2,0）,点B（0,）,确定∠ABO＝30°,证明△AOA'是等边三角形,得旋转角α＝60°,证明△COB'是30°的直角三角形,可得B'的坐标;（Ⅱ）依据旋转的性质可得∠BOB'＝∠AOA'＝α,OB＝OB',OA＝OA',即可得出∠OBB'＝∠OA'A ＝（180°﹣α）,再根据∠BOA'＝90°+α,四边形OBPA'的内角和为360°,即可得到∠BPA'＝90°,即AA'⊥BB';（Ⅲ）作AB的中点M（1,）,连接MP,依据点P的轨迹为以点M为圆心,以MP＝AB＝2为半径的圆,即可得到当PM∥y轴时,点P纵坐标的最小值为﹣2.【详解】解：（Ⅰ）如图1，过B'作B'C⊥x轴于C,∵OA ＝2,OB＝2,∠AOB＝90°,∴∠ABO＝30°,∠BAO＝60°,由旋转得：OA＝OA',∠A'＝∠BAO＝60°,∴△OAA'是等边三角形,∴α＝∠AOA'＝60°,∵OB＝OB'＝2,∠COB'＝90°﹣60°＝30°,∴B'C＝OB’＝,∴OC＝3,∴B'（3,）,（Ⅱ）证明：如图2,∵∠BOB'＝∠AOA'＝α,OB＝OB',OA＝OA',∴∠OBB'＝∠OA'A＝（180°﹣α）,∵∠BOA'＝90°+α,四边形OBPA'的内角和为360°,∴∠BPA'＝360°﹣（180°﹣α）﹣（90°+α）＝90°,即AA'⊥BB';（Ⅲ）点P纵坐标的最小值为-2．理由是：如图，作AB的中点M（1,）,连接MP,∵∠APB ＝90°,∴点P 的轨迹为以点M 为圆心,以MP ＝AB ＝2为半径的圆,除去点（2,2）,∴当PM ⊥x 轴时,点P 纵坐标的最小值为﹣2．【点睛】本题属于几何变换综合题,主要考查了旋转的性质,含30°角的直角三角形的性质,四边形内角和以及圆周角定理的综合运用,解决问题的关键是判断点P 的轨迹为以点M 为圆心,以MP 为半径的圆．7．如图①，抛物线y ＝ax 2+bx+c 经过点A （﹣2，0）、B （4，0）、C （0，3）三点．（1）试求抛物线的解析式；（2）点P 是y 轴上的一个动点，连接PA ，试求5PA+4PC 的最小值；（3）如图②，若直线l 经过点T （﹣4，0），Q 为直线l 上的动点，当以A 、B 、Q 为顶点所作的直角三角形有且仅有三个时，试求直线l 的解析式．【答案】（1）233384y x x =-++；（2）5PA+4PC 的最小值为18；（3）直线l 的解析式为334y x =+或334y x =--. 【解析】【分析】（1）设出交点式，代入C 点计算即可（2）连接AC 、BC ，过点A 作AE ⊥BC 于点E ，过点P 作PD ⊥BC 于点D ，易证△CDP ∽△COB ，得到比例式PC PD BC OB =，得到PD=45PC ，所以5PA+4PC ＝5（PA+45PC ）＝5（PA+PD ），当点A 、P 、D 在同一直线上时，5PA+4PC ＝5（PA+PD ）＝5AE 最小，利用等面积法求出AE=185，即最小值为18 （3）取AB 中点F ，以F 为圆心、FA 的长为半径画圆, 当∠BAQ ＝90°或∠ABQ ＝90°时，即AQ 或BQ 垂直x 轴，所以只要直线l 不垂直x 轴则一定找到两个满足的点Q 使∠BAQ ＝90°或∠ABQ ＝90°，即∠AQB ＝90°时，只有一个满足条件的点Q ，∴直线l 与⊙F 相切于点Q 时，满足∠AQB ＝90°的点Q 只有一个；此时，连接FQ ，过点Q 作QG ⊥x 轴于点G ，利用cos ∠QFT 求出QG ，分出情况Q 在x 轴上方和x 轴下方时，分别代入直接l 得到解析式即可【详解】解：（1）∵抛物线与x 轴交点为A （﹣2，0）、B （4，0）∴y ＝a （x+2）（x ﹣4）把点C （0，3）代入得：﹣8a ＝3∴a ＝﹣38∴抛物线解析式为y ＝﹣38（x+2）（x ﹣4）＝﹣38x 2+34x+3 （2）连接AC 、BC ，过点A 作AE ⊥BC 于点E ，过点P 作PD ⊥BC 于点D∴∠CDP ＝∠COB ＝90°∵∠DCP ＝∠OCB∴△CDP ∽△COB ∴PC PD BC OB= ∵B （4，0），C （0，3）∴OB ＝4，OC ＝3，BC∴PD ＝45PC ∴5PA+4PC ＝5（PA+45PC ）＝5（PA+PD ） ∴当点A 、P 、D 在同一直线上时，5PA+4PC ＝5（PA+PD ）＝5AE 最小∵A （﹣2，0），OC ⊥AB ，AE ⊥BC∴S △ABC ＝12AB•OC ＝12BC•AE ∴AE ＝631855AB OC BC ⨯==∴5AE ＝18∴5PA+4PC 的最小值为18．（3）取AB 中点F ，以F 为圆心、FA 的长为半径画圆当∠BAQ ＝90°或∠ABQ ＝90°时，即AQ 或BQ 垂直x 轴，∴只要直线l 不垂直x 轴则一定找到两个满足的点Q 使∠BAQ ＝90°或∠ABQ ＝90° ∴∠AQB ＝90°时，只有一个满足条件的点Q∵当Q 在⊙F 上运动时（不与A 、B 重合），∠AQB ＝90°∴直线l 与⊙F 相切于点Q 时，满足∠AQB ＝90°的点Q 只有一个此时，连接FQ ，过点Q 作QG ⊥x 轴于点G∴∠FQT ＝90°∵F 为A （﹣2，0）、B （4，0）的中点∴F （1，0），FQ ＝FA ＝3∵T （﹣4，0）∴TF ＝5，cos ∠QFT ＝35FQ TF = ∵Rt △FGQ 中，cos ∠QFT ＝35FG FQ = ∴FG ＝35FQ ＝95∴x Q ＝1﹣9455=-，QG ＝2222912FQ 355FG ⎛⎫-=-= ⎪⎝⎭①若点Q 在x 轴上方，则Q （41255-，）设直线l 解析式为：y ＝kx+b ∴4041255k b k b -+=⎧⎪⎨-+=⎪⎩ 解得：343k b ⎧=⎪⎨⎪=⎩ ∴直线l ：334y x =+ ②若点Q 在x 轴下方，则Q （41255--，） ∴直线l ：334y x =-- 综上所述，直线l 的解析式为334y x =+或334y x =--【点睛】本题是二次函数与圆的综合题，同时涉及到三角函数、勾股定理等知识点，综合度比较高，需要很强的综合能力，第三问能够找到满足条件的Q点是关键，同时不要忘记需要分情况讨论8．如图，在Rt△ABC中，点O在斜边AB上，以O为圆心，OB为半径作圆，分别与BC，AB相交于点D，E，连接AD．已知∠CAD＝∠B．（1）求证：AD是⊙O的切线；（2）若CD＝2，AC＝4，BD＝6，求⊙O的半径．【答案】（1）详见解析；（235.【解析】【分析】(1)解答时先根据角的大小关系得到∠1＝∠3，根据直角三角形中角的大小关系得出OD⊥AD ，从而证明AD为圆O的切线；(2)根据直角三角形勾股定理和两三角形相似可以得出结果【详解】（1）证明：连接OD，∵OB＝OD，∴∠3＝∠B，∵∠B＝∠1，∴∠1＝∠3，在Rt△ACD中，∠1+∠2＝90°，∴∠4＝180°﹣（∠2+∠3）＝90°，∴OD⊥AD，则AD为圆O的切线；（2）过点O作OF⊥BC，垂足为F，∵OF⊥BD∴DF＝BF＝12BD＝3∵AC＝4，CD＝2，∠ACD＝90°∴AD22AC CD5∵∠CAD＝∠B，∠OFB＝∠ACD＝90°∴△BFO∽△ACD∴BFAC = OB AD即3425∴OB＝352∴⊙O35．【点睛】此题重点考查学生对直线与圆的位置关系，圆的半径的求解，掌握勾股定理，两三角形相似的判定条件是解题的关键9．设C 为线段AB 的中点，四边形BCDE 是以BC 为一边的正方形，以B 为圆心，BD 长为半径的⊙B 与AB 相交于F 点，延长EB 交⊙B 于G 点，连接DG 交于AB 于Q 点，连接AD ．求证：（1）AD 是⊙B 的切线；（2）AD ＝AQ ；（3）BC 2＝CF×EG ．【答案】(1)证明见解析；（2）证明见解析；（3）证明见解析.【解析】【分析】()1连接BD ，由DC AB ⊥，C 为AB 的中点，由线段垂直平分线的性质，可得AD BD =，再根据正方形的性质，可得90ADB ∠=；()2由BD BG =与//CD BE ，利用等边对等角与平行线的性质，即可求得122.52G CDG BDG BCD ∠=∠=∠=∠=，继而求得67.5ADQ AQD ∠=∠=，由等角对等边，可证得AD AQ =； ()3易求得67.5GDE GDB BDE DFE ∠=∠+∠==∠，90DCF E ∠=∠=，即可证得Rt DCF ∽Rt GED ，根据相似三角形的对应边成比例，即可证得结论．【详解】证明：()1连接BD ，四边形BCDE 是正方形，45DBA ∴∠=，90DCB ∠=，即DC AB ⊥，C 为AB 的中点，CD ∴是线段AB 的垂直平分线，AD BD ∴=，45DAB DBA ∴∠=∠=，90ADB ∴∠=，即BD AD ⊥， BD 为半径，AD ∴是B 的切线；()2BD BG =，BDG G ∴∠=∠，//CD BE ，CDG G ∴∠=∠，122.52G CDG BDG BCD ∴∠=∠=∠=∠=， 9067.5ADQ BDG ∴∠=-∠=，9067.5AQB BQG G ∠=∠=-∠=， ADQ AQD ∴∠=∠，AD AQ ∴=；()3连接DF ，在BDF 中，BD BF =，BFD BDF ∴∠=∠，又45DBF ∠=，67.5BFD BDF ∴∠=∠=，22.5GDB ∠=，在Rt DEF 与Rt GCD 中，67.5GDE GDB BDE DFE ∠=∠+∠==∠，90DCF E ∠=∠=，Rt DCF ∴∽Rt GED ，CF CD ED EG∴=，又CD DE BC ==，2BC CF EG ∴=⋅．【点睛】本题考查了相似三角形的判定与性质、切线的判定与性质、正方形的性质以及等腰三角形的判定与性质.解题的关键是注意掌握数形结合思想的应用，注意辅助线的作法．10．如图1，⊙O 的直径AB =12，P 是弦BC 上一动点（与点B ，C 不重合），∠ABC =30°，过点P 作PD ⊥OP 交⊙O 于点D ．（1）如图2，当PD∥AB时，求PD的长；（2）如图3，当弧DC=弧AC时，延长AB至点E，使BE=12AB，连接DE．①求证：DE是⊙O的切线；②求PC的长．【答案】（1）26；（2）①证明见解析；②33﹣3．【解析】试题分析：（1）根据题意首先得出半径长，再利用锐角三角三角函数关系得出OP，PD的长；（2）①首先得出△OBD是等边三角形，进而得出∠ODE=∠OFB=90°，求出答案即可；②首先求出CF的长，进而利用直角三角形的性质得出PF的长，进而得出答案．试题解析：（1）如图2，连接OD，∵OP⊥PD，PD∥AB，∴∠POB=90°，∵⊙O的直径AB=12，∴OB=OD=6，在Rt△POB中，∠ABC=30°，∴OP=OB•tan30°=6×=2，在Rt△POD中，PD===；（2）①如图3，连接OD，交CB于点F，连接BD，∵，∴∠DBC=∠ABC=30°，∴∠ABD=60°，∵OB=OD，∴△OBD是等边三角形，∴OD⊥FB，∵BE=AB，∴OB=BE，∴BF∥ED，∴∠ODE=∠OFB=90°，∴DE是⊙O的切线；②由①知，OD⊥BC，∴CF=FB=OB•cos30°=6×=3，在Rt△POD中，OF=DF，∴PF=DO=3（直角三角形斜边上的中线，等于斜边的一半），∴CP=CF﹣PF=3﹣3．考点：圆的综合题。