2013-2014学年高一数学上学期第二次月考试题及答案(新人教A版 第260套)
人教版高一上学期第二次月考数学试卷及答案

高一上学期第二次月考数学试卷考试时间:120分钟满分:150分一、选择题:(本大题共12小题,每小题5分,共60分. ) 1. (2010年高考安徽卷)若集合A=,则?R A=( ) A.(-∞,0]∪(22,+∞) B.(22,+∞) C.(-∞,0]∪[22,+∞) D.[22,+∞) 答案:A2. 已知f(1-x1+x)=1-x21+x2,则f(x)的解析式可取为( )A.x1+x2 B.-2x1+x2 C.2x1+x2 D.-x1+x2答案:C3. 函数y=13x-2+lg (2x-1)的定义域是( ) A.[23,+∞) B.(12,+∞) C.(23,+∞) D(12,23) 答案:C4. 函数f(x)=22x-2的值域是( )A.(-∞,-1) B.(-1,0)∪(0,+∞)C.(-1,+∞) D.(-∞,-1)∪(0,+∞)答案:D5.函数x exxf 44)(的零点所在的区间为()A. (1,2)B. (0,1)C. (-1,0)D. (-2,-1) 答案:B6.下列函数在(0,1)上是减函数的是( )A.y=log0.5(1-x)B.y=x0.5 C.y=0.51-x D.y=12(1-x2) 答案:D7.已知偶函数f(x)在区间[0,+∞)上单调递增,则满足f(2x-1)<f(13).的x的取值范围为( )A.[0,13] B.(13,12] C.[12,23) D.(13,2 3)答案:D8.如图所示的直观图的平面图形ABCD是( ) (A)任意梯形(B)直角梯形(C)任意四边形(D)平行四边形答案:B9. 下列说法不正确的是( )(A)空间中,一组对边平行且相等的四边形一定是平行四边形(B)同一平面的两条垂线一定共面(C)过直线上一点可以作无数条直线与这条直线垂直,且这些直线都在同一个平面内(D)过一条直线有且只有一个平面与已知平面垂直D10. 半径为16,圆心角为180°的扇形围成圆锥的侧面,则圆锥的高是(A)82(B) 83 (C)85 (D)8 答案:B11. 一个底面是正三角形的三棱柱的正视图如图所示,则其体积等于( )(A)6 (B)2 (C)3(D)23答案:C12. 正四面体的内切球与外接球的半径之比为()A. 1∶3B. 1∶3C. 1∶9D. 1∶81答案:A二、填空题:(本大题共4小题,每小题5分,共20分.)13. 若函数f(x)=a x-x-a(a>0,且a≠1)有两个零点,则实数a的取值范围是________.答案:(1,+∞)14. 定义在R上的奇函数f(x),当x∈(0,+∞)时,f(x)=log2x,则不等式f(x)<-1的解集是________..答案:(-∞,-2)∪(0,12)15. 在空间四边形ABCD中,AD=BC=2,E,F分别是AB,CD的中点,EF=3,则异面直线AD与BC所成角的大小为_______.答案:60°16. 如图,将边长为1的正方形ABCD沿对角线AC折起,使得平面ADC⊥平面ABC,在折起后形成的三棱锥D-ABC中,给出下列三种说法:①△DBC是等边三角形;②AC⊥BD;③三棱锥D-ABC的体积是26. 其中正确的序号是________(写出所有正确说法的序号).答案:①②三、解答题:(本大题共6小题,共70分. ) 17.(本小题10分)已知集合A={x|2a-2<x<a},B={x|1<x<2},且A?R B,求实数a的取值范围.解:?R B={x|x≤1或x≥2}≠?,∵A?R B,∴分A=?和A≠?两种情况讨论.①若A=?,此时有2a-2≥a,∴a≥2.②若A≠?,则有?????2a-2<aa≤1或?????2a-2<a2a-2≥2.∴a≤1.综上所述,a≤1或a≥2.18.(本小题12分)设函数2()21x fxa???, ⑴求证: 不论a 为何实数()fx总为增函数;⑵确定a的值,使()fx为奇函数.18. 解: (1) ()f x的定义域为R, 12xx??,则121222()()2121xx fxfxaa???????=12122(22)(12)(12)xxxx????, 12xx?,??????,12()()0,fxfx???1212220,(12)(12)0xxxx即12()()fxfx?,所以不论a为何实数()fx总为增函数.…………6分 (2) ()f x为奇函数, ()()fxfx????,即222121xx aa???????, 解得: 1.a?2()1.21x fx????………………12分19.(12分)已知二次函数f(x)=4x2-2(p-2)x-2p2-p+1在区间[-1,1]内至少存在一个实数c,使f(c)>0,求实数p的取值范围.解析:二次函数f(x)在区间[-1,1]内至少存在一个实数c,使f(c)>0的否定是对于区间[-1,1]内的任意一个x都有f(x)≤0,∴f(-1)≤0且f(1)≤0整理得?????2p2+3p-9≥0,2p2-p-1≥0,解得p≥32或p≤-3,∴二次函数在区间[-1,1]内至少存在一个实数c,使f(c)>0的实数p的取值范围是(-3,32).20. 已知正方体ABCD-A1B1C1D1中,E,F分别为D1C1,C1B1的中点,AC∩BD=P,A1C1∩EF=Q.(1)求证: D,B,F,E四点共面;(2)若A1C交平面DBFE于R点,则P,Q,R三点共线.20.【证明】如图.(1)∵EF是△D1B1C1的中位线,∴EF∥B1D1.在正方体AC1中,B1D1∥BD,∴EF∥BD.∴EF、BD确定一个平面,即D,B,F,E四点共面.(2)正方体AC1中,设平面A1ACC1确定的平面为α,又设平面BDEF为β.∵Q∈A1C1,∴Q∈α.又Q∈EF,∴Q∈β.则Q是α与β的公共点,同理P是α与β的公共点,∴α∩β=PQ.又A1C∩β=R,∴R∈A1C.∴R∈α,且R∈β,则R∈PQ.故P,Q,R三点共线.21.(12分)如图所示的四棱锥P-ABCD中,底面ABCD为菱形,PA⊥平面ABCD,E为PC的中点,求证:(1)PA∥平面BDE; (2)平面PAC⊥平面PBD.21.【证明】(1)连接AC交BD于点O,连接OE. ∵四边形ABCD 是菱形,∴AO=CO.∵E为PC的中点,∴EO∥PA.∵PA平面BDE,EO?平面BDE, ∴PA∥平面BDE.(2)∵PA⊥平面ABCD,BD?平面ABCD,∴PA⊥BD,∵四边形ABCD是菱形,∴BD⊥AC.∵AC∩PA=A,∴BD⊥平面PAC. ∵BD?平面PBD,∴平面PAC⊥平面PBD.22. 如图,在棱长为a的正方体ABCD-A1B1C1D1中,E,F,G分别是CB,CD,CC1的中点.(1)求证:平面AB1D1∥平面EFG. (2)求EFGCD??二面角的正切值.22.(1)【证明】在正方体ABCD-A1B1C1D1中,连接BD.∵DD1∥B1B,DD1=B1B,∴四边形DD1B1B为平行四边形,∴D1B1∥DB.∵E,F分别为BC,CD的中点,∴EF∥BD,∴EF∥D1B1.∵EF?平面EFG,D1B1?平面EFG,∴D1B1∥平面EFG.同理AB1∥平面EFG. (2)2EFGCD 二面角的正切值为。
2013-2014学年高一数学上学期第二次月考试题及答案(新人教A版 第144套)

高一上学期第二次月考数学试题注意事项:1. 本试题卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,总分150分,考试时间90分钟.2. 答题前,考生须将自己的姓名、准考证号、考场号、座位号填写在本试题卷指定的位置上.2、下列说法正确的是 ( )A 、三点确定一个平面B 、四边形一定是平面图形C 、梯形一定是平面图形D 、平面α和平面β有不同在一条直线上的三个交点3、垂直于同一条直线的两条直线一定 ( )A 、平行B 、相交C 、异面D 、以上都有可能 4、在正方体1111ABCD A BC D -中,下列几种说法正确的是 ( )A 、11AC AD ⊥B 、11DC AB ⊥ C 、1AC 与DC 成45角D 、11AC 与1BC成60角 5、若直线l ∥平面α,直线a α⊂,则l 与a 的位置关系是 ( )A 、l ∥aB 、l 与a 异面C 、l 与a 相交D 、l 与a 没有公共点10、在棱长为1的正方体上,分别用过共顶点的三条棱中点的平面截该正方体,则截去8个三棱锥后,剩下的凸多面体的体积是 A 、23 B 、76 C 、45 D 、5611、如图是一个物体的三视图,则此物体的直观图是( ).12如图,在正方体1111ABCD A BC D 中,E F G H ,,,分别为1AA ,AB ,1BB ,11B C 的中点,则异面直线EF 与GH 所成的角等于( ) A.45° B.60° C.90° D.12°第Ⅱ卷(共90分)A FD BCGE 1BH1C1D1A二、填空题(每小题5分,共20分)18、(12分)已知E 、F 、G 、H 为空间四边形ABCD 的边AB 、BC 、CD 、DA 上的点,且EH∥FG.求证:EH ∥BD . (12分)19、(12分)已知ABC ∆中90ACB ∠=,SA ⊥面ABC ,AD SC ⊥,求证:AD ⊥面SBC .(12分) 20、(12分)已知ABCD 是矩形,PA ⊥平面ABCD ,2AB =,4PA AD ==,E 为BC 的中点.(1)求证:DE ⊥平面PAE ;(2)求直线DP 与平面PAE 所成的角.21、(12分)下图是一个几何体的三视图,已知侧视图是一个等边三角形,根据图中尺寸(单位:㎝),求该几何体的表面积和体H G FED BA CSDCB A 33侧视图正视图积。
2013-2014学年高一数学上学期第二次月考试题(9-21班使用)及答案(新人教A版 第272套)

普集高中2013-2014学年高一第一学期第二次月考数学试题(9—21班使用)一、选择题(每小题5 分,满分50分)1. 已知全集{}6,5,4,3,2,1=U ,集合{}6,4,3,1=A ,{}6,5,4,2=B ,则()B C A U ⋂等于( )A. {}3,1B. {}5,2C. {}4D. ∅2. 函数()x x f x 32+=的零点所在的一个区间是( )A. ()1,2--B. ()0,1-C. (0,1)D. (1,2)3. 已知函数()⎩⎨⎧≤>=020log 3x x x x f x,则=⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛91f f ( )A. 4B.41 C. -4D. 41-4. 已知幂函数()x f y =的图象过(4,2)点,则=⎪⎭⎫ ⎝⎛21f ( )A. 2B.21 C. 41 D.22 5. 函数()431ln 2+--+=x x x y 的定义域为( )A. (-4,-1)B. (-4,1)C. (-1,1)D. ]1,1(-6. 9log 4log 25log 532⋅⋅的值为( )A. 6B. 8C. 15D. 307. 已知函数()x f 对任意的R x ∈有()()0=-+x f x f ,且当0>x 时,()()1ln +=x x f ,则函数()x f 的大致图象为( )8. 设0.914y =,0.4828y =,3231()2y -=,则 ( )A .y 3>y 1>y 2B .y 2>y 1>y 3C .y 1>y 2>y 3D .y 1>y 3>y 29. 设2()f x x bx c =++,且(1)(3)f f -=,则 ( ) A .(1)(1)f c f >>- B .(1)(1)f c f <<- C .(1)(1)f f c >->D .(1)(1)f f c <-<10. 设函数()x f y =在()∞+∞-,内有定义,对于给定的正数K ,定义函数()()()()⎩⎨⎧>≤=K x f K K x f x f x f K ,,,取函数()||2x x f -=,当21=K 时,函数()x f K 的单调递增区间为( )A. ()0,∞-B. ()∞+,0C. ()1,-∞-D. ()∞+,1二、填空题(每小题4分,满分20分)11. 函数5()2log (3)f x x =++在区间[-2,2]上的值域是______12.已知01a <<,则函数|||log |x a y a x =-的零点的个数为___________.13.函数()log (3)1(0,a f x x a =++>且1)a ≠的图象恒过定点P ,则P 点的坐标是_____. 14.若f (x )=-x 2+2ax 与g (x )=ax +1在区间[1,2]上都是减函数,则a 的取值范围是_______.15. 已知)(x f 为偶函数,它在),0[+∞上是增函数.则不等式)1()(lg f x f >的解集是____. 三、解答题(共5小题,满分50+10分)16.(本题满分12分)计算:(1)21023213(2)(9.6)(3)0.148-----+; (2) 2.5log 6.25lg0.01++17.(本小题满分12分)已知[]2,1,432)3()(2-∈+⨯-=x x f x x ,求)(x f 的最大值与最小值;18.(本题满分13分)已知二次函数2()1(0)f x ax bx a =++>.(1)若(1)0f -=,且函数()f x 有且只有一个零点,求()f x 的表达式;(2)在(1)的条件下,当]2,2[-∈x 时,()()g x f x kx =-是单调函数,求实数k 的取值范围.19. (本题满分13分) 已知函数)10()3(log )1(log )(<<++-=a x x x f a a .(1)求函数)(x f 的定义域; (2)求函数)(x f 的零点;(3)若函数()f x 的最小值为2-,求a 的值.附加题:20.(本题满分10分) 已知函数1515)(+-=xx x f 。
2013-2014学年高一数学上学期第二次月考试题及答案(新人教A版 第120套)

江西省赣州市兴国县将军中学2013-2014学年高一数学上学期第二次月考试题新人教A 版说明:1.考试时间为120分钟,试卷满分为150分.试卷分Ⅰ,Ⅱ两卷,共21题. 2.答题前,务必将自己的姓名、班级和座位号填写在答题卡规定的位置上. 3.答选择题时,必须将答案书写在答题卡上对应的题号下面位置上.4.所有题目必须在答题卡上指定位置作答,在试题卷上或答题卡的其他地方答题无效.第Ⅰ卷一. 选择题(本大题共10小题,每小题5分,共50分,在每小题给出的四个选项中,只有一个是正确的,把正确选项的代号填在答题卡的指定位置上) 1. 已知集合{|0}1xM x x =≥-,2{|31,}N y y x x R ==+∈,则M N =( )A . ∅B . {|1}x x >C . {|1}x x ≥D . {|1x x ≥或0}x <2.函数y =12o g -x 的定义域为( )A .(,+∞) B .[1,+∞ C .( ,1 D .(-∞,1) 3.函数()x x x f 2log 4+-=的零点所在的区间是( )A.(0,1)B.(1,2)C.(2,3)D.(3,4)4.设函数),在(且0)10(|,|log )(∞-≠>=a a x x f a 上单调递增,则)2()1(f a f 与+的大小关系为( )A. )2()1(f a f =+B. )2()1(f a f >+C. )2()1(f a f <+D.不确定 5. ( )A B .2 C D 6. 已知0,0,122>>=+y x y x ,且n xm x aa =-=+11l og ,)1(l og ,则y al o g 等于( )A.()12m n -B.()12m n + C. m n - D.m n +7.设()xf x a =,13()g x x =,()log a h x x =,且a 满足2log (1)0a a ->,那么当1x >时必有( )A. ()()()h x g x f x <<B. ()()()h x f x g x <<C. ()()()f x g x h x <<D. ()()()f x h x g x <<8. 已知⎩⎨⎧≥<+-=)1(,)1(,1)2()(x a x x a x f x 满足对任意21x x ≠,都有0)()(2121>--x x x f x f 成立,那么a 的取值范围是( )A .3[,2)2B .3(1,]2C .(1,2) D.),1(+∞9. 已知函数53()353f x x x x =---+,若6)2()(>-+a f a f ,则实数a 的取值范围是 ( )A .1<aB .3<aC .1>aD .3>a10.已知函数)(x f 是定义在实数集R 上的偶函数,且对任意实数x 都有()()121+=+x f x f ,则()2012f 的值是( )A.1B. 0C. 1-D. 2-第Ⅱ卷二.填空题(本大题共5小题,每小题5分,共25分,将答案填写在正确的位置)11. 已知函数⎩⎨⎧=x x x f 3log )(2)0()0(≤>x x ,则)]41([f f 的值是 . 12.已知函数2log log )(32+-=x b x a x f ,若4)20121(=f ,则)2012(f 为 . 13.已知定义域为R 的偶函数)(x f 在区间),0[+∞上是增函数,若)(lg )1(x f f <,则实数x 的取值范围是 14. 函数11()22xf x a x =+--在(0,1)上有两个不同的零点,则实数a 的取值范围是 . 15. 下列命题:①始边和终边都相同的两个角一定相等. ② 是第二象限的角.③若,则4α是第一象限角. ④相等的两个角终边一定相同.⑤已知k =-)80cos(0,那么kk 21100tan --=.其中正确命题是 .(填正确命题的序号)三.解答题(本大题共6小题,共75分,解答应写出文字说明与演算步骤)16.(本小题满分12分)已知集合}2733|{≤≤=x x A ,2{|log 1}B x x =>. (Ⅰ)分别求A B C B A R )(,;(Ⅱ)已知集合{}1C x x a =<<,若C A ⊆,求实数a 的取值集合.17. (本小题满分12分)已知函数y =M , (1)求M ;(2)当M x ∈时,求函数2222()log log ()log f x x x a x =⋅+⋅的最大值。
2013年高一上学期数学月考试题及参考答案
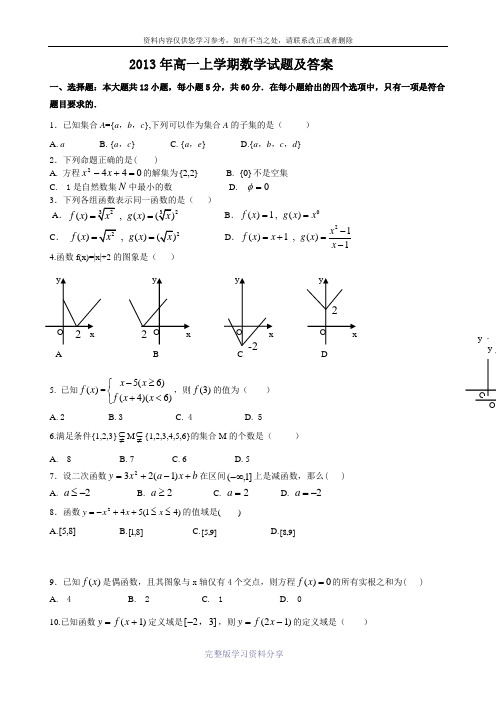
2013年高一上学期数学试题及答案一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合A ={a ,b ,c },下列可以作为集合A 的子集的是( ) A. a B. {a ,c } C. {a ,e } D.{a ,b ,c ,d } 2.下列命题正确的是( )A. 方程0442=+-x x 的解集为}2,2{B. }0{不是空集C. 1是自然数集N 中最小的数D. 0=φ 3.下列各组函数表示同一函数的是( ) A.2(),()f x g x ==B .0()1,()f x g x x ==C .2(),()f x g x == D .21()1,()1x f x x g x x -=+=-4.函数f(x)=|x|+2的图象是( )5. 已知()f x =5(6)(4)(6)x x f x x -≥⎧⎨+<⎩,则(3)f 的值为( )A. 2B. 3C. 4D. 56.满足条件{1,2,3}⊂≠M ⊂≠{1,2,3,4,5,6}的集合M 的个数是( )A. 8B. 7C. 6D. 57.设二次函数b x a x y +-+=)1(232在区间]1,(-∞上是减函数,那么( ) A. 2-≤a B. 2≥a C. 2=a D. 2-=a 8.函数)41(542≤≤++-=x x x y 的值域是( )A.]8,5[B.]8,1[C.]9,5[D.]9,8[9.已知)(x f 是偶函数,且其图象与x 轴仅有4个交点,则方程0)(=x f 的所有实根之和为( ) A. 4 B. 2 C. 1 D. 010.已知函数y f x =+()1定义域是[]-23,,则y f x =-()21的定义域是( )A BDy OyOA. ]35[,-B.[]-14,C. []052, D.[]-37, 11.集合A={x Z k k x ∈=,2} ,B={Z k k x x ∈+=,12} ,C={Z k k x x ∈+=,14} 又,,B b A a ∈∈则有( )A.(a+b )∈AB. (a+b )∈BC. (a+b )∈CD. (a+b )∈A 、B 、C 任一个 12.已知)(x f 在实数集R 上是减函数,若0≤+b a ,则下列正确的是( ) A .)]()([)()(b f a f b f a f +-≤+ B . )()()()(b f a f b f a f -+-≤+ C .)]()([)()(b f a f b f a f +-≥+ D .)()()()(b f a f b f a f -+-≥+二、填空题(本大题共4小题,每小题5分,共20分。
最新版高一数学上学期第二次月考试题及答案(新人教A版第120套

最新版高一数学上学期第二次月考试题及答案(新人教A版第120套啦啦啦啦啦啦啦啦啦江西省赣州市兴国县将军中学高一数学上学期第二次月考试题新人教A版说明:1.考试时间为120分钟,试卷满分为150分.试卷分Ⅰ,Ⅱ两卷,共21题.2.答题前,务必将自己的姓名、班级和座位号填写在答题卡规定的位置上.3.答选择题时,必须将答案书写在答题卡上对应的题号下面位置上.4.所有题目必须在答题卡上指定位置作答,在试题卷上或答题卡的其他地方答题无效.第Ⅰ卷一.选择题(本大题共10小题,每小题5分,共50分,在每小题给出的四个选项中,只有一个是正确的,把正确选项的代号填在答题卡的指定位置上)1.已知集合M{某|某0},N{y|y3某21,某R},则M某1N=()A.B.{某|某1}C.{某|某1}D.{某|某1或某0}2某1)的定义域为()2.函数y=log1(2A.(11,+∞)B.[1,+∞)C.(,1]D.(-∞,1)223.函数f某某4log2某的零点所在的区间是()A.(0,1)B.(1,2)C.(2,3)D.(3,4)0)4.设函数f(某)loga|某|,(a0且a1)在(,上单调递增,则f(a1)与f(2)的大小关系为()A.f(a1)f(2)B.f(a1)f(2)C.f(a1)f(2)D.不确定5.若一圆弧长等于其所在圆的内接正三角形的边长,则其圆心角的弧度数为()A.3B.2C.223D.26.已知某y1,某0,y0,且olgA.a(1某)m,olga1lg则on,1某ay等于()11mnB.mnC.mnD.mn22某7.设f(某)a,g(某)某,h(某)loga某,且a 满足loga(1a2)0,那么当某1时必有()13房东是个大帅哥啦啦啦啦啦啦啦啦啦A.h(某)g(某)f(某)B.h(某)f(某)g(某)C.f(某)g(某)h(某)D.f(某)h(某)g (某)(2a)某1,(某1)f(某1)f(某2)8.已知f(某)某满足对任意某1某2,都有0成立,某某12a,(某1)那么a的取值范围是()33A.[,2)B.(1,]C.(1,2)D.(1,)22539.已知函数f(某)某3某5某3,若f(a)f(a2)6,则实数a的取值范围是()A.a1B.a3C.a1D.a310.已知函数f(某)是定义在实数集R上的偶函数,且对任意实数某都有f某12f某1,则f2022的值是()A.1B.0C.1D.2第Ⅱ卷二.填空题(本大题共5小题,每小题5分,共25分,将答案填写在正确的位置)log2某(某0)1f(某)某11.已知函数,则f[f()]的值是.(某0)3412.已知函数f(某)alog2某blog3某2,若f(1)4,则f(2022)为.202213.已知定义域为R的偶函数f(某)在区间[0,)上是增函数,若f(1)f(lg某),则实数某的取值范围是14.函数f(某)a某某是.15.下列命题:①始边和终边都相同的两个角一定相等.②③若011在(0,1)上有两个不同的零点,则实数a的取值范围22是第二象限的角.,则4是第一象限角.④相等的两个角终边一定相同.01k2⑤已知co(80)k,那么tan100.k其中正确命题是.(填正确命题的序号)三.解答题(本大题共6小题,共75分,解答应写出文字说明与演算步骤)房东是个大帅哥啦啦啦啦啦啦啦啦啦16.(本小题满分12分)某已知集合A{某|3327},B{某|log2某1}.(Ⅰ)分别求AB,(CRB)A;(Ⅱ)已知集合C某1某a,若CA,求实数a的取值集合.17.(本小题满分12分)已知函数y2-某2某2的定义域为M,2某(1)求M;2(2)当某M时,求函数f(某)log2某log2(某)alog2某的最大值。
最新版高一数学上学期10月月考试题及答案(新人教A版 第26套)

雅安中学高一上期月考试题(10月)数学试题本试卷分为第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。
满分150分,考试时间120分钟。
考试结束后,将答题卷和机读卡一并收回。
第Ⅰ卷(选择题,共50分)一、选择题:共10小题,在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知{}4,3,2,1=U,{}4,3,1=A,{}4,3,2=B,那么=)(BACU()(A){}2,1(B){}4,3,2,1(C)φ(D){}φ2.如果A=}1|{->xx,那么()A.A⊆0 B.A∈}0{ C.A∈Φ D.A⊆}0{3.给出下列四个对应:其构成映射的是()A.只有①②B.只有①④ C.只有①③④D.只有③④4.下列图象中不能作为函数图象的是()5.设函数211()21x xf xxx⎧+≤⎪=⎨>⎪⎩,则((3))f f=()A.15B.3 C.23D.1396.已知函数y f x=+()1定义域是[]-23,,则y f x=-()21的定义域是()A.[]52, B.[]-14, C.[]-55, D.[]-37,7.下列函数中,既是奇函数又是增函数的为( )A .1y x =+B .2y x =-C .1y x=D .||y x x =9.已知不等式0622<+-k x kx ,若不等式的解集是R ,则k 的取值范围( ) A .),66()66,(+∞⋃--∞ B .)66,66(- C.)66,(--∞ D .),66(+∞ 10. 关于x 的方程a x x -=+-232有4个不同实数解,则a 的取值范围是( )A. )41,0(B. ),41(+∞-C. ]41,(-∞ D. )0,41(-第Ⅱ卷(非选择题,共100分)二、填空题:共5小题,把答案填在题中横线上.(25分)11.设集合}35|),{(},64|),{(-==+-==x y y x B x y y x A ,则B A = . 12.满足条件{1,2,3}⊂≠M ⊆{1,2,3,4,5,6}的集合M 的个数是 .13.函数14)(-+=x x x f 的值域是14.函数f (x ) =xx 0)1(++22++-x x 的定义域是 .15.若函数f(x)是定义在R 上的偶函数,在(-∞,0)上是增函数,且f(2)=0,则使f(x)<0的x 的取值范围是 .三、解答题:共6小题,解答应写出文字说明、证明过程或演算步骤.(75分) 16.(本小题13分)全集U=R ,若集合{}|310A x x =≤<,{}|27B x x =<≤,则(1)求A B ,AB , ()()U UC A C B ;(2)若集合C={|}x x a >,若A C A =⋂,求a 的取值范17.(本小题13分)设A ={x |x 2-ax +a 2-19=0},B ={x |x 2-5x +6=0},C ={x |x 2+2x -8=0}.(1)若A =B ,求a 的值;(2)若∅A ∩B ,A ∩C =∅,求a 的值 18 (本小题满分13分)已知函数2()22,[5,5].f x x ax x =++∈-(1)当1a =-时,求函数()f x 的最小值、最大值;(2) 当()f x 在[5,5]-上是单调函数时,求实数a 的取值范围。
高一数学上学期第二次月考试题含解析试题

智才艺州攀枝花市创界学校范家屯镇第一二零二零—二零二壹高一数学上学期第二次月考试题〔含解析〕一、选择题(每一小题5分,一共60分) 1.13sin6π的值是()A.12-B.12C. D.2【答案】B 【解析】 【分析】利用诱导公式可得所求之值.【详解】131sinsin 2sin 6662ππππ⎛⎫=+== ⎪⎝⎭,应选B. 【点睛】此题考察诱导公式,属于根底题.{}{}0,2,4,6,8,10,4,8A B ==,那么A B =A.{4,8}B.{02,6},C.{026,10},,D.{02468,10},,,, 【答案】C 【解析】试题分析:由补集的概念,得{}0,2,6,10A B =,应选C .【考点】集合的补集运算【名师点睛】研究集合的关系,处理集合的交、并、补的运算问题,常用韦恩图、数轴等几何工具辅助解题.一般地,对离散的数集、抽象的集合间的关系及运算,可借助韦恩图,而对连续的集合间的运算及关系,可借助数轴的直观性,进展合理转化.3cos 2απ⎛⎫-= ⎪⎝⎭sin(5)α-π+=〔〕A.23B.23-D.【答案】D 【解析】【分析】利用诱导公式可得sin 3α=,再化简sin(5)sin αα-π+==即可得解.【详解】由3cos 2απ⎛⎫-=⎪⎝⎭sin α-=,即sin 3α=.sin(5)sin αα-π+=-= 应选:D.【点睛】此题主要考察了诱导公式的化简,属于根底题. 4.sin1,cos1,tan1的大小关系为〔〕 A.tan1sin1cos1>> B.sin1tan1cos1>> C.sin1cos1tan1>>D.tan1cos1sin1>>【答案】A 【解析】单位圆中,1,42OM MP ATMOP OP OP OAπ∠=><<<,cos1sin1tan1∴<<,应选A.5.2tan α=,那么()cos cos 2a a ππ+⎛⎫+ ⎪⎝⎭的值是〔〕A.12-B.2-C.12D.2【答案】C 【解析】 【分析】直接利用诱导公式化简结合弦化切可得解.【详解】()cos cos 11sin tan 2cos 2a a a a a ππ+-===-⎛⎫+ ⎪⎝⎭,应选:C.【点睛】此题主要考察了诱导公式及同角三角函数根本关系,属于根底题. 6.31log 81等于〔〕 A.4 B.-4C.14D.14-【答案】B 【解析】 【分析】直接利用41381-=结合对数运算即可得解. 【详解】4331log log 3481-==-.应选:B.【点睛】此题主要考察了对数的运算,即可得解. 7.以下函数在区间〔0,2〕上必有零点的是〔〕 A.3y x =-B.2x y =C.3y x =D.lg y x =【答案】D 【解析】【分析】通过求函数的零点,验证是否在〔0,2〕即可得解. 【详解】对于A ,令30y x =-=,得3(0,2)x =∉,对于B ,20x y =>,所以不存在零点; 对于C ,令30y x ==,解得0(0,2)x =∉; 对于D ,令lg 0y x ==,得1(0,2)x =∈.应选:D.【点睛】此题主要考察了函数零点的概念,属于根底题.2sin x ≥0成立的x 的取值集合是()A.3|22,44x k x k k Z ππππ⎧⎫+≤≤+∈⎨⎬⎩⎭ B.7|22,44x k x k k Z ππππ⎧⎫+≤≤+∈⎨⎬⎩⎭C.5|22,44x k x k k Z ππππ⎧⎫-≤≤+∈⎨⎬⎩⎭ D.57|22,44x k x k k Z ππππ⎧⎫+≤≤+∈⎨⎬⎩⎭【答案】C 【解析】 【分析】首先对三角不等式进展恒等变换,变换成sin x 2≤,进一步利用单位圆求解.2sin x ≥0解得:sin x 2≤进一步利用单位圆解得:52244k x k ππππ-≤≤+〔k ∈Z 〕应选C .【点睛】此题考察的知识要点:利用单位元解三角不等式,特殊角的三角函数值. 9.5sin(2π)2y x =+的一条对称轴方程为〔〕 A.π2x =-B.π4x =-C.π8x =D.5π12x =【答案】A 【解析】 【分析】 令52π,22x k k Z ππ+=+∈,即可得解. 【详解】令52π,22x k k Z ππ+=+∈,解得:,2k x k Z ππ=-+∈. 当1k=时,轴为:π2x =-. 应选:A.【点睛】此题主要考察了正弦型函数的对称轴的求解,属于根底题.215()7sin()32f x x π=+是〔〕A.周期为3π的偶函数B.周期为2π的奇函数C.周期为3π的奇函数D.周期为43π的偶函数【答案】A 【解析】 【分析】化简函数2()7cos 3f x x =-,进而可得周期和奇偶性.【详解】函数21522()7sin()7sin()7cos 32323f x x x x ππ=+=-=-.周期2323T ππ==. 且22()7cos()7cos ()33f x x x f x -=--=-=,为偶函数.应选:A.【点睛】此题主要考察了诱导公式化简三角函数,及判断三角函数的奇偶性,属于根底题.π12cos?2y =-x 的最小值、最大值分别是()A.1,3-B.1,1-C.0,3D.0,1【答案】A 【解析】 由于π1cos 12x ≤≤-,故函数π12cos 2y x =-的最小值为121-=-,最大值为123+=. 应选A.27sin sin 4y x x =+-的最小值是〔〕 A.2 B.74C.14-D.不存在【答案】C 【解析】 【分析】令sin [1,1]tx =∈-,那么2271()242y t t t =-++=--+,再根据二次函数性质求最值即可. 【详解】令sin [1,1]t x =∈-,那么2271()242y t t t =-++=--+.当1t =-时,y 有最小值14-.应选:C.【点睛】此题主要考察了三角函数与二次函数的复合函数求最值,考察了换元法,属于根底题. 二、填空题(每一小题5分,一共20分)1tan 24y x π⎛⎫=-+ ⎪⎝⎭的单调递减区间是_______________.【答案】3(2,2),22k k k Z ππππ-++∈ 【解析】 【分析】由1tan 24y x π⎛⎫=-- ⎪⎝⎭,令1,2242k x k k Z πππππ-+<-<+∈,即可得解.【详解】11tan tan 2424y x x ππ⎛⎫⎛⎫=-+=-- ⎪ ⎪⎝⎭⎝⎭,令1,2242k x k k Z πππππ-+<-<+∈,解得322,22k x k k Z ππππ-+<<+∈.故答案为:3(2,2),22k k k Z ππππ-++∈.【点睛】此题主要考察了正切型函数的单调区间的求解,考察了整体代换的思想,属于根底题.的周长是6,中心角是1弧度,那么该扇形的面积为________. 【答案】2 【解析】试题分析:设扇形的弧长为l ,半径为r .那么有26,1lr lr+==,解得2l r ==.那么扇形的面积为1122222S lr ==⨯⨯=.考点:扇形的面积.α终边上一点(3,4)(0)P t t t ≠,那么sin α=______________.【答案】45± 【解析】 【分析】由任意角三角函数定义得4sin 5||tt α==,讨论0t >和0t <即可得解. 【详解】由任意角三角函数定义得:4sin 5||tt α==. 当0t>时,4sin 5α; 当0t <时,4sin 5α=-;故答案为:45±.【点睛】此题主要考察了任意角三角函数的定义,涉及分类讨论的思想,属于根底题. 16.tan 3α=,那么2212sin cos sin cos αααα+-的值是_______________.【答案】2 【解析】 【分析】 由22sin cos 1αα+=代入原式中交换1,再分子分母同时除以2cos α,结合正切值即可得解.【详解】由2222222212sin cos sin cos 2sin cos 12tan sin cos sin cos t 1an tan ααααααααααααα+++++==---. 因为tan 3α=,所以原式916291++==-.故答案为:2.【点睛】此题主要考察了同角三角函数关系22sin cos 1αα+=的妙用,属于根底题.三、解答题〔17题10分,18-22每一小题12分〕2cos(2)3y a x b π=-+的定义域是0,2π⎡⎤⎢⎥⎣⎦,值域是[]5,1-,求a ,b 的值.【答案】23a b =⎧⎨=-⎩或者21a b =-⎧⎨=-⎩【解析】【分析】先求得1cos(2)[,1]32x π-∈-,再讨论0a >和0a <两种情况求值域列方程求解即可. 【详解】当0,2x π⎡⎤∈⎢⎥⎣⎦时,ππ2π2[,]333x -∈-,1cos(2)[,1]32x π-∈-. 当0a>时,值域为:[,2][5,1]a b a b -++=-, 所以521a b a b -+=-⎧⎨+=⎩,解得23a b =⎧⎨=-⎩,当0a <时,值域为:[2,][5,1]a b a b +-+=-,所以251a b a b +=-⎧⎨-+=⎩,解得21a b =-⎧⎨=-⎩,综上:23a b =⎧⎨=-⎩或者21a b =-⎧⎨=-⎩.【点睛】此题主要考察了余弦型三角函数的值域问题,考察了分类讨论的思想及整体代换的思想,属于中档题.18.1sin cos ,,842x xx ππ=<<求以下各式的值: 〔1〕sin cos ;x x + 〔2〕cos sin .x x -【答案】〔1;〔2〕.【解析】 【分析】 〔1〕利用22sin cos 1x x +=,将sin cos x x +平方再根据角的范围开方即可得解;〔2〕将cos sin .x x -平方再根据角的范围开方即可得解 【详解】〔1〕由2225(sin cos )sin cos 2sin cos 12sin cos 4x x x x x x x x +=++=+=, 当42x ππ<<时,sin 0,cos 0x x >>,所以sin cos x x +=.〔2〕由2223(cos sin )sin cos 2sin cos 12sin cos 4x x x x x x x x -=+-=-=, 当42x ππ<<时,sin cos 0x x >>,所以cos sin x x -= 【点睛】此题主要考察了22sin cos 1x x +=的应用,属于根底题.19.3sin(3)cos(2)sin()2()cos()sin()f παππαααπαπα---+=----.(1)化简()f α.(2)假设α是第三象限角,且31cos()25πα-=,求()f α的值. (3)假设313απ=-,求()f α的值.【答案】〔1〕()cos f αα=-;〔2;〔3〕12-. 【解析】 【分析】〔1〕直接利用诱导公式化简即可得解;〔2〕利用诱导公式化简得1sin 5α=-,结合角的范围和同角三角函数关系可得解; 〔3〕直接代入313απ=-,结合诱导公式化简求值即可.【详解】(1)3sin(3)cos(2)sin()sin cos (cos )2()cos cos()sin()cos sin f παππαααααααπαπααα---+--===------.(2)31cos()sin 25παα-=-=,所以1sin 5α=-. 因为α是第三象限角,所以cos α==.所以()cos f αα=-=. (3)313απ=-时,31313111()cos()cos(10)cos()33332f πππππ-=--=--+=--=-. 【点睛】此题主要考察了诱导公式的化简及同角三角函数的关系的求解,属于根底题.20.()()4log 41x f x =-.〔1〕求()f x 的定义域;〔2〕讨论()f x 的单调性; 〔3〕.求()f x 在区间1,22⎡⎤⎢⎥⎣⎦上的值域. 【答案】〔1〕(0,)+∞;〔2〕在(0,)+∞上增函数;〔3〕4[0,log 15]【解析】【分析】〔1〕直接令真数大于0即可得解;〔2〕由41x t =-和4log y t =,结合同增异减即可得解;〔3〕直接利用〔2〕的单调性可直接得值域.【详解】〔1〕由()()4log 41x f x =-,得410->x ,解得0x >.所以定义域为:(0,)+∞;〔2〕由41x t =-在(0,)+∞上为增函数,且4log y t =为增函数, 所以()()4log 41x f x =-在(0,)+∞上为增函数;〔3〕由〔2〕知函数单调递增,1241log 4102f ⎛⎫⎛⎫=-= ⎪ ⎪⎝⎭⎝⎭,()()2442log 41log 15f =-=. 所以()f x 在区间1,22⎡⎤⎢⎥⎣⎦上的值域为4[0,log 15]. 【点睛】此题主要考察了对数与指数函数的复合函数,考察了复合函数的“同增异减〞的应用,属于根底题.()sin(2)f x x φ=+是奇函数,且02φπ<<.〔1〕求φ;〔2〕求函数f 〔x 〕的单调增区间.【答案】〔1〕φπ=;〔2〕3,,44k k k Z ππππ⎡⎤++∈⎢⎥⎣⎦〔开闭都对〕 【解析】【分析】〔1〕由(0)sin 0f φ==,结合02φπ<<可得解; 〔2〕令3222,22k x k k Z ππππ+≤≤+∈,可得解. 【详解】〔1〕函数()sin(2)f x x φ=+是奇函数,所以(0)sin 0f φ==, 解得:,k k Z φπ=∈. 又02φπ<<,所以φπ=; 〔2〕()sin(2)sin 2f x x x π=+=-. 令3222,22k x k k Z ππππ+≤≤+∈,解得:3,44k x k k Z ππππ+≤≤+∈. 所以增区间为:3,,44k k k Z ππππ⎡⎤++∈⎢⎥⎣⎦.〔开闭都对〕 【点睛】此题主要考察了三角函数的奇偶性和单调性,属于根底题. 22.sin ().cos x f x x= 〔1〕求函数f (x )的定义域;〔2〕判断函数f (x )的奇偶性,并说明理由;〔3〕在[],ππ-上作出函数f 〔x 〕的图像.【答案】〔1〕{|,}2x x k k Z ππ≠+∈;〔2〕奇函数;〔3〕见解析.【解析】【分析】〔1〕由分母不等于0即可得定义域;〔2〕利用奇函数定义判断()()f x f x -=-,从而得解; 〔3.【详解】〔1〕由可得:cos 0x ≠,所以,2xk k Z ππ≠+∈. 所以定义域为:{|,}2x x k k Z ππ≠+∈;〔2〕由〔1〕知函数的定义域关于原点对称,sin()sin ()()cos()cos x x f x f x x x---===--,所以()f x 为奇函数; 〔3〕tan ,22()tan ,22x x f x x x x ππππππ⎧-<<⎪⎪=⎨⎪--≤<-<≤⎪⎩或. 【点睛】此题主要考察了三角函数奇偶性的判断及正切函数的作图,涉及分段函数的表示,属于根底题.(1)求函数f (x )的最小正周期;(2)求函数f (x )在区间,64ππ⎡⎤-⎢⎥⎣⎦上的值域. 【答案】〔1〕π;〔2〕[0,3].【解析】【分析】〔1〕利用二倍角公式化简函数为()2sin(2)16f x x π=++,进而利用周期公式可得解; 〔2〕先求22,663x πππ⎡⎤+∈-⎢⎥⎣⎦,从而可得1sin(2),162x π⎡⎤+∈-⎢⎥⎣⎦,进而可得值域. 【详解】〔1〕2()2cos cos cos 22x x f x x x =+ 2sin(2)16x π=++.所以最小正周期为:22ππ=. 〔2〕由,64x ππ⎡⎤∈-⎢⎥⎣⎦,可得:22,663x πππ⎡⎤+∈-⎢⎥⎣⎦. 所以1sin(2),162x π⎡⎤+∈-⎢⎥⎣⎦. 所以f (x )在区间,64ππ⎡⎤-⎢⎥⎣⎦上的值域为:[0,3]. 【点睛】此题主要考察了三角函数的二倍角公式化简及整体代换求值域,属于根底题.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
望花高中2013-2014学年度上学期第二次月考测试题
高 一 数 学
满分:100分 时间:90分钟 第Ⅰ卷 客观题
一、选择题:(每小题4分,10道题,共40分)
1.设0.22()3a =,0.7
1.3b =,132()3
c =,则,,a b c 的大小关系为( )。
A .a b c <<
B .c a b <<
C .b c a <<
D .c b a << 2.函数2log (4)y x =-的定义域为( )。
A .(0,)+∞
B .(,4)-∞
C .(3,4)
D .(4,)+∞ 3.下面说法正确的是( )。
A 、不存在既不是奇函数,有又不是偶函数的幂函数;
B 、图象不经过点(-1,1)的幂函数一定不是偶函数;
C 、如果两个幂函数的图象有三个公共点,那么这两个幂函数相同;
D 、如果一个幂函数的图象不与y 轴相交,则y=αx 中α<0。
4.函数|21|x y =-在区间(k -1,k +1)内单调,则k 的取值范围是( )。
A .(,1]-∞-
B .[1,)+∞
C .(,1]-∞-∪[1,)+∞
D .[1,1]-
5.已知函数()f x =1
2x a
+-的图象恒过定点P ,则P 点的坐标为( )。
A 、(0,1)
B 、(-1,-1)
C 、(-1,1)
D 、(1,-1) 6.三棱锥A-BCD 中,以A
为顶点的三条侧棱两两垂直,且其长度分别为。
该三棱锥的四个顶点在同一个球面上,则这个球的表面积为
( ).
A .9π
B .12π
C .24π
D .36π
7.长方体中共一个顶点的三个面的面积分别是2、3、6,这个长方体
的体积是( )。
A 、23
B 、32
C 、6
D 、6
8. 一个四边形的斜二侧直观图是一个底角为45o ,腰和上底的长均为1的等腰梯形,那么原四边形的面积是( )。
装 订 线
A 、、、
22+、12
+ 9. 空间中,如果一个角的两边和另一个角的两边分别对应平行,那么这两个角的大小关系
为( )。
A .相等 B .互补 C .相等或互补 D .互余 10. 已知直线l ⊥平面α,m α⊂,则m 与l 不可能( )。
A 、垂直
B 、相交
C 、平行
D 、互为异面直线
第Ⅱ卷 主观题
二、填空题:(每小题5分,4道题,共20分)
11. 已知函数()log (3)a f x ax =-在[1,2]上是x 的减函数,则a 的取值范围
是 。
12. 如图,平面α∥β,A ,C ∈α,B ,D ∈β,直线AB 与CD 交于点P ,且AP=1,BP=4,
CD=6,那么CP= 。
13. 正方体ABCD -A B C D ''''的棱长为2,则三棱锥A '-BC D '的体积。
14.如图是正四棱锥P-ABCD 的三视图,其中主视图是边长为2的正三角形,则这个四棱锥的侧
棱长为 。
三、解答题:(每道小题10分,共4道小题,共40分) 15、已知2
()lg(1)f x x =-。
(1)求()f x 的定义域;
(2)求使()0f x >的x 取值范围。
16、已知在四面体ABCD 中,BD AC =,而且AC BD ⊥,H G F E ,,,分别是边
DA CD BC AB ,,,的中点.
求证:四边形EFGH 是正方形。
17.如右图,△BCD 中,∠BCD=90O , AB ⊥平面BCD ,E ,F 分别为AC ,AD 的中点。
求证:平面BEF ⊥平面ABC 。
18.正三棱锥的底面边长为6
装 订
侧面积。
望花高中2013-2014学年度上学期第二次月考测试题答题纸
高 一 数 学 满分:100分 时间:90分钟
第Ⅱ卷 主观题
二、填空题:(每小题5分,4道题,共20分) 11. 12. 13. 14.
三、解答题:(每小题10分,共4道小题,共40分) 装 订 线
线
2013-2014学年度上学期第二次月考测试题
高一数学参考答案
二、填空题:
11、312a <<
; 12、2; 13、8
3
; 14 三、解答题:
15.解:(1)令210x ->,解得1x <-或1x >。
………………………………3分
所以()f x 的定义域的定义域为(,1)
(1,)-∞+∞。
……………………2分
(2)因为lg y t =为(0,)+∞上的增函数,所以由()0f x >得211x ->,即 22x >,…………………………………………………………………2分
解得x <x >
2分
于是使()0f x >的x 取值范围是(,(2,)-∞+∞。
…………1分
16.证明:∵,E F 分别是边,AB BC 的中点,∴EF 是ABC ∆的中位线。
∴EF ∥AC ,EF 1
2AC =。
………………………………………………………2分 同理HG ∥AC ,HG 1
2
AC =。
……………………………………………………1分
∴EF ∥HG ,EF =HG 。
所以四边形EFGH 是平行四边形.……………………2分
∵BD AC =,EH 1
2
BD =,∴EF EH =. ………………………………………2分
∵AC BD ⊥,EH
BD ,∴EF EH ⊥. …………………………………………2分
所以四边形EFGH 是正方形。
………………………………………………………1分 17. 证明:∵AB ⊥平面BCD ,∴AB ⊥CD 。
………………………………………………2分 ∵∠BCD=90O ,∴CB ⊥CD 。
………………………………………………………………1分 ∵AB BC B =,AB ⊂平面ABC ,BC ⊂平面ABC ,∴CD ⊥平面ABC 。
……2分 ∵E ,F 分别为AC ,AD 的中点,∴EF ∥CD 。
……………………………………………2分 ∴EF ⊥平面ABC 。
…………………………………………………………………………1分 ∵EF ⊂平面BEF ,∴平面BEF ⊥平面ABC 。
…………………………………………2分
18. 解:如图,在正三棱锥S-ABC 中,设H 为ABC 的中心,连接SH ,则SH 为该 正三棱锥的高。
连接AH ,延长后交BC 于E ,则E 为BC 的中点,且AH BC ⊥。
………………………………………………………………………………………………1分
由于ABC ∆是边长为6的正三角形,∴62
AE =
=23AH AE ==
………………………………………………………………………………………………1分
在Rt SHA ∆中,SA =,AH =
所以SH =
……………………………………………………………2分
11
622
ABC S BC AE ∆=
⋅=⨯⨯= ………………………………………………………………1分
所以1
93
S ABC V -=⨯=。
………………………2分
连接SE ,则SE 为斜高,1
3
HE AE ==
在Rt SHE ∆中,SE
11
622
SBC S BC SE ∆=
⋅=⨯=3S =侧SBC S ∆=3分。
