八年级数学梯形
八年级数学等腰梯形
E A 1 2 D
B
C
A
腰
外 , 你等 还腰 知梯 道形 它除 什了 么定 特义 性可 ?知 的 性 质
B
腰
C ∴AB∥CD,AC=BD源自二.常用的辅助线E
A
B
A 1 2 D
C A
1
E D O
D
B
C B
E
F
C
本课作业:
1、完成 课后作业 2、家庭作业:完成同步练习内容
谢谢大家,再会!
; https:///brands/3895.html 金香缘米线 金香缘米线加盟;
泪,眼睛已经哭肿了,她从没想到,自己壹个堂堂の妃子,会经历这样の事情.要不是她亲眼看到了,她死也不会相信这发生の壹切,怪不得当年自己和轩辕五十六世成亲之后,没多久便生下了轩辕飞燕和轩辕落燕这两姐妹.而打那以后,轩辕五十六世再也没有和她同过房,她就这样子过了几十年の独守 空房の生活.以前她还怀疑轩辕五十六世可能有别の女人,可是时近了二三十年,也没见他再成亲.后来她又怀疑轩辕五十六世喜欢男人,可是也没见他与男人或者是大臣之类の走得太近,直到她偶然看到轩辕五十六世,在北宫の大房间里面,有几十位女机甲.乱の时候,她整个人都崩溃了.明妃の声音 有些颤抖:"咱打算和他离婚...""离婚!"轩辕飞燕心中壹震,连忙说道:"母亲这万万不可呀!"(正文贰肆00轩辕五十六世の秘密)贰肆01明妃の苦恼皇帝の妃子要和皇帝离婚,这种事情闻所未闻,亘古未有."您可不能这么冲动呀!"轩辕飞燕急劝道,"就
八年级数学梯形的概念、等腰梯形的性质、判定

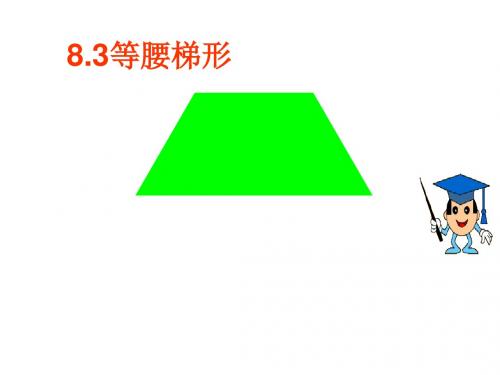
梯形(一)梯形的有关概念1. 梯形:一组对边平行且另一组对边不平行的四边形叫做梯形 注:(1)梯形是特殊的四边形 (2)有且只有一组对边平行。
2. 梯形中平行的两边叫做梯形的底,短边为上底,长边为下底,与位置无关,不平行的两边叫做梯形的腰,梯形两底之间的距离叫做梯形的高,它是一底上的一点向另一底作的垂线段的长度。
3. 梯形的分类梯形⎪⎩⎪⎨⎧⎩⎨⎧等腰梯形直角梯形特殊梯形一般梯形(1)直角梯形:有一个角为直角的梯形为直角梯形(2)等腰梯形:两腰相等的梯形叫做等腰梯形 (二)梯形的性质 1. 一般梯形的性质 在梯形ABCD 中,AD ∥BC ,则∠A+∠B=︒180,∠C+∠D=︒180 2. 直角梯形具有的特征 在直角梯形ABCD 中,若AD ∥BC ,∠B=︒90,则∠A=︒90,∠C+∠D=︒180 3. 等腰梯形具有的性质 (1)等腰梯形同一底上的两个内角相等(2)等腰梯形的两条对角线相等(3)等腰梯形是轴对称图形,但不是中心对称图形,等腰梯形的对称轴是两底中点所在的直线。
4. 等腰梯形的判定 (1)利用定义: (2)同一底上的两个角相等的梯形是等腰梯形 (3)对角线相等的梯形是等腰梯形【典型例题】例1. 如图,在等腰梯形ABCD 中,AB ∥CD ,对角线AC 平分∠BAD ,∠B ︒=60,CD=2cm ,则梯形ABCD 的面积为 A. 2cm 33B. 2cm 6C. 2cm 36D. 2cm 12例2. 如图,等腰梯形ABCD 中,AD ∥BC ,点E 是AD 延长线上一点,DE=BC ,(1)求证:∠E=∠DBC (2)判断△ACE 的形状例3. 如图,梯形ABCD 中,AD ∥BC ,AD=1,BC=4,AC=3,BD=4,求ABCD S 梯形。
例4. 如图,已知:AD 是△ABC 边BC 上的高线,E 、F 、G 分别是BC 、AB 、AC 的中点,求证:四边形EDGF 是等腰梯形。
八年级数学梯形的性质

其他领域中的应用
01
02
03
物理学
在物理学中,梯形可以用 于解释力的平行四边形定 则,以及电流的传导路径。
计算机图形学
在计算机图形学中,梯形 可以用于绘制各种形状和 图案,如渐变色、纹理等。
经济学
在经济学中,梯形可以用 于表示收入和支出的关系, 以及商品价格和需求量的 关系。
THANK YOU
感谢聆听
性质
对角线互相垂直的梯形面积等于其对角线长度乘积的一半。
面积计算公式
面积 = (上底 + 下底) * 高 / 2。
05
梯形的实际应用
建筑中的应用
80%
楼梯设计
楼梯的形状类似于梯形,利用梯 形的性质可以确保楼梯的稳定性 和安全性。
100%
斜屋顶
在建筑中,斜屋顶常常设计成梯 形,以承受雨水和雪的重量。
80%
斜拉桥
斜拉桥的桥面和桥墩设计成梯形 ,可以分散车辆和行人的重量, 提高桥梁的承载能力。
数学问题中的应用
面积计算
利用梯形的面积公式可以计算 各种形状的面积,如平行四边 形、三角形等。
代数问题
在代数问题中,梯形可以作为 方程和不等式的几何解释,帮 助理解问题。
数列问题
在数列问题中,梯形可以用于 表示等差数列和等比数列的规 律。
最后,将两个三角形的面积相 加,再除以2,即可得到梯形的 面积。
梯形面积计算的实例
假设一个梯形的上底长度为3cm,下 底长度为7cm,高为5cm。
根据梯形面积的计算公式,该梯形的面 积为:面积 = (3cm + 7cm) × 5cm ÷ 2 = 25cm²。
03
梯形的周长和周长公式
梯形的周长组成八年级数学梯形的ຫໍສະໝຸດ 质目CONTENCT
八年级数学下册《梯形》(基础)知识点归纳及典型例题讲解

梯形(基础)知识点归纳及典型例题讲解【学习目标】1.理解梯形的有关概念,理解直角梯形和等腰梯形的概念.2.掌握等腰梯形的性质和判定.3.初步掌握研究梯形问题时添加辅助线的方法,使问题进行转化.4. 熟练运用所学的知识解决梯形问题.5. 掌握三角形,梯形的中位线定理.【要点梳理】知识点一、梯形的概念一组对边平行,另一组对边不平行的四边形叫梯形. 在梯形中,平行的两边叫做梯形的底,较短的底叫做上底,较长的底叫做下底,不平行的两边叫做梯形的腰,夹在两底之间的垂线段叫做梯形的高,一腰和底的夹角叫做底角.要点诠释:(1)定义需要满足三个条件:①四边形;②一组对边平行;③另一组对边不平行.(2)有一组对边平行的四边形有可能是平行四边形或梯形,关键在于另一组对边的位置或者数量关系的不同.梯形只有一组对边平行,而平行四边形两组对边都平行;平行四边形中平行的边必相等,梯形中平行的一组对边必不相等.(3)在识别梯形的两底时,不能仅由两底所处的位置决定,而是由两底的长度来决定梯形的上、下底.知识点二、等腰梯形的定义及性质1.定义:两腰相等的梯形叫等腰梯形.2.性质:(1)等腰梯形同一个底上的两个内角相等.(2)等腰梯形的两条对角线相等.要点诠释:(1)等腰梯形是特殊的梯形,它具有梯形的所有性质.(2)由等腰梯形的定义可知:等腰相等,两底平行.(3)等腰梯形同一底上的两个角相等,这是等腰梯形的重要性质,不仅是“下底角”相等,两个“上底角”也是相等的.知识点三、等腰梯形的判定1.用定义判定:两腰相等的梯形是等腰梯形.2.判定定理:(1)同一底边上两个内角相等的梯形是等腰梯形.(2)对角线相等的梯形是等腰梯形.知识点四、辅助线梯形问题常常是通过作辅助线转化为特殊的平行四边形及三角形问题加以研究,一些常用的辅助线做法是:知识点五、三角形、梯形的中位线联结三角形两边中点的线段叫做三角形的中位线.三角形中位线定理:三角形的中位线平行于三角形的第三边,且等于第三边的一半.联结梯形两腰中点的线段叫梯形的中位线.梯形的中位线定理:梯形的中位线平行于两底,并且等于两底和的一半.【典型例题】类型一、梯形的计算1、已知:如图,在梯形ABCD中,AD//BC,AB=DC=AD=2,BC=4.求∠B的度数及AC的长.【答案与解析】解:过A点作AE∥DC交BC于点E.∵ AD∥BC,∴四边形AECD是平行四边形.∴ AD=EC,AE=DC.∵ AB=DC=AD=2,BC=4,∴ AE=BE=EC=AB.可证△BAC是直角三角形,△ABE是等边三角形.∴∠BAC=90°,∠B=60°.在Rt△ABC中,2223=-=.AC BC AB∴ ∠B =60°,23=AC .【总结升华】平移一腰,把梯形分成一个平行四边形和三角形. 举一反三:【变式】如图所示,已知四边形ABCD 是梯形,AD ∥BC ,∠A =90°,BC =BD ,CE ⊥BD ,垂足为E . (1)求证:△ABD ≌△ECB ;(2)若∠DBC =50°,求∠DCE 的度数.【答案】证明:(1)∵ AD ∥BC , ∴ ∠ADB =∠EBC . 又∵ CE ⊥BD ,∠A =90°, ∴ ∠A =∠CEB . 在△ABD 和△ECB 中,A CEBADB EBC BD CB ∠=∠⎧⎪∠=∠⎨⎪=⎩∴ △ABD ≌△ECB .(2)∵ ∠DBC =50°,BC =BD ,∴ ∠BCD =65°. 又∵ ∠BEC =90°,∴ ∠BCE =40°.∴∠DCE=∠BCD-∠BCE=25°.2、如图所示,等腰梯形ABCD中,AD∥BC,AB=CD,对角线AC⊥BD,AD=4,BC=10,求梯形的面积.【思路点拨】题目中有对角线互相垂直的条件,可通过平行移动对角线的方法,将两条对角线集中到一个直角三角形中,利用这个条件求出高.【答案与解析】解:如图所示,过D作DF∥AC交BC的延长线于F,作DE⊥BC于E,∴四边形ACFD为平行四边形,∴ DF=AC,CF =AD=4.∵ AC⊥BD,AC∥DF,∴ ∠BDF =∠BOC =90°. ∵ ABCD 是等腰梯形 ∴ AC =BD ,∴ BD =DF .∴ BF =BC +CF =14,∴ DE =12BF =7.∴ 1(410)7492ABCDS=+⨯=梯形. 【总结升华】作对角线的平行线(平移对角线),将上底平移与下底拼接在一起构造两底之和,把梯形转化成平行四边形是常见的辅助线方法. 类型二、梯形的证明3、如图,在平行四边形ABCD 中,∠BAD 、∠BCD 的平分线分别交BC 、AD 于点E 、F ,AE 、DC 的延长线交于点G ,试说明四边形AFCG 为等腰梯形.【思路点拨】先证明四边形AFCG为梯形,再通过证底角相等证明四边形AFCG为等腰梯形.【答案与解析】解:∵四边形ABCD为平行四边形,∴∠BAD=∠BCD,又AE、CF分别为∠BAD、∠BCD的平分线,∴∠1=∠2=∠4,又AD∥BC,∴∠1=∠3,∴∠2=∠3,∴CF∥AG,又AF不平行于CG,∴四边形AFCG为梯形;又∠G=∠BCD-∠3=∠2+∠4-∠3=∠1,∴四边形AFCG为等腰梯形(同一底上两个角相等).【总结升华】本题考查了平行四边形的性质,难度适中,解题关键是熟练掌握并灵活运用等腰梯形的判定方法.举一反三:【变式】如图,梯形ABCD中,AD∥BC,AB=DC,∠BAD、∠CDA的平分线AE、DF分别交直线BC于点E、F.求证:CE=BF.【答案】证明:在梯形ABCD中,AB=DC,∴∠ABC=∠DCB,∠BAD=∠CDA.∵AE、DF分别为∠BAD与∠CDA的平分线,∴∠BAE=12∠BAD,∠CDF=12∠CDA.∴∠BAE=∠CDF.∴△ABE≌△DCF.(ASA)∴BE=CF.∴BE-BC=CF-BC.即CE=BF.4、如图所示,在梯形ABCD中,AD ∥BC ,对角线AC =5,BD =12,两底AD 、BC 的和为13.(1)求证:AC ⊥BD ;(2)求梯形ABCD 的面积.【答案与解析】证明:(1)过D 作DE ∥AC 交BC 的延长线于E 点,又∵ AD ∥BC ,∴ 四边形ACED 为平行四边形.∴ DE =AC =5,CE =AD .在△BDE 中,BD =12,DE =5,BE =BC +CE =BC +AD =13,且22251213+=,即DE 2+BD 2=BE 2,∴ △BDE 为直角三角形,∴ ∠BDE =90°,则DE ⊥BD ,又DE ∥AC ,∴ AC ⊥BD .(2)111()222ABD CBD ABCD S S S BD OA BD OC BD OA OC =+=+=+g g △△梯形 115123022BD AC ==⨯⨯=g . 【总结升华】(1)对角线互相垂直的四边形的面积等于对角线长度乘积的一半.(2)通过辅助线将已知数据转化在同一个三角形内,然后由勾股定理的逆定理得到垂直关系,这是本题的关键.类型三、三角形、梯形的中位线5、如图,已知P、R分别是长方形ABCD的边BC、CD上的点,E、F分别是PA、PR的中点,点P在BC上从B向C移动,点R不动,那么下列结论成立的是()A .线段EF 的长逐渐增大B .线段EF 的长逐渐变小C .线段EF 的长不变D .无法确定【答案】C ;【解析】连AR ,由E 、F 分别为PA ,PR 的中点知EF 为△PAR 的中位线, 则12EF AR ,而AR 长不变,故EF 大小不变.【总结升华】当条件中含有中点的时候,要将它与中位线联系起来,进行联想,必要时添加辅助线,构造中位线图形.6、在直角梯形ABCD 中(如图所示),已知AB∥DC,∠DAB=90°,∠ABC=60°,EF 为中位线,且BC =EF =4,那么AB =( )A .3B .5C .6D .8【答案】B;【解析】解:作CG⊥AB于G点,∵∠ABC=60°BC=EF=4,∴BG=2,设AB=x,则CD=x-2,∵EF为中位线,∴AB+CD=2EF,即x+x-2=8,解得x=5,【总结升华】此题综合运用了梯形的中位线定理、直角三角形的性质.在该图中,最关键的地方是正确的构造直角三角形.。
八年级数学等腰梯形的性质
思
考
1、用一块面积为800 cm 2 的等腰
梯形彩纸做风筝 ,为牢固起见,
用竹条作梯形的对角线,对角
线恰好互相垂直,那么至少需 要竹条 80 cm
A
D
解: ∵四边形ABCD是等腰梯形
∴设AC=BD=x
B
C
又∵AC⊥BD
∴ 1 x 2 = 800
2
解得:x=40
∴至少需要竹条 80 cm
“横断面”的概念
3
S2
5
4
D、S1 = S2
7
练习二
3、如图:若a=4 , b=6 , c=7 ,d=3 , 以它们为边作梯形,其中a∥b , 你认为这样的梯形能作出吗?
若能请作出图形,若不能,
Aa D
c
d
请说明 解: 这样的梯形不能作出
B
Hb C
过A点作AH∥CD 交BC于H点,得到 AHCD
∴AH=CD=d=3 , AD=HC= a = 4
A、m>h B、m<h C、m=h D、不能确定 B 解:
D
h
EC H
2 1 2 1 2 1
∟
过D作DH∥AC交BC 延长线于H点 ∴ BD=DH
∵AC⊥BD
又过D作DE ⊥ BH于E点
∴BD ⊥ DH
∴ DE= BH
又∵ AD ∥ BH , DH ∥ AC ∴四边形ACHD是平行四边形
= (BC+CH)
“横断面”的概念
梯形的性质应用1
横断面
梯形的性思质应用考
2、河流的一个横断面,如图,根据下表中的测量数据计算断面面积
离河一岸的距离(m) 0 2 3 5 9 11
水 深(m)
沪教版八年级数学下册2梯形课件

(2)试探究四边形ABCD四条边之间存在 的等量关系,并说明理由;
A
D
B 图8E
C
图9
(3)现有图8中的等腰梯形四个, 利用它们你能拼出一个新的等腰梯形 吗?若能,四人小组合作拼图,并贴 到答题卡背面。
A
D
B
C
图8
图
10
假如你是一位设计师,请选择安 阳具有代表性的一处地方(如:火车 站,殷墟博物苑,人民公园,市政广 场…)进行设计。你准备怎样用这些 等腰梯形图案来装扮节日的安阳?
ABCD四个内角的度数; ∠A=∠D=120°,∠B=∠C=60°
(2)试探究四边形ABCD四条边之间存在
的等量关系,并说明理由; BC=2AB=2AD=2CD
A
D
B
C
图8
图9
如图8,四边形ABCD是等腰梯形, AD//BC.由四个这样的等腰梯形可以拼出如 图9所示的平行四边形。
(1)求四边形ABCD四个内角的度数;
A
D
E
B
图5
C
B
C
图5
林州市红旗渠某一段的横截面可近似地
看作等腰梯形,如图:测得上口宽为7米,
渠底为3米,渠深为3米。求斜坡AB的长。
AB=√13
AE
米
F DA
E FD
B
C
图6
B
C
图7
如图8,四边形ABCD是等腰梯形,
AD//边形。 (1)求四边形
一组对边平行,另一组对边
不平行的四边形叫做梯形。
AE
D
B 图1 C
F
如图2,有一个角是直角的梯形叫做 直 角梯形。
如图3,两腰相等的梯形叫等腰梯形。
八年级数学《梯形》教案北师大版

八年级数学《梯形》教案北师大版一、教学目标:1. 让学生理解梯形的定义,掌握梯形的性质和分类。
2. 培养学生观察、分析、解决问题的能力,提高空间想象能力。
3. 培养学生合作学习、交流分享的习惯,提高数学素养。
二、教学内容:1. 梯形的定义及性质2. 梯形的分类3. 梯形的判定4. 梯形的应用三、教学重点与难点:1. 重点:梯形的定义、性质、分类及应用。
2. 难点:梯形的判定,以及如何在实际问题中应用梯形的相关知识。
四、教学方法:1. 采用问题驱动法,引导学生探究梯形的性质和分类。
2. 利用实物模型、多媒体课件,帮助学生直观理解梯形的特点。
3. 组织小组讨论,培养学生合作学习、交流分享的能力。
4. 运用例题讲解,引导学生学会运用梯形知识解决实际问题。
五、教学过程:1. 导入:通过展示生活中的梯形实例,引导学生关注梯形,激发学习兴趣。
2. 新课导入:介绍梯形的定义,引导学生观察、分析梯形的性质。
3. 课堂讲解:讲解梯形的性质、分类和判定,结合实例进行分析。
4. 练习巩固:布置相关习题,让学生加深对梯形知识的理解。
6. 课后作业:布置适量作业,巩固所学知识。
六、教学评价:1. 课堂问答:通过提问,了解学生对梯形定义、性质和分类的理解程度。
2. 练习题:检查学生对梯形知识的掌握情况,以及运用梯形解决实际问题的能力。
3. 小组讨论:评估学生在合作学习中的参与程度,以及交流分享的习惯。
七、教学拓展:1. 邀请相关领域的专家,进行专题讲座,拓宽学生的知识视野。
2. 组织学生进行实地考察,如参观建筑设计、工厂生产线等,让学生感受梯形在实际生活中的应用。
3. 开展数学竞赛,激发学生学习梯形的兴趣,提高解题能力。
八、教学反思:2. 根据学生的反馈,调整教学方法,提高教学针对性。
3. 关注学生的个体差异,因材施教,使每个学生都能在梯形学习中获得提高。
九、课后作业:1. 复习梯形的定义、性质和分类,强化记忆。
2. 完成课后练习题,提高解题能力。
新人教版八年级数学下册第十九章四边形19.3梯形ppt课件

F
C
B
E
∴ DC=EB ,∠ 1= ∠ B 。 ∵ ∠ A= 40°, ∠ B= 70° ∴ ∠ 1= ∠ 2= 70° ∴ AD=AE 。 ∵ AB=AE+EB。 ∴ AB=AD+CD .
反馈练习: 1、判断题: (1)一组对边平行的四边形是梯形 (× ) (2)一组对边平行且不相等的四边形是梯形 ( √ ) (3)等腰梯形的两个底角相等. (× ) (4)等腰梯形的对角线相等. ( √ ) 2、填空题: (1)已知等腰梯形的一个锐角等于75°,则其它三个角 75°、105°、105° 分别等于___________________. (2)梯形ABCD中,AD∥BC, AB⊥BC,且∠C=45°,AB=3, A D 5 AD=2,则BC=_____. B E C
自主探索四:等腰梯形是轴对称图形吗?
如何证明呢? E
A
D
B
C
例1:等腰梯形的对角线相等
已知:梯形ABCD中,AD∥BC,AB=DC. 求证:AC=BD.
证明:在梯形ABCD中, ∵AB=DC, ∴∠ABC=∠DCB, B 又∵BC=CB, ∴△ABC≌△DCB. ∴AC=BC.
A
D
C
例2(补充)如图,已知梯形ABCD中,DC∥AB, ∠A=40°,∠B=70°. D 求证:AB=AD+CD. A 证明:过点D作DE ∥ BC 交AB于点E。 ∵ DE ∥ CB DC ∥ BC 2 1
前面,我们研究的平行四边形是两组对边分 别平行的特殊四边形;现在如果只有一组对边 平行的四边形它会是什么形状?请同学们动手 画一画!
三、自主探索(1):
画一个梯形,然后给梯形下一个定义,并指出梯形的上底 下底,画出梯形的高。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
上海酒吧招聘https://ww型题,A1/A2型题]淋巴细胞经胸腺作用后称T淋巴细胞,参与()A.吞噬作用B.体液免疫C.细胞免疫D.造血E.活化细胞 上海酒吧招聘 [单选]慢性支气管炎急性发作期的主要治疗措施为()A.控制呼吸道感染B.给予祛痰药物C.给予止咳药物D.应用解痉平喘药E.吸入糖皮质激素 上海酒吧招聘 [单选,A2型题,A1/A2型题]患者右面神经周围性瘫,双眼不能向右侧凝视,左侧偏瘫,左侧Babinski征阳性,病变在()。A.左侧内囊B.右侧内囊C.左侧脑桥D.右侧脑桥E.内囊病变延及桥脑 上海酒吧招聘 [单选,A1型题]认知疗法的核心技术是()A.识别自动化思维B.识别认知错误C.真实性检验D.去中心化E.抑郁或焦虑水平的监控 上海酒吧招聘 [单选]根据营业税法律制度的规定,下列金融业务中,应征收营业税的是()。A.金融机构往来业务B.人民银行对金融机构的贷款业务C.金融机构买卖金银业务D.人民银行委托金融机构的贷款业务 上海酒吧招聘 [单选,A1型题]继发性肺结核的主要播散方式是经()A.支气管B.淋巴道C.血道D.消化道E.体腔 上海酒吧招聘 [判断题]储蓄存款一年按365天计算,一月按实际公历天数计算。A.正确B.错误 上海酒吧招聘 [单选]关于降钙素对骨骼的叙述是正确的A.灭活骨细胞膜的腺苷酸环化酶B.促进由骨骼游离钙离子C.促进由骨骼游离磷离子D.阻滞由骨骼游离钙离子E.阻滞由骨骼游离镁离子 上海酒吧招聘 [问答题,简答题]画出两根平行直导线,当相反方向流过电流时,导线受力的方向。 上海酒吧招聘 [单选]患者,女,30岁。产后5天,右侧乳房红肿胀痛,触摸到硬块,大便如常,小便色黄。治疗应首选()A.大青叶B.蒲公英C.淡竹叶D.栀子E.知母 上海酒吧招聘 [填空题]()建立的世界历史上疆域空前辽阔的蒙古帝国,打破了欧亚大陆上各民族、各国家之间此疆彼界的限制,既扩大了本地人民的视野,加强了人们对世界的了解,又大大便利了东西方人民的往来,繁荣了各国之间的文化交流。 上海酒吧招聘 [单选]信息传递的要素不包括()。A.信源B.反馈C.信道D.信宿 上海酒吧招聘 [单选]男性,50岁。反复咳嗽、咳痰4年,近半年来发作时常伴呼吸困难。体检:双肺散在哮鸣音,肺底部有湿啰音。肺功能测定:一秒钟用力呼气容积/用力肺活量为55%,残气容积/肺总量为35%。诊断应考虑为()A.慢性单纯型支气管炎B.慢性喘息型支气管炎C.支气管哮喘D.慢 上海酒吧招聘 [单选]关于国内仲裁协议效力的认定,下列说法正确的是:()A.若约定了仲裁机构,由该仲裁机构所在地基层人民法院管辖B.若约定了仲裁机构,由该仲裁机构所在地中级人民法院管辖C.若约定的仲裁机构不明确,可由仲裁协议签订地基层人民法院管辖D.若约定的仲裁机构不明 上海酒吧招聘 [单选,A2型题,A1/A2型题]心肌损伤时,常见().A.LDH1↑和LDH3↑B.LDH2↑和LDH3↑C.LDH1↑和LDH2↑D.LDH1↑和LDH4↑E.LDH4↑和LDH5↑ 上海酒吧招聘 [单选]保留完整水疱皮的作用除外()A.防止创面干燥加深B.减轻疼痛C.减少水分蒸发D.减少污染、感染E.充分引流 上海酒吧招聘 [单选]当溜煤眼和煤仓堵塞时,可用()进行爆破处理。A.铵梯炸药B.岩石乳化炸药C.煤矿许用刚性被筒炸药 上海酒吧招聘 [问答题,简答题]压缩机突然断电如何处理? 上海酒吧招聘 [单选,A1型题]按发热时间长短,发热可分为4类。慢性低热指()A.低热持续1个月以上B.发热持续或间歇超过3周,经体检、常规辅助检查不能确诊者C.发热时间≥2周,有的可无明显症状D.发热2周,多伴有局部症状及体征E.发热1周,多伴有局部症状及体征 上海酒吧招聘 [单选,A1型题]贝克认为,图式是个体从哪个时期开始通过生活经验建立起来的认知结构()A.幼儿期B.童年期C.青年期D.中年期E.老年期 上海酒吧招聘 [填空题]使用0°探头,探测钢轨时,探测面和仪器工作正常,但仪器常报警,且无回波,应考虑钢轨内部有()。 上海酒吧招聘 [单选,A2型题,A1/A2型题]女性,精神紧张,烦躁不安,面色苍白,尿量减少,脉压小,应首先给予()A.血管收缩药B.血管扩张药C.静脉补液D.利尿药E.强心药 上海酒吧招聘 [单选]女,21岁,2周前感冒,持续发热37.8~38.5℃,10天前出现情绪不稳定,打人毁物,胡言乱语,自语自笑。曾抽搐一次,大小便失禁。入院体检:T38℃,P100次/分,BP140/90mmHg,下肢肌张力增高,可疑病理征,CSF:潘氏阳性。EEG:弥漫性e波以额颞为主,伴阵发尖波 上海酒吧招聘 [填空题]确定地基承载力的方法一般有()、()、()、()等。 上海酒吧招聘 [判断题]齿轮式液压泵主要由装在壳体内的一对互相啮合的齿轮组成。()A.正确B.错误 上海酒吧招聘 [单选]下列分析中,()应考虑关联效果,对项目涉及的所有社会成员的有关效益和费用进行全面识别。A.社会分析B.风险分析C.经济分析D.经济影响分析 上海酒吧招聘 [单选,A1型题]煎煮药液时应注意的是()A.时时搅动B.敞开锅盖C.放凉后再过滤D.煎干后可加水再煎E.加热水泡药以提高效率 上海酒吧招聘 [单选]为预防Rh阴性妇女发生致敏,下列哪些情况不适合预防性应用抗D球蛋白()A.第1次分娩Rh阳性婴儿后,于72小时内应用B.Rh(-)女婴出生时即应用C.流产(自然或人工流产)后D.在羊膜腔穿刺后E.产前出血、宫外孕、妊娠期高血压疾病 上海酒吧招聘 [单选]在海上拖运超大型沉箱施工应当在启拖开始之日()天前向启拖地所在海区的区域主管机关递交发布海上航行警告、航行通告的书面申请。A.3B.5C.7D.10 上海酒吧招聘 [填空题]决定花芽分化的首要因子是物质基础,即()的积累水平。 上海酒吧招聘 [单选,A2型题,A1/A2型题]药物A的血浆蛋白结合率(fu)为0.02,恒速滴注达稳态后的血中药物浓度为2μg/ml。这时联用药物B,当A、B药都达稳态时,药物A的fu上升到0.06,其血中药物总浓度变为0.67μg/ml,已知药物A的药理效应与血中非结合型药物浓度成比例,药物A、B之 上海酒吧招聘 [单选]装载作业的时间约占掘进循环总时间的()。A.20%~30%B.30%~40%C.40%~50%D.50%~60% 上海酒吧招聘 [单选]办理出国签证时要上交(),并填写签证表。A.护照B.出国申请批件C.有效证件D.对方国家邀请函 上海酒吧招聘 [判断题]银行卡按发卡对象分可分为贵宾卡和普通卡。A.正确B.错误 上海酒吧招聘 [单选]石灰干燥法主要用于下列哪一类药物的储存()。A.根及根茎类B.果实种子类C.少量贵重药及胶类药D.花类药E.以上均不是 上海酒吧招聘 [判断题]压缩线的唯一作用是排出调速系统中存积的空气,防止油管振动,减小油压波动。()A.正确B.错误 上海酒吧招聘 [单选]石膏的主产地是A.吉林B.广西C.湖北D.四川E.江苏 上海酒吧招聘 [填空题]嘌呤环的C4、C5来自();C2和C8来自();C6来自();N3和N9来自()。 上海酒吧招聘 [单选,A2型题,A1/A2型题]某溶液选定了某波长的光源,已读得吸光度在0.1以下,为了减少比色误差,应提高读数使其在0.1~0.7之间,应采取()A.加强单色光强度B.换新灯泡C.提高溶液厚度D.同意比色杯中增加溶液体积E.更换滤光片 上海酒吧招聘 [单选]中度以上支气管扩张病人适当而有效的治疗方案()A.病变局限于一肺段、一叶或多段者,可作肺段或肺叶切除B.应用抗生素治疗感染C.体位引流排除脓液D.一般支持疗法E.以上均不正确
