最新数学分析考试试卷答案样本(A卷)讲课稿
数学分析试卷(A)

数学分析试卷(A)s 一、选择题(每小题3分,共18分) 1.设2{|60}Mxxx, {|11}Rxx,则MR为( ) A.{|3}xx B.{|2}xx C.{|21}xx D.{|1}xx 2.21lim(1)xxx( ) A.1 B.0 C. D.e 3.设2xyzexy,则zx( )
A.2xyxyye B.2xyxxe C.2xyxye D.2xyxyxe 4.幂级数1(1)nnnxn的收敛区间是( ) A.(1,1) B.[1,1) C.(1,1] D.[1,1] 5.设D由平面曲线yx及2yx所围,则二重积分(,)Dfxyd化为二次积分为( )
A.210(,)xxdxfxydy B.210(,)xxdxfxydy C.210(,)xxdyfxydx D.10(,)yydyfxydx 6.20xedx( ) A.12 B.12 C.2 D.-2 二、填空题(每小题3分,共15分) 1.设()(1)()fxxxxn,则(0)f .
2.3cossinxexdx .
3.若常数项级数110nnu,则limnnu . 4.设2lnxzy,则(1,2)|dz . 5.平面曲线32616yxx的拐点是 . 三、计算题(每小题9分,共45分)
1.求2201arctanln(1)2limxxxxx. 2.设函数()fx处处连续,且满足方程2011()sin2cos222xftdtxxxx(x为任意实数),试计算()4f和()4f. 3.求240secxxdx. 4.将()(1)(12)xfxxx展开成x的幂级数. 5.22xyDedxdy,其中D是圆环形区域2214xy. 四、证明题(10分) 设0ba,证明不等式22arctanarctan11babababa. 五、应用题(12分) 在椭圆2244xy上求一点,使其到直线:2360Lxy的距离最小,并求此距离.
数学分析试题及答案解析,(1)

数学分析试题及答案解析,(1)20xx ---20XX学年度第二学期《数学分析2》A试卷学院班级学号(后两位)姓名题号一二三四五六七八总分核分人得分一. 判断题(每小题3分,共21分)(正确者后面括号内打对勾,否则打叉) 1.若在连续,则在上的不定积分可表为(). 2.若为连续函数,则().3. 若绝对收敛,条件收敛,则必然条件收敛().4. 若收敛,则必有级数收敛()5. 若与均在区间I上内闭一致收敛,则也在区间I上内闭一致收敛().6. 若数项级数条件收敛,则一定可以经过适当的重排使其发散于正无穷大().7. 任何幂级数在其收敛区间上存在任意阶导数,并且逐项求导后得到的新幂级数收敛半径与收敛域与原幂级数相同(). 二. 单项选择题(每小题3分,共15分) 1.若在上可积,则下限函数在上() A.不连续 B. 连续 C.可微 D.不能确定 2. 若在上可积,而在上仅有有限个点处与不相等,则() A. 在上一定不可积;B. 在上一定可积,但是;C. 在上一定可积,并且;D. 在上的可积性不能确定. 3.级数 A.发散 B.绝对收敛C.条件收敛 D. 不确定 4.设为任一项级数,则下列说法正确的是() A.若,则级数一定收敛;B. 若,则级数一定收敛;C. 若,则级数一定收敛;D. 若,则级数一定发散;5.关于幂级数的说法正确的是() A. 在收敛区间上各点是绝对收敛的;B. 在收敛域上各点是绝对收敛的;C. 的和函数在收敛域上各点存在各阶导数;D. 在收敛域上是绝对并且一致收敛的;三.计算与求值(每小题5分,共10分) 1. 2.四. 判断敛散性(每小题5分,共15分) 1. 2.3. 五. 判别在数集D上的一致收敛性(每小题5分,共10分) 1. 2. 六.已知一圆柱体的的半径为R,经过圆柱下底圆直径线并保持与底圆面角向斜上方切割,求从圆柱体上切下的这块立体的体积。
(本题满10分)七. 将一等腰三角形铁板倒立竖直置于水中(即底边在上),且上底边距水表面距离为10米,已知三角形底边长为20米,高为10米,求该三角形铁板所受的静压力。
数学分析试卷及答案6套

数学分析试卷及答案6套第一套试卷一、选择题(共20题,每题4分,共80分)1. 若函数f(x) = 3x^2 + 2x - 1,求f(-1)的值是多少?A. -4B. 4C. 0D. 12. 函数f(x) = ln(x^2 + 1)在区间(-∞, 0)上的最小值是多少?A. ln(1)B. ln(0)C. ln(-1)D. 不存在最小值3. 已知函数f(x)在区间[0, 5]上连续,且f(0) = 2, f(5) = 1,证明在该区间上存在一个点c,使得f(c) = 3.(请写出证明过程)4. 求不等式2x - 5 < 3x + 2的解集。
A. x < -7B. x > -7C. x > -3D. x < -35. 设函数f(x)在区间[a, b]上连续,且f(a) = f(b),证明在该区间上至少存在两个不同的点c和d,使得f(c) = f(d).(请写出证明过程)..................第一套答案一、选择题1. B2. A3. (证明过程略)4. A5. (证明过程略)二、填空题(共5题,每题4分,共20分)1. 若e^x = 2,则x = ln(2);2. 设a, b为实数,若a^2 + 2ab + b^2 = 0,则a = -b;3. lim(x→∞) (x^2 - 2x - 3)/(3x + 1) = 1;4. 若函数f(x) = x^2 + 3x - 2,则f(-1) = -6;5. 若f(x) = √(2x + 1),则f'(x) = 1/√(2x + 1)。
三、解答题(共3题,每题20分,共60分)1. 设函数f(x) = x^3 - 2x + 1在区间[-2, 2]上的一个驻点为c,请求该驻点c的值以及f(c)的极值。
(请写出解题过程)2. 求函数f(x) = x^3 - 3x + 1的所有零点。
(请写出解题过程)3. 若函数f(x) = 3x^4 + 4x^3 - 12x^2 + 4在区间[0, 3]上的导函数f'(x)恰有一个零点c,并且f(c) = 2,求函数f(x)在该区间上的最大值。
数学分析(1)试题(A卷)

数学分析(上)试题 班级____________姓名____________序号_______成绩____________ 一、求解下列各题(每题4分共40分) 1.!limnncn(0c为常数)
2.xxxxxsintan)sin(sin)tan(tanlim0 3.xxxx)1cos1(sinlim 4.求ba,使0120)(xexbaxxfx在点0x可导。 5.求155345xxxy在]2,1[上的最大值与最小值。 6.dxxxx221arctan
7.11)1ln(lim4sin002xdttxx 8.])1(cos2coscos1[1limnnxnnxnxn
(Rx)
9.0dxexxn(Nn) 10.baxbaxdx))(((ba) 二(10分)、设)(xf在区间I上有界,记 )(inf,)(supxfmxfMIxIx
称mMIf),(为函数f在区间I上振幅。证明 )()(sup),(,xfxfIfIxx
三(10分)、设)(xf在有限开区间),(ba上连续,证明)(xf在),(ba上一致连续的充要条件是)(limxfax与)(limxfbx都存在且有限。(提示使用一致连续性定理)
四(10分)、证明:方程033cxx(c为常数)在区间]1,0[内不可能有两个不同的实根。
五(10分)、设)(xf在)(0xU连续,在)(00xU可导,证明:如果)0(0xf存在,则)(0xf也存在,且)0()(00xfxf。并由此结论证明,如果)(xf在区间I上可导,则)(xf不存在第一类间断点。
六(10分)、设)(xf为],[ba上的非负连续函数,证明:如果0)(badxxf,则0)(xf。
七(10分)、设f在],[ba上有界,],[baan,cannlim,证明:若f在],[ba上只有),2,1(nan为其间断点,则f在],[ba上可积。
第一学期数学分析A考卷A答案
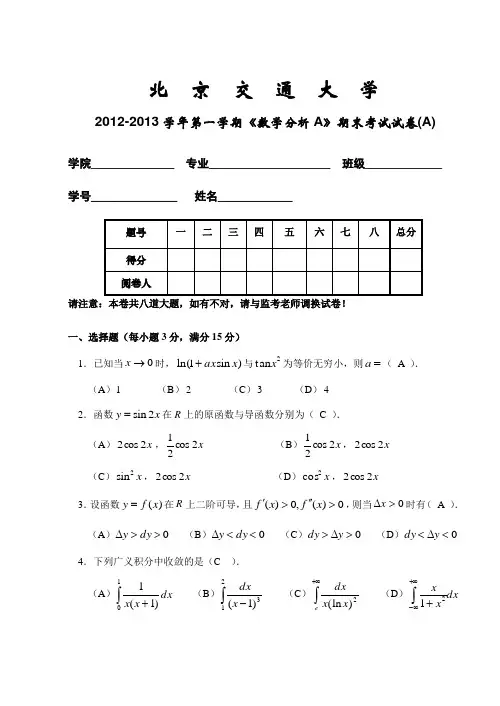
北 京 交 通 大 学2012-2013学年第一学期《数学分析A 》期末考试试卷(A)学院_____________ 专业___________________ 班级____________ 学号_______________ 姓名_____________请注意:本卷共八道大题,如有不对,请与监考老师调换试卷! 一、选择题(每小题3分,满分15分)1.已知当0→x 时,)sin 1ln(x ax +与2tan x 为等价无穷小,则=a ( A ). (A )1 (B )2 (C )3 (D )4 2.函数x y 2sin =在R 上的原函数与导函数分别为( C ). (A )x 2cos 2,x 2cos 21 (B )x 2cos 21,x 2cos 2 (C )x 2sin ,x 2cos 2 (D )x 2cos ,x 2cos 23.设函数)(x f y =在R 上二阶可导,且0)(,0)(>''>'x f x f ,则当0>∆x 时有( A ). (A )0>>∆dy y (B )0<<∆dy y (C )0>∆>y dy (D )0<∆<y dy 4.下列广义积分中收敛的是(C ).(A )⎰+10)1(1dx x x (B )⎰-213)1(x dx (C )⎰+∞e x x dx 2)(ln (D )dx x x⎰+∞∞-+215.设函数)(x f 在点0=x 处连续,下列命题中正确的个数是( C ).① 若xx f x )(lim0→存在,则0)0(=f .② 若xx f x )(lim 0→存在,则)0(f '存在.③ 若xx f x f x )()(lim 0-+→存在,则0)0(=f .④ 若xx f x f x )()(lim 0--→存在,则)0(f '存在.(A )1 (B )2 (C )3 (D )4 二、填空题(每小题3分,满分15分) 1.=++∞→n nnn 321lim 3 .2.若)100()2)(1()(+++=x x x x x f ,则=')0(f 100! .3.=-+⎰-dx x x x )1cos (11232π. 4.若点)3,1(是曲线23bx ax y +=的拐点,则=),(b a ⎪⎭⎫⎝⎛-29,23 . 5.微分方程12='-''y y 的通解为=y x e C C x2212++- . 三、(每小题6分,满分12分)求下列极限1.设24053111)(2xx dt e x x f xt +-=⎰-,求)(lim 0x f x →.解:222322544003333311lim ()limlim lim 3155xt x x Lx x x x e dt x x e x e x f x x x x ---→→→→-+-+-+===⎰ 20301lim 101422lim 5122x e x x xe x x x x L--=+-=-→-→101=;2.设xx e e x f x x 1sin ||12)(2+++=,求)(lim x f x -∞→,)(lim x f x +∞→,)(lim x f x ∞→.解:11211sin lim 12lim 1sin 12lim )(lim 22=-=-++=⎪⎪⎭⎫ ⎝⎛-++=-∞→-∞→-∞→-∞→x x e ex x e ex f x x xx x xx x ; 11011sinlim 12lim 1sin 12lim )(lim 22=+=+++=⎪⎪⎭⎫ ⎝⎛+++=+∞→+∞→+∞→+∞→xx e e x x e e x f x x xx x x x x ;由单侧极限与极限关系可得:1)(lim =∞→x f x .四、(每小题6分,满分12分)求下列导数或微分 1.设1ln 2++=x x y ,求dy 与y ''.解:显然,)1ln(212++=x x y .由复合函数求导法则与四则运算求导法则可得: 121)21211(1121222+=⋅++++⋅='x x x x x y , dx x dy 1212+= ,3222)1(22121)11(21+-=⋅+⋅+-=''x xx x x y . 2.设)(x y y =是由⎩⎨⎧=++=-+01,0)1(y te t t x y 所确定的函数,求0=t dx dy.解:当0=t 时,1,0-==y x .由0)1(=-+t t x 可得:t t x -=2,1|)12()0(0-=-='=t t t x ;由01=++y te y对t 求导可得:0='+'+t t y y y y te e ,1)0(--='e y t ,由参量函数求导法可得:10)0()0(-==''=e x y dx dy t t t .五、(本题满分12分)求下列积分: 1.dx x ⎰arctan.解:⎰=tdt t I arctan 2⎰⎰+-==dt tt t t t td 22221arctan )(arctan C t t t C t t t t +-+=++-=arctan )1(arctan arctan 22C x x x +-+=arctan )1(2.dx x x ⎰-π53sin sin .解: 注意到|cos |sin )sin 1(sin sin sin 32353x x x x x x ⋅=-=-,故 ⎰⎰-=πππ2232023cos sin cos sin xdx x xdx x I 54|sin 52|sin 522252025=-=πππx x . 六、(本题满分13分)(I )判定函数x xe x f -=)(的单调性,并求其极值;(II )讨论方程x ae x =的实根个数.解:(I )∵⎪⎩⎪⎨⎧><==<>-='-,1,0,1,0,1,0)1()(x x x e x x f x ∴),1()(),1,()(+∞∈↓-∞∈↑x f x f ,且极大值为ef f 1)1(max ==. (II )x ae x =的实根个数xxe y -=⇔与a y =的交点个数.由(I )及-∞==-∞→-∞→xx x e xx f lim)(lim ()()(+∞⋅-∞),01lim lim )(lim ===+∞→+∞→+∞→x x L x x x ee x xf , 可知 ① 当0≤a 或ea 1=时,原方程只有一个实根;② 当ea 10<<时,原方程有两个实根; ③ 当ea 1>时,原方程没有实根. 七、(本题满分13分)(I )求曲线x y ln =与其在点)1,(e 处的切线、x 轴所围成的平面图形G 的面积A ;(II )求上述平面图形G 绕x 轴旋转所得的旋转体的体积V . 解:(I )∵e y x y 1)0(,1='=',∴切线方程为)(11e x e y -=-,即exy =. ⎰-=exdx e A 1ln 212|)]1(ln [21-=--=e x x e e. (II )⎰-=e xdx e V 12ln 31ππ]1ln 2|ln [31112dx x x x x x e ee⎰⋅⋅--=ππ]|)1(ln 2[31)ln 2(3111e ex x e e dx x e e ---=--=⎰ππππ )31(2)2(31e e e -=--=πππ.八、(本题满分8分)设函数)(x f 在]1,0[上连续,在)1,0(内可导,且(0)(1)0f f ==,112f ⎛⎫= ⎪⎝⎭,证明:存在点)1,0(∈ξ,使得1)(='ξf . 证:设x x f x F -=)()(,则]1,0[)(C x F ∈,且1)1(,21)21(,0)0(-===F F F . ① ∵111()[,1],()0,(1)10222F x C F F ∈=>=-<, ∴由零点定理可知:存在点)1,21(∈η,使得0)(=ηF .② ∵)()0(),,0()(],,0[)(ηηηF F D x F C x F =∈∈,∴由罗尔定理可知:存在点)1,0(),0(⊂∈ηξ,使得0)(='ξF ,即1)(='ξf .。
数学分析3考试题及答案

数学分析3考试题及答案一、选择题(每题3分,共30分)1. 函数f(x)=x^2在区间[0,1]上是:A. 增函数B. 减函数C. 常数函数D. 非单调函数2. 极限lim(x→0) (sin(x)/x)的值是:A. 0B. 1C. -1D. ∞3. 以下哪个级数是收敛的:A. 1 + 1/2 + 1/4 + 1/8 + ...B. 1 - 1/2 + 1/3 - 1/4 + ...C. 1 + 2 + 3 + 4 + ...D. 1/2 + 1/4 + 1/8 + 1/16 + ...4. 函数f(x)=x^3-3x在区间(-∞,+∞)上:A. 有唯一极值点B. 有两个极值点C. 有三个极值点D. 没有极值点5. 函数f(x)=x^2在x=0处的导数是:A. 0B. 1C. -1D. 26. 函数f(x)=|x|在x=0处:A. 连续B. 可导C. 不连续D. 不可导7. 函数f(x)=x^2+2x+1的不定积分是:A. (x^3+x^2)/3 + CB. (x^3+x^2+2x)/3 + CC. (x^3+x^2+2x+1)/3 + CD. (x^3+x^2+x)/3 + C8. 以下哪个函数是周期函数:A. f(x)=x^2B. f(x)=sin(x)C. f(x)=e^xD. f(x)=ln(x)9. 函数f(x)=x^3在x=1处的泰勒展开式是:A. 1 + 3(x-1) + 3(x-1)^2 + (x-1)^3B. 1 + 3(x-1) + 3(x-1)^2C. 1 + 3(x-1) + (x-1)^3D. 1 + 3(x-1) + 3(x-1)^2 + 6(x-1)^310. 函数f(x)=x^2在区间[0,1]上的定积分是:A. 1/3B. 1/2C. 2/3D. 1二、填空题(每题4分,共20分)1. 函数f(x)=x^3在x=1处的导数值为______。
2. 函数f(x)=sin(x)在x=π/2处的二阶导数值为______。
数学分析期末A卷
期末(A)试卷 课程名称 数学分析(3) A 卷 考试形式 闭 卷 考核类型 考试 本试卷共 3 大题,卷面满分100分,答题时间120分钟。
一、计算题:(共6小题,每小题6分,共36分)
题号 一 二 三 总分 复核人 得分
得分 评卷人
………………………密……………………封…………………………装…………………订…
…
…………………线………………………
系别 专业(班级) 姓名 学号
2401xdxx
4.计算
222213.,.2xyzdydzdxdxxyz
设 求
223322,.xyxyfxyxy1.讨论函数的极限
zyyu=x+sin+e.22.计算函数的全微分 二、综合应用题:(共6小题,每小题8分,共48分)
得分 评卷人
6.()d,0(0,0),A(1,0),B(1,1)LxysL计算其中是以为顶点的三角形。20xedx
5.计算
33 3 zxyxy1.求的极值。 22sin,sin.cos,cos4xtyttztt2.求曲线 在的点处的切线和法平面。
221zxy3.求曲面在点(2,1,4)处的切平面和法线方程.
2,210.Dxydxdyyxxyxx4.求其中D是由曲线 , 和 () 围成的平面闭区域 三、证明题:(第1.2小题,每小题5分,第3小题6分
共16分)
得分 评卷人
2222s
16.I=,z.dsxyzah求曲面积分其中S是球面
被平面z=h(0
222222222(),1.Ixyzdxdydzxyzxyz5.求其中是上半球面
(z0)与圆锥面所围成的立体 221.sin(),.uuxuuyxyxxyy设证明y
2(,)[,;,]()(,) [,]bafxyabcdIyfxydxcd证明:若在矩形上连续,则是上的连续函数。
222222223.x+y+z=x+y=tanz证明:,(常数),球面
