基于SPSS多元线性回归分析的案例
SPSS多元回归分析实例
t i e an dl l t 多元回归分析在大多数的实际问题中,影响因变量的因素不是一个而是多个,我们称这类回问题为多元回归分析。
可以建立因变量y 与各自变量x j (j=1,2,3,…,n)之间的多元线性回归模型:其中:b 0是回归常数;b k (k =1,2,3,…,n)是回归参数;e 是随机误差。
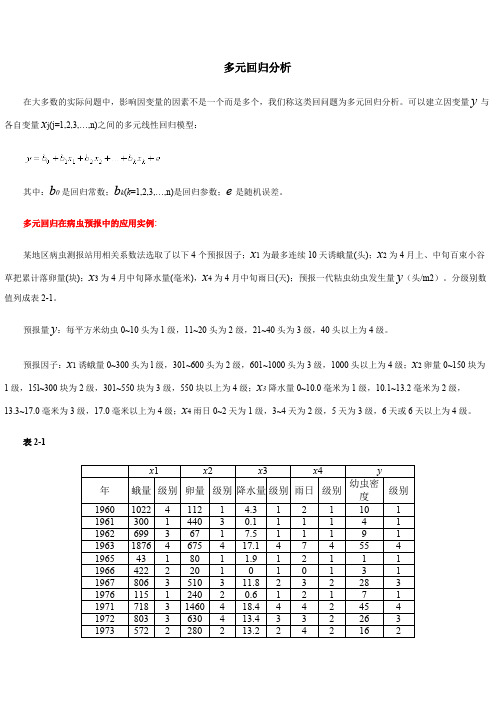
多元回归在病虫预报中的应用实例:某地区病虫测报站用相关系数法选取了以下4个预报因子;x 1为最多连续10天诱蛾量(头);x 2为4月上、中旬百束小谷草把累计落卵量(块);x 3为4月中旬降水量(毫米),x 4为4月中旬雨日(天);预报一代粘虫幼虫发生量y (头/m2)。
分级别数值列成表2-1。
预报量y :每平方米幼虫0~10头为1级,11~20头为2级,21~40头为3级,40头以上为4级。
预报因子:x 1诱蛾量0~300头为l 级,301~600头为2级,601~1000头为3级,1000头以上为4级;x 2卵量0~150块为1级,15l~300块为2级,301~550块为3级,550块以上为4级;x 3降水量0~10.0毫米为1级,10.1~13.2毫米为2级,13.3~17.0毫米为3级,17.0毫米以上为4级;x 4雨日0~2天为1级,3~4天为2级,5天为3级,6天或6天以上为4级。
表2-1x 1x 2x 3x 4y 年 蛾量 级别 卵量 级别 降水量 级别 雨日 级别 幼虫密度级别1960102241121 4.31211011961300144030.111141196269936717.511191196318764675417.14745541965431801 1.9121111966422220101013119678063510311.82322831976115124020.612171197171831460418.444245419728033630413.433226319735722280213.224216219742641330342.243219219751981165271.84532331976461214017.515328319777693640444.7432444197825516510101112数据保存在“DATA6-5.SAV”文件中。
spss多元回归分析案例

spss多元回归分析案例SPSS多元回归分析案例。
在统计学中,多元回归分析是一种用于探究多个自变量与因变量之间关系的方法。
通过多元回归分析,我们可以了解不同自变量对因变量的影响程度,以及它们之间的相互作用情况。
在本篇文档中,我将通过一个实际案例来介绍如何使用SPSS软件进行多元回归分析。
案例背景:假设我们是一家电子产品公司的市场营销团队,在推出新产品之前,我们希望了解不同因素对产品销量的影响。
我们收集了一些数据,包括产品的售价、广告投入、竞争对手的售价、季节等因素,以及产品的销量作为因变量。
数据准备:首先,我们需要将数据录入SPSS软件中。
在SPSS中,我们可以通过导入Excel文件的方式将数据导入到软件中,并进行必要的数据清洗和处理。
确保数据的准确性和完整性对于后续的多元回归分析非常重要。
模型建立:接下来,我们需要建立多元回归模型。
在SPSS中,我们可以通过依次选择“分析”-“回归”-“线性回归”来进行多元回归分析。
在“因变量”栏中输入销量,然后将所有自变量依次输入到“自变量”栏中。
在建立模型之前,我们还需要考虑是否需要进行变量转换或交互项的添加,以更好地拟合数据。
模型诊断:建立模型后,我们需要对模型进行诊断,以确保模型的准确性和有效性。
在SPSS中,我们可以通过查看残差的正态性、异方差性以及自相关性来进行模型诊断。
如果模型存在严重的偏差或违反了多元回归分析的假设,我们需要进行相应的修正或改进。
模型解释:最后,我们需要解释多元回归模型的结果。
在SPSS的输出结果中,我们可以看到各个自变量的系数、显著性水平、调整R方等统计指标。
通过这些指标,我们可以了解不同自变量对销量的影响程度,以及它们之间的相互作用情况。
同时,我们还可以进行各种假设检验,来验证模型的有效性和可靠性。
结论:通过以上多元回归分析,我们可以得出不同自变量对产品销量的影响程度,以及它们之间的相互作用情况。
这些结果对于我们制定产品的定价策略、广告投放策略以及市场营销策略都具有重要的指导意义。
4.3.4 多元线性回归的实用案例[共4页]
![4.3.4 多元线性回归的实用案例[共4页]](https://img.taocdn.com/s3/m/9c6b619b2e3f5727a4e96231.png)
195 他筛选方法结合使用。
因此,尽管它是一种比较高效的方法,但使用者较少。
4.3.4 多元线性回归的实用案例1.案例要求对于如图4-39所示的“大学学习状态测试.sav ”文档,请分析作业情况、上网时间、游戏时间、性别、爱好、认知风格与数学成绩之间的关系。
如果可能,请构造回归方程,并评价回归分析的效果。
图4-39 待进行线性回归分析的原始数据2.分析解决方案分析图4-39中所示的“大学学习状态测试.sav ”数据,依据案例要求以“数学”成绩为结果变量(因变量)、以“作业情况”“上网时间”“游戏时间”“性别”“爱好”“认知风格”作为因素变量(自变量),构造多元线性回归方程。
最后,根据回归结果,借助判定系数、F 值和T 值评价回归方程的质量。
根据线性回归分析对自变量的规范性要求,需要在执行线性回归分析前对字符型自变量进行数值化编码,而且在编码过程中尽可能依据某种规范把字符型变量转化为定序型数据。
3.操作流程首先,以SPSS 打开“大学学习状态测试.sav ”文档,使之处于“数据视图”状态。
然后,检查题目中要求的每个自变量,对于字符型变量“性别”“爱好”“认知风格”进行数值化编码,使之成为定序的数值型量,新变量名称为“Sex ”“S 爱好”“S 风格”。
第三,利用菜单【分析】—【回归】—【线性】命令,启动“线性回归”对话框,如图4-40所示。
第三,按照图4-40所示的界面,把变量“数学”添加到【因变量】列表框中,把变量“上网时间”“游戏时间”“作业情况”“Sex ”“S 爱好”“S 风格”添加到【自变量】列表框中。
第四,在右侧中部的“方法”组合框中,选择自变量的筛选方式为“逐步”。
最后,单击底部的【确定】按钮,启动线性回归过程。
获得如图4-41~图4-45所示的一组处理结果。
基于SPSS多元线性回归分析的案例
农民收入影响因素的多元回归分析自改革开放以来,虽然中国经济平均增长速度为9.5 % ,但二元经济结构给经济发展带来的问题仍然很突出。
农村人口占了中国总人口的70 %多,农业产业结构不合理,经济不发达,以及农民收入增长缓慢等问题势必成为我国经济持续稳定增长的障碍。
正确有效地解决好“三农”问题是中国经济走出困境,实现长期稳定增长的关键。
其中,农民收入增长是核心,也是解决“三农”问题的关键。
本文力图应用适当的多元线性回归模型,对有关农民收入的历史数据和现状进行分析,寻找其根源,探讨影响农民收入的主要因素,并在此基础上对如何增加农民收入提出相应的政策建议。
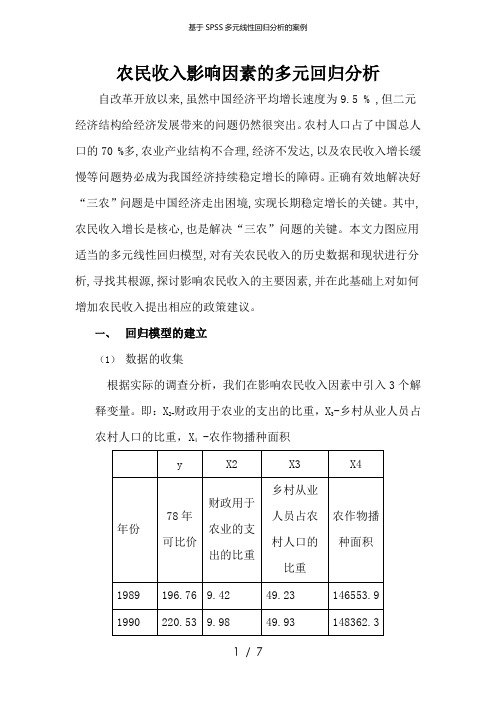
一、回归模型的建立(1)数据的收集根据实际的调查分析,我们在影响农民收入因素中引入3个解释变量。
即:X2-财政用于农业的支出的比重,X3-乡村从业人员占农村人口的比重,X4 -农作物播种面积1991223.2510.2650.92149585.8 1992233.1910.0551.53149007.1 1993265.679.4951.86147740.7 1994335.169.252.12148240.6 1995411.298.4352.41149879.3 1996460.688.8253.23152380.6 1997477.968.354.93153969.2 1998474.0210.6955.84155705.7 1999466.88.2357.16156372.8 2000466.167.7559.33156299.9 2001469.87.7160.62155707.9 2002468.957.1762.02154635.5 2003476.247.1263.721524152004499.399.6765.64153552.6 2005521.27.2267.59155487.7(1)回归模型的构建Y i=1+2X2+3X3+4X4+u i二、回归模型的分析(1)多重共线性检验系数a(2)模型异方差的检验异方差产生的原因有:数据质量原因、模型设定原因。
SPSS多元回归分析报告实例
多元回归分析在大多数的实际问题中,影响因变量的因素不是一个而是多个,我们称这类回问题为多元回归分析。
可以建立因变量y与各自变量x j(j=1,2,3,…,n)之间的多元线性回归模型:其中:b0是回归常数;b k(k=1,2,3,…,n)是回归参数;e是随机误差。
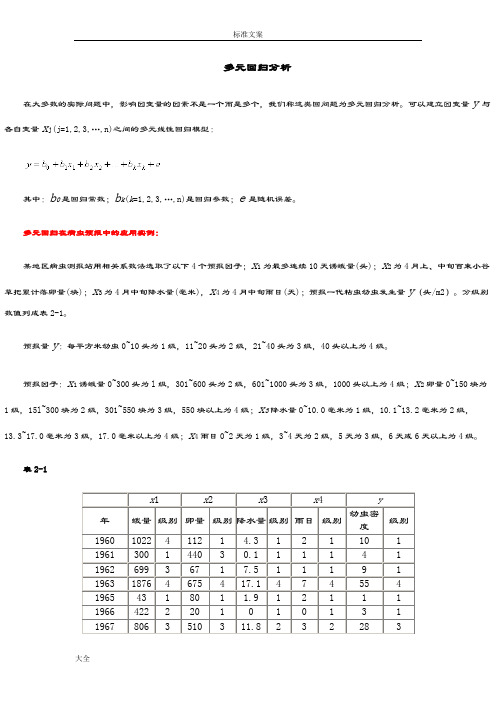
多元回归在病虫预报中的应用实例:某地区病虫测报站用相关系数法选取了以下4个预报因子;x1为最多连续10天诱蛾量(头);x2为4月上、中旬百束小谷草把累计落卵量(块);x3为4月中旬降水量(毫米),x4为4月中旬雨日(天);预报一代粘虫幼虫发生量y(头/m2)。
分级别数值列成表2-1。
预报量y:每平方米幼虫0~10头为1级,11~20头为2级,21~40头为3级,40头以上为4级。
预报因子:x1诱蛾量0~300头为l级,301~600头为2级,601~1000头为3级,1000头以上为4级;x2卵量0~150块为1级,15l~300块为2级,301~550块为3级,550块以上为4级;x3降水量0~10.0毫米为1级,10.1~13.2毫米为2级,13.3~17.0毫米为3级,17.0毫米以上为4级;x4雨日0~2天为1级,3~4天为2级,5天为3级,6天或6天以上为4级。
表2-1x1 x2 x3 x4 y年蛾量级别卵量级别降水量级别雨日级别幼虫密度级别1960 1022 4 112 1 4.3 1 2 1 10 1 1961 300 1 440 3 0.1 1 1 1 4 1 1962 699 3 67 1 7.5 1 1 1 9 1 1963 1876 4 675 4 17.1 4 7 4 55 4 1965 43 1 80 1 1.9 1 2 1 1 1 1966 422 2 20 1 0 1 0 1 3 1 1967 806 3 510 3 11.8 2 3 2 28 3数据保存在“DATA6-5.SAV”文件中。
1)准备分析数据在SPSS数据编辑窗口中,创建“年份”、“蛾量”、“卵量”、“降水量”、“雨日”和“幼虫密度”变量,并输入数据。
SPSS中多元回归分析实例解析

SPSS中多元回归分析实例解析多元回归分析是一种统计方法,用于研究一个因变量与多个自变量之间的关系。
在SPSS中,可以使用该方法来构建、估计和解释多元回归模型。
下面将以一个实例来解析SPSS中的多元回归分析。
假设我们想要研究一个教育投资项目的效果,该项目包括多个自变量,例如教育资金、教育设施、学生人数等,并且我们希望预测该项目对学生学习成绩的影响。
首先,我们需要准备好数据并导入SPSS中。
数据应包含每个教育投资项目的多个观测值,以及与之相关的自变量和因变量。
例如,可以将每个项目作为一个观测值,并将教育资金、教育设施、学生人数等作为自变量,学生学习成绩作为因变量。
在SPSS中,可以通过选择“Analyze”菜单中的“Regression”选项来打开回归分析对话框。
然后,选择“Linear”选项来进行多元回归分析。
接下来,可以将自变量和因变量添加到对话框中。
在自变量列表中,选择教育资金、教育设施、学生人数等自变量,并将它们移动到“Independent(s)”框中。
在因变量框中,选择学生学习成绩。
然后,点击“OK”按钮开始进行分析。
SPSS将输出多元回归的结果。
关键的统计指标包括回归系数、显著性水平和拟合度。
回归系数表示每个自变量对因变量的影响程度,可以根据系数的大小和正负来判断影响的方向。
显著性水平表示自变量对因变量的影响是否显著,一般以p值小于0.05为标准。
拟合度指示了回归模型对数据的拟合程度,常用的指标有R方和调整后的R方。
在多元回归分析中,可以通过检查回归系数的符号和显著性水平来判断自变量对因变量的影响。
如果回归系数为正且显著,表示该自变量对因变量有正向影响;如果回归系数为负且显著,表示该自变量对因变量有负向影响。
此外,还可以使用其他方法来进一步解释和验证回归模型,例如残差分析、模型诊断等。
需要注意的是,在进行多元回归分析时,需要满足一些前提条件,例如自变量之间应该独立、与因变量之间应该是线性关系等。
spss多元回归分析案例

spss多元回归分析案例SPSS多元回归分析是一种常用的统计方法,可以通过分析多个自变量对一个或多个因变量的影响程度,帮助研究者理解变量之间的关系以及预测变量之间的变化情况。
以下是一个关于人们消费意愿的多元回归分析的案例。
假设我们想研究人们的消费意愿受到收入水平、年龄和受教育水平的影响程度。
我们收集了100个参与者的数据,包括他们的收入、年龄、受教育水平以及消费意愿。
下面将介绍如何使用SPSS进行多元回归分析。
首先,在SPSS软件中打开数据文件,并选择"回归"菜单下的"线性回归"选项。
然后将因变量(消费意愿)拉入"因变量"框中,将自变量(收入、年龄、受教育水平)拉入"自变量"框中。
其次,点击"统计"按钮,在弹出的对话框中勾选"无多重共线性检验"、"离群值"和"样本相关矩阵"选项,并点击"确定"按钮。
接下来,点击"模型"按钮,在弹出的对话框中选择"全量"和"因素样本相关系数"选项,并点击"确定"按钮。
然后,点击"保存"按钮,在弹出的对话框中输入保存路径和文件名,并勾选"标准化残差"、"标准化预测值"和"离群值的DFITS"选项,并点击"确定"按钮。
最后,点击"OK"按钮开始进行多元回归分析。
在分析结果中,我们可以查看每个自变量的回归系数、标准误、t值以及显著性水平。
还可以查看整体模型的解释力、统计显著性和调整R 平方。
根据分析结果,我们可以得出结论:收入水平、年龄和受教育水平对消费意愿有显著影响。
收入水平对消费意愿的影响最大,其次是受教育水平,年龄对消费意愿的影响较小。
SPSS多元回归分析实例(最新整理)

多元回归分析在大多数的实际问题中,影响因变量的因素不是一个而是多个,我们称这类回问题为多元回归分析。
可以建立因变量y与各自变量x j(j=1,2,3,…,n)之间的多元线性回归模型:其中:b0是回归常数;b k(k=1,2,3,…,n)是回归参数;e是随机误差。
多元回归在病虫预报中的应用实例:某地区病虫测报站用相关系数法选取了以下4个预报因子;x1为最多连续10天诱蛾量(头);x2为4月上、中旬百束小谷草把累计落卵量(块);x3为4月中旬降水量(毫米),x4为4月中旬雨日(天);预报一代粘虫幼虫发生量y(头/m2)。
分级别数值列成表2-1。
预报量y:每平方米幼虫0~10头为1级,11~20头为2级,21~40头为3级,40头以上为4级。
预报因子:x1诱蛾量0~300头为l级,301~600头为2级,601~1000头为3级,1000头以上为4级;x2卵量0~150块为1级,15l~300块为2级,301~550块为3级,550块以上为4级;x3降水量0~10.0毫米为1级,10.1~13.2毫米为2级,13.3~17.0毫米为3级,17.0毫米以上为4级;x4雨日0~2天为1级,3~4天为2级,5天为3级,6天或6天以上为4级。
表2-1x1 x2 x3 x4 y年蛾量级别卵量级别降水量级别雨日级别幼虫密度级别1960102241121 4.3121101 1961300144030.111141 196269936717.511191 196318764675417.1474554 1965431801 1.912111 19664222201010131 19678063510311.8232283 1976115124020.612171 197171831460418.4442454 19728033630413.4332263 19735722280213.224216219742641330342.243219219751981165271.84532331976461214017.515328319777693640444.7432444197825516510101112数据保存在“DATA6-5.SAV”文件中。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
农民收入影响因素的多元回归分析
自改革开放以来,虽然中国经济平均增长速度为9.5 % ,但二元经济结构给经济发展带来的问题仍然很突出。
农村人口占了中国总人口的70 %多,农业产业结构不合理,经济不发达,以及农民收入增长缓慢等问题势必成为我国经济持续稳定增长的障碍。
正确有效地解决好“三农”问题是中国经济走出困境,实现长期稳定增长的关键。
其中,农民收入增长是核心,也是解决“三农”问题的关键。
本文力图应用适当的多元线性回归模型,对有关农民收入的历史数据和现状进行分析,寻找其根源,探讨影响农民收入的主要因素,并在此基础上对如何增加农民收入提出相应的政策建议。
一、回归模型的建立
(1) 数据的收集
根据实际的调查分析,我们在影响农民收入因素中引入3个解释变量。
即: X财政用于农业的支出的比重, X-乡村从业人员占农村人口的比重, X -2-34 农作物播种面积
y X2 X3 X4
乡村从业人员78年可比财政用于农业农作物播年份占农村人口的价的支出
的比重种面积比重
1989 196.76 9.42 49.23 146553.9
1990 220.53 9.98 49.93 148362.3
1991 223.25 10.26 50.92 149585.8
1992 233.19 10.05 51.53 149007.1
1993 265.67 9.49 51.86 147740.7
1994 335.16 9.2 52.12 148240.6
1995 411.29 8.43 52.41 149879.3
1996 460.68 8.82 53.23 152380.6
1997 477.96 8.3 54.93 153969.2
1998 474.02 10.69 55.84 155705.7
1999 466.8 8.23 57.16 156372.8
2000 466.16 7.75 59.33 156299.9
2001 469.8 7.71 60.62 155707.9
2002 468.95 7.17 62.02 154635.5
2003 476.24 7.12 63.72 152415
2004 499.39 9.67 65.64 153552.6
2005 521.2 7.22 67.59 155487.7
(1) 回归模型的构建
Y=ββX+βX+βX+u i1+223344i
二、回归模型的分析
(1) 多重共线性检验
a系数
非标准化系数标准系数共线性统计量模型 B 标准误差试用版 t Sig. 容差 VIF
1 (常量) -2983.479 803.141 -3.715 .003
X2 -14.221 15.007 -.141 -.948 .361 .579 1.726
X3 5.201 3.760 .258 1.383 .190 .368 2.717
X4 .021 .006 .614 3.677 .003 .459 2.177 a. 因变量: y 表1
多重共线性是指解释变量之间存在相关关系,判断解释变量之间的多重共线性一般可看方差膨胀因子VIF和容忍度这两个指标,如果解释变量之间存在多重共线性,一般采用逐步剔除VIF最大的解释变量来消除解释变量之间多重共线性的问
题。
从表1可知,解释变量,X1,X2,X3三者的方差膨胀因子VIF分别为
1.726,
2.717和2.177,均小于10。
且三者的容忍度均大于0.1。
所以可以判断解释变量X1,X2,X3三者之间不存在多重共线性。
(2)模型异方差的检验
异方差产生的原因有:数据质量原因、模型设定原因。
由异方差引起的后果一般会导致回归系数估计结果误差较大、有关统计检验失去意义、模型的预测失效等危害,所以在建立模型的过程中必须要检验模型之间是否存在异方差。
若存在异方差解决办法——加权最小二乘法。
从上表散点图判断模型的解释变量之间是否存在异方差,但从上表可以看
到散点图之间的特征不是特别明显。
不易于做出结论,故采用|e|与X的等级相关系数进行判定。
表2
从表2可知,在95%的置信水平下,检验统计量与为标准化残差的绝对值(|e|)之间的显著性水平P值均大于0.05,则接受原假设,检验统计量与|e|之间是独立的,不存在相关关系。
说明模型不存在异方差。
(3)模型序列相关的检验
序列相关是指各随机误差项之间不独立,则称其存在自相关或序列相关性。
自相关产生的原因有:经济变量的惯性、省略解释变量的影响、错误的函数形式的影响、滞后效应、其他原因等。
如果随机误差之间存在自相关,则可能导致OLS估计值不具有最小方差性; 很可能高估R2;t-检验与F-检验结果都变得无效;等影响。
所以必须检验所构造模型是否存在自相关性。
a系数
非标准化系数标准系数
模型 B 标准误差试用版 t Sig.
1 (常量) -.355 7.59
2 -.047 .963
REST1 1.226 .251 1.252 4.889 .068
REST2 -.676 .252 -.686 -2.680 .073
a. 因变量: RES
在上表中REST1为e(t-1),REST2为e(t-2),用e(t)与e(t-1),和e(t-2)进行回归分析,得到上表。
显著性水平均P均为接受原假设,既回归方程的各部分系数均为0,既认定模型不存在序列关。
三、回归模型的确定及解释
a系数
非标准化系数标准系数共线性统计量模型 B 标准误差试用版 t Sig. 容差 VIF
1 (常量) -2983.479 803.141 -3.715 .003
X2 14.221 15.007 -.141 -.948 .361 .579 1.726
X3 5.201 3.760 .258 1.383 .190 .368 2.717
X4 .021 .006 .614 3.677 .003 .459 2.177 a. 因变量: y
由上表可以确立,线性模型的方程为。
Y=-2983.47+14.221X+5.201X+0.021X 234
从构建的模型可以知道,农民的收入水平与X财政用于农业的支出2-
的比重成正相关的关系,财政每增加一元用于农业,农民的收入增加14,。
221元。
X-乡村从业人员占农村人口的比重增加1%,农民收入增加5.201%,3
农民的收入与虽与作物的播种面积成正比比例关系,但是作用较少。
