电工技术第四章正弦交流电路习题解答
电工电子技术1-4章习题题

uC () US R2 8 V R1 R2
( R1 / / R2 R3 )C 0.02 s
uc (t ) uc () [uc (0 ) uc ()]et / 8 4e50t
i1 (t ) 4 2 50 t e A 3 3
计算I、 US 、R。
12A R 9A 12Ω 6A 3Ω 18A 15A 3A 1Ω I =6A
12×3V-9R-15×1V=0 R=7/3Ω -US- 12×3V- 18×3V=0 US=-90V
《电工电子技术》1-4章复习指导
4
第二章 电路的分析方法
已知:R1=25Ω,R4=30Ω, R5=15Ω, R7=70Ω,R8=35Ω,R9=17.5Ω。 求Rab。
《电工电子技术》 1-4章复习指导
黄诗浩 信息科学与工程学院
《电工电子技术》1-4章复习指导
1
第一章 电路的基本概念和基本定律
电路图如图1所示,试写出电路中Uab 和电流I 的关系。
解: Uab =-US -IR
解: Uab =US +IR
《电工电子技术》1-4章复习指导
2
第一章 电路的基本概念和基本定律
R4
a
R1
R8
R7
R9
R5
b
R7=10+20+10x20/5=70Ω R8=5+20+5x20/10=35Ω R9=10+5+10x5/20=17.5Ω Rab=25+R8||(30||R7+15||R9)=36.25 Ω
《电工电子技术》1-4章复习指导
5
电工学部分习题参考答案

电工学部分习题参考答案第1章 习题习 题1-1 单项选择题1. 一个220V 、40W 的灯泡和一个220V 、60W 的灯泡串联起来接到220V 的电源上,请问哪个灯泡会比较亮?( )A .220V ,40W 的灯泡比较亮B .220V ,60W 的灯泡比较亮C .一样亮2. 一个220V 、40W 的灯泡和一个220V 、60W 的灯泡并联起来接到220V 的电源上,请问哪个灯泡会比较亮?( )A .220V ,40W 的灯泡比较亮B .220V ,60W 的灯泡比较亮C .一样亮3. 空间中有a 、b 、c 三点,已知V 2ab =U ,V 3bc =U ,求ac U 的电压。
( ) A. 1V B. 5V C. -1V4. 已知V 2ab =U ,V 3bc =U ,如果以b 点作为电位参考点,求a 、b 、c 三点电位。
( )A .a 点电位为0V ,b 点电位为2V ,c 点电位为3V B. a 点电位为2V ,b 点电位为0V ,c 点电位为3V C .a 点电位为2V ,b 点电位为0V ,c 点电位为-3V D. a 点电位为5V ,b 点电位为3V ,c 点电位为0V 5. 如图T1.1所示,A 10S =I ,V 5S =U ,Ω=1R ,问电压源和电流源各起什么作用。
( )A .电压源起负载作用,电流源起电源作用。
B .电压源起电源作用,电流源起电源作用。
C. 电压源起电源作用,电流源起负载作用。
1-2 判断题(正确的请在每小题后的圆括号内打“√”,错误的打“×”)1. 如果没有参考方向,只说某支路中的电流为-1A ,这种说法没有意义。
( )2. 电路中某两点的电位很高,因此这两点间的电压也很高。
( )3. 实际电流源允许开路运行,它对外不输出功率,自身也不消耗功率。
( )图T1.1 习题1-1(5)图图T1.2 习题1-3图4. 电压和电位的单位都是伏特,但是它们在概念上没有联系。
电工学—电工技术课后答案1

第二章电路的分析方法
P39 习题二
2-1
题2-1图题2-1等效图
解:
①
②
,
①
,
, ,
代入 ①
另外,戴维南等效图
回归原图 ,所以
2-2答 由并联输出功率400
所以每个R获得功率
改串联后:
2-3
题2-3等效图
,
2-4
题2-4 △-Y变换(一)图
题2-4 △-Y变换(二)图
题2-4 △-Y变换(三)图
解: ,闭合后,为零输入响应。
,
3-4
解: , ,为零状态响应。
3-5
解:本题为零状态响应。
,
3-6
解: ,
所以:
3-7解:
,
所以
3-8
解:
,
所以:
3-9 如图所示电路中,t=0时,开关S闭合,试求 时,
(1)电容电压 ;
(2)B点的电位 和A点的电位 的变化规律。假设开关闭合前电流已处于稳态。
习题3-9图
题4-11图
解:由已知有: ,则 ,
又
解得: ,
两表的读数均为 。
4.12 已知题4-12图所示电路中 ,电流表A的读数为2A。电压表 的读数均为200V。求参数R、L、C,并作出该电路的相量图。并写出 的瞬时值表达式。
题4-12 图
解: 同理
,整理得: , ,即
由相量图可知电流超前端电压 ,
4.13 求图4-13两图中的电流 。
时
所以电流表的读数约为1.43A
2-13 应用戴维南定理求图中1Ω电阻的电流。
解: 由于1 为研究对象,所以与电流源串联的2 和理想电压源并联的5 每个电阻对1 不起作用,因此电路图为(b)图
电工学课后第1-6章习题答案
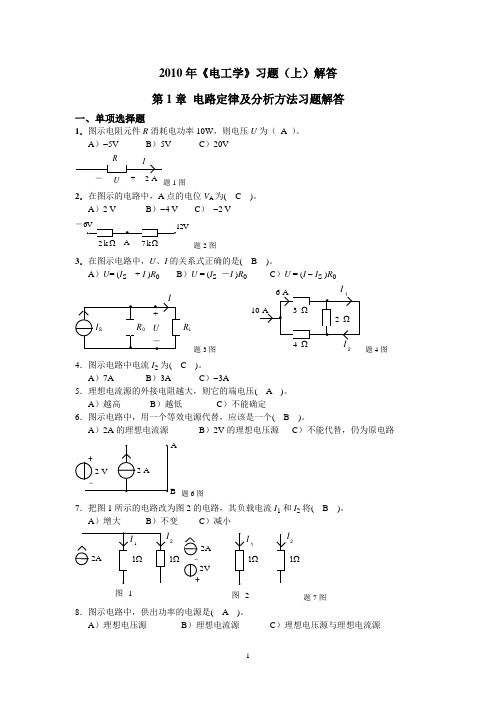
2010年《电工学》习题(上)解答 第1章 电路定律及分析方法习题解答一、单项选择题1.图示电阻元件R 消耗电功率10W ,则电压U 为( A )。
A )-5V B )5V C )20VUR 题1图2.在图示的电路中,A 点的电位V A 为( C )。
A )2 V B )-4 V C ) -2 V- 2 k 7 k ΩΩ题2图3.在图示电路中,U 、I 的关系式正确的是( B )。
A )U = (I S + I )R 0 B )U = (I S -I )R 0 C )U = (I - I S )R 0R L题3图I 2题4图4.图示电路中电流I 2为( C )。
A )7AB )3AC )-3A5.理想电流源的外接电阻越大,则它的端电压( A )。
A )越高 B )越低 C )不能确定6.图示电路中,用一个等效电源代替,应该是一个( B )。
A )2A 的理想电流源 B )2V 的理想电压源 C )不能代替,仍为原电路2 V题6图7.把图1所示的电路改为图2的电路,其负载电流I 1和I 2将( B )。
A )增大B )不变C )减小221Ω2V 2A图 1图 2+题7图8.图示电路中,供出功率的电源是( A )。
A )理想电压源 B )理想电流源C )理想电压源与理想电流源U4VS题8图S题9图9.在图示电路中,各电阻值和U S 值均已知。
欲用支路电流法求解流过电阻R G 的电流I G ,需列出独立的电流方程数和电压方程数分别为( B )。
A )4和3 B )3和3 C )3和410.在计算线性电阻电路的电压和电流时,用叠加原理。
在计算线性电阻电路的功率时,加原理( B )。
A )可以用 B )不可以用 C )有条件地使用11.在图示电路中,已知U S =12V ,I S =2A 。
A 、B 两点间的电压U AB 为( A )。
A )-18VB )18VC )-6VU I SS+题11图SA题12图12.在图示电路中,当开关S 闭合时A 点的电位V A ( C )。
电工学 秦曾煌第七版 第四章

正误判断
u 1s 0 i0 tn × U
瞬时值
复数
U 5e j1 0 × 552 0 sit n 1 ) (5
复数
瞬时值
(4-39)
正误判断
已知: i1s0i nt(45 )
j45
× 则: I 10 45 2 有效值
× Im10e45
已知: u21s0i(n t15) -j15
(4-11)
§4.1.3 正弦波特征量之三 —— 初相位
i2Isi nt
(t ):正弦波的相位角或相位。
: t = 0 时的相位,称为初相位或初相角。
i
t
说明: 给出了观察正弦波的起点或参考点,
常用于描述多个正弦波相互间的关系。
(4-12)
两个同频率正弦量间的相位差( 初相差)
i1 i2
t
1 2
设: U1 U11 U2 U22
则:
U1 U2
U1 U2
(1 2)
例 : U 1 9 3 , U 2 0 3 7 , U U 0 1 / U 2 3 4
(4-30)
# 计算器上的复数运算操作
代数式→极坐标形式
-3+j4 = 5 /126.9°
3 +/- a 4 b 2nd →rθ
i1 Im1sint1 i2 Im2sint2
t 2 t 1 2 1 (4-13)
两种正弦信号的相位关系
相
i2
位
超
前 1 2
i1 120
t
i i 超前于
1
2
相 位
i1
滞 后
2 1
i2
120
t
i i 滞后于
《电工技术》任务4.1.3相量与相量图

4 143.1
A 4 j3 5 / 36.9
arctan(b )
a 36.9
2、极坐标→三角函数→代数式时的正确转换
A A A (cos jsin )
A cos j A sin
已知复数A的模a=5,幅角ψ=53.1°,试写出 复数A的极坐标形式和代数形式表达式。
相量辐角=正弦量的初相角
•
如Um Um u Um sin(t )
——幅值相量
•
如U U u 2U sin(t )
——有效值相量
大写字母头上 加点
可不画坐标轴
2)相量图:用复平面的矢量表示相量
•
如: I 5600 A
•
U 10 1200 V
•
•
U 落后于I1800
注意:只有同频率的正弦量才能画在同一相量图上。 才可以比较幅值和相位。
Re
本节小结:
1、正弦量的4种表示法; 2、复数的4种表示形式及运算规则; 3、相量表示法及相量图; 4、相量法及相量图法。
实训4-2:正弦交流信号的仿真测试
实训流程:
(1)本实训采用测量仪器中的函数信号发生器来产生正弦交流信号。双 击信号发生器面板可设置参数:波形为正弦波,频率1kHz,振幅10Vp (最大值),如图4.20左下角所示。
②乘除运算:以及坐标形式进行
乘法:模相乘,辐角相加 除法:模相除,辐角相减
例:
A1 r11 A2 r2 2 A1 A2 r1.r21 2 A1 A2 r1 r21 2
4)复数四则运算
已知复数A=5 ∠53.1 °,求:jA。
A 553.1
jA 190 553.1
5(53.1 90) 5143.1
电工电子技术习题四

习题十四14-1 当一交流铁芯线圈接在f =50Hz 的正弦电源上时,铁芯中磁通的最大值φm =2.25× 10-3Wb 。
在此铁芯上再绕一个200匝的线圈。
当此线圈开路时,求其两端电压?解:由公式 4.44m UE fN ≈=Φ 34.4450200 2.251099.9U -=⨯⨯⨯⨯=V14-2 将一铁芯线圈接于U =100V , f =50Hz 的交流电源上,其电流I 1=5A ,COS ϕ =0.7。
若将此线圈中的铁芯抽出,再接于上述电源上,则线圈中电流I 2=10A ,COS ϕ =0.05。
试求此线圈在具有铁芯时的铜损和铁损。
解:设有铁心时的铁损为:Fe P ∆;有铁心时的铜损为:Cu P ∆由于线圈上无外接负载,故有功功率是有铁损和铜损来消耗的1111cos Fe Cu P U I P P ϕ∴==∆+∆ 即:10050.7F e C u P P ⨯⨯=∆+∆=350W 当电流由5A 变为10A 时,由于铁心已被抽去,FeP ∆=0W ,但铜损同电流平方成正比,故有:22210cos 505Cu P U I ϕ⎛⎫∆== ⎪⎝⎭得Cu P ∆=12.5W35012.5337.5Fe P ∆=-=W14-3有一台10000/230V 的单相变压器,其铁芯截面积S =120cm 2,磁感应强度最大值B m =1T ,电源频率为f =50Hz 。
求原、副绕组的匝数N 1、N 2 各为多少?解:由已知:110000U =V ,2230U =V44.44 4.44 4.4450112010m m U E fN fNB S N -≈=Φ==⨯⨯⨯⨯⨯13754N ⇒=由1122U N U N = 得:287N =14-4 有一单相照明变压器,容量为10KV A ,额定电压为3300 /220V 。
(1)求原、副绕组的额定电流?(2)今欲在副边接上220V 、40W 的白炽灯(可视为纯电阻),如果要求变压器在额定情况下运行,这种电灯最多可接多少盏?解:NN N S U I = 13300N U =V ,2220N U =V ,得1 3.03N I A =,245.45N I A =;每盏灯通过的电流400.18220I A ==灯,所以在副边上可以并联的白炽灯数目为:245.452520.18N I I ==灯盏. 14-5 在图14-10中,将R =8Ω的扬声器接在变压器的副边,已知N 1 =300,N 2 =100,信号源电动势E =6V ,内阻R 0=100Ω。
电工学第七版第4章 正弦交流电路(南昌大学期末考试必考知识点其他学校只供参考)PPT课件

4.3 单一参数的交流电路
⑶波形关系
ui u
⑷相量关系
UU0 II0 O
i
ωt
U I
U I
R
欧姆定律的相量表示式: U RI
⑸相量图
I U
制作群
21
主 页 总目录 章目录 上一页 下一页 退 出
4.3 单一参数的交流电路
⒉ 功率关系 ⑴瞬时功率p
ui u
电压瞬时值u与电流
i
O
瞬时值i的乘积。
p ui UmImsi2nωt p
R
u
-
R
正半周
负半周
图中虚线箭头代表电流的实际方向;
、 代表电压的实际方向(极性)。
正弦量:正弦电压和电流等物理量统称为正弦量。
制作群
5
主 页 总目录 章目录 上一页 下一页 退 出
4.1 正弦电压与电流
正弦量的特征表现在:
变化的快慢 大小 初始值
频率 幅值
正弦量的三要素
初相位
设正弦交流电流:
i Im
第4章 正弦交流电路
4.1 正弦电压与电流 4.2 正弦量的相量表示法 4.3 单一参数的交流电路 4.4 电阻、电感与电容元件串联的交流电路 4.5 阻抗的串联与并联 *4.6 复杂正弦交流电路的分析与计算 4.7 交流电路的频率特性 4.8 功率因数的提高 4.9 非正弦周期电压和电流
制作群
1
主 页 总目录 章目录 上一页 下一页 退 出
4.2 正弦量的相量表示法
4.2.2 相量
表示正弦量的复数称相量。
相量只是表示正弦量,而不等于正弦量。
⒈ 相量式
设正弦量:uU m si(n ω tψ ) 电压幅值相量表示: U mUm ejψUm ψ 电压有效值相量表示: UUejψUψ
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
tωAi /A222032πtAi /A 2032π6πA102i 1i 第四章 正弦交流电路[练习与思考]4—1-1 在某电路中,()A t i 60 314sin 2220-=⑴指出它的幅值、有效值、周期、频率、角频率及初相位,并画出波形图。
⑵如果i 的参考方向选的相反,写出它的三角函数式,画出波形图,并问⑴中各项有无改变? 解:⑴ 幅值 A I m 2220有效值 A I 220=频率 3145022f Hz ωππ===周期 10.02T s f==角频率 314/rad s ω=题解图4。
01初相位 s rad /3πψ-=波形图如题解图4.01所示 (2) 如果i 的参考方向选的相反, 则At i ⎪⎭⎫ ⎝⎛+=32 314sin 2220π,初相位改变了,s rad /32πψ=其他项不变。
波形图如题解图 4.02所示。
题解图4。
024—1-2已知A)120314sin(101 -=t i ,A )30314sin(202+=t i⑴它们的相位差等于多少?⑵画出1i 和2i 的波形。
并在相位上比较1i 和2i 谁超前,谁滞后。
解:⑴ 二者频率相同,它们的相位差︒-=︒-︒-=-=1503012021i i ψψϕ+1+1(2)在相位上2i 超前,1i 滞后。
波形图如题解图4.03所示。
题解图4。
03 4—2—1 写出下列正弦电压的相量V )45(sin 2201 -=t u ω,)V 45314(sin 1002 +=t u 解:V U ︒-∠=•4521101 V U ︒∠=•4525024-2-2 已知正弦电流)A60(sin 81 +=t i ω和)A 30(sin 62 -=t i ω,试用复数计算电流21i i i +=,并画出相量图.解:由题目得到A j j j j I I I m m m ︒∠=+=-++=︒-︒+︒+︒=︒-∠+︒∠=+=•••1.231093.32.9)32.5()93.64()30sin 630cos 6()60sin 860cos 8(30660821 所以正弦电流为)A 1.23(sin 101 +=t i ω题解图4.04 相量图如题解图4.04所示。
4-2-3 指出下列各式的错误。
A I 3010∠=, )V 45sin 100 +=t ( U ωA e I j 3010=, A )20314sin 10 +=t (I解:A I 3010∠= 应改为 A I ︒∠=•3010)V 45sin 100 +=t ( U ω 应该为 )V 45sin 100 +=t ( u ω A eI j 3010= 应该为 A e I j ︒•=3010A )20314sin 10 +=t (I 应该为 A )20314sin 10 +=t (i4—3—1 已知H 1=L 的电感接在400Hz/100V 的正弦电源上,u 的初相位为200,求电流并画出电流、电压的相量图。
解:已知VU ︒∠=•20100A j jX U I L ︒-∠=⨯⨯︒∠==••7004.01400220100π电流、电压的相量图如题解图4。
05所示。
4-3-2 指出下列各式哪些是对的,哪些是错的?L X i u = ,L j I U ω=,L X IU =••,L Uj I ω••-=dt di Lu = ,C X I U =,C I U ω=,Cj I U ω••-=题解图4.05解:L X i u = 此式错 应改为 L X IU =L j IU ω= 此式错 应改为 L j IUω=••L X IU =••此式错 应改为L jX IU =••L UjI ω••-= 此式正确 dtdiL u = 此式正确C X IU = 此式正确C IUω= 此式错 应改为 C I U ω1=C j IU ω••-= 此式错 应改为 CI jU ω••-=4-3-3 试列表比较RLC 三元件在正弦电源激励下各自表现的特性及其关系。
解:4-4—1 假设R 、L 、C 已定,电路性质能否确定?阻性?感性?容性?解:不能.还跟电路的频率有关。
4—4-2 RLC 串联电路的ϕcos 是否一定小于1? 解:还可能等于1.4—4—3 RLC 串联电路中是否会出现U U >R ,U U >L ,U U >C 的情况? 解:会出现U U >L 和U U >C 的情况,不会出现U U >R 的情况。
4-4-4 在RLC 串联电路中,当C L >时,u 超前i ,当C L <时,u 滞后i ,这样分析对吗?解:在RLC 串联电路中,当C L >,电路呈感性,u 超前i ;当C L <时,电路呈容性,u 滞后i 。
所以上面的分析是正确的。
4-4-5 有一RLC 串联的交流电路,已知Ω===10C L X X R ,A I 1=,试求其两端的电压U 。
解:此电路为纯阻性,所以V IR U 10101=⨯==4—4-6 有一RC 串联电路,已知Ω=4R ,Ω=3C X ,电源电压V 0100 ∠=•U ,试求电流i 。
解:Aj jX R U I C ︒∠=︒-∠︒∠=-∠︒∠=-︒∠=-=••9.36209.365010043arctan 501003401004—5-1图4-20所示的四个电路,每个电路图下的电压、电流和电路阻抗模的答案对不对?各图中给定的电路电压、阻抗是否正确?Ω=7Z VU 14=Ω=14Z VU 70=Ω=2Z A I 8= Ω=2Z A I 8=(a ) (b) (c ) (d )图4—17 练习与思考4—5-1图 解:(a )Ω=5Z VU 10=(b)两个元件性质相同,容抗和电压可以直接相加.图中给定的电路电压、阻抗是正确。
(c )图中给定的电路电压、阻抗是正确.(d)两个元件性质不同,图中给定的电路电压、阻抗是不正确。
•︒45I •LI •RI •2•I 4—5-3 两个阻抗串联时,在什么情况下21Z Z Z += 成立?两个阻抗并联时,在什么情况下21111Z Z Z+=成立?解:当两个阻抗的阻抗角相等的时候,上面2个式子成立。
Ω===2C L R X X ,4—5—4 图4-21所示电路中,已知电流表A 1的读数为3A ,试问:⑴A 2和A 3的读数为多少? ⑵并联等效阻抗Z 为多少?图4-18 练习与思考4-5—4图解:⑴此题为RLC 并联电路,Ω===2C L R X X ,所有各元件中电流的大小是相等的,即R C L I I I ==,相量图如题解图4。
06所示。
由相量图知,电流表1A 所测量的的总电流1I 就是电阻电流R I ,所以A I I I R C L 3===,所以电流表3A 的读数为3A 。
电流表2A 测量的是R I •和C I •的总和.由相量图可知2A 的读数为4.24A 。
题解图4.06⑵212121211111=-+=-+=j j jX jX R Z C L 则并联等效阻抗Ω=2Z4—6-1 对于感性负载,能否采取串联电容器的方式提高功率因数?解:电容电感串联能够提高电路总的功率因数,但是会改变感性负载的工作状态。
4-6-2 试用相量图说明,并联电容量过大,功率因数反而下降的原因.解:从题解图4。
07相量图上可知,当并联合适的电容时,总电压和总电流的夹角ϕ减小,使得功率因数提高,直到提高到1,这时继续增加并联的电容值,电路由感性变为容性,功率因数反而下降。
•CI •1••ϕ•I)(a •CI •1•••I)(b •CI •1••ϕ•I)(c题解图4。
074—6—3 提高功率因数时,如将电容器并联在电源端(输电线始端),是否能取得预期效果? 解:电容并联在输电线始端,只能减少电源的无功电流,提高了电源的功率因数,但是连接负载的的输电线路(可能很长)电流并无改变,仍然存在原来的功率损耗,因此达不到提高功率因数的预期效果。
4—6-4 功率因数提高后,线路电流减小了,瓦时计会走的慢些(省电)吗?解:不会。
因为瓦时计测量的是有功功率,提高功率因数后,电路的有功功率不变。
4—7—1 电路基本定律的相量形式是什么? 解:KCL 定理: 0=∑•IKVL 定理:0=∑•U欧姆定律:Z IU =••4—7—2分析正弦交流电路一般采用什么方法?解: 1.根据原电路图画出相量模型图(电路结构不变)R R →、L jX L →、C jX C -→•→U u 、•→I i 、•→E e2.根据电路基本定律的相量形式,列出相量方程式或画相量图 3.用相量法或相量图求解 4.将结果变换成要求的形式4—7-3 分析复杂正弦交流电路采用什么方法?解:同第2章计算复杂直流电路一样,支路电流法、结点电压法、叠加原理、戴维宁定理等方法也适用于计算复杂交流电路。
所不同的是电压和电流用相量表示,电阻、电感和电容及组成的电路用阻抗或导纳来表示,采用相量法计算。
4-7—4 能否用直流电路中学过的弥尔曼定理和支路电流法分析正弦交流电路?如果能用,使用时应注意什么问题?解:可以。
注意:电压和电流用相量表示,电阻、电感和电容及组成的电路用阻抗或导纳来表示,采用相量法计算。
4—8—1 串联谐振时,电路对外呈电阻性,无功功率为零,能否认为电感和电容的无功功率也为零? 解:不能。
电路总的无功功率为零,电感和电容的无功功率大小相等,方向相反。
4—8-2 试说明当频率低于或高于谐振频率时,RLC 串联电路是电容性还是电感性的?t解:当0f f <时,C L X X <,电路呈容性; 当0f f =时,C L X X <,电路发生谐振; 当0f f >时,C L X X >,电路呈感性。
4—8-3 有一2000PF 的电容和一个10Ω的电阻及0.2mH 的线圈,将它们接成并联谐振电路,求谐振时的阻抗和谐振频率。
解:s rad .LCω/1058.110200020117150⨯=⨯⨯==-K Ω.RC L Z -101020001010201230=⨯⨯⨯==-习 题该电4-1 已知某正弦电压当其相位角为6π时,其值为5V ,压的有效值是多少?若此电压的周期为10ms,且在t=0时正处于由正值过渡到负值时的零值,写出电压的瞬时值表达式。
解:设正弦电压的瞬时值表达式为V t U u m )sin(ψω+=由题目知6sin5πm U =,所以V U m 10=, 有效值V U 07.7=s rad f /6280010110223=⨯⨯==-ππω 由t=0时正处于由正值过渡到负值时的零值得到πψ= 得到电压的瞬时值表达式V t u )62800sin(10π+= 4—2 已知某负载的电流和电压的有效值和初相位分别是6A 、-30o ;48V 、45o ,频率均为50Hz 。
