小学数学有趣算式
小学数学四年级上册《探索与发现(一)-有趣的算式》知识要点

1.用计算器进行大数目运算;
2.说出算式中的规律;
3.根据规律进行计算;
4.用化难为易的方法解决问题。
1.算:用计算器进行大数目运算;
2.说:算式中的规律;
3.算:根据规律进行计算;
4.想:用化难为易的方法解决问题。
用化难为易的方法解决问题。
用计算器计算一般都是算一些比较复杂的,很简单的计算我们可以直接用口算。
化难为易:当数很大时,我们可以化繁为简,从简单的算式中发现规律,再用规律来帮助我们解决问题。
表达
1.用计算器计算;
2.用语言描述算式中的规律;
3.用规律计算。
1.算:用计算器算;
2.说:用语言描述算式中的规律;
3.算:用规律计算。
8.说:计算的结果;
9.看:观察积的特点及与因数的关系;
10.说:积的特点及与因数的关系;
11.写:142857×5=142857×4=
12.算:999999999×999999999=;
13.说:当数很大时,我们可以化繁为简,从简单的算式中发现规律,再用规律来帮助我们解决问题;
14.算:计算器算99×99=999×999=
小学数学四年级上册《探索与发现(一)—有趣的算式》知识要点
教学点
陈述性知识
程序性知识
策略性知识
认知
1、第一组算式:积的位数是两个因数位数之和-1,积的最高位和最低位都是1,中间的数字为因数的位数,两边的数字相同并依次减1。(此为回文数)
2、第二组算式:积都由1、4、2、8、5、7几个数字组成,而且前后排列的顺序不变,只需要确定末位数字就可以算出积(如果能直接推算出首位数字则更好)
15.说:计算的结果;
16.猜:9999×9999的结果;
小学数学四年级上册有趣的算式习题第4课时

小学数学四年级上册《有趣的算式》习题一、基础题奇妙的宝塔。
(1-3题用计算器算,后两题按规律直接写出)1×1=111×11=111×111=1111×1111=11111×11111=奇怪的142857。
(1-3题用计算器算,后三题按规律直接写出)142857×1=142857×3=142857×2=142857×4=142857×5=142857×6=二、综合题神奇的9。
9×9=99×99=999×999=9999×9999=99999×99999=999999×999999 =三、提高题寻找神秘的数。
在0、1、2、3、4、5、6、7、8、9这十个数字中,随意选取4个数字。
运算规则:将四个数字组成数字不重复的最大四位数和最小的四位数。
如:1、3、7、8 最大四位数:8731 最小四位数:1378然后两数相减,并把结果的四个数字重新组成一个最大的四位数与最小的数,再次相减……,在这样不断重复的过程中,你能找到一个神秘的数吗?( )- ( )= ( )( )- ( )= ( )( )- ( )= ( )( )- ( )= ( )( )- ( )= ( )( )- ( )= ( )参考答案一、基础题略二、综合题略三、提高题9753-3579=61747641-1467=6174…..。
小学数学四年级《有趣的算式》教案
活动二:不计算,找规律(有趣的数字9)1.首学:学生用计算器计算结果。
99×99=9801 999×999=998001 9999×9999=99980001学生发现通过计算器计算无法得出9999×9999= 准确结果。
2.互学:学生讨论寻求解决问题的方法。
以小组为单位讨论,寻找规律。
3.群学:小组代表汇报结果。
4.共学:师生一起总结规律根据规律,直接写出以下算式的得数。
99999×99999999999×9999999999999×9999999 99999999×99999999活动三:找规律,并用计算器验证(有趣的数字142857)1.首学:自主计算并探索规律。
2.再观察积是由什么数字组成,是怎么变化的?3.最后观察算式的变化与积的变化有什么联系。
活动二:不计算,找规律(有趣的数字9)1.首学:让学生用计算器计算:99×99= 999×999= 9999×9999=2.互学:猜一猜:9999×9999的结果。
学生根据以上两个算式,猜测规律得出:9999×9999=9998000199999×99999=99998000013.群学:学生汇报交流,教师点拨。
指导学生按照“先看宣算式、再看积、最后看算式和积的变换关系”的逻辑顺序进行探索。
4.共学:归纳并总结规律:他们的结果都以数字89开头,以1结尾,中间填0,0的个数是算式中一个乘数里9的个数减去1得来的。
活动三:找规律,并用计算器验证1.首学:出示神秘的算式。
142857×1=142857142857×2=285714142857×3=428571142857×4=571428142857×5=?142857×6=?。
趣味数学300题第一章给小学的同学们
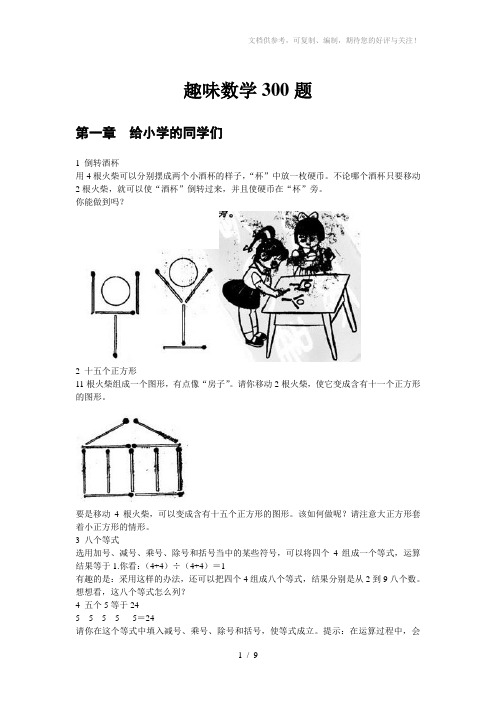
趣味数学300题第一章给小学的同学们1 倒转酒杯用4根火柴可以分别摆成两个小酒杯的样子,“杯”中放一枚硬币。
不论哪个酒杯只要移动2根火柴,就可以使“酒杯”倒转过来,并且使硬币在“杯”旁。
你能做到吗?2 十五个正方形11根火柴组成一个图形,有点像“房子”。
请你移动2根火柴,使它变成含有十一个正方形的图形。
要是移动4根火柴,可以变成含有十五个正方形的图形。
该如何做呢?请注意大正方形套着小正方形的情形。
3 八个等式选用加号、减号、乘号、除号和括号当中的某些符号,可以将四个4组成一个等式,运算结果等于1.你看:(4+4)÷(4+4)=1有趣的是:采用这样的办法,还可以把四个4组成八个等式,结果分别是从2到9八个数。
想想看,这八个等式怎么列?4 五个5等于245 5 5 5 5=24请你在这个等式中填入减号、乘号、除号和括号,使等式成立。
提示:在运算过程中,会出现小数。
5 放哨有十五名少先队员,在一块方形的玉米地四周放哨。
队长决定,每一条边都应该有五名队员看守。
他注意布置各哨位的人数,果然达到了要求。
请看下图。
后来,又来了两名队员,队长调整了哨位上的人数,每边仍然是五名队员看守。
过不久,抽走了四名队员,队长又调整一次哨位上的人数,每边仍然是五名队员看守。
队长是怎么调整哨位的?6 四个等式围一围请看下图,方框的每一边都是一个等式,只是还没填上数字。
请你将从1到8的八个数字填上去,使四个等式成立。
做数学题,要善于寻找突破口,才能较快地找到正确的答案。
要是不加分析,胡乱填几个数字,再来凑结果,会浪费很多时间。
好好想一想,突破口在哪里呢?7 填数字请将从1到8八个数字填到图里。
有一个要求:每一线段两端的两个数字之差必须大于1.8 消防设备九座仓库,有十三条路连接。
为了防火,打算在这些仓库中放两套消防设备。
一座仓库放了消防设备,凡是与它有路连接的仓库,都可以就近使用。
请你想一想,这两套消防设备应该放在哪里,才能使九座仓库都用得上。
小学数学趣味规律100例(一)

1 趣味平方数探秘如果规定1×1=12,2×2=22,3×3=32,…………我们就称12,22,32,……分别是1的平方,2的平方,3的平方,…….关于数的平方有许多很有趣的规律.在这里,我们一起来研究两组算式,看都有怎样的规律.(1)这是一组有趣的算式:1=12,1+2+1=22,1+2+3+2+1=32,1+2+3+4+3+2+1=42,…………想一想,再往下写,会是怎样的算式?你还能接着往下写吗?(2)下面有一组竖式:…………如果把它们改写成横式就是:12=1,112=121,1112=12321,…………想一想,下一个算式该怎样写呢?像这样的算式还能写几个?【规律】1+2+3+4+5+4+3+2+1=52,1+2+3+4+5+6+5+4+3+2+1=62,一般地,有1+2+3+……+n+……+3+2+1=n2(其中字母n代表任意的自然数).11112=1234321.像这样的算式还能继续写上五个:111112=123454321,1111112=12345654321,11111112=1234567654321,111111112=123456787654321,1111111112=12345678987654321.2 两个自然数游戏不必计算,就能说出算式6759×78437843-7843×67596759的得数来.你有这个本领吗?其实这并不困难,只要你认真研究了下面的这几组算式的结果就可以了.请先观察算式的特点,再算出算式的得数.(1)1×22-2×11 2×33-3×22 3×44-4×33 …………(2)11×2222-22×1111 12×3434-34×1212 56×7878-78×5656 …………第1页(3)222×333333-333×222222 124×234234-234×123123 …………(4)1234×56785678-5678×12341234 …………这些算式的答案如何?它们当中的奥秘是什么?【规律】这些算式的答案都是0.由两自然数连续写上两遍所得的数,那么这些算式及它们的得数都有下面的规律:因此,就有6759×78437843-7843×67596759=0.【练习】1.速算下列各题.(1)(1993×19941994-1994×19931993)÷1995(2)1×22+2×33+3×44+……+98×9999-2×11-3×22-4×33-……-99×9898(3)2345×67896789-6789×234523452.研究下列各题.(1)25×484848-48×252525(2)25×48484848-48×252525253 三个等距自然数如果今年是1994年,那么与今年相差1年的年份应该是1993年和1995年;与今年相差2年的年份是1992年和1996年;与今年相差3年的年份是1991年和1997年…….我们就称1993和1995是1994的一组等距数,1是它们的等距;1992和1996也是1994的一组等距数,2是它们的等距;1991和1997也是1994的一组等距数,3是它们的等距…….关于等距数有许多十分有趣的规律.如,任何一个数的2倍等于它的一对等距数的和.像1994这个数就有:1994×2=1993+1995;1994×2=1992+1996;1994×2=1991+1997;…………现在我们有这样一个猜想:与一个数等距的两个数的乘积会等于这个数自乘的积(即这个数的平方)吗?就拿上面的1994这个数来说,1994的平方会等于1993和1995的乘积吗?还会等于1992和1996的乘积或1991和1997的乘积吗?如果不相等,那么会相差多少呢?相差的数是不是有规律?请你先考察完下面的例子后再作结论.为了减少计算上的麻烦,我们在例子里都选用较小的数.第2页(1)等距是1.2×2-1×3=()3×3-2×4=()4×4-3×5=()5×5-4×6=()…………(2)等距是2.3×3-1×5=()4×4-2×6=()5×5-3×7=()6×6-4×8=()…………(3)等距是3.4×4-1×7=()5×5-2×8=()6×6-3×9=()7×7-4×10=()…………(4)假设等距用a表示,那么一个数的一对等距数的乘积与这个数自乘的积相差多少呢?请你用含有a的式子表示出来.会吗?【规律】一个数(用字母b表示)的一对等距数(可用b+a和b-a表示)的乘积与这个数自乘的积不相等.它们相差等距a的平方.用式子表示就是b2-(b+a)×(b-a)=a2.【练习】请直接写出下列各题的得数.(1)19942-1993×1995(2)19942-1992×1996(3)19942-1991×1997(4)1+(22-1×3)+(32-2×4)+(42-3×5)+……+(19942-1993×1995)(5)(152-10×20)+(252-20×30)+(352-30×40)+……+(952-90×100)4 分数性质的推论分数的基本性质是:如果分数的分子和分母都乘以或者都除以相同的数(零除外),那么分数的大小不变.而有人还希望下面的说法也是正确的:分数的分子和分母都加上或者减去相同的数,分数的大小不变.这实际上是错误的.但为了满足这些人的愿望,我们只要将上面的说法稍加修正就能得到一条正确的规律.怎样修正呢?读者朋友,分数的分子和分母要同时加上或减去什么样的数,分数的大小才会不变呢?【规律】分数的分子和分母同时各自加上或减去原来的相同倍数(减去时,这个倍数小于1),分数的大小不变.用字母表示出这条规律就是很明显,这条规律可由分数的基本性质直接导出:因此,我们这条规律是分数基本性质的推论.第3页5 探讨组数的规律用几个不同的数字可以组成多少个不同的若干位数(在同一个数中不能重复使用同一个数字).这是我们本节需要研究的问题.让我们先来考察一个例子.用1~9九个不同的数字,可以组成多少个各位数字不同的两位数?因为1~9九个数字选作两位数的个位和十位都有可能,因此,我们按照一定的顺序来考察实际组数的情况.假如,我们先在十位上选取1~9中的某个数字,比如1吧,那么,以1作十位数的两位数,它的个位数字就只有其余9-1=8(个)数字(2、3、4、5、6、7、8、9)可供选择,这样的两位数就有8个.而十位上的数字是有九个数字可供选择的,因此,总共就可以得到9×8=72(个)各位数字不同的两位数.这72个两位数就是:值得我们思考的是,如果我们只用1~9这些数字中的某八个数字、七个数字、六个数字、……,那么,分别可以组成多少个各位数字不同的两位数?按上面的做法,用八个不同数字组成两位数,先选十位上的数字有八种可能的方法,接着选个位上的数字还有七种可能的方法(也可以先选个位上的数字,再选十位上的数字),因此,共可以组成8×7=56(个)不同的两位数.同理,用七个不同的数字就可以组成7×6=42(个)各位数字不同的两位数.下面的情形不必由我写出,读者可能也推想到了.那么,我希望用下面的符号记录出上面的各种情形:用m个不同的数字,可以组成多少个各位数字不同的两位数?请读者写出答案.再来考察一个例子.用1~9九个数字,可以组成多少个各位数字不同的三位数?九个数字选作三位数的各位数字都有可能.假如,百位上选数字1,十位选数字2,个位上就还有除1、2以外的其余9-2=7(个)数字可以选择,就可得7个三位数.图示如下页。
二年级数学巧算100题(10篇)

二年级数学巧算100题(10篇)我们总是觉得数学是一门很枯燥、没有精彩点的学科。
其实不然,如果我们深入了解数学、研究数学你就会发现里面也有十分有趣的地方。
昨天,妈妈下班回家给我看了一个有趣的信息,信息里是一些阿拉伯数字组成的金字塔一样的题目,看了这些奇妙的数字,我不由得赞叹不已,就这些简单的数字竟能拼成这么完美的形状出来。
然后妈妈选了一组来给我做题,说要让我亲自做做题目,自己感受一下它的奇妙。
题目是:1×9+2=?、12×9+3=?、123×9+4=?、1234×9+5=?以此类推一直到×9+10=?;我看到这些题目就说:“这也没什么特别奇妙的啊。
”妈妈听到就说:“那好,我们把它竖起来写。
”哈哈,这个题目就有趣多吧,然后我就拿起笔开始计算起来了,刚算了两题就把我难住了,妈妈看到我为难的样子,就从身后拿出了计算机说到:“我知道四年级的小朋友还没教到3位数以上的乘法,但是今天我们不是来做算数题目的,我们是来体验数学的奇妙的,来,下面的题目就用计算机算吧。
”我迫不及待的拿过计算机“啪啪啪”的按着计算机上的按钮开始计算了。
当我开始计算第6题时,妈妈一把拿走计算机:“接下来4道题你自己充分发挥现象来做吧,这下我傻眼了:“个、十、百、千、万、十万、十万位的数字叫我怎么算啊?”我心里正纳闷着,妈妈看到我为难的样子就笑了:“欣芸看看上面5道题的得数有什么规律啊?”我刚才只顾着计算题目,还没注意到呢,结果一看,傻眼了,怎么都是1啊?而且一道比一道多一个1。
妈妈接着补充说到:“先看看每道题的规律,然后结合规律、充分发挥现象来做题喔。
”我发现每道题前面多加一位数,后面的得数也就会多出一个1来,这个会不会就是解题的规律呢?我半信半疑地按着这个规律做完了后面的题目,做完之后,我赶紧用计算机检查了一遍,得数居然都是对的,我的心里美滋滋的。
今天数学小测试,我认真地答题,仔细地计算,字迹也比较工整。
【四年级上册数学】《有趣的算式》教学设计

《有趣的算式》教学设计【教学内容】:《义务教育课程标准实验教科书•数学》北师大版四年级上册第37-38页。
【教材与学情分析】:本课是在北师大版四年级上册“乘法”这个单元的最后一个课时,安排在学生已经学习了“计算器”后的一课时内容。
在探究“有趣的算式”过程中,需要借助计算器计算大数,彰显“有趣”、“有意”的学习过程。
教材所选的三个例子中既体现了算式的有趣,还包含结果的有趣。
这些问题的重点不是进行计算,而是通过计算结果的观察发现有趣的规律,以培养学生的探究能力。
四年级学生已经具备使用计算器的基本能力,在本课学习中,学生可以先用计算器算出几个简单算式的结果,重点通过观察发现规律,去推算较复杂算式的结果,必要时还可以用计算器验证,从而培养学生合理使用计算工具解决问题的意识。
学习此部分知识时,学生已经掌握了乘法运算的知识和经验,也积累了较丰富的找规律的探究活动经验。
在经历探索与发现的过程中,学生可以感受数学的奇妙,也有利于培养他们善于观察、乐于思考、勇于实践的精神。
【教学目标】:1、通过有趣的探索活动,体会计算器不仅是计算工具,而且也是探索数学、学习数学的工具。
2、通过观察、比较、归纳,发现有趣的乘法算式中蕴含的规律,并有条理地进行归纳概括,发展合情推理能力。
3、在发现规律的过程中,感受数学的有趣和神奇,激发学习数学的兴趣。
【教学过程】:一、开门见山,引出主题1、谈话:在数学王国里有许多有趣的算式,今天这节课,我们就一起去探索算式中的奥秘。
2、揭题:有趣的算式——探索规律【设计意图:课始即开门见山,引出主题,由此奏响了本节课堂的主旋律——活泼灵动、简约高效。
】二、探索发现,掌握方法1、观察感知,发现规律(1)学生借助计算器依次计算:1×1 11×11 111×111 1111×1111……(2)学生观察算式,尝试概括规律。
(3)组织全班交流:你发现了什么?(引导学生从“乘数、积的特点和变化规律”去观察,用自己的语言有条理地说清即可。
北师大版小学数学四年级上册第三单元《有趣的算式》教学设计教学建议

有趣的算式(用计算器探索规律)学习目标1.通过有趣的探索活动,体会计算器不仅是计算工具,而且也是探索数学、学习数学的工具。
2.能发现有趣的乘法算式中蕴含的规律,并有条理地进行归纳概括,发展合情推理能力。
3.在发现规律的过程中,感受数学的有趣和神奇,激发学习数学的兴趣。
编写说明推理是数学的基本思想之一,是重要的数学思维方式,也是一种主要的数学方法。
因此,教科书结合使用计算器的教学,设计了多组有趣的算式,让学生用计算器进行大数的运算,并通过观察、比较、归纳,发现并表达每组算式的规律,培养学生的合情推理能力。
教科书提出了四个问题:第一个问题和第二个问题都是先用计算器计算,然后观察算式发现规律,再根据规律继续写出这样的算式和结果;第三个问题是先观察和发现算式蕴含的规律,再用计算器进行验证;第四个问题是交流探索“有趣的算式”的体会与收获。
·算一算,然后认真观察,说一说你发现了什么。
已知1×1=1,使用计算器计算11×11=121,111×111=12321后,观察这些算式,发现积的规律。
再让学生尝试用自己的语言表达所发现的规律,进而继续写出后两个算式的结果。
·不计算,你能直接写出99999×99999,999999×999999的积吗?先用计算器计算前三道题:99×99=9801,999×999=998001,9999×9999=99980001。
观察这三个算式与结果,发现规律。
发现了规律,就能够不计算,直接写出所求的积。
·观察下面的算式和得数分别有什么特点,你能在写出几个这样的算式吗?用计算器验证结果。
观察前三个算式和结果,发现规律,继续写出后面的算式和结果:1234×9+5=11111,12345×9+6=111111,123456×9+7=1111111。
进而使用计算器检验结果。
