三向应力状态简介
空间应力状态分析简介
目录
应力状态和强度理论\空间应力状态分析简介
最大切应力为
max
1
3
2
170 MPa
由单元体的三个主应力，绘出三向应力圆如图b所示。
目录
力学
综上可知，单元体任意 斜截面上的应力，总可以用
三个应力圆的圆周上某点或由它们围成的阴影线区域内某点的坐标
来表示。这三个应力圆称为三向应力圆。其中由1和3绘出的应力
圆①称为主应力圆。ຫໍສະໝຸດ 目录应力状态和强度理论\空间应力状态分析简介
1.2 最大正应力和最大切应力
由图示三向应力圆可见，在一点处
的三个主应力中，1是通过该点的
最大切应力为
max
1
3
2
90 MPa
目录
应力状态和强度理论\空间应力状态分析简介 【例7.6】 单元体各个面上的应力如图所示，试求主应力和最
大切应力，并绘出三向应力圆。
目录
应力状态和强度理论\空间应力状态分析简介
【解】 该单元体有一个已知主应力，
即z = 120 MPa。单元体的x平面（左、右
于1和3，相当于平面应力状态，如图c所示。
目录
应力状态和强度理论\空间应力状态分析简介
可用以（1，0）和 （3，0）两点间的线段为
直径绘出的应力圆①（图d） 上各点的坐标来表示。
理论分析证明：对于 与三个主应力均不平行的 任意斜截面，其上的应力 可用位于三个应力圆围成 的阴影线区域里某一相应 点的坐标来表示。
所有截面上的正应力中的最大值，
3是通过该点的所有截面上的正应
力中的最小值。即
max = 1，min = 3
而通过该点的所有截面上的切应
力中的最大值为
三向应力状态
2
min
例7-1 试求中所示单元体的主应力和最大剪应力。 （1）求主应力
x 10MPa, y 30MPa, x 20MPa max x + y x - y 2 + x 2 2 min
10 + 30 10 - 30 + 202 2 2 + 42.4MPa（ 拉 应 力 ） - 2.4MPa（ 压 应 力 ）
2 2
a 0对应 max
x + y
2
a 0 + 90 对应 min
x + y
2
三、最大和最小剪应力
d a 0 da
2
x - y
2
cos 2a - 2 xy sin 2a 0
x - y tg 2a 2 xy
max
x - y 2 + + xy 2 x - y 2 - 2 + xy
3
a 0 12143'
3
（2）求最大剪应力
1 42.4 2 0 MPa - 2.4 3
1
(a)
max
1 - 3
2
22 .4 MPa
3、 纯剪切应力状态
- 2 x tg 2a 0 - x - y
a0 135
五、不等于零的情况。
二向应力状态：三对主应力中有两对主应力不等
于零的情况。
三向应力状态：三对主应力皆不等于零的情况。
7-2 平面应力状态分析—解析法
一、斜截面上的应力
已知：单元体 x，y，xyyx， a 研究与z轴平行的任一斜截面c e上的应力。 符号规则： q 角：从x轴正方向反时针转至斜截面的 外法线方向为正，反之为负。 正应力：拉为正，压为负。 剪应力：使微元体或其局部产生顺时针方 向转动趋势者为正，反之为负。
三向应力
1 2 3
y
(s 1 s 3 )
3
30
E
s 3
(s
2
s 1 )
30
1 E
s 30 s 120 s z ) （
30
x
120
1 E
1 E
s 120 s 30 s z ) （
z
x1
dx
dy
y1
y
ds
x1
x
y1
ds
1
d ( l1 )
d ( l1 ) x d x c o s
dx
xdx
1
x d x s in
ds
x c o s s in
x
y
再 研 究 y 对 微 分 线 段 d s的 影 响
x1
dx
dy
y1
1） x1 方 向 的 线 应 变 ； .沿 2）x1 y 1角 的 剪 应 变 。 .
dx
f ( x , y , z , xy , ) g ( x , y , z , xy , )
y1
y
x1
dy
x
y
先 研 究 x 对 微 分 线 段 d s的 影 响
b
a
A
E
c
d
D
D1
1 AOD BOE
b x cos b / sin a x sin a /cos
三向应力
z
s z s 30 s 120 ) （
我们应该把X，Y，Z理解 成任意三个垂直的方向
特例（主单元体）
s
2
s3
s1
s
2
s1
1 2 3
1 E 1 E 1 E (s 1 s 2 ) (s s 1 )
s1
1 2 3
1 E 1 E 1 E (s 1 0 )
xy
2 xy
x y
例： 已知一点在某一平面内的 1、 2、 3、方向上的应变 1、
2、 3，三个线应变，求该面内的主应变。
解：由
x cos i y sin i
2 2
i
xy
sin i cos i
i =1,2,3这三个方程求出 x， y， x y；然后在求主应变。
2
co s 2
xy
2
sin 2
x y
2
sin 2
y
xy
2
co s 2
2 s x s t
2
s
s x s
s x s
2
y
cos 2 t xy sin 2
y
sin 2 t xy cos 2
二、应变分析图解法——应变圆（ Strain Circle）
1） x1 方 向 的 线 应 变 ； .沿 2）x1 y 1角 的 剪 应 变 。 .
dx
f ( x , y , z , xy , ) g ( x , y , z , xy , )
y1
y
x1
dy
三向应力状态简介
变形比能： 1 u 2
2
1 1 1 u 1 1 2 2 3 3 2 2 2
1 3
变形比能： 1 1 1 u 1 1 2 2 3 3 2 2 2
1 2 2 1 2 2 3 2 ( 1 2 2 3 3 1 ) 2E 1
例：求图示应力状态的主应力和最大剪应力
（应力单位为MPa）。
解： 1 50MPa
2 50MPa 3 50MPa max 1 3
2 50MPa
CL10TU33
例：求图示应力状态的主应力和最大剪应力
（应力单位为MPa）。
CL10TU34
解：
120 40 2 2
3(1 2 ) 2 1 2 2 m ( 1 2 3 ) uv 2E 6E
u f u uv
12 2 2 2 m ( 1 2 ) ( 2 3 ) ( 3 1 ) 6E
m
1 2 3
3
3 ( 1 2 ) 1 2 3 m 变形比能 = 体积改变比能 + 形状改变比能 E 3 K u = u + u
v
f CL10TU41
1 2 2 u 1 2 2 3 2 ( 1 2 2 3 3 1 ) 2E
1 式中：
E 1 体积弹性模量 K 3 (12 2 ) 2 （ 3 1 ） E 1 2 3 m 1 3 3 （ 1 2 ） 3 E 当 05 . 时， 0
2
3 1
1 3
三向应力状态简介4广义胡克定律5
三、应力状态的研究方法
取单元体 1、单元体特征 单元体的尺寸无限小，
2
1 3 2
3 1
每个面上应力均匀分布
任意一对平行平面上的应力相等 2、主单元体 各侧面上切应力均为零的单元体
3、主平面 4、主应力 说明:
切应力为零的截面 主平面上的正应力
重要结论：
(1) 同一面上不同点的应力各不相同;
(2) 同一点不同方向面上的应力也是各不相同
一点的应力状态
过一点不同方位面上应力的总和，称为这一点的应力 状态。
二、研究应力状态的目的
1. 解决复杂应力状态下的强度计算问题 2. 有助于理解和解释某些破坏现象 例如
为什么塑性材料拉伸时会出现滑移线？
(2)当x<y 时 ， 0 是x与min之间的夹角
3. 最大切应力
令
x y
2 x y 2
x y
2
cos 2 x sin 2
sin 2 x cos 2
x y d 2[ cos 2 x sin 2 ] 0 d 2
F
t
0
dA ( x dAcos )cos
( x dA cos )sin ( y dA sin )sin ( y dA sin )cos 0
化简以上两个平衡方程最后得
x y
2 x y 2
x y
2
cos 2 x sin 2
sin 2 x cos 2
不难看出
90 x y
即两相互垂直面上的正应力之和保持一个常数
材料力学第七章
若应力状态由主应力表示，并且在max 0 和 min 0 的情况下，则式（7-7） 成为
max min
max
min
2
1 3
2
进一步讨论，由式（7-4）和式（7-6）可知
tan
21
1 tan 20
上式表明1 与 0 之间有如下关系：
1
0
4
可见，切应力取得极值的平面与主平面之间的夹角为 45 。
若三个主应力中，只有一个主应力不等于零，这样的应力状态称为 单向应力状态。若三个主应力中有两个不等于零，称为二向应力状态或 平面应力状态。若三个主应力皆不为零，称为三向应力状态或空间应力 状态。
第二节 平面应力状态分析——解析法
一、斜截面上的应力
图 7-1 所示为平面应力状态的最一般情况。已知 x ， y ， xy 和 yx 。现 在研究图中虚线所示任一斜截面上的应力，设截面上外法向 n 与 x 轴的夹角 为 。
令 d /d 0 ，由式（7-1）可得
x
2
y
sin
2
xy
cos 2
0
解得
（7-3）
tan 20
2 xy x y
通过运算，可以得到斜截面上正应力的极值为
（7-4）
max min
x
y 2
x
2
y
2
2 xy
（7-5）
由式（7-4）可知， 取得极值的角0 有两个，二者相差 90 ，即最大正应 力 max 和最小正应力 min ，二者分别作用在两个相互垂直的截面上。当 0 ， 取得极值时，该斜截面上的切应力 0 ，即正应力就是主应力。
（a）
（b） 图7-6
例 7-4 悬臂梁受力如图 7-7（a）所示。试求截面 n n 上 A 点处的主应力 大小和方向，并按主平面画出单元体。
简述应力状态的类型
一、根据主单元体上三个主应力中有几个是非零的数值，可将应力状态分为三类：
1.单向应力状态只有一个主应力不等于零。
2.二向应力状态有两个主应力不等于零。
3.三向应力状态三个主应力都不等于零。
单向应力状态又称为简单应力状态，二向和三向应力状态统称为复杂应力状态。
单向及二向应力状态又称为平面应力状态。
二、一点的应力状态：通过受力构件内一点的所有截面上的应力情况称为一点的应力状态。
三、一点的应力状态的表示法—
单元体：围绕所研究的点，截取一个边长为无穷小的正六面体，用各面上的应力分量表示周围材料对其作用。
称为应力单元体。
特点：
1.单元体的尺寸无限小，每个面上的应力为均匀分布。
2.单元体表示一点处的应力，故相互平行截面上的应力相同。
四、主平面、主应力、主单元体：主平面单元体中剪应力等于零的平面。
主应力主平面上的正应力。
可以证明：受力构件内任一点，均存在三个互相垂直的主平面。
三个主应力用σl、σ2和σ3表示，且按代数值排列即σl>σ2>σ3。
主单元体用三对互相垂直的主平面取出的单元体。
第九章三向应力状态(6,7,8)
§9-7 强度理论及其相当应力
一.单参数强度条件的局限性
1.单参数强度条件
max [ ]
max [ ]
2.单参数强度条件的局限性
（1）破坏形式与应力状态有关 铸铁的拉压破坏说明同种材料不同的 受力方式破坏形式不同；
（2）材料的破坏方式与材料性能有关。 铸铁和低碳钢的扭转破坏说明相同的受力方式材料不 同破坏方式不同。 2. 材料破坏的形式 材料破坏的形式主要有两类： 断裂面为主应力作用面的正断-- 脆性破坏 断裂面为主切应力作用面的剪断-- 塑性破坏
（c）在三向压应力接近相等的情况下，都可以引起
塑性变形，所以应该采用第三或第四强度理论。
（d）在两向拉伸的脆性材料，常采用第二强度理论。 对于拉压性能不同的材料，在一个方向拉而另一个方向压 时采用摩尔理论。 这些强度理论的应用条件也不是绝对的，一方面要视 具体工程上的要求，另一方面，脆性破坏和塑性破坏 会因不同条件而发生转化
] 1 E [ 1 （ 2 3） 1 ] 2 [ 2 （ 3 1） E 3 1 [ 3 （ 1 2） ] E
变形比能=体积改变比能+形状改变比能
2
v vV vd
m
1
2 m
1 2 vu 2 s 6E
v f vu
屈服破坏条件是：
1 2 2 2 ( 1 2 ) ( 2 3 ) ( 3 1 ) s 2
第四强度理论：
1 2 2 2 ( 1 2 ) ( 2 3 ) ( 3 1 ) [ ] 2
数情况下远比此为小。
4.形状改变比能理论(第四强度理论)
三向应力状态简介
动力应力状态
动力应力状态是指岩体在受 到周期性或非周期性的外力 作用时，其内部应力不断发
生变化的状态。
动力应力状态通常由地震、 车辆振动、机器振动等动态 因素引起，其特点是各向应 力随时间变化，岩体可能发
生动态变形或破坏。
在动力应力状态下，岩体内 部应力的分布和大小均随时 间变化，需要采取相应的减 震、隔震措施以减小岩体的 动态响应。
发展多尺度、跨层次的理论模型
结合微观、细观和宏观尺度，研究三向应力状态下材料在不同尺度上的响应和演化规律。
探索复杂环境因素对三向应力状态的影响
考虑温度、湿度、化学环境等复杂因素，建立更为真实的理论模型，以模拟实际工程中 的复杂应力状态。
实验技术的发展
开发高精度、高分辨率的实验测试技术
发展新型传感器和测量方法，提高对三向应力状态的测量精度和可靠性。
03 三向应力状态的影响因素
地质构造
地质构造是影响三向应力状态的重要 因素之一。地壳中的板块运动、断层 活动、褶皱等地质构造过程会导致岩 层中应力的变化，从而影响三向应力 状态。
不同地区的地质构造特征不同，因此 三向应力状态也会存在差异。例如， 在板块边界、断裂带等地区，岩层中 的应力通常较高，而在盆地、平原等 地区则较低。
03
在地下工程中，三向应力状态可用于分析隧道、地下洞室等结构的稳定性，预 测结构变形和破坏的可能性。
石油工程
石油工程是研究石油和天然气的勘探 、开发和生产的科学，三向应力状态 在石油工程中具有重要应用。在石油 工程中，三向应力状态是指地层中的 岩石在三个方向的应力作用下处于平 衡状态。
在石油工程中，三向应力状态可用于 分析地层的稳定性、预测地层破裂的 可能性以及评估地层压力。例如，在 钻井工程中，三向应力状态可用于分 析井壁的稳定性，预测井壁坍塌的可 能性。
三向应力状态最大主应力方向计算
三向应力状态最大主应力方向计算（最新版）目录1.引言2.三向应力状态的定义和意义3.最大主应力方向的计算方法4.应用实例5.结论正文【引言】在材料力学中，应力状态是指材料内部各点的应力分布情况。
三向应力状态是指材料在某一点处受到三个大小相等、方向相互垂直的应力作用。
这种应力状态在实际工程中非常常见，如压力容器、桥梁等结构。
对于三向应力状态，最大主应力方向的计算是一个关键问题，它直接影响到结构的强度和稳定性。
本文将介绍三向应力状态的最大主应力方向计算方法。
【三向应力状态的定义和意义】三向应力状态是指材料内部某一点处受到三个大小相等、方向相互垂直的应力作用。
在这种应力状态下，材料内部的应力分布呈现出一种特殊的规律，即最大主应力方向位于三个应力方向的交点处。
三向应力状态在实际工程中具有重要意义，因为它可以反映出材料在复杂应力环境下的强度和稳定性。
【最大主应力方向的计算方法】计算三向应力状态下最大主应力方向的方法有多种，其中较为常用的是莫尔法和屈服准则法。
1.莫尔法莫尔法是一种基于应力圆的概念来计算最大主应力方向的方法。
在三向应力状态下，三个应力方向分别对应三个应力圆。
最大主应力方向位于三个应力圆的交点处，可以通过求解这三个交点来得到最大主应力方向。
2.屈服准则法屈服准则法是一种基于材料屈服特性来计算最大主应力方向的方法。
在三向应力状态下，材料的屈服方向通常是沿着最大主应力方向。
因此，可以通过求解材料的屈服准则来得到最大主应力方向。
【应用实例】假设一个压力容器在顶部受到三个大小相等、方向相互垂直的应力作用，我们需要计算最大主应力方向。
首先，我们可以通过实验或数值模拟得到应力分布情况。
然后，根据莫尔法或屈服准则法，求解最大主应力方向。
最后，根据最大主应力方向，可以判断压力容器在顶部的强度和稳定性。
【结论】对于三向应力状态，最大主应力方向的计算是一个关键问题。
通过莫尔法或屈服准则法，可以有效地计算出最大主应力方向。
岩石三向应力状态
岩石三向应力状态在地球内部，岩石经常受到各种各样的力的作用。
这些力可以导致岩石发生变形和破裂，并对地壳构造和山脉形成产生重要影响。
为了了解岩石内部的三向应力状态，我们需要研究和分析地质力学。
地质力学是研究岩石在地球内部受力和变形规律的学科。
在地球内部，岩石受到三个方向的应力：水平应力、垂直应力和剪切应力。
以下是相关参考内容：1. 水平应力：在地质构造中，水平应力是地壳中最重要的一个力。
它是沉积物和岩石的自重、地壳板块构造运动、火山活动等因素所产生的。
水平应力作用在岩石中，会使岩石产生挤压和拉伸的应变，导致岩石的变形和断裂。
2. 垂直应力：垂直应力是指垂直于地表的力，也就是岩石的地表压力。
它是岩石承受重力和地质力学过程中的岩层远离或靠近地表所产生的。
垂直应力作用在岩石中，会使岩石发生压缩或拉伸的应变，导致岩石的变形和断裂。
3. 剪切应力：剪切应力是指作用在岩石中，使其产生滑动或剪切变形的力。
剪切应力是由板块运动、断层活动等因素所产生的。
当剪切应力作用在岩石中，会引起岩石中的切割和滑动，导致岩石的块状破裂和岩层错动。
4. 应力张量：应力张量可以描述和分析岩石的三向应力状态。
它是一个矩阵，包含了岩石受到的各个方向的应力。
通过对应力张量的分析，可以研究岩石的应力分布、应力场、地震活动等。
5. 线性弹性理论：线性弹性理论是地质力学中常用的一种理论方法。
它假设岩石在小应变下的变形是可逆的，岩石具有线弹性性质。
根据线性弹性理论，可以推导出岩石的应力应变关系，从而研究岩石受力和变形的规律。
6. 应力解析：应力解析是通过计算和模拟来分析岩石的应力状态和变形。
它使用数学方法和地质力学实验来确定岩石中的应力分布和变形机制。
通过应力解析，可以计算出岩石的应力张量和主应力方向，从而预测岩石的变形和断裂。
以上是有关岩石三向应力状态的一些相关参考内容。
研究和理解岩石的应力状态对于地质地质工程、地震预测和资源勘探等有重要意义。
三向应力状态简介
2 1
m m
2 m
1 m
3
m
3 m
m
1
2
3
3
变 形3 比(1 能=2 体)积 改1 变 比能2+ 形状3改变比m 能
u E = uv 3+
uK f CL10TU41
u 2 1 E1 2 2 2 3 2 2 (12 23 31 )
uv
3(12)
2E
2m
1 6E 2(123)2
uf uuv
1 6 2E ( 1 1 2 ) 2 m(2 m 3 ) 2 (3 1 1 ) 2 m
变为 0，则外力偶ｍ＝？
m
CL10mTU60
解：(1)将应变片贴于与母线成45°角的外表面上
(2) 1 ,2 0 ,3
1E 11(23) max
min
1
E
1
E
m
d3
0
16
m d 3E 0 16(1 )
例：钢制封闭圆筒，在最大内压作用下测 得圆筒表面任一点的εx＝1.5×10－4。已知 E=200GPa，μ＝0.25，［σ］＝160MPa，按第 三强度理论校核圆筒的强度。
y x
CL10TU61
解：y 2x
xE 1(xy)1.5104
由上两式可求得 x 6 0 M P a , y 1 2 0 M P a
故 1 1 2 0 M P a , 2 6 0 M P a , 3 0
r 3 1 3 1 2 0 M P a < [] y
1
至于与三个主方向都不平行的任意斜截面， 弹性力学中已证明，其应力σn和τn可由图中阴 影面内某点的坐标来表示。
3
2
1
第九章三向应力状态(6,7,8)
(5) 强度理论的相当应力
上述四个强度理论所建立的强度条件可统一写 作如下形式：
影响材料的脆性和塑性的因素很多，例如低温能提 高脆性，高温一般能提高塑性； 在高速动载荷作用下 脆性提高，在低速静载荷作用下保持塑性。 无论是塑性材料或脆性材料：
在三向拉应力接近相等的情况下，都以断裂的形式破坏， 所以应采用最大拉应力理论；
在三向压应力接近相等的情况下，都可以引起塑性变形， 所以应该采用第三或第四强度理论。
于是，第四强度理论的屈服判据为 vd vdu
1 vd ( 1 2 ) 2 ( 2 3 ) 2 ( 3 1 ) 2 6E
对于由单轴拉伸试验可测定屈服极限s的材料，注 意到试验中1＝ s， 2＝3＝0，而相应的形状改 变能密度的极限值为 1 vdu 2 s2 6E 故屈服判据可写为
1 1 E 1 （ 2 3） 1 2 （ 3 1） 2 E 3 1 3 （ 1 2） E
1 2 2 2 v 1 2 3 2 ( 1 2 2 3 3 1 ) 2E
1 1 2 2 2 1 2 2 3 3 1 2 s2 62 1 2 2 3 3 1 s 2 此式中，1、2、3是构成危险点处的三个主应力， 相应的强度条件则为
§9-7 强度理论及其相当应力
一、强度理论的概念
三向应力状态定义
三向应力状态定义
描述应力的时候是需要定义截面的，截面的面积、方向都会影响应力，也就是与所取微元体的方向位置有关。
题主描述的主应力状态仅是在材料
某一点上一种特殊的应力状态，非特殊情况时就会包含切应力。
可以从最简单的单向应力状态进行理解，例如杆件两端受拉。
我们可
以找到一个微元体的状态，使得仅存在一个主平面上的主应力不为零，可
以认为这个状态与拉力方向呈0°。
当我们取的微元体与拉力方向呈45°时，存在切应力且切应力达到最大值。
一般材料力学书都有提到这块内容。
那么三向应力状态也是同理，受力构件任意一点一定存在一个微元体
状态，使三个相互垂直平面切应力为0，即三个相互垂直的主平面，然后
当微元体稍有偏转，就会出现切应力。
三向应力状态应力圆的画法
三向应力状态应力圆的画法应力圆是一种用于描述材料内部应力分布的图形方法，它可以直观地展示材料在不同方向上的应力大小和方向关系。
在三向应力状态下，应力圆的画法可以帮助我们更好地理解材料的应力分布情况。
在三向应力状态下，材料同时受到三个方向上的应力作用，这三个方向可以是任意的，通常分别称为x、y、z方向。
为了绘制应力圆，我们需要确定这三个方向上的应力大小和方向，并将其表示在一个平面上。
我们选择一个平面作为绘制应力圆的基准平面，通常选择x-y平面。
在这个平面上，我们可以用一个坐标系来表示应力的大小和方向。
在x-y平面上，我们以x轴为横轴，y轴为纵轴建立坐标系。
接下来，我们需要确定应力圆的中心位置。
在三向应力状态下，应力圆的中心位置通常表示为(x0, y0)，即应力圆的圆心坐标。
根据材料的应力状态，我们可以计算出x、y方向上的应力值，然后将其代入应力圆方程中，求解出圆心坐标。
在得到圆心坐标后，我们可以绘制出应力圆的圆心。
圆心表示的是材料在该点上的平均应力状态。
接下来，我们需要确定应力圆的半径。
在三向应力状态下，应力圆的半径表示的是切应力的大小。
根据材料的应力状态，我们可以计算出x、y方向上的切应力值，然后将其代入应力圆方程中，求解出半径值。
在得到半径值后，我们可以绘制出应力圆的圆周。
圆周表示的是材料在该点上的切应力大小和方向。
还可以在应力圆上标注出一些特殊点和线。
例如，我们可以标注出主应力方向，即切应力达到最大或最小值的方向；我们还可以标注出主应力值，即切应力的最大或最小值。
通过绘制应力圆，我们可以直观地了解材料在不同方向上的应力分布情况。
这对于工程设计和材料分析都是非常重要的。
通过对应力圆的分析，我们可以判断材料的强度和稳定性，进而优化设计方案，提高材料的使用寿命。
应力圆的画法是一种用于描述材料内部应力分布的图形方法。
在三向应力状态下，应力圆可以帮助我们更好地理解材料的应力分布情况。
通过绘制圆心、圆周和标注特殊点和线，我们可以清晰地了解材料在不同方向上的应力大小和方向关系。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
uv
3(12)
2E
2m
1 6E 2(123)2
uf uuv
1 6 2E ( 1 1 2 ) 2 m(2 m 3 ) 2 (3 1 1 ) 2 m
3
m
.
3 m
§10-7 强度理论的概念
max [ ] max [ ]
流动破坏 材料破坏的形式主要有两类：
断裂破坏
.
§10-8 常用的四种强度理论
• 由此导出失效条件的应力表达式为：
1 (2 3 ) b
[ ] b
n
• 第二强度条件： 1(23 ) []
.
煤、石料或砼等材料在轴向压缩试验时，如 端部无摩擦，试件将沿垂直于压力的方向发生 断裂，这一方向就是最大伸长线应变的方向， 这与第二强度理论的结果相近。
单 位 体 积 的 体 积 改 变 为 :
V1 V0
V0
123
3 a
b 1 c
也 称 为 体 积 应 变 。 .
CL10TU30
1231E 2(123)
3(12)123 m
式 当 中 Km： 0 3.(5 1E 213时 1E2， EEE1113 )2 体 0 1323积 3.弹 （（（性模213量 K231
材料破坏的基本形式有两种：流动、断裂 相应地，强度理论也可分为两类：
一类是关于脆性断裂的强度理论； 另一类是关于塑性屈服的强度理论。 一、关于脆断的强度理论
.
1.最大拉应力理论（第一强度理论）
• 它假定：无单向拉伸断裂时 的极限应力σu，材料即破坏。
.
2.最大伸长线应变理论（第二强度理论）
• 它假定，无论材料内各点的应变状态如何， 只要有一点的最大伸长线应变ε1达到单向拉 伸断裂时应变的极限值 εu，材料即破坏。
• 所以发生脆性断裂的条件是 ε1 ≥ εu • 若材料直到脆性断裂都是在线弹性范围内工
作，则
1 E 11 （ 2.3 ） , uE uE b
m ax1 2347.2M Pa
.
例：求图示应力状态的主应力和最大剪应力 （应力单位为MPa）。
解： 1 5 0 M P a
2 50M Pa
3 50M Pa
max
1 3 2
50M Pa
.
CL10TU33
例：求图示应力状态的主应力和最大剪应力 （应力单位为MPa）。
.
CL10TU34
.
3
2
1
.
这样，单元体上与主应力之一平行的各个 斜截面上的正应力和剪应力，可由三个应力圆 圆周上各点的坐标来表示。
3
2
1
.
至于与三个主方向都不平行的任意斜截面， 弹性力学中已证明，其应力σn和τn可由图中阴 影面内某点的坐标来表示。
3
2
1
.
• 在三向应力状态情况下：
2
max 1
min 3
1
2
1 E
2 （ 3 1）
3
1 E
3 （ 1 2） .
2 1
m m
2 m
1 m
3
m
3 m
m
1
2
3
3
变 形3 比(1 能=2 体)积 改1 变 比能2+ 形状3改 变比m 能
u E = uv 3+ .
uK f CL10TU41
u 2 1 E1 2 2 2 3 2 2 (12 23 31 )
.
对于二向应力状态：
1 1 E ( 1 2 )
2
1 E
(
2
1)
3 E ( 1 2 )
.
2 1
CL10TU30
下 面 考 虑 体 积 变 化 ：
V0abc
V 1 a ( 1 1 ) b ( 1 2 ) c ( 1 3 ) 2
a b c ( 1 1 23 )
解：
2 1 1 12 20 02 2 4 40 0 1 2 0 2 4 0 23 021 3 3 0 0M M P a 3 3 30 0M MP Pa a
m ax1 2380M Pa
.
§10-5 广义胡克定律
纵向应变：
E
横向应变：
E .
CL10TU35
下 面 计 算 沿 1 方 向 的 应 变 ：
• 在单向拉伸时，极限应力 σu =σb
• 失效条件可写为 σ1 ≥ σb
[ ] b
n
• 第一强度强度条件： .
1 []
试验证明，这一理论与铸铁、岩石、砼、 陶瓷、玻璃等脆性材料的拉断试验结果相符， 这些材料在轴向拉伸时的断裂破坏发生于拉应 力最大的横截面上。脆性材料的扭转破坏，也 是沿拉应力最大的斜面发生断裂，这些都与最 大拉应力理论相符，但这个理论没有考虑其它 两个主应力的影响。
max
1
3
2
3
• τmax 作用在与σ2平行且与σ1和σ3的方向成45°
角的平面上，以τ1，3表示 .
CL10TU31
例：求图示应力状态的主应力和最大剪应力 （应力单位为MPa）。
.
CL10TU32
解：
1 330 220 30 220 2402 5 4 2 2 .2 .2M M P a
25500M M PPaa
1引 起 的 应 变 为 1
1
E
2
2 、 3 引 起 的 应 变 为
1
2
E
1
3
E
1 3
当 三 个 主 应 力 同 时 作 用 时 ：
1E 11（ 2 . 3）
CL10TU30
广义胡克定律：
1
1 E
1 （ 2 3）
2
1 E
2
（
3
）
1
3
1 E
3 （ 1 2）
2
3
3
1
1 1
3 2
. 3
2
3
2
1
.
同理，在平行于 σ2 的各个斜截面上，其 应力对应于由主应力 σ1 和 σ3 所画的应力圆圆 周上各点的坐标。
2
3
1
1
3 2.
3
2
1
.
在平行于 σ1 的各个斜截面上，其应力对应 于由主应力 σ2 和 σ3 所画的应力圆圆周上各点 的坐标。
2
3
1
1
3 2
§10-4 三向应力状态简介
主单元体：六个平面都是主平面
2
1 3
若三个主应力已知，求任. 意斜截面上的应CL力10T: U30
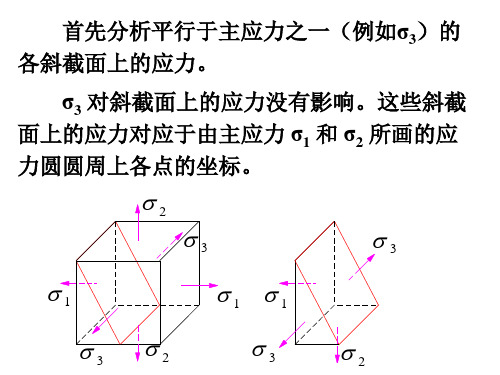
首先分析平行于主应力之一（例如σ3）的 各斜截面上的应力。
σ3 对斜截面上的应力没有影响。这些斜截 面上的应力对应于由主应力 σ1 和 σ2 所画的应 力圆圆周上各点的坐标。
） ） ）
§10-6 复杂应力状态下的变形比能
P
拉压变形能：
U1Pl1PPl P2l
2
2 EA 2EA
变形比能：
P
l l
uU P2l
2
1
V 2EAAl 2E 2
. CL10TU40
变形比能：
u 1
2
u2 1112 1222 133 2
1 3
.
变形比能：
u21112122 2133
2 1 E 1 2 1 E12 2 13 2 2 （(1 2 2 3 ）23 31 )