第九章应力状态(3,4,5)分解
合集下载
材料力学第九章动荷载和交变应力

kd 1 a g 1 2.5 9.8 1.26
st FNst / A W2 / A 127.3MPa d kd st 160.4MPa 1.05[ ]
∴ 钢索满足强度要求。
2.5m
FNd W2
W2 g
a
2.5m a
W2
2.梁的强度校核
W1
kd 1 a g 1 2.5 9.8 1.26
求σdmax、△Dd。不计梁的自重。 A
解:1.计算静态的△Cst、Mmax和
σstmax
W
h
D
2l / 3 l
C
B
l/3
由 w Fb(l 2 b2 ) x Fb x3
6EIl
6EIl
得
Δ Cst
W
l [l 2 ( l )2]
3
3
6EIl
2l 3
Wl 3
6EIl
( 2l )3 3
4Wl 3 0.19mm 243EI
结论:梁满足强度要求。
三、提高构件抗冲击能力的措施
d kdst Fd kdW d kd st
kd 1
1 2h — —竖向冲击动荷因数
st
kd
v2 水平冲击动荷因数
gst
在静应力不变的情况下,减小动荷系数可以减小冲击应力。
即加大冲击点沿冲击方向的静位移: 被冲击物采用弹性模量低、变形大的材料制作; 或在被冲击物上垫上容易变形的缓冲附件。
W
h C
z Iz = 1130cm4 Wz =141cm3
A
B
1.梁本身的变形
1.5m
1.5m
k
ΔCst1
Wl 3 48EI
0.474mm
2.支座缩短量
第九章 梁的应力

38
第二节 梁的切应力、切应力强度条件
◆例题
例 7 : FS = 15 b = 120 mm,d 20 mm, yC
= 45 mm。试求 :tmax ;腹板与翼
缘交接处切应力 ta
解:
Sz ,max
d (d
b 2
yC )2
9.03 105
b(h02 h2 ) 2d (h2 4 y2 )
第九章
37
第二节 梁的切应力、切应力强度条件 ◆ 梁的正应力与梁的剪应力比较
s max
Fl bh2
6Fl bh2
6
t max
3F 2 bh
s max t max
6Fl bh2
2bh 3F
4
l h
第九章
当 l >> h 时,smax >> tmax
E
ymax
2. 应力计算
第九章
D d 0.701m
22
ymax
d
2
1.0 103 m
s max
E
ymax
285 MPa
10
第一节 梁的正应力、正应力强度条件
静力学方面
ysdA M
A
联立求解得:
E y2dA M
A
1
M EI z
结 论:
中性层曲率:
22
ymax
d
2
1.0 103 m
s max
E
ymax
285 MPa
3. 弯矩计算
1 M
第九章 预应力混凝土构件

裂缝宽度与钢筋应力基本成正比,一般
Ms=(0.6~0.8)My,如配筋按正截面承载力计算,Ms作用
下sss=(0.5~0.7)fy。对于HPB335级钢筋,fy
=300MPa,sss=150~210MPa,裂缝宽度已达(0.15~ 0.25) mm。如采用RRB400级高强钢筋,fy=580MPa, 则sss= 290 ~406 MPa,裂缝宽度已远远超过容许限值。 故钢筋混凝土结构限制了高强材料的应用,限制
无粘结预应力束
3.预应力螺纹钢筋 也称精轧螺纹钢筋,是用热轧、轧后余热 处理或热处理工艺制作成带有不连续无纵肋的 外螺纹的直条钢筋,该钢筋在任意截面处均可 带有匹配的内螺纹的连接器或锚具进行连接或 锚固。直径为18~50mm,具有高强度、高韧性 等特点。
预应力钢筋
9.1.4施加预应力的方法
一、先张法
根据力的平衡条件
spcI
spcAc spAp ssAs scon sl aEspc Ap aES仍处 于受压状态,不会出现开裂;
s c s pc 0
受拉边缘应力虽然受拉,但拉应力小于混 凝土的抗拉强度,一般不会出现开裂;
0 s c s pc ftk
s c s pc ftk
受拉边缘应力超过混凝土的抗拉强 度,虽然会产生裂缝,但比钢筋混 凝土构件(Np =0)的开裂明显推迟, 裂缝宽度也显著减小。
' cu
9.3预应力混凝土轴心受拉构件的计算
预应力混凝土的计算分两部分 一、使用阶段计算 ⑴承载力计算。对于预应力轴心受拉构件,应进行正 截面受拉承载力计算;对于预应力受弯构件,应进行 正截面受弯承载力和斜截面受剪承载力计算。 ⑵裂缝控制验算。对于正常使用阶段不允许开裂的构 件,应进行抗裂验算;对于允许开裂的构件,则应进 行裂缝宽度验算。 ⑶变形验算。对预应力受弯构件,应进行挠度验算。 二、施工阶段验算 预应力混凝土构件在制作、运输和安装等施工过 程中,应对其承载力和抗裂性进行验算。
第9章 梁的应力

中性层
中 性 轴
6
3.假设和推论 (1)平面假设:横截面变形后仍为平面,只是绕中性轴发生
转动.
(2)假设纵向纤维之间无挤压,各条纤维仅发生简单的拉伸
或压缩。材料服从虎克定律σ=Eε。
推论: (1)距中性轴等高处,变形相等。 (2) 横截面上只有正应力。
F
F
m
n
4、梁的正应力公式推导
m
n
中性轴
B
L 2 L 2
A
F
h 6
a
b
C
h 2
h
c
b
3
FL
1
a
M B ya IZ
FL
h
MB
1 2
FL
IZ
bh
12
2 3 3 1.65MPa bh 12 1 h
b 0
c
M B yc IZ
FL
2 3 2 bh 12
2.47MPa
(压)
12
例题2
试计算图示简支矩形截面木梁平放与竖放时的最大 正应力,并加以比较。
F A
F
cos
2
同一点在斜截面上时:
2
sin 2
即使同一点在不同方位截面上,它的应力也各不相同
45
3、梁上任一点应力状态的分析
符号规定: 正应力:拉应力为正,压应力为负 切应力:使单元体顺时针方向转动为正;反之为负 α自x轴开始到斜截面的外法线方向逆时针转向为正,反之为负
第九章 梁的应力
1
概
述
钢筋混凝土梁拉裂破坏 1、弯曲构件横截面上的应力 剪力V 内力 剪应力τ
第九章梁的应力

的过渡层--------称为中 性层 。
中间层与横截面 的交线
--中性轴
梁的弯曲变形实际上是各截面绕各自的中性轴转
动了一个角度,等高度的一层纤维的变形完全相同。
4、纵向线应变的变化规律
(纵向线段的变化规律)
A1B1 AB
AB
A1B1 OO1 OO1
(y)dd d
y
y (1)
——横截面上各点的纵向线应变 与它到中性轴的距离成正比
三、纯弯曲理论的推广
纯弯曲时梁横截面上 My
正应力的计算公式
Iz
横力弯曲时
1、由于切应力的存在,梁 的横截面发生翘曲;
2、横向力还使各纵向线之 间发生挤压。
A
B
1m
2m
平面假设和纵向线之 间无挤压的假设实际上都 不再成立。
实验和弹性理论的研究结果表明:
对于细长梁(跨高比 l / h > 5 ),剪力的影响可以忽 略,纯弯曲时的正应力计算公式用于横力弯曲情况,其结
a
c
o
o1
AB
b
d
dx
中性层
y
中
性
层
曲
率
d
半
径
y
A1
B1
E Ey
——横截面上各点的正应力沿截面高度 按线性规律变化
梁弯曲时横截面上正应力分布图: M
中性层
σmax
Z
σmax
y
中性轴的位置?
梁变形后中性层的曲率 1 ?
M Z
M
E
Ey
y
(三)、静力平衡条件
zdAdA x 由横截面上的弯矩和正应力的关系
只是相对转动了一个角度
且仍与纵向线正交。 3、假设:
中间层与横截面 的交线
--中性轴
梁的弯曲变形实际上是各截面绕各自的中性轴转
动了一个角度,等高度的一层纤维的变形完全相同。
4、纵向线应变的变化规律
(纵向线段的变化规律)
A1B1 AB
AB
A1B1 OO1 OO1
(y)dd d
y
y (1)
——横截面上各点的纵向线应变 与它到中性轴的距离成正比
三、纯弯曲理论的推广
纯弯曲时梁横截面上 My
正应力的计算公式
Iz
横力弯曲时
1、由于切应力的存在,梁 的横截面发生翘曲;
2、横向力还使各纵向线之 间发生挤压。
A
B
1m
2m
平面假设和纵向线之 间无挤压的假设实际上都 不再成立。
实验和弹性理论的研究结果表明:
对于细长梁(跨高比 l / h > 5 ),剪力的影响可以忽 略,纯弯曲时的正应力计算公式用于横力弯曲情况,其结
a
c
o
o1
AB
b
d
dx
中性层
y
中
性
层
曲
率
d
半
径
y
A1
B1
E Ey
——横截面上各点的正应力沿截面高度 按线性规律变化
梁弯曲时横截面上正应力分布图: M
中性层
σmax
Z
σmax
y
中性轴的位置?
梁变形后中性层的曲率 1 ?
M Z
M
E
Ey
y
(三)、静力平衡条件
zdAdA x 由横截面上的弯矩和正应力的关系
只是相对转动了一个角度
且仍与纵向线正交。 3、假设:
第九章应力状态(3,4,5)
E
广义虎克定律: 3. 广义虎克定律:
σ2
σ1 σ3
当 个 应 同 作 时 三 主 力 时 用 :
1 ε1 = [σ1 − µ( 2 + σ 3)] σ E 1 另两个方向 ε2 = [σ2 − µ( 3 +σ1 ] σ ) E 1 ] ε3 = [σ3 − µ( 1 +σ2) σ E
CL10TU30
一.斜方向的应变 设 件 一 处 应 构 内 点 的 ε ε γ 变 x、 y和 xy皆 已 为 知 。 求 α和 α 量 现 ε γ
伸长的线应变和使直 角减小的剪应变规定 为正。 为正。
α
CL10TU27
1. 斜方向应力
σ x +σ y σ x −σ y σ α α + cos 2 −τ x sin 2 α= 2 2 σ −σ y τα = x sin 2 +τ x cos 2 α α 2 1 1 π π σ π = (σx +σ y ) + (σx −σ y ) cos 2(α + ) −τ x sin 2(α + ) α+ 2 2 2 2 2
σ2 σ 3
σ1 σ3 σ 2 σ1
τ
σ3
σ2
σ σ1
这样, 这样,单元体上与主应力之一平行的各个 斜截面上的正应力和剪应力, 斜截面上的正应力和剪应力,可由三个应力圆 圆周上各点的坐标来表示。 圆周上各点的坐标来表示。
τ
σ3
σ2
σ1
σ
至于与三个主方向都不平行的任意斜截面, 至于与三个主方向都不平行的任意斜截面, 弹性力学中已证明,其应力σ 弹性力学中已证明,其应力 n和τn可由图中阴 影面内某点的坐标来表示。 影面内某点的坐标来表示。
广义虎克定律: 3. 广义虎克定律:
σ2
σ1 σ3
当 个 应 同 作 时 三 主 力 时 用 :
1 ε1 = [σ1 − µ( 2 + σ 3)] σ E 1 另两个方向 ε2 = [σ2 − µ( 3 +σ1 ] σ ) E 1 ] ε3 = [σ3 − µ( 1 +σ2) σ E
CL10TU30
一.斜方向的应变 设 件 一 处 应 构 内 点 的 ε ε γ 变 x、 y和 xy皆 已 为 知 。 求 α和 α 量 现 ε γ
伸长的线应变和使直 角减小的剪应变规定 为正。 为正。
α
CL10TU27
1. 斜方向应力
σ x +σ y σ x −σ y σ α α + cos 2 −τ x sin 2 α= 2 2 σ −σ y τα = x sin 2 +τ x cos 2 α α 2 1 1 π π σ π = (σx +σ y ) + (σx −σ y ) cos 2(α + ) −τ x sin 2(α + ) α+ 2 2 2 2 2
σ2 σ 3
σ1 σ3 σ 2 σ1
τ
σ3
σ2
σ σ1
这样, 这样,单元体上与主应力之一平行的各个 斜截面上的正应力和剪应力, 斜截面上的正应力和剪应力,可由三个应力圆 圆周上各点的坐标来表示。 圆周上各点的坐标来表示。
τ
σ3
σ2
σ1
σ
至于与三个主方向都不平行的任意斜截面, 至于与三个主方向都不平行的任意斜截面, 弹性力学中已证明,其应力σ 弹性力学中已证明,其应力 n和τn可由图中阴 影面内某点的坐标来表示。 影面内某点的坐标来表示。
应力状态分析和强度理论

03
弹性极限
材料在弹性范围内所能承受的最大应力状态,当超过这一极限时,材料会发生弹性变形。
01
屈服点
当物体受到一定的外力作用时,其内部应力状态会发生变化,当达到某一特定应力状态时,材料会发生屈服现象。
02
强度极限
材料所能承受的最大应力状态,当超过这一极限时,材料会发生断裂。
应力状态对材料强度的影响
形状改变比能准则
04
弹塑性材料的强度分析
屈服条件
屈服条件是描述材料在受力过程中开始进入屈服(即非弹性变形)的应力状态,是材料强度分析的重要依据。
根据不同的材料特性,存在多种屈服条件,如Mohr-Coulomb、Drucker-Prager等。
屈服条件通常以等式或不等式的形式表示,用于确定材料在复杂应力状态下的响应。
最大剪切应力准则
总结词
该准则以形状改变比能作为失效判据,当形状改变比能超过某一极限值时发生失效。
详细描述
形状改变比能准则基于材料在受力过程中吸收能量的能力。当材料在受力过程中吸收的能量超过某一极限值时,材料会发生屈服和塑性变形,导致失效。该准则适用于韧性材料的失效分析,尤其适用于复杂应力状态的失效判断。
高分子材料的强度分析
01
高分子材料的强度分析是工程应用中不可或缺的一环,主要涉及到对高分子材料在不同应力状态下的力学性能进行评估。
02
高分子材料的强度分析通常采用实验方法来获取材料的应力-应变曲线,并根据曲线确定材料的屈服极限、抗拉强度等力学性能指标。
03
高分子材料的强度分析还需要考虑温度、湿度等环境因素的影响,因为高分子材料对环境因素比较敏感。
02
强度理论
总结词
该理论认为最大拉应力是导致材料破坏的主要因素。
应力状态

x
-
yx
xy
y
即又一次证明了剪应力的互等定理。
材料力学
应力状态/应力圆
三、应 力 圆
(Mohr’s Circle for Stresses)
1、应力圆方程
x y x - y cos 2 - xy sin 2 2 2
(1)
xy -30MPa. y -40MPa,
试求(1)斜面上的应力;(2)主应力、主平面; (3)绘出主应力单元体。
40
D
A
30MPa 60MPa
材料力学
应力状态/应力圆
解: (一)、图解法 3 -48.3MPa
40
30MPa
1 68.3MPa
a(-40,30)
60MPa
由平衡即可确定任意方向面上的正
应力和切应力。
材料力学
应力状态/应力状态的概念及其描述
示例一 F
S平面
F
1
1
1
材料力学
F A
应力状态/应力状态的概念及其描述 S平面 n
F
1
F
1
90
同一点的应力状态可以有各种各样的描述方式.
材料力学
应力状态/应力状态的概念及其描述
材料力学
应力状态/应力状态的概念及其描述
应力的三个重要的概念 1、应力的面的概念 2、应力的点的概念 3、应力状态的概念
材料力学
应力状态/应力状态的概念及其描述
(二)、一点应力状态的描述
• 微元
(Element)
dx , dy, dz 0
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
s min
2 2
2 t x
解:
s 2 50MPa s 1 s 2 50MPa
s 3 50MPa
t max s1 s 3
2 50MPa
[例9-14]求图示应力状态的主应力和最大 剪应力(应力单位为MPa)。
s max
解:
s min
s x s y
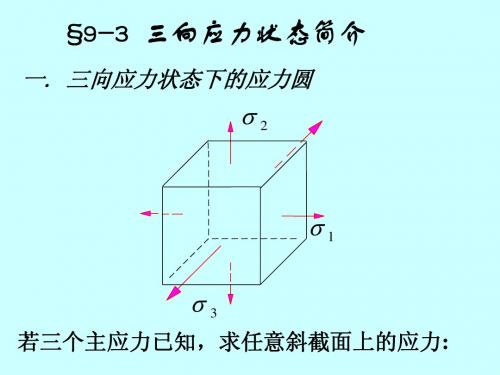
§9-3 空间应力状态的概念
当一点处的三个主应力都不等于零时,称该点 处的应力状态为空间应力状态(三向应力状态);钢 轨在轮轨触点处就处于空间应力状态(图a)。
空间应力状态最一 般的表现形式如图所 示;正应力sx、sy、sz 的下角标表示其作用 面,切应力txy、txz、tyx、 tyz、tzx、tzy的第一个下角标表示其作用面,第二个 下角标表示切应力的方向。
现在来导出一般空 间应力状态(图a)下的广 义胡克定律。因为在线 弹性,小变形条件下可以 应用叠加原理,故知x方 向的线应变与正应力之 间的关系为
s y sz 1 ex s x s y s z E E E E 同理有 1 1 e y s y s x s z ,e z s z s x s y E E sx
图中所示的正应力和切应力均为正的,即正应力以拉应 力为正。如果某作用面的外法线是沿着坐标轴的正向,则该 面上的切应力分量就以沿坐标轴正向时为正,相反,如果某 截面上的外法线是沿着坐标轴的负向,则该面上的切应力分 量就以沿坐标轴负向时为正。这样剪应力互等定理的表达式 就可不加负号了。
最一般表现形式的空间应力状态中有9个应力 分量,但根据切应力互等定理有txy=tyx,tyz=tzy , txz=tzx,因而独立的应力分量为6个,即sx、sy、sz、 tyx、tzy、tzx。
当空间应力状态的三个主应 力s1、s2、s3已知时(图a),与 任何一个主平面垂直的那些斜截 面(即平行于该主平面上主应力 的斜截面)上的应力均可用应力 圆显示。
三向应力状态下的应力圆
s2
s1 s3
若三个主应力已知,求任意斜截面上的应力:
首先分析平行于主应力之一σ3的斜截面上的应力。
σ3 对斜截面上的应力没有影响。这些斜截面上的 应力对应于由主应力 σ1 和 σ2 所画的应力圆圆周上各 点的坐标。
s2
s1 s1 s3
s3
s2
t
s
s3
s2
s1
同理,在平行于 σ2 的各个斜截面上,其应力对应于
由主应力 σ1 和 σ3 所画的应力圆圆周上各点的坐标。
主单元体:六个平面都是主平面
s2 s 3
s1 s3 s1
t
s3
s2
s1
s
s2
在平行于 σ1 的各个斜截面上,其应力对应于由主
应力 σ2 和 σ3 所画的应力圆圆周上各点的坐标。
s2
s1 s
s3
在三向应力状态情况下:
s2
s max s 1 s min s 3
t max s1 s3 2
s3
s2
s3
s1
s1
τmax 作用在与σ2平行且与σ1和σ3的方向成45° 角的平面上,以τ1,3表示。
[例9-12]求图示应力状态的主应力和最大 应力(应力单位为MPa)。 s max s x s y s x s y 2 解:
s2 s 3
s1 s3 s1
t
s3
s2
s1
s
s2
这样,单元体上与主应力之一平行的各个斜截 面上的正应力和剪应力,可由三个应力圆圆周上各 点的坐标来表示。
t
s3
s2
s
s1
至于与三个主方向都不平行的任意斜截面,弹性 力学中已证明,其应力σn和τn可由图中阴影面内某点 的坐标来表示。
t
s1 s3
s2
n
2
s min
2
2
2 t x
s 1 30 20 30 20 52.2 2 40 42.2 MPa s3 2 2
s 2 50MPa
t max
s1 s3 47.2MPa 2
[例9-13]求图示应力状态的主应力和最大 剪应力(应力单位为MPa)。s max s x s y s x s y 2
关于应力分量的正负已于§7-3中讲述;至于应 变分量的正负为了与应力分量的正负相一致,规定: 线应变ex , ey , ez以伸 长变形为正,切应变 gxy、gyz 、gzx 以使单 元体的直角∠xOy 、 ∠yOz 、∠zOx减小 为正。
本节讨论在线弹性范围内,且为小变形的条件 下,空间应力状态的应力分量与应变分量之间的关 系,即广义胡克定律。
一. 单向应力状态虎克定律和剪切虎克定律
纵向应变: e
横向应变:
s
E
s
s
σ ε νε ν E
τ Gγ
二. 各向同性材料的广义胡克定律
对于各向同性材料,它在任何方向上的弹性性 质相同,也就是它在各个方向上应力与应变之间的 关系相同。因此,对于各向同性材料:
(1) 在正应力作用下,沿正应力方向及与之垂 直的方向产生线应变,而在包含正应力作用面在内 的三个相互垂直的平面内不会发生切应变; (2) 在切应力作用下只会在切应力构成的平面 内产生切应变,而在与之垂直的平面内不会产生切 应变;也不会在切应力方向和与它们垂直的方向产 生线应变。
至于切应变与切应力 的关系,则根据前面 所述可知,切应变只 与切应变平面内的切 应力相关,因而有
g xy
t xy
G
,g yz
t yz
G
,g zx
t zx
G
1 ε x [σ x ν (σ y σ z )] E 1 ε y σ y ν σ x σ z E 1 εz σ z ν σ x σ y E
2
s x s y 2 t x 2
ቤተ መጻሕፍቲ ባይዱ
2
s 1 120 40 120 40 130 2 30 30 MPa s2 2 2
2
s 3 30MPa s1 s3 t max 80MPa
2
§9-4 应力与应变间的关系
前已讲到,最一般表现形式的空间应力状态有6 个独立的应力分量: sx 、sy 、sz 、txy 、 tyz 、tzx;与之相应 的有6个独立的应变 分量:ex、ey 、ez、 gxy 、gyz 、gzx。
2 2
2 t x
解:
s 2 50MPa s 1 s 2 50MPa
s 3 50MPa
t max s1 s 3
2 50MPa
[例9-14]求图示应力状态的主应力和最大 剪应力(应力单位为MPa)。
s max
解:
s min
s x s y
§9-3 空间应力状态的概念
当一点处的三个主应力都不等于零时,称该点 处的应力状态为空间应力状态(三向应力状态);钢 轨在轮轨触点处就处于空间应力状态(图a)。
空间应力状态最一 般的表现形式如图所 示;正应力sx、sy、sz 的下角标表示其作用 面,切应力txy、txz、tyx、 tyz、tzx、tzy的第一个下角标表示其作用面,第二个 下角标表示切应力的方向。
现在来导出一般空 间应力状态(图a)下的广 义胡克定律。因为在线 弹性,小变形条件下可以 应用叠加原理,故知x方 向的线应变与正应力之 间的关系为
s y sz 1 ex s x s y s z E E E E 同理有 1 1 e y s y s x s z ,e z s z s x s y E E sx
图中所示的正应力和切应力均为正的,即正应力以拉应 力为正。如果某作用面的外法线是沿着坐标轴的正向,则该 面上的切应力分量就以沿坐标轴正向时为正,相反,如果某 截面上的外法线是沿着坐标轴的负向,则该面上的切应力分 量就以沿坐标轴负向时为正。这样剪应力互等定理的表达式 就可不加负号了。
最一般表现形式的空间应力状态中有9个应力 分量,但根据切应力互等定理有txy=tyx,tyz=tzy , txz=tzx,因而独立的应力分量为6个,即sx、sy、sz、 tyx、tzy、tzx。
当空间应力状态的三个主应 力s1、s2、s3已知时(图a),与 任何一个主平面垂直的那些斜截 面(即平行于该主平面上主应力 的斜截面)上的应力均可用应力 圆显示。
三向应力状态下的应力圆
s2
s1 s3
若三个主应力已知,求任意斜截面上的应力:
首先分析平行于主应力之一σ3的斜截面上的应力。
σ3 对斜截面上的应力没有影响。这些斜截面上的 应力对应于由主应力 σ1 和 σ2 所画的应力圆圆周上各 点的坐标。
s2
s1 s1 s3
s3
s2
t
s
s3
s2
s1
同理,在平行于 σ2 的各个斜截面上,其应力对应于
由主应力 σ1 和 σ3 所画的应力圆圆周上各点的坐标。
主单元体:六个平面都是主平面
s2 s 3
s1 s3 s1
t
s3
s2
s1
s
s2
在平行于 σ1 的各个斜截面上,其应力对应于由主
应力 σ2 和 σ3 所画的应力圆圆周上各点的坐标。
s2
s1 s
s3
在三向应力状态情况下:
s2
s max s 1 s min s 3
t max s1 s3 2
s3
s2
s3
s1
s1
τmax 作用在与σ2平行且与σ1和σ3的方向成45° 角的平面上,以τ1,3表示。
[例9-12]求图示应力状态的主应力和最大 应力(应力单位为MPa)。 s max s x s y s x s y 2 解:
s2 s 3
s1 s3 s1
t
s3
s2
s1
s
s2
这样,单元体上与主应力之一平行的各个斜截 面上的正应力和剪应力,可由三个应力圆圆周上各 点的坐标来表示。
t
s3
s2
s
s1
至于与三个主方向都不平行的任意斜截面,弹性 力学中已证明,其应力σn和τn可由图中阴影面内某点 的坐标来表示。
t
s1 s3
s2
n
2
s min
2
2
2 t x
s 1 30 20 30 20 52.2 2 40 42.2 MPa s3 2 2
s 2 50MPa
t max
s1 s3 47.2MPa 2
[例9-13]求图示应力状态的主应力和最大 剪应力(应力单位为MPa)。s max s x s y s x s y 2
关于应力分量的正负已于§7-3中讲述;至于应 变分量的正负为了与应力分量的正负相一致,规定: 线应变ex , ey , ez以伸 长变形为正,切应变 gxy、gyz 、gzx 以使单 元体的直角∠xOy 、 ∠yOz 、∠zOx减小 为正。
本节讨论在线弹性范围内,且为小变形的条件 下,空间应力状态的应力分量与应变分量之间的关 系,即广义胡克定律。
一. 单向应力状态虎克定律和剪切虎克定律
纵向应变: e
横向应变:
s
E
s
s
σ ε νε ν E
τ Gγ
二. 各向同性材料的广义胡克定律
对于各向同性材料,它在任何方向上的弹性性 质相同,也就是它在各个方向上应力与应变之间的 关系相同。因此,对于各向同性材料:
(1) 在正应力作用下,沿正应力方向及与之垂 直的方向产生线应变,而在包含正应力作用面在内 的三个相互垂直的平面内不会发生切应变; (2) 在切应力作用下只会在切应力构成的平面 内产生切应变,而在与之垂直的平面内不会产生切 应变;也不会在切应力方向和与它们垂直的方向产 生线应变。
至于切应变与切应力 的关系,则根据前面 所述可知,切应变只 与切应变平面内的切 应力相关,因而有
g xy
t xy
G
,g yz
t yz
G
,g zx
t zx
G
1 ε x [σ x ν (σ y σ z )] E 1 ε y σ y ν σ x σ z E 1 εz σ z ν σ x σ y E
2
s x s y 2 t x 2
ቤተ መጻሕፍቲ ባይዱ
2
s 1 120 40 120 40 130 2 30 30 MPa s2 2 2
2
s 3 30MPa s1 s3 t max 80MPa
2
§9-4 应力与应变间的关系
前已讲到,最一般表现形式的空间应力状态有6 个独立的应力分量: sx 、sy 、sz 、txy 、 tyz 、tzx;与之相应 的有6个独立的应变 分量:ex、ey 、ez、 gxy 、gyz 、gzx。
