第九章应力状态与应变状态分析
应力及应变状态
19Βιβλιοθήκη 一、一点附近应力表示法4. 主应力和应力不变量 已知单元体的应力状态为：
és x t xy t xz ù és x t xy t xz ù ê ú ê ú s ij = êt yx s y t yz ú = ê s y t yz ú êt zx t zy s z ú ê sz ú û ë û ë
s 1 = s 0 × cos a
F
单向拉伸时轴向应力随截面方位变化
16
外载荷不变的情况下， 应力的数值取决于其所 作用平面的方位。
一、一点附近应力表示法
3. 直角坐标系下一点的应力状态
s ij =
és x t xy t xz ù êyx s y t yz ú t êt yx s y t yz ú êt zx t zy s z ú ë û
应力状态和应变状态分析
内容
l塑性加工应力分析 — 一点附近应力表示方法 l平衡微分方程 l塑性加工应变分析 --- 点的应变状态分析
2
F
预测金属变形？载荷？缺陷？ 应力和应变分析 变形区域内接触应力 变形力F
平衡方程 Forging F 塑性条件 物理方程 几何方程 边界条件
Extrusion
三维空间问题 （十三个未知数，十三个方程） 轴对称问题 （九个未知数，九个方程） 平面问题 3 （三个未知数，三个方程）
一、一点附近应力表示法
1.基本概念
外力： 外部施加作用在物体上的力。（接触力，摩擦力，重力等） 内力： 外力作用下，物体各点之间产生相互作用的力。 应力： 变形体中单位面积上的内力。
4
一、一点附近应力表示法 外力分析
正压力—工具与工件接触面上的垂直作用力
第九章应力状态(3,4,5)分解
2 2
2 t x
解：
s 2 50MPa s 1 s 2 50MPa
s 3 50MPa
t max s1 s 3
2 50MPa
[例9-14]求图示应力状态的主应力和最大 剪应力（应力单位为MPa）。
s max
解：
s min
s x s y
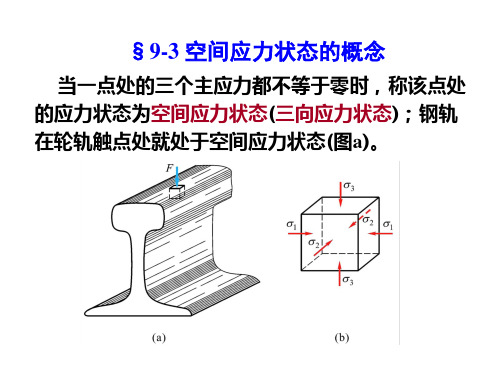
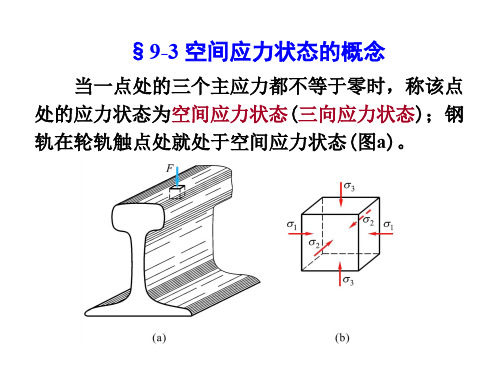
§9-3 空间应力状态的概念
当一点处的三个主应力都不等于零时，称该点 处的应力状态为空间应力状态(三向应力状态)；钢 轨在轮轨触点处就处于空间应力状态(图a)。
空间应力状态最一 般的表现形式如图所 示；正应力sx、sy、sz 的下角标表示其作用 面，切应力txy、txz、tyx、 tyz、tzx、tzy的第一个下角标表示其作用面，第二个 下角标表示切应力的方向。
现在来导出一般空 间应力状态(图a)下的广 义胡克定律。因为在线 弹性,小变形条件下可以 应用叠加原理，故知x方 向的线应变与正应力之 间的关系为
s y sz 1 ex s x s y s z E E E E 同理有 1 1 e y s y s x s z ，e z s z s x s y E E sx
图中所示的正应力和切应力均为正的，即正应力以拉应 力为正。如果某作用面的外法线是沿着坐标轴的正向，则该 面上的切应力分量就以沿坐标轴正向时为正，相反，如果某 截面上的外法线是沿着坐标轴的负向，则该面上的切应力分 量就以沿坐标轴负向时为正。这样剪应力互等定理的表达式 就可不加负号了。
最一般表现形式的空间应力状态中有9个应力 分量，但根据切应力互等定理有txy＝tyx，tyz＝tzy ， txz＝tzx，因而独立的应力分量为6个，即sx、sy、sz、 tyx、tzy、tzx。
应力应变状态
应力应变状态
作为一名小学生，我不太懂“应力应变状态”这个词呀，这对我来说太难啦！这难道不是大人们在工程学或者物理学里才会研究的东西吗？
不过我可以想象一下，“应力应变状态”就好像我们做游戏时的规则和我们的表现。
比如说，玩跳绳的时候，绳子就像一个有规则的“应力”，我们跳的动作和速度就是“应变”。
如果绳子甩得太快或者太慢，这就是一种特别的“应力状态”，而我们能不能跟上节奏跳过去或者被绊倒，就是我们的“应变状态”啦。
再比如搭积木，积木的材质和结构承受的压力就是“应力”，而积木会不会变形、倒塌就是“应变”。
如果我们堆得太高，积木承受不住了，这不就是一种不好的“应力应变状态”吗？
哎呀，我真的不太确定我说的对不对。
我去问问我的小伙伴们。
我找到小明，问他：“小明，你知道应力应变状态吗？”小明挠挠头说：“我不知道呀，这听起来好难！”我又跑去问小红，小红眨眨眼睛说：“我好像在哥哥的书上看到过，但是不太懂呢。
”
我想，也许“应力应变状态”就像一个神秘的密码，等着我们长大后去解开。
它是不是像一个隐藏在深处的宝藏，只有掌握了特殊的知识和技能才能找到？
对于现在的我来说，虽然不太明白这个复杂的概念，但我相信，只要我努力学习知识，总有一天能搞清楚的！我可不会被它难倒，我一定要弄明白！。
应力和应变状态
由应力圆可计算出： 1 5P， 2 P
例3 已知受力构件的A点处于平面应力状态，过A点两斜截面上 的应力圆如图，试用应力圆求该点的主应力、主平面和最大剪应 力。
解：
1 OA1 232.5MPa
3 OB1 107.5MPa
100
max 170MPa R
四、三向应力状态和最大剪应力
若单元体是主单元体，即各面上的应力为主应力； 各方向的主应变为：
1 2
3
1
E 1
E 1
E
1 2 3
2 1 2
3 3 1
各平面的剪应变为零
12 23 31 0.
例1、测得A点处的x=400×10-6，y=-120×10-6 （）。已知： E=200GPa，=0.3，求A点在x和y方向上的正应力。
3）夹角关系：圆上某两条半径夹角等于单元体上对 应截面外法线夹角的两倍，且转向相同。
3.应力圆的应用:
1）确定单元体上任一斜截面上的正应力σα、 剪应力τα；
2）确定两个主应力的大小和方位；
3）确定两个最大最小剪应力的大小和方位；
例1 σx=60MPa,τxy=20.6MPa ,σy= 0 , 用图解法求： 1）该点的主应力和主平面的方位； 2）求与轴线方向成-450的应力σ-450、τ -450 ？
100 (80) sin 600 40cos600 2
97.64(MPa)
4）计算σmax、σmin及主平面方位角
max
min
x
y
2
x
2
y
2
2 xy
10888.5.（5 MPa）
1 108 .5, 2 0, 3 88.5
t g20
2xy x y
9第九章 应力、应变分析、强度理论123
第九章 应力、应变分析、强度理论一、是非题9-1、单元体最大正应力面上的剪应力恒等于零。
（ ）9-2、单元体最大剪应力面上的正应力恒等于零。
（ ）9-3、依照剪应力互等定理，一单元体中两个平面上的剪应力数值相等，符号相反，则这两平面必定相互垂直。
（ ）9-4、 只要构件横截面上的轴力N=0，则该横截面正应力处处为零。
（ ）9-5、 梁受横力弯曲时，其横截面上各点处的主应力必定是σ1≥0，σ3≤0。
（ ）9-6、 等截面圆杆受纯扭转时，杆内任一点处只有剪应力，而无正应力。
（ ）9-7、若受力构件中一点处，某方向上的线应变为零，则该方向上的正应力必为零。
（ ）9-8、若受力钢质构件中的一点处，某相互垂直方向的剪应变为零，则该方向上的剪应力必为零。
（ ） 9-9、若各向同性材料单元体的三个正应力σx >σy >σz ，则对应的三个线应变也有εx >εy >εz 。
（ ） 9-10、 各向同性单元体的三个主应变为ε1≠0，ε2≠0，ε3=0，若（1）、当ε1>0，则必有σ1>0；（ ）（2）、当ε1>ε2，则必有σ1>σ2；（ ）（3）、当ε1>ε2>0，则()()21max 12εεμτ-+=E 。
（ ） 9-11、各向同性材料在三向均匀压缩或拉伸时，其形状改变比能恒等于零。
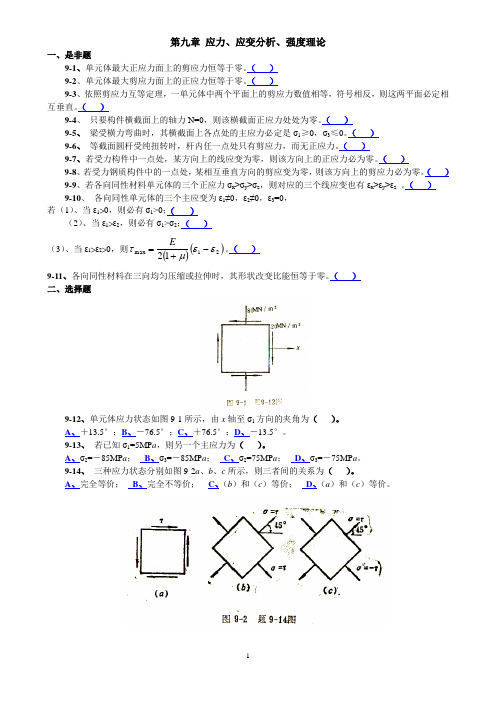
（ ）二、选择题9-12、单元体应力状态如图9-1所示，由x 轴至σ1方向的夹角为（ ）。
A 、＋13.5°；B 、－76.5°；C 、＋76.5°；D 、－13.5°。
9-13、 若已知σ1=5MP a ，则另一个主应力为（ ）。
A 、σ2=－85MP a ；B 、σ3=－85MP a ；C 、σ2=75MP a ；D 、σ3=－75MP a 。
9-14、 三种应力状态分别如图9-2a 、b 、c 所示，则三者间的关系为（ ）。
A 、完全等价；B 、完全不等价；C 、（b ）和（c ）等价；D 、（a ）和（c ）等价。
第九章应力状态(3,4,5)
s
3
e3
1 E
s
3
s 1
s 2
例 9-17
边长a =0.1 m的铜质立方体，置于刚性很大的 钢块中的凹坑内(图a)，钢块与凹坑之间无间隙。 试求当铜块受均匀分布于顶面的竖向荷载F =300 kN时，铜块内的主应力，最大切应力，以及铜块 的体应变。已知铜的弹性模量E =100 GPa，泊松比
1 2
E
sx sy sz
思考: 各向同性材料制成的构件内一点处，
三个主应力为s1＝30 MPa，s2＝10 MPa，s3＝-40
MPa。现从该点处以平行于主应力的截面取出边 长均为a的单元体，试问：(1) 变形后该单元体的 体积有无变化？(2) 变形后该单元体的三个边长之 比有无变化？
弹性,小变形条件下可以
应用叠加原理，故知x方 向的线应变与正应力之
间的关系为
e x
sx
E
sy
E
sz
E
1 E
sx
sy
sz
同理有
e y
1 E
s
y
s x
s z ，e z
1 E
sz
sx
s
最一般表现形式的空间应力状态中有9个应力
分量，但根据切应力互等定理有txy＝tyx，tyz＝tzy ， txz＝tzx，因而独立的应力分量为6个，即sx、sy、sz、 tyx、tzy、tzx。
当空间应力状态的三个主应
力s1、s2、s3已知时(图a)，与
任何一个主平面垂直的那些斜截
面(即平行于该主平面上主应力
第九章应变、力与
Rl 忽略
R
计时： R Rl
R S S R Rl '
S
R
应对灵敏度加以修正
5、减小读数漂移 使电桥电密尽可能对称。良好的接地。 6、电磁干扰 如有电磁场，可能是仪表发生误差。
7、测点的选择 对于被测体，如何选择测点，是正确测量的一个重要环节。一 般以最少的测点达到真实反映结构受力状态的原则来选点。 （1）对被测结构进行受力分析。找出其主要处的受力和变形 部位。 （2）对应力集中部位，应适当多分布测点。 （3）利用对称性，可减少测点。 （4)利用已知应变，应力的位置。可检查结果的正确性。
电阻应变仪分类
类 别
静态电阻应变仪 静动态电阻应变仪 动态电阻应变仪 超动态电阻应变仪 遥测应变仪
测量应变信号
静态应变 单点动态应变测量 周期或非周期动态应变 多通道 动态应变：爆炸、高速冲击 无线电传输信号原理 测量旋转体、运动件
测量频率范围
0 ~ 15Hz < 200Hz < 5KHz
几十 KHz
(3) 应变片自补偿法 粘贴在被测部位上的是一种特殊应变片，当温 度变化时，产生的附加应变为零或相互抵消，这种 特殊应变片称为温度自补偿应变片。 ①选择式自补偿应变片 ②双金属敏感栅自补偿应变片 这种应变片也称组合式自补偿应变片。这是利用 两种电阻丝材料的电阻温度系数不同(一个为正，一 个为负)的特性，将二者串联绕制成敏感栅。
h
H1 H 3 2
0
对每一个记录幅值，都可同样办法计算其对应的应变值。
第二节
力的测量
通过对机械零件和机械结构的力的测量，可以分析其受力状 况和工作状态，验证设计计算，确定工作过程和某些物理现 象的机理。力的测量方法可以归纳为利用力的静力效应和动 力效应两种。
材料力学：第九章 应力状态分析
τx
C
F
Me
d
C
(a)
·
σx
(b)
C
T
F
解：C点所在横截面上的正应力和切应力的分布规律如图 所示， 点所在横截面上的正应力和切应力的分布规律如图b所示 点所在横截面上的正应力和切应力的分布规律如图 所示， 其值为
FN 500 × 103 N σx = = = 63.7 × 106 Pa=63.7MPa π 2 A 0.1m ) ( 4
经整理后得到 ）、（2） ）、（ （1） 由（1）、（ ）式，可以求出单 ） 元体各个截面上的应力。（ 。（即 点 元体各个截面上的应力。（即a点 （2） 处各个方向上的应力） ） 处各个方向上的应力）
∑F = 0
t
τ =τ′
σ α = −τ sin 2α
τ α = τ cos 2α
定义：构件内一点处各个方向上的应力集合， 定义：构件内一点处各个方向上的应力集合，称为该点处的 应力状态。 应力状态。
F F
横截面上只有正应力，且 横截面上只有正应力， 均匀分布 计算公式： 计算公式：
m
σ
F
FN
FN σ= A
等直圆杆扭转时横截面上的应力： 等直圆杆扭转时横截面上的应力：
Me m Me
m
横截面上只有切应力，呈 横截面上只有切应力， 线性分布
T
o
τρ
τmax
T⋅ρ 计算公式： 计算公式： τρ = Ip
R
τ
T 16 M e τ= = WP πd3
为了研究a点处各个方向的应力，围绕a点取一个各边长均为无 为了研究 点处各个方向的应力，围绕 点取一个各边长均为无 点处各个方向的应力 限小的六面体（称为单元体）。 限小的六面体（称为单元体）。 径向截面
第九章应力状态(3,4,5)
广义虎克定律： 3. 广义虎克定律：
σ2
σ1 σ3
当 个 应 同 作 时 三 主 力 时 用 ：
1 ε1 = [σ1 − µ（ 2 + σ 3）] σ E 1 另两个方向 ε2 = [σ2 − µ（ 3 +σ1 ] σ ） E 1 ] ε3 = [σ3 − µ（ 1 +σ2） σ E
CL10TU30
一.斜方向的应变 设 件 一 处 应 构 内 点 的 ε ε γ 变 x、 y和 xy皆 已 为 知 。 求 α和 α 量 现 ε γ
伸长的线应变和使直 角减小的剪应变规定 为正。 为正。
α
CL10TU27
1. 斜方向应力
σ x +σ y σ x −σ y σ α α + cos 2 −τ x sin 2 α= 2 2 σ −σ y τα = x sin 2 +τ x cos 2 α α 2 1 1 π π σ π = (σx +σ y ) + (σx −σ y ) cos 2(α + ) −τ x sin 2(α + ) α+ 2 2 2 2 2
σ2 σ 3
σ1 σ3 σ 2 σ1
τ
σ3
σ2
σ σ1
这样， 这样，单元体上与主应力之一平行的各个 斜截面上的正应力和剪应力， 斜截面上的正应力和剪应力，可由三个应力圆 圆周上各点的坐标来表示。 圆周上各点的坐标来表示。
τ
σ3
σ2
σ1
σ
至于与三个主方向都不平行的任意斜截面， 至于与三个主方向都不平行的任意斜截面， 弹性力学中已证明，其应力σ 弹性力学中已证明，其应力 n和τn可由图中阴 影面内某点的坐标来表示。 影面内某点的坐标来表示。
材料力学-应力状态与应变状态分析
s2 引起 1 s 2 E 2 s 2 E 3 s 2 E
s3 引起 1 s 3 E 2 s 3 E 3 s 3 E
小变形 i i i i i 1,2,3
1
1 E
s1
(s 2
s 3 )
广
2
1 E
s 2
(s 3
s1 )
义 虎 克 定
3
1 E
s 3
(s 1
s 2)
t T ＝ 1 πD3 (1－a4) 16
1
＝
1 E
[s1－
(s2＋s3)]
＝
1＋
E
t
T＝8.38 kN·m
二、体积应变
单元体边长：dx、dy、dz
体积：V0 = dx·dy·dz
dy
dx → dx +△dx = dx + 1dx = (1 + 1) dx
dy → dy +△dy = dy + 2dy = (1 + 2) dy
体积的绝对增量：△V = V－V0 = V0 (1+ 2+ 3)
单位体积增量：
V V0
1 2
3
体积应变 体积的相对增量
1 2
E
(s1
s2
s
3)
讨论：
V V0
1 2
E
(s1 s 2
s 3)
⒈ 若 s1 + s2 + s3＞0，
则 ＞0 →△V ＞0，即体积增大；
若 s1 + s2 + s3＜0，
s2
s3 dsz 1
dx
dz → dz +△dz = dz + 3dz = (1 + 3) dz
9 应力状态及应变状态分析
9 应力状态及应变状态分析通过对前几章的讨论，我们已经了解了杆件在基本变形时横截面上的应力情况。
实际上一点的应力情况除与点的位置有关以外，还与通过该点所截取的截面方位有关。
为了讨论一点在不同截面上的应力情况，为讨论组合变形打下一定的理论基础，本章介绍：应力状态、应变状态的概念；应力状态、应变状态分析；复杂应力状态下一点的应力与应变的关系——广义虎克定律，复杂应力状态下的变形比能。
在此基础上介绍强度理论的概念及常用的四种强度理论。
9.1 应力状态的概念9.1.1 一点处的应力状态受力构件内任意一点、在不同方位各个截面上的应力情况，称为该点处的应力状态。
判断一个受力构件的强度，必须了解这个构件内各点处的应力状态，即了解各个点处不同截面的应力情况，从而找出哪个点、哪个面上正应力最大，或剪应力最大。
据此建立构件的强度条件，这就是研究应力状态的目的。
9.1.2 通过单元体分析一点的应力状态如上所述，应力随点的位置和截面方位不同而改变，若围绕所研究的点取出一个单元体（如微小正六面体），因单元体三个方向的尺寸均为无穷小，所以可以认为：单元体每个面上的应力都是均匀分布的，且单元体相互平行的面上的应力都是相等的，它们就是该点在这个方位截面上的应力。
所以，可通过单元体来分析一点的应力状态。
图9.1应力状态的一般情况和已知三个主应力的应力状态9.1.3 主应力及应力状态的分类包括受力构件内的某点，所截取出的单元体，一般来说，各个面上既有正应力，又有剪应力（图9.1a ）。
以下根据单元体各面上的应力情况，介绍应力状态的几个基本概念。
① 主平面 如果单元体的某个面上只有正应力，而无剪应力，则此平面称为主平面。
② 主应力 主平面上的正应力称为主应力。
③ 主单元体 若单元体三个相互垂直的面皆为主平面，则这样的单元体称为主单元体。
可以证明：从受力构件某点处，以不同方位截取的诸单元体中，必有一个单元体为主单元体。
主单元体在主平面上的主应力按代数值的大小排列，分别用1σ，2σ和3σ表示，即321σσσ≥≥（图9.1b ）。
第九章：复杂应力状态及强度理论
杆在周向截面上没有应力。又由切应力互等定理可知， 杆在径向截面上 B 点处应该有与相等的切应力。于是 此单元体各侧面上的应力如图.
第一节：应力状态概念
三、主平面、主应力、应力状态的分类
主单元体：在一般情况下，表示一点处应力状态的应力单元体在其各个表面上同时 存在有正应力和切应力。但是可以证明：在该点处以不同方式截取的各个单元体中， 必有一个特殊的单元体，在这个单元体的侧面上只有正应力而没有切应力。这样的 单元体称为该点处的主应力单元体或主单元体。
sin 2 cos 2
当 450 时， max
当 00 时， max
低碳钢试件扭转破坏是被剪断的，且其抗剪能力低于其抗拉能力。 铸铁试件扭转破坏是被拉断的，且其抗拉能力低于其抗剪能力。
第二节：二向应力状态分析
例 9-3 图示单元体，x =100MPa，x = – 20MPa， y =30MPa。试求：1） =40º的斜截面上的 和 ；2）确定 A 点处的max、max 和它们所在的
由单向应力状态胡克定律可知：主应力 1、 2和 3 单独作用时，分别对 应的纵向线应变为1/E、2/E和 3/E；令横向变形系数 ，则主应力 2 将引起 1 方向相应的线应变为 – 2 /E；其它同理。故 1 由1 的纵向线 应变与 2、3 分别引起的 1 方向相应的横向线应变三项叠加而成。
主应力表示的 广义胡克定律
第三节：三向应力状态分析
第三节：三向应力状态分析
复杂应力状态下一点处的最大应力 1、一点处的最大正应力
设一点处的主应力单元体如图 a 所示，研究证明，当主应力按 1 2 3
排列时，则有
max 1
min 3
第三节：三向应力状态分析
2、一点处的最大切应力
7__应力状态及应变状态分析
7.2 平面应力状态分析－－－－解析法
平面一般应力状态，即空间应力状态中，z方向的 应力分量全部为零；或只存在作用于x-y平面内的 应力分量。
y
y
7.2.1平面一般应力状态斜截面上应力
斜截面平行于z轴且与x面成倾角 ，由力的平衡条件 可求得斜截面上应力σ ，τ 。
x
y
t 0
( x - y )sin cos + x (cos - sin )
2 2
1 ( x - y ) sin 2 + x cos 2 2
例 一单元体如图所示，试求在 = 30的斜截面 上的应力。
x 10 MPa, y 30 MPa , x 20 MPa, y -20 MPa, 30
２．一点处的应力状态：是指通过一点不同截面 上的应力情况的集合。
二、单元体分析法
一点处的应力状态可用围绕该点截取的微单元 体（微正六面体）上三对互相垂直微面上的应力情况 来表示。
轴向拉伸杆件内围绕点截取的两种微元体。
特点：
1、微元体三个方向的尺寸均无穷小；
2、每个面上的应力是均匀的；
3、微元体内相互平行的截面上，应力相同； 4、互相垂直的两个侧面上剪应力服从剪切互等关系。
7 应力状态及应变状态分析
7.1 应力状态概述
一、一点的应力状态
1．凡提到“应力”，必须指明：
在哪一点；在哪个面；在哪个方向。
7.1 应力状态概述
一、一点的应力状态
1．凡提到“应力”，必须指明：
在哪一点；在哪个面；在哪个方向。
目的：判断受力构件在那个点，那个方向最危险， 以便解决构件在复杂受力情况下的强度问题。
应力状态图和应变状态图
3
2
1 约定： 1 2 3
应力状态图和应变状态图
一、应力状态图
主应力表示的应力状态
可能的主应力状态
6.在各种受力情况下，可能的主应力状态图共有九种：
一种零应力状态、二种线性应力状态、三种平面应力状态、四种立
体应力状态。
应力状态图和应变状态图
二、塑性变形体积不变定律
1.定律的应用：它可以应用于计算毛料尺寸，也可以用于塑性理论的各种计算，并用来判断应变状态。
z
z
zx zy
xz yz
x x
xy
yx
y y
应力状态图和应变状态图
一、应力状态图
3.主平面:只有正应力而无剪应 力存在的坐标面称为主平面。
4.点的主应力状态图:是表示所 研究的点，在各主轴方向上，有无主 应力及其主应力性质的定性图形。
5.主应力性质:是指拉或压应力， 通常规定，拉应力为正，其箭头向外； 压应力为负，其箭头指向内。
主应变状态图
2.根据塑性变形体积不变定律方程可得如下结论
（1）主应变状态图只存在三种形式。
（2）无论何种应变状态，总有一个主应变的符号与其他两个主应变
的符号相反，且其绝对值最大。
谢谢观看！
应力状态图和应变状态图
1
应力状态图
2
塑性变形体积不变定律
3
最小阻力定律
4
应变状态图
应力状态图和应变状态图
一、应力状态图
1.点的应力状态:是指物体内的 任意一个质点附近不同方位上所承受 的应力情况。
（实心截面）
T
Ip
应力状态图和应变状态图
一、应力状态图
2.应力状态图:在立方体的三个 互相垂直的截面上，用箭头定性地表 示有无应力及应力方向的图形，称为 应力状态图。
应力与应变分析课件
03
边界元法
边界元法是一种基于边界积分方程的数值方法，适用于解决各种物理问
Байду номын сангаас
题。未来，边界元法将在更多领域得到应用，例如流体力学、电磁场等
问题。
考虑材料非线性的影响
材料非线性是指材料的应力-应变关系不是线性的，需要考虑 材料内部结构、相变等因素的影响。未来，研究人员将进一 步考虑材料非线性的影响，以更准确地预测材料的力学性能 。
解方程
通过加权残值法，求解方程中 的参数，使得残值的平方和最
小化。
05
应力与应变分析在工 程中的应用
结构优化设计
总结词
提高结构性能与稳定性
详细描述
应力与应变分析在结构优化设计中具有重要作用，通过分析可以评估结构的强 度、刚度和稳定性，发现潜在的薄弱环节，为结构设计和改进提供依据，从而 提高结构的性能与稳定性。
应力分类
根据作用力的来源和性质，应力 可以分为多种类型，如正应力、 剪应力、弯曲应力等。
应力与应变的关系
应力的作用
应力作用在物体上，会导致物体 内部发生形变，即应变。
应变分类
应变分为线应变和角应变，分别表 示物体形状和大小的改变。
弹性力学基本方程
描述应力与应变之间关系的方程， 如胡克定律（Hooke's law）。
应力应变关系。
04
应变分析的基本方法
直接方法
定义应变分量
根据物体的形状和受力情况，将物体分为多个小的单元，并定义 每个单元的应变分量。
建立方程
根据弹性力学方程和应变分量的定义，建立物体整体的应变方程。
解方程
根据方程的解，得到每个点的应变值。
最小二乘法
确定目标函数
工程力学 第9章 应力状态分析 习题及解析
习题9-1图 x15-'x x'σy'x'τ 1.25MPa15 (b-1)15a 4MP15-y'x'τx'x'σa1.6MP x (a-1) 习题9-2图302MPa 0.5MPa-60x'σ'x ''y x τ 工程力学（工程静力学与材料力学）习题与解答第9章 应力状态分析9－1 木制构件中的微元受力如图所示，其中所示的角度为木纹方向与铅垂方向的夹角。
试求： 1．面内平行于木纹方向的切应力；2．垂直于木纹方向的正应力。
知识点：平面应力状态、任意方向面上的应力分析 难度：易 解答：（a ）平行于木纹方向切应力6.0))15(2cos(0))15(2sin(2)6.1(4=︒-⨯⋅+︒-⨯---=''y x τMPa 垂直于木纹方向正应力84.30))15(2cos(2)6.1(42)6.1(4-=+︒-⨯---+-+-='x σMPa （b ）切应力08.1))15(2cos(25.1-=︒-⨯-=''y x τMPa正应力625.0))15(2sin()25.1(-=︒-⨯--='x σMPa9－2 层合板构件中微元受力如图所示，各层板之间用胶粘接，接缝方向如图中所示。
若已知胶层切应力不得超过1MPa 。
试分析是否满足这一要求。
知识点：平面应力状态、任意方向面上的应力分析 难度：易 解答：55.1))60(2cos(5.0))60(2sin(2)1(2-=︒-⨯⋅+︒-⨯---=''y x τMPa 1MPa 55.1||>=''y x τMPa ，不满足。
9－3 结构中某点处的应力状态为两种应力状态的叠加结果。
试求叠加后所得应力状态的主应力、面内最大切应力和该点处的最大切应力。
知识点：平面应力状态分析 难度：难 解答：习题9-2图yσxσxyτ=yσxσxyτx=yσxσxyτ=左微元⎪⎪⎪⎩⎪⎪⎪⎨⎧-='-='-=-='+=--+='000000022cos 122sin )2sin(222cos 10)2cos(22σθσσσσθθστσθθσσσx y xy x 叠加 ⎪⎪⎪⎩⎪⎪⎪⎨⎧-=+'=-=+=+=+'=''000022cos 1022sin 022cos 3σθσσσθττσθσσσy y y x xy x x0)cos 1()cos 1( )22sin (4)22cos 122cos 3(21222cos 122cos 330020202021=⎩⎨⎧-+=-+--+±-++=⎭⎬⎫σσθσθσθσθθσθθσσ 面内最大切应力：θσσστcos 2021max=-='该点最大切应力：031max2cos 12σθσστ+=-=左微元0023))30(2sin()(ττσ=︒-⨯-='x ，0230τσσ-='-='x y ，2))30(2cos(00τττ=︒-⨯='xy 右微元0023)302sin()(ττσ=︒⨯-=''x，0230τσσ-=''-=''x y ，2))30(2cos()(00τττ-=︒⨯-=''xy 叠加 03τσσσ='+'=y x x ，03τσσσ-=''+'=y y y ，0=''+'=xyxy xy τττ 013τσ=，02=σ，033τσ-= 面内031max32||τσστ=-='xABOσOσαα(a)习题9-4图A60CB60100-x σxσyxτxyτ92MPa(a)习题9-5图该点031max 32||τσστ=-=叠加[]⎪⎪⎪⎩⎪⎪⎪⎨⎧=⎥⎦⎤⎢⎣⎡︒-⨯--+==--+==⎥⎦⎤⎢⎣⎡︒-⨯--+-++=MPa 30))45(2sin(2)30(5070MPa 1010)3050(0MPa 90))45(2cos(2)30(502)30(5080xy y x σσσ主应力0MPa 0MPa100304)]100(90[212109022231=⎩⎨⎧=⨯+-±+=⎭⎬⎫σσσ面内及该点：5021002||||31max max=-=-=='σσττMPa9－4 已知平面应力状态的最大正应力发生在与外力作用的自由表面AB 相垂直的面上，其值为0σ。
应力状态与应变状态分析
应变状态分析对应力状态分析起到补充作用，特别是在复杂受力情况下，能够更 准确地描述物体的变形行为。
应变状态的分类
单轴应变
物体在单向受力过程中发 生的应变，只有一个方向 的长度变化。
双轴应变
物体在双向受力过程中发 生的应变，长度变化发生 在两个相互垂直的方向上。
三轴应变
物体在三向受力过程中发 生的应变，长度变化发生 在三个相互垂直的方向上。
塑性变形
在某些高应力状态下，材料可能 会发生塑性变形，影响其机械性 能和稳定性。
断裂韧性
材料的断裂韧性可能会受到其内 部应力的影响，高应力状态可能 降低材料的断裂韧性，导致材料 更容易断裂。
02
应变状态分析
定义与概念
定义
应变状态分析是研究物体在受力过程中内部应变的分布和变化情况，以及应变与 应力之间的关系。
详细描述
在塑性行为下，材料发生屈服，即应力达到某一特定值后，应变开始急剧增加。这种行为通常发生在 材料承受的应力高于其屈曲点时。
脆性行为
总结词
当材料受到外力作用时，它可能会突然断裂，而不会发生显著的形变。
详细描述
在脆性行为下，材料在较低的应力状态下就会断裂，且断裂前几乎没有明显的塑性变形。这种行为常见于某些脆 性材料，如玻璃或陶瓷。
弹性行为
总结词
当材料受到外力作用时，会发生形变， 但当外力去除后，材料能够完全恢复 其原始形状和尺寸。
详细描述
在弹性行为下，材料的应力和应变之 间呈线性关系，即应力与应变成正比。 这种行为通常发生在材料承受的应力 低于其屈服点时。
塑性行为
总结词
当材料受到外力作用时，会发生形变，并且当外力去除后，材料不能完全恢复其原始形状和尺寸。
《工程力学(工程静力学与材料力学)(第3版)》习题解答：第9章 应力状态分析
MPa
MPa
2．
MPa
MPa
9－13图示外径为300mm的钢管由厚度为8mm的钢带沿20°角的螺旋线卷曲焊接而成。试求下列情形下，焊缝上沿焊缝方向的切应力和垂直于焊缝方向的正应力。
1．只承受轴向载荷FP = 250kN；
2．只承受内压p=5.0MPa（两端封闭）
3．同时承受轴向载荷FP = 250kN和内压p=5.0MPa（两端封闭）
难度：一般
解答：
（1）当 = 40℃
mm＜
mm＜
所以铝板内无温度应力，
（2）当 = 80℃
mm＞
mm＞
∴ （1）
（2）
所以解得qx = qy=70MPa（压）
， MPa
MPa
9－18对于一般平面应力状态，已知材料的弹性常数E、 ，且由实验测得 和 。试证明：
知识点：广义胡克定律、 三者之间的关系
难度：一般
难度：一般
解答：
正确答案是C。
（A）不满足切应力互等定律；
（B）不满足平衡；
（C）既可满足切应力互等，又能达到双向的平衡；
（D）不满足两个方向的平衡。
9－27微元受力如图所示，图中应力单位为MPa。试根据不为零主应力的数目，它是：
（A）二向应力状态；
（B）单向应力状态；
（C）三向应力状态；
（D）纯切应力状态。
MPa
9－7受力物体中某一点处的应力状态如图所示（图中p为单位面积上的力）。试求该点处的主应力。
知识点：应力圆的应用
难度：难
解答：
应力圆半径
9－8从构件中取出的微元，受力如图所示。试：
1．求主应力和最大切应力；
2．确定主平面和最大切应力作用面位置。
应力分析与应变分析
应力分析与应变分析概述应力分析和应变分析是材料力学与结构设计中重要的分析方法。
通过研究材料内部的应力和应变分布情况，可以评估材料的强度和稳定性，为结构设计提供依据。
本文将介绍应力分析和应变分析的基本概念、方法和应用领域。
应力分析应力的概念应力是材料内部的内力状态，是材料中单元体受到的单位面积上的力的大小。
常见的应力类型有正应力、剪切应力和法向应力。
正应力指的是垂直于面元的力，剪切应力指的是在面元平面上的切应力，法向应力是正应力的一种特殊情况。
应力分布材料内部的应力分布可以通过应力场来描述。
应力场是指空间中各点的应力分布情况。
常见的应力场模型包括均匀应力场、线性应力场和非线性应力场。
弹性力学弹性力学是研究材料受力后的变形和应力恢复的一门学科。
通过弹性力学理论，可以计算材料在受力后的应力分布和变形情况。
应力分析的应用应力分析在工程领域有广泛的应用。
例如，在结构设计中，可以通过应力分析来评估结构的强度和稳定性，确定合理的结构形式和尺寸。
此外，应力分析也用于材料疲劳寿命预测、断裂力学研究等领域。
应变分析应变的概念应变是材料内部形变程度的度量，是材料内部单位长度的变化量。
常见的应变类型有线性应变、剪切应变和体积应变。
线性应变指的是材料在受力后的线性变形；剪切应变是材料在受到切应力作用时沿切应力方向发生的形变；体积应变是材料在受力后发生的体积变化。
应变分布类似于应力分布，应变分布可以通过应变场来描述。
应变场是指空间中各点的应变分布情况。
应变分析的方法应变分析的常用方法包括拉伸试验、剪切试验、压缩试验和扭转试验等。
通过这些试验可以获取材料在不同受力状态下的应变数据，进而进行应变分析。
应变测量应变测量是应变分析中的重要环节。
常用的应变测量方法有电阻式应变计、光栅应变计和激光测量等。
这些方法可以准确地获取材料受力后的应变数据，并用于应变分析和应变场重构。
应变分析的应用应变分析在材料研究和工程设计中起着重要的作用。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
向
面
应
应
力
力
状 特例 状
态
态
单向应力状态
特例
纯剪应力状态
常用术语 主平面
x1
x1
面上只有正应力
主单元体
三个主平面相 互垂直
主应力 单元体的某个面上剪应力等于零时的正应力;
约定：
12 3
应力状态
空间（三向）应力状态： 三个主应力均不为零； 平面（二向）应力状态： 两个主应力不为零； 单向应力状态：一个主应力不为零;
两种材料的扭转试验
低碳钢扭转
铸铁扭转
为什么脆性材料扭转时沿45º螺旋面断开？
为什么要研究应力状态 试件的破坏不只在横截面，
有时也沿斜截面发生破坏；
不仅要研究横截面上的应力， 而且也要研究斜截面上的应力。
三、如何描述一点的应力状态
微元
微元及其各面上的应力来描 述一点的应力状态。
dz
dy
dx
约定:
哪一个面上？ 哪一点？
指明
哪一点？ 哪个方向面？
应力状态:
——过同一点不同方向面上应力的集合，称 为这一点的应力状态；
二、为什么要研究应力状态？
请看下列实验现象：
低碳钢和铸铁的拉伸实验 低碳钢和铸铁的扭转实验
两种材料的拉伸试验
铸铁拉伸
低碳钢拉伸
塑性材料拉伸时为什么会出现滑移线？ (P18 图2.16)
应力的面的概念
轴向拉压
F
同一横截面上各点应力相等： F
A
F
同一点在斜截面上时： co2s
2
sin2
应力的面的概念
——过同一点不同方向面上的应力 各不相同；
受轴向拉力作用的杆件，受力之前,表面的正方形
FP
FP
受拉后，正方形变成了矩形，直角没有改变。 横截面上没有剪应力；
应力的面的概念
受拉之前,表面斜置的正方形
9.1 应力状态概述
9.1 应力状态的基本概念 一、什么是应力状态？ 二、为什么要研究应力状态? 三、如何描述一点的应力状态?
一、什么是应力状态？
应力的点的概念: ——同一截面上不同点的应力 各不相同;
FQ
Mz
横截面上的正应力分布
横截面上的剪应力分布
结果表明：
同一面上不同点的应力各不相同，即应力的点的概念。
FP
FP
受力之后,在其表面斜置的正方形在受拉后， 变成了菱形。
这表明：拉杆的斜截面上存在剪应力。
应力的面的概念
受扭之前，圆轴表面的圆
Mx Mx
受扭后，变为一斜置椭圆，长轴方向伸长， 短轴方向缩短。这是为什么？
轴扭转时，其斜截面上存在着正应力。
根据微元的局部平衡
y' x x'
x' y'
x
x
拉中有切 x
微元体的体积为无穷小； 相对面上的应力等值、反向、共线;
一般三向（空间）应力状态
z
z
zx zy
xz yz
x x
xy
yx
y y
一般平面（二向）应力状态
σy
τyx
τ xy
x
σx
yx xy
y
一般单向应力状态或纯剪应力状态
y
x
x
y
yx xy
x
单向应力状态
纯剪力状态
一点的应力状态
三
平
3 2
1
本章难点 提取危险点处应力状态； 应力状态是一剪应力分析的基础；
1 提取拉压变形杆件一点的应力状态
x
F A
单向应力状态
2 提取拉压变形杆件一点的应力状态-斜截面上
co2s
2
sin2
3 提取扭转变形杆件一点的应力状态
T IP
T Wt
纯剪应力状态
4 提取横力弯曲变形杆件下边缘一点的应力状态
M Wz
单向应力状态
5 提取横力弯曲变形杆件任意一点的应力状态
My Iz
F
s
S
* z
bI z
平面应力状态
6 提取工字形截面梁上一点的应力状态
FP S平面
l/2
l/2
5
FQ
FP 2
S平面
5
4
4
3
3
Mz
FP l 4
2
2
1
1
x1
1
2
x2
3
3 3
2 2
2 2
4
x2
x1
5
7 同一点的应力状态可以有各种各样的描述方式. S平面
F
F
1
F
A
1
S平面
n
F
1
F
1
90
Mx Mx
根据微元的局部平衡
y ' yx
x'
xy
xy
切中有拉
x' y' x'
yx
x'y'
x'
xy
x'y'
x'
yx
x
微元平衡分析结果表明：
即使同一点不同方向面上的应力也是各不相同的，此即应 力的面的概念。
不仅横截面上存在应力，斜截面上也存在应力。
应力的点的概念与面的概念
应力