第九章 应力状态与强度理论
应力状态与强度理论

理论理论能很好的解释石料或混凝土等脆性材 料受轴向压缩时的断裂破坏。
3、最大剪应力理论(第三强度理论):
理论认为最大剪应力是引起塑性屈服的主要 因素,只要最大剪应力τmax达到与材料性质 有关的某一极限值,材料就发生屈服。
单向拉伸下,当与轴线成45。的斜截面上的
τmax= s/2时
任意应力状态下
莫尔强度条件为:
1
Байду номын сангаас
t c
3
t
对于拉压强度不同的脆性材料,如铸铁、 岩石和土体等,在以压为主的应力状态下, 该理论与试验结果符合的较好。
综合以上强度理论所建立的强度条件, 可以写出统一的形式: σr≤[σ]
σr称为相当应力
r1 1
r2 1 2 3
r3 1 3
r4
1 2
理论理论能很好的解释石料或混凝土等脆性材 料受轴向压缩时,沿纵向发生的断裂破坏。
2、最大伸长线应变理论(第二强度理论):
理论认为最大伸长线应变是引起断裂的主要因素。
拉断时伸长线应变的极限值为
断裂准则为:
1
1 E
1
2
11
b
E
3
1 2 3 b
第二强度理论的强度条件:
1 2 3
max
1 3
2
屈服准则: 1 3 s
2
2
1 3 s
第三强度理论建立的强度条件为:
1 3
在机械和钢结构设计中常用此理论。
4、形状改变比能理论(第四强度理论):
第四强度理论认为: 形状改变比能是引起塑性屈服的主要因素。
单向拉伸时,
1
3E
s
2的形状改变比能。
应力状态和强度理论

7.10 强度理论概述 低碳钢在拉伸、压缩和扭转时 低碳钢在拉伸、压缩和扭转时, 当试件的应力达 到屈服点后, 就会发生明显的塑性变形, 到屈服点后 就会发生明显的塑性变形 使其失 去正常的工作能力, 去正常的工作能力 这是材料破坏的一种基本形 塑性屈服。 叫做塑性屈服 式, 叫做塑性屈服。 铸铁拉伸或扭转时, 铸铁拉伸或扭转时 在未产生明显的塑性变形的 情况下就突然断裂, 材料的这种破坏形式, 情况下就突然断裂 材料的这种破坏形式 叫做 脆性断裂。 脆性断裂 。 石料压缩时的破坏也是这种破坏形 式。
混凝土压缩时的力学性能 使用标准立方体试块测定
端面未润滑时的破 端面润滑时的 坏形式 破坏形式
(三)最大剪应力(第三强度)理论 最大剪应力(第三强度) 认为构件的屈服是由最大剪应力引起的。 认为构件的屈服是由最大剪应力引起的。当最 最大剪应力引起的 大剪应力达到单向拉伸试验的极限剪应力时, 大剪应力达到单向拉伸试验的极限剪应力时, 构件就破坏了。 构件就破坏了。 σ1 −σ3 σ s = =τs τ max = τ s τ max =
[
]
1+µ 2 = τ E
E ∴G= 2(1+µ )
7.10 强度理论概述
1.材料破坏的基本形式
在前面的实验中, 在前面的实验中 曾接触过一些材料的 破坏现象, 破坏现象 如果以低碳钢和铸铁两种材料 为例, 它们在拉伸(压缩 压缩)和扭转试验时的破 为例 它们在拉伸 压缩 和扭转试验时的破 坏现象虽然各有不同, 坏现象虽然各有不同 但都可把它归纳为 两类基本形式, 塑性屈服和脆性断裂。 两类基本形式 即塑性屈服和脆性断裂。
第一类强度理论-----脆性断裂的理论 脆性断裂的理论 第一类强度理论
第一强度理论---第一强度理论 最大拉应力理论 第二强度理论---第二强度理论 最大伸长线应变理论
材料力学第9章 强度理论
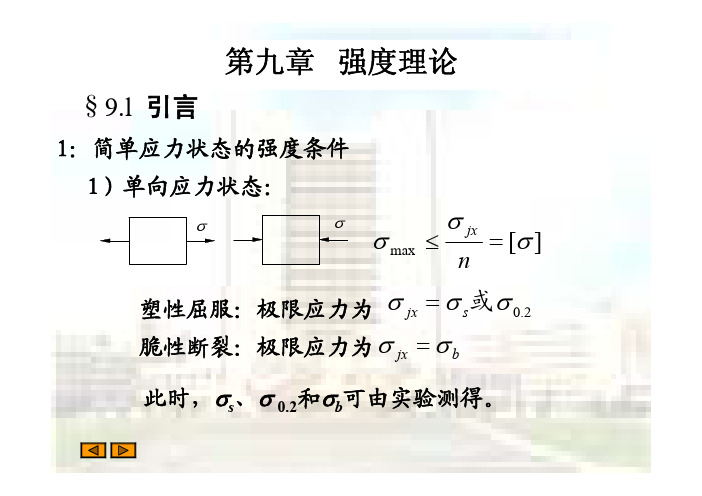
由于物体在外力作用下所发生的弹性变形既包括 物体的体积改变,也包括物体的形状改变,所以可推 断,弹性体内所积蓄的变形比能也应该分成两部分: 一部分是形状改变比能(畸变能) ,一部分是体积改 变比能 。 在复杂应力状态下,物体形状的改变及所积蓄的 形状改变比能是和三个主应力的差值有关;而物体体 积的改变及所积蓄的体积改变比能是和三个主应力的 代数和有关。
注意:图示应力状态实际上为弯扭组合加载对 应的应力状态,其相当应力如下:
r 3 2 4 2 [ ] 2 2 [ ] r 4 3
可记住,便于组合变形的强度校核。
例1 对于图示各单元体,试分别按第三强度理论及第四强度理论 求相当应力。
120 MPa 140 MPa
r4
1 2 2 2 [(0 120) ( 120 120) ( 120 0) ] 120MPa 2
140 MPa
(2)单元体(b)
σ1 140MPa
σ 2 110MPa
σ3 0
110 MPa
σr 3 σ1 σ 3 140MPa 1 2 2 2 σr 4 [30 110 ( 140) ] 128MPa 2
1u
1u
E
b
E
1 1 1 2 3 E
1u
1u
E
b
E
1 2 3 b
强度条件为: 1 2 3
b
n
[ ]
实验验证: a) 可解释大理石单压时的纵向裂缝; b) 脆性材料在双向拉伸-压缩应力状态下,且压应 力值超过拉应力值时,该理论与实验结果相符合。
σ1 94 .72MPa σ 3 5 .28MPa
第九章第六节梁弯曲时的应力及强度计算(上课用)

m
V
( Stresses in Beams)
m
m
M
V
m m
只有与剪应力有关的切向内力元素 d V = dA 才能合成剪力
只有与正应力有关的法向内力元素 d FN = dA 才能合成弯矩
剪力V 内力 弯矩M 正应力 剪应力
所以,在梁的横截面上一般
既有 正应力, 又有 剪应力
先观察下列各组图
所以,可作出如下 假设和推断:
1、平面假设:
2.单向受力假设: 各纵向纤维之间互不挤压,纵向纤维均处于单向受拉或受压的状态。 因此梁横截面上只有正应力σ而无剪应力τ
各横向线代表横截面,实验表 明梁的横截面变形后仍为平面。
梁在弯曲变形时,上面部分纵向纤维缩短,下面部分纵向纤维伸长,必 有一层纵向纤维既不伸长也不缩短,保持原来的长度,这一纵向纤维层称为 中性层. 中性层与横截面的交线称为中性轴,中性轴通过截面形心,是一条形心轴。 且与截面纵向对称轴y垂直,将截面分为受拉区及受压区。梁弯曲变形时, 各横截面绕中性轴转动。
(3)横截面上任一点处的剪应力计算公式(推导略)为
V S I zb
Z
V——横截面上的剪力
Iz——整个横截面对中性轴的惯性矩
b——需求剪应力处的横截面宽度 S*Z——横截面上需求剪应力处的水平线 以外(以下或以上)部分面积A*(如图 )对 中性轴的静矩
V
3V 4 y2 (1 2 ) 2bh h
应力状态按主应力分类:
(1)单向应力状态。在三个相对面上三个 主应力中只有一个主应力不等于零。 (2)双向应力状态。在三个相对面上三个 主应力中有两个主应力不等于零。
(3)三向应力状态。其三个主应力都不等于零。例 如列车车轮与钢轨接触处附近的材料就是处在三向应 力状态下.
9第九章 应力、应变分析、强度理论123
第九章 应力、应变分析、强度理论一、是非题9-1、单元体最大正应力面上的剪应力恒等于零。
( )9-2、单元体最大剪应力面上的正应力恒等于零。
( )9-3、依照剪应力互等定理,一单元体中两个平面上的剪应力数值相等,符号相反,则这两平面必定相互垂直。
( )9-4、 只要构件横截面上的轴力N=0,则该横截面正应力处处为零。
( )9-5、 梁受横力弯曲时,其横截面上各点处的主应力必定是σ1≥0,σ3≤0。
( )9-6、 等截面圆杆受纯扭转时,杆内任一点处只有剪应力,而无正应力。
( )9-7、若受力构件中一点处,某方向上的线应变为零,则该方向上的正应力必为零。
( )9-8、若受力钢质构件中的一点处,某相互垂直方向的剪应变为零,则该方向上的剪应力必为零。
( ) 9-9、若各向同性材料单元体的三个正应力σx >σy >σz ,则对应的三个线应变也有εx >εy >εz 。
( ) 9-10、 各向同性单元体的三个主应变为ε1≠0,ε2≠0,ε3=0,若(1)、当ε1>0,则必有σ1>0;( )(2)、当ε1>ε2,则必有σ1>σ2;( )(3)、当ε1>ε2>0,则()()21max 12εεμτ-+=E 。
( ) 9-11、各向同性材料在三向均匀压缩或拉伸时,其形状改变比能恒等于零。
( )二、选择题9-12、单元体应力状态如图9-1所示,由x 轴至σ1方向的夹角为( )。
A 、+13.5°;B 、-76.5°;C 、+76.5°;D 、-13.5°。
9-13、 若已知σ1=5MP a ,则另一个主应力为( )。
A 、σ2=-85MP a ;B 、σ3=-85MP a ;C 、σ2=75MP a ;D 、σ3=-75MP a 。
9-14、 三种应力状态分别如图9-2a 、b 、c 所示,则三者间的关系为( )。
A 、完全等价;B 、完全不等价;C 、(b )和(c )等价;D 、(a )和(c )等价。
第九章强度理论

第九章 强度理论1.图示应力状态,用第三强度理论校核时,其相当应力为:(A )213τσγ=; (B )=3γστ;(C )=3γστ213; (D )=3γσ2τ;正确答案是 。
2和许用拉应力的关系为:(A )[τ] = [σ]; (B )[τ] =[σ] / 2 ;(C )[τ] = [σ] / 213; (D )[τ] = [σ] / 3 ;正确答案是 。
3.塑性材料的下列应力状态中,那一种最易发生剪切破坏:45.第三强度理论和第四强度理论的相当应力分别为3γσ 及4γσ ,对于纯剪应力状态,恒有3γσ / 4γσ= 。
6.按第三强度理论计算图示单元体的相当应力3γσ= 。
7.图示①、②、③为三个平面应力状态的应力圆,试画出各应力圆所对应的主平面微元体上的应力。
8.图示为承受气体压力p 的封闭薄壁圆筒,平均直径为D ,壁厚t ,气体压强p 均为已知,用第三强度理论校核筒壁强度的相当应力3γσ= 。
9.单元体如图,已知αττσ42−==xy y 。
证明:2/3/=y x σσ ;6/7/=x σσα。
τx10.证明线弹性材料的泊松比μ满足关系式:0<μ<0.511.图(a )、(b )表示同一材料的两个单元体。
材料的屈服极限s σ= 275 MPa 。
试根据第三强度理论求两个单元体同时进入屈服极限时拉应力σ 与剪应力τ的值。
若σ> τ。
(a) (b)12.图示受扭圆轴的d = 30 mm ,材料的弹性模量 ,v =0.3 ,屈服极限MPa E 5101.2×=S σ= 240MPa ,实验测得a b 方向的应变为 0002.0=ε 。
试按第三强度理论确定设计该轴时采用的安全系数。
13.从低碳钢零件中某点处取出一单元体,其应力状态如图所示,试按第三、四强度理论计算单元体的相当应力。
单元体上的应力为60=ασ,80−=βσ,(°+=90αβ),40−=ατ (单位:MPa 。
应力状态分析和强度理论

03
弹性极限
材料在弹性范围内所能承受的最大应力状态,当超过这一极限时,材料会发生弹性变形。
01
屈服点
当物体受到一定的外力作用时,其内部应力状态会发生变化,当达到某一特定应力状态时,材料会发生屈服现象。
02
强度极限
材料所能承受的最大应力状态,当超过这一极限时,材料会发生断裂。
应力状态对材料强度的影响
形状改变比能准则
04
弹塑性材料的强度分析
屈服条件
屈服条件是描述材料在受力过程中开始进入屈服(即非弹性变形)的应力状态,是材料强度分析的重要依据。
根据不同的材料特性,存在多种屈服条件,如Mohr-Coulomb、Drucker-Prager等。
屈服条件通常以等式或不等式的形式表示,用于确定材料在复杂应力状态下的响应。
最大剪切应力准则
总结词
该准则以形状改变比能作为失效判据,当形状改变比能超过某一极限值时发生失效。
详细描述
形状改变比能准则基于材料在受力过程中吸收能量的能力。当材料在受力过程中吸收的能量超过某一极限值时,材料会发生屈服和塑性变形,导致失效。该准则适用于韧性材料的失效分析,尤其适用于复杂应力状态的失效判断。
高分子材料的强度分析
01
高分子材料的强度分析是工程应用中不可或缺的一环,主要涉及到对高分子材料在不同应力状态下的力学性能进行评估。
02
高分子材料的强度分析通常采用实验方法来获取材料的应力-应变曲线,并根据曲线确定材料的屈服极限、抗拉强度等力学性能指标。
03
高分子材料的强度分析还需要考虑温度、湿度等环境因素的影响,因为高分子材料对环境因素比较敏感。
02
强度理论
总结词
该理论认为最大拉应力是导致材料破坏的主要因素。
工程力学(静力学和材料力学)第2版课后习题答案 范钦珊主编 第9章 应力状态与强度理论

τ max =
σ1 −σ 3
2
=
380 1 2 + 100 2 + 4τ xy < 160 4 4
解得 | τ xy | <120MPa
所以,取 | τ xy | <120MPa。 9- 6 图示外径为 300mm 的钢管由厚度为 8mm 的钢带沿 20°角的螺旋线卷曲焊接而
成。试求下列情形下,焊缝上沿焊缝方向的剪应力和垂直于焊缝方向的正应力。 1.只承受轴向载荷 FP = 250 kN; 2.只承受内压 p = 5.0MPa(两端封闭) *3.同时承受轴向载荷 FP = 250kN 和内压 p = 5.0MPa(两端封闭)
εt =
2 π ( r + Δ r ) − 2 πr Δ r = 2 πr r 1 Δr = ε t ⋅ r = [σ t −νσ m ] E 1 = (118.72 − 0.33 × 59.36 ) × 254 = 0.336mm 75 ×103
9- 8
构件中危险点的应力状态如图所示。 试选择合适的准则对以下两种情形作强度校
9- 7
承受内压的铝合金制的圆筒形薄壁容器如图所示。 已知内压 p = 3.5MPa, 材料
的 E = 75GPa, ν = 0.33。试求圆筒的半径改变量。
5
习题 9-7 图
解:
σm =
3.5 × (254 × 2 + 7.6) = 59.36 MPa 4 × 7.6 3.5 × (254 × 2 + 7.6) = 118.72 MPa σt = 2 × 7.6
σ r4 =
1 (100 2 + 20 2 + 120 2 ) = 111.4 MPa 2
2. σ =
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
由分离体平衡得:
Fn 0
s Ss xScos2t xyScossin s ySsin 2t yxSsincos0
图1
考虑切应力互等和三角变换:
s
sx
y
sy
ttxy
n
Ox
t
图2
t xy t yx;
cos2 1 cos2 ;
2
sin2 1 cos2 ;
2
2sin cos sin 2
sy
s 6095MPa t 6025 3MPa
t
s
x
s
2
y
sin2
t
xy
cos2
五、梁的主应力及主应力迹线
P1
P2
q
1
2 3 4
5
如图,已知梁发生剪切弯 曲(横力弯曲),其上M、 Q>0,试确定截面上各点主 应力大小及主平面位置。
单元体:
s
x
My Iz
t
xy
QS bI
z
z
s s
1 3
s x
2
(s x)2t
实线表示拉主应力迹线; 虚线表示压主应力迹线。
拉力
s3 s1
两组曲线正交.
压力
y
1234
i
a
b
c
d
n
主应力迹线的画法: x
1234
i
n
截面截面截面截面 截面 截面
q
s1 s3
§9–4 三向应力状态简介
1、空间应力状态
y
s1
t
s2
s3
z
x
s3
s2
s
s1
2、三向应力分析
t
y
s1
t max
s2
s3
s3
y
面的法线 应力圆的半径
Ox
t n D( s , t
2
C
x
两面夹角 两半径夹角2 ;
A(sx ,txy) s
且转向一致。
O
B(sy ,tyx)
点面对应,转向相同,转角二倍
四、在应力圆上标出极值应力
t
t max
x
21
A(sx ,txy)
OC
s3 s2
20 s1 s
B(sy ,tyx)
t m in
s s
sy
y
主单元体(Principal body):
sx
各侧面上切应力均为零的单元体。
sz
z
s2
s3
主平面(Principal Plane):
切应力为零的截面。 x
主应力(Principal Stress ):
主平面上的正应力。
s1
主应力排列规定:按代数值大小,
s 1s 2 s 3
三向应力状态( Three—Dimensional State of Stress): 三个主应力都不为零的应力状态。
1
1 E
s
1
s
2
s
3
2
1 E
s
2
s
3
s
1
3
1 E
s
3
s
2
s
1
方向一致
tg2
0
xy x y
2t xy s x s
y
tg2
0
四、平面状态下的应力---应变关系:
s
x
E
1
2
x
y
s z t yzt zx 0
s
y
E
1
2
y x
t xyG xy
主应力与主应变方向一致?
tg2
0
2t xy s x s y
在坐标系内画出点A(s x,txy)和 B(sy,tyx)
AB与s 轴的交点C便是圆心。
2
C
A(sx ,txy) s
以C为圆心,以AC为半径画
O
圆——应力圆;
B(sy ,tyx)
圆心(s
x
s
2
y
,0);半径 (s
x
s
2
y
)2 t
2 xy
sy
n 三、单元体与应力圆的对应关系
s
sx
t txy
面上的应力(s ,t ) 应力圆上一点(s ,t )
25 3
s2
45 B 95
A
150° 0 25 3
s1
B(45,25 3)
AB的垂直平分线与
s 轴的交点C便是
圆心,以C为圆心, 以AC为半径画 圆——应力圆
t (MPa)
B
s3
O
s2
A
20
C
20MPa
s1
s
(MPa)
主应力及主平面如图
s 1 120 s 220 s 30 0 30
25 3
s2
长线应变达到单向拉伸试验下的极限应变时,构件就断了。
1
u
sb
E
; (1 0)
1
1 E
s 1
s 2
s 3
sb
E
1、破坏判据:s 1 s 2 s 3 s b
2、强度准则:s 1 s 2 s 3 s
3、适用范围:适用于破坏形式为脆断的构件。
同时考虑了s1、s2、s3,适用于脆性材料(一般非金属)。 不适用于两向拉、压。
二向应力状态(Plane State of Stress): 一个主应力为零的应力状态。
单向应力状态(Unidirectional State of Stress): 一个主应力不为零的应力状态。
sx B sx
tzx
txz
sx
sx
A
§9–2 二向应力状态分析——解析法
y
sy
sy
txy sx
等价 y
第九章 应力状态与强度理论
§9–1 引言 §9–2 二向应力状态分析——解析法 §9–3 二向应力状态分析——图解法 §9–4 三向应力状态简介 §9–5 广义虎克定律 §9–6 复杂应力状态的应变能密度 §9–7 四种常用的强度理论 §9–8 莫尔强度理论
§9–1 引 言
一、引言 1、铸铁与低碳钢的拉、压、扭试验现象是怎样产生的?
ds
d
sx s y
sin 2 2t xy cos2
0时,s有最大最小值。
s取得极值时,t 0极值正应力就是主应力!
主平面法线与X轴夹角:
tg20
2t xy sx s y
可求出相差90º的两个0 ,定两个互相垂直 平面,分别对应最大、最小主应力:
ssmm
ax in
s
x
s y
±
s
(x
2
E
1
2
2 xyG [( x y )(1
)] (
xy x
y
)
tg2
0
一、概述: §9–7 四种常用的强度理论
(一)、简单变形时强度条件的建立:
1、铸铁与低碳钢的拉、压、扭试验
P 铸铁拉伸
铸铁压缩
P M
低碳钢
铸铁
确定破坏(极限)应力,得许P用应力,建立相应的强度条件, P
2、组合变形杆将怎样破坏? M
2
2 xy
1
s3 s3
0 s1
s3
3 –45°
s1s3
0 s1 5 s1
t
D1 A2
A1 D2
CO
s
D1
t
A2
20
A1
CO
s
D1 t
D2
D1
CO
20= –90°
s
D2
t
D2 A2
A1 D1
OC
s
t
A2
20
O
D1 A1
C
s
D2
主应力迹线(Stress Trajectories):
主应力方向线的包络线——曲线上每一点的切线都指示 着该点的拉主应力方位(或压主应力方位)。
yz zx 0
txy
Hale Waihona Puke zx三、复杂状态下的应力 --- 应变关系
sy
x
1 E
s
x
s
y
s
z
y
sx
sz
txy
z
x
依叠加原理,得:
x
s x
E
sy
E
sz
E
y
1 E
s
y
s
z
s
x
z
1 E
s
z
s
x s
y
x
y
t
xy
G
y
z
t
yz
G
zx
t zx
G
1 E
s
x
s
y
s
z
主应力 --- 主应变关系
45 B 95
A
150° 0 25 3
s1
t (MPa)
B
s3
O
s2
A
2s0
C
20MPa
s1
s
(MPa)
解法2—解析法:分析——建立坐标系如图
25 3
45 95
60°
150° 25 3
s s
1 2
s
x
s
2
y
(s
x
s
2
y
)2 t
2 xy
s y 45MPa
t yx25 3MPat xy
y Ox
s x ?
(二)、强度理论:是关于“构件发生强度失效起因”的假说 。 找到原因后,利用简单应力状态的实验结果,建立复杂应力
