第十章-三向应力状态简介(材料力学课件)
合集下载
材料力学三向应力状态PPT课件
第243页/共72页
90 45 0
直角应变花： x 0 ， y 90
由 45
x
y
2
xy
2
可求得:
xy 0 90 2 45
第254页/共72页
CL10TU28
§9-6 复杂应力状态下的变形比能
一、微元体应变能
1.单向拉伸变形比能：
v
1
2
2
2、微元体变形功
dy
3 dx
CL10TU50
3.最大剪应力理论（第三强度理论）
假设：无论材 料 内 各 点的 应 力 状 态 如何 ， 只 要 有 一点 的 最 大 剪 应力 τ max达到 单 向 拉 伸屈服剪应力τS时，材料就在该处出现明显塑性变形或屈服。
屈服破坏条件是：
max s
max
1
2
3
,
s
s 2
用应力表示的屈服破坏条件：
应变的实测：
用应变仪直接测出三个选定方向 1、 2、 3的线应变 1 、 2 、 3 ，由下式
1
2
3
x x x
y
2
y
2
y
2
x x x
y
2
y
2
y
2
cos2 1 cos2 2 cos2 3
xy
2
xy
2
xy
2
sin 2 1 sin 2 2 sin 2 3
求出 x 、 y 、 xy
3
2
1
第21页/共72页
同理，在平行于 σ2 的各个斜截面上，其应力对应于由主应力 σ1 和 σ3 所画的 应力圆圆周上各点的坐标。
主单元体：六个平面都是主平面
材料力学应力状态
材料力学应力状态关键词：单元体的取法，莫尔应力圆的前提有那么一个单元体后（单元体其中的一对截面上主应力=0（平面）或平衡（空间），也就是单元体的一对截面为主平面），才有这么一个隔离体，才有那么一个莫尔应力圆和表达式也就是：取的单元体不同，则单元体的应力特点不一样，从而用截面法求任意截面上的应力取隔离体列平衡方程时，隔离体的受力特点不同，从而球出来的表达式也不同，只有这种表达式才适合莫尔应力圆。
因此拿到一个单元体后，不要急着应用莫尔应力圆，要先看它的特点适合不适合莫尔应力圆，也就是σα和τα的表达式球出来以后还是不是下面的这个公式。
特别还要记住，这个公式里的夹角α是斜截面的外法线与σx作用平σy的形式。
比如，面的外法线之间的夹角，这样公式中才是σx—当α表示的是斜截面的外法线与σ1所在平面的夹角，那么公式就是σ1—σ2的形式；不论是谁减谁，应力圆的性状都不变；1.首先，先有主平面和主应力的概念，剪应力为0的平面为主平面，主平面上的正应力为主应力；2.然后，由于构件受力情况的不同，各点的应力状态也不一样，可以按三个主应力中有几个不等于零而将一点处的应力状态划分为三类：∙单向应力状态：只有一个主应力不等于零，如受轴向拉伸和压缩的直杆及纯弯曲的直杆内各点的应力状态。
∙二向应力状态(平面应力状态)：有两个主应力不等于零，如受扭的圆轴，低压容器器壁各点的应力状态。
∙三向应力状态：三个主应力都不等于零，如高压容器器壁内各点的应力状态。
3.然后，根据受力宏观判断是单轴应力状态还是平面应力状态还是三轴应力状态，取单元体关键，单元体取的不同，单元体上的应力也不同，做莫尔圆的繁简程度也不同，对于平面应力状态，当然要用主应力=0的那个截面参与单元体截取；4.单轴应力状态、平面应力状态、三轴应力状态是由主应力等于零的个数决定的，不受单元体取法的影响，也不是看单元体的三对截面上是否都存在正应力；比如单轴应力状态下，也可以取出一个单元体，让这个单元体的各平面上都有正应力和切应力，但是它仍然是单轴应力状态；同样，平面应力状态下，也可以取出一个单元体，让其各平面上都有正应力和剪应力，但它仍然是平面应力状态；5.按不同方位截取的单元体，尽管作用在这些单元体上的应力不同，但是在它们之间却存在着一定的关系：因为二者表示的是同一点的应力状态，因而可以从一个单元体上的应力求出另一个与其方向不同的单元体上的应力。
材料力学课件 强度理论讲诉
n
[s ]
可见：a) 与s2、s3无关； b) 应力su可用单向拉伸试样发生脆性断裂的
试验来确定。
实验验证：铸铁：单拉、纯剪应力状态下的破坏与 该理论相符；平面应力状态下的破坏和该理论基本 相符。
存在问题：没有考虑s2、s3对脆断的影响，无法解
释石料单压时的纵向开裂现象。
2）最大伸长线应变理论(第二强度理论)
1
2
s1
s 2 2
s 2
s 3 2
s1
s 3 2
ss
n
[s ]
实验验证： a) 较第三强度理论更接近实际值；
b) 材料拉压性能相同时成立。
强度理论的统一形式： s r [s ]
sr称为相当应力，分别为：
• 最大拉应力(第一强度)理论：
s r1 s1
• 最大伸长线应变(第二强度)理论：
可见：材料破坏的形式不仅与材料有关，还与 应力状态有关。
5）强度理论
根据一些实验资料，针对上述两种破坏形式， 分别针对它们发生破坏的原因提出假说，并认为不 论材料处于何种应力状态，某种类型的破坏都是由 同一因素引起，此即为强度理论。
常用的破坏判据有：
脆性断裂： s l max 塑性断裂： max
研究复杂应力状态下材料破坏的原因，根据一 定的假设来确定破坏条件，从而建立强度条件，这 就是强度理论的研究内容。
4）材料破坏的形式 常温、静载时材料的破坏形式大致可分为：
• 脆性断裂型： 例如： 铸铁：拉伸、扭转等； 低碳钢：三向拉应力状态。
• 塑性屈服型： 例如： 低碳钢：拉伸、扭转等； 铸铁：三向压缩应力状态。
s r2 s1 s 2 s 3
• 最大切应力(第三强度)理论： s r3 s1 s 3
[s ]
可见：a) 与s2、s3无关； b) 应力su可用单向拉伸试样发生脆性断裂的
试验来确定。
实验验证：铸铁：单拉、纯剪应力状态下的破坏与 该理论相符；平面应力状态下的破坏和该理论基本 相符。
存在问题：没有考虑s2、s3对脆断的影响，无法解
释石料单压时的纵向开裂现象。
2）最大伸长线应变理论(第二强度理论)
1
2
s1
s 2 2
s 2
s 3 2
s1
s 3 2
ss
n
[s ]
实验验证： a) 较第三强度理论更接近实际值；
b) 材料拉压性能相同时成立。
强度理论的统一形式： s r [s ]
sr称为相当应力，分别为：
• 最大拉应力(第一强度)理论：
s r1 s1
• 最大伸长线应变(第二强度)理论：
可见：材料破坏的形式不仅与材料有关，还与 应力状态有关。
5）强度理论
根据一些实验资料，针对上述两种破坏形式， 分别针对它们发生破坏的原因提出假说，并认为不 论材料处于何种应力状态，某种类型的破坏都是由 同一因素引起，此即为强度理论。
常用的破坏判据有：
脆性断裂： s l max 塑性断裂： max
研究复杂应力状态下材料破坏的原因，根据一 定的假设来确定破坏条件，从而建立强度条件，这 就是强度理论的研究内容。
4）材料破坏的形式 常温、静载时材料的破坏形式大致可分为：
• 脆性断裂型： 例如： 铸铁：拉伸、扭转等； 低碳钢：三向拉应力状态。
• 塑性屈服型： 例如： 低碳钢：拉伸、扭转等； 铸铁：三向压缩应力状态。
s r2 s1 s 2 s 3
• 最大切应力(第三强度)理论： s r3 s1 s 3
三向应力状态
2
2
min
例7-1 试求中所示单元体的主应力和最大剪应力。 （1）求主应力
x 10MPa, y 30MPa, x 20MPa max x + y x - y 2 + x 2 2 min
10 + 30 10 - 30 + 202 2 2 + 42.4MPa（ 拉 应 力 ） - 2.4MPa（ 压 应 力 ）
2 2
a 0对应 max
x + y
2
a 0 + 90 对应 min
x + y
2
三、最大和最小剪应力
d a 0 da
2
x - y
2
cos 2a - 2 xy sin 2a 0
x - y tg 2a 2 xy
max
x - y 2 + + xy 2 x - y 2 - 2 + xy
3
a 0 12143'
3
（2）求最大剪应力
1 42.4 2 0 MPa - 2.4 3
1
(a)
max
1 - 3
2
22 .4 MPa
3、 纯剪切应力状态
- 2 x tg 2a 0 - x - y
a0 135
五、不等于零的情况。
二向应力状态：三对主应力中有两对主应力不等
于零的情况。
三向应力状态：三对主应力皆不等于零的情况。
7-2 平面应力状态分析—解析法
一、斜截面上的应力
已知：单元体 x，y，xyyx， a 研究与z轴平行的任一斜截面c e上的应力。 符号规则： q 角：从x轴正方向反时针转至斜截面的 外法线方向为正，反之为负。 正应力：拉为正，压为负。 剪应力：使微元体或其局部产生顺时针方 向转动趋势者为正，反之为负。
2
min
例7-1 试求中所示单元体的主应力和最大剪应力。 （1）求主应力
x 10MPa, y 30MPa, x 20MPa max x + y x - y 2 + x 2 2 min
10 + 30 10 - 30 + 202 2 2 + 42.4MPa（ 拉 应 力 ） - 2.4MPa（ 压 应 力 ）
2 2
a 0对应 max
x + y
2
a 0 + 90 对应 min
x + y
2
三、最大和最小剪应力
d a 0 da
2
x - y
2
cos 2a - 2 xy sin 2a 0
x - y tg 2a 2 xy
max
x - y 2 + + xy 2 x - y 2 - 2 + xy
3
a 0 12143'
3
（2）求最大剪应力
1 42.4 2 0 MPa - 2.4 3
1
(a)
max
1 - 3
2
22 .4 MPa
3、 纯剪切应力状态
- 2 x tg 2a 0 - x - y
a0 135
五、不等于零的情况。
二向应力状态：三对主应力中有两对主应力不等
于零的情况。
三向应力状态：三对主应力皆不等于零的情况。
7-2 平面应力状态分析—解析法
一、斜截面上的应力
已知：单元体 x，y，xyyx， a 研究与z轴平行的任一斜截面c e上的应力。 符号规则： q 角：从x轴正方向反时针转至斜截面的 外法线方向为正，反之为负。 正应力：拉为正，压为负。 剪应力：使微元体或其局部产生顺时针方 向转动趋势者为正，反之为负。
六、 材料力学应力状态分析(2)
(MPa)
τ σ
（0，-100）
tmax
（300，100）
τmax = 180MPa；
Hale Waihona Puke σOσσ三向应力状态 特例分析
作为三向应力状态的特例,平面应力状态特点：
σ =0 σ、σ 、σ σ1 、σ 2、σ3
广义胡克定律
1、胡克定律、横向变形与泊松比
y
sx x = ; E sx y = x = ； E — 泊松比
tmax
（-300，50）
300
(MPa)
τ
σ
σ
（-200，-50）
σ
O
σ
三向应力状态 特例分析
例3、如图平面应力状态，求： 主应力s1、s2 、 s3和最大切 应力tmax。
300 100
解：如图作应力圆 Ｒ＝180MPa； s1 = 330MPa； s2 = 0； s3 = -30MPa；
A
2、平衡方法是分析一点处应 力状态最重要、最基本的方法
A
论证A－A截面上 必然存在切应力，而 且是非均匀分布的； 怎样证明A－A截 面上各点的应力状态 不会完全相同。
结论与讨论
A
ζ
ζ η
A
关于A点的应力状态有多种答 案、请用平衡的概念分析哪 一种是正确的。
η
η
ζ
结论与讨论
3、怎样将应力圆作为一 种分析问题的重要 手段，求解较为复杂的 应力状态问题
P
x =
由变形方程： x =
1 [s x (s y s z )] = 0； E s x = s z = 0.3( 60) = 18 MPa
P σx σy
所以铅块主应力为: ζ1 = 0；ζ2 = -18MPa; ζ3 = -60MPa;
材料力学课件PPT
力学性质：在外力作用下材料在变形和破坏方面所 表现出的力学性能
一
试
件
和
实
常
验
温
条
、
件
静
载
材料拉伸时的力学性质
材料拉伸时的力学性质
二 低 碳 钢 的 拉 伸
材料拉伸时的力学性质
二 低碳钢的拉伸（含碳量0.3%以下）
e
b
f 2、屈服阶段bc（失去抵抗变 形的能力）
b
e P
a c s
s — 屈服极限
（二）关于塑性流动的强度理论
1．第三强度理论（最大剪应力理论） 这一理论认为最大剪应力是引起材料塑性流动破坏的主要
因素，即不论材料处于简单还是复杂应力状态，只要构件危险 点处的最大剪应力达到材料在单向拉伸屈服时的极限剪应力就 会发生塑性流动破坏。
这一理论能较好的解释塑性材料出现的塑性流动现象。 在工程中被广泛使用。但此理论忽略了中间生应力 2的影响， 且对三向均匀受拉时，塑性材料也会发生脆性断裂破坏的事 实无法解释。
许吊起的最大荷载P。
CL2TU8
解： N AB
A [ ]
0.0242 4
40 106
18.086 103 N 18.086 kN
P = 30.024 kN
6.5圆轴扭转时的强度计算
圆轴扭转时的强度计算
▪ 最大剪应力：圆截面边缘各点处
max
Tr
Ip
max
Wp T
Wp
Ip r
—
抗扭截面模量
3、强化阶段ce（恢复抵抗变形
的能力）
o
b — 强度极限
4、局部径缩阶段ef
明显的四个阶段
1、弹性阶段ob
第十章-三向应力状态简介(材料力学课件)
应力与许用拉应力之比 [ ] 0.5 [ ]
• 用第四强度理论可得出：塑性材料的许用剪
应力与许用拉应力之比 [ ] 0.577 [ ]
例：填空题。
石料在单向压缩时会沿压力作用方向的纵 截面裂开，这与第 二 强度理论的论述基本 一致。
例：填空题。
一球体在外表面受均布压力p = 1 MPa 作用，则在球心处的主应力 1 = －1 MPa， 2 = －1 MPa， 3 = －1 MPa。
1.最大拉应力理论（第一强度理论） • 它假定：无论材料内各点的应力状态如何，
只要有一点的主应力σ1 达到单向拉伸断裂时 的极限应力σu，材料即破坏。
• 在单向拉伸时，极限应力 σu =σb
• 失效条件可写为 σ1 ≥ σb
[ ] b
n
• 第一强度强度条件： 1 [ ]
试验证明，这一理论与铸铁、岩石、砼、 陶瓷、玻璃等脆性材料的拉断试验结果相符， 这些材料在轴向拉伸时的断裂破坏发生于拉应 力最大的横截面上。脆性材料的扭转破坏，也 是沿拉应力最大的斜面发生断裂，这些都与最 大拉应力理论相符，但这个理论没有考虑其它 两个主应力的影响。
V 2EA Al 2E 2
CL10TU40
变形比能：
u 1
2
u
1 2
1
1
1 2
2
2
1
2
3
3
2
1 3
变形比能：
u
1 2
1
1
1
2
2
2
1
2
3
3
• 用第四强度理论可得出：塑性材料的许用剪
应力与许用拉应力之比 [ ] 0.577 [ ]
例：填空题。
石料在单向压缩时会沿压力作用方向的纵 截面裂开，这与第 二 强度理论的论述基本 一致。
例：填空题。
一球体在外表面受均布压力p = 1 MPa 作用，则在球心处的主应力 1 = －1 MPa， 2 = －1 MPa， 3 = －1 MPa。
1.最大拉应力理论（第一强度理论） • 它假定：无论材料内各点的应力状态如何，
只要有一点的主应力σ1 达到单向拉伸断裂时 的极限应力σu，材料即破坏。
• 在单向拉伸时，极限应力 σu =σb
• 失效条件可写为 σ1 ≥ σb
[ ] b
n
• 第一强度强度条件： 1 [ ]
试验证明，这一理论与铸铁、岩石、砼、 陶瓷、玻璃等脆性材料的拉断试验结果相符， 这些材料在轴向拉伸时的断裂破坏发生于拉应 力最大的横截面上。脆性材料的扭转破坏，也 是沿拉应力最大的斜面发生断裂，这些都与最 大拉应力理论相符，但这个理论没有考虑其它 两个主应力的影响。
V 2EA Al 2E 2
CL10TU40
变形比能：
u 1
2
u
1 2
1
1
1 2
2
2
1
2
3
3
2
1 3
变形比能：
u
1 2
1
1
1
2
2
2
1
2
3
3
应力应变分析ppt课件
某点处所有截面上的正应力，其极大值为1， 极小值为3
17
单向、双向、三向应力状态
18
2 .某点单元体的最大切应力 由斜面应力公式 (10.2) 求导
45ºS
x
y
2
sin 2
x cos 2
d d
( x
y ) cos2 2 x sin 2
0
cot 2S
2 x x y
tan 2 P
y
y
( , ) 2
Dx x , x
R
O x y
C
2
Dy y , x
27
从应力圆上还可找到：主应力，主方向，主切应力
主应力：
, ,0 1, 2, 3
主方向：
P1, P2 , z 方向 pi
0
最大切应力： O
max
1
2
3
Dy
y , x
2 P 2 C
D ,
2 Dx x , x
y
2
2
2
x
y
2
2
2 x
x
2
y
2
2
R2
圆的方程：圆心 ( x y ,
2
圆的半径： R
(
x
2
y
)2
2 x
0)
上式在应力坐标系 中为一圆，称为应力圆(莫尔圆)
24
应力圆的画法：
已知某点的平面应力状态为 x , y , x
y
x面坐标 Dx（ x , x） 两点连线与
（2）单向压缩
-
单压 单拉
31
例题
例题2
§10 应力应变分析与应力应变关系
某点单元体应力状态如图，确 定该点的主应力、主方向，画 出主单元体及其上的应力，并 在应力圆上标出图示截面上的 应力，（单位： MPa ）
17
单向、双向、三向应力状态
18
2 .某点单元体的最大切应力 由斜面应力公式 (10.2) 求导
45ºS
x
y
2
sin 2
x cos 2
d d
( x
y ) cos2 2 x sin 2
0
cot 2S
2 x x y
tan 2 P
y
y
( , ) 2
Dx x , x
R
O x y
C
2
Dy y , x
27
从应力圆上还可找到：主应力，主方向，主切应力
主应力：
, ,0 1, 2, 3
主方向：
P1, P2 , z 方向 pi
0
最大切应力： O
max
1
2
3
Dy
y , x
2 P 2 C
D ,
2 Dx x , x
y
2
2
2
x
y
2
2
2 x
x
2
y
2
2
R2
圆的方程：圆心 ( x y ,
2
圆的半径： R
(
x
2
y
)2
2 x
0)
上式在应力坐标系 中为一圆，称为应力圆(莫尔圆)
24
应力圆的画法：
已知某点的平面应力状态为 x , y , x
y
x面坐标 Dx（ x , x） 两点连线与
（2）单向压缩
-
单压 单拉
31
例题
例题2
§10 应力应变分析与应力应变关系
某点单元体应力状态如图，确 定该点的主应力、主方向，画 出主单元体及其上的应力，并 在应力圆上标出图示截面上的 应力，（单位： MPa ）
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
§10-9 莫尔强度理论
1
[ [
t c
] ]
3
[
t
]
rM
1
[ [
t c
] ]
3
例：填空题。
冬天自来水管冻裂而管内冰并未破裂， 其原因是冰处于 三向压 应力状态，而水管 处于 二向拉 应力状态。
例：填空题。
• 在纯剪切应力状态下：
• 用第三强度理论可得出：塑性材料的许用剪
应力与许用拉应力之比 [ ] [ ]
1 2E
121
122 E
2 3
2( 1
1 （ 2
2 2 3
3）
3 1)
2
1 E
2
（
3
）
1
3
1 E
3 （ 1 2 ）
2 1
m m
2 m 1 m
3
m
3 m
m
1
2
3
3
变形3比(1能 =2体)积改1变比能2 +形状3 改 变比m 能
u E= uv 3 +
uK f CL10TU41
2.最大伸长线应变理论（第二强度理论）
• 它假定，无论材料内各点的应变状态如何， 只要有一点的最大伸长线应变ε1达到单向拉 伸断裂时应变的极限值 εu，材料即破坏。
• 所以发生脆性断裂的条件是 ε1 ≥ εu • 若材料直到脆性断裂都是在线弹性范围内工
作，则
1
1 E
1 （ 2 3 ）
• 它假定，复杂应力状态下材料的形状改变比 能达到单向拉伸时使材料屈服的形状改变比 能时，材料即会发生屈服。
• 屈服破坏条件是： u f uu
u f
1
6E
( 1 2 ) 2 ( 2 3 ) 2 ( 3 1 ) 2
• 简单拉伸时： 1 s , 2 3 0
uu
1
四个强度理论的强度条件可写成统一形式：
r [ ]
r 称为相当应力
r1 1 r2 1 ( 2 3 ) r3 1 3
r4
1 2
( 1 2 ) 2
( 2 3 ) 2
( 3 1 ) 2
• 一般说来，在常温和静载的条件下，脆性材 料多发生脆性断裂，故通常采用第一、第二 强度理论；塑性材料多发生塑性屈服，故应 采用第三、第四强度理论。
[ ] s
n
• 第三强度条件： 1 3 [ ]
第三强度理论曾被许多塑性材料的试验结 果所证实，且稍偏于安全。这个理论所提供的 计算式比较简单，故它在工程设计中得到了广 泛的应用。该理论没有考虑中间主应力σ2的影 响，其带来的最大误差不超过15％，而在大多 数情况下远比此为小。
2.形状改变比能理论(第四强度理论)
单位体积的体积改变为:
V1 V0 V0
1 2 3
b 1
3
c
a
也称为体积应变。
CL10TU30
1
2
3
1 2
E
( 1
2
3)
3(1 2) 1 2 3 m
式当中Km：03.(51E213时1E2，EEE1113)2
1
3
（
2
K 3
）
体2 积 弹（性模3量 1）
3
3 （ 1 2 ）
,
u
u
E
b
E
• 由此导出失效条件的应力表达式为：
1 ( 2 3 ) b
[ ] b
n • 第二强度条件： 1 ( 2 3 ) [ ]
煤、石料或砼等材料在轴向压缩试验时，如 端部无摩擦，试件将沿垂直于压力的方向发生 断裂，这一方向就是最大伸长线应变的方向， 这与第二强度理论的结果相近。
§10-4 三向应力状态简介
主单元体：六个平面都是主平面
2
1 3
若三个主应力已知，求任意斜截面上的应CL力10T:U30
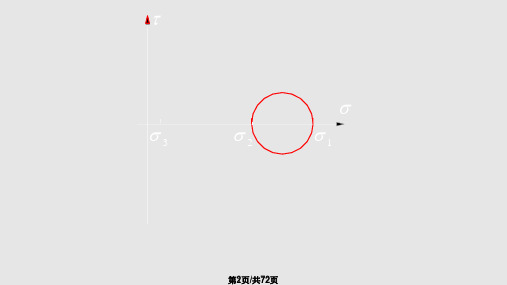
首先分析平行于主应力之一（例如σ3）的 各斜截面上的应力。
σ3 对斜截面上的应力没有影响。这些斜截 面上的应力对应于由主应力 σ1 和 σ2 所画的应 力圆圆周上各点的坐标。
2
3
3
1
1 1
3 2
3
2
3
2
1
同理，在平行于 σ2 的各个斜截面上，其 应力对应于由主应力 σ1 和 σ3 所画的应力圆圆 周上各点的坐标。
2
3
1
1
3 2
3
2
1
在平行于 σ1 的各个斜截面上，其应力对应 于由主应力 σ2 和 σ3 所画的应力圆圆周上各点 的坐标。
2
3
1
1
3 2
3
2
1
这样，单元体上与主应力之一平行的各个 斜截面上的正应力和剪应力，可由三个应力圆 圆周上各点的坐标来表示。
3 50MPa
max
1 3
2
50MPa
CL10TU33
例：求图示应力状态的主应力和最大剪应力 （应力单位为MPa）。
CL10TU34
解：
1 120 40
2
2
120 40 2 2
302
130 MPa
30
3 30MPa
max
1 3
2
80MPa
§10-5 广义胡克定律
m
m CL10TU60
解：(1)将应变片贴于与母线成45°角的外表面上
(2) 1 , 2 0, 3
1
1 E
1 ( 2
3)
max
min
1
E
1
E
m
d3
0
16
m d 3E 0 16(1 )
例：钢制封闭圆筒，在最大内压作用下测 得圆筒表面任一点的εx＝1.5×10－4。已知 E=200GPa，μ＝0.25，［σ］＝160MPa，按第 三强度理论校核圆筒的强度。
流动破坏 材料破坏的形式主要有两类：
断裂破坏
§10-8 常用的四种强度理论
材料破坏的基本形式有两种：流动、断裂 相应地，强度理论也可分为两类：
一类是关于脆性断裂的强度理论； 另一类是关于塑性屈服的强度理论。 一、关于脆断的强度理论
1.最大拉应力理论（第一强度理论） • 它假定：无论材料内各点的应力状态如何，
体的体积改变有四种答案： （A）变大 （B）变小 （C）不变 （D）不确定
1 2 3 m
K
例： 圆轴直径为d，材料的弹性模量为E， 泊松比为 μ ，为了测得轴端的力偶ｍ之值，但 只有一枚电阻片。 (1) 试设计电阻片粘贴的位置和方向； (2) 若按照你所定的位置和方向，已测得线应
变为 0，则外力偶ｍ＝？
y
x
CL10TU61
解： y 2 x
x
1 E
( x
y)
1.5 104
由上两式可求得 x 60MPa, y 120MPa
故 1 120MPa, 2 60MPa, 3 0
r3 1 3 120MPa < [ ]
故满足强度条件。
y x
作业（P182-187）
•2 • 4（b、d） • 5（b、d） • 10，11，12，14（b、c），15，17，18 • 20，23，25，30
• 用第四强度理论可得出：塑性材料的许用剪
应力与许用拉应力之比 [ ] [ ]
解：在纯剪切应力状态下，三个主应力分别为
1 , 2 0, 3
第三强度理论的强度条件为：
1 3 ( ) 2 [ ] 由此得： [ ]
2
剪切强度条件为： [ ] 按第三强度理论可求得： [ ] [ ]
例：填空题。
三向应力状态中，若三个主应力都等于σ，材
料的弹性模量和泊松比分别为E和 μ ，则三个 主
应变为
。
1
1 E
1 （ 2 3 ）
2
1 E
2 （ 3 1）
3
1 E
3 （ 1 2 ）
例：填空题。
第三强度理论和第四强度理论的相当应 力分别为σr3及σr4，对于纯剪应力状态，恒有 σr3／σr4＝＿＿＿。
3
1 E
3 （ 1 2 ）
对于二向应力状态：
1
1 E
( 1
2)
2
1 E
( 2
1 )
3 E ( 1 2 )
2 1
CL10TU30
下面考虑体积变化：
V0 a b c
V1 a(1 1) b(1 2 ) c(1 3 ) 2 a b c (1 1 2 3 )
6E
2 s2
• 屈服破坏条件是：
1
2
( 1 2 ) 2 ( 2 3 ) 2 ( 3 1 ) 2
s
• 第四强度条件：
1
2
( 1 2 ) 2 ( 2 3 ) 2 ( 3 1 ) 2
[ ]
这个理论和许多塑性材料的试验结果相符， 用这个理论判断碳素钢的屈服失效是相当准确 的。
0
§10-6 复杂应力状态下的变形比能
P
拉压变形能：
U 1 P l 1 P P l P2l
2
2 EA 2EA
变形比能：
P
l l
uU
P2l
2
1
V 2EA Al 2E 2
CL10TU40
变形比能：
u 1
2
u
1 2
1
1
1 2
2
2
1
2
3
3
2
1 3
变形比能：
u
1 2
1
1
1
2
2
2
1
2
3
3
u 1 2E
2 1
2 2
2 3
2( 1 2 2 3 3 1)