正弦型函数y=Asin(ωx+φ)的图像
函数y=Asin(ωx+φ)图像变换优质课课件

在振动控制领域,函数y=asin(ωx+φ)可以用于设计振动控制器。通过调整控制器的参数, 可以实现振动的有效抑制或放大,提高机械设备的稳定性和可靠性。
振动信号处理
在振动信号处理中,函数y=asin(ωx+φ)可以用于信号的调制和解调。通过对信号进行变换, 可以实现信号的增强、降噪和特征提取,为故障诊断和状态监测提供依据。
控制系统稳定性分析
利用函数y=asin(ωx+φ)可以分析控制系统的稳定性。通过分析系统的极点和零点分布,可以判断系统的稳定性和动态性 能,为控制系统校正和优化提供指导。
控制系统校正与优化
在控制系统设计中,函数y=asin(ωx+φ)可以用于控制系统校正与优化。通过调整控制器的参数,可以提 高系统的性能指标,如响应速度、超调和稳态误差等,使系统更好地适应实际应用需求。
ω<0的周期变换
无界周期
当ω<0时,函数y=asin(ωx+φ)的周 期是无界的,这意味着函数在x轴上的 移动是无限循环的。
波形变化
随着ω的减小,函数的波形会变得更加 平缓或尖锐,这取决于绝对值的大小。
04 振幅变换
A>1的振幅变换
总结词
当振幅系数A大于1时,函数y=asin(ωx+φ)的图像将呈现放大 的效果。
φ=0的相位变换
总结词
当相位φ等于0时,函数图像不发生平移。
详细描述
当相位φ的值等于0时,函数y=asin(ωx+φ)就变成了标准正弦函数y=asin(ωx),图 像没有发生平移。这是因为此时函数的周期性没有改变,所以图像在x轴方向上没有 移动。
03 周期变换
ω>1的周期变换
周期缩短
高中数学必修四第一章 (三)正弦型函数y=Asin(ωx+φ)的图象

人大附中分校高一数学导学学案题目 1.3.1正弦型函数y =A sin (ωx +φ)的图象课型 新授课 教材 数学B 版必修4§1.3.1学 习 要 求 1.理解振幅、周期、频率、初相的定义;2.理解振幅变换、相位变换和周期变换的规律;3.会用“五点法”画出y =A sin(ωx +φ)的简图,明确A 、ω和φ对函数图象的影响作用;重 点 难 点重点:熟练地对y =sin x 进行振幅、周期和相位变换。
难点:理解振幅变换、周期变换和相位变换的规律。
导 学 学 案一.自学课本P44~45,通过观察、考虑观缆车,得出振幅、周期、频率、初相的概念。
在函数)sin(φω+=t R y 中,点P 旋转一周所需要的时间ωπ2=T ,叫做点P 的转动周期。
在1秒内,点P 转动的周数πω21==T f ,叫做转动的频率。
0OP 与x 轴正方向的夹角φ叫做初相。
二.归纳总结:函数y =A sin(ωx +φ),其中0,0>>ωA 表示一个振动量时,A 就表示这个量振动时离开平衡位置的最大距离,通常称为这个振动的振幅; 往复一次所需的时间ωπ2=T ,称为这个振动的周期;单位时间内往复振动的次数πω21==T f ,称为振动的频率; φω+x 称为相位; 0=x 时的相位φ称为初相。
三.例题:例1.在同一坐标系中,画出函数y =2sin x x ∈R ;y =21sin x x ∈R 的图象(简图) (比较它们的振幅的大小与A 的关系)y =sin x -112ππyxO结论:一般地,函数x A y sin =的值域是[],,A A -最大值是A ,最小值是A -,由此可知,A 的大小,反映曲线x A y sin =波动幅度的大小。
因此A 也称为振幅。
函数yAsin(ωxφ)的图像与性质

图像的形状与特点
01
02
03
04
周期性
函数y=asin(ωxφ)具有周期性, 其图像呈现为一系列重复的波
形。
振幅
振幅与ω有关,ω越大,振幅 越大;反之,ω越小,振幅越
小。
相位
相位与φ有关,φ决定了波形 在水平方向上的位置。
单调性
在每个周期内,函数是单调的 ,先增后减。
参数ω和φ对图像的影响
参数ω
函数y=asin(ωxφ)表示一个正弦函数经过平移、伸 缩和旋转后的变换。其中,ω控制正弦函数的伸缩, φ控制正弦函数的平移,而asin则表示正弦函数经 过了反相变换。
φ是实数,表示正弦函数的平移量,当φ>0时,正 弦函数向右平移,当φ<0时,正弦函数向左平移。
ω是正实数,表示正弦函数的伸缩系数,当ω>1时, 正弦函数被压缩,当0<ω<1时,正弦函数被拉伸。
余弦函数
y=asin(ωxφ)的图像与标准余弦函数y=cos(x)的图像也具有相似性,同样可以 通过调整参数来改变其形状和位置。
03 函数y=asin(ωxφ)的性 质
周期性
函数y=asin(ωxφ)具有周期性,其周 期为2π/∣ω∣。这意味着函数图像将 按照一定的规律重复出现。
周期性是三角函数的重要性质之一, 它有助于我们更好地理解函数的图像 和变化规律。
在未来的应用前景
在物理学中的应用
可以应用于描述物理现象,如波动、振动等。
在工程学中的应用
可以应用于信号处理、图像处理等领域。
在金融领域的应用
可以应用于金融数据分析、股票价格预测等领域。
THANKS FOR WATCHING
感谢您的观看
正弦型函数y=Asin(ψx φ)的图象与应用

π 例 1 将函数 y=sin x 的图象上所有的点向右平行移动 个单 10 位长度,再把所得各点的横坐标伸长到原来的 2 倍(纵坐标不变), 所得图象的函数解析式是 ( C ) π π 2x- 2x- A .y=sin 10 B .y=sin 5 1 π 1 π x- x- C .y=sin 2 10 D .y=sin 2 20
6 5 D.向右平移 个长度单位 6
本节课你收获了什么?
一:函数y=Asin(ωx+φ)的图象及变换
小 结
二:由图象求函数y=Asin(ωx+φ)的解析式
三:y=函数Asin(ωx+φ)的性质应用
C
).
π A.T=6π,φ=6 π C.T=6,φ=6
π B.T=6π,φ=3 π D.T=6,φ=3
当堂检测
1.为得到函数 y cos( x ) 的图象,只需将 y 3 的图象( A ) A.向左平移 6 个长度单位 B.向右平移 6 个长度单位
sin x
C.向左平移 5 个长度单位
例2 函数f(x)=Asin(ωx+φ)(A,ω,φ为常数,A>0,ω>
6. 0)的部分图象如图所示,则f(0)的值是________ 2
【对点演练2】
1.已知简谐运动
π f(x)=Asin(ωx+φ)|φ|<2的部分图象如图所
示,则该简谐运动的最小正周期 T 和初相 φ 分别为(
【对点演练1】
1.要得到函数 y=cos (
D
π 2x+ 的图象,只需将函数 6
y=cos 2x 的图象
)
π A.向右平移 个单位 6 π C.向左平移 个单位 6
π B.向右平移 个单位 12 π D.向左平移 个单位 12
函数y=Asin(ωx+φ)的图象课件

1 2
参数ω对周期的影响 随着ω的增大,函数y=asin(ωx+φ)的周期会减 小;反之,随着ω的减小,函数的周期会增大。
参数φ对相位的影响 当φ增加时,函数图像会沿x轴向右移动;反之, 当φ减小时,图像会向左移动。
3
参数a对振幅的影响
a的大小决定了函数图像的振幅。当a增大时,图 像的振幅增大;反之,当a减小时,振幅减小。
使用数学软件绘制图像
MATLAB
MATLAB是一款强大的数学软件,可以用来绘制各种复杂的函数图像,包括函数 y=asin(ωx+φ)。使用MATLAB,用户可以自定义ω和φ的值,观察图像的变化。
Python (Matplotlib)
Matplotlib是Python的一个绘图库,也可以用来绘制函数y=asin(ωx+φ)。通过 Matplotlib,用户可以轻松地定制图像的样式和颜色。
在通信系统中,信号的传输通常会受到噪声和其他干扰的影响。利用函数 y=asin(ωx+φ)进行信号调制可以提高信号的抗干扰能力和传输质量。例如,在调 频(FM)通信中,调制信号的频率会随着声音信号的变化而变化,解调后可以得到 还原的声音信号。
04 函数y=asin(ωx+φ)的变 种形式
多参数变化的影响
函数图像的基本特征
周期性
极值点
由于正弦函数的周期性,函数 y=asin(ωx+φ)的图像也具有周期性, 周期取决于ω的取值。
函数图像在每个周期内有两个极值点, 极值点的位置和高度取决于参数ω、 φ的取值。
对称性
函数图像具有对称性,包括轴对称和 中心对称,具体对称轴和对称中心取 决于参数φ的取值。
02 函数y=asin(ωx+φ)的图 像绘制
6. 正弦型函数y=Asin(ωx+φ)的图象及应用
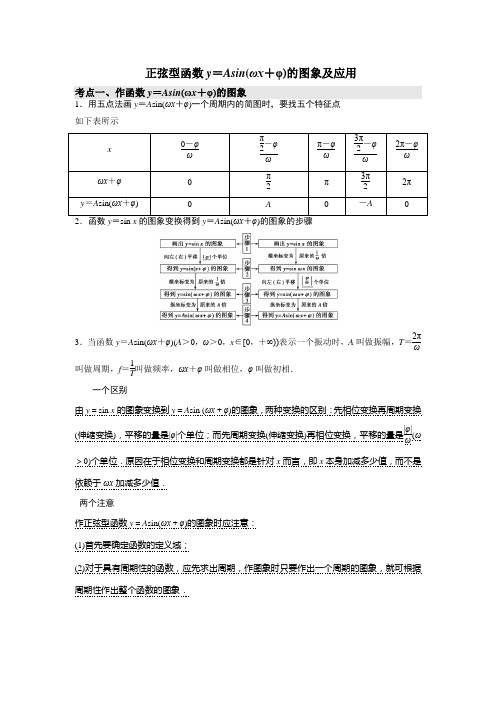
正弦型函数y =Asin (ωx +φ)的图象及应用考点一、作函数y =Asin (ωx +φ)的图象1.用五点法画y =A sin(ωx +φ)一个周期内的简图时,要找五个特征点 如下表所示x0-φω π2-φω π-φω 3π2-φω 2π-φω ωx +φ 0 π2 π 3π2 2π y =A sin(ωx +φ)A-A3.当函数y =A sin(ωx +φ)(A >0,ω>0,x ∈[0,+∞))表示一个振动时,A 叫做振幅,T =2πω叫做周期,f =1T叫做频率,ωx +φ叫做相位,φ叫做初相.一个区别由y =sin x 的图象变换到y =A sin (ωx +φ)的图象,两种变换的区别:先相位变换再周期变换(伸缩变换),平移的量是|φ|个单位;而先周期变换(伸缩变换)再相位变换,平移的量是|φ|ω(ω>0)个单位.原因在于相位变换和周期变换都是针对x 而言,即x 本身加减多少值,而不是依赖于ωx 加减多少值. 两个注意作正弦型函数y =A sin(ωx +φ)的图象时应注意: (1)首先要确定函数的定义域;(2)对于具有周期性的函数,应先求出周期,作图象时只要作出一个周期的图象,就可根据周期性作出整个函数的图象.- 2 -【例题】1. 已知函数f (x )=3sin ⎝⎛⎭⎫12x -π4,x ∈R .(1)画出函数f (x )在长度为一个周期的闭区间上的简图; (2)将函数y =sin x 的图象作怎样的变换可得到f (x )的图象?考点二、求函数y =Asin (ωx +φ)的解析式A 由最值确定;ω由周期确定;ϕ由图象上的特殊点确定,【例题】1.函数f (x )=A sin(ωx +φ)(A ,ω,φ为常数,A >0,ω>0)的部分图象如图所示,则f (0)的值是________.2.已知函数y =A sin(ωx +φ)(A >0,|φ|<π2,ω>0)的图象的一部分如图所示.(1)求f (x )的表达式;(2)试写出f (x )的对称轴方程.考点三、函数y =A sin (ωx +φ)的图象与性质的综合应用研究函数sin()y A x ωϕ=+性质的方法:类比于研究sin y x =的性质,只需将sin()y A x ωϕ=+中的x ωϕ+看成sin y x =中的x ,但在求sin()y A x ωϕ=+的单调区间时,要特别注意A 和ω的符号,通过诱导公式先将ω化正. 【例题】1.设函数f (x )=sin(ωx +φ)⎝⎛⎭⎫ω>0,-π2<φ<π2,给出以下四个论断: ①它的图象关于直线x =π12对称;②它的图象关于点⎝⎛⎭⎫π3,0对称;③它的周期为π;④在区间⎣⎡⎦⎤-π6,0上是增函数. 以其中两个论断作为条件,余下论断作为结论,写出你认为正确的两个命题: (1)________________;(2)________________.2.(1)已知函数f (x )=2sin(ωx +φ)(ω>0)的图象关于直线x =π3对称,且f ⎝⎛⎭⎫π12=0,则ω的最小值为________.(2)设ω>0,函数y =sin ⎝⎛⎭⎫ωx +π3+2的图象向右平移4π3个单位后与原图象重合, 则ω的最小值是________.(3)已知f (x )=sin ⎝⎛⎭⎫ωx +π3(ω>0),f ⎝⎛⎭⎫π6=f ⎝⎛⎭⎫π3,且f (x )在区间⎝⎛⎭⎫π6,π3有最小值,无最大值, 则ω=________.(4)已知ω>0,函数f (x )=sin ⎝⎛⎭⎫ωx +π4在⎝⎛⎭⎫π2,π上单调递减.则ω的取值范围是________. 3.(1)要得到函数cos()24x y π=-的图象,只需把函数sin 2xy =的图象向__平移____个单位. (2)将函数72sin(2)13y x π=-+图像,按向量a 平移后得到的函数图像关于原点对称,求出模最小的向量a .4.已知函数f (x )=sin 2⎝⎛⎭⎫x -π6+cos 2⎝⎛⎭⎫x -π3+sin x cos x ,x ∈R . (1)求f (x )的最大值及取得最大值时的x 的值;(2)求f (x )在[0,π]上的单调增区间.5.已知函数f (x )=sin ⎝⎛⎭⎫2x +π6-cos ⎝⎛⎭⎫2x +π3+2cos 2x . (1)求f ⎝⎛⎭⎫π12的值;(2)求f (x )的最大值及相应x 的值.考点四、三角函数模型的应用三角函数应用题与解三角形中的问题不一样,主要是构造三角函数,并利用三角函数的性质解决相关问题,多与能建立形如y =A sin(ωx +φ)+B (或y =A cos(ωx +φ)+B )等形式的函数问题有关.【例题】1.如图为一个缆车示意图,该缆车半径为4.8 m,圆上最低点与地面距离为0.8 m,60秒转动一圈,图中OA与地面垂直,以OA为始边,逆时针转动θ角到OB,设B点与地面距离是h.(1)求h与θ间的函数关系式;(2)设从OA开始转动,经过t秒后到达OB,求h与t之间的函数关系式,并求缆车到达最高点时用的时间.2.如图,某市拟在长为8 km的道路OP的一侧修建一条运动赛道,赛道的前一部分为曲线段OSM,该曲线段为函数y=A sinωx(A>0,ω>0),x∈[0,4]的图象,且图象的最高点为S(3,2);赛道的后一部分为折线段MNP.为保证参赛运动员的安全,限定∠MNP=120°.(1)求A,ω的值和M,P两点间的距离;(2)应如何设计,才能使折线段赛道MNP最长?- 4 -。
函数y=Asin(ωx φ)的图像(第二课时)课件-2022-2023学年高一上学期数学必修第一册

“第五点”为ωx+φ=2π.
函数y Asin(x )图像与性质的应用
4.对称性:利用函数y=sinx的对称中心为(k,0), k Z,函数y=sinx的对称轴为x= k(k Z),
2 (1)令x =k,k Z,解得x的解为函数
y A sin(x )对称中心的横坐标; (2)令x = k(k Z)解得x的解为函数
y
1 2
sin
x
图象上各点横坐标 伸长为原来的2倍
y 1 sin 1 x 22
1 y 1 sin x 2
2
3
4
O
x
y 1 sin 1 x
1
y sin x
22
法二:
图象上各点横坐标
y sin x 伸长为原来的2倍
y sin 1 x 图象上各点纵坐标 2 缩短为原来的一半
y 1 sin 1 x 22
2
“第五点”为ωx+φ=2π.
函数y A sin(x )图像与性质的应用
2.周期:正弦曲线、余弦曲线相邻两对称中心、相邻
两对称轴之间的距离是半个周期,相邻的对称中心与 对称轴之间的距离是 1 个周期.
4 3.奇偶性:若f(x)=Asin(ωx+φ)(A,ω≠0),则
(1)当=k(k Z)时, 函数y A sin(x )= A sin x为奇函数;
A 如图所示,则( )
A.y=2sin 2x-π6
B.y=2sin 2x-π3
x+π C.y=2sin 6
x+π D.y=2sin 3
以寻找“五点法”中的特殊点作为突破口:
“第一点”(即图象上升时与x轴的交点)为ωx+φ=0; “第二点”(即图象的最高点)为ωx+φ= ;
2
函数y=Asin(ωx φ)的图象

函数 y=sinx (>0且0) 的图象可以看作 是把 y=sinx 的图象上所有点的横坐标缩短 (当>1时)或伸长(当0< <1时)到原来的1/ 倍(纵坐标不变)而得到的.
所有的点横坐标缩短(>1)
y=sinx
或伸长(0< <1) 1/倍 纵坐标不变
y=sinx
决定函数的周期:T 2
探究: A 对函数图象的影响
D.纵坐标伸长到原来的2倍,横坐标不变.
作正弦型函数y=Asin(x+) 的图象的方法: (1)用“五点法”作图 (2)利用变换关系作图
函数y=Asin(ωx+φ)的图象 平移伸缩变化欣赏
想一想?
问题:把y=sin2x的图象经过怎样的变换就得到
y=sin(2x+ 3
)的图象?
)的图象
(横坐标不变)
y=3sin(
1 2
x
-
4
)的图象
练习2. 为了得到y=3sin(2x+π/5)的图象,只需将函数
y=3sin(x+π/5)的图象上各点的 ( B)而得到.
A.横坐标伸长到原来的2倍,纵坐标不变. B.横坐标缩短到原来的1/2倍,纵坐标不变. C.纵坐标伸长到原来的1/2倍,横坐标不变.
函数y=Asin(ωx+φ)的图象
(1)y=sinx与y=sin(x+)的图象关系; (2)y=sinx与y=sinx的图象关系; (3)y=sinx与y=Asinx的图象关系; (4)y=sinx与y=Asin(x+)的图象关系.
***复习回顾***
y sin x, x [0,2 ]的图象
关键点: (0,0),( ,1),( ,0),( 3 ,1),(2 ,0)
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
)
的定义域是__________,值域是________,周期是________,振幅是________,频率是
________,初相是_________.
7.如果函数
y=sin2x+acos2x
的图象关于直线
π x=-8
对称,那么 a=_________.
8.函数 y=sin2x 的图象向左平移
π 6
A.-sin x B.sin x C.-cos x D.cos x
解析 由图象的平移得 g(x)=cosx+2π=-sin x.
答案 A
4.设 ω>0,函数 y=sinωx+π3+2 的图象向右平移43π个单位后与原图象重合,则 ω 的最小值是( ).
2 A.3
4 B.3
3 C.2
D.3
解析 y=sinωx+π3+2 向右平移43π个单位后得到 y1=sinωx-43π+π3+2=sinωx+π3-43πω+2,又 y 与 y1 的图象
π y=4cos(2x-6
);
(2)y=f(x )是以 2π 为最小正周期的周期函数;
(3)y=f(x ) 的图象关于点(-π6 ,0)对称;
(4)y=f(x )
的图象关于确的命题序号是___________.
一、选择题:
1.函数
π y=sin(2x+6
)的图象可看成是把函数 y=sin2x 的图象做以下平移得到(
)
A.向右平移π6
B.
向左平移
π 12
C.
向右平移
π 12
D. 向左平移π6
2.函数
π y=sin(4
-2x)的单调增区间是(
)
3π 3π A. [kπ- 8 , kπ+ 8 ]
(k∈Z)
B.
π 5π [kπ+8 , kπ+ 8 ]
例题讲解
1.(人教 A 版教材习题改编)y=2sin2x-π4 的振幅、频率和初相分别为( ).
A.2,1π,-π4
B.2,21π,-π4
C.2,1π,-π8
D.2,21π,-π8
答案 A
2.已知简谐运动 f(x)=Asin(ωx+φ)|φ|<π2的部分图象如图所示,则该简谐运动的最小正周期 T 和初相 φ 分别为( ).
综上知,存在 a=32符合题意.
课上练习
一、选择题
1.为了得到函数 y=cos(x+ ),x∈R 的图象,只需把余弦曲线 y=cosx 上的所有的点 ( ) 3
(A) 向左平移 个单位长度 3
(B) 向右平移 个单位长度 3
(C) 向左平移 1 个单位长度 3
(D) 向右平移 1 个单位长度 3
(k∈Z)
π 3π C. [kπ-8 , kπ+ 8 ]
(k∈Z)
D.
3π 7π [kπ+ 8 , kπ+ 8 ]
(k∈Z)
3.函数
3π y=sin(x+ 2
)的图象是(
A. 关于 x 轴对称
C. 关于原点对称
)
B. 关于 y 轴对称
D.
关于
3 x=-2
π 对称
4.函数 f(x)=cos(3x+φ)的图像关于原点中心对称的充要条件是( )
13.已知函数 y=2sin( k x+5)周期不大于 1,求正整数 k 的最小值. 3
*14. 已知 N(2, 2 )是函数 y=Asin(ωx+φ)(A>0,ω>0)的图象的最高点,N 到相邻最低点的图象曲线与 x 轴交于 A、B,其 中 B 点的坐标(6,0),求此函数的解析表达式.
课后练习
3.当函数 y=Asin(ωx+φ)(A>0,ω>0,x∈[0,+∞))表示一个振动时,A 叫做振幅,T=2ωπ叫做周期,f=T1叫 做频率,ωx+φ 叫做相位,φ 叫做初相.
4.图象的对称性 函数 y=Asin(ωx+φ)(A>0,ω>0)的图象是轴对称也是中心对称图形,具体如下: (1)函数 y=Asin(ωx+φ)的图象关于直线 x=xk(其中 ωxk+φ=kπ+2π,k∈Z)成轴对称图形. (2)函数 y=Asin(ωx+φ)的图象关于点(xk,0)(其中 ωxk+φ=kπ,k∈Z)成中心对称图形. 一种方法 在由图象求三角函数解析式时,若最大值为 M,最小值为 m,则 A=M-2 m,k=M+2 m,ω 由周期 T 确定,即由2ωπ =T 求出,φ 由特殊点确定. 一个区别 由 y=sin x 的图象变换到 y=Asin (ωx+φ)的图象,两种变换的区别:先相位变换再周期变换(伸缩变换),平移的
基础梳理
1.用五点法画 y=Asin(ωx+φ)一个周期内的简图时,要找五个特征点
如下表所示
x
0-φ ω
π2-φ ω
ωx+φ
0
π 2
y=Asin(ωx+φ)
0
A
2.函数 y=sin x 的图象变换得到 y=Asin(ωx+φ)的图象的步骤
π-φ ω
π 0
32π-φ ω
3π 2
-A
2π-φ ω
2π 0
解决这类问题常常借助三角函数的有界性或转化为我们所熟悉的函数,如二次函数等来解决.
【试一试】 是否存在实数 a,使得函数 y=sin2x+acos x+58a-32在闭区间0,π2上的最大值是 1?若存在,求出对应
的 a 值?若不存在,试说明理由.
[尝试解答] y=-cos x-21a2+a42+58a-12,
量是|φ|个单位;而先周期变换(伸缩变换)再相位变换,平移的量是|ωφ|(ω>0)个单位.原因在于相位变换和周期变 换都是针对 x 而言,即 x 本身加减多少值,而不是依赖于 ωx 加减多少值.
两个注意
作正弦型函数 y=Asin(ωx+φ)的图象时应注意: (1)首先要确定函数的定义域; (2)对于具有周期性的函数,应先求出周期,作图象时只要作出一个周期的图象,就可根据周期性作出整个函数 的图象.
(A) f(x)=sin(3x+6)+2 (B) f(x)=sin(3x-6)-2 (C) f(x)=sin(3x+2)+2 (D) f(x)=sin(3x-2)-2
二. 填空题
7.函数 y=3sin(2x-5)的对称中心的坐标为
;
8.函数 y=cos( 2 x+ )的最小正周期是
;
34
9.函数 y=2sin(2x+ )(x∈[-π,0])的单调递减区间是
(B) y=3cos(2x+ ) (C) y=3cos(2x+ 2 ) (D) y= 1 cos( 1 x+ )
3
3
3 26
5.已知函数 y=Asin(ωx+φ)(A>0,ω>0)在同一周期内,当 x= 时,ymax=2;当 x= 7 时,,ymin=-2.那么函数的解析式为
12
12
()
(A) y=2sin(2x+ ) 3
π A. φ=2
B. φ= kπ(k∈Z)
π C. φ= kπ+2
(k∈Z)
π D. φ= 2kπ-2
(k∈Z)
5.函数
1 y=5
sin2x 图象的一条对称轴是(
π A.x= - 2
π B. x= - 4
π C. x = 8
) 5π
D. x= - 4
二、填空题:
6.函数
1 y=5
π sin(3x-3
,所得的曲线对应的函数解析式是__________.
9.要得到 y=sin2x-cos2x 的图象,只需将函数 y=sin2x+cos2x 的图象沿 x 轴向____移___________个单位.
10.关于函数
π f(x)=4sin(2x+3
)
(x∈R),有下列命题:
(1)y=f(x
)的表达式可改写为
(B) y=2sin( x - ) 26
(C) y=2sin(2x+ ) 6
(D) y=2sin(2x- ) 3
*6. 把 函 数 f(x) 的 图 象 沿 着 直 线 x+y=0 的 方 向 向 右 下 方 平 移 2 2 个 单 位 , 得 到 函 数 y=sin3x 的 图 象 , 则
()
2.函数 y=5sin(2x+θ)的图象关于 y 轴对称,则 θ=
(A) 2kπ+ (k∈Z) 6
(B) 2kπ+ π(k∈Z)
(C) kπ+ (k∈Z) 2
() (D) kπ+ π(k∈Z)
3. 函数 y=2sin(ωx+φ),|φ|< 的图象如图所示,则 2
(A) ω= 10 ,φ= 11 6
当 0≤x≤π2时,0≤cos x≤1,令 t=cos x,则 0≤t≤1,
∴y=-t-21a2+a42+58a-12,0≤t≤1.
当 0≤a2≤1,即 0≤a≤2 时,则当 t=a2,即 cos x=a2时. ymax=a42+58a-12=1,解得 a=32或 a=-4(舍去). 当a2<0,即 a<0 时,则当 t=0,即 cos x=0 时, ymax=58a-12=1,解得 a=152(舍去). 当a2>1,即 a>2 时,则当 t=1,即 cos x=1 时, ymax=a+58a-32=1,解得 a=2103(舍去).
;
6
*10.函数 y=sin2x 的图象向右平移 φ(φ>0)个单位,得到的图象恰好关于直线 x= 对称,则 φ 的最小值是
.
6
三. 解答题
11.写出函数 y=4sin2x (x∈R)的图像可以由函数 y=cosx 通过怎样的变换而得到.(至少写出两个顺序不同的变换)
