【免费下载】双因素方差分析模型
第四章双因素方差分析

ab
ab
2
(yi y)(yj y)2
(yi y)(yij yi yj y)
i1 j1
i1 j1
ab
2
(yj y)(yij yi yj y)
=0
i1 j1
=0
=0
可以验证三个的两两交叉项的累加和均为零
ab
(yiy)(yijyiyj y)
第四章 双因素方差分析
第一节 双因素无重复方差分析
一、数据描述
表4.1
B水 平
A水平 A1
A2
…
双因素无重复实验的典型数据
B1
B2
…
Bj
…
y11
y12
…
y1j
…
y21
y22
…
y2j
…
…
…
…
…
…
Ai
yi1
yi2
…
yij
…
…
…
…
…
…
…
Aa
ya1
ya2
…
yaj
…
…
y.j
y.1
y.2
y.j
…
Bb
yi.
y1b
ST
a
i1
b j1
yij2
T2 N
ab
T yij i1 j1
因素A总差分解:
ab
a
SA (yiy)2b (yiy)2
i1j1
i1
a
SAb (yi22yiyy2)
i1
a
a
a
SAb yi22by yib y2
所以 FB Fa(3,6).
(完整word版)两因素方差分析.
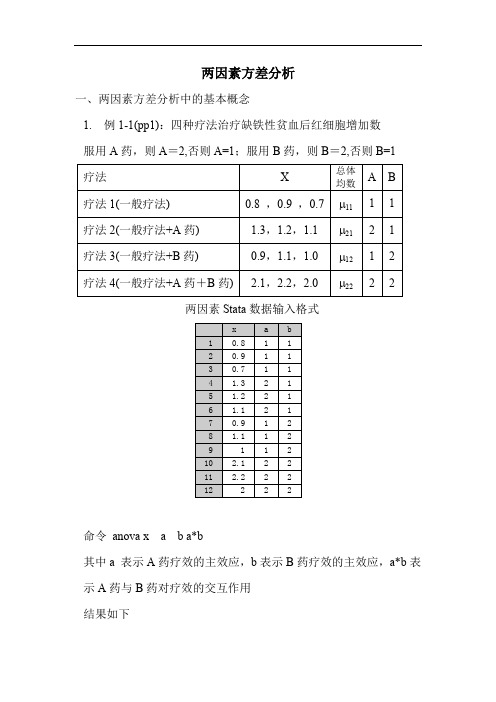
两因素方差分析一、两因素方差分析中的基本概念1. 例1-1(pp1):四种疗法治疗缺铁性贫血后红细胞增加数服用A药,则A=2,否则A=1;服用B药,则B=2,否则B=1两因素Stata数据输入格式命令anova x a b a*b其中a 表示A药疗效的主效应,b表示B药疗效的主效应,a*b表示A药与B药对疗效的交互作用结果如下结果表明:对于 =0.05而言H10:没有交互作用并且A药和B药疗效的主效应都没有差异H11:有交互作用或A药主效应有差异或B药主效应有差异F Model=98.75,P值<0.05,因此认为模型是有效的(或有交互作用或有主效应)。
H20:没有交互作用H21:有交互作用F A×B=36.75,P值=0.0003<0.05,因此A药与B药的疗效有交互作用,并且有统计意义。
H30:A药没有差异H31:A药主效应有差异F A=168.75,P值<0.05,A药的主效应有统计意义H40:B药没有差异H41:B药主效应有差异F B =90.75,P 值<0.05,B 药的主效应也有统计意义。
问题:模型是什么? 模型:..()ab a b ab μμαβαβ=+++其中μab 是x 的总体均数,αa 称为A 因素的主效应,βb 称为B 因素的主效应,(αβ)ab 称为A 因素和B 因素对因变量x(观察指标变量)的交互作用。
2. 主效应的意义A 药B 药平均A 主效应表示未服用服用 未服用 μ11μ1211121.2μμμ+=1...1μμα=+服用 μ21 μ22 21222.2μμμ+= 2...2μμα=+ 平均1121.12μμμ+= 1222.22μμμ+= 11122122..4μμμμμ+++= B 主效应 .1..1μμβ=+ .2..2μμβ=+称α1和α2为A 因素的主效应,β1和β2为B 因素的主效应。
并且可以验证:α1+α2=0(即:α1=-α2)以及β1+β2=0(β1=-β2) 若α1=α2(即α1=α2=0),则对应A 因素的主效应没有作用。
【免费下载】双因素方差分析模型

从模型1、模型2 可以看出, 在通常的教学质量评价过程中, 人们只注重对教师教学水平的点评,而对评课人的素质和水平几乎没有讨论。
但事实上, 教师教学水平的高低及提高, 与评课人的水平是密切相关的, 只有评课人与指导者水平高, 对教师教学水平的评价才有较高的可靠性, 教师的教学水平也才会得到提高。
方差分析的结论告诉我们:不但教师之间的水平有显著差异, 评课人的水平也是有显著差异的, 因而要想对被评教师做出客观公正的结论, 不能忽视评课者的素质。
请看下例:某高校评估小组(8人)对该校某教研室教师(6人) 上学期教学水平的评分成绩如表2 所示。
表2 对某教研室教师教学水平的评分教师评课人1234567818.959.088.988.958.959.159.108.9528.809.108.758.859.008.728.958.8138.889.108.758.859.008.728.958.8148.838.608.738.408.758.738.859.0258.958.938.959.058.988.928.958.9869.109.159.158.859.259.209.159.25试对教师之间的教学水平和评估人之间的水平做出你的评价。
这是一个无重复试验的双因素方差分析问题, 因素A是教师,有6个水平A1,A2,,A6;因素B是评课人,有8个水平B1,B2,,B8。
X ij(i=1,2,,6,j=1,2,,8)是因素A,B的水平的每对组合(A i,B j)做一次试验的数据, 其数学模型为检验假设H0A:α1=α2=…=α6= 0,H1A:α1,α2 ,…,α6不全为0;H0B:β1=β2=…=β7 = 0, H1B:β1,β2,…,β7不全为0。
经计算得:S T=2.21073, S A=0.98644, S B=01500 09,S E=S T-S A-S B=017242,从而得方差分析表如表3 所示。
双因素方差分析共43页文档

▪
29、勇猛、大胆和坚定的决心能够抵得上武器的精良。——达·芬奇
▪
30、意志是一个强壮的盲人,倚靠在明眼的跛子肩上。——叔本华
谢谢!
43
双因素方差分析
•
6、黄金时代是在我们的前面,而不在 我们的 后面。
•
但某些时候请收 敛。
•
9、只为成功找方法,不为失败找借口 (蹩脚 的工人 总是说 工具不 好)。
•
10、只要下定决心克服恐惧,便几乎 能克服 任何恐 惧。因 为,请 记住, 除了在 脑海中 ,恐惧 无处藏 身。-- 戴尔. 卡耐基 。
▪
26、要使整个人生都过得舒适、愉快,这是不可能的,因为人类必须具备一种能应付逆境的态度。——卢梭
▪
27、只有把抱怨环境的心情,化为上进的力量,才是成功的保证。——罗曼·罗兰
▪
28、知之者不如好之者,好之者不如乐之者。——孔子
双因素试验方差分析课件

未来将结合其他统计方法,如回归 分析、聚类分析等,以更全面地揭 示多因素对试验结果的影响。
THANKS
感谢您的观看
重复原则
在相同条件下重复进行试 验,提高试验的可靠性和 准确性。
对照原则
设置对照组,以消除非试 验因素的影响,突出试验 因素的作用。
试验的分类
STEP 02
STEP 03
多因素试验
同时考虑多个因素对试验 结果的影响。
STEP 01
双侧双因素试验
同时考虑两个因素对试验 结果的影响。
单侧双因素试验
只考虑两个因素中的一个 因素对试验结果的影响。
结果解释
根据方差分析的结果,解释各因素 对观测值的影响程度和显著性,得 出结论。
双因素试验方差分析的注意事项
数据的正态性和同方差性
样本量和试验精度
在进行方差分析之前,需要检验数据 是否符合正态分布和同方差性,以确 保分析结果的准确性。
适当增加样本量可以提高试验精度和 降低误差,对方差分析的结果产生积 极影响。
方差分析的步 骤
01
02
03
04
计算平均值和方差
计算各组的平均值和方差。
检验假设条件Βιβλιοθήκη 检查是否满足方差分析的假设 条件。
进行方差分析
使用适当的统计软件或公式进 行方差分析,并解释结果。
结论与建议
根据分析结果得出结论,并提 出相应的建议。
双因素试验方差分析
双因素试验方差分析的步骤
确定试验因素
明确试验的两个因素,并确定每个 因素的取值水平。
试验设计
根据试验目的和因素水平进行试验 设计,确保每个因素的每个水平都 被充分考虑。
数据收集
双因素方差分析

这种各个因素的不同水平的搭配所产生的新的影响 在统计上称为交互作用. 各因素间是否存在交互作用是 多因素方差分析新产生的问题.
一、无交互作用的方差分析
考虑的因素记为A的第i种效应和因素B的第j 种效应分 别记作αi , βj,试验误差记作εij,其数据结构如下:
第7.3节 双因素方差分析
一、无交互作用的方差分析 二、有交互作用的方差分析 三、利用Excel进行双因素方差分析的步骤
在许多实际问题中, 往往需要同时考察几个因素对指 标的影响,这种同时研究两个因素对试验指标影响的方 差分析,就是 双因素方差分析 (double factor analysis of variance)问题.
B1
B2
B3
A1
390 380 440 420 370 350
A2
390 410 450 430 370 380
解 由Excel软件依次单击:工具-数据分析-方差分析:可重 复双因素方差分析, 如下图
单击“确定”后,得分析结果如下:
由此可见,因素B显著,而因素A和A与B交互作用都 不显著.下面着重考察因素B.
方差来源 平方和 自由度
A B 误差 总和
Q1
r-1
Q2
s-1
Q3 (r-1)(s-1)
Q
rs-1
均方 S12 S22 S32
F值 S12/S32 S22/S32
显著性
二、有交互作用的方差分析
如果因素A 和因素B 没有交互作用, 则只需要在各 个组合水平下各做一次试验就可以进行方差分析.
但是如果因素A 和因素B 有交互作用,这时必须在 各个组合水平下做重复试验方可进行方差分析.
双因素方差分析课件
双原因无反复(无交互作用)试验资料表
原因 B 原因 A
B1
A1
X11
...
...
Aa
X a1
a
T. j X ij T.1 i 1
X. j T. j a X .1
b
B2 ... Bb Ti. X ij X i. Ti. b j 1
X12 ... X1b
T1.
X 1.
... ... ... ...
➢ 有交互作用旳双原因试验旳方差分析
有检验交互作用旳效应,则两原因A,B旳不同水 平旳搭配必须作反复试验。
处理措施:把交互作用当成一种新原因来处理,
即把每种搭配AiBj看作一种总体Xij。
基本假设(1)X ij 相互独立;
(2)Xij ~ N ij , 2 ,(方差齐性)。
线性统计模型
原因B
总平均 旳效应
53 58 48
a
T. j Xij 197 232 183 i 1
b
Ti. X ij j 1 165 143 145 159
T 612
X i. Ti. b
55.0 47.7 48.3 53.0
X. j T. j a 49.3 58.0 45.8
X 51
解 基本计算如原表
a b
双原因方差分析措施
双原因试验旳方差分析
在实际应用中,一种试验成果(试验指标)往往 受多种原因旳影响。不但这些原因会影响试验成果, 而且这些原因旳不同水平旳搭配也会影响试验成果。
例如:某些合金,当单独加入元素A或元素B时, 性能变化不大,但当同步加入元素A和B时,合金性 能旳变化就尤其明显。
统计学上把多原因不同水平搭配对试验指标旳 影响称为交互作用。交互作用在多原因旳方差分析 中,把它当成一种新原因来处理。
双因素方差分析模型
从模型1、模型2 可以看出, 在通常的教学质量评价过程中, 人们只注重对教师教学水平的点评,而对评课人的素质和水平几乎没有讨论。
但事实上, 教师教学水平的高低及提高, 与评课人的水平是密切相关的, 只有评课人与指导者水平高, 对教师教学水平的评价才有较高的可靠性, 教师的教学水平也才会得到提高。
方差分析的结论告诉我们:不但教师之间的水平有显著差异, 评课人的水平也是有显著差异的, 因而要想对被评教师做出客观公正的结论, 不能忽视评课者的素质。
请看下例:某高校评估小组(8人)对该校某教研室教师(6人) 上学期教学水平的评分成绩如表2 所示。
表2 对某教研室教师教学水平的评分试对教师之间的教学水平和评估人之间的水平做出你的评价。
这是一个无重复试验的双因素方差分析问题, 因素A是教师,有6个水平A1,A2,,A6;因素B是评课人,有8个水平B1,B2,,B8。
X ij(i=1,2,,6,j=1,2,,8)是因素A,B的水平的每对组合(A i,B j)做一次试验的数据, 其数学模型为检验假设H0A:α1=α2=…=α6= 0,H1A:α1,α2,…,α6不全为0;H0B:β1=β2=…=β7 = 0, H1B:β1,β2,…,β7不全为0。
经计算得:S T=2.21073, S A=0.98644, S B=01500 09,S E=S T-S A-S B=017242,从而得方差分析表如表3 所示。
取α=0.05,有F A(r-1,(r-1)(s-1))=F0.05(5,35)=2.30F A(s-1,(r-1)(s-1))=F0.05(7,35)=2.14由于F A=10.89529 > 2.30=F0.05(5,35),F B=4.14248 > 2.14=F0.05(7,35) ,因此以95% 的置信度可以认为教师之间的教学水平有显著差异, 同时评课小组成员之间的水平也有显著差异。
由于评课小组成员之间的水平有显著差异, 因此可以讨论如何定量地去比较他们水平的高低。
双因素方差分析
三、双因素方差分析
在上述误差平方和的基础上计算均方,也就是将各平方和除 以相应的自由度。与各误差平方和相对应的自由度分别为:
SST的自由度为kr-1,SSR的自由度为k-1,SSC的自由度 为r-1,SSE的自由度为(k-1)(r-1)。
为构造检验统计量,需要计算下列各均方: ①行因素的均方,记为MSR。 ②列因素的均方,记为MSC。 ③随机误差的均方,记为MSE。
三、双因素方差分析
二、 无交互作用的双因素方差分析
1. 数据结构
在无交互作用的双因素方差分析中,由于有两个 因素,因而在获取数据时,需要将一个因素安排在“ 行”的位置,称为行因素;另一个因素安排在“列” 的位置,称为列因素。设行因素有k个水平,列因素 有r个水平,行因素和列因素的每一个水平都可以搭配 成一组,观察它们对试验指标的影响,共抽取kr个观 察数据,其数据结构见表7-8。
三、双因素方差分析
“全因子”单选按钮为系统默认项,用 来建立全模型。全模型中包括因素之间的交 互作用。如果选择分析两个因素的交互作用 ,则必须在每种水平组合下取得两个以上的 试验数据,才能实现两个因素的交互作用的 分析。如果不考虑因素间的交互作用,则应 当选择自定义模型。
三、双因素方差分析
“设定”单选按钮用来自定义模型,本例选择此项并激活下面的各项操 作,如图7-12所示。
三、双因素方差分析
2. 分析步骤
与单因素方差分析类似,双因素方差分析也包括提出假设、构造检验 统计量和决策分析等步骤。
(1)提出假设。
为了检验两个因素的影响,需要对两个因素分别提出如下假设:
①对行因素提出假设。
H0∶μ1=μ2=…=μk=μ
行因素(自变量)对因变量没有显著影响
双因素重复试验方差分析
S I /((r 1)( s 1)) 从而有FB ~ F ((r 1)( s 1), rs (l 1)) Se /(rs(l 1))
对给定的显著性水平 ,拒绝域分别为
WA {FA : FA F ((r 1), rs(l 1))} WB {FB : FB F (( s 1), rs(l 1))} WI {FI : FI F ((r 1)( s 1), rs(l 1))}
行面和-平方-和-均值
列面和-平方-和-均值
纵向和-平方-和-均值 总平方和
1 R xijk l i 1 j 1 k 1
r s l
2 W xijk i 1 j 1 k 1 r s l
2
可以证明:
S A QA P S B QB P
r
s
l
l ( X ij X i X j X ) 2
i 1 j 1
r
ST [( X ijk X ij ) ( X i X ) ( X j X )
i 1 j 1 k 1
r
s
l
( X ij X i X j X )]2
第k次试验的结果列表如下:
B1 A1 A2 Ar
B2
Bs X 1sk X 2 sk X rsk
X 11k X 12 k X 21k X 22 k X r 1k X r 2 k
假设 X ijk ~N ( ij , 2 ), i 1,, r , j 1,, s, k 1,, t .
(3)
S A /(r 1) 从而有FA ~ F (r 1, rs(l 1)) Se /(rs(l 1)) S 2 当H 02成立时, B ~ ( s 1).且S B与Se相互独立 2
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
从模型1、模型2 可以看出, 在通常的教学质量评价过程中, 人们只注重对教师教学水平的点评,而对评课人的素质和水平几乎没有讨论。
但事实上, 教师教学水平的高低及提高, 与评课人的水平是密切相关的, 只有评课人与指导者水平高, 对教师教学水平的评价才有较高的可靠性, 教师的教学水平也才会得到提高。
方差分析的结论告诉我们:不但教师之间的水平有显著差异, 评课人的水平也
是有显著差异的, 因而要想对被评教师做出客观公正的结论, 不能忽视评课者的素质。
请看下例:某高校评估小组(8人)对该校某教研室教师(6人) 上学期教学水平的评分成绩如表2 所示。
表2 对某教研室教师教学水平的评分
教师
评课人
12345678
18.959.088.988.958.959.159.108.95
28.809.108.758.859.008.728.958.81
38.889.108.758.859.008.728.958.81
48.838.608.738.408.758.738.859.02
58.958.938.959.058.988.928.958.98
69.109.159.158.859.259.209.159.25
试对教师之间的教学水平和评估人之间的水平做出你的评价。
这是一个无重复试验的双因素方差分析问题, 因素A是教师,有6个水平A1,A2,,A6;因素B是评课人,有8个水平B1,B2,,B8。
X ij(i=1,2,,6,j=
1,2,,8)是因素A,B的水平的每对组合(A i,B j)做一次试验的数据, 其数学模型为
检验假设
H0A:α1=α2=…=α6= 0,H1A:α1,α2 ,…,α6不全为0;
H0B:β1=β2=…=β7 = 0, H1B:β1,β2,…,β7不全为0。
经计算得:
S T=2.21073, S A=0.98644, S B=01500 09,S E=S T-S A-S B=017242,从而得方差分析表如表3 所示。
取α=0.05,有
F A(r-1,(r-1)(s-1))=F0.05(5,35)=2.30
F A(s-1,(r-1)(s-1))=F0.05(7,35)=2.14
由于F A=10.89529 > 2.30=F0.05(5,35),
F B=4.14248 > 2.14=F0.05(7,35) ,
因此以95% 的置信度可以认为教师之间的教学水平有显著差异, 同时评课小组成员之间的水平也有显著差异。
由于评课小组成员之间的水平有显著差异, 因此可以讨论如何定量地去比较他们水平的高低。
表3 方差分析表
方差来源平方和自由度均方和 F 值
因素A S A=0.98644r-1=5S A=S A/5=0.16441F A=S A/S E=10.89529因素B S B=0.50009s-1=7S A=S B/7=0.01509F B=S B/S E=4.14248误差S E=0.7242(r-1)(s-1)=35S E=S E/35=07242
总和S T=2.21073rs-1=34
X*j为第j个成员对每位教师评分的平均值, 显然不能根据它的大小来度量该成员水平的高低。
考虑到X ij=X i*的含义(第j个成员对第i名
教师评分与所有成员对第i 名教师评分的平均值之差),用
来评价第j名评课人水平的高低是合适的,
δj越小水平越高, δj越大水平则越低对于本例计算D j如表4 所示。
表4 评课人的水平排名
结论: 第1名评课人水平最高,第4名评课人水平最低
评课人δj水平排名
10.0107191
20.0976036
30.0236792
40.4430798
50.0690194
60.0926995
70.0458793
80.1069397附录:
双因素方差分析法计算过程。
