圆的切线测试题
初三圆的切线试题及答案

初三圆的切线试题及答案
一、选择题
1. 下列说法正确的是()
A. 圆的切线垂直于过切点的半径
B. 圆的切线与过切点的半径垂直
C. 圆的切线与过切点的直径垂直
D. 圆的切线与过切点的弦垂直
答案:B
2. 经过圆外一点作圆的切线,下列说法正确的是()
A. 只能作一条
B. 能作两条
C. 能作无数条
D. 不能作
答案:B
二、填空题
3. 已知圆的半径为5,圆心到切线的距离为3,则切线的长度为______。
答案:4√2
4. 圆的直径为10,切线与直径的夹角为30°,则切线的长度为______。
答案:5√3
三、解答题
5. 已知圆O的半径为2,点A在圆外,OA=4,求经过点A的圆O的切
线长。
答案:首先,连接OA,设切点为B。
由题意知,OA=4,OB=2。
在直角
三角形OAB中,根据勾股定理,AB²=OA²-OB²=4²-2²=12,所以
AB=2√3。
由于切线与半径垂直,所以切线长为2√3。
6. 圆的半径为3,圆心到切线的距离为2,求切线与圆心的夹角。
答案:设切线与圆心的夹角为θ,根据切线的性质,圆心到切线的距
离等于半径乘以sinθ,即2=3sinθ。
解得sinθ=2/3。
由于θ在0°到90°之间,所以θ=arcsin(2/3)。
中考压轴题圆的切线证明与计算(中考真题)
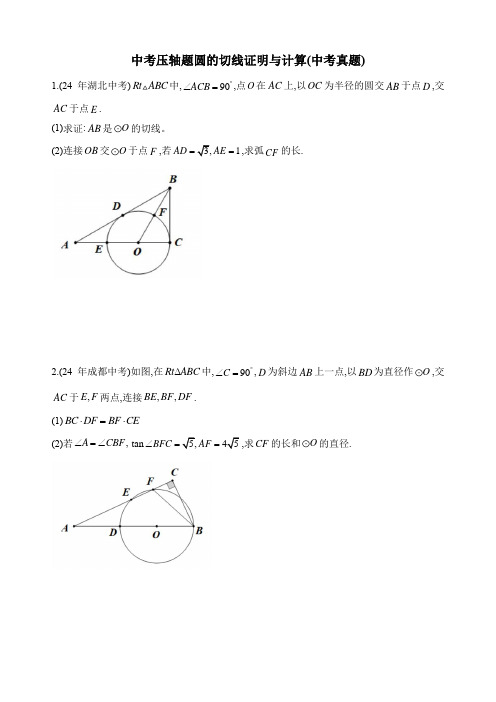
中考压轴题圆的切线证明与计算(中考真题)1.(24年湖北中考)Rt ABC 中,90ACB ︒∠=,点O 在AC 上,以OC 为半径的圆交AB 于点D ,交AC 于点E .(1)求证:AB 是O 的切线。
(2)连接OB 交O 于点F ,若1AD AE ==,求弧CF 的长.2.(24年成都中考)如图,在Rt ABC ∆中,90C ︒∠=,D 为斜边AB 上一点,以BD 为直径作O ,交AC 于,E F 两点,连接,,BE BF DF .(1)BC DF BF CE ⋅=⋅(2)若,A CBF ∠=∠tan BFC AF ∠==,求CF 的长和O 的直径.3.(24年浙江中考)如图,在圆内接四边形ABCD中,AD<AC,ADC BAD∠<∠,延长AD至点E,使AE=AC,延长BA至点F,连结EF,使AFE ADC∠=∠.(1)若60O∠的度数.∠=,CD为直径,求ABDAFE(2)求证:①EF∥BC ②EF=BD.4.(24年辽宁中考)如图,O是ABC的外接圆,AB是O的直径,点D在BC上,AC BD=,E ∠=∠.在BA的延长线上,CEA CAD(1)如图1,求证:CE是O的切线OA=,求BD的长.(2)如图2,若2CEA DAB∠=∠,85.(24年安徽中考)如图,O 是ABC ∆的外接圆,D 是直径AB 上一点,ACD ∠的平分线交AB 于点E ,交O 于另一点,.F FA FE =(1)求证:;CD AB ⊥(2)设FM AB ⊥,垂足为M ,若1OM OE ==,求AC 的长.6.(24年新疆中考)如图,在O 中,AB 是O 的直径,弦CD 交AB 于点E,AD BD =.(1)求证:△ACD ∽△ECB.(2)若AC=3,BC=1,求CE 的长.7.(24年江西中考)如图,AB 是半圆O 的直径,点D 是弦AC 延长线上一点,连接BD BC ,,60D ABC ∠=∠=︒.(1)求证:BD 是半圆O 的切线.(2)当3BC =时,求AC 的长.8.(24年呼伦贝尔中考)如图,在ABC 中,以AB 为直径的O 交BC 于点,D DE AC ⊥,垂足为E . O 的两条弦,FB FD 相交于点,F DAE BFD ∠∠=.(1)求证:DE 是O 的切线;(2)若30,C CD ∠=︒=,求扇形OBD 的面积.9.(24年扬州中考)在综合实践活动中,“特殊到一般”是一种常用方法,我们可以先研究特殊情况,猜想结论,然后再研究一般情况,证明结论.如图,已知ABC ,CA CB =, O 是ABC 的外接圆,点D 在O 上(AD BD >),连接AD ,BD ,CD .【特殊化感知】(1)如图1,若60ACB ∠=︒,点D 在AO 延长线上,则AD BD -与CD 的数量关系为________【一般化探究】(2)如图2,若60ACB ∠=︒,点C ,D 在AB 同侧,判断AD BD -与CD 的数量关系并说明理由【拓展性延伸】(3)若ACB α∠=,直接写出AD ,BD ,CD 满足的数量关系.(用含α的式子表示)10.(24年赤峰中考)如图,ABC中,90ACB∠=︒,AC BC=,O经过B,C两点,与斜边AB交于点E,连接CO并延长交AB于点M,交O于点D,过点E作EF CD∥,交AC于点F.(1)求证:EF是O的切线;(2)若BM=,1tan2BCD∠=,求OM的长.11.(24年绥化中考)如图1,O是正方形ABCD对角线上一点,以O为圆心,OC长为半径的O 与AD相切于点E,与AC相交于点F.(1)求证:AB与O相切.(2)若正方形ABCD1,求O的半径.(3)如图2,在(2)的条件下,若点M是半径OC上的一个动点,过点M作MN OC⊥交CE于点N.当:1:4CM FM=时,求CN的长.12.(24年河北中考)已知O的半径为3,弦MN=ABC中.∠=︒==在平面上,先将ABC和O按图1位置摆放(点B与点N重90,3,ABC AB BC合,点A在O上,点C在O内),随后移动ABC,使点B在弦MN上移动,点A始终在O上=.随之移动,设BN x(1)当点B与点N重合时,求劣弧AN的长.(2)当OA MN∥时,如图2,求点B到OA的距离,并求此时x的值.(3)设点O到BC的距离为d.①当点A在劣弧MN上,且过点A的切线与AC垂直时,求d的值.①直接写出d的最小值.13.(24年滨州中考)【教材呈现】现行人教版九年级下册数学教材85页“拓广探索”第14题: 如图,在锐角ABC 中,探究sin a A ,sin b B ,sin c C之间的关系.(提示:分别作AB 和BC 边上的高.)【得出结论】sin sin sin a b c A B C==. 【基础应用】在ABC 中,75B ∠=︒,45C ∠=︒,2BC =,利用以上结论求AB 的长;【推广证明】进一步研究发现,sin sin sin a b c A B C==不仅在锐角三角形中成立,在任意三角形中均成立,并且还满足2sin sin sin a b c R A B C===(R 为ABC 外接圆的半径). 请利用图1证明:2sin sin sin a b c R A B C ===.【拓展应用】如图2,四边形ABCD 中,2AB =,3BC =,4CD =,90B C ∠=∠=︒.求过A,B,D 三点的圆的半径.14.(24年苏州中考)如图,ABC 中,AB =为AB 中点,BAC BCD ∠=∠cos ADC ∠=. O 是ACD 的外接圆.(1)求BC 的长(2)求O 的半径.15.(24年乐山中考)如图,O 是ABC 的外接圆,AB 为直径,过点C 作O 的切线CD 交BA 延长线于点D,点E 为CB 上一点,且AC CE =.(1)求证:DC AE ∥;(2)若EF 垂直平分OB ,3DA =,求阴影部分的面积.16.(24年武汉中考)如图,ABC ∆为等腰三角形,O 是底边BC 的中点,腰AC 与半圆O 相切于点D ,底边BC 与半圆O 交于E ,F 两点.(1)求证:AB 与半圆O 相切(2)连接OA .若4CD =,2CF =,求sin OAC ∠的值.17.(24年甘肃武威中考)如图,AB 是O 的直径,BC BD =,点E 在AD 的延长线上,且ADC AEB ∠=∠.(1)求证:BE 是O 的切线;(2)当O 的半径为2,3BC =时,求tan AEB ∠的值.18.(24年深圳中考)如图,在ABD △中,AB BD =,O 为ABD △的外接圆,BE 为O 的切线,AC 为O 的直径,连接DC 并延长交BE 于点E .(1)求证:DE BE ⊥(2)若AB =5BE =,求O 的半径.19.(24年盐城中考)如图,点C 在以AB 为直径的O 上,过点C 作O 的切线l,过点A 作AD l ⊥,垂足为D,连接AC BC 、.(1)求证:ABC ACD △△∽;(2)若5AC =,4CD =,求O 的半径.20.(24年广西中考)如图,已知O 是ABC ∆的外接圆,AB AC =.点D,E 分别是BC ,AC 的中点,连接DE 并延长至点F,使DE EF =,连接AF .(1)求证:四边形ABDF 是平行四边形(2)求证:AF 与O 相切(3)若3tan 4BAC ∠=,12BC =,求O 的半径. 21.(24年四川广安中考)如图,点C 在以AB 为直径的O 上,点D 在BA 的延长线上,DCA CBA ∠=∠.(1)求证:DC 是O 的切线;(2)点G 是半径OB 上的点,过点G 作OB 的垂线与BC 交于点F ,与DC 的延长线交于点E ,若4sin 5D =,2DA FG ==,求CE 的长.22.(24年四川南充中考)如图,在O 中,AB 是直径,AE 是弦,点F 是AE 上一点,AF BE =,,AE BF 交于点C,点D 为BF 延长线上一点,且CAD CDA ∠=∠.(1)求证:AD 是O 的切线.(2)若4,BE AD ==求O 的半径长.23.(24年四川泸州中考)如图,ABC ∆是O 的内接三角形,AB 是O 的直径,过点B 作O 的切线与AC 的延长线交于点D,点E 在O 上,AC CE =,CE 交AB 于点F .(1)求证:CAE D ∠=∠;(2)过点C 作CG AB ⊥于点G,若3OA =,BD =求FG 的长.24.(24年四川德阳中考)已知O 的半径为5,B C 、是O 上两定点,点A 是O 上一动点,且60,BAC BAC ∠=︒∠的平分线交O 于点D .(1)证明:点D 为BC 上一定点;(2)过点D 作BC 的平行线交AB 的延长线于点F .①判断DF 与O 的位置关系,并说明理由;①若ABC 为锐角三角形,求DF 的取值范围.25.(24年四川宜宾中考)如图,ABC 内接于O ,10AB AC ==,过点A 作AE BC ∥,交O 的直径BD 的延长线于点E,连接CD .(1)求证:AE 是O 的切线;(2)若1tan 2ABE ∠=,求CD 和DE 的长.26.(24年内蒙古通辽中考)如图,ABC 中,90ACB ∠=︒,点O 为AC 边上一点,以点O 为圆心,OC 为半径作圆与AB 相切于点D ,连接CD .(1)求证:2ABC ACD ∠=∠;(2)若8AC =,6BC =,求O 的半径.27.(24年四川达州中考)如图,BD 是O 的直径.四边形ABCD 内接于O .连接AC ,且AB AC =,以AD 为边作DAF ACD ∠=∠交BD 的延长线于点F .(1)求证:AF 是O 的切线;(2)过点A 作AE BD ⊥交BD 于点E .若3CD DE =,求cos ABC ∠的值.28.(24年四川遂宁中考)如图,AB 是O 的直径,AC 是一条弦,点D 是AC 的中点,DN AB ⊥于点E ,交AC 于点F ,连结DB 交AC 于点G .(1)求证:AF DF =;(2)延长GD 至点M ,使DM DG =,连接AM .①求证:AM 是O 的切线;①若6DG =,5DF =,求O 的半径.29.(24年包头中考)如图,AB 是O 的直径,,BC BD 是O 的两条弦,点C 与点D 在AB 的两侧,E 是OB 上一点(OE BE >),连接,OC CE ,且2BOC BCE ∠=∠.(1)如图1,若1BE =,CE =求O 的半径;(2)如图2,若2BD OE =,求证:BD OC ∥.(请用两种证法解答)30.(24年四川自贡中考)在Rt ABC △中,90C ∠=︒,O 是ABC 的内切圆,切点分别为D,E,F .(1)图1中三组相等的线段分别是CE CF =,AF =________,BD =________;若3AC =,4BC =,则O 半径长为________;(2)如图2,延长AC 到点M,使AM AB =,过点M 作MN AB ⊥于点N .求证:MN 是O 的切线.31.(24年山东枣庄中考)如图,在四边形ABCD 中,AD BC ∥,60DAB ∠=︒,22AB BC AD ===. 以点A 为圆心,以AD 为半径作DE 交AB 于点E ,以点B 为圆心,以BE 为半径作EF 所交BC 于点F ,连接FD 交EF 于另一点G ,连接CG .(1)求证:CG 为EF 所在圆的切线(2)求图中阴影部分面积.(结果保留π)32.(24年青海中考) 如图,直线AB经过点C,且OA OB=.=,CA CB(1)求证:直线AB是O的切线;(2)若圆的半径为4,30∠=︒,求阴影部分的面积.B中考压轴题圆的切线证明与计算答案1.(24年湖北中考)【答案】(1)略 (2)弧CF 的长为3π2.(24年成都中考)【答案】(1)略(2)CF =;O 的直径为3.(24年浙江中考)【答案】(1)30o (2)证明略4.(24年辽宁中考)【答案】(1)见详解 (2)2π5.(24年安徽中考)【答案】(1)略 (2).6.(24年新疆中考)【答案】(1) 略 (2)CE =.7.(24年江西中考)【答案】(1)见解析 (2)2π8.(24年呼伦贝尔中考)【答案】(1)略 (2)43π 9.(24年扬州中考)【答案】(1)AD BD CD -=.(2)AD BD CD -=(3)当D 在BC 上时,2sin 2CD AD BD α⋅=-.当D 在AB 上时,2sin 2CD AD BD α⋅=+10.(24年赤峰中考)【答案】(1)略 (2)OM =11.(24年绥化中考)【答案】(1)证明略 (2)12.(24年河北中考)【答案】(1)π (2)点B 到OA 的距离为2;3 (3)①3d =2313.(24年滨州中考)【答案】教材呈现:见解析;基础应用:AB =;推广证明:见解析;拓展应用:6R =.14.(24年苏州中考)【答案】(1)4BC = (2)O 的半径为715.(24年乐山中考)【答案】(1)略 (2)3π-16.(24年武汉中考)【答案】(1)略 (2)4517.(24年甘肃武威中考)【答案】(1)略 (2)tan 3AEB ∠=18.(24年深圳中考)【答案】(1)略 (2)19.(24年盐城中考)【答案】(1)略 (2)25620.(24年广西中考)【答案】(1)略 (2)略 (3)1021.(24年四川广安中考)【答案】(1)略 (2)1422.(24年四川南充中考)【答案】(1)略 (2)23.(24年四川泸州中考)【答案】(1)证明略 (2)45 24.(24年四川德阳中考)【答案】(1)证明略(2)①DF 与O 相切,理由见解析;①DF 的取值范围为2DF <<25.(24年四川宜宾中考)【答案】(1)略 (2)CD =DE =. 26.(24年内蒙古通辽中考)【答案】(1)证明略 (2)327.(24年四川达州中考)【答案】(1)证明略 28.(24年四川遂宁中考)【答案】(1)证明略 (2)①证明略,①O 的半径为203. 29.(24年包头中考)【答案】(1)3 (2)略30.(24年四川自贡中考)【答案】(1)AD ;BE ;1 (2)略31.(24年山东枣庄中考)【答案】(1)略 3π32.(24年青海中考) 【答案】(1)详见解析 (2) 83S π=阴影。
圆的切线的性质和判定-练习题-含答案.doc

D.不能确定的切线的性质与判定副标题 题号 * 总分 得分一、选择题(本大题共2小题,共6.0分)1.己知半径为5的圆,其圆心到直线的距离是3,此时直线和圆的位置关系为() A.相离 B.相切 C.相交 D.无法确定【答案】C 【解析】解:半径r = 5,圆心到直线的距离d=3,v 5 > 3, BPr > d,二直线和圆相交,故选C.由直线和圆的位置关系:r>d,可知:直线和圆相交.本题考查了直线和圆的位置关系,判断的依据是半径和直线到圆心的距离的大小关系: 设。
的半径为厂,圆心。
到直线/的距离为丈 ①直线/和0。
相交②直线 /和。
相切od=r ;③直线/和。
0相离^d>r.2. 在中,zC= 90°, BC=3cm, AC=4cm,以点 C 为圆心,以2.5cm 为半径画圆,则。
C 与直线AB 的位置关系是() A,相交 B.相切 C.相离 【答案】A 【解析】解:过C 作CD LAB 于。
,如图所示: A ABC 中,L.C — 90, AC= 4, BC = 3, ・・・AB =、泌=5,7 A ABC^Jm=^-ACxBC=预8x CD, 2 2・•. 3 X 4 = 5 CD ,CD= 2.4<2.5, 即』< r, .••以2.5为半径的。
C 与直线AB 的关系是相交; 故选A.过C 作CD LAB 于C,根据勾股定理求出AB,根据三角形的面积公式求出CD,得出 d<r,根据直线和圆的位置关系即可得出结论.本题考查了直线和圆的位置关系,用到的知识点是勾股定理,三角形的面积公式;解此 题的关键是能正确作出辅助线,并进一步求出CO 的长,注意:直线和圆的位置关系有: 相离,相切,相交.二、填空题(本大题共3小题,共9.0分)3, 如图,已知。
是MBC 的内切圆,切点为。
、E 、 尸,如果AE=2, CD= 1, BF= 3,则内切圆的半 径『= .BD【答案】1【解析】解:・.・。
圆的切线练习题

圆的切线练习题一、选择题1. 已知圆的半径为5,点P到圆心的距离为10,则点P与圆的位置关系是()。
A. 点P在圆内B. 点P在圆上C. 点P在圆外2. 圆的切线与圆相切于点A,若切线与圆心的距离为6,则圆的半径是()。
A. 3B. 6C. 12D. 9二、填空题1. 若圆的半径为r,点P到圆心的距离为d,当d等于r时,点P与圆的位置关系是________。
2. 已知圆的切线在圆上与点A相切,若切线与圆心的距离为d,圆的半径为r,则切线与圆心的距离d等于________。
三、计算题1. 已知圆的半径为7,圆上一点A的坐标为(3,4),求过点A的圆的切线方程。
2. 圆心坐标为(0,0),半径为5,求过点(3,3)的圆的切线方程。
四、证明题1. 证明:圆的切线垂直于经过切点的半径。
2. 证明:若两圆相切于点A,且两圆的半径分别为r1和r2,点P在两圆的公共切线上,且PA=PB,则PA=PB=r1+r2。
五、应用题1. 一个圆的半径为10,圆心在原点(0,0),求过点(6,8)的圆的切线方程。
2. 已知两圆外切,圆心分别为O1(-3,0)和O2(3,0),半径分别为5和3,求两圆的公共切线方程。
六、综合题1. 在平面直角坐标系中,圆C的圆心在(1,2),半径为3。
点A的坐标为(4,0),求过点A的圆C的切线方程。
2. 圆心在(2,3)的圆与x轴相切,求圆的半径,并求出切点坐标。
七、探索题1. 探索:若圆的半径为定值,当圆上一点到圆心的距离逐渐增大时,过该点的圆的切线数量会如何变化?2. 探索:若两圆相切,且已知一圆的半径和两圆心的距离,如何求另一圆的半径?八、开放性问题1. 若圆的切线与圆心构成一个直角三角形,求切线的长度与圆的半径之间的关系。
2. 设想一个实际问题,其中涉及到圆的切线,并尝试构建一个数学模型来解决这个问题。
请注意,以上题目仅为示例,具体题目应根据实际教学大纲和学生水平进行适当调整。
初三圆的切线试题及答案

初三圆的切线试题及答案一、选择题1. 圆的切线与圆相切于一点,该点称为切点。
圆的切线有以下哪个特征?A. 切线与半径垂直B. 切线与直径平行C. 切线与切点的半径垂直D. 切线与圆心的距离等于半径答案:C2. 已知圆的半径为5,点A到圆心的距离为7,那么点A到圆的切线距离是多少?A. 2B. 3C. 4D. 5答案:A二、填空题1. 圆的切线与圆相切于______,并且切线与该点的半径垂直。
答案:切点2. 如果圆的半径为r,点P到圆心的距离为d,当d > r时,点P到圆的切线距离为d - r;当d < r时,点P到圆的切线距离为______。
答案:r - d三、解答题1. 如图,圆O的半径为3,点P在圆O上,PA是圆O的切线,PA垂直于OP,求PA的长度。
解:由于PA是圆O的切线,根据切线的性质,我们知道PA与OP 垂直,且PA的长度等于OP的长度减去半径的长度。
因此,PA的长度为OP - 3。
由于OP是半径,所以OP = 3。
代入公式得PA = 3 - 3 = 0。
但这个结果显然是错误的,因为PA不可能为0。
这里需要重新审视题目,如果题目没有错误,那么可能是题目本身存在问题。
2. 已知圆的半径为5,点A在圆上,点B在圆外,AB是圆的切线,且AB垂直于过圆心的直线l,求点B到圆心O的距离。
解:由于AB是圆的切线,且AB垂直于过圆心的直线l,我们可以知道OA = 5(半径),并且由于AB垂直于l,根据勾股定理,我们可以计算出OB的长度。
设OB = x,那么根据勾股定理,我们有:\[ x^2 = OA^2 + AB^2 \]由于AB垂直于OA,所以AB的长度等于OA的长度,即AB = 5。
代入公式得:\[ x^2 = 5^2 + 5^2 = 50 \]解得x = √50 ≈ 7.07。
结束语:通过上述试题,我们可以看到圆的切线问题涉及到切线的性质、勾股定理以及几何图形的构造。
解决这类问题需要对圆的性质有深入的理解,并且能够灵活运用几何知识。
中考数学专项练习圆的切线长定理(含解析)

中考数学专项练习圆的切线长定理(含解析)一、单选题1.如图,△ABC是一张周长为17cm的三角形的纸片,BC=5cm,⊙O 是它的内切圆,小明预备用剪刀在⊙O的右侧沿着与⊙O相切的任意一条直线MN剪下△AMN,则剪下的三角形的周长为()A.12cm B.7cm C.6cm D.随直线MN的变化而变化2.下列说法正确的是()A.过任意一点总能够作圆的两条切线 B.圆的切线长确实是圆的切线的长度C.过圆外一点所画的圆的两条切线长相等 D.过圆外一点所画的圆的切线长一定大于圆的半径3.如图,PA,PB切⊙O于A,B两点,CD切⊙O于点E,交PA,PB 于C,D.若⊙O的半径为1,△PCD的周长等于2 ,则线段AB的长是()A.B.3C. 2D. 34.如图,圆和四边形ABCD的四条边都相切,且AB=16,CD=10,则四边形ABCD的周长为()A.5B.52C.54D.565.如图,PA,PB,CD与⊙O相切于点为A,B,E,若PA=7,则△P CD的周长为()A.7B.14C.10.5D.106.如图,PA,PB切⊙O于点A,B,PA=8,CD切⊙O于点E,交PA,PB 于C,D两点,则△PCD的周长是()A.8B.18C.16D.147.如图,四边形ABCD中,AD平行BC,∠ABC=90°,AD=2,AB= 6,以AB为直径的半⊙O 切CD于点E,F为弧BE上一动点,过F点的直线MN为半⊙O的切线,MN交BC于M,交CD于N,则△MCN的周长为()A.9B.1C. 3D. 28.圆外切等腰梯形的一腰长是8,则那个等腰梯形的上底与下底长的和为()A.4B.8C.12D.169.如图,△ABC是一张三角形的纸片,⊙O是它的内切圆,点D是其中的一个切点,已知AD=10cm ,小明预备用剪刀沿着与⊙O相切的任意一条直线MN剪下一块三角形(△AMN),则剪下的△AMN的周长为()A.20cmB.15cmC.10cm D.随直线MN的变化而变化二、填空题10.如图,PA、PB是⊙O的两条切线,A、B是切点,若∠APB=60°,PO=2,则⊙O的半径等于________.11.PA、PB分别切⊙O于点A、B,若PA=3cm,那么PB=________cm.12.如图,一圆内切于四边形ABCD,且AB=16,CD=10,则四边形A BCD的周长为________.13.如图,小明同学测量一个光盘的直径,他只有一把直尺和一块三角板,他将直尺、光盘和三角板如图放置于桌面上,并量出AB=3cm,则此光盘的直径是________cm.14.如图,PA,PB是⊙O的两条切线,切点分别是A、B,PA=10,CD 是⊙O的切线,交PA于点C,交PB于点D,则△PCD的周长是________.15.如图,AB,AC,BD是⊙O的切线,P,C,D为切点,假如AB=5,AC=3,则BD的长为________.16.如图,一圆外切四边形ABCD,且AB=16,CD=10,则四边形的周长为________.答案解析部分一、单选题1.【答案】B【考点】切线长定理【解析】【解答】解:设E、F分别是⊙O的切点,∵△ABC是一张三角形的纸片,AB+BC+AC=17cm,⊙O是它的内切圆,点D是其中的一个切点,BC=5cm,∴BD+CE=BC=5cm,则AD+AE=7cm,故DM=MF,FN=EN,AD=AE,∴AM+AN+MN=AD+AE=7(cm).故选:B.【分析】利用切线长定理得出BC=BD+EC,DM=MF,FN=EN,AD=AE,进而得出答案.2.【答案】C【考点】切线长定理【解析】【解答】解:A、过圆外任意一点总能够作圆的两条切线,过圆上一点只能做圆的一条切线,过圆内一点不能做圆的切线;故A错误,不符合题意;B、圆的切线长确实是,过圆外一点引圆的一条切线,这点到切点之间的线段的长度确实是圆的切线长;故B错误,不符合题意;C、依照切线长定理:过圆外一点所画的圆的两条切线长相等;故C是正确的符合题意;D、过圆外一点所画的圆的切线长取决于点离圆的距离等,故不一定大于圆的半径;故D错误,不符合题意;故答案为:C。
圆的切线训练题1

圆的切线训练题11.如图,四边形ABCD内接于⊙O,BD是⊙O的直径,AE⊥CD,垂足为E,DA平分∠BDE.①求证:AE是⊙O的切线;②若∠DBC=300,DE=1cm,求BD的长;③AE=4,BD=10,求CD的长度2.如图,AB为⊙O的直径,PD切⊙O于点C,与BA的延长线交于点D,DE⊥PO交PO延长线于点E,连接PB,∠EDB=∠EPB.①求证:PB是⊙O的切线.②若PB=3,DB=4,求DE的长3.已知,如图,AB为⊙O的直径,PD切⊙O于点C,与AB的延长线交于点D,DE⊥PO交PO延长线于点E,连接PA,且∠EDB=∠EPA.①求证:PA是⊙O的切线;②若PA=6,DA=8,求⊙O的半径4.在Rt△ABC中,∠ACB=90°,D是AB边上一点,以BD做为直径作⊙O交AC于点E,连接DE并延长交BC的延长线于点F,且BD=BF.①求证:AC与⊙O相切;②若BC=6,AD=4,求⊙O的面积5.已知:如图,AB是⊙O的直径,C是⊙O上一点,OD⊥BC于点D,过点C作⊙O的切线,交OD的延长线于点E,连接BE.①求证:BE与⊙O相切;②连接AD并延长交BE于点F,若OB=9,sin∠ABC=2/3,求BF的长6.如图,在Rt△ABC中,∠C=900,AC=12,BC=16.∠BAC的平分线AD交BC于D,经过A、D两点的⊙O交AB于E,且点O在AB上.①求证:BC是⊙O的切线;②求AF的长7.如图,在Rt△ABC中,∠C=90°,∠BAC的平分线AD交BC于点D,点E是AB上一点,以AE为直径的⊙O过点D,且交AC于点F.①求证:BC是⊙O的切线;②若CD=6,AC=8,求AE8.如图,在△ABC中,∠C=90°,∠BAC的平分线AD交BC于D,过点D作DE⊥AD交AB于E,以AE为直径作⊙O.①求证:点D在⊙O上;②求证:BC是⊙O的切线;③若AC=6,BC=8,求△BDE的面积9.如图,在Rt△ABC中,∠B=90°,∠BAC的平分线交BC于点D,E为AB上的一点,DE=DC,以D为圆心,DB 长为半径作⊙D,AB=10,EB=6.①求证:AC是⊙D的切线;②求线段AC的长10.如图,点P是⊙O外一点,PA为⊙O的切线,A为切点,直线PO交⊙O于点E、F,弦AB⊥PF,垂足为D,延长BO交⊙O于点C,连接AC,BF.①求证:PB与⊙O相切;②若AC=12,tan∠F=1/2,求⊙O的直径圆的切线训练题1答案1.分析:(1)连接OA,根据角之间的互余关系可得∠OAE=∠DEA=900,故AE⊥OA,即AE是⊙O的切线;(2)根据圆周角定理,可得在Rt△AED中,∠AED=900,∠EAD=300,有AD=2DE;在Rt△ABD中,∠BAD=900,∠ABD =300,有BD=2AD=4DE,即可得出答案;(3)先利用三个角是直角的四边形是矩形,得出OF=AE=4,再用勾股定理求出DF即可得出CD.解:(1)证明:连接OA,∵DA平分∠BDE,∴∠BDA=∠EDA.∵OA=OD,∴∠ODA=∠OAD,∴∠OAD=∠EDA,∴OA∥CE.∵AE⊥CE,∴AE⊥OA.∴AE是⊙O的切线.(2)解:∵BD是直径,∴∠BCD=∠BAD=900.∵∠DBC=300,∠BDC=600,∴∠BDE=1200.∵DA平分∠BDE,∴∠BDA=∠EDA=600.∴∠ABD=∠EAD=300.∵在Rt△AED中,∠AED=900,∠EAD=300,∴AD=2DE.∵在Rt△ABD中,∠BAD=900,∠ABD=300,∴BD=2AD=4DE.∵DE的长是1cm,∴BD的长是4cm.(3)解:如图2,连接OA,过O点作OF垂直CD于F,∴∠OFE=900,CD=2DF,∵AE 是⊙O的切线.∴∠OAE=900,∵AE⊥CD,∴∠AED=900,∴∠OFE=∠OAE=∠AED=900,∴四边形OAEF是矩形,∴OF=AE=4,在Rt△ODF中,OD=BD=5,∴DF==3,∴CD=2DF=6.2.分析:(1)由已知角相等,及对顶角相等得到三角形DOE与三角形POB相似,利用相似三角形对应角相等得到∠OBP为直角,即可得证;(2)在直角三角形PBD中,由PB与DB的长,利用勾股定理求出PD的长,由切线长定理得到PC=PB,由PD﹣PC求出CD的长,在直角三角形OCD中,设OC=r,则有OD=8﹣r,利用勾股定理列出关于r的方程,求出方程的解得到r的值,然后通过相似三角形的性质即可得到结论.解:(1)证明:∵在△DEO和△PBO中,∠EDB=∠EPB,∠DOE=∠POB,∴∠OBP=∠E=90°,∵OB为圆的半径,∴PB为圆O的切线;(2)解:在Rt△PBD中,PB=3,DB=4,根据勾股定理得:PD==5,∵PD与PB 都为圆的切线,∴PC=PB=3,∴DC=PD﹣PC=5﹣3=2,在Rt△CDO中,设OC=r,则有DO=4﹣r,根据勾股定理得:(4﹣r)2=r2+22,解得:r=,∴OP==,∵∠E=∠PBO,∠DPE=∠OPB,∴△DEP∽△OBP,∴,∴DE=3.分析:(1)欲证明PA是⊙O的切线,只需推知∠PAD=90°即可;通过相似三角形△APO~△EDO的对应角相等证得结论即可;(2)在直角△PAD中,由PA与DA的长,利用勾股定理求出PD的长,由切线长定理得到PC=PA,由PD﹣PC求出CD的长,在直角△OCD中,设OC=r,则有OD=8﹣r,利用勾股定理列出关于r的方程,求出方程的解得到r的值,即为圆的半径.解:(1)证明:∵∠EDB=∠EPA,DE⊥PO,∴∠EDO=∠APO,∠DEO=90°.又∵∠POA=∠DOE,∴△APO~△EDO,∴∠PAO=∠DEO=90°.又∵OA是半径,∴PA是⊙O的切线;(2)解:在Rt△PAD中,若PA=6,DA=8,根据勾股定理得:PD==10,∵PD与PA都为圆的切线,∴PC=PA=6,∴DC=PD﹣PC=10﹣6=4,在Rt△CDO中,设OC=r,则有DO=8﹣r,根据勾股定理得:(8﹣r)2=r2+42,解得:r=3,则圆的半径为3.4.分析:(1)连接OE,求出OE∥BF推出∠AEO=90°,根据切线的判定推出即可;(2)证△AOE∽△ABC,得出关于r的方程,求出方程的解即可.解:证明(1)连接OE,∵OD=OE,∴∠ODE=∠OED,∵BD=BF,∴∠ODF=∠F,∴∠OED=∠F,∴OE∥BF,∴∠AEO=∠ACB=90°,∴AC与⊙O相切;(2)解:∵由(1)可知,∠AEO=∠ACB,又∠A=∠A,∴△AOE∽△ABC,∴=,设⊙O的半径为r,则=,解得r=4(负数舍去),∴⊙O的面积为π×42=16π.5.分析:(1)连接OC,先证明△OCE≌△OBE,得出EB⊥OB,从而可证得结论.(2)过点D作DH⊥AB,根据sin ∠ABC=,可求出OD=6,OH=4,HB=5,然后由△ADH∽△AFB,利用相似三角形的性质得出比例式即可解出BF的长.解:证明:(1)连接OC,∵OD⊥BC,∴∠COE=∠BOE,在△OCE和△OBE中,∵,∴△OCE≌△OBE,∴∠OBE=∠OCE=90°,即OB⊥BE,∵OB是⊙O半径,∴BE与⊙O相切.(2)过点D作DH⊥AB,连接AD又∵sin∠ABC 并延长交BE于点F,∵∠DOH=∠BOD,∠DHO=∠BDO=90°,∴△ODH∽△OBD,∴==.=,OB=9,∴OD=6,易得∠ABC=∠ODH,∴sin∠ODH=,即=,∴OH=4,∴DH==2,又∵△ADH∽△AFB,∴=,=,∴FB=.6.分析:(1)连OD,先证明OD∥AC,再证明OD⊥DC.(2)过D点作DG⊥AB于G点.在直角三角形BDG中利用勾股定理求出CD.作OM⊥AF于M,在直角三角形OAM中利用勾股定理求出OA,则可求出AM,而AF=2AM.解:(1)证明:连接OD,∵OA=OD,∴∠OAD=∠ODA.∵AD平分∠BAC,∴∠OAD=∠CAD.∴OD∥AC.∵∠C=90°,∴OD⊥BC于D.∴BC是⊙O的切线.(2)解:过D作DG⊥AB于G,∴DG=DC,AG=AC.设DC=x,则BD =16﹣x,BG=8,∴82+x2=(16﹣x)2,∴x=6.设半径为r,则(12﹣r)2+62=r2,∴r=7.5.∴EG=3.连接DE,DF,易证△DGE≌△DCF,∴CF=3,∴AF=9.(2)证法2:(如图)连OD,OF,作OM⊥AF于M;设DC=x,(x的求法同于前面)∴x=6;∵OM⊥AF,OD⊥BC,则MC=OD=R,OM=DC=6,AM=12﹣R,∴R2=(12﹣R)2+62,∴R=7.5,∴AM=12﹣7.5=4.5,∴AF=2AM=9.证法3:(如图)连EF,与OD交于H点,设DC=x,∴x=6,(求法同前);在Rt△BOD中,BO=20﹣R,OD=R,BD=10;∴(20﹣R)2=R2+102,∴R=7.5,∴AE=15;∵EF =2FH=2CD=12,在Rt△EAF中,AF2=AE2﹣EF2=152﹣122=81,∴AF=9.证法4,(如图)连EF;设DC=x,∴x=6,(求法同前)∴EF=2FH=2CD=12;∵S△BEF+S梯形EFCB=S△ABC,,∴AF=9.7.分析:(1)连接OD,根据平行线判定推出OD∥AC,推出OD⊥BC,根据切线的判定推出即可;(2)求出AD,连接DE,证△DCA∽△EDA,得出比例式,代入求出即可.解:(1)证明:连接OD,∵OA=OD,∴∠OAD=∠ODA,∵AD平分∠BAC,∴∠BAD=∠CAD,∴∠ODA=∠CAD,∴OD∥AC,∵∠C=90°,∴∠ODC=90°,∴OD⊥BC,∵OD为半径,∴BC是⊙O切线;(2)解:在Rt△ADC中,AC=8,CD=6,由勾股定理得:AD=10.连接DE,∵AE为直径,∴∠EDA=∠C=90°,∵∠CAD=∠EAD,∴△DCA∽△EDA,∴=,∴=,AE=12.5.8.分析:(1)连接OD,由DO为直角三角形斜边上的中线,得到OD=OA=OE,可得出点D在圆O上;(2)由AD 为角平分线,得到一对角相等,再由OD=OA,利用等边对等角得到一对角相等,等量代换得到一对内错角相等,利用内错角相等两直线平行得到OD与AC平行,根据两直线平行同位角相等即可得到∠ODB为直角,即BC与OD 垂直,即可确定出BC为圆O的切线;(3)过E作EH垂直于BC,由OD与AC平行,得到△ACB与△ODB相似,设OD=OA=OE=x,表示出OB,由相似得比例列出关于x的方程,求出方程的解得到x的值,确定出OD与BE的长,进而确定出BD的长,再由△BEH与△ODB相似,由相似得比例求出EH的长,△BED以BD为底,EH为高,求出面积即可.解:(1)证明:连接OD,∵△ADE是直角三角形,OA=OE,∴OD=OA=OE,∴点D在⊙O上;(2)证明:∵AD 是∠BAC的角平分线,∴∠CAD=∠DAB,∵OD=OA,∴∠OAD=∠ODA,∴∠CAD=∠ODA,∴AC∥OD,∴∠C=∠ODB=90°,∴BC是⊙O的切线;(3)解:在Rt△ACB中,AC=6,BC=8,∴根据勾股定理得:AB=10,设OD=OA=OE=x,则OB=10﹣x,∵AC∥OD,△ACB∽△ODB,∴==,∴=,解得:x=,∴OD=,BE=10﹣2x=10﹣=,∵=,即=,∴BD=5,过E作EH⊥BD,∵EH∥OD,∴△BEH ∽△BOD,∴=,∴EH=,∴S△BDE=BD•EH=.9.分析:(1)过点D作DF⊥AC于F,求出BD=DF(半径),即可得出AC是⊙D的切线.(2)先证明△BDE≌△DCF (HL),根据全等三角形对应边相等及切线的性质的AB=AF,得出AB+EB=AC即可.解:(1)证明:过点D作DF⊥AC于F;如图所示:∵AB为⊙D的切线,∴∠B=90°,∴AB⊥BC,∵AD平分∠BAC,DF⊥AC∴BD=DF,∴AC是⊙D的切线;(2)解:在Rt△BDE和Rt△DCF中,,∴Rt△BDE≌Rt△DCF(HL),∴EB=FC.∵AB=AF,∴AB+EB=AF+FC,即AB+EB=AC,∴AC=10+6=16.10.分析:(1)证明:连接OA,由弦AB⊥PF,AD=BD,得到PA=PB,根据三角形全等得到∠PAO=∠PBO.由于PA为⊙O的切线,得到∠PAO=90°,即可得到结果;(2)根据三角形的中位线的性质得到OD=AC=6,由tan∠F=,设BD=x,则DF=2x,OB=OF=DF﹣OD=6,在R t△BOD中,由勾股定理列方程即可得到结论.解:(1)证明:连接OA,∵弦AB⊥PF,AD=BD,∴PA=PB,在△APO和△BPO中,,∴△APO≌△BPO(SSS),∴∠PAO=∠PBO.∵PA为⊙O的切线,∴∠PAO=90°.∴∠PBO=90°∴PB与⊙O相切;(2)∵AD=BD,BO=CO,∴OD=AC=6,∵tan∠F=,∴设BD=x,则DF=2x,AB=2x,在R t△BOD中,OB2=BD2+OD2,∴(2x﹣6)2=x2+62,解得:x=8,∴OB=10,∴⊙O的直径是2BO=2×10=20.。
初三数学 圆的切线长定理测试题

初三数学检测(2)满分:100班级__________ 姓名__________ 考号___________一、填空题(每题5分)1.如图,PA切⊙O于点A,若∠APO=30°,OP=2,则⊙O半径是_________ 2.一个点到圆的最大距离为11cm,最小距离为5cm,则圆的半径为______3. 点O是△ABC的内心,∠BOC为130°,则∠A的度数为________4. 正五边形的一个中心角的度数是________5. 如图,已知∠AOB=30°,M为OB边上任意一点,以M为圆心,•2cm•为半径作⊙M,•当OM=______cm时,⊙M与OA相切.6. 如图,⊙O内切于△ABC,切点为D,E,F.已知∠B=50°,∠C=60°,•连结OE,OF,DE,DF,那么∠EDF等于_________7. AB是⊙O的弦,∠AOB=80°则弦AB所对的圆周角是__________8. 已知:如图,AB为⊙O直径,BC交⊙O于点D,DE⊥AC于E,要使DE是⊙O的切线,•那么图中的角应满足的条件为_______(只需填一个条件)9.一个三角形的三边长分别为3cm,4cm,4cm,其内切圆半径为0.5cm,则这个三角形的面积为____________10.如图,AB、AC分别与⊙O相切于B、C,∠A=50°,点P是圆上异于B,C的动点,则∠BPC的度数是_______11.在Rt△ABC中,∠C=90°,AC=3,AB=5,则它的内切圆与外接圆半径分别为________12.ΔABC中,AB=6,BC=8,AC=12,⊙O与ΔABC三边AB,BC,CA分别切于D、E、,F,则AD=13. 如图,已知⊙O 的半径为5cm ,两弦AB、CD相交于AB的中点E,且AB=8cm,CE:ED=4:9,则圆心到弦CD的距离为________.14如图,⊙O的直径为10弦AB=8,P是弦AB上的一个动点,那么OP长的取值范围是.15. 如图1,PA,PB切⊙O于A,B,点 C、E分别在PA、PB上,且CE切⊙O于D,若PA=5cm ,则ΔPCE周长为;·ABCDEOA BO16. 如图,CD 切⊙O 于B ,CO 的延长线交⊙O 于A , 若∠C=36°,则∠ABD 的度数是___________ 三、解答题(每题10分)17.如图4,ΔABC 中,AB=AC ,以AB 为直径作⊙O 交BC 于D ,DE ⊥AC 于E 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
圆的切线测试题一、选择题1. 如图,AB 是⊙O 的弦,AO 的延长线交过点B 的⊙O 的切线于点C ,如果∠ABO =20°,则∠C 的度数是( ) A . 70° B .50° C .45° D .20°2. 如图,圆形铁片与直角三角尺、直尺紧靠在一起平放在桌面上.已知铁片的圆心 为O ,三角尺的直角顶点C 落在直尺的10cm 处,铁片与直尺的唯一公共点A 落在直尺的14cm 处,铁片与三角尺的唯一公共点为B ,下列说法错误的是( ) A . 圆形铁片的半径是4cm B . 四边形AOBC 为正方形 C . 弧AB 的长度为4πcm D . 扇形OAB 的面积是4πcm 23.如图,PA 和PB 是⊙O 的切线,点A 和B 的切点,AC 是⊙O 的直径,已知∠P =40°,则∠ACB 的大小是( ) A . 40° B . 60° C .70° D .80°4. 如图,在⊙O 中,AB 为直径,BC 为弦,CD 为切线,连接OC .若∠BCD =50°,则∠AOC 的度数为( ) A . 40° B .50° C .80° D .100°5. 如图,点P 在⊙O 外,PA 、PB 分别与⊙O 相切于A 、B 两点,∠P =50°,则∠AOB 等于( ) A . 150° B .130° C .155° D .135°6. 如图,AC ,BE 是⊙O 的直径,弦AD 与BE 交于点F ,下列三角形中,外心不是点O 的是( ) A .△ABE B .△ACF C .△ABD D .△ADE7.如图,△ABC 中,AB =5,BC =3,AC =4,以点C 为圆心的圆与AB 相切,则⊙C 的半径为( )A . 2.3B . 2.4C .2.5D . 2.6 8.如图,∠O =30°,C 为OB 上一点,且OC =6,以点C 为圆心,半径为3的圆与OA 的位置关系是( ) A . 相离 B . 相交 C . 相切 D . 以上三种情况均有可能第1题图 第2题图 第3题图 第4题图第5题图 第6题图 第7题图第8题图9.如图,两个同心圆,大圆的半径为5,小圆的半径为3,若大圆的弦AB 与小圆有公共点,则弦AB 的取值范围是( ) A . 8≤AB ≤10 B . 8<AB ≤10 C . 4≤AB ≤5 D . 4<AB ≤510. 如图,在矩形ABCD 中,AB =4,AD =5,AD ,AB ,BC 分别与⊙O 相切于E ,F ,G 三点,过点D 作⊙O 的切线BC 于点M ,切点为N ,则DM 的长为( ) A .B .C .D . 2二、填空题 11. 如图,AB 是⊙O 的直径,过B 点作⊙O 的切线,交弦AE 的延长线于点C ,作AC OD ⊥,垂足为D ,若︒=∠60ACB ,4=BC , 则DE 的长为 .12.如图,在矩形ABCD 中,AB =8,AD =12,过点A ,D 两点的⊙O 与BC 边相切于点E ,则⊙O 的半径为13.在Rt △ABC 中,∠C =90°,BC =3,AC =4,点P 在以C 为圆心,5为半径的圆上,连结PA ,PB 。
若PB =4,则PA 的长为14.已知,如图,过⊙O 外一点P 作⊙O 的两条切线PA 、PB,切点分别为A 、B.下列结论中:①OP 垂直平分AB ;②∠BOP =∠APB ;③△ACP ≌△BCP ;④若∠APB =800,则∠ABO =400;⑤PA=AB .正确的有 (只填正确答案的序号) 三、解答题15. 如图,已知在△ABC 中,∠A =90°(1)请用圆规和直尺作出⊙P ,使圆心P 在AC 边上,且与AB ,BC 两边都相切(保留作图痕迹,不写作法和证明). (2)若∠B =60°,AB =3,求⊙P 的面积.16. 已知△ABC 内接于⊙O ,过点A 作直线EF .(1)如图①所示,若AB 为⊙O 的直径,要使EF 成为⊙O 的切线,还需要添加的一个条件是(至少说出两种):__________或者___________; (2)如图②所示,如果AB 是不过圆心O 的弦,且∠CAE =∠B ,那么EF 是⊙O 的切线吗?试证明你的判断.PAB OC 第14题OACBDE第11题图 第9题图 第10题图 第12题图17. 如图 ,以线段AB 为直径作⊙O ,CD 与⊙O 相切于点E , 交AB 的延长线于点D , 连接BE ,过点O 作OC ∥BE 交切线DE 于点C ,连接AC .(1)求证:AC 是⊙O 的切线 ; (2)若BD =OB =4 ,求弦AE 的长.18. 如图,已知BC 是⊙O 的直径,AC 切⊙O 于点C ,AB 交⊙O 于点D ,E 为AC 的中点,连结DE .(1)若AD =DB ,OC =5,求切线AC 的长; (2)求证:ED 是⊙O 的切线.19. ⊙O 为△ABC 的外接圆,请仅用无刻度的直尺,根据下列条件分别在图1,图2中画出一条弦,使这条弦将△ABC 分成面积相等的两部分(保留作图痕迹,不写作法). (1) 如图1,AC=BC ;(2) 如图2,直线l 与⊙O 相切于点P ,且l ∥BC .l图2图1PAO OCBBCA20. 如图,在△ABC 中,BA =BC ,以AB 为直径的⊙O 分别交AC 、BC 于点D 、E ,BC 的延长线于⊙O 的切线AF 交于点F . (1)求证:∠ABC =2∠CAF ;(2)若AC =210,CE :EB =1:4,求CE 的长.21. 如图,在Rt ABC ∆中,90ABC ∠=︒,AC 的垂直平分线分别与AC ,BC 及AB 的延长线相交于点D ,E ,F ,且BF BC =.⊙O 是BEF ∆的外接圆,EBF ∠的平分线交EF 于点G , 交⊙O 于点H ,连接BD ,FH . (1)求证:ABC EBF ∆≅∆; (2)试判断BD 与⊙O 的位置关系,并说明理由.22. 已知如图,以Rt △ABC 的AC 边为直径作⊙O 交斜边AB 于点E , 连接EO 并延长交BC 的延长线于点D ,点F 为BC 的中点,连接EF . (1)求证:EF 是⊙O 的切线; (2)若⊙O 的半径为3,∠EAC =60°,求AD 的长.23. 如图,在△ACE 中,CA =CE ,∠CAE =30°,⊙O 经过点C ,且圆的直径AB 在线段AE 上.(1)试说明CE 是⊙O 的切线;(2)若△ACE 中AE 边上的高为h ,试用含h 的代数式表示⊙O 的直径AB ;(3)设点D 是线段AC 上任意一点(不含端点),连接OD ,当CD +OD 的最小值为6时,求⊙O 的直径AB 的长.DE FO A C B GHOE D A FCB圆的切线测试题参考答案一、选择题 题号 1 2 3 4 5 6 7 8 9 10 答案BDCCBBBCAA二、填空题 11. 3 12.25413. 3或73 14. ①③④ 三、解答题 15. 解:(1)如图所示,则⊙P 为所求作的圆. (2)∵∠B =60°,BP 平分∠ABC ,∴∠ABP =30°, ∵tan ∠ABP =,∴AP =,∴S ⊙P =3π.16. 解:(1)①∠BAE =90°,②∠EAC =∠ABC , 理由是:①∵∠BAE =90°,∴AE ⊥AB , ∵AB 是直径,∴EF 是⊙O 的切线; ②∵AB 是直径,∴∠ACB =90°, ∴∠ABC +∠BAC =90°,∵∠EAC =∠ABC ,∴∠BAE =∠BAC +∠EAC =∠BAC +∠ABC =90°,即AE ⊥AB ,∵AB 是直径,∴EF 是⊙O 的切线;(2)EF 是⊙O 的切线.证明:作直径AM ,连接CM ,则∠ACM =90°,∠M =∠B ,∴∠M +∠CAM =∠B +∠CAM =90°, ∵∠CAE =∠B ,∴∠CAM +∠CAE =90°,∴AE ⊥AM ,∵AM 为直径,∴EF 是⊙O 的切线.17. (1)证明:连接OE ,∵CD 与圆O 相切,∴OE ⊥CD ,∴∠CEO =90°, ∵BE ∥OC ,∴∠AOC =∠OBE ,∠COE =∠OEB ,∵OB =OE ,∴∠OBE =∠OEB ,∴∠AOC =∠COE ,在△AOC 和△EOC 中,,∴△AOC ≌△EOC (SAS ),∴∠CAO =∠CEO =90°,则AC 与圆O 相切; (2)在Rt △DEO 中,BD =OB ,∴BE =OD =OB =4,∵OB =OE ,∴△BOE 为等边三角形,∴∠ABE =60°,∵AB 为圆O 的直径,∴∠AEB =90°,∴AE =BE •tan 60°=4.18. (1)连接CD ,∵BC 是⊙O 的直径, ∴∠BDC =90°,即CD ⊥AB ,∵AD =DB ∴AC =BC =2OC =10. (2)连接OD , ∵∠ADC =90°,E 为AC 的中点, ∴DE =EC =AC , ∴∠1=∠2,∵OD =OC , ∠3=∠4,∵AC 切⊙O 于点C ,∴AC ⊥OC .∴∠1+∠3=∠2+∠4,即DE ⊥OD ,∴DE 是⊙O 的切线. 19. 解:(1)如右图所示.图1,∵AC =BC ,∴AC BC ∴点C 是AB 的中点,连接CO ,lEDAO OA交AB 于点E ,由垂径定理知,点E 是AB 的中点,延长CE 交⊙O 于点D , 则CD 为所求作的弦;(2)图2,∵l 切⊙O 于点P , 作射线PO ,交BC 于点E ,则PO ⊥l , ∵l ∥BC , ∴PO ⊥BC , 由垂径定理知,点E 是BC 的中点,连接AE 交⊙O 于F ,则AF 为所求作的弦. 20. (1)略;(2)如图,连接AE ,∴∠AEB =90°,设CE =x , ∵CE :EB =1:4,∴EB =4x ,BA =BC =5x ,AE =3x , 在Rt △ACE 中,,即,∴x =2.∴CE =2.21. 解:(1)由已知条件易得,DCE EFB ∠=∠,ABF EBF ∠=∠,又BC BF =,∴ABC EBF ∆≅∆(ASA );(2)BD 与⊙O 相切。
