动力学复习题1-2 lq解析
2020版高考物理大一轮复习练习:牛顿第二定律两类动力学问题Word版含解析

基础课2牛顿第二定律两类动力学问题一、选择题(1〜5题为单项选择题,6〜9题为多项选择题)1. (2017苏州高三检测)关于力学单位制的说法中正确的是()A. kg、m/s、N是导出单位B. kg、m、J是基本单位C. 在国际单位制中,质量的基本单位是kg,也可以是gD. 只有在国际单位制中,牛顿第二定律的表达式才是 F = ma解析kg是质量的单位,它是基本单位,所以A错误;国际单位制规定了七个基本物理量。
分别为长度、质量、时间、热力学温度、电流、发光强度、物质的量。
它们在国际单位制中的单位称为基本单位,J是导出单位,B错误;g也是质量的单位,但它不是质量在国际单位制中的基本单位,所以C错误;牛顿第二定律的表达式F二ma,是在其中的物理量都取国际单位制中的单位时得出的,所以D正确。
答案D2. (2017自贡市月考)如图1所示,两轻质弹簧a、b悬挂一小铁球处于平衡状态,a弹簧与竖直方向成30°角,b弹簧水平,a、b两弹簧的劲度系数分别为匕、k2,重力加速度为g,则()A • a b两弹簧的伸长量之比为k;B. a、b两弹簧的伸长量之比为瓷图1C. 若弹簧b的左端松脱,贝U松脱瞬间小球的加速度为D. 若弹簧b的左端松脱,贝U松脱瞬间小球的加速度为解析设弹簧a、b的弹力分别为T a、T b,将弹簧a的弹力沿水平和竖直方向分解,则T a cos 30=mg, T a s in 30 =T a,结合胡克定律可求得a、b两弹簧的伸长量之比为~ki,结合牛顿第二定律可求得弹簧b的左端松脱瞬间小球的加速度为3-yg,选项B正确,A、C、D错误。
答案B3. 一物体沿倾角为a的斜面下滑时,恰好做匀速直线运动,若物体以某一初速度冲上斜面,则上滑时物体加速度大小为()A. gsin aB. gtan aC. 2gsin aD. 2gtan a解析对物体下滑时进行受力分析,如图甲。
由于恰好做匀速直线运动,根据平衡知识得:mgsin a f物体以某一初速度冲上斜面,对物体受力分析,如图乙物体的合力F 合=mgsin a+ f = 2mgsin aF合根据牛顿第二定律得:a = ~m a 2gsin a故选C答案C4. 如图2所示,质量为4 kg的物体A静止在竖直的轻弹簧上面。
动力学力的分析与计算练习题与解析

动力学力的分析与计算练习题与解析动力学是物理学的一个重要分支,主要研究物体在受力作用下的运动规律。
力是物体发生运动的原因,因此对于动力学中力的分析与计算是非常重要的。
下面将给出一些动力学力的分析与计算练习题,同时给出详细解析。
题目一:一个质量为2kg的物体沿着x轴正方向受到一个5N的恒力作用,已知物体的初始速度为2m/s,求物体在3秒后的速度。
解析:根据牛顿第二定律可以知道,物体在受力作用下的加速度与作用力成正比,与物体的质量成反比。
所以可以使用以下公式求解:F = m * a其中F为作用力,m为物体质量,a为物体加速度。
根据题意可知,作用力F为5N,物体质量m为2kg。
代入公式可以得到:5 = 2 * a解得加速度a为2.5 m/s²。
再根据运动学中的相关公式可以求得物体的速度。
v = u + a * t其中v为物体的速度,u为物体的初始速度,a为物体的加速度,t 为时间。
代入数据得到:v = 2 + 2.5 * 3 = 9.5 m/s答案为9.5m/s。
题目二:一个质量为3kg的物体受到一个20N的恒力作用,物体的初始速度为4m/s,求物体在5秒后的速度。
解析:同样根据牛顿第二定律可以得到:F = m * a代入已知数据可得:20 = 3 * a解得加速度a为6.67m/s²。
再根据运动学公式求得物体的速度:v = u + a * t代入已知数据得到:v = 4 + 6.67 * 5 = 36.7 m/s答案为36.7m/s。
题目三:一个质量为2kg的物体受到一个20N的作用力,物体的初始速度为8m/s,求物体在4秒后的速度。
解析:同样根据牛顿第二定律可以得到:F = m * a代入已知数据可得:20 = 2 * a解得加速度a为10m/s²。
再根据运动学公式求得物体的速度:v = u + a * t代入已知数据得到:v = 8 + 10 * 4 = 48 m/s答案为48m/s。
物理化学动力学测试卷

,
得此结论的理由是 基元反应的反应级数等于反应分子数
。
2.对峙反应 A
B,其正反应的速率可表示为: r 正=k1[A]
;逆
反应的速率为: r 逆=k-1[B] ,该对峙反应的净速率可表示为: r= r 正-r 逆
=k1[A]- k-1[B] ;当反应达到平衡时,正、逆反应速率常数之间的关系可表示为
k1[A]- k-1[B] 或 k1/ k-1 = [B]/ [A] =K
1
《动力学部分》题库及题解
一、填空题:
1.何为具有简单级数的反应:反应速率只与浓度有关,且组分级数和反应总级数
为零或正整数 ,某反应 A+B=P 为基元反应,则该反应的反应级数为: 二级 ,
该反应的反应速率与反应物浓度的关系可表示为 r=k[A][B]
,得此关系
的理由是 基元反应遵守质量作用定律 ,该反应的分子数为: 二
反应是……( D)
A.一级反应
B.二级反应
C.零级反应
D.3/2 级反应
∵3/2 级反应的 t = 2/k([A]01/2-[A]1/2/[A]01/2[A]1/2) t1/t 2=2.22≈2
10、若某反应进行完全所需的时间是有限的,且等于 c0/k,则此反应为……(C )
A.一级反应
B.二级反应
是:测 不同温度下的速率常数 k ,作 lnk~1/T 关系图,通过斜率求
得活化能。
4.某气体反应 A+B—→3C 的速率方程为 r ==kCαACβB,为确定α、β值在常温 下进行实验,当初始压力为 PA,0=102Pa,PB,0=105Pa 时,作反应的 lnPA~t(时间) 图为一直线,当初始压力为 PA,0= PB,0=5×102Pa 时,仍作反应的 lnPA~t 图仍为一 直线,则α= 1 ,β= 0 。(lnc~t 成直线关系的是一级反应)
【理论力学】动力学典型习题集+答案解析
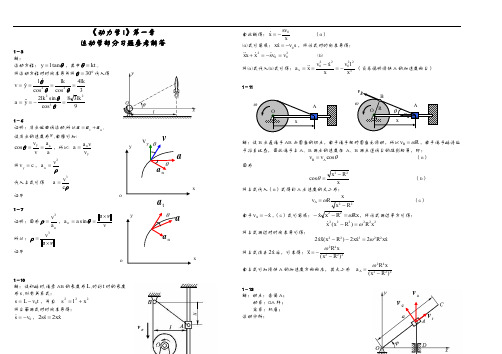
《动力学I 》第一章 运动学部分习题参考解答1-3 解:运动方程:θtan l y =,其中kt =θ。
将运动方程对时间求导并将030=θ代入得34cos cos 22lklk l y v ====θθθ 938cos sin 2232lk lk y a =-==θθ1-6证明:质点做曲线运动,所以n t a a a +=, 设质点的速度为v ,由图可知:a a vv y n cos ==θ,所以: yv v a a n = 将c v y =,ρ2n v a =代入上式可得 ρc v a 3= 证毕 1-7证明:因为n2a v=ρ,va a v a ⨯==θsin n所以:va ⨯=3v ρ证毕1-10解:设初始时,绳索AB 的长度为L ,时刻t 时的长度 为s ,则有关系式:t v L s 0-=,并且 222x l s +=将上面两式对时间求导得: 0v s-= ,x x s s 22= 由此解得:xsv x-= (a ) (a)式可写成:s v x x 0-= ,将该式对时间求导得: 2002v v s x x x =-=+ (b)将(a)式代入(b)式可得:3220220xlv x x v x a x -=-==(负号说明滑块A 的加速度向上)1-11解:设B 点是绳子AB 与圆盘的切点,由于绳子相对圆盘无滑动,所以R v B ω=,由于绳子始终处于拉直状态,因此绳子上A 、B 两点的速度在 A 、B 两点连线上的投影相等,即: θcos A B v v = (a ) 因为xR x 22cos -=θ (b ) 将上式代入(a )式得到A 点速度的大小为: 22Rx x Rv A -=ω (c )由于x v A -=,(c )式可写成:Rx R x xω=--22 ,将该式两边平方可得: 222222)(x R R x xω=- 将上式两边对时间求导可得:x x R x x R x xx 2232222)(2ω=-- 将上式消去x2后,可求得:22242)(R x xR x --=ω由上式可知滑块A 的加速度方向向左,其大小为 22242)(R x xR a A -=ω1-13解:动点:套筒A ;动系:OA 杆; 定系:机座; 运动分析:o va ve vr vxovxo t绝对运动:直线运动; 相对运动:直线运动; 牵连运动:定轴转动。
动力学习题汇总-1-1,2级反应精品PPT课件

t=0: pA,0
pB,0
0
t=t: pA
pB
pA,0- pA
则时间t时的总压力为 pt = pA+ pB+ pA,0 - pA= pB+ pA,0
因为 pA,0= pB,0 符合化学计量系数比,所以 pA= pB
则
pt = pA + pA,0
故
pA= pB= pt -pA,0
代入速率微分方程,得
dpA dt
(1)t1=t1/2/2; (2)t2=2t1/2 。
解:一级反应 kt ln 1 1 xA
设反应物初浓度为cA,0
t1/2= ln2/k
二级反应 kt 1 ( 1 1)
cA,0 1 xA
(1)t1=t1/2/2
t1/2=1/(kcA,0)
一级:
kt1
ln 2 2
ln 1 1 xA
1-xA=0.707=70.7%
闭容器中,系统初始压力为3 kPa,经50s后容器内压力
为2 kPa,问经150s后容器中pB为若干?
解:nA,0/ nB,0 = vA/ vB= 2/1;则 nA / nB=pA / pB = 2
-dpB / dt = kpA1.5pB0.5 = k(2pB)1.5pB0.5 = 21.5kpB2 = k’pB2 k 't 1 1 pB pB,0
8-1-8
已知气相反应
2A +
B 2Y的速率方程为 dpA dt
kpA pB 。
将气体A和B按物质的量比2:1引入一抽空的反应器中,反应温
度保持400 K。反应经10min后测得系统压力为84 kPa,经很长
时间反应完了后系统压力为63 kPa。试求:
动力学概念题lq分解课件

lq分解法的改进方向
01
开发更稳健的算法
针对lq分解法对初值和噪声敏感的问题,可以开发更稳健的算法。例如,
可以采用自适应步长策略、阻尼技术等方法来提高算法的稳定性和鲁棒
性。
02
结合其他算法
可以考虑将lq分解法与其他算法相结合,以获得更好的性能。例如,可
以将lq分解法与优化算法、滤波算法等相结合,以处理更复杂、更高维
机器人控制
在机器人控制领域,LQR方法被用于 设计机器人的最优控制器,实现机器 人的稳定运动和精确控制。
车辆控制
在车辆控制领域,LQR方法被用于设 计自动驾驶车辆的最优控制器,实现 车辆的稳定行驶和路径规划。
电力控制
在电力控制领域,LQR方法被用于设 计电力系统的最优控制器,实现电力 系统的稳定运行和优化调度。
实际应用
在实际应用中,许多系统都可以近似为线性系统,因此LQR 方法具有广泛的应用价值。例如,在航天、机器人、车辆控 制等领域,LQR方法已经被广泛应用于实现系统的最优控制。
动力学概念题lq分解的应用领域
航空航天
LQR方法在航空航天领域中用于设计 飞行器的最优控制器,实现飞行器的 稳定控制和轨迹优化。
由于lq分解法将系统分解为多个子系 统,因此可以很方便地进行并行计算。 通过将子系统分配给不同的处理器或 计算机,可以显著加速计算过程。
lq分解法的缺点
对初值敏感
lq分解法是一种迭代算法,对初值的选择比较敏感。如果初值选择不当,可能会导致算法 不收敛或收敛到非期望的解。因此,在应用lq分解法时,需要仔细选择合适的初值。
02
动力学基本原理
牛顿第二定律
总结词
描述物体运动状态变化的关键定律
详细描述
动力学两类基本问题(高考复习)
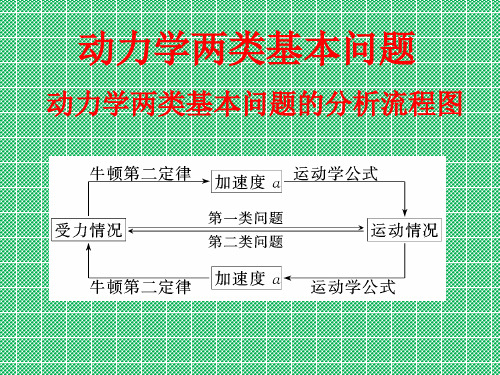
(1)试管塞从静止开始到离开试管口的总位移; (2)试管塞受到的滑动摩擦力与其重力的比值. 解析 (1)试管塞开始与试管一起运动了位移:x1=H=0.80 m 之后又独立运动了位移:x2=l-h=(0.21-0.01)m=0.20 m 所以总位移:x=x1+x2=(0.80+0.20)m=1.0 m
小物体做初速度为 v=10 m/s、加速度为 a1 的匀加速直线
运动由 x-x1=vt2+12a1t22 得:11=10t2+12×2t22=10t2+t22
解得 t2=1 s
(2 分)
所以,小物体从 A 端运动到 B 端的时间为:t=t1+t2=2 s.
[答案] (1)4 s (2)4 s (3)2 s
•【变式1】
•质量为1吨的汽车在平直公路上以10 m/s的速
度匀速行驶.阻力大小不变,从某时刻开始, 汽车牵引力减少2 000 N,那么从该时刻起经 过6 s,汽车行驶的路程是( ).
•A.50 m
B.42 m
•C.25 m
D.24 m
解析 牵引力减少 2 000 N 后,物体所受合力为 2 000 N,由 F =ma,2 000=1 000a,a=2 m/s2,汽车需 t=va=120 s=5 s 停下 来,故 6 s 内汽车前进的路程 x=2va2=21×002 m=25 m,C 正确. 答案 C
[答案] (1)4 s (2)4 s (3)2 s
(1 分)
•【变式】 传送带与水平面夹角为37°,皮带 以12 m/s的速率沿顺时针方向转动,如图3-310所示.今在传送带上端A处无初速度地放上 一个质量为m的小物块,它与传送带间的动摩 擦因数为0.75,若传送带A到B的长度为24 m, g取10 m/s2,则小物块从A运动到B的时间为多 少?
动力学练习题与解析

动力学练习题与解析动力学是物理学的一个重要分支,研究物体运动的原因和规律。
本篇文章将针对动力学训练题进行解析,帮助读者更好地理解和掌握这一领域的知识。
1. 以下哪个公式描述了物体的牛顿第二定律?A. F = maB. F = m∆v/∆tC. F = mvD. F = m∆x/∆t答案:A. F = ma解析:牛顿第二定律描述了物体的加速度是由物体所受的合力除以其质量得到的。
因此,正确的公式是 F = ma。
2. 一个质量为2 kg的物体受到20 N的恒力作用,经过8秒钟后物体速度改变了多少?A. 2 m/sB. 4 m/sC. 10 m/sD. 16 m/s答案:B. 4 m/s解析:根据牛顿第二定律 F = ma,可以得出 a = F/m = 20 N / 2 kg = 10 m/s²。
速度的变化∆v 可以用公式∆v = a∆t 得到,即∆v = 10 m/s² × 8 s = 80 m/s。
因此,物体的速度改变了 80 m/s,即 4 m/s。
3. 一个质量为5 kg的物体通过一个水平面上的绳子受到10 N的拉力,如果物体与水平面之间的摩擦力为6 N,那么物体的加速度为多少?A. 2 m/s²B. 1 m/s²C. 4 m/s²D. 3 m/s²答案:A. 2 m/s²解析:物体所受的净力等于拉力减去摩擦力,即 F = 10 N - 6 N = 4 N。
根据牛顿第二定律 F = ma,可以得出 a = F/m = 4 N / 5 kg = 0.8 m/s²。
因此,物体的加速度为 0.8 m/s²,即 2 m/s²。
4. 一个质量为3 kg的物体在水平面上受到水平方向的18 N的力和重力作用,如果物体的摩擦系数为0.2,那么物体的加速度为多少?A. 2 m/s²B. 3 m/s²C. 4 m/s²D. 5 m/s²答案:C. 4 m/s²解析:物体所受的净力等于水平力减去摩擦力和重力分量,即 F =18 N - μmg = 18 N - 0.2 × 3 kg × 9.8 m/s² = 18 N - 5.88 N = 12.12 N。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
“动力学”计算题(7)
长为l、质量为m的均质细杆静止直立于光滑水平面上。 当杆受微小干扰而倒下。求杆刚刚到达地面时的角速度、角 加速度和地面约束力。(20分)
分析要点:
C
A
(1)根据动能定理求角速度 ; (2)由刚体平面运动微分方程求角加速度和地面约束力。 5
“动力学”计算题(7)解答
1. 求杆刚刚到达地面时的角速度
F1x
m1g
9
“动力学”计算题(9) ,
如图所示,缠绕在半径为R的滚子B上的不可伸长的细绳,跨过半径 为r的定滑轮A,另端系一质量为m1的重物D。定滑轮A和滚子B可分别视 为质量为m2和m3的均质圆盘,滚子B可沿倾角为的固定斜面无滑动的滚 动,滚子中心系一刚度系数为k的弹簧。假设弹簧和绳子的倾斜段均与斜 面平行,绳子与滑轮间无相对滑动,轴承O处摩擦和绳子、弹簧的质量都 不计,如果在弹簧无变形时将系统静止释放,物块D开始下落。
杆的水平轴线夹角 。 如果将BE绳突然剪断,求 此
瞬时AB杆的角加速度 A和B AD绳的拉力T ?
D
A
E
B
11
“动力学”计算题(1)
D
E
求: AB ?
A
B
分析要点:
T ?
(1)采用平面运动微分方程求解; (2)找补充方程: AB杆上运动学关系。
12
“动力学”计算题(1)
BE绳突然剪断,求: AB 和AD绳的拉力T ?
Nn
3 mg sin 4
C G
Nn
1 2
mg(1 3cos )
3
“动, 力学”计算题(6)
匀质杆AB质量m,长度l,可绕过O点的水平轴转动,O 点在AB杆的1/3位置。开始时,杆静止于水平位置,试求突然 释放后,AB杆转至=60时轴承O处的约束力。
A O
分析要点:
B
(1) 根据动能定理求ω; (2) 根据动量矩定理求ε; (3) 由质心运动定理求O处反力
3g sin
9
d
.
6 并注意运动的初始条件:
2l
0 , 0
d
d 3g sind
0
0 2l
3g (1 cos ) l
O B
C A
(将2)再由和质心的运表动达mm定aa式CC理n分方别程代,FF入n即上列两mm式66ll , 2 即NN可n m求gm得sginc:os
N
N BO
解: (4)找补充方程 AB杆上运动学关系:
D
a
n A
aCy aCnA aCx
E
aC
aCx
aA
aCy
aC A aCnA
1.求加速度aD
M
设系统由静止开始运动,故初动能T1=0
O2
O1
物块D上升距离s时,系统的动能T2为:
B
A
T2
1 2
J112
1 2
m2vC2
1 2
J
2
CC
1 2
m3vD2
C
其中vC=vD , rω1=2vD , RωC=vC
T2
1 4
(4m1
3m2
2m3 )vD2
D
W
M
(m2
,m3 )Wgs
2Ms r
将上式沿铅垂方向投影,得:
aC
aC A
1 l
2
联立求解得:
FN
1 mg 4
3g
2l
C
vA
vC
A
FN aA
ε
C
A
aC
mg
6
“动力学”计算题(8)
在图示机构中,匀质轮O1质量为m1,半径为r。不计轮O2质量,其半 径也为r。匀质轮C的质量为m2,半径为R,物块D的质量为m3。在匀质轮O1 上作用常力偶矩M,试求:
(m2
m3 ) gs
代入动能定理: T2 m2
2m3 )v, D2
W0
2Ms r
(m2
m3 ) gs
1
2
(4m1
3m2
2m3
)vD
a
DW
[
2M r
(m2
m3 ) g ]
ds dt
aD
4M 2(m2 (4m1 3m2
m3 )gr 2m8 3 )r
“动力学”计算题(8)解答
杆刚刚到达地面时,A点为瞬心,则
vC
1 2
l
T
1 2
mvC2
1 2
JC 2
1 6
ml2 2
由动能定理得: 1 ml22 1 mgl
6
2
3g l
2. 求杆刚刚到达地面时的地面约束力
由刚体平面运动微分方程得: mg FN maC
FN
l 2
1 12
ml 2
A、C两点速度关系: aC aA aC A aCnA
A
O B
分析要点:
(1) 根据动能定理求ω; (2) 根据动量矩定理求ε; (3) 由质心运动定理求O处反力
2
“动力学”计算题(5)解答
(1)由刚体定轴转动微分方程: IO mz (F)
OC 1 l 6
IO
1 ml 2 12
m( l )2 6
1 ml 2 9
A
1 ml2 mg l sin
“动力学”计算题一
(一)动能定理 (二)动量原理 (三)动量矩定理 (四)DAlembert原理
1
“动, 力学”计算题(5)
匀质杆AB质量m,长度l,可绕过O点的水平轴转动,O 点在AB杆的1/3位置。开始时,杆静止于铅直位置,受轻微扰 动后而转动,试求:(1)AB杆转至任意位置时的角速度和角 加速度;(2)轴承O处的约束力。
试求:(1)滚子中心C沿斜面上升距离s 时,点C的加速度;(2)轴承O的 反力;(3)此时滚子与斜面间的摩擦力的大小。
分析要点:
(1)根据动能定理求aC ; (2)取A滑轮,根据动量矩定理
和质心运动定理求轴承O的反力。
(3)取滚子B,由平面运动方程
求斜面间的摩擦力。
10
“动力学”计算题(1)
均质杆质量m,长l , A、B两端用绳索悬挂,绳与
(1)物块D上升的加速度;
(2)求水平绳索拉力和轴承O1处的约束力。 (绳索拉力和轴承处约束力可表示成加速度aD的函数)(24分)
M
O2
O1
B
A 分析要点:
(1)根据动能定理求加速度aD ;
C
(2)取轮O1为分离体,应用动
量矩定理和质心运动定理,求绳
D
索拉力和轴承O1处约束力。 7
“动力学”计算题(8)解答
解: (1) 研究AB杆 (2)画受力图
D
T
(3)列出平面运动微分方程:
maCx T cos ① A
maCy T sin mg ②
E
C
B
mg
IC AB T sin l / 2 ③
四个未知量aCx、aCy、εAB、T,只有三个方程;
需要找一个补充方程 ?
13
求: AB ? T= ?
2. 求水平绳索拉力和轴承O1处约束力
取轮O1为分离体
对固定点O1应用动量矩定理得:
JO1O1 M FT r 其中 2aD rO1
FT
1 (M r
JO1O1)
应用质心运动定理得:
0 N1x FT
0 N1y m1g
N1x
M r
m1aD
N1y m1g
O2
B
M
O1
A
C
D
F1y
FT
M
O1
