中考数学压轴题-二次函数动点问题.docx
动点问题中考真题(四川绵阳)(解析版)

动点问题中考真题(四川绵阳)1.如图,二次函数2224y x x a =--+-的图象与一次函数2y x =-的图象交于点A 、B (点B 在右侧),与y 轴交于点C ,点A 的横坐标恰好为a .动点P 、Q 同时从原点O 出发,沿射线OB t 秒后,以PQ 为对角线作矩形PMQN ,且矩形四边与坐标轴平行.(1)求a 的值及1t =秒时点P 的坐标;(2)当矩形PMQN 与抛物线有公共点时,求时间t 的取值范围;(3)在位于x 轴上方的抛物线图象上任取一点R ,作关于原点()0,0的对称点为'R ,当点M 恰在抛物线上时,求'R M 长度的最小值,并求此时点R 的坐标.2.如图,抛物线过点A (0,1)和C ,顶点为D ,直线AC 与抛物线的对称轴BD 的交点为B 0),平行于y 轴的直线EF 与抛物线交于点E ,与直线AC 交于点F ,点F BDEF 为平行四边形.(1)求点F 的坐标及抛物线的解析式;(2)若点P 为抛物线上的动点,且在直线AC 上方,当△PAB 面积最大时,求点P 的坐标及△PAB 面积的最大值;(3)在抛物线的对称轴上取一点Q ,同时在抛物线上取一点R ,使以AC 为一边且以A ,C ,Q ,R 为顶点的四边形为平行四边形,求点Q 和点R 的坐标.3.如图,在矩形ABCD 中,对角线相交于点O ,⊙M 为△BCD 的内切圆,切点分别为N ,P ,Q ,DN =4,BN =6.(1)求BC ,CD ;(2)点H 从点A 出发,沿线段AD 向点D 以每秒3个单位长度的速度运动,当点H 运动到点D 时停止,过点H 作HI ∥BD 交AC 于点I ,设运动时间为t 秒.①将△AHI 沿AC 翻折得△A H ¢I ,是否存在时刻t ,使点H ¢恰好落在边BC 上?若存在,求t 的值;若不存在,请说明理由;②若点F 为线段CD 上的动点,当△OFH 为正三角形时,求t 的值.4.如图,在以点O 为中心的正方形ABCD 中,4=AD ,连接AC ,动点E 从点O 出发沿O C ®以每秒1个单位长度的速度匀速运动,到达点C 停止.在运动过程中,ADE D 的外接圆交AB 于点F ,连接DF 交AC 于点G ,连接EF ,将EFG D 沿EF 翻折,得到EFH D .(1)求证:DEF D 是等腰直角三角形;(2)当点H 恰好落在线段BC 上时,求EH 的长;(3)设点E 运动的时间为t 秒,EFG D 的面积为S ,求S 关于时间t 的关系式.5.在平面直角坐标系中,将二次函数()20y ax a =>的图象向右平移1个单位,再向下平移2个单位,得到如图所示的抛物线,该抛物线与x 轴交于点A 、B (点A 在点B 的左侧),1OA =,经过点A 的一次函数()0y kx b k =+¹的图象与y 轴正半轴交于点C ,且与抛物线的另一个交点为D ,ABD D 的面积为5.(1)求抛物线和一次函数的解析式;(2)抛物线上的动点E 在一次函数的图象下方,求ACE D 面积的最大值,并求出此时点E 的坐标;(3)若点P 为x 轴上任意一点,在(2)的结论下,求35PE PA +的最小值.6.如图,已知△ABC 的顶点坐标分别为A (3,0),B (0,4),C (-3,0).动点M ,N 同时从A 点出发,M 沿A→C,N 沿折线A→B→C ,均以每秒1个单位长度的速度移动,当一个动点到达终点C 时,另一个动点也随之停止移动,移动时间记为t 秒.连接MN.(1)求直线BC的解析式;(2)移动过程中,将△AMN沿直线MN翻折,点A恰好落在BC边上点D处,求此时t值及点D的坐标;(3)当点M,N移动时,记△ABC在直线MN右侧部分的面积为S,求S关于时间t的函数关系式.7.如图,已知△ABC中,∠C=90°,点M从点C出发沿CB方向以1cm/s的速度匀速运动,到达点B停止运动,在点M的运动过程中,过点M作直线MN交AC于点N,且保持∠NMC=45°,再过点N作AC的垂线交AB于点F,连接MF,将△MNF关于直线NF对称后得到△ENF,已知AC=8cm,BC=4cm,设点M运动时间为t(s),△ENF与△ANF重叠部分的面积为y(cm2).(1)在点M的运动过程中,能否使得四边形MNEF为正方形?如果能,求出相应的t 值;如果不能,说明理由;(2)求y关于t的函数解析式及相应t的取值范围;(3)当y取最大值时,求sin∠NEF的值.8.如图,在边长为2的正方形ABCD中,G是AD延长线上的一点,且DG=AD,动点M从A出发,以每秒1个单位的速度沿着A→C→G的路线向G点匀速运动(M不与A、G重合),设运动时间为t秒.连接BM并延长交AG于N.(1)是否存在点M,使△ABM为等腰三角形?若存在,分析点M的位置;若不存在,请说明理由;(2)当点N在AD边上时,若BN⊥HN,NH交∠CDG的平分线于H,求证:BN=NH;(3)过点M分别用AB、AD的垂线,垂足分别为E、F,矩形AEMF与△ACG重叠部分的面积为S,求S的最大值.参考答案:1.(1)a =()1,2-;(2)112t ££+;(3,312æö-±ç÷ç÷èø【分析】(1)将(),2a a -,代入2224y x x a =--+-,求出a ,即可得到抛物线解析式,当1t =秒时,OP =P 的坐标为(),x y ,建立方程求解即可;(2)经过t 秒后,OP ,OQ =,由(1)方法知,P 的坐标为(),2t t -,Q 的坐标为()2,4t t -进而得出M 的坐标为()2,2t t -,N 的坐标为(),4t t -将()2,2M t t -代入222y x x -=-+,将(),4N t t -代入222y x x -=-+,解方程即可得到答案;(3)设(),R m n ,则R 关于原点的对称点为()',R m n --,当点M 恰好在抛物线上时,M 坐标为()1,1-.过'R 和M 作坐标轴平行线相交于点S ,如图③则'R M ==222n m m =--+得2(1)3m n +=-,消去m得'R M ==【详解】解:(1)由题意知,交点A 坐标为(),2a a -,代入2224y x x a =--+-,解得a =∴抛物线解析式为222y x x -=-+.当1t =秒时,OP =P 的坐标为(),x y ,则2252x y y xìï+==í=-ïî,解得12x y =ìí=-î或12x y =-ìí=î(舍),所以P 的坐标为()1,2-.(2)经过t 秒后,OP ,OQ =,由(1)方法知,P 的坐标为(),2t t -,Q 的坐标为()2,4t t -,由矩形PMQN 的邻边与坐标轴平行可知,M 的坐标为()2,2t t -,N 的坐标为(),4t t -.矩形PMQN 在沿着射线OB 移动的过程中,点M 与抛物线最先相交,如图①,然后公共点变为2个,点N 与抛物线最后相离,然后渐行渐远.如图②,将()2,2M t t -代入222y x x -=-+,得2210t t +-=,解得12t =,或1t =-(舍),将(),4N t t -代入222y x x -=-+,得()213t -=,解得1t =1t =.所以,当矩形PMQN 与抛物线有公共点时,时间t 的取值范围是112t ££.(3)设(),R m n ,则R 关于原点的对称点为()',R m n --,当点M 恰好在抛物线上时,M 坐标为()1,1-.过'R 和M 作坐标轴平行线相交于点S ,如图③则'R M ==222n m m =--+得2(1)3m n +=-,消去m 得'R M ====,当32n =时,'R M此时,23222n m m =--+=,解得1m =-,所以,点R 的坐标是312æö-±ç÷ç÷èø.【点睛】本题主要考查了二次函数的综合,待定系数法求函数解析式,二次函数的最值,勾股定理,矩形的性质,中心对称等等,解题的关键在于能够熟练掌握相关知识进行求解.2.(1)﹣13);y =﹣x 2 (2),4712) (3)Q 443ö-÷ø,R 373æö-ç÷èø或Q ﹣10),R 373-)【分析】(1)由待定系数法求出直线AB 的解析式为y =,求出F 点的坐标,由平行四边形的性质得出﹣3a+1=163a ﹣8a+1﹣(﹣13),求出a 的值,则可得出答案;(2)设P (n ,﹣n 2),作PP'⊥x 轴交AC 于点P',则P'(n ,n+1),得出PP'=﹣n 2,由二次函数的性质可得出答案;(3)联立直线AC 和抛物线解析式求出C﹣43),设Qm ),分两种情况:①当AQ 为对角线时,②当AR 为对角线时,分别求出点Q 和R 的坐标即可.【详解】解:(1)设抛物线的解析式为y =ax 2+bx+c (a≠0),∵A (0,1),B0),设直线AB 的解析式为y =kx+m ,∴m 0m 1+==ïî,解得k m ì=ïíï=î,∴直线AB 的解析式为y =,∵点F∴F 点纵坐标为=﹣13,∴F ﹣13),又∵点A 在抛物线上,∴c =1,对称轴为:x =﹣2b a =,∴b =﹣,∴解析式化为:y =ax 2﹣,∵四边形DBFE 为平行四边形.∴BD =EF ,∴﹣3a+1=163a ﹣8a+1﹣(﹣13),解得a =﹣1,∴抛物线的解析式为y =﹣x 2;(2)设P (n ,﹣n 2),作PP'⊥x 轴交AC 于点P',则P'(n,),∴PP'=﹣n2,S△ABP=12OB•PP'=272+n=2n,∴当n时,△ABP,此时P,4712).(3)∵21 y xy xì=+ïíï=-++î,∴x=0或x∴C﹣43),设Qm),①当AQ为对角线时,∴R(73m+),∵R在抛物线y=2(x-+4上,∴m+73=﹣2æçè+4,解得m=﹣443,∴Q443ö-÷ø,R373æö-ç÷èø;②当AR为对角线时,∴R73m-),∵R 在抛物线y =2(x -+4上,∴m ﹣273=-+4,解得m =﹣10,∴Q ﹣10),R 373-).综上所述,Q 443ö-÷ø,R 373æö-ç÷èø;或Q ﹣10),R 373-).【点睛】本题是二次函数综合题,考查了待定系数法,二次函数的性质,二次函数图象上点的坐标特征,平行四边形的性质等知识,熟练掌握二次函数的性质及方程思想,分类讨论思想是解题的关键.3.(1)8;6 (2)①存在;2512s ②(4s 【分析】(1)由切线长定理得出BP =BN =6,DQ =DN =4,CP =CQ ,BD =BN+DN =10,设CP =CQ =a ,由勾股定理得出BC 2+CD 2=BD 2,得出方程,解方程即可;(2)①由折叠的性质得∠AH'I =∠AHI ,AH'=AH =3t ,证明△AIH'∽△AH'C ,则AH'2=AI×AC ,证△AIH ∽△AOD ,求出AI =158t ,得出(3t )2=158t×10,解方程即可;②作PH ⊥OH 于H ,交OF 的延长线于P ,作OM ⊥AD 于M ,PN ⊥AD 于N ,证出FH =FP =OF ,HP ,DN =DM =4,证明△OMH ∽△HNP ,求出HN =DH =HN ﹣DN =4,得出AH =AD ﹣DH =12﹣【详解】解:(1)∵⊙M 为△BCD 的内切圆,切点分别为N ,P ,Q ,DN =4,BN =6,∴BP =BN =6,DQ =DN =4,CP =CQ ,BD =BN+DN =10,设CP =CQ =a ,则BC =6+a ,CD =4+a ,∵四边形ABCD 是矩形,∴∠BCD =90°,∴BC 2+CD 2=BD 2,即(6+a )2+(4+a )2=102,解得:a =2,∴BC =6+2=8,CD =4+2=6;(2)①存在时刻t =2512s ,使点H′恰好落在边BC 上;理由如下:如图1所示:由折叠的性质得:∠AH'I=∠AHI,AH'=AH=3t,∵四边形ABCD是矩形,∴AD=BC=8,AD∥BC,∠BCD=90°,OA=OC=12AC,OB=OD=12BD,AC=BD,∴AC=BD10,OA=OD=5,∴∠ADO=∠OAD,∵HI∥BD,∴∠AHI=∠ADO,∴∠AH'I=∠AHI=∠ADO=∠OAD=∠ACH',∴△AIH'∽△AH'C,∴AHAC¢=AIAH¢,∴AH'2=AI×AC,∵HI∥BD,∴△AIH∽△AOD,∴AIAO=AHAD,即5AI=38t,解得:AI=158t,∴(3t)2=158t×10,解得:t=25 12,即存在时刻t=2512s,使点H′恰好落在边BC上;②作PH⊥OH于H,交OF的延长线于P,作OM⊥AD于M,PN⊥AD于N,如图2所示:则OM∥CD∥PN,∠OMH=∠HNP=90°,OM是△ACD的中位线,∴OM=12CD=3,∵△OFH是等边三角形,∴OF =FH ,∠OHF =∠HOF =60°,∴∠FHP =∠HPO =30°,∴FH =FP =OF ,HP ,∴DF 是梯形OMNP 的中位线,∴DN =DM =4,∵∠MHO+∠MOH =∠MHO+∠NHP =90°,∴∠MOH =∠NHP ,∴△OMH ∽△HNP ,∴OMHN =OH HP,∴HN =∴DH =HN ﹣DN =4,∴AH =AD ﹣DH =12﹣∴t =AH3=4即当△OFH 为正三角形时,t 的值为(4s .【点睛】本题是圆的综合题目,考查了切线长定理、矩形的性质、折叠的性质、勾股定理、相似三角形的判定与性质、等边三角形的性质、含30°角的直角三角形的性质、等腰三角形的判定、三角形中位线定理等知识;本题综合性强,熟练掌握切线长定理、相似三角形的判定与性质以及勾股定理是解题的关键.4.(1)证明见解析;(2)EH =-(3)EFGS D =.【分析】(1)由正方形的性质可得45DAC CAB Ð=Ð=o ,再根据圆周角定理即可证得结论;(2)设OE t =,连接OD ,通过证明DOE DAF D D :可得AF =,再证明AEF ADG D D :可得AG 与t 的关系式,进一步可表示EG 的长,由AF CD ∥得比例线段FG AFDG CD=,进而求出t 的值,然后代入EG 的表达式可求EH 的值;(3)由(2)知EG 与t 的关系式,再过点F 作FK AC ^于点K ,易证DOE EKF D @D ,于是FK OE t ==,再根据三角形的面积公式即可求解.【详解】(1)证明:∵四边形ABCD 是正方形,∴45DAC CAB Ð=Ð=o ,∵FDE CAB Ð=Ð,DFE DAC Ð=Ð,∴45FDE DFE Ð=Ð=o ,∴90DEF Ð=o ,∴DEF D 是等腰直角三角形;(2)设OE t =,连接OD ,如图,则90DOE DAF Ð=Ð=o ,∵OED DFA Ð=Ð∴DOE DAF D D :,∴OE OD AF AD ==,∴AF =,又∵AEF ADG Ð=Ð,EAF DAG Ð=Ð,∴AEF ADG D D :,∴AE AFAD AG=,∴AG AE AD AF ×=×=,又∵AE OA OE t =+=,∴AG =,∴EG AE AG =-=当点H 恰好落在线段BC 上时,454590DFE HFE Ð+Ð=+=o o o ,∴ADF BFH D D :,∴FH FD =∵AF CD ∥,∴FG AF DG CD ==∴FG DF =∵FG =FH ,=解得:1t =2t =舍去),∴EG EH ====(3)过点F 作FK AC ^于点K ,由(2)得EG =∵DE EF =,90DEF Ð=o ,∴DEO EFK Ð=Ð,∴()DOE EKF AAS D @D ,∴FK OE t ==,∴12EFGS EG FK D =×=【点睛】本题是四边形综合题,重点考查了正方形的性质、圆周角定理、全等三角形的判定与性质、相似三角形的判定和性质、等腰直角三角形的判定与性质、一元二次方程的求解和三角形的面积等知识,涉及的知识点多,难度较大,属于试卷的压轴题,第(2)小题具有相当的难度,解题的关键是灵活应用相似三角形的判定与性质,学会利用参数构建方程解决问题.5.(1)21322y x x =--;1122y x =+;(2)ACE D 的面积最大值是2516,此时E 点坐标为315,28æö-ç÷èø;(3)35PE PA +的最小值是3.【分析】(1)先写出平移后的抛物线解析式,再把点()1,0A -代入可求得a 的值,由ABD D 的面积为5可求出点D 的纵坐标,代入抛物线解析式可求出横坐标,由A 、D 的坐标可利用待定系数法求出一次函数解析式;(2)作EM y P 轴交AD 于M ,如图,利用三角形面积公式,由ACE AME CME S S S D D D =-构建关于E 点横坐标的二次函数,然后利用二次函数的性质即可解决问题;(3)作E 关于x 轴的对称点F ,过点F 作FH AE ^于点H ,交x 轴于点P ,则BAE HAP HFE Ð=Ð=Ð,利用锐角三角函数的定义可得出35EP AP FP HP +=+,此时FH 最小,求出最小值即可.【详解】解:(1)将二次函数()20y ax a =>的图象向右平移1个单位,再向下平移2个单位,得到的抛物线解析式为()212y a x =--,∵1OA =,∴点A 的坐标为()1,0-,代入抛物线的解析式得,420a -=,∴12a =,∴抛物线的解析式为()21122y x =--,即21322y x x =--.令0y =,解得11x =-,23x =,∴()3,0B ,∴4AB OA OB =+=,∵ABD D 的面积为5,∴152ABD D S AB y D =×=,∴52D y =,代入抛物线解析式得,2513222x x =--,解得12x =-,24x =,∴54,2D æöç÷èø,设直线AD 的解析式为y kx b =+,∴5420k b k b ì+=ïíï-+=î,解得:1212k b ì=ïïíï=ïî,∴直线AD 的解析式为1122y x =+.(2)过点E 作EM y P 轴交AD 于M ,如图,设213,22E a a a æö--ç÷èø,则11,22M a a æö+ç÷èø,∴221113132222222EM a a a a a =+-++=-++,∴112ACE AME CME S S S EM D D D =-=´×()22113121342224a a a a æö=-++´=---ç÷èø,213254216a æö=--+ç÷èø,∴当32a =时,ACE D 的面积有最大值,最大值是2516,此时E 点坐标为315,28æö-ç÷èø.(3)作E 关于x 轴的对称点F ,连接EF 交x 轴于点G ,过点F 作FH AE ^于点H ,交x 轴于点P ,∵315,28E æö-ç÷èø,1OA =,∴35122AG =+=,158EG =,∴5421538AG EG ==,∵90AGE AHP Ð=Ð=o ,∴3sin 5PH EG EAG AP AE Ð===,∴35PH AP =,∵E 、F 关于x 轴对称,∴PE PF =,∴35PE AP FP HP FH +=+=,此时FH 最小,∵1515284EF =´=,AEG HEF Ð=Ð,∴4sin sin 5AG FH AEG HEF AE EF Ð=Ð===,∴415354FH =´=.∴35PE PA +的最小值是3.【点睛】主要考查了二次函数的平移和待定系数法求函数的解析式、二次函数的性质、相似三角形的判定与性质、锐角三角函数的有关计算和利用对称的性质求最值问题.解(1)题的关键是熟练掌握待定系数法和相关点的坐标的求解;解(2)题的关键是灵活应用二次函数的性质求解;解(3)题的关键是作E 关于x 轴的对称点F ,灵活应用对称的性质和锐角三角函数的知识,学会利用数形结合的思想和转化的数学思想把求35PE PA +的最小值转化为求FH 的长度.6.(1)y=43x+4;(2)D (-1511,2411);(3)①当0<t≤5时,S=25t2,②当5<t≤6时,S=25t2+325t-12.【分析】(1)利用待定系数法即可解决问题;(2)如图1中,连接AD 交MN 于点O’.想办法求出点D 坐标,利用待定系数法即可解决问题;(3)分两种情形①如图2中,当0<t≤5时,△ABC 在直线MN 右侧部分是△AMN .②如图3中,当5<t≤6时,△ABC 在直线MN 右侧部分是四边形ABNM .分别求解即可.【详解】(1)设直线BC 的解析式为y kx b =+,则430b k b =ìí-+=î,解得434k b ì=ïíï=î,\直线BC 的解析式为443y x =+.(2)如图,连接AD 交MN 于点'O .由题意:四边形AMDN 是菱形,()3,0M t -,3(35N t -,4)5t ,4'(35O t \-,2)5t ,8(35D t -,4)5t ,Q 点D 在BC 上,44834535t t æö\=´-+ç÷èø,解得3011t =.3011t s \=时,点A 恰好落在BC 边上点D 处,此时15(11D -,24)11.(3)如图2中,当05t <…时,ABC D 在直线MN 右侧部分是AMN D ,2142··255S t t t ==.如图3中,当56t <…时,ABC D 在直线MN 右侧部分是四边形ABNM .()()2114232646·451222555S t t t t éù=´´-´---=-+-êúëû.【点睛】考查一次函数综合题、待定系数法、菱形的判定和性质、相似三角形的判定和性质、锐角三角函数、三角形的面积等知识,解题的关键是灵活运用所学知识解决问题,学会用分类讨论的思想思考问题.7.(1)85;(2)2212 (02)41416(24)1233t t t y t t t ì-+<<ïï=íï-+££ïî;(3.【详解】试题分析:(1)由已知得出CN =CM =t ,FN ∥BC ,得出AN =8﹣t ,由平行线证出△ANF ∽△ACB ,得出对应边成比例求出NF =12AN =12(8﹣t ),由对称的性质得出∠ENF =∠MNF =∠NMC =45°,MN =NE ,OE =OM =CN =t ,由正方形的性质得出OE =ON =FN ,得出方程,解方程即可;(2)分两种情况:①当0<t ≤2时,由三角形面积得出2124y t t =-+ ;②当2<t ≤4时,作GH ⊥NF 于H ,由(1)得:NF =12(8﹣t ),GH =NH ,GH =2FH ,得出GH =23NF =13(8﹣t ),由三角形面积得出21(8)12y t =-(2<t ≤4);(3)当点E 在AB 边上时,y 取最大值,连接EM ,则EF =BF ,EM =2CN =2CM =2t ,EM =2BM ,得出方程,解方程求出CN =CM =2,AN =6,得出BM =2,NF =12AN =3,因此EM =2BM =4,作FD ⊥NE 于D ,由勾股定理求出EB=EF =12EBDF 的长,在Rt △DEF 中,由三角函数定义即可求出sin ∠NEF 的值.试题解析:解:(1)能使得四边形MNEF 为正方形;理由如下:连接ME 交NF 于O ,如图1所示:∵∠C =90°,∠NMC =45°,NF ⊥AC ,∴CN =CM =t ,FN ∥BC ,∴AN =8﹣t ,△ANF ∽△ACB ,∴84AN AC NF BC == =2,∴NF =12AN =12(8﹣t ),由对称的性质得:∠ENF =∠MNF =∠NMC =45°,MN =NE ,OE =OM =CN =t ,∵四边形MNEF 是正方形,∴OE =ON =FN ,∴t =12×12(8﹣t ),解得:t =85;即在点M 的运动过程中,能使得四边形MNEF 为正方形,t 的值为85;(2)分两种情况:①当0<t ≤2时,y =12×12(8﹣t )×t =2124t t -+,即2124y t t =-+(0<t ≤2);②当2<t ≤4时,如图2所示:作GH ⊥NF 于H ,由(1)得:NF =12(8﹣t ),GH =NH ,GH =2FH ,∴GH =23NF =13(8﹣t ),∴y =12NF ′GH =12×12(8﹣t )×13(8﹣t )=21(8)12t -,即21(8)12y t =-(2<t ≤4);综上所述:2212 (02)41416(24)1233t t t y t t t ì-+<<ïï=íï-+££ïî .(3)当点E 在AB 边上时,y 取最大值,连接EM ,如图3所示:则EF =BF ,EM =2CN =2CM =2t ,EM =2BM ,∵BM =4﹣t ,∴2t =2(4﹣t ),解得:t =2,∴CN =CM =2,AN =6,∴BM =4﹣2=2,NF =12AN =3,∴EM =2BM =4,作FD ⊥NE 于D ,则EB==△DNF 是等腰直角三角形,∴EF =12EBDFNF=,在Rt △DEF 中,sin ∠NEF =DF EF点睛:本题是四边形综合题目,考查了正方形的判定与性质、相似三角形的判定与性质、勾股定理、三角函数、三角形面积的计算、等腰直角三角形的判定与性质等知识;本题综合性强,有一定难度.8.(1)详见解析;(2)详见解析;(3)当t=秒时,S的最大值为.【详解】试题分析:(1)△ABM为等腰三角形有三种情况,①AM=BM,②AB=BM,③AM=AB,根据这三种情况确定M的位置.(2)根据同角的的余角相等可证∠ABN=∠DNH,再证∠BKN=∠NDH=135º,BK=DN,利用ASA可判定△BNK≌△NHD,进而根据全等三角形的对应边相等可得BN=NH.(3)矩形AEMF与△ACG重叠部分分两种情况,①当点M在AC 上时,即0<t≤时,当点M在CG上时,即<t<时,分别求出在这两种情况时矩形AEMF与△ACG重叠部分的面积S与运动时间t之间的函数关系式,利用二次函数的性质求得这两种情况各自的最大值,再进行比较,找出最大的即为本题答案.试题解析:(1)当点M为AC中点时,有AM=BM,则△ABM为等腰三角形;当点M与点C重合时,AB=BM,则△ABM为等腰三角形;当点M在AC上且AM=2时,AM=AB,则△ABM为等腰三角形.证明:在AB上取点K,使AK=AN,连接KN.∵AB=AD,BK=AB-AK,ND=AD-AN,∴BK=DN.又DH平分直角∠CDG,∴∠CDH=45º,∴∠NDH=90º+45º=135º.∴∠BKN=180-∠AKN=135º,∴∠BKN=∠NDH.∵在Rt△ABN中,∠ABN+∠ANB=90º,又BN⊥NH,即∠BNH=90º∴∠ANB+∠DNH=180º-∠BNH=180º-90º=90º∴∠ABN=∠DNH.∴△BNK≌△NHD(ASA),∴BN=NH.①当点M在AC上时,即0<t≤时,易知:△AMF为等腰直角三角形.∵AM=t,∴AF=FM=.∴S=.当点M在CG上时,即<t<时,CM=t-,MG=-t.∵AD=DG,∠ADC=∠CDG,CD=CD,∴△ACD≌△GCD(SAS),∴∠ACD=∠GCD=45º∴∠ACM=∠ACD+∠GCD=90º∴∠G=90-∠GCD=90º-45º=45º∴△MFG为等腰直角三角形.∴②在0<t≤范围内,当t=时,S的最大值为.在<t<范围内,,当时,S的最大值为.∵82 3>,∴当t=秒时,S的最大值为.考点:四边形、三角形、二次函数综合题.。
完整版中考数学二次函数动点问题

.模式1:平行四边形分类标准:讨论对角线例如:请在抛物线上找一点p使得A、B、C、P四点构成平行四边形,那么可分成以下几种情况〔1〕当边AB是对角线时,那么有AP//BC〔2〕当边AC是对角线时,那么有AB//CP〔3〕当边BC是对角线时,那么有AC//BP例题1:〔山东省阳谷县育才中学模拟10〕此题总分值14分〕在平面直角坐标系中,抛物线经过A(-4,0),B(0,-4),C(2,0)三点.(1)求抛物线的解析式;(2)假设点M为第三象限内抛物线上一动点,点M的横坐标为m,△AMB的面积为S.求S关于m的函数关系式,并求出 S的最大值;(3)假设点P是抛物线上的动点,点 Q是直线y=-x上的动点,判断有几个位置能使以点P、Q、B、0为顶点的四边形为平行四边形,直接写出相应的点Q的坐标.Word资料.练习:如图1,抛物线y x22x 3与x轴相交于A、B两点〔点 A在点B的左侧〕,与y轴相交于点C,顶点为D.〔1〕直接写出A、B、C三点的坐标和抛物线的对称轴;〔2〕连结BC,与抛物线的对称轴交于点E,点P为线段BC上的一个动点,过点P作PF//DE交抛物线于点,设点P 的横坐标为m.F①用含m的代数式表示线段PF的长,并求出当m为何值时,四边形PEDF为平行四边形?②设△BCF的面积为S,求S与m的函数关系.模式2:梯形分类标准:讨论上下底例如:请在抛物线上找一点p使得A、B、C、P四点构成梯形,那么可分成以下几种情况〔1〕当边AB是底时,那么有AB//PC〔2〕当边AC是底时,那么有AC//BP〔3〕当边BC是底时,那么有BC//APWord资料例题2:,矩形OABC在平面直角坐标系中位置如图1所示,点A的坐标为(4,0),点C的坐标为(0,2),直线y 2x与边BC相交于点D.3(1)求点D的坐标;(2)抛物线yax 2bx c经过点、、O,求此抛物线的表达式;AD(3)在这个抛物线上是否存在点M ,使、、A、M为顶点的四边形是梯形?假设存在,请求出O D所有符合条件的点M的坐标;假设不存在,请说明理由.练习:二次函数的图象经过A 〔2,0〕、(0,12)两点,且对称轴为直线=4,设顶点C x为点P,与x轴的另一交点为点B.〔1〕求二次函数的解析式及顶点P的坐标;〔2〕如图 1,在直线y=2x上是否存在点D,使四边形OPBD为等腰梯形?假设存在,求出点的坐标;假设不存在,请说明理由;〔3〕如图2,点M是线段OP上的一个动点〔O、P两点除外〕,以每秒2个单位长度的速度由点P 向点O运动,过点M作直线MN//x轴,交PB于点.将△PMN沿直线MN对NWord资料折,得到△P1MN.在动点M的运动过程中,设△P1MN与梯形OMNB的重叠局部的面积为S,运动时间为t秒,求S关于t的函数关系式.模式3:直角三角形分类标准:讨论直角的位置或者斜边的位置例如:请在抛物线上找一点p使得A、B、P三点构成直角三角形,那么可分成以下几种情况1〕当A为直角时,ACAB2〕当B为直角时,BCBA3〕当C为直角时,CACB例题3:如图1,抛物线y=x2+bx+c与x轴交于A、B两点〔点A在点B左侧〕,与 y轴交于点C(0,-3),对称轴是直线x=1,直线BC与抛物线的对称轴交于点D.1〕求抛物线的函数表达式;2〕求直线BC的函数表达式;〔3〕点E为y轴上一动点,CE的垂直平分线交CE于点F,交抛物线于P、Q两点,且点P在第三象限.3AB时,求tan∠CED的值;①当线段PQ4Word资料.②当以C、D、E为顶点的三角形是直角三角形时,请直接写出点P的坐标.练习:如图1,直线y 4x4和x轴、y轴的交点分别为B、C,点A的坐标是〔-2,30〕.〔1〕试说明△ABC是等腰三角形;〔2〕动点M从A出发沿x轴向点B运动,同时动点N从点B出发沿线段BC向点C运动,运动的速度均为每秒1个单位长度.当其中一个动点到达终点时,他们都停止运动.设M运动t 秒时,△MON的面积为S.①求S与t的函数关系式;②设点M 在线段OB上运动时,是否存在=4的情形?假设存在,求出对应的t值;假设不存在S请说明理由;③在运动过程中,当△MON为直角三角形时,求t的值.Word资料.模式4:等腰三角形分类标准:讨论顶角的位置或者底边的位置例如:请在抛物线上找一点p使得A、B、P三点构成等腰三角形,那么可分成以下几种情况1〕当A为顶角时,ACAB2〕当B为顶角时,BCBA3〕当C为顶角时,CACB例题4::如图 1,在平面直角坐标系x Oy中,矩形OABC的边OA在y轴的正半轴上,OC在x轴的正半轴上,OA=2,OC=3,过原点O作∠AOC的平分线交AB于点D,连接DC,过点D作DE⊥DC,交OA于点E.〔1〕求过点E、D、C的抛物线的解析式;〔2〕将∠EDC 绕点D按顺时针方向旋转后,角的一边与y轴的正半轴交于点,另一边与线F段OC交于点G.如果DF与〔1〕中的抛物线交于另一点M,点M的横坐标为6,那么EF=52GO是否成立?假设成立,请给予证明;假设不成立,请说明理由;Word资料.〔3〕对于〔2〕中的点G,在位于第一象限内的该抛物线上是否存在点Q,使得直线GQ与AB的交点P与点C、G构成的△PCG是等腰三角形?假设存在,请求出点Q的坐标;假设不存在成立,请说明理由.练习:〔2021江汉市中考模拟〕抛物线y =2+bx+(>0)经过点(12,0)和(0,-ax ca B C6),对称轴为x=2.(1)求该抛物线的解析式.(2)点D 在线段AB上且=,假设动点P从A出发沿线段AB以每秒1个单位长度的速度匀AD AC速运动,同时另一个动点Q以某一速度从C出发沿线段CB匀速运动,问是否存在某一时刻,使线段PQ被直线CD垂直平分?假设存在,请求出此时的时间t(秒)和点Q的运动速度;假设存在,请说明理由.(3)在(2)的结论下,直线x=1上是否存在点M,使△MPQ为等腰三角形?假设存在,请求出所有点M的坐标;假设不存在,请说明理由.yA PO DBx CQ模式5:相似三角形突破口:寻找比例关系以及特殊角例题5:〔据荆州资料第58页第2题改编〕在梯形ABCD中,AD∥BC,BA⊥AC,∠B= 450,AD=2,BC=6,以BC所在直线为x轴,建立如下图的平面直角坐标系,点A在y轴Word资料.上。
(完整word版)初三二次函数动点问题(教师版)

(完整 word 版)初三二次函数动点问题(教师版)二次函数动点问题1、如图,已知二次函数 y= 1 x 2 3 x 4 的图象与 y 轴交于点 A,与 x 轴交于 B、C 两点,其对称轴与 x 轴交于点 D, 42连接 AC. (1)点 A 的坐标为_______ ,点 C 的坐标为_______ ; (2)线段 AC 上是否存在点 E,使得△EDC 为等腰三角形?若存在,求出所有符合条件的点 E 的坐标;若不存在,请说明理由; (3)点 P 为 x 轴上方的抛物线上的一个动点,连接 PA、PC,若所得△PAC 的面积为 S,则 S 取何值时,相应的点 P 有且只有2 个?2、已知抛物线 y ax2 bx c(a 0)经过点 B(2,0)和点 C(0,8),且它的对称轴是直线 x 2 。
(1)求抛物线与 x 轴的另一交点 A 坐标; (2)求此抛物线的解析式;(3)连结 AC、BC,若点 E 是线段 AB 上的一个动点(与点 A、点 B)不重合,过点 E 作 EF∥AC 交 BC 于点 F,连结 CE, 设 AE 的长为 m,△CEF 的面积为 S,求 S 与 m 之间的函数关系式;(4)在(3)的基础上试说明 S 是否存在最大值,若存在,请求出 S 的最大值,并求出此时 点 E 的坐标,判断此时△BCE 的形状;若不存在,请说明理由。
3、如图,四边形 ABCD 是平行四边形,AB=4,OB=2,抛物线过 A、B、C 三点,与 x 轴交于另一点 D.一动点 P 以每秒1 个单位长度的速度从 B 点出发沿 BA 向点 A 运动,运动到点 A 停止,同时一动点 Q 从点 D 出发,以每秒 3 个单位长度的速度沿 DC 向点 C 运动,与点 P 同时停止.(1)求抛物线的解析式;(2)若抛物线的对称轴与 AB 交于点 E,与 x 轴交于点 F,当点 P 运动时间 t 为何值时,四边形 POQE 是等腰梯形?(3)当 t 为何值时,以 P、B、O 为顶点的三角形与以点 Q、B、O 为顶点的三角形相似?1/7(完整 word 版)初三二次函数动点问题(教师版)4、如图 1,已知抛物线经过坐标原点 O 和 x 轴上另一点 E,顶点 M 的坐标为 (2,4);矩形 ABCD 的顶点 A 与点 O 重合,AD、AB 分别在 x 轴、y 轴上,且 AD=2,AB=3。
中考数学:二次函数动点相关的压轴题.doc

中考数学:二次函数动点相关的压轴题在平面直角坐标系中,抛物线y=﹣x2/2+bx+c与x轴交于点A,B,与y轴交于点C,直线y=x+4经过A,C两点.(1)求抛物线的解析式;
(2)在AC上方的抛物线上有一动点P.
①如图1,当点P运动到某位置时,以AP,AO为邻边的平行四边形第四个顶点恰好也在抛物线上,求出此时点P 的坐标;
②如图2,过点O,P的直线y=kx交AC于点E,若PE:OE=3:8,求k的值.
考点分析:
二次函数综合题.
题干分析:
(1)由直线的解析式y=x+4易求点A和点C的坐标,把A和C的坐标分别代入y=﹣x2/2+bx+c求出b和c的值即可得到抛物线的解析式;
(2)①若以AP,AO为邻边的平行四边形的第四个顶点Q恰好也在抛物线上,则PQ∥AO,再根据抛物线的对称轴可求出点P的横坐标,由(1)中的抛物线解析式,进而可求出其纵坐标,问题得解;
②过P点作PF∥OC交AC于点F,因为PF∥OC,所以△PEF∽△OEC,由相似三角形的性质:对应边的比值相等可
求出PF的长,进而可设点点F(x,x+4),利用(﹣x2/2-x+4)-(x+4)=3/2,可求出x的值,解方程求出x的值可得点P的坐标,代入直线y=kx即可求出k的值.。
【中考数学压轴题专题突破02】二次函数中的动点问题
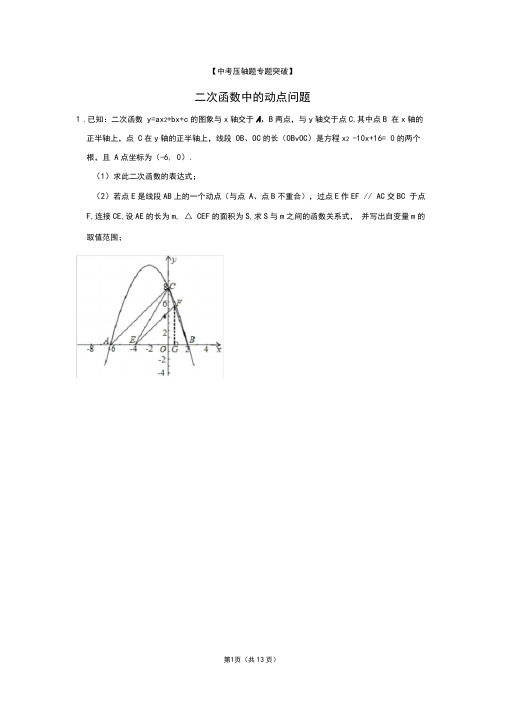
【中考压轴题专题突破】二次函数中的动点问题1.已知:二次函数y=ax2+bx+c的图象与x轴交于A、B两点,与y轴交于点C,其中点B 在x轴的正半轴上,点C在y轴的正半轴上,线段OB、OC的长(OBvOC)是方程x2 -10x+16= 0的两个根,且A点坐标为(-6, 0).(1)求此二次函数的表达式;(2)若点E是线段AB上的一个动点(与点A、点B不重合),过点E作EF // AC交BC 于点F,连接CE,设AE的长为m, △ CEF的面积为S,求S与m之间的函数关系式,并写出自变量m的取值范围;2.如图是二次函数y= ( x+m) 2+k的图象,其顶点坐标为M (1, -4).(1)求出图象与x轴的交点A, B的坐标;(2)在二次函数的图象上是否存在点P,使S APAB=—S;AMAB?若存在,求出P点的坐标,4若不存在,请说明理由;(3)点C在x轴上一动点,以BC为边作正方形BCDE ,正方形BCDE还有一个顶点(除点B外)在抛物线上,请写出满足条件的点E的坐标;(4)将二次函数的图象在x轴下方的部分沿x轴翻折,图象的其余部分保持不变,得到一个新的图象,请你结合这个新的图象回答:当直线y=x+b与此图象至少有三个公共点时,请直接写出b的取值范围是 .即圄2 邺3.如图,二次函数图象的顶点为坐标系原点O,且经过点A (3, 3), 一次函数的图象经过点A和点B (6, 0).(1)求二次函数与一次函数的解析式;(2)如果一次函数图象与y轴相交于点C,点D在线段AC上,与y轴平行的直线DE 与二次函数图象相交于点巳/ CDO = / OED ,求点D的坐标;(3)当点D在直线AC上的一个动点时,以点O、C、D、E为顶点的四边形能成为平行四边形吗?请说明理由.4.如图,二次函数y=ax2+bx+c (a^0)的图象与x轴交于A (- 3, 0)、B (1, 0 与y轴相交点C (0,近).(1)求该二次函数解析式;(2)连接AC、BC,点M、N分别是线段AB、BC上的动点,且始终满足BM = 接MN.①将4BMN沿MN翻折,B点能恰好落在AC边上的P处吗?若能,请判断四边形的形状并求出PN的长;若不能,请说明理由.②将^ BMN沿MN翻折,B点能恰好落在此抛物线上吗?若能,请直接写出此时于MN的对称点Q的坐标;若不能,请说明理由.两点,BN,连BMPNB点关5.如图,在平面直角坐标系中,抛物线y=』!x2-2F3x-代与x轴交于A、B两点(点3 3(1)判断△ ABC的形状,并说明理由;(2)如图(1),点P为直线BC下方的二次函数图象上的一个动点(点P与B、C不重合),过点p作Y轴的平行线交X轴于点E.当△ PBC面积的最大值时,点F为线段BC 一点(不与点BC重合),连接EF,动点G从点E出发,沿线段EF以每秒1个单位的速度运动到点F,再沿FC以每秒2工3个单位的速度运动到点C后停止,当点F的坐标| 3是多少时,点G在整个运动过程中用时最少?(3)如图2,将4ACO沿射线CB方向以每秒个单位的速度平移,记平移后的△ ACO 为AA l C l O l连接AA1,直线AA1交抛物线与点M,设平移的时间为t秒,当^ AMC 1为等腰三角形时,求t的值.6.如图,二次函数y=—x2+bx- -的图象与x轴交于点A (-3, 0)和点B,以AB为边在2 2x轴上方作正方形ABCD ,点P是x轴上一动点,连接DP ,过点P作DP的垂线与y轴交于点E.(1)b=;点D的坐标:;(2)线段AO上是否存在点P (点P不与A、。
中考数学压轴题 二次函数动点问题 专题练习

中考数学压轴题二次函数动点问题专题练习二次函数的动点问题已知抛物线经过原点O和x轴上另一点A,它的对称轴x=2与x轴交于点C,直线y=-2x-1经过抛物线上一点B(-2,m),且与y轴、直线x=2分别交于点D、E。
1) 求m的值及该抛物线对应的函数关系式。
通过点B(-2,m)在直线y=-2x-1上,可以求得m的值以及点B的坐标,进而求得抛物线的解析式。
解析式为y=x^2-x。
2) 求证:①CB=CE;②D是BE的中点。
通过分别求得CB和CE的长度来说明CB=CE。
过点B作BG∥x轴,与y轴交于F、直线x=2交于G,过点E作EH∥x轴,交y轴于H。
由△DFB≌△DHE,证得D是BE的中点。
3) 若P(x,y)是该抛物线上的一个动点,是否存在这样的点P,使得PB=PE?若存在,请求出所有符合条件的点P的坐标;若不存在,请说明理由。
若存在点P使得PB=PE,则点P必在线段BE的中垂线CD上。
动点P又在抛物线上。
通过解直线CD和抛物线对应的函数关系式所联立的方程组,其解即为所求点的坐标。
符合条件的点P应是直线CD与该抛物线的交点。
1.将点D(0,-1)和C(2,0)代入直线方程组,解得直线CD对应的函数关系式为y=x-1.另外,符合条件的点P的坐标为(3+5/22,1/2)或(3-5/22,-1/2)。
2.(1) 直线BC的解析式为y=-2x+5.2) 由三角形面积公式可得△ABC的面积为6.3) 设点M到点B的距离为x,则点N到点C的距离为2x。
由三角形面积公式可得△MNB的面积为(1/2)x(5-x)。
对该函数求导可得其最大值为5/8,此时x=5/4.因此,当点M运动1.25秒时,△MNB的面积最大,最大面积为1.5625.3.(1) 由平行四边形的性质可得FE∥AB,因此∠XXX∠CEG,且XXX。
因此,ΔBEF∽ΔCEG。
2) 当点E在线段BC上运动时,△BEF和△XXX的周长之间的比值为BE/CE,即x/(x+5)。
二次函数动点问题

二次函数动点问题二次函数是数学中的一个重要概念,也有很多实际应用。
在二次函数中,我们经常会遇到一种问题,即动点问题。
该问题要求我们根据给定的二次函数,确定函数图像上某个动点的坐标。
问题描述在二次函数动点问题中,我们通常会给出二次函数的方程和一个动点的初始位置。
我们需要通过计算,确定动点在函数图像上的位置。
具体来说,我们要求解动点的横坐标和纵坐标。
解决方法为了解决二次函数动点问题,我们可以采用以下步骤:1. 首先,我们需要根据二次函数的方程,确定函数的具体形式。
二次函数的一般形式为 $y = ax^2 + bx + c$,其中 $a$、$b$、$c$ 为已知常数。
2. 接下来,我们需要确定动点的初始位置。
动点通常以坐标的形式给出,例如 $(x_0, y_0)$。
我们将动点的初始位置代入二次函数的方程,得到动点的纵坐标 $y_0$。
3. 然后,我们需要计算动点的横坐标。
根据函数图像的对称性,动点的横坐标为二次函数的顶点的横坐标。
顶点的横坐标可以通过以下公式计算:$x_v = -\frac{b}{2a}$。
4. 最后,我们可以得到动点在函数图像上的位置。
动点的横坐标为 $x_v$,纵坐标为 $y_0$。
实例演示以下是一个示例,演示了如何解决二次函数动点问题:已知二次函数的方程为 $y = x^2 + 2x + 1$,动点的初始位置为$(2, y_0)$。
我们可以按照以下步骤求解动点的位置:1. 将动点的横坐标代入二次函数的方程,得到动点的纵坐标:$y_0 = 2^2 + 2 \cdot 2 + 1 = 9$。
2. 计算二次函数的顶点的横坐标:$x_v = -\frac{2}{2 \cdot 1} = -1$。
3. 动点的位置为 $(x_v, y_0) = (-1, 9)$。
通过以上计算,我们得到了动点在函数图像上的位置。
结论二次函数动点问题是一个常见的数学问题。
通过确定二次函数的形式和动点的初始位置,我们可以计算出动点在函数图像上的位置。
二次函数动点问题压轴题专题汇编(含答案)

二次函数动点问题压轴题专题汇编(含答案)二次函数的动态问题(动点)正方形ABCD的顶点A,B的坐标分别为(0,10),(8,4),顶点C,D在第一象限。
点P从点A出发,沿正方形按逆时针方向匀速运动,同时,点Q从点E(4,0)出发,沿x轴正方向以相同速度运动。
当点P到达点C时,P,Q两点同时停止运动,设运动的时间为t秒。
1) 求正方形ABCD的边长。
解:作BF⊥y轴于F。
则FB=8,FA=6,AB=10.2) 当点P在AB边上运动时,△OPQ的面积S(平方单位)与时间t(秒)之间的函数图象为抛物线的一部分。
求P,Q两点的运动速度。
解:由图可知,点P从点A运动到点B用了10秒。
又AB=10,故P,Q两点的运动速度均为每秒1个单位。
3) 求(2)中面积S(平方单位)与时间t(秒)的函数关系式及面积S取最大值时点P的坐标。
解:方法一:作PG⊥y轴于G,则PG∥BF。
由相似三角形可得:GA/AP=FA/AB,即6/10=t/AP,故GA=3/5t。
又OG=10-3/5t,OQ=4+t。
则S=1/2×OQ×OG=1/2×(t+4)×(10-3/5t)=-3/10t²+19/5t+20.对XXX求导得:S'=(-6/5)t+19/5,令其为0,解得t=19/3.此时S有最大值。
此时GP=76/15,OG=31/5,P的坐标为(76/15,31/5)。
方法二:当t=5时,OG=7,OQ=9,S=63/2.设所求函数关系式为S=at²+bt+20.抛物线过点(5,63/2),则a=-3/10,b=19/2.代入可得S=-3/10t²+19/2t+20.同样可得最大值时t=19/3,P的坐标为(76/15,31/5)。
4) 若点P,Q保持(2)中的速度不变,则点P沿着AB边运动时,∠XXX的大小随着时间t的增大而增大;沿着BC边运动时,∠XXX的大小随着时间t的增大而减小。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
二次函数压轴题
1.如图:抛物线经过 A(-3 ,0)、 B(0,4)、 C(4,0)三点 .
(1)求抛物线的解析式 .
(2)已知 AD = AB( D 在线段 AC上),有一动点 P 从点的速度移动;同时另一个动点Q以某一速度从点B 沿线段PQ被 BD垂直平分,求 t 的值;A 沿线段 AC以每秒 1 个单位长度BC移动,经过 t 秒的移动,线段
(3)在(2)的情况下,抛物线的对称轴上是否存在一点 M,使 MQ+MC的值最小?若存在,请求出点 M的坐标;若不存在,请说明理由。
2. 如图 9,在平面直角坐标系中,二次函数的图象的顶点为D点,与 y 轴交于 C 点,与 x 轴交于
A、B 两点, A 点在原点的左侧, B 点的坐标为( 3, 0),
OB=OC ,tan ∠ACO=.
(1)求这个二次函数的表达式.
()经过、两点的直线,与x 轴交于点
E,在该抛物线上是否存在这样的点 F,使以点 A、
2 C D
C、E、F 为顶点的四边形为平行四边形?若存在,请求出点 F 的坐标;若不存在,请说明理
由.
(3)如图 10,若点 G( 2, y)是该抛物线上一点,点 P 是直线 AG下方的抛物线上一动点,当点 P 运动到什么位置时,△ APG的面积最大?求出此时 P 点的坐标和△ APG的最大面积 .
3. 如图,已知抛物线与x 轴交于 A(- 1, 0)、 B(3,0)两点,与 y 轴交于点 C(0,3)。
⑴求抛物线的解析式;
⑵设抛物线的顶点为 D,在其对称轴的右侧的抛物线上是否存在点 P,使得△ PDC是等腰三角形?若存在,求出符合条件的点 P 的坐标 ; 若不存在,请说明理由 ;
⑶若点 M是抛物线上一点,以B、C、D、M为顶点的四边形是直角梯形,试求出点M的坐标。
4.已知:抛物线 y=ax2+bx+c 与 x 轴交于 A、B 两点,与 y 轴交于点 C,其中点 B 在 x 轴的正半
轴上,点 C 在 y 轴的正半轴上,线段OB、OC的长( OB OC)是方程 x2-x+=
0的两个根,
<1016
且抛物线的对称轴是直线x=- 2.
(1)求 A、B、C 三点的坐标;
(2)求此抛物线的表达式;
(3)求△ ABC的面积;
(4)若点 E 是线段 AB上的一个动点(与点 A、点 B 不重合),过点 E 作 EF∥AC交 BC于点F,连接 CE,设 AE 的长为 m,△ CEF的面积为 S,求 S 与 m之间的函数关系式,并写出自变量 m 的取值范围;
(5)在( 4)的基础上试说明 S 是否存在最大值,若存在,请求出 S的最大值,并求出此时点
E 的坐标,判断此时△ BCE的形状;若不存在,请说明理由.
5.已知抛物线与轴的一个交点为 A(-1,0) ,与 y 轴的正半轴交于点 C.
⑴直接写出抛物线的对称轴,及抛物线与轴的另一个交点 B 的坐标;⑵
当点 C 在以 AB为直径的⊙P 上时,求抛物线的解析式;
⑶坐标平面内是否存在点,使得以点M和⑵中抛物线上的三点 A、 B、 C 为顶点的四边形是平行
四边形?若存在,请求出点的坐标;若不存在,请说明理由.
6、如图,已知抛物线y x 2bx c 与x轴负半轴交于点A,与y轴正半轴交于点B,且 OA=OB.
(1)求 b + c的值;
(2)若点 C 在抛物线上,且四边形 OABC是平行四边形,求抛物线的解析式;
(3)在(2)条件下,点 P(不与 A、C重合)是抛物线上的一点,点 M是y轴上一点,当△ BPM 是等腰直角三角形时,求点M的坐标 .
7、如图,已知抛物线y=ax2 +bx+c(a≠0)与 x 轴相交于点 A(-2 , 0) 和点 B,与 y 轴相交于点 C,
9
顶点 D(1 ,- 2).
(1)求抛物线对应的函数关系式;
(2)求四边形 ACDB的面积;
(3)若平移 (1) 中的抛物线,使平移后的抛物线与坐标轴
...
仅有两个交点,请直接写出一个平移后的抛物线的关系式.]
8、如图a,在平面直角坐标系中,A,
6)
, B,
0).
(0(4
( 1)按要求画图:在图 a 中,以原点 O为位似中心,按比例尺1:2 ,将△ AOB缩小,得到△
DOC,使△ AOB与△ DOC在原点 O的两侧;并写出点 A 的对应点 D的坐标
为,点B
的对应点 C的坐标为;
(2)已知某抛物线经过 B、 C、D三点,求该抛物线的函数关系式 , 并画出大致图象;
(3)连接 DB,若点 P 在 CB上,从点 C 向点 B 以每秒 1 个单位运动,点 Q 在 BD上,从点 B 向点 D以每秒 1 个单位运动,若 P、Q两点同时分别从点 C、点 B 点出发,经过 t 秒,当 t 为何值时,△ BPQ是等腰三角形?
、(
2013江苏扬州弘扬中学二模)如图所示,已知抛物线y 1 x2x k 的图象与y轴相交于
9
4
点B(0,1),点 C(m,n)在该抛物线图象上,且以 BC为直径的⊙ M恰好经过顶点 A.
(1)求 k 的值;( 2)求点 C 的坐标;( 3)若点 P 的纵坐标为 t ,且点 P 在该抛物线的对称
轴 l 上运动,
试探索:①当 S1< S< S2时,求 t 的取值范围
(其中: S 为△ PAB的面积, S1为△ OAB的面积, S2为四边形 OACB的面积);
②当 t 取何值时,点 P 在⊙ M上.(写出 t 的值即可)
10如图 1,在平面直角坐标系xOy中,顶点为M的抛物线y=ax2+bx(a> 0)经过点A和x轴正半轴上的点 B, AO= BO=2,∠ AOB=120°.
(1)求这条抛物线的表达式;
(2)连结OM,求∠AOM的大小;
(3)如果点C在x轴上,且△ABC与△AOM相似,求点C的坐标.
11
如图 1,已知抛物线 y
1 x 2
1
(b 1)x
b
( b 是实数且 b >2)与 x 轴的正半轴分别交于点
A 、
4 4 4 (点 位于点
B 是左侧),与
y 轴的正半轴交于点 .
BA
C
( 1)点 B 的坐标为 ______,点 C 的坐标为 __________(用含 b 的代数式表示);
( 2)请你探索在第一象限内是否存在点P ,使得四边形 PCOB 的面积等于 2b ,且△ PBC 是以点 P 为直
角顶点的等腰直角三角形?如果存在,求出点P 的坐标;如果不存在,请说明理由;
( 3)请你进一步探索在第一象限内是否存在点Q ,使得△ QCO 、△ QOA 和△ QAB 中的任意两个三角形
均相似(全等可看作相似的特殊情况)?如果存在,求出点Q 的坐标;如果不存在,请说明理由.
12 如图 1,已知抛物线的方程
C 1: y
1
(x 2)( x m) ( m > 0) 与 x 轴交于点 B 、C ,与 y 轴交于点
m
E ,且点 B 在点 C 的左侧.
( 1)若抛物线 C 1 过点 M (2, 2) ,求实数 m 的值;
( 2)在( 1)的条件下,求△ BCE 的面积;
(3)在( 1)的条件下,在抛物线的对称轴上找一点
H ,使得 BH + EH 最小,求出点 H 的坐标;
( 4)在第四象限内,抛物线 C 1 上是否存在点 F ,使得以点 B 、 C 、 F 为顶点的三角形与△ BCE 相似?若存在,求 m 的值;若不存在,请说明理由.
13 . 如图 1,已知梯形 OABC ,抛物线分别过点 O (0, 0)、 A (2, 0)、 B ( 6, 3).
(1)直接写出抛物线的对称轴、解析式及顶点M的坐标;
(2)将图 1 中梯形OABC的上下底边所在的直线OA、CB以相同的速度同时向上平移,分别交抛物线
于点O1、A1、 C1、 B1,得到如图 2 的梯形O1A1B1C1.设梯形O1A1B1C1的面积为S,A1、B 1的坐标分别为(x1,y1)、( x2,y2).用含S的代数式表
示
x2- x1,并求出当S=36时点A1的坐标;
(3)在图 1 中,设点D的坐标
为(1 ,3) ,动点P 从点B出发,以每
秒
1 个单位长度的速度沿着线段
BC运动,动点 Q从点 D出发,以与点 P相同的速度沿着线段DM运动. P、Q两点同时出发,当点
M时, P、Q两点同时停止运动.设P、Q两点的运动时间为t ,是否存在某一时刻t ,使得直线AB、x轴围成的三角形与直线PQ、直线 AB、抛物线的对称轴围成的三角形相似?若存在,请求出
Q到达点PQ、直线t 的值;
若不存在,请说明理由.
14.如图 1,抛物线经过点A(4 ,0) 、B( 1, 0) 、C(0,- 2)三点.
(1)求此抛物线的解析式;
(2)P是抛物线上的一个动点,过P作PM⊥x轴,垂足为M,是否存在点P,使得以A、P、M为顶点
的三角形与△相似?若存在,请求出符合条件的点
P 的坐标;若不存在,请说明理由;
OAC
(3)在直线上方的抛物线是有一点,使得△的面积最大,求出点的坐标.AC D DCA D
,。
