铝化炸药非理想爆轰的简化模型
新爆轰模型及其实验验证_胡绍鸣

4.1
2 10 (2.6210 CJ
24
关联宏观爆速 D 与细观粒子速度 u 爆轰区剖面上各个粒子的速度 ui 大小和方向不
10)
, 爆轰过程终点仍然是点 ‘2’. 这是
由于阿伏伽德罗数 N A 太大 , 也就是单位体积中的分 子数目太多, 分子理化特性不足以影响统计结果[12]. 王竹溪 [13] 指出 : 热力学中的一个基本现象是趋 向平衡态, 这是一个显著的不可逆过程. 不可逆过程 的例子包括各种爆炸过程 . 力学中的平衡态只是单 纯静止的问题; 在热力学中的平衡态不但要静止, 而 且要所有能观察到的性质都不随时间改变 . 作为典 型的热现象 , 爆轰过程终点应该是热力学平衡的静 止态. 静止态粒子平均速度为 u2 0. (6) u 为粒子速度. 代入质量守恒关系式(3): ( D u2 ) / v2 ( D u0 ) / v0 , D 为爆速; 下标 0, 炸药. 因为炸药粒子速度为 u0 =0, 则可得
2011 年
第 41 卷
第 10 期: 1230 ~ 1238
《中国科学》杂志社
SCIENCE CHINA PRESS
www.sc胡绍鸣*, 田清政, 肖川, 苏健军, 王辉, 杨凯, 袁建飞, 孔军利, 宋浦, 齐存秀, 王建灵, 郭炜, 赵洁
中国科学: 物理学 力学 天文学
2011 年
第 41 卷
第 10 期
2 LADM 模型简介
如图 1 所示, 爆轰波阵面和反应区粒子运动极为 复杂, 阵面不光滑, 存在横波、微爆炸、紊流、热点、 间断面、纵向不稳定等等 (本文统称复杂运动 ), 用牛 顿力学方法分析力的关系很困难 . 爆轰波反应区除 化学反应外, 还存在摩擦、扩散和热传导等物理过程 (本文统称输运效应), 它们使各个爆轰产物粒子之间 出现动量、质量和能量的传递. 复杂运动强化了输运 效应 , 使有序的动能和化学能迅速耗散成了无序的 热能. 要描述如此复杂的爆轰图像非常困难, 传统方 法是简化为一维层流并忽略输运效应. LADM 模型认为 , 复杂运动和输运效应在爆轰 过程中起重要作用 , 提出用熵原理概括输运效应的 结果, 确定爆轰过程终点; 用 Hamilton 原理描述爆轰 产物粒子复杂运动 , 确定有序能量耗散成热能的真 实过程
非理想爆轰波阵面传播的LevelSet方法在爆轰驱动计算中的应用研究

非理想爆轰波阵面传播的Level Set方法在爆轰驱动计算中的应用研究姜洋*,钟敏,孙承纬,李平,柏劲松(中国工程物理研究院流体物理研究所,四川绵阳 621900)摘要:基于爆轰冲击波动力学(DSD)理论,研究了计算二维贴体坐标系中非理想爆轰波阵面传播问题的Level Set方法。
根据Hamilton-Jacobi方程的Godunov差分格式,提出了非正交的贴体坐标系中Level Set函数方程的差分格式及其相应的数值方法。
将Level Set方法应用于自行研制的二维流体动力学程序TDY2D得到编码TDY_DSD,对爆轰波的传播及爆轰驱动的实验模型进行了数值模拟计算,所得的计算值均与实验值符合较好,具有较高精度。
关键词:爆炸力学;爆轰驱动;DSD理论;Level-Set方法;贴体坐标系;数值模拟中图分类号:O241;O382;O383文献标识码:AApplication of the Level Set method for propagation of non-ideal detonation to the numerical simulation for acceleration of metals by detonation waveAbstract:Based on the DSD (Detonation Shock Dynamics) theory, the Level Set method in body-fitted coordinate for propagation of non-ideal detonation is studied in this paper. According to the Hamilton-Jacobi formulation of the Godunov’s scheme, the finite difference method and algorithm for the propagation equation of non-ideal detonation in non-orthogonal body-fitted coordinate are studied. Then the Level Set method is incorporated into the 2D hydrodynamic code TDY2D to form a combination code TDY_DSD and it is used to compute some models about the propagation of detonation wave and the motion of flyers driven by explosive. The computation results are in good agreement with the experimental data and the precision in calculation is high.Key words: Mechanics of explosion; Acceleration by detonation products; DSD theory; Level set method; Body-fitted coordinate; Numerical simulation*作者简介:姜洋(1976-),女,助理研究员,博士生 从事计算流体力学、计算爆炸力学的理论和数值计算方法方面研究通信地址:四川绵阳919信箱105分箱 邮编621900电话:***********Email:**********************0引言对复杂几何形状炸药中爆轰波阵面传播过程的描述是炸药驱动装置设计中的一个重要课题,在军事及工程研究中具有重要的实际应用价值。
含铝炸药能量释放的简化模型

含铝炸药能量释放的简化模型
周俊祥;徐更光;王廷增
【期刊名称】《爆炸与冲击》
【年(卷),期】2005(025)004
【摘要】为了在水下爆炸效应中反映出非理想爆轰特性的影响,建立了含铝炸药非理想爆轰能量释放的简化模型.该模型以CJ爆轰理论和二次反应理论为基础,把含铝炸药化学反应划分为快速反应和慢速反应,以释放的化学能和慢反应速率常数作为非理想特征参数,并应用于一维数值模拟.计算结果与基本实验结果一致,冲击波峰值的计算误差不大于10%,衰减时间常数的误差小于5%,冲击波能与实验值也具有良好的一致性.简化模型合理地描述了含铝炸药非理想爆轰的主要过程及非理想特性,可应用于含铝炸药的设计和爆炸效应的分析.
【总页数】4页(P309-312)
【作者】周俊祥;徐更光;王廷增
【作者单位】北京理工大学机械电子工程系,北京,100081;北京理工大学机械电子工程系,北京,100081;北京理工大学机械电子工程系,北京,100081
【正文语种】中文
【中图分类】O381
【相关文献】
1.分层开采煤矿的矿震能量释放模型与能量释放谱 [J], 李铁;蔡美峰;蔡明
2.含铝炸药Miller能量释放模型的应用 [J], 辛春亮;徐更光;刘科种;秦健
3.含铝炸药爆压及能量释放过程的研究 [J], 韩勇;韩敦信;卢校军;黄毅民;何碧;关立峰
4.DNAN基含铝炸药烤燃实验与数值模拟 [J], 吴浩;段卓平;白孟璟;黄风雷
5.含铝炸药装药杀爆战斗部爆炸威力评估 [J], 肖师云;丁华;华绍春;陈文;刘俞平因版权原因,仅展示原文概要,查看原文内容请购买。
含铝炸药在密实介质中爆炸响应的FE-SPH耦合算法模拟研究

含铝炸药在密实介质中爆炸响应的FE-SPH耦合算法模拟研究爆炸效应在工程技术中有广泛的应用,如爆破拆除、爆炸成型、爆炸焊接、破岩和破冰等。
爆炸问题涉及到高温、高压、强冲击以及大变形等问题,爆炸荷载作用下的材料往往容易发生大变形、破碎和飞溅等现象。
鉴于实验研究耗费高、周期长和测取参量有限,为了弥补实验的不足以及在炸药制备前开展大量的规律性研究,数值模拟成为炸药研究过程中的重要手段之一。
目前,针对含铝炸药已开展的数值模拟研究主要是以传统的基于网格的数值方法为主,但有限元法对于大变形问题往往会产生单元畸变,其求解精度和效率都会明显降低。
光滑粒子法对大变形问题具有很强的求解能力,能够有效再现材料的破碎和飞溅等复杂物理现象,但在计算效率和边界条件的处理方面不如有限元法。
耦合有限元法与光滑粒子法,可以充分利用两者的优势,为大变形问题的模拟提供有效途径。
首先,本文应用轴对称FE-SPH自适应耦合算法对含铝炸药在混凝土介质中的爆炸响应过程进行模拟研究。
含铝炸药的爆炸过程采用JWL状态方程结合Miller反应速率方程来描述,同时采用接触处理算法避免爆炸响应后转化的SPH 粒子点间形成非物理穿透,并对不同含铝量炸药在不同埋深下的爆炸响应过程进行了数值模拟。
结果表明,轴对称FE-SPH自适应耦合算法能够稳定再现含铝炸药在混凝土介质中的爆炸响应过程,响应的特征参量也与试验数据相吻合,可以为含铝炸药在混凝土介质中爆炸问题的数值模拟研究提供新的有效途径。
其次,由于国内外对含铝炸药在混凝土复合介质中的爆炸毁伤效应研究相对较少。
因此,本文将应用三维FE-SPH自适应耦合算法模拟研究含铝炸药在混凝土复合介质中的爆炸毁伤规律,并与实验数据进行比较,验证数值分析模型的有效性。
在此基础上研究含铝炸药在爆轰过程中的压力特性以及铝粉含量和炸药埋深等因素对爆炸毁伤规律的影响。
研究结果表明,在药量一定的条件下,混凝土复合介质毁伤效应受炸药铝粉含量、炸药埋深的影响较大。
3.3炸药的爆轰理论
炸药径向间隙效应
视频1 视频2
可采取选用爆速大的炸药和大直径药 卷及坚固外壳等措施,实现稳定爆轰。
视频1
视频2
七、爆速的测定方法
炸药的爆速是衡量炸药爆炸性能的重 要标志量,也是目前可以比较准确测定的 一个爆轰参数。
测量方法 (1)导爆索法 (2)电测法 (3)高速摄影法
视频1 视频2
l
h
导爆索法测爆速
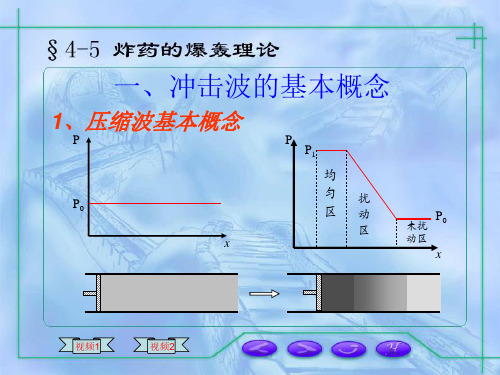
一、冲击波的基本概念
1、压缩波基本概念
P P
P1
P0 x
均 匀 区
扰 动 区
未扰 动区
P0 x
视频1
视频2
在无限长气筒活塞右侧充满压力为P0 的气体,当活塞在F力的作用下向右运动 时,活塞右侧气体存在三个区域: 压力为P1的均匀区 压力介于P1与P0之间的扰动区 压力仍为P0的未扰动区
视频1
视频2
视频1 视频2
2
1 0
使介质运动的力是波阵面两边的压力差 PH P0 在单位时间内流进波阵面的介质质量为 0 ( D u0 ) 其速度的变化为 ( D u 0 ) ( D u H ) u H u 0 根据动量守恒定律有:
PH P0 0 ( D u 0 )( u H u 0 )
已反应的药包
视频1 视频2
未反应的药包
1)炸药达到稳定爆轰前有 一个不稳定的爆炸区。
2)在特定的条件下,每种 炸药都会有一个不变的炸 药特征爆速Di。 3) 每种炸药都存在一个最 小的临界爆速Dc。波速低 于Dc后,冲击波将衰减为 音波而导致爆轰熄灭。
炸药包在冲击波激发下的爆轰过程
视频1 视频2
(2)爆轰波模型
H ( D u H )[ E H
RDX基铝纤维炸药空中爆炸性能

空中爆炸实验采用直径为2.4 m、长为4.5 m 的空中爆炸容器,测试装置包括压力传感 器、恒 流 源 和示波器。固定传感器时确保传感器水平,传感器的平面部分平行 于 铅 垂 面,传 感 器 指 向 被 测 药 柱,并
与药柱处于同一水平面上,实验装置如图1所示。为了对比研究铝纤维 炸 药 与 铝 粉 炸 药 以 及 基 体 炸 药 RDX 空中爆炸性能参数和衰减规律,在距离药柱0.7 m 处安放传感器,并测得压力时程曲线。
国 标 学 科 代 码 :1303520
文 献 标 志 码 :A
对空武器的装药选取需要考虑多方面因素,其中重要的性能指标 有 冲 击 波 压 力 峰 值 和 冲 量。有 学 者对不同等效距离上的 TNT 压力峰值 的 实 验 和 理 论 值 进 行 了 总 结,得 到 不 同 的 压 力 峰 值 经 验 计 算 公 式。H.L.Brode等 总 [1] 结的压力峰值经验公式计算结果与实验验 数 据 有 较 大 的 偏 差,因 此 无 法 直 接 应 用到战斗部威力评估中。於津等 提 [2] 出的压力峰值经 验 公 式 虽 然 精 度 有 所 提 高,但 由 于 缺 乏 大 量 实 验 数据导致其经 验 公 式 的 适 用 范 围 较 小。 张 陶 等 分 [3] 别 测 试 了 油 气 炸 弹 (fuelairexplosives,FAE)和 TNT 爆炸场压力峰值,结果表明 FAE 爆炸场压力分布规律与 TNT 有显著区别。牛余雷等 测 [4] 量 了 3 种 双 元 炸 药 空 中 爆 炸 冲 击 波 压 力 时 程 曲 线 ,并 与 单 一 炸 药 进 行 比 较 ,结 果 表 明 双 元 炸 药 的 装 药 结 构 可 使 两部分装药之间产生能量耦合,从 而 提 高 装 药 的 能 量 输 出。 仲 倩 等 对 [5] 于 不 同 装 药 量 的 TNT 冲 击 波 压力进行测定,提出了压力峰值与比 例 距 离 关 系 的 改 良 经 验 公 式,其 与 文 献 数 据 相 对 偏 差 的 平 均 值 为 5.61%。传统上,对于非 TNT 炸药,可通过实验得到其冲击波压力峰值,并与 TNT 炸药的压力峰值进 行比较,从而求出该炸药的爆炸威力(TNT 当量 比)[6],但 这 种 方 法 仅 对 理 想 炸 药 适 用。 空 中 武 器 装 填 的 炸 药 由 于 类 型 并 不 相 同 ,不 同 类 型 的 炸 药 在 空 中 爆 炸 时 爆 轰 特 性 以 及 冲 击 波 衰 减 规 律 也 不 尽 相 同 ,按 照冲击波压力峰值进行估算炸药威力往往会得出错误结论,因此需要对不 同 类 型 的 炸 药 进 行 空 中 爆 炸 实验 。 [7] 有学者对如何提高炸药爆炸后在介质中产生 的 压 力 以 及 冲 击 波 冲 量 进 行 了 深 入 研 究,认 为 在 炸 药 中 加 入 金 属 粉 末 可 以 在 爆 炸 中 额 外 释 放 出 能 量 ,虽 然 这 部 分 能 量 对 爆 速 和 爆 压 均 无 贡 献 ,但 可 以 增 强炸药在周围介质中形成的冲击 波 压 力 和 冲 击 波 冲 量 。 [8] 本 文 中,将 传 统 含 铝 炸 药 (RDX/Al)中 的 铝 粉用铝纤维替代,得到新型铝纤维炸药[9],通过对铝纤 维 炸 药 与 传 统 含 铝 炸 药 以 及 基 体 炸 药 RDX 进 行 空 中 爆 炸 实 验 ,分 析 三 者 空 中 爆 炸 性 能 的 差 异 ,以 期 为 进 一 步 提 高 含 铝 炸 药 的 性 能 提 供 参 考 。
Ansys_AUTODYN计算求解一般步骤中文解析

MO-Granular 强度模型
常用于干土、沙子、岩石、混凝土和陶瓷等材料。
压强硬化
10 点分段屈服应力-压强曲线 密度硬化 10 点分段屈服应力-密度曲线
剪切模量变量
10 点分段剪切模量-密度曲线
一般问题的分析步骤-第二步 定义材料(续) Johnson-Holmquist 模型
C 和γ是常数
失 效 概 率
C γε P=1-exp - γ e
• γ 由用户定义
• C 通过计算得到
• 分布类型:
– Fixed–每一时刻相同 – Random-任意
JWL 状态方程用于爆炸产物
用于拉格朗日和 SPH 求解器。
一般问题的分析步骤-第二步 定义材料(续) 用户自定义状态方程
用户自定义状态方程 子程序 EXEOS 定义 通过公共块使用其它的变量 提供子程序构架
一般问题的分析步骤-第二步 定义材料(续)
材料强度类型
None
用单精度来满足求解效率和内存的需要:
避免出现压力低于10-6的单位制;
避免出现单元质量低于10-6的单位。
缺省单位:
长度 质量 时间 速度 mm mg ms m/s
力 mN
压强 密度 能量 kPa g/cm3 mJ
一般问题的分析步骤-第二步 定义材料
第一种方式:材料库选择材料模型
– Miller 模型表达了这种能量释放
P A(1
w
R1V
)e R1V B(1
w
R2V
)e R2V
w ( E Q)
V
d a (1 ) m P n dt
Q= a = m= n = 附加的比能, 能量释放常数, 能量释放指数, 压力指数
爆炸与炸药的基本理论ppt课件

通常采取相对某种已知的炸药作比较 来确定炸药的威力。
相对重量威力
相对体积威力
通常情况下仅有10%的炸药发挥了功效。损失原因如下:
1.化学损失 2.热损失 3.无效的机械损失
表示侧向飞散 带走部分未反应炸药 损失能量的50% 包括振动 抛掷 冲击波
炸药的爆炸性能
猛度 破碎能力。
爆速越高 猛度越大 岩石破碎度越高
炸药的爆轰理论
爆轰波的基本方程(冲击波分析法)
质量守恒: 动量守恒:
0 D H (D D H )
P HP 0 D H
能量守恒:
E H E 0 Q 1 2 (H 0 )V ( 0 V H )
ρ0 ----- 初始炸药密度
ρH ----- 反应区炸药密度 DH ----- 爆轰气体流速 D ----- 爆速 V0 ----- 炸药初始质量体积
炸药的爆炸性能
消除沟槽效应的方法:
1. 采取提高爆速的手段 使爆轰波的传递速度大于等离子波的传播速度。
(V>4500m/s)
2. 提高外包装质量。
提高包装外壳的强度 爆速将上升 沟槽效应下降
即提高了抵御等离子波的压缩穿透作用。
3. 堵塞等离子波的传播。
炮孔中设置卡环 炮孔中填充炮泥
增大药卷直径
工业生产最小药卷 Φ25 cm
沟槽效应产生的原因 1. 爆炸产物压缩药卷和孔壁间的空气,产生冲击波,它超前于爆轰波
并压缩药卷, 从而抑制爆轰。 2.美国学者认为:沟槽效应是由于药卷外部炸药爆轰产生的等离子体
影响。即炸药起爆后 在爆轰波阵面的前方有一等离子层,对后面未 反应的药卷表层产生压缩作用,妨碍该层炸药的完全反应。 (以上两种说法都有一定的实验依据 但还需要进一步发展完善)
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
铝化炸药非理想爆轰的简化模型摘要:本文以CJ 爆轰理论和二次反应理论为基础,建立了铝化炸药非理想爆轰的简化模型。
该模型把铝化炸药化学反应划分为快速反应和慢速反应,并以释放的化学能和慢反应速率常数作为非理想特征参数。
应用于一维数值模拟的计算结果与基本实验事实相一致,表明简化模型合理地描述了铝化炸药非理想爆轰的主要过程及非理想特性。
关键词:铝化炸药;非理想爆轰;数值模拟1引言铝化炸药是典型的非理想炸药,其各组分化学能的释放速率存在显著差异,且较慢的反应过程显著低于流体动力学特征时间。
因此,以经典热力学为基础的CJ 爆轰理论不能描述铝化炸药的非理想爆轰过程,化学反应动力学行为已成为铝化炸药爆轰性能和爆炸效应分析中的重要因素。
但由于炸药在高温、高压下反应过程的复杂性,目前对反应机理以及反应速率函数关系的认识还是唯象的和经验性的。
在应用化学反应流体动力学所作的理论分析中,对氧化剂的分解和铝粒子的氧化等主要的化学和物理过程必须做出适当的假设[1]。
在以WK 爆轰理论为基础的动力学模型中,化学能的释放则被分解为快、慢两个过程,并采用形式相同的反应速率函数[2]。
这些处理方法在分析爆轰波与化学反应间的相互作用方面是非常有效的,爆轰性能的计算结果与实验值具有良好的一致性。
而在铝化炸药爆炸效应的数值分析中,常常沿用点火-燃烧-快反应三项式反应速率函数描述能量释放过程[3],明显地缺乏与非理想爆轰特征相对应的物理意义。
本文以CJ 爆轰理论和铝化炸药二次反应理论为基础,建立了一种能表述主要非理想特性的简化模型。
2非理想爆轰的简化模型炸药冲击起爆以及爆轰建立过程的化学动力学分析模型一般包含如下内容:未反应炸药的状态方程;爆轰产物状态方程;混合物规则和反应速率方程。
设未反应炸药比内能为χe ,爆轰产物比内能为p e ,已反应炸药的质量分数(反应进程度)为λ,则混合物的比内能为()p χ1e e e λλ+-= (1) 其中 ()p p ,q v p e e -= (2)()v p e ,为某种形式的爆轰产物状态方程,p 为压力,v 为比容,p q 为单位质量炸药释放的化学能。
铝化炸药的组成通常可划分为快反应的理想组分(如RDX ,HMX )和慢反应的非理想组分(如AP ,Al ,粘结剂等)。
AP 的分解以及Al 的氧化速率通常比RDX 的分解速率低二个数量级,但能量水平较高。
因此,可以认为铝化炸药的化学变化过程主要由非理想组分的慢反应所控制,即相当数量的化学能在CJ 点之后持续释放是其主要的非理想特性。
根据铝化炸药的二次反应理论,假设理想组分在CJ 点全部反应完毕,CJ 点之后的稀疏波区只是非理想组分的反应区域。
由于可认为理想组分的分解是次要的能量释放过程,可进一步假设其反应速率为无穷大,即可以不再考虑炸药的冲击起爆和稳态反应区内的变化过程。
设理想组分的初始质量分数为0I λ,在t 时刻非理想组分反应的质量分数为NI λ,则有N I 0I λλλ+= (3)代入(1)式,可得()()()N I N I I 0I χ,1q qv p e e e λλλλ+-+-= (4)式中I q 、NI q 分别为理想组分和非理想组分的反应热,并有化学能释放为N I N I I 0I p q q q λλ+= (5)因此,(3)、(5)两式明确地反映了铝化炸药非理想爆轰的进程及能量释放过程,根据上述假设,可进一步令()()()v p e e v p e ,1,,χλλλ+-= (6) 即可采用一个与λ相关的状态方程描述爆轰产物从CJ 点开始的非等熵膨胀。
则由(1)式表示的爆轰产物比内能改写为()()λλp ,,q v p e e -= (7)由(3)式可知,非理想组分的反应速率即为铝化炸药的反应速率。
对铝化炸药具有普适性的是与压力相关的反应速率方程[4]()61211d d p a tλλ-= (8)式中a 为反应速率常数,是单位压力下的初始反应速率。
按上述方法,铝化炸药非理想爆轰的动力学分析主要包括两部分内容:与λ相关的爆轰产物状态方程和非理想组分的反应速率方程,具体关系式为(3)、(5)、(7)、(8)式。
这个简化的分析模型是针对铝化炸药的非理想爆轰建立的,并包含着可评价铝化炸药非理想程度的特征参数:理想组分和非理想组分的化学能以及非理想组分的反应速率常数,因而具有了明确的物理意义。
两类化学能可由热力学计算得出,反应速率方程中的各项参数则可根据相应的水下爆炸实验数据分析得到[5]。
可以看出,若(8)式中的速率常数a →∞,则该简化模型退化为CJ 模型。
3在一维数值分析中的应用铝化炸药在无限水域中的爆炸效应可以采用方便、快捷的一维非定常数值分析。
以一维球对称拉格朗日型流体动力学方程为基础,将简化的非理想爆轰模型纳入其中,则可以明确地分析各种非理想因素对水下爆炸能量特性的影响。
建立与反应进程λ相关的爆轰产物状态方程的有效方法是将状态方程中的各项参数视为λ的线性函数。
采用JWL 状态方程v e e v R B e v R A p v R v R ωρωρωρρ+⎪⎪⎭⎫ ⎝⎛-+⎪⎪⎭⎫ ⎝⎛-=--020******* (9) 并分别确定对应于0=λ和1=λ时的两条等熵线,则反应过程任一中间状态的参数A 、B 、1R 、2R 、ω为两条等熵线间的线性差值[6]。
以PBX 型铝化炸药RDX/AP/Al/HTPB 为计算实例,密度为 1.79g/cm 3,装药质量为0.5Kg 。
在非理想组分不参与爆轰的情况下,爆速为5.7Km/s ,爆压为12GPa ,爆温为3150K ,JWL 爆轰产物状态方程的各项参数如表1所示。
设炸药各组分的质量百分比不变,则理想组分和非理想组分的化学能为定值, 分别为I q =3.015 KJ/g ,NI q =8.19 KJ/g ,而反应速率只取决于反应速率常数的大小。
表1 JWL 状态方程参数 Table 1 Parameters for JWL EOS0=λ1=λA (GPa ) 778.3 652.7B (GPa ) 7.071 10.64 1R4.4855.1523 2R1.068 1.0305 ω0.30.1551图1为PBX 铝化炸药与RDX 距装药中心0.5m 处的水中冲击波计算结果。
可以看出,在爆炸总能量相同的情况下,由于铝化炸药按简化模型改变了爆炸能量的释放过程,从而降低了压力波的峰值压力m p ,增大了衰减时间常数θ,这与试验结果相一致。
爆炸冲击波的超压取决于炸药的爆速和爆压,即能量的动态释放特性,而与铝化炸药对应的这部分能量是理想组分释放的化学能。
与RDX 相比,铝化炸药降低了这部分能量,故造成冲击波峰值压力的下降。
故可以预计,特别是在近距离处,铝化炸药水中爆炸冲击波的能量耗散将低于RDX 装药。
此外,非理想组分的化学变化是流体膨胀过程中的放热反应,必然会减缓压力的衰减速率,有助于增大冲击波能量s E 。
200400600800100020406080100120RDX/AP/Al/HTPBRDXp r e s s u r e /M P atime/μs 020040060080020406080100a = 5.0a = 0.001a = 0.025p r e s s u r e /M P atime/μs图1 0.5m 处的水中冲击波历史 图2 0.5m 处不同反应速率的水中冲击波历史 Fig. 1 Shock wave time histories within water Fig. 2 Shock wave time histories within waterat 0.5m at 0.5m versus reaction rate不同反应速率下的爆炸冲击波历史及冲击波特性的计算结果如图2和表2所示。
结果表明,反应速率对冲击波的峰值压力和衰减时间常数都有不同程度的影响。
当反应速率常数由0.025减少到它的1/25时,峰值压力没有明显变化,压力衰减速率却有大幅度的增加。
当反应速率常数大于0.025时,峰值压力和压力衰减速率都增加了相同的幅度。
对于存在能量慢速释放过程的铝化炸药,当慢速反应速率过低时,将减少爆炸作用的有效能量,而当慢速反应速率过高时,则会更多地表现出理想爆轰的特征。
因此,爆轰产物与水介质的动力学耦合要求慢速反应速率应控制在一定的范围之内,才能满足对冲击波特性的设计要求。
表2中的数据明显地表明,只有当反应速率常数大于某个阈值时,慢速释放的能量才能转换为爆炸冲击波能。
若取90%的最大冲击波能对应的反应速率常数为阈值,则本算例的速率常数阈值为0.025(×10MPa)-1/61μs -⋅。
表2 水下冲击波特征参数Table 2 Characteristic parameters of shock wave within watera /(×10MPa)-1/61μs -⋅ μs /θm p /MPas E /MJKg-10.001 47.2 85.0 0.92 0.005 74.0 85.2 1.23 0.025 98.6 85.0 1.80 0.5 74.6 107 2.05 1.075.01052.004 结论简化模型由CJ 模型和铝化炸药二次反应理论相结合而得到,该模型以CJ 点为界,把铝化炸药的能量释放过程划分为理想组分的快速释放和非理想组分的慢速释放两个过程,并以两步释放的化学能和慢速释放速率作为评价铝化炸药非理想特性的参数。
将简化模型应用于一维数值分析中,与理想炸药相比,铝化炸药水下爆炸冲击波的时间衰减常数增大,冲击波的能量耗散减小,可以获得更大的冲击波能量。
此外,铝化炸药化学能向冲击波能的转换程度受慢速反应速率的制约,且速率常数存在阈值。
这些计算结果与基本试验事实和理论分析相一致,且非理想特征参数能够体现出不同非理想程度下的水下爆炸效应。
因此,简化模型合理地描述了铝化炸药非理想爆轰的主要过程,快速和慢速释放的化学能以及慢速反应速率能够有效地体现铝化炸药的非理想程度。
该模型应用于水下爆炸效应的计算分析,对铝化炸药的设计具有一定的指导意义。
参考文献:[1] D. John Pastine ,etc. A model of nonideal detonation in aluminized explosives, Proc. of 11th Symp.(Int.) onDetonation, 1998, p204-213.[2] W. Michael Howard, etc. Kinetic modeling of non-ideal explosives with CHEETAH, Proc. of 11th Symp.(Int.)on Detonation, 1998, p998-1006.[3] J ing Ping Lu, David L. Kennedy. Modeling of PBXW-115 using kinetic CHEETAH and the DYNA codes.DSTO-TR-1496, 2003.[4] D. John Pastine. Energetics of late chemical reactions in non-ideal underwater detonations. ADA309088, 1995. [5] R. Guirguis , R. McKeown. A closed water-filled cylinder to characterize non-ideal explosives, Proc. of 12thSymp.(Int.) on Detonation, 2002, p344-352[6] Guirguis, R. H., Miller, P. J., Time-dependent equations of state for aluminized underwater explosives, Proc. of10th Symp.(Int.) on Detonation, 1993, p675-682.。
