浙江省湖州长兴县农用化肥(折纯)施用量、机耕面积和有效灌溉面积数据分析报告2019版
长兴县2009年国民经济和社会发展统计公报

长兴县2009年国民经济和社会发展统计公报2009年,面对外部环境的急剧变化和严峻考验,全县上下认真贯彻落实科学发展观,紧紧围绕“保增长、抓转型、增活力、重民生、促和谐、强保障”,经济运行实现企稳回升,经济社会呈现和谐共进的发展局面。
一、综合国民经济运行平稳。
初步核算,2009年全县实现地区生产总值(GDP)242.32亿元,按可比价格计算,比上年增长11.0%。
其中,第一产业增加值22.17亿元,增长3.7%;第二产业增加值135.22亿元,增长10.0%;第三产业增加值84.92亿元,增长14.3%。
三次产业结构从2008年9.0:57.1:33.9调整为9.2:55.8:35.0,第三产业比重比上年提高1.1个百分点。
按户籍人口计算人均生产总值39132元,比上年增长10.5%,按平均汇率计算折合5729美元。
2009年长兴县三次产业结构第一产业二、农业农业经济发展良好。
全县实现农林牧渔业总产值40亿元,比上年增长6.1%;实现农业增长值22.17亿元,比上年增长3.7%。
全年农作物播种面积132.63万亩,其中粮食播种面积63.57万亩,总产量27.5万吨,油料作物播种面积24.06万亩,总产量3.28万吨。
农业扶持力度不断加大,全年预算内支农财政总支出3.2亿元。
现代农业成效明显。
七大特色产业新发展6.75万亩、总产值达到25.8亿元。
全年新发展农民专业合作社32家,新增市级以上示范性农民合作组织7家、重点农业龙头企业5家,新增省级以上无公害、绿色、有机农产品25只,我县成为“中国果菜无公害十强县”。
主要农产品产量如下:农业基础条件不断改善。
水利工程建设进一步加强,2009年水利总投入3.02亿元,其中农村水利建设资金0.5亿元。
全年农田灌溉面积44.86千公顷,完成河道清淤143公里,建设标准堤防43公里。
年末实有固定机电排灌站2135处。
农业物质装备水平不断提高,年末拥有农机总动力34.56万千瓦,耕地机械动力5.93万千瓦,机耕面积54.1万亩,机收面积56.83万亩。
统计案例分析报告及典型例题

统计案例分析及典型例题§11.1 抽样方法1.为了了解所加工的一批零件的长度,抽取其中200个零件并测量了其长度,在这个问题中,总体的一个样本是 . 答案 200个零件的长度2.某城区有农民、工人、知识分子家庭共计2 004户,其中农民家庭1 600户,工人家庭303户,现要从中抽取容量为40的样本,则在整个抽样过程中,可以用到下列抽样方法:①简单随机抽样,②系统抽样,③分层抽样中的 . 答案 ①②③3.某企业共有职工150人,其中高级职称15人,中级职称45人,初级职称90人.现采用分层抽样抽取容量为30的样本,则抽取的各职称的人数分别为 . 答案 3,9,184.某工厂生产A 、B 、C 三种不同型号的产品,其相应产品数量之比为2∶3∶5,现用分层抽样方法抽出一个容量为n 的样本,样本中A 型号产品有16件,那么此样本的容量n= . 答案 80例1 某大学为了支援我国西部教育事业,决定从2007应届毕业生报名的18名志愿者中,选取6人组成志愿小组.请用抽签法和随机数表法设计抽样方案. 解 抽签法:第一步:将18名志愿者编号,编号为1,2,3, (18)第二步:将18个号码分别写在18张外形完全相同的纸条上,并揉成团,制成号签; 第三步:将18个号签放入一个不透明的盒子里,充分搅匀; 第四步:从盒子中逐个抽取6个号签,并记录上面的编号;基础自测第五步:所得号码对应的志愿者,就是志愿小组的成员. 随机数表法:第一步:将18名志愿者编号,编号为01,02,03, (18)第二步:在随机数表中任选一数作为开始,按任意方向读数,比如第8行第29列的数7开始,向右读;第三步:从数7开始,向右读,每次取两位,凡不在01—18中的数,或已读过的数,都跳过去不作记录,依次可得到12,07,15,13,02,09.第四步:找出以上号码对应的志愿者,就是志愿小组的成员.例2 某工厂有1 003名工人,从中抽取10人参加体检,试用系统抽样进行具体实施. 解 (1)将每个人随机编一个号由0001至1003. (2)利用随机数法找到3个号将这3名工人剔除. (3)将剩余的1 000名工人重新随机编号由0001至1000. (4)分段,取间隔k=100001=100将总体均分为10段,每段含100个工人.(5)从第一段即为0001号到0100号中随机抽取一个号l.(6)按编号将l ,100+l ,200+l,…,900+l 共10个号码选出,这10个号码所对应的工人组成样本. 例3 (14分)某一个地区共有5个乡镇,人口3万人,其中人口比例为3∶2∶5∶2∶3,从3万人中抽取一个300人的样本,分析某种疾病的发病率,已知这种疾病与不同的地理位置及水土有关,问应采取什么样的方法?并写出具体过程.解 应采取分层抽样的方法.3分过程如下:(1)将3万人分为五层,其中一个乡镇为一层.5分(2)按照样本容量的比例随机抽取各乡镇应抽取的样本. 300×153=60(人);300×152=40(人); 300×155=100(人);300×152=40(人); 300×153=60(人),10分因此各乡镇抽取人数分别为60人,40人,100人,40人,60人.12分(3)将300人组到一起即得到一个样本.14分练习:一、填空题1.(安庆模拟)某校高中生共有900人,其中高一年级300人,高二年级200人,高三年级400人,现分层抽取容量为45的样本,那么高一、高二、高三年级抽取的人数分别为 .答案15,10,202.某牛奶生产线上每隔30分钟抽取一袋进行检验,则该抽样方法为①;从某中学的30名数学爱好者中抽取3人了解学习负担情况,则该抽样方法为②.那么①,②分别为 .答案系统抽样,简单随机抽样3.下列抽样实验中,最适宜用系统抽样的是(填序号).①某市的4个区共有2 000名学生,且4个区的学生人数之比为3∶2∶8∶2,从中抽取200人入样②某厂生产的2 000个电子元件中随机抽取5个入样③从某厂生产的2 000个电子元件中随机抽取200个入样④从某厂生产的20个电子元件中随机抽取5个入样答案③4.(2013·重庆文)某校高三年级有男生500人,女生400人,为了解该年级学生的健康情况,从男生中任意抽取25人,从女生中任意抽取20人进行调查,这种抽样方法是 .答案分层抽样法5.某中学有高一学生400人,高二学生300人,高三学生200人,学校团委欲用分层抽样的方法抽取18名学生进行问卷调查,则下列判断不正确的是(填序号).①高一学生被抽到的概率最大②高三学生被抽到的概率最大③高三学生被抽到的概率最小④每名学生被抽到的概率相等答案①②③6.某商场有四类食品,其中粮食类、植物油类、动物性食品类及果蔬类分别有40种、10种、30种、20种,现从中抽取一个容量为20的样本进行食品安全检测,若采用分层抽样的方法抽取样本,则抽取的植物油类与果蔬类食品种数之和是 .答案 67.(天津文,11)一个单位共有职工200人,其中不超过45岁的有120人,超过45岁的有80人.为了调查职工的健康状况,用分层抽样的方法从全体职工中抽取一个容量为25的样本,应抽取超过45岁的职工 人. 答案 108.将参加数学竞赛的1 000名学生编号如下0001,0002,0003,…,1000,打算从中抽取一个容量为50的样本,按系统抽样的方法分成50个部分,如果第一部分编号为0001,0002,…,0020,从第一部分随机抽取一个号码为0015,则第40个号码为 . 答案 07959.某政府机关有在编人员100人,其中副处级以上干部10人,一般干部70人,工人20人,上级机关为了了解政府机构改革意见,要从中抽取一个容量为20的样本,试确定用何种方法抽取,如何抽取? 解 用分层抽样抽取. (1)∵20∶100=1∶5, ∴510=2,570=14,520=4∴从副处级以上干部中抽取2人,一般干部中抽取14人,从工人中抽取4人.(2)因副处级以上干部与工人人数较少,可用抽签法从中分别抽取2人和4人;对一般干部可用随机数表法抽取14人.(3)将2人、4人、14人编号汇合在一起就得到了容量为20的样本.10.某单位有工程师6人,技术员12人,技工18人,要从这些人中抽取一个容量为n 的样本.如果采用系统抽样法和分层抽样法抽取,不用剔除个体;如果样本容量增加一个,则在采用系统抽样时,需要在总体中先剔除1个个体,求样本容量n.解 总体容量为6+12+18=36.当样本容量是n 时,由题意知,系统抽样的间隔为n36,分层抽样的比例是36n ,抽取工程师36n ×6=6n (人),抽取技术人员36n ×12=3n (人),抽取技工36n×18=2n (人).所以n 应是6的倍数,36的约数即n=6,12,18,36.当样本容量为(n+1)时,在总体中剔除1人后还剩35人,系统抽样的间隔为135+n ,因为135+n 必须是整数,所以n 只能取6,即样本容量为6.总体分布的估计与总体特征数的估计1.一个容量为20的样本,已知某组的频率为0.25,则该组的频数为 . 答案 52.(2008·山东理)右图是根据《山东统计年鉴2007》中的资料作成的1997年至2006年我省城镇居民百户家庭人口数的茎叶图.图中左边的数字从左到右分别表示城镇居民百户家庭人口数的百位数字和十位数字,右边的数字表示城镇居民百户家庭人口数的个位数字.从图中可以得到1997年至2006年我省城镇居民百户家庭人口数的平均数为 . 答案 303.63.在抽查产品的尺寸过程中,将其尺寸分成若干组,[a ,b )是其中的一组,抽查出的个体在该组上的频率为m,该组在频率分布直方图的高为h ,则|a-b|= . 答案 hm4.(2008·山东文,9)从某项综合能力测试中抽取100人的成绩,统计如表,则这100人成绩的标准差为 .答案 51025.为了了解某地区高三学生的身体发育情况,抽查了该地区100名年龄为17.5岁~18岁的男生体重(kg ),得到频率分布直方图如下:根据上图可得这100名学生中体重在[56.5,64.5)的学生人数是 . 答案 40基础自测典型例题:例1 在学校开展的综合实践活动中,某班进行了小制作评比,作品上交时间为5月1日至30日,评委会把同学们上交 作品的件数按5天一组分组统计,绘制了频率分布直方图(如图所示),已知从左到右各长方形高的比为2∶3∶4∶6∶4∶1,第三组的频数为12,请解答下列问题: (1)本次活动共有多少件作品参加评比? (2)哪组上交的作品数量最多?有多少件?(3)经过评比,第四组和第六组分别有10件、2件作品获奖,问这两组哪组获奖率高? 解 (1)第三组的频率为1464324+++++=51又因为第三组的频数为12,∴参评作品数为5112=60.(2)根据频率分布直方图,可以看出第四组上交的作品数量最多,共有60×1464326+++++=18(件).(3)第四组的获奖率是1810=95,第六组上交的作品数量为60×1464321+++++=3(件),∴第六组的获奖率为32=96,显然第六组的获奖率高.例4(14分)某化肥厂甲、乙两个车间包装肥料,在自动包装传送带上每隔30 min 抽取一包产品,称其重量,分别 记录抽查数据如下: 甲:102, 101, 99, 98, 103, 98,99;乙:110, 115, 90,85,75,115, 110.(1)这种抽样方法是哪一种? (2)将这两组数据用茎叶图表示;(3)将两组数据比较,说明哪个车间产品较稳定. 解 (1)因为间隔时间相同,故是系统抽样. 2分(2)茎叶图如下:5分(3)甲车间: 平均值:1x =71(102+101+99+98+103+98+99)=100,7分方差:s 12=71[(102-100)2+(101-100)2+…+(99-100)2]≈3.428 6.9分乙车间:平均值:2x =71(110+115+90+85+75+115+110)=100,11分方差:s 22=71[(110-100)2+(115-100)2+…+(110-100)2]≈228.571 4.13分∵1x =2x ,s 12<s 22,∴甲车间产品稳定.14分练习:1.为了了解小学生的体能情况,抽取了某小学同年级部分学生进行跳绳测试,将所得数据整理后,画出频率分布直方图如图所示,已知图中从左到右前三个小组的频率分别是0.1,0.3,0.4,第一小组的频数为5.(1)求第四小组的频率;(2)参加这次测试的学生人数是多少?(3)在这次测试中,学生跳绳次数的中位数落在第几小组内? 解 (1)第四小组的频率=1-(0.1+0.3+0.4)=0.2. (2)设参加这次测试的学生人数是n, 则有n=第一小组频率第一小组频数=5÷0.1=50(人).(3)因为0.1×50=5,0.3×50=15,0.4×50=20,0.2×50=10,即第一、第二、第三、第四小组的频数分别为5、15、20、10,所以学生跳绳次数的中位数落在第三小组内. 练习:一、填空题1.下列关于频率分布直方图的说法中不正确的是 . ①直方图的高表示取某数的频率②直方图的高表示该组上的个体在样本中出现的频率 ③直方图的高表示该组上的个体数与组距的比值④直方图的高表示该组上的个体在样本中出现的频率与组距的比值 答案 ①②③2.甲、乙两名新兵在同样条件下进行射击练习,每人打5发子弹,命中环数如下:甲:6,8,9,9,8;乙:10,7,7,7,9.则这两人的射击成绩 比 稳定. 答案 甲 乙4.某班50名学生在一次百米测试中,成绩全部介于13秒与19秒之间,将测试结果分成六组:右图是得到的频率分布直方图.设成绩小于17秒的学生人数占全班总人数的百分比为x,成绩大于等于15秒且小于17秒的学生人数为y ,则从频率分布直方图中可分析出x 和y 分别为 . 答案 0.9, 356.甲、乙两名同学在5次体育测试中的成绩统计的茎叶图如图所示,若甲、乙两人的平均成绩分别是x 甲、x 乙,则x 甲 x 乙, 比 稳定. 答案 < 乙 甲7.(上海,9)已知总体的各个体的值由小到大依次为2,3,3,7,a ,b ,12,13.7,18.3,20,且总体的中位数为10.5.若要使该总体的方差最小,则a 、b 的取值分别是 . 答案 10.5、10.5二、解答题10.为了了解高一学生的体能情况,某校抽取部分学生进行一分钟跳绳次数测试,将所得数据整理后,画出频率分布直方图(如图所示),图中从左到右各小长方形面积之比为2∶4∶17∶15∶9∶3,第二小组频数为12.(1)第二小组的频率是多少?样本容量是多少?(2)若次数在110以上(含110次)为达标,试估计该学校全体高一学生的达标率是多少? (3)在这次测试中,学生跳绳次数的中位数落在哪个小组内?请说明理由. 解 (1)由于频率分布直方图以面积的形式反映了数据落在各小组内的频率大小, 因此第二小组的频率为:391517424+++++=0.08.又因为频率=样本容量第二小组频数, 所以样本容量=第二小组频率第二小组频数=08.012=150. (2)由图可估计该学校高一学生的达标率约为39151742391517++++++++×100%=88%.(3)由已知可得各小组的频数依次为6,12,51,45,27,9,所以前三组的频数之和为69,前四组的频数之和为114,所以跳绳次数的中位数落在第四小组内.线性回归方程1.下列关系中,是相关关系的为 (填序号). ①学生的学习态度与学习成绩之间的关系;基础自测②教师的执教水平与学生的学习成绩之间的关系;③学生的身高与学生的学习成绩之间的关系;④家庭的经济条件与学生的学习成绩之间的关系.答案①②2.为了考察两个变量x、y之间的线性相关关系,甲、乙两同学各自独立地做10次和15次试验,并利用最小二乘法求得回归直线分别为l1和l2.已知在两人的试验中发现变量x的观测数据的平均值恰好相等,都为s,变量y的观测数据的平均值也恰好相等,都为t,那么下列说法中正确的是(填序号).①直线l1,l2有交点(s,t)②直线l1,l2相交,但是交点未必是(s,t)③直线l1,l2由于斜率相等,所以必定平行④直线l1,l2必定重合答案①3.下列有关线性回归的说法,正确的是(填序号).①相关关系的两个变量不一定是因果关系②散点图能直观地反映数据的相关程度③回归直线最能代表线性相关的两个变量之间的关系④任一组数据都有回归直线方程答案①②③4.下列命题:①线性回归方法就是由样本点去寻找一条贴近这些样本点的直线的数学方法;②利用样本点的散点图可以直观判断两个变量的关系是否可以用线性关系表示;③通过回归直线yˆ=bˆx+aˆ及回归系数bˆ,可以估计和预测变量的取值和变化趋势. 其中正确命题的序号是 .答案①②③5.已知回归方程为yˆ=0.50x-0.81,则x=25时,yˆ的估计值为 .答案11.69例1下面是水稻产量与施化肥量的一组观测数据:施化肥量15 20 25 30 35 40 45水稻产量320 330 360 410 460 470 480(1)将上述数据制成散点图;(2)你能从散点图中发现施化肥量与水稻产量近似成什么关系吗?水稻产量会一直随施化肥量的增加而增长吗?解(1)散点图如下:(2)从图中可以发现施化肥量与水稻产量具有线性相关关系,当施化肥量由小到大变化时,水稻产量由小变大,图中的数据点大致分布在一条直线的附近,因此施化肥量和水稻产量近似成线性相关关系,但水稻产量只是在一定范围内随着化肥施用量的增加而增长.例2(14分)随着我国经济的快速发展,城乡居民的生活水平不断提高,为研究某市家庭平均收入与月平均生活支出的关系,该市统计部门随机调查了10个家庭,得数据如下:(1)判断家庭平均收入与月平均生活支出是否相关?(2)若二者线性相关,求回归直线方程.解(1)作出散点图:5分观察发现各个数据对应的点都在一条直线附近,所以二者呈线性相关关系. 7分(2)x =101 (0.8+1.1+1.3+1.5+1.5+1.8+2.0+2.2+2.4+2.8)=1.74,y=101(0.7+1.0+1.2+1.0+1.3+1.5+1.3+1.7+2.0+2.5)=1.42,9分bˆ=∑∑==-∙-ni ini i i x n xyx n y x 1221≈0.813 6,aˆ=1.42-1.74×0.813 6≈0.004 3,13分 ∴回归方程yˆ=0.813 6x+0.004 3.14分例3 下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量x(吨)与相应的生产能耗y (吨)标准煤的几组对照数据.(1)请画出上表数据的散点图;(2)请根据上表提供的数据,用最小二乘法求出y 关于x 的线性回归方程yˆ=b ˆx+a ˆ; (3)已知该厂技改前100吨甲产品的生产能耗为90吨标准煤.试根据(2)求出的线性回归方程,预测生产100吨甲产品的生产能耗比技改前降低多少吨标准煤? (参考数值:3×2.5+4×3+5×4+6×4.5=66.5) 解 (1)散点图如下图:(2)x =46543+++=4.5,y =45.4435.2+++=3.5∑=41i ii yx =3×2.5+4×3+4×5+6×4.5=66.5.∑=412i ix=32+42+52+62=86∴bˆ=24124144x x yx yx i i i ii -∙-∑∑===25.44865.45.345.66⨯-⨯⨯-=0.7aˆ =y -bˆx =3.5-0.7×4.5=0.35. ∴所求的线性回归方程为yˆ=0.7x+0.35. (3)现在生产100吨甲产品用煤 y=0.7×100+0.35=70.35,∴降低90-70.35=19.65(吨)标准煤.1.科研人员为了全面掌握棉花新品种的生产情况,查看了气象局对该地区年降雨量与年平均气温的统计数据(单位分别是mm,℃),并作了统计.(1)试画出散点图;(2)判断两个变量是否具有相关关系. 解 (1)作出散点图如图所示,(2)由散点图可知,各点并不在一条直线附近,所以两个变量是非线性相关关系.2.在研究硝酸钠的可溶性程度时,对于不同的温度观测它在水中的溶解度,得观测结果如下:由资料看y 与x 呈线性相关,试求回归方程. 解 x =30,y =50.1283.1120.850.767.66++++=93.6.bˆ=25125155x xyx yx i ii ii -∙-∑∑==≈0.880 9.aˆ=y -bˆx =93.6-0.880 9×30=67.173. ∴回归方程为yˆ=0.880 9x+67.173.3.某企业上半年产品产量与单位成本资料如下:(1)求出线性回归方程;(2)指出产量每增加1 000件时,单位成本平均变动多少? (3)假定产量为6 000件时,单位成本为多少元? 解 (1)n=6,∑=61i i x =21,∑=61i i y =426,x =3.5,y =71,∑=612i i x =79,∑=61i i i y x =1 481,bˆ=26126166x xyx yx i ii ii -∙-∑∑===25.3679715.364811⨯-⨯⨯-=-1.82.aˆ=y-bˆx=71+1.82×3.5=77.37.回归方程为yˆ=aˆ+bˆx=77.37-1.82x.(2)因为单位成本平均变动bˆ=-1.82<0,且产量x的计量单位是千件,所以根据回归系数b的意义有: 产量每增加一个单位即1 000件时,单位成本平均减少1.82元.(3)当产量为6 000件时,即x=6,代入回归方程:yˆ=77.37-1.82×6=66.45(元)当产量为6 000件时,单位成本为66.45元.一、填空题1.观察下列散点图,则①正相关;②负相关;③不相关.它们的排列顺序与图形对应顺序是 .答案a,c,b2.回归方程yˆ=1.5x-15,则下列说法正确的有个.①y=1.5x-15②15是回归系数a③1.5是回归系数a④x=10时,y=0答案 13.(2009.湛江模拟)某地区调查了2~9岁儿童的身高,由此建立的身高y(cm)与年龄x(岁)的回归模型为yˆ=8.25x+60.13,下列叙述正确的是 .①该地区一个10岁儿童的身高为142.63 cm②该地区2~9岁的儿童每年身高约增加8.25 cm③该地区9岁儿童的平均身高是134.38 cm④利用这个模型可以准确地预算该地区每个2~9岁儿童的身高答案 ②4.三点(3,10),(7,20),(11,24)的回归方程是 .答案 yˆ=1.75x+5.75 5.某人对一地区人均工资x(千元)与该地区人均消费y(千元)进行统计调查,y 与x 有相关关系,得到回归直线方程yˆ=0.66x+1.562.若该地区的人均消费水平为7.675千元,估计该地区的人均消费额占人均工资收入的百分比约为 . 答案 83%6.某化工厂为预测产品的回收率y,需要研究它和原料有效成分含量x 之间的相关关系,现取8对观测值,计算,得∑=81i i x =52, ∑=81i i y =228, ∑=812i i x =478, ∑=81i i i y x =1 849,则其线性回归方程为 .答案 yˆ=11.47+2.62x 7.有下列关系:①人的年龄与他(她)拥有的财富之间的关系;②曲线上的点与该点的坐标之间的关系;③苹果的产量与气候之间的关系;④森林中的同一种树木,其断面直径与高度之间的关系.其中,具有相关关系的是 . 答案 ①③④8.已知关于某设备的使用年限x 与所支出的维修费用y(万元),有如下统计资料:若y 对x 呈线性相关关系,则回归直线方程yˆ=b ˆx+a ˆ表示的直线一定过定点 . 答案 (4,5) 二、解答题9.期中考试结束后,记录了5名同学的数学和物理成绩,如下表:(1)数学成绩和物理成绩具有相关关系吗?(2)请你画出两科成绩的散点图,结合散点图,认识(1)的结论的特点. 解 (1)数学成绩和物理成绩具有相关关系.(2)以x 轴表示数学成绩,y 轴表示物理成绩,可得相应的散点图如下:由散点图可以看出,物理成绩和数学成绩对应的点不分散,大致分布在一条直线附近. 10.以下是某地搜集到的新房屋的销售价格y 和房屋的面积x 的数据:(1)画出数据对应的散点图;(2)求线性回归方程,并在散点图中加上回归直线. 解 (1)数据对应的散点图如图所示:(2)x =109,y =23.2,∑=512i i x =60 975,∑=51i iiy x=12 952,bˆ=25125155x xyx yx i ii ii -∙-∑∑==≈0.196 2aˆ=y -bˆx ≈1.814 2 ∴所求回归直线方程为yˆ=0.196 2x+1.814 2.11.某公司利润y 与销售总额x(单位:千万元)之间有如下对应数据:(1)画出散点图; (2)求回归直线方程;(3)估计销售总额为24千万元时的利润. 解 (1)散点图如图所示:(2)x =71(10+15+17+20+25+28+32)=21,y=71(1+1.3+1.8+2+2.6+2.7+3.3)=2.1,∑=712i ix=102+152+172+202+252+282+322=3 447,∑=71i iiy x=10×1+15×1.3+17×1.8+20×2+25×2.6+28×2.7+32×3.3=346.3,bˆ=27127177x x yx yx i i i ii -∙-∑∑===221744731.22173.346⨯-⨯⨯-≈0.104, aˆ=y -bˆx =2.1-0.104×21=-0.084, ∴yˆ=0.104x-0.084. (3)把x=24(千万元)代入方程得,yˆ=2.412(千万元).∴估计销售总额为24千万元时,利润为2.412千万元.12.某种产品的广告费支出x 与销售额y(单位:百万元)之间有如下对应数据:(1)画出散点图;(2)求回归直线方程;(3)试预测广告费支出为10百万元时,销售额多大? 解 (1)根据表中所列数据可得散点图如下:(2)列出下表,并用科学计算器进行有关计算:因此,x =525=5,y =5250 =50,∑=512i i x =145, ∑=512i i y =13 500, ∑=51i i i y x =1 380.于是可得:bˆ=25125155x xyx yx i ii ii -∙-∑∑===55514550553801⨯⨯-⨯⨯-=6.5;aˆ=y -bˆx =50-6.5×5=17.5. 因此,所求回归直线方程为:yˆ=6.5x+17.5. (3)根据上面求得的回归直线方程,当广告费支出为10百万元时,yˆ=6.5×10+17.5=82.5(百万元),即这种产品的销售收入大约为82.5百万元.§11.4 统计案例1.对有线性相关关系的两个变量建立的回归直线方程y ˆ=a ˆ+b ˆx 中,回归系数bˆ与0的大小关系为 .(填序号) ①大于或小于 ②大于 ③小于 ④不小于答案 ①2.如果有90%的把握说事件A 和B 有关系,那么具体计算出的数据 2 2.706.(用“>”,“<”,“=”填空) 答案 >3.对两个变量y 与x 进行回归分析,分别选择不同的模型,它们的相关系数r 如下,其中拟合效果最好的模型是 .①模型Ⅰ的相关系数r 为0.98 ②模型Ⅱ的相关系数r 为0.80 ③模型Ⅲ的相关系数r 为0.50 ④模型Ⅳ的相关系数r 为0.25 答案 ①4.下列说法中正确的有:①若r >0,则x 增大时,y 也相应增大;②若r <0,则x 增大时,y 也相应增大;③若r=1或r=-1,则x 与y 的关系完全对应(有函数关系),在散点图上各个点均在一条直线上 . 答案 ①③基础自测例1 (14分)调查339名50岁以上人的吸烟习惯与患慢性气管炎的情况,获数据如下:试问:(1)吸烟习惯与患慢性气管炎是否有关? (2)用假设检验的思想给予证明. (1)解 根据列联表的数据,得到χ2=))()()(()(2c d b d c a b a bc ad n ++++-2分 =13428356205)1316212143(3392⨯⨯⨯⨯-⨯⨯=7.469>6.6356分 所以有99%的把握认为“吸烟与患慢性气管炎有关”.9分(2)证明 假设“吸烟与患慢性气管炎之间没有关系”,由于事件A={χ2≥6.635}≈0.01,即A 为小概率事件,而小概率事件发生了,进而得假设错误,这种推断出错的可能性约有1%.14分例2 一台机器使用时间较长,但还可以使用.它按不同的转速生产出来的某机械零件有一些会有缺点,每小时生产有 缺点零件的多少,随机器运转的速度而变化,下表为抽样试验结果:(1)对变量y 与x 进行相关性检验;(2)如果y 与x 有线性相关关系,求回归直线方程;(3)若实际生产中,允许每小时的产品中有缺点的零件最多为10个,那么,机器的运转速度应控制在什么范围内?解 (1)x =12.5,y =8.25,∑=41i iiy x=438,4x y =412.5,∑=412i i x =660,∑=412i i y =291,所以r=)4)(4(42412241241y yx xyx yx i ii ii ii --∙-∑∑∑====)25.272291()625660(5.412438-⨯--=25.6565.25≈62.2550.25≈0.995 4.因为r >r 0.05,所以y 与x 有很强的线性相关关系.(2)yˆ=0.728 6x-0.857 1. (3)要使yˆ≤10⇒0.728 6x-0.857 1≤10, 所以x ≤14.901 3.所以机器的转速应控制在14.901 3转/秒以下.例3 下表是某年美国旧轿车价格的调查资料,今以x 表示轿车的使用年数,y 表示相应的年均价格,求y 关于x 的回归 方程.解 作出散点图如图所示.可以发现,各点并不是基本处于一条直线附近,因此,y 与x 之间应是非线性相关关系.与已学函数图象比较,用y ˆ=e a x b ˆˆ来刻画题中模型更为合理,令zˆ=ln y ˆ,则z ˆ=b ˆx+a ˆ,题中数据变成如下表所示:相应的散点图如图所示,从图中可以看出,变换的样本点分布在一条直线附近,因此可以用线性回归方程拟合.由表中数据可得r ≈-0.996.|r|>r 0.05.认为x 与z之间具有线性相关关系,由表中数据得bˆ≈-0.298,a ˆ≈8.165,所以z ˆ=-0.298x+8.165,最后回代z ˆ=ln y ˆ,即y ˆ=e -0.298x+8.165为所求.1.某班主任对全班50名学生学习积极性和对待班级工作的态度进行了调查,统计数据如下表所示:(1)如果随机抽查这个班的一名学生,那么抽到积极参加班级工作的学生的概率是多少?抽到不太主动参加班级工作且学习积极性一般的学生的概率是多少?(2)试运用独立性检验的思想方法分析:学生的学习积极性与对待班级工作的态度是否有关系?说明理由.解 (1)随机抽查这个班的一名学生,有50种不同的抽查方法,由于积极参加班级工作的学生有18+6=24人,所以有24种不同的抽法,因此由古典概型的计算公式可得抽到积极参加班级工作的学生的概率是P 1=5024=2512,又因为不太主动 参加班级工作且学习积极性一般的学生有19人,所以抽到不太主动参加班级工作且学习积极性一般的学生的概率是P 2=5019.(2)由2χ统计量的计算公式得2χ=25252624)761918(502⨯⨯⨯⨯-⨯⨯≈11.538,由于11.538>10.828,所以可以有99.9%的把握认为“学生的学习积极性与对待班级工作的态度有关系”.2.某个体服装店经营某种服装,一周内获纯利y (元)与该周每天销售这种服装的件数x 之间的一组数据如下:已知∑=712i i x =280, ∑=712i i y =45 309, ∑=71i i i y x =3 487,此时r 0.05=0.754.(1)求x ,y ;(2)判断一周内获纯利润y 与该周每天销售件数x 之间是否线性相关,如果线性相关,求出回归直线方程.解 (1)x =71(3+4+5+6+7+8+9)=6,y=71 (66+69+73+81+89+90+91)≈79.86.(2)根据已知∑=712i i x =280, ∑=712i i y =45 309, ∑=71i i i y x =3 487,得相关系数 r=)86.79730945)(67280(86.7967487322⨯-⨯-⨯⨯-≈0.973.由于0.973>0.754,所以纯利润y与每天销售件数x 之间具有显著线性相关关系. 利用已知数据可求得回归直线方程为yˆ=4.746x+51.386.3.某种书每册的成本费y (元)与印刷册数x (千册)有关,经统计得到数据如下:检验每册书的成本费y 与印刷册数的倒数x1之间是否具有线性相关关系,如有,求出y 对x 的回归方程.解 首先作变量置换,令u=x1,题目所给数据变成如下表所示的10对数据:然后作相关性检验.经计算得r ≈0.999 8>0.75,从而认为u 与y 之间具有线性相关关系.由公式得aˆ≈1.125,b ˆ≈8.973, 所以yˆ=1.125+8.973u, 最后回代u=x1,可得y ˆ=1.125+x973.8,这就是题目要求的y 对x 的回归曲线方程.回归曲线的图形如图所示,它是经过平移的反比例函数图象的一个分支.一、填空题1.对于独立性检验,下列说法中正确的是 . ①2χ的值越大,说明两事件相关程度越大 ②2χ的值越小,说明两事件相关程度越小 ③2χ≤2.706时,有90%的把握说事件A 与B 无关 ④2χ>6.635时,有99%的把握说事件A 与B 有关 答案 ①②④2.工人月工资y (元)依劳动生产率x(千元)变化的回归方程为y ˆ=50+80x ,下列判断正确的是 .①劳动生产率为1 000元时,工资为130元。
17化肥施用强度(折纯)

17、化肥施用强度(折纯)指标要求:化肥施用强度(折纯)<250千克/公顷完成情况:近年来为了指导农民科学施肥,纠正常规生产中存在的施肥不合理,氮、磷用量较高等问题,努力提高肥料利用率,实现节本增效、增产增收。
我县全面推广以“节氮、控磷、增钾”为重点的施肥模式,在肥料应用上一方面积极做好测土配方施肥技术的推广率和到位率工作;另一方面,大力提倡秸秆还田、鼓励增加有机肥用量和种植绿肥,减少化肥用量,改善耕地土壤质量。
通过几年的努力,我县农田面源污染得到有效控制,为创建国家生态县,加快农业产业结构调整,大力发展无公害、绿色、有机农产品打下了扎实的基础。
根据有关统计资料,2006-2009年我县化肥施用强度分别为:190.38、179.32、196.96、196.75千克/公顷,已达到生态县建设指标要求。
数据来源:(1)2006-2008年《溧水统计年鉴》有关种植业生产情况、化肥施用情况的资料(2)溧水县农林局统计资料农作物化肥施用强度指标情况表溧水县化肥使用强度指标完成情况总结长期以来,我县农业生产盲目施肥、过量施肥现象普遍,不仅造成农业生产成本增加,而且带来严重的环境污染,威胁农产品质量安全。
近年来,随着“三品”生产基地建设的推进,化肥的使用问题越来越受到重视。
尤其是07年测土配方施肥项目、08年的商品有机肥推广应用和绿肥推广种植项目实施以来,化肥的施用逐步规范化、科学化。
化肥的合理使用不仅节省投入增加农民收入,还大大提高了农产品的品质。
一、开展测土配方施肥项目,指导农民科学施肥自2006年测土配方施肥项目实施以来,土肥站对全县土壤进行家底摸清,掌握土壤的供肥性能,本着缺什么补什么,多什么控什么的原则实行配方施肥。
测土配方施肥主要围绕“测土、配方、配肥、供肥、施肥指导”五个环节开展十一项工作。
对土壤类型按肥力的高、中、低对稻麦(油)主推广品种进行无氮基础地力试验、精确施氮试验、3414田间肥效小区试验、示范对比和配方校正试验。
农业技术进步与要素禀赋的耦合协调度测算

农业技术进步与要素禀赋的耦合协调度测算魏金义;祁春节【摘要】要素禀赋条件是农业发展的根本制约,技术进步是实现我国农业发展方式转变的巨大动力,两者间的高度耦合协调是我国农业现代化的必然要求.改革开放以来,我国农业要素禀赋和技术条件都有所变化.本文从耦合关系的视角,利用耦合协调模型,建立相应的指标体系,分析了改革开放以来我国农业技术进步和要素禀赋的耦合协调性,并对各地区间两者的耦合协调关系进行了比较.结果发现:在过去一段时间内,我国农业要素禀赋结构的优化速度滞后于技术进步的步伐;农业技术进步与要素禀赋的耦合性没有发生明显波动,一直处于颉颃阶段,且呈现出“U”型的变化趋势;1981-2011年间,我国农业技术进步和要素禀赋的耦合协调度逐年提高,已由改革开放初的低度耦合协调发展成为高度耦合协调;各地区间农业技术进步和要素禀赋的耦合性存在一定差异,多数地区两者间耦合协调关系属于中度耦合协调型,北京和西藏两地仍处于低水平耦合阶段,仅江苏、山东、河南、广东四省为高度耦合协调型.在农业改革过程中,应着重强调发挥市场在促进农业技术进步和要素禀赋结构升级中的决定性作用,为实现两者的高度耦合创造良好的制度环境.同时,应充分考虑我国各地区农业要素禀赋条件的差异性,选择与当地要素禀赋相适应的技术类型,以期最大限度地发挥生产要素的作用和技术本身的效率.【期刊名称】《中国人口·资源与环境》【年(卷),期】2015(025)001【总页数】7页(P90-96)【关键词】农业技术进步;农业要素禀赋;耦金度;耦合协调【作者】魏金义;祁春节【作者单位】华中农业大学经济管理学院,湖北武汉430070;湖北农村发展研究中心,湖北武汉430070;华中农业大学经济管理学院,湖北武汉430070【正文语种】中文【中图分类】F304改革开放以来,我国农业发展取得了举世瞩目的成就,农业要素禀赋条件也发生了深刻的变化。
2012年12月召开的中央农村工作会议强调我国农业发展进入到资源环境约束趋紧的新阶段。
长兴县土地利用现状分乡镇分类面积统计表

29
资料来源:长兴县土地利用现状变更资料(1996年)
注:* 县域合计数包括南湖林场和外县插花地。
** 本县合计指扣除南湖林场和外县插花地后属长兴县管辖范围的土地面积。
*** 其它小计指南湖林场和外县插花地的合计数。
30
资料来源:《长兴县土地统计年报》1992-1996年。
本研究整理。
注:* 全县总计中包括南湖林场以及少量的外县插花地。
**小计中不含南湖林场和外县插花地。
***其它未利用土地指的是南湖林场以及少量的外县插花地。
** 本县合计指扣除南湖林场和外县插花地后属本县管辖范围的土地面积。
*** 其它小计指南湖林场和外县插花地的合计数。
** 本县合计指扣除南湖林场和外县插花地后属本县管辖范围的土地面积。
*** 其它小计指南湖林场和外县插花地的合计数。
注:其它包括南湖林场和少量外县插花地。
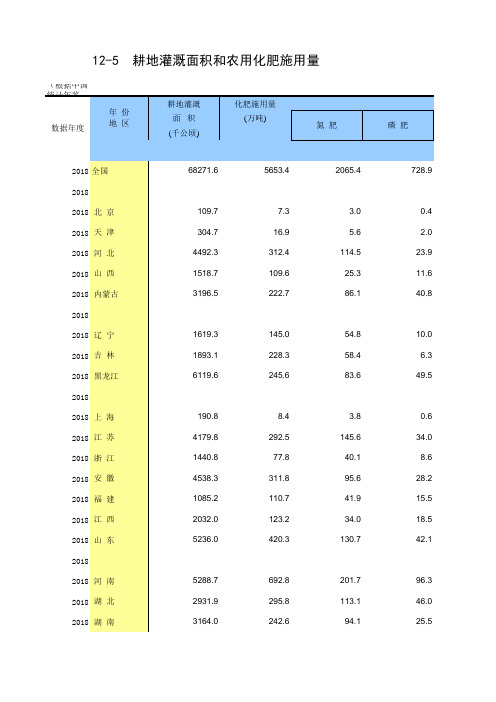
12-5 中国统计年鉴数据处理:耕地灌溉面积和农用化肥施用量(全国与各省级指标,2007-2018多年数据分析对比)
93.2 235.2
89.5 217.4
5.2
229.6 83.2 8.3 38.4
255.0
5859.4
8.5 18.0 322.0 112.0 235.0
145.5 231.0 251.2
8.9
88.6 73.8 14.8
45.9 112.1
40.1 105.0
1.5
88.9 33.2
3.5 16.4 109.9
24.0
150.0
9.0
63.8
18.4
77.2
11.8
68.4
14.0
149.6
34.7
77.9
0.3
3.8
17.2
95.7
6.1
22.9
27.9
160.1
21.9
31.4
17.9
52.9
35.6
211.9
57.4
337.3
29.1
107.7
41.6
81.4
2018 广 东 2018 广 西 2018 海 南 2018 2018 重 庆 2018 四 川 2018 贵 州 2018 云 南 2018 西 藏 2018 2018 陕 西 2018 甘 肃 2018 青 海 2018 宁 夏 2018 新 疆 2018 2017 全国 2017 2017 北 京 2017 天 津 2017 河 北 2017 山 西 2017 内蒙古 2017 2017 辽 宁 2017 吉 林 2017 黑龙江 2017 2017 上 海
12-5 耕地灌溉面积和农用化肥施用量
(根据中国 统计年鉴
数据年度
年份 地区
耕地灌溉 面积 (千公顷)
2020年长兴县国民经济和社会发展统计公报

2019年,面对复杂严峻的国内外发展形势,全县上下认真贯彻落实中央和省、市各项决策部署,紧紧围绕建设“环太湖发展高地、长三角经济强县”目标,实字当头、一干到底,深入开展“双提十攻坚”行动,扎实做好“三服务”工作,全县经济运行总体稳健,呈现“稳中承压、稳中有质”态势,高质量发展的基础进一步夯实。
一、综合国民经济。
初步核算,全年地区生产总值(GDP)为693.28亿元,按可比价格计算,同比增长8.2%。
其中,第一产业增加值35.03亿元,同比增长3.1%;第二产业增加值355.64亿元,同比增长8.1%;第三产业增加值302.6亿元,同比增长8.9%,三次产业占比为5.1:51.3:43.6,第三产业对GDP增长贡献率为45.7%。
按户籍人口计算,人均生产总值为108861元,可比价增长7.9%,按平均汇率折算为15780美元。
图一 2014-2019年长兴县地区生产总值及增长速度图二 2019年长兴县三次产业增加值比重财政。
全年财政总收入114.38亿元,同比增长11.4%;地方财政收入65.83亿元,同比增长10.9%。
地方财政收入中,税收收入55.87 亿元,同比增长11.5%,占比为84.9%,其中增值税、企业所得税、个人所得税分别为24.67亿元、9.43亿元和3.86亿元,分别增长13.2%、21.7%和13.7%。
财政支出81.1亿元,同比增长13.3%,其中教育、科技、社会保障和就业、卫生健康分别支出15.57亿元、3.61亿元、7.79亿元和5.43亿元。
二、农业农业经济。
全年农林牧渔业总产值 62.6亿元,同比增长4.6% ,经济作物播种面积53.9万亩,其中油料作物播种面积6.1万亩,总产量 9497吨。
粮食播种面积45.7万亩,总产量19.5万吨。
现代农业成效明显,粮食生产功能区提标改造1.62万亩,新发展和改造提升农业七特色产业1.8万亩。
吕山乡入选国家级农业产业强镇创建,创建市级以上示范性农民专业合作社7家、市级以上示范性家庭农场16家、市级以上农业龙头企业4家;新增“三品”基地1.65万亩、产品28只(含绿色食品6只),认定通过农产品地理标志“胥仓雪藕”1只。
分省年度数据(化肥施用量)

数据库:分省年度数据指标:农用化肥施用折纯量(万吨)地区2013年2012年2011年2010年2009年2008年2007年2006年2005年2004年北京市12.7813.6713.8413.6713.8213.6313.9914.8414.8414.46天津市24.3424.4524.3925.5425.9625.8825.8224.5623.2922.85河北省331.04329.33326.28322.86316.17312.4311.87304.89303.39289.88山西省121.02118.28114.57110.37104.32103.4100.8398.2795.793.44内蒙古自治区202.42189.04176.94177.24171.42154.1140.29128.51116.72104.35辽宁省151.76146.9144.64140.08133.61128.77127.47121.08119.86117.85吉林省216.79206.73195.2182.8174.18163.84154.39146.7138.1159.09黑龙江省244.96240.28228.44214.89198.87180.73175.2162.2150.92143.81上海市10.7810.9911.9711.8412.5614.3214.0814.5314.4415.02江苏省326.83330.95337.21341.11344340.76342.03342.01340.81336.8浙江省92.4392.1592.0792.293.692.9892.8293.9894.2793.34安徽省338.4333.53329.67319.77312.79307.35305.02294.29285.67277.56福建省120.57120.87120.93121.04120.68118.67119.69120.86122.02121.67江西省141.58141.26140.77137.62135.76132.97132.65132.58129.39123.53山东省472.66476.26473.64475.32472.86476.33500.34489.82467.63450.96河南省696.37684.43673.71655.15628.67601.68569.68540.43518.14493.16湖北省351.93354.89354.89350.77340.26327.66299.9292.48285.83281.92湖南省248.19249.11242.49236.57231.6223.38219.58214.72209.87203.18广东省243.91245.38241.3237.29233.16226.6219.64212.13204.62201.3广西壮族自治区255.7249.04242.71237.16229.32222.58220.84210.66201.25195.22海南省47.5745.5347.7346.4346.2945.6241.6739.4937.3141.06重庆市96.6496.0295.5891.8291.1788.1484.3280.5479.0577.02四川省251.14253.03251.23248247.97242.84238.17228.16220.92214.71贵州省97.4298.1794.0886.5386.5483.0982.0580.2377.4174.31云南省219.02210.21200.47184.58171.39167.67158.27150.39142.65137.24西藏自治区 5.7 4.99 4.79 4.74 4.69 4.6 4.58 4.4 4.21 3.98陕西省241.73239.8207.27196.79181.32165.9158.81149.73147.3143.13甘肃省94.7192.1387.2485.2682.981.3780.1476.575.9272.39青海省9.89.38.278.767.968.117.557.17 6.99 6.57宁夏回族自治区40.4439.4438.2437.9335.5434.7534.6331.9229.9327.61新疆维吾尔自治区203.22192.7183.68167.56154.98148.89131.52119.65107.7799.17数据来源:国家统计局注:1.2003年以后,农林牧渔业总产值包括农林牧渔服务业产值。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
浙江省湖州长兴县农用化肥(折纯)施用量、机耕面积和有效灌溉面积数据分析报告2019版
前言
本报告主要收集权威机构数据如中国国家统计局,行业年报等,通过整理及清洗,从数据出发解读湖州长兴县农用化肥(折纯)施用量、机耕面积和有效灌溉面积现状及趋势。
湖州长兴县农用化肥(折纯)施用量、机耕面积和有效灌溉面积数据分析报告相关知识产权为发布方即我公司天津旷维所有,其他方引用我方报告均需要注明出处。
湖州长兴县农用化肥(折纯)施用量、机耕面积和有效灌溉面积数据分析报告深度解读湖州长兴县农用化肥(折纯)施用量、机耕面积和有效灌溉面积核心指标从农用化肥(折纯)施用量,机耕面积,有效灌溉面积等不同角度分析并对湖州长兴县农用化肥(折纯)施用量、机耕面积和有效灌溉面积现状及发展态势梳理,相信能为你全面、客观的呈现湖州长兴县农用化肥(折纯)施用量、机耕面积和有效灌溉面积价值信息,帮助需求者提供重要决策参考及借鉴。
目录
第一节湖州长兴县农用化肥(折纯)施用量、机耕面积和有效灌溉面积现状 (1)
第二节湖州长兴县农用化肥(折纯)施用量指标分析 (3)
一、湖州长兴县农用化肥(折纯)施用量现状统计 (3)
二、全省农用化肥(折纯)施用量现状统计 (3)
三、湖州长兴县农用化肥(折纯)施用量占全省农用化肥(折纯)施用量比重统计 (3)
四、湖州长兴县农用化肥(折纯)施用量(2016-2018)统计分析 (4)
五、湖州长兴县农用化肥(折纯)施用量(2017-2018)变动分析 (4)
六、全省农用化肥(折纯)施用量(2016-2018)统计分析 (5)
七、全省农用化肥(折纯)施用量(2017-2018)变动分析 (5)
八、湖州长兴县农用化肥(折纯)施用量同全省农用化肥(折纯)施用量(2017-2018)变动对
比分析 (6)
第三节湖州长兴县机耕面积指标分析 (7)
一、湖州长兴县机耕面积现状统计 (7)
二、全省机耕面积现状统计分析 (7)
三、湖州长兴县机耕面积占全省机耕面积比重统计分析 (7)
四、湖州长兴县机耕面积(2016-2018)统计分析 (8)
五、湖州长兴县机耕面积(2017-2018)变动分析 (8)
六、全省机耕面积(2016-2018)统计分析 (9)
七、全省机耕面积(2017-2018)变动分析 (9)
八、湖州长兴县机耕面积同全省机耕面积(2017-2018)变动对比分析 (10)
第四节湖州长兴县有效灌溉面积指标分析 (11)
一、湖州长兴县有效灌溉面积现状统计 (11)
二、全省有效灌溉面积现状统计分析 (11)
三、湖州长兴县有效灌溉面积占全省有效灌溉面积比重统计分析 (11)
四、湖州长兴县有效灌溉面积(2016-2018)统计分析 (12)
五、湖州长兴县有效灌溉面积(2017-2018)变动分析 (12)
六、全省有效灌溉面积(2016-2018)统计分析 (13)
七、全省有效灌溉面积(2017-2018)变动分析 (13)
八、湖州长兴县有效灌溉面积同全省有效灌溉面积(2017-2018)变动对比分析 (14)
图表目录
表1:湖州长兴县农用化肥(折纯)施用量、机耕面积和有效灌溉面积现状统计表 (1)
表2:湖州长兴县农用化肥(折纯)施用量现状统计表 (3)
表3:全省农用化肥(折纯)施用量现状统计表 (3)
表4:湖州长兴县农用化肥(折纯)施用量占全省农用化肥(折纯)施用量比重统计表 (3)
表5:湖州长兴县农用化肥(折纯)施用量(2016-2018)统计表 (4)
表6:湖州长兴县农用化肥(折纯)施用量(2017-2018)变动统计表(比上年增长%) (4)
表7:全省农用化肥(折纯)施用量(2016-2018)统计表 (5)
表8:全省农用化肥(折纯)施用量(2017-2018)变动统计表(比上年增长%) (5)
表9:湖州长兴县农用化肥(折纯)施用量同全省农用化肥(折纯)施用量(2017-2018)变动对比统计表 (6)
表10:湖州长兴县机耕面积现状统计表 (7)
表11:全省机耕面积现状统计表 (7)
表12:湖州长兴县机耕面积占全省机耕面积比重统计表 (7)
表13:湖州长兴县机耕面积(2016-2018)统计表 (8)
表14:湖州长兴县机耕面积(2017-2018)变动统计表(比上年增长%) (8)
表15:全省机耕面积(2016-2018)统计表 (9)
表16:全省机耕面积(2017-2018)变动统计表(比上年增长%) (9)
表17:湖州长兴县机耕面积同全省机耕面积(2017-2018)变动对比统计表(比上年增长%) (10)
表18:湖州长兴县有效灌溉面积现状统计表 (11)
表19:全省有效灌溉面积现状统计分析表 (11)
表20:湖州长兴县有效灌溉面积占全省有效灌溉面积比重统计表 (11)
表21:湖州长兴县有效灌溉面积(2016-2018)统计表 (12)
表22:湖州长兴县有效灌溉面积(2017-2018)变动分析表(比上年增长%) (12)
表23:全省有效灌溉面积(2016-2018)统计表 (13)
表24:全省有效灌溉面积(2017-2018)变动分析表(比上年增长%) (13)
表25:湖州长兴县有效灌溉面积同全省有效灌溉面积(2017-2018)变动对比统计表(比上年增长%) (14)。
