7刚体动力学
刚体动力学

●
刚体基本动力学量
现在取 Axyz 坐标系为一个平动参考系 , 则刚体上的 R 点相对速度为 v r R =× R
dV
【定理】刚体相对动量为 p r =× mt R C
证明:pr =∫ v r R dV =∫ × R R dV
=×∫ R R dV =×m t RC(证毕)
⇒ L'A =∫ R2 I − R R ⋅ R dV =[∫ R2 I − R R R dV ]⋅
= J A⋅
(证毕)
1 1 ' 【定理】刚体相对动能为 T r = ⋅L A= ⋅J A⋅ 2 2
证明: T r=
1 1 2 v r R dV = ∫ v r⋅v r R dV ∫ 2 2 1 1 × R ⋅ v R dV = R × v r ⋅ R dV ∫ ∫ r 2 2
【推论】匀质刚体如果有一过 A 的镜像对称面,则过 A 且 与该镜像面垂直的轴是主轴;如果过 A 有两个正交的 镜像面,则两镜像面过 A 点的法线以及镜像面的交线 构成主轴系;匀质旋转体的旋转轴和任意与之正交的 两正交轴构成主轴系 . (请自己根据定义证明) 【定理】假定角速度在主轴坐标系下表示为
d d' J A⋅ 是矢量, J A⋅ = J A⋅× J A⋅ dt dt
⇒⋯⇒ J A⋅ = J XZ X J YZ Y J ZZ Z = ˙ Z ˙
d e ⋅M A ⇒ Z⋅ J A⋅= J ZZ = ≡M Z ¨ Z dt
2
J lk = J kl
(证毕)
因为:
lk =kl , Rl R k = Rk Rl
注:一般把 Jlk 称为惯量系数,由于对称性,只有 6 个是独立的 注:如果 AXYZ 不是固连在刚体上的坐标系,则 R 相对 AXYZ 有 转动,那么在 AXYZ 上看到的质量分布一般会随时间改变, 故在这个坐标系中惯量系数依赖于时间 . 注:如果 AXYZ 不是固连在刚体上的坐标系,在少数有良好对称性 的情况下 AXYZ 上看到的质量分布可能不随时间改变,此时在 这个坐标系中惯量系数是常数 .
《刚体动力学 》课件

牛顿第二定律
物体的加速度与作用在物 体上的力成正比,与物体 的质量成反比。
牛顿第三定律
对于任何两个相互作用的 物体,作用力和反作用力 总是大小相等,方向相反 ,作用在同一条直线上。
刚体的平动
刚体的平动是指刚体在空间中 的位置随时间的变化而变化, 而刚体的形状和大小保持不变
的运动。
刚体的平动具有三个自由度 ,即三个方向的平动。
05
刚体的动力学方程
刚体的动力学方程
牛顿第二定律
刚体的加速度与作用力成正比,与刚体质量 成反比。
刚体的转动定律
刚体的角加速度与作用力矩成正比,与刚体 对转动轴的转动惯量成反比。
刚体的动量方程
刚体的动量变化率等于作用力对时间的积分 。
刚体的自由度与约束
自由度
描述刚体运动的独立变量,如平动自由度和转动 自由度。
约束
限制刚体运动的条件,如固定约束、滑动约束等 。
约束方程
描述刚体运动受约束的数学表达式。
刚体的动力学方程的求解方法
解析法
通过代数运算求解动力学方程,适用于简单问 题。
数值法
通过迭代逼近求解动力学方程,适用于复杂问 题。
近似法
通过近似模型求解动力学方程,适用于实际问题。
06
刚体动力学中的问题与实例 分析
人工智能和机器学习的发展将为刚体 动力学的研究提供新的思路和方法, 有助于解决复杂动力学问题。
感谢您的观看
THANKS
船舶工程
在船舶工程中,刚体动力学 用于研究船舶的航行稳定性 、推进效率以及船舶结构的 安全性等。
兵器科学与技术
在兵器科学与技术领域,刚 体动力学用于研究弹药的发 射动力学、火炮的射击精度 和稳定性等。
刚体动力学
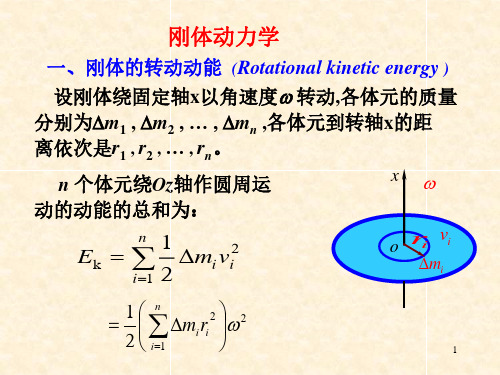
n i 1
1 2
Δmi
vi2
o ri vi
mi
1 2
n i 1
Δmi ri 2
2
1
式中
n
mi
ri2
称为刚体对转轴的转动惯量
。
i 1
用J 表示:
n
J mi ri2
i 1
代入动能公式中, 得到刚体转动动能的一般表达式
Ek
1 2
J2
Ek
1 2
mv2
刚体转动动能与质点运动动能在表达形式上是相
3
若刚体的质量连续分布 , 转动惯量中的求和号 用积分号代替
J r 2dm r 2 dV
单位:kg.m2
讨论:1.质量越大,转动惯量越大。 2.在总质量一定的条件下,刚体的质元分布 离轴越远,转动惯量越大。和质量分布有关。 3.转轴位置不一样,转动惯量不同。
与转动惯量有关的因素:
0
R 2πr 3 d r
0
2π R r3 d r 1 mR2
0
2
9
三、力矩作的功
力 矩 (moment of force)
力矩
M
r
F
大小 M= F r sinθ= F d
方向 右手定则
力臂:从转轴Z与截面
的交点O到力F的作用
线的垂直距离d称为力
对转轴的力臂
M
i 1
矩的代数和, 也就是作用于刚体的外力对转轴的合外
力矩Mz 。14来自如果刚体在力矩Mz 的作用下绕固定轴从位置1转 到2 , 在此过程中力矩所作的功为
《刚体动力学》课件

单击此处输入你的项正文,文字是您思想的提炼。
应用场景:碰撞、打击、爆炸等 角动量定理 角动量定理
定义:角动量是物体转动惯量和角速度的乘积 单击此处输入你的项正文,文字是您思想的提炼。
角动量定理公式:L=Iω
单击此处输入你的项正文,文字是您思想的提炼。
应用场景:行星运动、陀螺仪等
刚体的滚动和滑动摩擦
刚体滚动:刚体在平面内绕固定点转动,滚动摩擦力产生的原因和影响
刚体滑动摩擦:刚体在平面内滑动时产生的摩擦力,滑动摩擦系数与接触面材料和粗糙度等因素 的关系
刚体滚动和滑动摩擦的应用实例:例如,汽车轮胎与地面之间的滚动摩擦力,以及机械零件之间 的滑动摩擦力等
刚体滚动和滑动摩擦的实验研究:通过实验研究刚体滚动和滑动摩擦力的影响因素和规律,为实 际应用提供理论支持
04
刚体动力学基本原理
牛顿第二定律
定义:物体加速度的大小跟作用 力成正比,跟物体的质量成反比
应用:解释物体运动状态变化的 原因
添加标题
添加标题
公式:F=ma
添加标题
添加标题
注意事项:只适用于宏观低速运 动的物体
动量定理和角动量定理
定义:动量是物体质量与速度的乘积
单击此处输入你的项正文,文字是您思想的提炼。
刚体动力学研究内容
刚体的定义和性质 刚体运动的基本形式 刚体动力学的基本方程 刚体动力学的研究方法
刚体动力学发展历程
早期发展:古代力学对刚体的研究 经典力学时期:牛顿、伽利略等经典力学大师对刚体动力学的研究 弹性力学时期:弹性力学的发展对刚体动力学的影响 现代发展:计算机技术和数值模拟方法在刚体动力学中的应用
课程内容:刚体 的平动、转动、 碰撞等动力、力学等相关专 业的本科生和研 究生
刚体运动的基本原理与动力学分析

刚体运动的基本原理与动力学分析刚体运动是物理学中的重要概念,研究刚体的基本原理和动力学分析对于理解力学运动规律具有重要意义。
本文将从刚体的定义、刚体运动的基本原理,以及刚体的动力学分析等方面展开论述。
一、刚体的定义刚体是指在力的作用下,保持形状和体积不变的物体。
刚体的特点是不易变形,内部各点之间的相对位置保持不变。
二、刚体运动的基本原理1. 平动和转动刚体运动可以分为平动和转动两种形式。
平动是指刚体上所有点按照相同方向和相同距离运动,转动是指刚体绕着某个轴旋转。
2. 受力和力矩刚体的运动受到外力的作用,外力可以分为接触力和非接触力。
接触力是指物体之间直接接触施加的力,非接触力是指物体间通过场的相互作用施加的力,如重力和电磁力等。
另外,刚体的转动还受到力矩的影响。
力矩是由作用力与力臂的乘积,用来描述力对刚体的转动效果。
力矩的方向由右手定则确定,大小等于力的大小与力臂的长度之积。
3. 刚体的运动学方程刚体的运动学方程描述了刚体在运动过程中各个部分的位置、速度和加速度之间的关系。
根据牛顿第二定律和运动学关系可以得到刚体的运动学方程。
三、刚体的动力学分析1. 平动的动力学分析刚体的平动运动可以通过牛顿第二定律进行动力学分析。
根据牛顿第二定律可知,刚体所受的合外力等于刚体的质量与加速度的乘积。
2. 转动的动力学分析刚体的转动运动需要通过力矩和转动惯量进行动力学分析。
根据牛顿第二定律可知,刚体所受的合外力矩等于刚体的转动惯量与角加速度的乘积。
此外,刚体的角动量和动能也是进行动力学分析的重要物理量。
角动量等于刚体的转动惯量与角速度的乘积,动能等于刚体的转动惯量与角速度的平方的乘积的一半。
四、刚体运动的应用刚体运动的研究在工程、医学等领域有广泛应用。
例如在机械工程中,对机械零件的运动进行分析可以用于设计和优化机械结构;在生物医学中,对人体骨骼系统的运动学和动力学分析可以用于疾病的诊断和康复治疗。
总结:刚体运动的基本原理和动力学分析是研究力学运动规律中的重要内容。
刚体力学基础

非专业训练,请勿模仿
例 解 由转动定律得
1 mgl sin J 2 1 2 式中 J ml 3 3g sin 得 2l
角加速度与质量无关,与长 度成反比,竹竿越长越安全。
-------------------------------------------------------------------------------
刚体的一般运动 质心的平动
+
绕质心的转动
-------------------------------------------------------------------------------
二、刚体绕定轴转动定律
F外力 F内力 mi ai
ai :质元绕轴作圆运动
-------------------------------------------------------------------------------
二、定轴转动的角动量守恒定律
质点角动量(相对O点)
定轴转动刚体
L r p r mv
-------------------------------------------------------------------------------
解:
M 1l gdl cos M mgL cos 2 m g1 l cos dl cos mgl M 2 3g cos L 1 22 J 2l M ml L g 3 cos L 2 3g cos d d d d 1 2 l dt cos d d mgL dt 2
2 法向: F cos F cos m r 法向力的作用线过转轴 i i i i. 内力 ,其力矩为零 外力 切向:F外力 sin i F内力 sin i mi ri
刚体动力学

刚体动力学
刚体动力学是指研究力和质量对刚体运动的影响,它涉及物理
和数学,主要研究力对物体运动的影响。
它广泛应用于工程和物理领域,用于描述物体在局部或全局中的运动状态。
如何利用运动学理论
来分析和解释物理世界中物体的运动轨迹,最终揭示物体运动的物理
原理至关重要。
在刚体动力学的概念中,物体的运动被建模为一种力对对对象的
瞬时影响。
通过应用力,物体的运动可以得到估计。
瞬时力是指在特
定时空会给物体造成瞬时影响的力。
可以从特征定律出发,将其用于
物体运动分析。
这些定律涉及到物理力学,牛顿力学和拉普拉斯力学,上述定律可将物体的运动状态的分类。
与此同时,通过测量物体的加
速度、速度和位移,有可能解释其运动轨迹,解析物体的运动和定义
有关的物理参数,这些物理参数的累积可以描述物体的运动状态,从
而揭示物体运动的原理。
刚体动力学的原理也可以用来处理运动学中更加抽象的问题,例
如变换,尤其是物体受力时联合受力的问题。
此外,它还可以用于研
究物理系统中某些复杂的力的运动模式,包括动量、角动量、能量和
声学等。
可以说,它是物理上最基本的模型,用于解释物体的局部或
全局运动。
利用刚体动力学的原理,可以研究物体运动在各种复杂条
件下的变化,从而揭示物体运动的物理原理。
动量定理应用

动量定理应用动量定理是物理学中的一个基本原理,它描述了物体的动量随时间的变化关系。
在本文中,我们将探讨动量定理在碰撞分析、弹道计算、交通事故分析、工业生产、抛射体运动、游戏物理、刚体动力学和流体力学等方面的应用。
1.碰撞分析动量定理可以用于分析碰撞过程中的能量和动量变化。
在碰撞中,物体的动量会发生瞬时变化,而动量定理可以描述这个变化的过程。
通过动量定理,我们可以判断碰撞是否符合物理规律,从而帮助我们理解物体的碰撞行为。
2.弹道计算动量定理可以用于计算炮弹、子弹等抛射体的运动轨迹和速度。
在枪械和火箭发射中,抛射体的速度和轨迹是决定射击精度和发射角度的重要因素。
通过动量定理,我们可以精确地计算出抛射体的运动轨迹和速度,从而提高枪械和火箭的射击精度。
3.交通事故分析动量定理可以用于分析交通事故中车辆碰撞时的能量和动量变化。
在交通事故中,车辆碰撞时的能量和动量是判断事故责任和损伤程度的重要依据。
通过动量定理,我们可以分析碰撞过程中车辆的能量和动量变化,从而帮助判断事故责任和损伤程度。
4.工业生产动量定理可以用于计算压力容器和机械臂等工业生产设备的力和运动轨迹。
在工业生产中,压力容器和机械臂的运动轨迹和力度是决定产品质量和效率的重要因素。
通过动量定理,我们可以精确地计算出设备的运动轨迹和力度,从而提高生产效率和产品质量。
5.抛射体运动动量定理可以用于分析抛射体运动的轨迹和速度。
在抛射体运动中,物体的速度和轨迹是决定射击精度的重要因素。
通过动量定理,我们可以精确地计算出抛射体的运动轨迹和速度,从而提高射击精度。
6.游戏物理动量定理可以用于制作更加真实的游戏物理效果,包括碰撞反弹、物块运动等。
在游戏中,物理效果的真实与否直接影响到游戏的整体质量。
通过动量定理,我们可以模拟出更加真实的物理效果,从而提高游戏的整体质量。
7.刚体动力学动量定理可以用于计算刚体运动过程中的力和运动轨迹。
在刚体动力学中,物体的力和运动轨迹是决定物体运动状态的重要因素。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
7.刚体动力学在前一篇文章中,我们直接设置了刚体的角速度和角加速度让它进行旋转,现在的问题是:刚体的角加速度究竟是由什么决定的?物理知识如下图所示,若外力F (图中的箭头表示)的作用线通过物体质心且刚体绕质心的初始角速度为零,则物体只做平动,可应用质心运动定理,建立刚体平动的动力学微分方程:F 外=m a =m d v C dt式中v c 为质心的运动速度矢量。
若如下图所示外力作用线不过质心O ,刚体就要旋转,如果O 是固定的,这在物理学上称为刚体定轴转动。
我们发现:在这个力的作用下,刚体的转动效果不仅与F 的大小有关,还和F 的作用线到转轴的距离有关,因此我们提出一个新的物理量——力矩(moment ,torque ),在高中物理中力矩定义为力与力臂的乘积,力臂的定义为力的作用线与转轴的距离,即图中的d 。
公式如下:M =Fd在高中物理中不讨论力矩是否是矢量,只说明若假设顺时针力矩为正,则逆时针力矩取为负值,事实上是将力矩作为标量处理的。
但是大学物理告诉我们,力矩是一个矢量,它定义为转动轴到着力点的矢量与力矢量的叉乘,公式为:M =r ×F (公式1)在右手坐标系中(即XNA 使用的坐标系),M 的方向是由右手螺旋定则进行判断的,即将右手拇指伸直,四指弯曲由r 转向F ,这时大拇指方向就是力矩的方向,上图中的力矩方向为竖直向下,即-z 方向。
若处理的是刚体定轴转动,那么力矩只有两个方向,这也是高中物理用带符号的标量表示力矩的原因。
而在2D 物理引擎中处理的也是这种情况,若你想要实现的是3D 物理引擎,就需要讨论更复杂的刚体定点转动,目前还用不到。
在质点运动学中我们曾经讨论过:力F 可以使质点产生加速度a ,而物体的质量表示速度v 改变的难易程度,公式为F =m a 。
类似的情况有:在转动中,力矩M 可以使刚体产生角加速度α,表示物体角速度ω改变难易程度的物理量叫做转动惯量I ,所以刚体转动的动力学方程为:M =I α=I d ωdt至于如何求物体的转动惯量,还是去翻大学物理书吧。
目前这个引擎要用到的是:1.均匀矩形板以中心为转轴的转动惯量为m(a 2+b 2)/12,其中m 为板的质量,a 、b 分别为板长和板宽;2.均匀薄圆盘,转轴为中心与盘面垂直的情况下,转动惯量为mR 2/2,其中R 为圆盘的半径。
若刚体内所有的运动点都平行于某一平面,则这种运动叫做刚体的平面平行运动。
而2D 物理引擎处理的就是这种运动。
归纳起来,刚体平面平行运动可分解为质心的运动和绕质心的转动,二者的动力学方程分别为质心运动定理:F 外=m a =m d v C dt绕质心的转动:M =I α=I d ωdt故应用以上两个方程,即可建立刚体一般运动的微分方程。
再利用欧拉运动学方程和初始条件,即可确定刚体在空间的一般运动规律。
在前面的质点动力学中,我们不仅讨论了牛顿定律,还讨论了适用范围更广的动量定理:I =F t =Δp =m Δv ,在转动中也有对应的规律。
与动量p 对应的叫做角动量J ,定义为J =I ω(对应p =m v );与冲量I 对应的叫做角冲量,又叫冲量矩,定义为M t (对应I =F t ),对应动量定理是角动量定理:∫M dt =I(ω-ω0) (公式2)即角冲量等于角动量的增量。
在Stun2Dphyisics 中的实现有了以上的物理知识,我们开始在引擎中添加新的代码。
1.在Body 类中添加转动惯量/// <summary>/// Body 的转动惯量。
/// <para>2D 空间中的转动惯量是一个标量,表示body 绕质心转动的难易程度。
</para> /// <para>不同形状的物体转动惯量也不同。
对于诸如圆、矩形之类的基本形状来说,有公式/// 可以根据形状属性(圆半径或矩形的长宽)计算转动惯量。
</para>/// <para>若Body 不是基本形状,通常也可以使用接近的基本形状进行近似模拟。
/// 还可以使用更高级的算法计算非基本形状的转动惯量。
</para>/// </summary>/// <exception cref="ArgumentException">M转动惯量不能小于等于0</exception>public float MomentOfInertia{get { return momentOfInertia; }set{if (value <= 0)throw new ArgumentException("转动惯量不能为小于等于0", "value");momentOfInertia = value;if (isStatic)inverseMomentOfInertia = 0;elseinverseMomentOfInertia = 1f / value;}}/// <summary>/// 转动惯量的倒数(1/<see cref="MomentOfInertia"/>)/// </summary>public float InverseMomentOfInertia{get { return inverseMomentOfInertia; }}额外设置一个转动惯量倒数的原因和设置一个质量倒数的原因是一样的。
2.添加工厂类自动创建Body你可以手动创建一个Body,代码如下:Body body=new Body();Body.Mass=1;// 若Body为质量为1,长宽各为1的矩形,根据以上物理知识,它的转动惯量为// 1*(12+12)/12=1/6Body. MomentOfInertia=1/6;但是为了使用更方便,我们可以将这个计算公式整合到引擎中,所以在引擎项目中新建名为Factories的文件夹,在这个文件夹中新建一个名为BodyFactory.cs的类,代码如下:namespace Stun2DPhysics.Factories{/// <summary>/// 便于创建Body的工厂方法/// </summary>public class BodyFactory{private static BodyFactory _instance;private BodyFactory(){}public static BodyFactory Instance{get{if (_instance == null){_instance = new BodyFactory();}return _instance;}}#region 矩形/// <summary>/// 创建一个矩形Body。
/// </summary>/// <param name="physicsSimulator">物理引擎。
</param>/// <param name="width">矩形宽。
</param>/// <param name="height">矩形高。
</param>/// <param name="mass">质量。
</param>/// <returns></returns>public Body CreateRectangleBody(PhysicsSimulator physicsSimulator, float width, float height, float mass){Body body = CreateRectangleBody(width, height, mass);physicsSimulator.Add(body);return body;}/// <summary>/// 创建一个矩形Body。
/// </summary>/// <param name="width">矩形宽。
</param>/// <param name="height">矩形高。
</param>/// <param name="mass">质量。
</param>/// <returns></returns>public Body CreateRectangleBody(float width, float height, float mass){if (width <= 0)throw new ArgumentOutOfRangeException("width", "矩形宽必须大于0");if (height <= 0)throw new ArgumentOutOfRangeException("height", "矩形高必须大于0");if (mass <= 0)throw new ArgumentOutOfRangeException("mass", "质量必须大于0");Body body = new Body();body.Mass = mass;// 设置矩形的转动惯量。
body.MomentOfInertia = mass * (width * width + height * height) / 12;return body;}#endregion#region 圆形/// <summary>/// 创建一个圆形Body。
/// </summary>/// <param name="physicsSimulator">物理引擎。
</param>/// <param name="radius">圆半径。
</param>/// <param name="mass">质量。
</param>/// <returns></returns>public Body CreateCircleBody(PhysicsSimulator physicsSimulator, float radius, float mass){Body body = CreateCircleBody(radius, mass);physicsSimulator.Add(body);return body;}/// <summary>/// 创建一个圆形Body。
