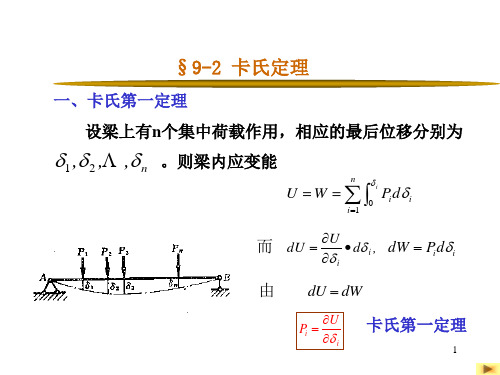
卡氏定理与超静定
合集下载
材料力学卡式定理
l
(2)
于是(1)式改写为
y / l
(3)
3
梁内任一点处的比能
u
1 2
E 2
1 2
E 2
l2
y2
(4)
梁的应变能
l
U VudV 0 (AudA)dx
l 1 E 2
( 02
l2
y2dA)dx 1 EI 2
A
2l
(5)
由卡氏第一定理
m U 1 EI (2 ) EIθ
(6)
2 lx)
2
dx
1 ( 5PL3 RC L3 ) 0
EI 48
3
RC
5P 16
能量法求解超静定结构,适 用任意荷载作用下、线性或 非线性弹性杆系、刚架或曲 杆等超静定系统。
14
2.求 wB
① 求内力
M
AB ( x)
5P 16
(L
x)
P(0.5L
x)
M BC ( x)
5P 16
Px L EI Px
1 EI
x 0
P(L
x1 ) ( x1
x)dx1
P
x3 [
(L
x)x2
Lx 2 ]
EI 3
2
12
例6 等截面梁如图,用卡氏定理求B 点的挠度。
P 0.5 L
B
A
L
解:1.依 wC 0 求多余反力,
卡氏定理解 ① 取静定基如图 C 超静定结构
② 求内力
M AB ( x) RC (L x) P(0.5L x)
L x1
O
x
w
①求内力 M AB ( x1) P(L x1) Px ( x x1) M BC ( x1) P(L x1)
材料力学第三章 能量法

三、卡氏第二定理(线弹性体)
Di
Vc Fi
在线弹性范围内
余能定理 Vc V
Di
V Fi
卡氏第二定理: 线弹性杆件或杆系的应变能对于 作用在该杆件或杆系上的某一荷 载的变化率,就等于与该荷载相 应的位移。
卡氏第二定理适用于一切受力状态下的线弹性体。
卡氏第二定理公式D及i 含义VF:i
若结构的应变能 V 表示为F1、F2 …Fi …的函数,则应变 能对任一载荷Fi的偏导数等于Fi作用点沿Fi方向位移。
C
与需求位移相应的虚设外力
F。求偏导后令其为零。
(2)列弯矩方程
M
x
F 2
ql 2
x
qx 2 2
0
x
l 2
M
x
F 2
ql 2
x
qx 2 2
0
x
l 2
(3)求梁的应变能
M 2 l/2
x
1
V 2 0
dx
2EI
EI
l/2
0
F 2
ql 2
x
qx 2 2
2 dx
1 EI 1 EI
V W
一、杆件基本变形的应变能
(一)轴向拉伸(压缩)
1、杆的应变能
轴力沿轴线不变的情况:
dW Fd(Dl) W Dl1 Fd(Dl) 0
线弹性范围内 W 1 FDl
1
2
V
F
W
FN
2
F Dl Dl
FNl EA
应变能
V
FN2l 2EA
F
l
Dl
F
Dl d (Dl)
Dl1
Dl
(一)轴向拉伸(压缩)
卡氏定理材料力学

2Ma 3EI
(
)
DF FD
CD段:
M (x)
Mx , 2a
M (x) F
x,
MC
CB段: M (x) M ,
M (x) 2a x, a F
2a
C
M
AB段: M (x) 0,
M (x) x, F
a
B
A FAx
(4)带入卡氏定理求解。
Dx
l
M (x) M (x) d x EI F
FAy
2a
MC, 在D截面虚设一水平力F 。 MC
DF
C
(2)取刚架为研究对象, a
受力图如图所示。
M
FD
FAx F
B
a
A FAx
FAy
FD
F
1 2a
(M
MC)
FAy
(3)分段列出弯矩方程及偏导方程。
2a
CD段:
MC
M
( x1 )
[F
1 2a
(M
MC
)]x1
Cx aM 2
x
1
DF FD
M (x1) F
新位移 i 上也做功,系统的总的应变能为
V
Fi
i
1 2
Fi
i
(2)
由(1)=(2),并忽略二阶小量,得
V Fi
i
V Fi
i
若将结构的应变能表示为载荷F1,F2, ,Fn 的 函数,则应变能对任一载荷Fi的偏导数,等于Fi作用
点沿Fi作用方向的位移 i ,称为卡氏第二定理。
说明 (1)卡氏定理只适用线弹性结构。
i
V Fi
FN (x) FN (x) d x L EA Fi
材料力学卡式定理

M
AB
(x)
P
11 x 3 L 16
M
BC
(x)
P
5( L x ) 16
③ 变形
wB U P
0
M ( x ) M ( x ) EI P
2
dx
L
L
1 EI
0 .5 L
P(
11 x 3 L 16
) dx
0 .5 L
P( ) ( L x ) dx 16 5
荷载之变化率,就等于与该荷载相应的位移。
适用条件:适用一切受力状态下的弹性杆件,其中, Pi ——作用在杆件上的广义力;
i ——与 Pi 相应的广义位移。
用卡氏定理的注意事项
①U——整体结构在外载作用下的线
P1 P2
弹性变形能 ② Pi 视为变量,结构反力和变形能
等都必须表示为 Pi的函数 ③ i为 Pi 作用点的沿 Pi 方向的变形。
dx M ( x ) M ( x ) EI Pn
L
M n ( x ) M n ( x ) GI
P
L
Pn
dx
L
例5 结构如图,用卡氏定理求A 面的挠度和转角。 P A 解:求挠度,建坐标系 ①求内力 M ( x ) xP A xP
EI
L
x
O
②将内力对PA求偏导
M ( x ) PA x
(
1 E 2 l
2
2
0
y dA ) dx
2 A
1 EI 2 l
2
(5)
由卡氏第一定理
m U 1 EI 2 l ( 2 ) EI θ l
AB
(x)
P
11 x 3 L 16
M
BC
(x)
P
5( L x ) 16
③ 变形
wB U P
0
M ( x ) M ( x ) EI P
2
dx
L
L
1 EI
0 .5 L
P(
11 x 3 L 16
) dx
0 .5 L
P( ) ( L x ) dx 16 5
荷载之变化率,就等于与该荷载相应的位移。
适用条件:适用一切受力状态下的弹性杆件,其中, Pi ——作用在杆件上的广义力;
i ——与 Pi 相应的广义位移。
用卡氏定理的注意事项
①U——整体结构在外载作用下的线
P1 P2
弹性变形能 ② Pi 视为变量,结构反力和变形能
等都必须表示为 Pi的函数 ③ i为 Pi 作用点的沿 Pi 方向的变形。
dx M ( x ) M ( x ) EI Pn
L
M n ( x ) M n ( x ) GI
P
L
Pn
dx
L
例5 结构如图,用卡氏定理求A 面的挠度和转角。 P A 解:求挠度,建坐标系 ①求内力 M ( x ) xP A xP
EI
L
x
O
②将内力对PA求偏导
M ( x ) PA x
(
1 E 2 l
2
2
0
y dA ) dx
2 A
1 EI 2 l
2
(5)
由卡氏第一定理
m U 1 EI 2 l ( 2 ) EI θ l
材料力学第27讲 Chapter3-2第三章 能量法(卡氏定理)

F
f (x) x M AB ( y) M AB ( y)dy
0 EI
F
F 0
x
1 EI
[P(L y)][(x y)]dy
0
P EI
x
[
y2
(L
x)
y
11
解(2): 用卡氏第一定理
关键: V V (Ax , Ay )
1
Ax
450
2 l2
l1 Ay
变形协调关系
Ax l1; Ay sin 450 Ax cos 450 l2
450
V
FN21l1 FN22l2 2EA 2EA
EA 2l1
l12
EA 2l2
l22
l FNl
EA
EA 2l1
材料力学 II
(2)
Energy Method—Part 2
第廿七讲
1
内容
1. 应变能和余能的计算 2. 卡氏定理 3. 用能量法解超静定系统 4. 虚位移原理及单位力法
2
线弹性问题应变能的普遍表达式
V
FN 2 (x)dx L 2EA
T 2 (x)dx L 2GIP
M 2 (x)dx L 2EI
Ay (2
2 1)Ax
1
l1
Ax
1 2l2
Ay Ax
0
Ax
2
1 2
Ay Ax
0
1
l2
Ay Ax
2P EA
Ay
Ax
2
2Pl EA
l2 2l1 2l
Ax
Pl , EA
Ay (2
2 1) Pl EA
与解法一结果相同
14
II. 卡氏第二定理
f (x) x M AB ( y) M AB ( y)dy
0 EI
F
F 0
x
1 EI
[P(L y)][(x y)]dy
0
P EI
x
[
y2
(L
x)
y
11
解(2): 用卡氏第一定理
关键: V V (Ax , Ay )
1
Ax
450
2 l2
l1 Ay
变形协调关系
Ax l1; Ay sin 450 Ax cos 450 l2
450
V
FN21l1 FN22l2 2EA 2EA
EA 2l1
l12
EA 2l2
l22
l FNl
EA
EA 2l1
材料力学 II
(2)
Energy Method—Part 2
第廿七讲
1
内容
1. 应变能和余能的计算 2. 卡氏定理 3. 用能量法解超静定系统 4. 虚位移原理及单位力法
2
线弹性问题应变能的普遍表达式
V
FN 2 (x)dx L 2EA
T 2 (x)dx L 2GIP
M 2 (x)dx L 2EI
Ay (2
2 1)Ax
1
l1
Ax
1 2l2
Ay Ax
0
Ax
2
1 2
Ay Ax
0
1
l2
Ay Ax
2P EA
Ay
Ax
2
2Pl EA
l2 2l1 2l
Ax
Pl , EA
Ay (2
2 1) Pl EA
与解法一结果相同
14
II. 卡氏第二定理
卡氏第二定理线性弹性体对于线性弹性体

0a
(FPBB x1 EI
)
(
x1
)dx1
a2a
FPBB
x2
FP(
EI
x2
a)(
x2
)dx2
令:FB=F
By
a 0
Fx12 EI
dx1
2a a
2F
x22 Fax2 EI
dx2
7Fa3 2EI
二、求B 处的转角
由于 B 处没有相应的力偶与 转角相对应,可假设在 B 作用一 力偶 M f ( M f 为附加力偶)。
P 2l 3 3EI
P2l 3 2GI P
3、利用功能原理求位移
U
W
1 2
P
Cy
P2l3 3EI
P2l3 2GI P
P 2
Cy
,
x
Cy
2Pl 3 3EI
Pl 3 GI P
x
例 桁架如图所示,各杆EA相同,利用功能原理求D点的 垂直位移。
解 1、各杆内力
C
FN1 FN 5
dx
段的应变能:
dU
1 2
FN
EA
(x) (dx)
FN2 (x)dx 2EA
FN
FF
FN (x) FN (x) dx
x
FN (x)
dU
1 2
FN
(x) (dx)
FN2 (x)dx 2EA
比能:
u(x) dU FN2 (x)dx 1 (x) (x)
dV 2EA Adx 2
材料力学第8章-能量法3-1

d
FN dx d(l) = EA
0 N
Mdx d EI
0
Tdx d GI p
0 S 0
1 F d l M d F d T d
F FN T T M M dx dx dx EA EI GI p
0 N 0 0
2.力和位移应理解为广义力和广义位移。
能量法/虚功原理 单位力法 图乘法
上节回顾
1、可能内力,可能位移,虚位移 2、虚功原理
在外力作用下处于平衡的结构,任意给它一个虚位移, 则外力在虚位移上所做的虚功,等于结构内力在虚变形上所 作的功。
W Wi
* e
e
*
外力虚功
内力虚功
l
W
Fi
5 M a 3
0 1c
2 Fa a
M
0 2c
3 a 2
Fa a 3 2 2 0 M 3c a 3
能量法/虚功原理 单位力法 图乘法
A
EI1
a
C
EI 2
a
F B
1
2Fa Fa
1
2a 5a/3
2
3a/2
-
2a/3
3
根据图乘法,自由端的挠度为:
1 1 0 0 yB 1M1c 2 M 2c EI 3M 30c EI1 2 1 Fa a 5 3 1 Fa a 2a a Fa a a EI1 2 3 2 EI 2 2 3
能量法/超静定问题 力法 例 如图超静定梁, EI为常数,试求B点的约束反力。
第八章
一、杆件的应变能
超静定问题的概念

超静定问题的概念
超静定问题是指具有多余约束的几何结构问题。
在力学中,超静定问题是指系统的约束数多于方程数,即系统的自由度被多限制的问题。
相较于静定问题,超静定问题更加复杂,因为除了平衡方程外,还需要考虑多余约束条件。
在工程中,超静定问题通常出现在结构力学、弹性力学等领域。
例如,一个简单的悬臂梁就是超静定问题,因为它的端部受到固定约束,但只有两个平衡方程来描述其行为。
为了解决超静定问题,我们需要使用额外的约束条件来建立方程,从而得到唯一解。
超静定问题的研究有助于我们更好地理解结构的稳定性、抵抗外部载荷的能力以及结构的变形等重要问题。
因此,在工程设计和实践中,超静定问题的解决具有重要的实际意义。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Fi
M 2(x)dx
2EI
M(x) M(x)
dx
EI Fi
河南理工大学土木工程学院
材料力学
第12章 能量法与超静定问题
平面桁架
δi
V Fi
n FNj l j j1 EA
FNj Fi
组合变形
δi
V
Fi
[ FN2( x)dx
——卡氏定理。
河南理工大学土木工程学院
材料力学
说明
第12章 能量法与超静定问题
(1) 卡氏第二定理只适用于线性弹性体
δi
V Fi
(2) Fi 为广义力, i 为相应的位移
一个力
一个力偶
一对力
一对力偶
一个线位移
一个角位移
河南理工大学土木工程学院
相对线位移 相对角位移
材料力学
第12章 能量法与超静定问题
材料力学
第12章 能量法与超静定问题
材料力学
第12章 能量法与超静定问题
2019年5月21日
河南理工大学土木工程学院
材料力学
第12章 能量法与超静定问题
第十二章 能量法
§12-1 概述 §12-2 杆件变形能的计算 §12-3 卡氏定理 §12-4 能量法解超静定问题
河南理工大学土木工程学院
材料力学
T 2( x)dx
M 2( x)dx ]
Fi l 2EA
l 2GIp
l 2EI
FN( x) FN( x)dx T ( x) T ( x)dx M ( x) M ( x)dx
EA Fi
GIp Fi
EI Fi
河南理工大学土木工程学院
材料力学
第12章 能量法与超静定问题
② 附加力法求位移
A l
q
B
C
a
河南理工大学土木工程学院
材料力学
第12章 能量法与超静定问题
A
l
q
F
x
B
xC
a
BC:弯曲变形
qx2 M ( x) -Fx -
2
AB:弯曲与扭转的组合变形
M ( x) - x F
M(x) ( qa)x
M ( x) x F
V
dFi
d i
1 2 dFi
d i
(b)
由式(a)=(b),可得: 河南理工大学土木工程学院
材料力学
第12章 能量法与超静定问题
V
V Fi
dFi
V
dFi
d i
1 2 dFi
di
略去二阶微量:
1 2
dFi
d,i 求得: i
V
Pi
例12-1 图示各杆的直径均为d,材料的弹性常数E、G。试
用卡氏第二定理求 A 端的铅垂位移(不计剪力对位移的影响)。
l
y
B
C
F xA
a
y
O z
x
① 直接求位移
解:AB段的弯矩方程及其对F 的偏导数分别为
M (x) -Fx , M (x) -x F
(0≤ x≤ l)
河南理工大学土木工程学院
弹性体内所产生的变形能为:1
2
dFi
d i
在 F1、F2…
Fn
的作用过程中,由 F1、F2… Fn 对弹性体的作用效果并
不因先前作用了 dFi 而有所改变, 同时由于 在这一过程中
dFi 始终作用在弹性体上,因此该过程中,弹性体内再次
产生的变形能应为: V
1 2
dFi
di
,而总的变形能应为:
1 2
F3δ3
河南理工大学土木工程学院
材料力学
只给 Fi 一个增量 Fi . 结构应变能的增量为
V
Fi dFi
原有的所有力完成的功为
V
V
Fi
dFi
(a)
第12章 能量法与超静定问题
2
F2
F3
F1
3 1
河南理工大学土木工程学院
材料力学
第12章 能量法与超静定问题
如先作用 dFi, 而后作用 F1、F2… Fn 。由于 dFi 的作用,
第12章 能量法与超静定问题
§12-1 概述
一、能量方法
能量法是求位移的普遍方法,可以求结构上任意点沿任意 方向的位移。
二、基本原理
V W
河南理工大学土木工程学院
材料力学
第12章 能量法与超静定问题
§12-2 杆件变形能的计算
1、轴向拉压的变形能
V
FN2l 2EA
2、扭转杆内的变形能
T 2l V 2GIp
材料力学
第12章 能量法与超静定问题
BC段的弯矩和扭矩方程及其对F 的偏导数分别为
M ( y) -Fy , M ( y) - y F
l
T( y) -Fa , T ( y) -a
y
F
B
A 端的铅垂位移为
ΔAy
1[ EI
a Fx2 d x
0
l Fy2 d y] 1
(3) 卡氏第二定理的应用
轴向拉、压
δi
V Fi
Fi
FN2(x)dx 2EA
FN (x) FN (x) dx EA Fi
扭转
δi
V Fi
Fi
T 2(x)dx
2GIp
T(x) T(x)
dx
GIp Fi
弯曲
δi
V Fi
0
GIp
l Fa2 d y
0
Fa3 Fl 3 Fla2 3EI 3EI GIp
C
F xA
a
河南理工大学土木工程学院
材料力学
第12章 能量法与超静定问题
例题12-2 圆截面杆ABC,(ABC=90°)位于水平平面内, 已知杆截面直径 d 及材料的弹性常数 E , G . 求C 截面处的铅垂 位移. 不计剪力的影响。
4、组合变形的变形能
V
FN2 ( x) dx l 2EA( x)
T 2(x) dx
l 2GIp ( x)
M 2(x) dx
l 2EI( x)
二、变形能的普遍表达式
V
1 2
(F1δ1
F2δ2
F3δ3 )
F--广义力 包括力和力偶
δ--广义位移 包括线位移和角位移
—— 克拉贝隆原理(只限于线性结构)
河南理工大学土木工程学院
材料力学
第12章 能量法与超静定问题
§12-3 卡氏定理
设弹性结构在支座的约束下无任何
刚性位移.
作用有外力:
F1
F1 ,F2 , ,Fi , 相应的位移为:
1 , 2 , , i ,
结构的变形能
2
F2
F3
3 1
V
W
1 2
F1δ1
1 2
F2δ2
河南理工大学土木工程学院
材料力学
第12章 能量法与超静定问题
3、 弯曲变形的变形能
Me
纯弯曲
θ
Me
Me
Me
V
W
1 2
Me θ
1 2
Me
Mel EI
Me2l 2EI
横力弯曲
V
Me2 ( x)dx l 2EI( x)
河南理工大学土木工程学院
材料力学
第12章 能量法与超静定问题
