1、图1圆截面直杆的横截面面积为A,长度为 ,弹性模量为E
轴向拉伸 习题

轴向拉伸(压缩)的内力及强度计算一、判断题1.力是作用于杆件轴线上的外力。
()图 12.力越大,杆件越容易被拉断,因此轴力的大小可以用来判断杆件的强度。
()3.图1所示沿杆轴线作用着三个集中力,其m—m截面上的轴力为 N=-F。
()4.在轴力不变的情况下,改变拉杆的长度,则拉杆的绝对变化发生变化,而拉杆的纵向线应变不发生变化。
()5.轴力是指杆件沿轴线方向的内力。
()6.内力图的叠加法是指内力图上对应坐标的代数相加。
()7.轴力越大,杆件越容易被拉断,因此轴力的大小可以用来判断杆件的强度。
()8.两根等长的轴向拉杆,截面面积相同,截面形状和材料不同,在相同外力作用下它们相对应的截面上的内力不同()。
9.如图所示,杆件受力P作用,分别用N1、N2、N3和σ1、σ2、σ3表示截面I-I、II-II、III-III上的轴力和正应力,则有(1)轴力N1> N2> N3()(2)正应力σ1>σ2>σ 3 ()图 2 图 310.A、B两杆的材料、横截面面积和载荷p均相同,但L A > L B , 所以△L A>△L B(两杆均处于弹性范围内),因此有εA>εB。
()11.因E=σ/ε,因而当ε一定时,E随σ的增大而提高。
()12.已知碳钢的比例极限σp=200MPa,弹性模量E=200Pa,现有一碳钢试件,测得其纵向线应变ε=0.002,则由虎克定律得其应力σ=Eε=200×10×0.002=400Mpa。
()13.塑性材料的极限应力取强度极限,脆性材料的极限应力也取强度极限。
()14.现有低碳钢和铸铁两种材料,杆1选用铸铁,杆2选用低碳钢。
()图 415.一等直拉杆在两端承受拉力作用,若其一半段为钢,另一半段为铝,则两段的应力相同,变形相同。
()16.一圆截面轴向拉杆,若其直径增加一倍,则抗拉强度和刚度均是原来的2倍。
()17.铸铁的许用应力与杆件的受力状态(指拉伸或压缩)有关。
《材料力学》第2章轴向拉(压)变形习题解答

其方向。 解:斜截面上的正应力与切应力的公式为:
ασσα20cos = αστα2sin 2 = 式中,MPa mm N A N 1001001000020===σ,把α的数值代入以上二式得:
[习题 2-7] 一根等直杆受力如图所示。已知杆的横截面面积 A 和材料的弹性模量 E 。试作轴力图,并求杆端点 D 的位移。 解: (1)作轴力图
[习题 2-9] 一根直径 mm d 16=、长 m l 3=的圆截面杆,承受轴 向拉力 kN F 30=,其伸长为 mm l 2.2=?。试求杆横截面上的应 力与材料的弹性模量 E 。 解:(1)求杆件横截面上的应力 MPa mm N A N 3.1491614.34 110302 23=???==σ (2)求弹性模量 因为:EA Nl l = ?, 所以:GPa MPa l l l A l N E 6.203)(9.2035902 .23000 3.149==?=??=???=σ。 [习题 2-10] (1)试证明受轴向拉伸(压缩)的圆截面杆横截 面沿圆周方向的线应变 s ε等于直径方向的线应变 d ε。 (2)一根直径为 mm d 10=的圆截面杆,在轴向力 F 作用下,直 径减小了 0.0025mm 。如材料 的弹性模量 GPa E 210=,泊松比 3.0=ν,试求该轴向拉力 F 。 (3)空心圆截面杆,外直径 mm D 120=,内直径 mm d 60=,材 料的泊松比 3.0=ν。当其轴向拉伸时,已知纵向线应变 001.0=, 试求其变形后的壁厚。 解:(1)证明 d s εε= 在圆形截面上取一点 A ,连结圆心 O 与 A 点,则 OA 即代表直 径方向。过 A 点作一条直线 AC 垂直于 OA ,则 AC 方向代表圆周方向。νεεε-==AC s(泊
材料力学填空与判断题解

实用文档第1 章 绪论一、是非判断题1-1 材料力学是研究构件承载能力的一门学科。
( √ ) 1-2 材料力学的任务是尽可能使构件安全地工作。
( × ) 1-3 材料力学主要研究弹性范围内的小变形情况。
( √ )1-4 因为构件是变形固体,在研究构件的平衡时,应按变形后的尺寸进行计算。
(×) 1-5 外力就是构件所承受的载荷。
( × )1-6 材料力学研究的内力是构件各部分间的相互作用力。
( × )1-7 用截面法求内力时,可以保留截开后构件的任一部分进行平衡计算。
( √ ) 1-8 压强是构件表面的正应力。
( × ) 1-9 应力是横截面上的平均内力。
( × )1-10 材料力学只研究因构件变形引起的位移。
( √ ) 1-11 线应变是构件中单位长度的变形量。
( × ) 1-12 构件内一点处各方向线应变均相等。
( × )1-13 切应变是变形后构件中任意两根微线段夹角的变化量。
( × ) 1-14 材料力学只限于研究等截面直杆。
( × )1-15 杆件的基本变形只是拉(压)、剪、扭和弯四种。
如果还有另一种变形,必定是这四种变形的某种组合。
( √ )第 2 章 轴向拉伸与压缩 一、是非判断题2-1 使杆件产生轴向拉压变形的外力必须是一对沿杆轴线的集中力。
(×) 2-2 拉杆伸长后,横向会缩短,这是因为杆有横向应力存在。
(×) 2-3 虎克定律适用于弹性变形范围内。
(×) 2-4 材料的延伸率与试件尺寸有关。
(√)2-5 只有超静定结构才可能有装配应力和温度应力。
(√) 二、填空题2-6 承受轴向拉压的杆件,只有在(加力端一定距离外)长度范围内变形才是均匀的。
2-7 根据强度条件][σσ≤可以进行(强度校核、设计截面、确定许可载荷)三方面的强度计算。
2-8 低碳钢材料由于冷作硬化,会使(比例极限)提高,而使(塑性)降低。
工程力学历年真题

⼯程⼒学历年真题全国⾼等教育⾃学考试真题集⼯程⼒学(⼆)强⼤的符易整理全国2012年4⽉⾼等教育⾃学考试⼯程⼒学(⼆)试题课程代码:02391⼀、单项选择题(本⼤题共10⼩题,每⼩题2分,共20分)在每⼩题列出的四个备选项中只有⼀个是符合题⽬要求的,请将其代码填写在题后的括号内。
错选、多选或未选均⽆分。
1.图⽰结构中,AD 杆D 端作⽤⽔平⼒F ,⽀座B 对折杆BC 的约束⼒⽅向应为( ) A.⽔平⽅向 B.沿BC 连线 C.铅垂⽅向D.沿BD 连线2.平⾯汇交⼒系如图所⽰,其合⼒应为 ( ) A.100NB.50NC.253ND.03.图⽰外伸梁C 端作⽤⼀个⼒偶,其⼒偶矩为m ,则B 处⽀座反⼒⼤⼩应为 ( ) A.m aB.23m aC.2m a D.3m a4.图⽰物块重量为Q ,⽔平拉⼒P=0.3Q ,若物块与⽔平⾯间摩擦系数f=0.35,则重物与⽔平⾯间的摩擦⼒应为 ( ) A.Q B.0.35Q C.0.3Q D.05.如图所⽰,铅垂⼒F 的作⽤点A 的坐标x A =a ,y A =b ,z A =0,⼒F 对三个坐标轴之矩⼤⼩应为 ( ) A.m x (F)=Fa ,m y =(F)=Fb ,m z (F)=0 B.m x (F)=0,m y =(F)=Fa ,m z (F)=Fb C.m x (F)=Fb ,m y (F)=Fa ,m z (F)=0D.m x (F)=Fa ,m y =(F)=Fb ,m z (F)=22F a b +6.图⽰结构为 ( ) A.静定结构B.⼀次超静定结构C.⼆次超静定结构D.三次超静定结构 7.材料的许⽤应⼒[]=unσσ(n 为安全系数),对于塑性材料,极限应⼒σn取材料的( )A.屈服极限B.弹性极限C.⽐例极限D.强度极限8.图⽰矩形截⾯对z 轴的静矩S z 为 ( )A.2bhB.312b hC.312bhD.22bh9.图⽰某纯弯曲梁横截⾯上A 点处的正应⼒为2MPa ,z 轴为中性轴,则B 点处的正应⼒为 ( ) A.2MPaB.4MPaC.6MPaD.8MPa10.图⽰梁跨中点C 处的竖向位移为( )A.33Fa EIB.0C.36Fa EI -D.33Fa EI-⼆、填空题(本⼤题共10⼩题,每⼩题2分,共20分)请在每⼩题的空格中填上正确答案。
材料力学习题01拉压剪切

拉伸与压缩一、 选择题 (如果题目有5个备选答案选出其中2—5个正确答案,有4个备选答案选出其中一个正确答案。
)1.若两等直杆的横截面面积为A ,长度为l ,两端所受轴向拉力均相同,但材料不同,那么下列结论正确的是( )。
A .两者轴力相同应力相同B .两者应变和仲长量不同C .两者变形相同D .两者强度相同E .两者刚度不同2.一圆截面直杆,两端承受拉力作用,若将其直径增大一倍,其它条件不变,则( )。
A .其轴力不变B .其应力将是原来的1/4C .其强度将是原来的4倍D .其伸长量将是原来的1/4E .其抗拉强度将是原来的4倍3.设ε和1ε分别表示拉压杆的轴向线应变和横向线应变,μ为材料的泊松比,则下列结论正确的是( )。
A .εεμ1=B .εεμ1-=C .εεμ1= D .εεμ1-= E .常数时,=≤μσσ p 4.钢材经过冷作硬化处理后,其性能的变化是( )。
A .比例极限提高 B .屈服极限提高C .弹性模量降低D .延伸率提高E .塑性变形能力降低5.低碳钢的拉伸σ-ε曲线如图1-19所示若加载至强化阶段的C 点,然后卸载,则应力回到零值的路径是( )。
A .曲线cbaoB .曲线cbf (bf ∥oa )C .直线ce (ce ∥oa )D .直线cd (cd ∥o σ轴)6.低碳钢的拉伸σ-ε曲线如图l —19,若加载至强化阶段的C 点时,试件的弹性应变 和塑性应变分别是( )。
A .弹性应变是ofB .弹性应变是oeC .弹性应变是edD .塑性应变是ofE .塑性应变是oe7.图l-2l 表示四种材料的应力—应变曲线,则: (1)弹性模量最大的材料是( );(2)强度最高的材料是( ); (3)塑性性能最好的材料是( )。
8.等截面直杆承受拉力,若选用三种不同的截面形状:圆形、正方形、空心圆,比较材料用量,则( )。
A .正方形截面最省料B .圆形截面最省料C .空心圆截面最省料D .三者用料相同9.若直杆在两外力作用下发生轴向拉伸(压缩)变形,则此两外力应满足的条件是 A .等值 B .反向 C .同向D .作用线与杆轴线重合E .作用线与轴线垂直 10.轴向受拉杆的变形特征是( )。
工程力学第8章 变形及刚度计算

结构构件在满足强度要求条件下,若其变形过大, 会影响正常使用。本章将学习杆件的变 形及刚度计算。
1
8.1 轴向拉压杆的变形
杆件在发生轴向拉伸或轴向压缩变形时,其纵向尺 寸和横向尺寸一般都会发生改变,现分别予以讨论。 8.1.1 轴向变形 图8.1所示一等直圆杆,变形前原长为l,横向直径 为d;变形后长度为l′,横向直径为d′,则称
8.8 题8.8图所示一直径为d的圆轴,长度为l,A端 固定,B端自由,在长度方向受分布力偶m 作用发生扭 转变形。已知材料的切变模量为G,试求B端的转角。
56
8.9 某传动轴,转速 n=150 r/min,传递的功率 P =60 kW,材料的切变模量为 G =80GPa,轴的单位长度 许用扭转角[θ]=0.5(°)/m,试设计轴的直径。
30
例 8.9 简支梁受力如图 8.11所示
31
8.4 简单超静定问题
8.4.1 超静定问题的概念 前面几章所研究的杆或杆系结构,其支座反力和内 力仅仅用静力平衡条件即可全部求解出来,这类问题称 为静定问题(staticallydeterminateproblem)。例如,图 8.12所示各结构皆为静定问题。在工程实际中,有时为 了提高强度或控制位移,常常采取增加约束的方式,使 静定问题变成了超静定问题或静不定问题 (staticallyindeterminateproblem)。超静定问题的特点 是,独立未知力的数目大于有效静力平衡方程式的数目, 仅仅利用静力平衡条件不能求出全部的支座反力和内力。
52
8.5 高为l的圆截面锥形杆直立于地面上,如题8.5图 所示。已知材料的重度γ和弹性模量E,试求杆在自重作 用下的轴向变形Δl。
53
54
《建筑力学》第4章计算题

计 算 题( 第四章 )试作图示各杆的轴力图。
图题4. 1图示等截面混凝土的吊柱和立柱,已知横截面面积A 和长度a ,材料的重度γ,受力如图示,其中10F Aa γ=。
试按两种情况作轴力图,并求各段横截面上的应力,⑴不考虑柱的自重;⑵考虑柱的自重。
图题一起重架由100×100mm2 的木杆BC 和直径为30mm 的钢拉杆AB 组成,如图所示。
现起吊一重物WF =40kN 。
求杆AB 和BC 中的正应力。
图题图示钢制阶梯形直杆,各段横截面面积分别为21100mm A =,2280mm A =,23120mm A =,钢材的弹性模量GPa E 200=,试求:(1)各段的轴力,指出最大轴力发生在哪一段,最大应力发生在哪一段;(2)计算杆的总变形;图题4.5 图示短柱,上段为钢制,长200mm ,截面尺寸为100×100mm2;下段为铝制,长300mm ,截面尺寸为200×200mm 2。
当柱顶受F 力作用时,柱子总长度减少了0.4mm 。
试求F 值。
已知:(E 钢=200GPa ,E 铝=70GPa)。
4.6 图示等直杆AC ,材料的容重为ρg ,弹性模量为E ,横截面积为A 。
求直杆B 截面的位移ΔB 。
题图 题图两块钢板用四个铆钉连接,受力kN 4=F 作用,设每个铆钉承担4F 的力,铆钉的直径mm 5=d ,钢板的宽mm 50=b ,厚度mm 1=δ,连接按(a )、(b )两种形式进行,试分别作钢板的轴力图,并求最大应力max σ。
题图用钢索起吊一钢管如图所示,已知钢管重kN10=G F ,钢索的直径mm 40=d ,许用应力[]MPa 10=σ,试校核钢索的强度。
正方形截面的阶梯混凝土柱受力如图示。
设混凝土的320kN m γ=,载荷kN 100=F ,许用应力[]MPa 2=σ。
试根据强度选择截面尺寸a 和b 。
题图 题图图示构架,30=α,在A 点受载荷kN 350=F 作用,杆AB 由两根槽钢构成,杆AC 由一根工字钢构成,钢的许用拉应力[]MPa 160t =σ,许用压应力[]MPa 100c =σ,试为两杆选择型钢号码。
华中科技大学材料力学答案1
解:桁架结构各杆均为二力杆(拉压杆)
FAx
E
FAy
A FNAE FAy FNAC
求支反力
Fx 0 FAx 0
FB
220 4 2208
M B (F ) 0 FAy
12
220kN
MA(F) 0
FB
220 4 2208 12
220kN
求杆AC和CD的轴力:
由A点的平衡条件: FNAC
-
2F
A
F +
(d) 等截面杆,最大应力在轴力最大的截 面上:
max
33
2F A
30MPa
2-4 图示一等直矩形截面杆受拉,已知F=10kN,b=5mm,h=20mm。试求α= ±45o、±135o 等四个斜截面(图示虚线)上的正应力和切应力。
解:求横截面上的应力:
F
b
F
h
F
F
10 103
100 MPa
FN3 3
F 2 2F
3F 画内力图时,可用与基线垂直的具有标长的直
3
3F
2F
FN :
+
+
+
线段表示该线段所在截面内力值的大小。切记 不可画成阴影线(剖面线)。
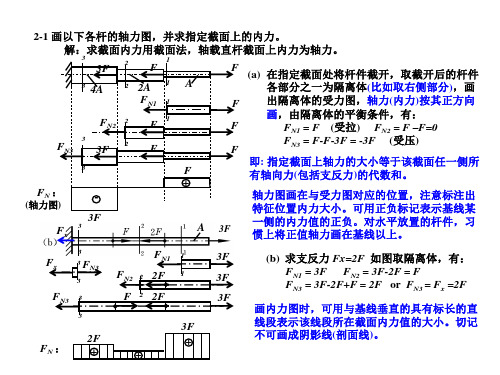
2-1 画以下各杆的轴力图,并求指定截面上的内力。
2 A 2F
F1
2F
(c) 如图取隔离体,有:
2
FN2 2
1
FN1 1
2F
2F F 1
2F
解:本题实质上是要考察斜截面上的应力。由斜截面应力公式,有:
cos2
2
sin 2
由题义,要求: 2
则有: cos2 2 sin 2 tan 1
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
162 第十一能量法
授课学时:8学时
一、 内容提要
1. 杆件的变形能表达式
轴向拉压
扭转
弯曲
组合变形
说明:
(1)变形能是广义力或广义位移的二次函数,不能简单叠加。
(2)变形能仅与外力的最终值有关,而与加力次序无关。
(3)当杆件的各段截面不相同或内力由不同函数表示时,应分段计算变形能。
(4)杆件是满足虎克定律的线弹性体,如对非线弹性体变形能将变为
2. 卡氏定理
弹性系统的总变形能 是由所有作用于弹性系统的广义力
引起的。
令在 的作用点沿 方向引起的广义位移为 ,根据卡氏定理,按下式计算广义位移
说明:
(1)广义力与广义位移须相对应。
(2)当所求位移的截面处没有相应的集中力或集中力偶时,可采用附加力 的方法。
二、 基本要求
1. 理解功能原理,掌握杆件变形能的计算方法。
2. 掌握用卡氏定理求结构位移的方法。
3.理解并掌握用能量法解超静定问题的方法。
三、 典型例题分析
例1 钢架ABCD 承受一对P 力作用(如图1),其抗弯刚度EI 、抗拉刚度EA 以dx
EA x N U l ⎰=2)
(2dx
EI
x M U l ⎰=2)(2
dx
GI x M U l p n ⎰=2)
(2
),,,(21n P P P U U ⋅⋅⋅=),,2,1(n i P i ⋅⋅⋅=i P i δi
i P U
∂∂=δi P 0,
=P l l a D
A -δ⎰+⎰+⎰=i l p n l EI x M dx GI x M dx EA x N U 2)(2)(2)(2
2
2
⎰+⎰⎰+∆=l l l n Md d M l Nd U θ
φ)(
163
及 、 均已知,试利用功能原理求截面A 、D 之间的相对水平位移 。
图1 解:(1)内力分量 AB (CD )段: BC 段: (2)变形能计算
(3) 的计算
由
得
例2 杆件受力如图2,抗弯刚度EI ,试用卡氏定理计算B 截面的竖直位移 。
Pa
x M =)(Px x M =)(P
x N =)(CD
BC AB U U U U ++=⎰+⎰+⎰=l l a EA dx P EI dx Pa EI dx Px 02020222)(2)(2EA l P EI l a P EI a P 2232
2232+
+=D A -δD A P W U -==δ2
1
EA Pl EI l Pa EI Pa D A ++=-2
332δBy δx
P
P
P
P
164 图2
解法一 为了区分梁上的两个力,可将作用于B 截面的力标为 BC 段
AC 段
令 则
解法二:在截面上施加一附加力
BC 段
AC 段
令 则
例3 图3a 中,各杆长均为 ,抗拉压刚度均为 ,求铅垂力作用时各杆的内力
1P 212202111011
)()()()(dx P x M EI x M dx P x M EI x M P U a a By ∂∂⎰+∂∂⎰=∂∂=δ2
12)(x P x M =∂∂)2(2a x a ≤≤1
11)(x P x M =11
1)
(x P x M =∂∂)0(1a x ≤≤)()(2212a x P x P x M --=[]2
202
22110111)(dx EI x a x P x P dx EI x x P a a ⎰⋅--+⎰⋅=P P =1)(6113
↑=
EI
Pa
By δ2
1
2)
(x P x M =∂∂)
2(2a x a ≤≤0
,
=y P 1
,
111)(x P x P x M y +=1
11)
(x P x M =∂∂)0(1a x ≤≤)()(22,
212a x P x P x P x M y --+=212202111011
)
()()()(dx P x M EI x M dx P x M EI x M P U a a By
∂∂⎰+∂∂⎰=∂∂=
δ[
]
2
20222,
2110
11,
11)()(dx EI
x a x P x P x P dx EI x x P x P a y a y ⎰⋅--++⎰⋅+=0,=y P )(6113
↑=EI
Pa By δl EA
165
图3a
解:此为一次超静定结构,采用解除内力约束的方法。
在3杆任意截面处切开,多余未知力为 。
(图3b )
由静力学条件
则系统的变形能
由卡氏定理
两斜杆所受轴向压力
说明:此题也可解除外约束,如解除B 支座铅垂方向的约束, 如图3c 所示,多余未
知力为约束反力 ,变形协调条件为B 点的铅垂位移等于0 。
四、 作业题
1 圆截面直杆的横截面面积为A ,长度为 ,弹性模量为E 。
上端
固定,下端受中心拉力P 作用,设直杆自重为P 答案:
EA
l
P U 672
=
3N 2/)(321N P N N -==[]
EA
l
N P EA l N U 22/)(22232
3-⋅
+=0)(333=--=∂∂EA l N P EA l N N U 23P N =P N N 4
22
1==3X l 3
X
166
2 试求图2悬臂梁B 截面的挠度及转角。
设EI 为常数。
图2
答案: (向下) (顺时针方向)
3 图3悬臂梁受集中力偶矩 的作用。
若 均为已知,试利用功能原理
求自由端C 截面的转角 。
答案: (顺时针)
图3
4
等截面直杆AB 和BC 组成的构架受力如图4。
若两杆的抗拉(压)刚度均为EA , 设
P 、 、E 、A 都已知。
试利用功能原理求B 的竖直位移。
答案: (向下)
图4
EI qa
y B 2474=EI qa B 63
=θ0M l EI 、c θEI l
M c 430=θl EA Pl
B 9.1=
δB
P
167
5 抗弯刚度为EI 的刚架受力如图5,试求刚架A 截面的水平位移 、竖直
位移 、转角 。
答案: ( )
图5
Ax δAy δA θ)(22
→=EI Pbh Ax δ)(↑-=EI
Pabh Ay
δEI Pbh A =θ。
