材料力学B试题10超静定系统
材料力学-力法求解超静定结构

力法求解超静定结构时,可以根据计算结果优化结构设计,提高结构的强度和稳定性。
结论与总结
力法是求解超静定结构的有效方法,通过合理应用材料力学基础和力法的原理,我们能够准确求解反力分布并 分析结构的应力情况。
样例分析
结构:桥梁
使用力法求解桥梁上的悬臂梁,计算主梁的支座反 力和悬臂梁的应力分布。
结构:楼房
将力法应用于楼房结构,确定楼板的支座反力并分 析楼梯的受力情况。
实用提示和技巧
1 标定自由度
在应用力法时,正确标定结构的自由度是成功求解反力的重要步骤。
2 验证计算结果
对计算得到的反力进行验证,确保结果的准确性,避免错误的设计决策。
材料力学-力法求解超静 定结构
超静定结构的定义
超静定结构是指具有不止一个不可靠支持反力的结构。它们挑战了传统的结构分析方法,需要使用力法进行求 解。
材料力学基础
材料力学研究材料的受力和变形规律,包括弹性力学、塑性力学和损伤力学。 这些基础理论为力法求解超静定结构提供了必要的工具。
力法的原理
力法是一种基于平衡原理和支座反力法则的结构分析方法。它通过对超静定结构施加虚位移,建立受力平衡方 程,求解未知反力。
超静定结构应用力法求解的步骤
1
确定结构类型
了解结构是否为超静定结构,并确定不
计算反力
2
可靠支持反力的个数。
根据力法原理,建立并求解受力平衡方
程,计算未知反力。
3
验证平衡
通过检查受力平衡方程是否满足等式的
确定应力分布
4
要求,验证计算的反力是否正确。
பைடு நூலகம்
根据已知反力和结构的几何特性,计算 并绘制应力分布图。
材料力学_超静定结构

B1
1
B
C1 No
C
a
IAm1 ag2e
A
a
l
e
C1
C'
3
B1
1
C1
A1
2
l1 = l2
B C
A
l C1
3
l3 e
C''
(1)变形几何方程为 Δl1 Δl3 Δe
(2)物理方程
Δl1
FN1l1 EA
Δl3
FN3l E3 A3
FN1
B'
(3)补充方程
FN3l Δe FN1l
E3 A3
EA
FN3 C' FN2 A'
判断下列结构属于哪类超静定
(a)
外力超静定
(b)
内力超静定
(c)
混合超静定
(d)
外力超静定
(e)
内力超静定
(f)
混合超静定
三、工程中的超静定结构( Statically indeterminate structure in engineering)
在机械和工程结构中常采用超静定结构增加系统的刚度,提 高构件的承载能力 .
A
(3)补充方程
l ΔT
l
FRB l EA
(4)温度内力
FRA A
FRB EA l ΔT
由此得温度应力
T
FRB A
l E ΔT
B
lT B'
lF
B
B'FRB
§2-3 简单超静定梁的解法—变形比较法
求解超静定梁的步骤
q
(procedure for solving a statically
材料力学 简单的超静定问题

FN 3 l 3 E 3 A3
FN1
FN3
a a A
A1 FN2
l3
FN 3l3 E 3 A3
(3)
(4)补充方程:由几何方程和物理方程得:
F N 1l1 E1 A1
2
cos a
(5)联解(1)、(2)、(3)式,得:
FN 1 FN 2 E1 A1 F cos a 2 E1 A1 cos a E 3 A3
第六章
简单的超静定问题
1
第六章
§6-1
§6-2
简单的超静定问题
超静定问题及其解法
拉压超静定问题
§6-3 §6-4
扭转超静定问题 简单超静定梁
2
§6-1
超静定问题及其解法
1.单纯依靠静力平衡方程能够确定全部未知力(支反 力、内力)的问题,称为静定问题。 相应的结构称为静定结构。
2.单纯依靠静力平衡方程不能确定全部未知力(支反 力、内力)的问题,称为超静定问题。 相应的结构称为超静定结构。
3
F N3 A3 9F 14 A [ ]
F
[F ]
14 9
14 9
[ ] A
[ ] A
11
[例6-2-4]木制短柱的四角用四个40404的等边角钢 加固,角钢和木材的许用应力分别为[]1=160MPa和 []2=12MPa,弹性模量分别为E1=200GPa 和 E2 =10GPa;求许可载荷P。 解:(1)以压头为研究对象, 设每 个角钢受力为FN1,木柱受力为FN2.
14
B
1
D
C
3 2
(2) 几何方程
l1 ( l 3 ) cos a
材料力学B-第7-10章自测题参考答案

材料力学B 材料力学 B
(第7-10章自测题答案)
北京 北京理工大学宇航学院力学系 大学宇航学院力学系
韩斌
§7
§7
能量法 (3) (D) (4) (D)
§8
q qa FGy () 2
qa FAy () 2
5qa2 () MG 16
5qa2 MA () 16
自测题5* 答案 答案:
qa4 qa4 Cx (), ) Cy () 56EI 16EI
9
§9 压杆稳定
§9自测题1
b xz 1 答案: (1) Fcr 116.61 kN ; (2) h 2 xy
EI Kd v , P 3g Pa
最大动弯矩为: M d max C截面的动转角为:
49 24
Pa v EIP Kd 2 2 ag
Cd K d Cst
Pav 2 ( ) EIg g
12
§10自测题4
§10
动载荷
2 65 Pa 3 / 8 EI K d (1 1 )3 3 65 Pa / 12 EI
(2) d 84 MPa
答案: (1) K d 21 (3) h 3.99
§10自测题2
mm
答案: 答案 d max K d st max
11.5 8.30
95.50 MPa [ ] 100 MPa
结论:结构强度安全。
11
§10
§10自测题3
动载荷
答案:
材料力学试卷试题(附参考答案)
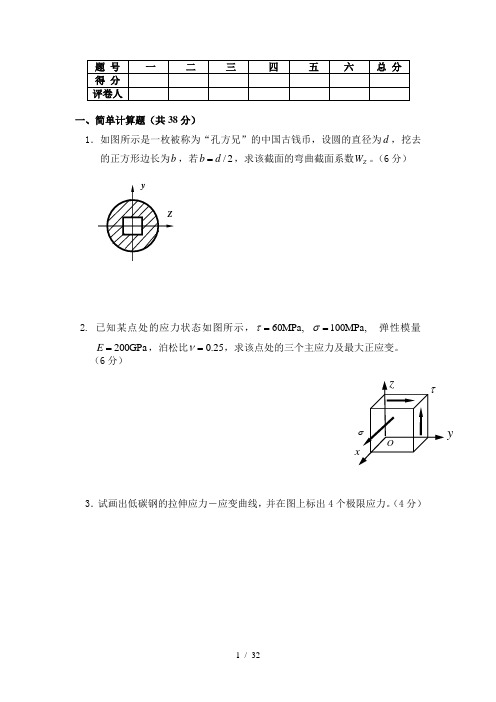
一、简单计算题(共38分)1.如图所示是一枚被称为“孔方兄”的中国古钱币,设圆的直径为d ,挖去的正方形边长为b ,若2/d b =,求该截面的弯曲截面系数Z W 。
(6分)2. 已知某点处的应力状态如图所示,,MPa 100,MPa 60==στ弹性模量GPa 200=E ,泊松比25.0=ν,求该点处的三个主应力及最大正应变。
(6分)3.试画出低碳钢的拉伸应力-应变曲线,并在图上标出4个极限应力。
(4分)y4.已知交变应力的,MPa 5,MPa 3min max -==σσ, 求其应力循环特征r 及应力幅度a σ。
(4分)5.如图所示为矩形截面悬臂梁,在梁的自由端突然加一个重为Q 的物块,求梁的最大弯曲动应力。
(4分)Qhb6.如图所示为两根材料相同的简支梁,求两梁中点的挠度之比b a w w /。
(4分)7.两块相同的钢板用5个铆钉连接如图所示,已知铆钉直径d ,钢板厚度t ,宽度b ,求铆钉所受的最大切应力,并画出上钢板的轴力图。
(6分))(b2/L 2/L )(a P8.超静定结构如图所示,所有杆件不计自重,AB为刚性杆,试写出变形协调方程。
(4分)Pa a a 2/AF二、作图示梁的剪力图与弯矩图。
(10分)三、不计剪力的影响,已知EI ,试用能量法求图示悬臂梁自由端的挠度A w 。
(12分)四、铸铁梁的载荷及截面尺寸如图所示,其中4cm 5.6012,mm 5.157==Z C I y 。
2A C已知许用拉应力MPa 40][=t σ,许用压应力MPa 160][=C σ。
试按正应力条件校核梁的强度。
若载荷不变,但将截面倒置,问是否合理?为什么? (14分)五、圆截面直角弯杆ABC 放置于图示的水平位置,已知cm 50=L ,水平力(单位:mm )200kN 40=F ,铅垂均布载荷m /kN 28=q ,材料的许用应力MPa 160][=σ,试用第三强度理论设计杆的直径d 。
超静定问题典型习题解析

5
由变形协调条件
∆B
= 0 得 FBx
=
F π
CF
C1
F/π F/2
F/π 1/π
F/2
1/2
(e)
题5图
1/π 1/2
3、计算 C 点沿 F 力方向的位移 ∆C
在相当系统上,有
0 ≤ ϕ ≤ π : M (ϕ) = − F R(1− cosϕ) + F R sinϕ ;
2
2
π
在基本系统 C 点处沿 F 力方向加单位集中力,则
超静定问题分析
典型习题解析
1 试判断下列结构中为几度静不定,给出基本结构并列出相应的变形协调条件。
A
B
C
(a)
(b)
题1图
(a) 解Ⅰ:梁有四个约束反力,有三个有效的平衡方程,但尚有一个条件,即在中间铰
B 处的内力弯矩为零,故为静定梁。
解Ⅱ:去掉任何一个约束,该梁成为几何可变机构,所以是 1-1=0 度静不定,即
=
6EIk∆a + 3EIFa 2 2a3k + 6 2EI
。
3、计算弹簧回复到其原长时的 F 的大小
令 X = 0 ,即 6EIk∆ − kFa3 = 0 ,得 F = 6EI∆
2ka3 + 6EI
a3
7
MA
=
1 2
ql 2
−
FBy l
=
1 2
× 20 ×103 N/m × (4m)2
− 8.75 ×103 N × 4m
= 125 ×103 N ⋅ m = 125kN ⋅ m(逆时针)
( ) FC = FP + FBy = 40 ×103 N + 8.75 ×103 N=48.75 ×103 N = 48.75kN ↑
材料力学简单的超静定问题

§6-4 简单超静定梁
1.基本概念: 超静定梁:支反力数目大于有效平衡方程数目的梁 多余约束:从维持平衡角度而言,多余的约束 超静定次数:多余约束或多余支反力的数目。 相当系统:用多余约束力代替多余约束的静定系统 2.求解方法: 解除多余约束,建立相当系统——比较变形,列变 形协调条件——由物理关系建立补充方程——利用 静力平衡条件求其他约束反力。
1Δ2l3cos
②
(3)代入物理关系,建立补充方程
1
N1 1 E1 A1
N1
E1 A1 cos
③
3
N3 E3 A3
13
2
A
2
1
3
A
§6-2 拉压超静定问题
(2)建立变形协调方程:如图三杆铰结, 画A节点位移图,列出变形相容条件。要 1 注意所设的变形性质必须与受力分析所 中设定的力的性质一致。由对称性知
C
(b)
F
B
F C
B
C
(c)
FBy
(c)
FBy FF
BB B
(d) (d) B
F CC C
C
(d) FBy
F(2a)2
1F 43a
(w B)F
(9a2a)
6EI
3EI
(wB)FBy
8FBya3 3EI
所以
14Fa3 8FBya3 0 3EI 3EI
FBy
7 4
F
4)由整体平衡条件求其他约束反力
M AF 2(a), F Ay 4 3F ( )
FCFFB 408.75
4.875kN
M C0 , M C2 F 4 F B 0
MC 4FB 2F
48.75240115kN.m
西南交10秋学期《材料力学B》离线作业

《材料力学B》第1次作业一、单项选择题(只有一个选项正确,共6道小题)1. 图示结构,其中杆AD发生的变形为:(A) 弯曲变形(B) 压缩变形(C) 弯曲与压缩的组合变形(D) 弯曲与拉伸的组合变形2. 以下结论中正确的是哪一个?(A) 杆件某截面上的内力是该截面上应力的代数和(B) 杆件某截面上的应力是该截面上内力的平均值(C) 应力是内力的集度(D) 内力必大于应力3. 关于下列结论的正确性:1、同一截面上正应力s 与切应力t必相互垂直。
2、同一截面上各点的正应力s必定大小相等,方向相同。
3、同一截面上各点的切应力t必相互平行。
现有四种答案:(A) 1对(B) 1、2对(C) 1、3对(D) 2、3对4. 关于下列结论:1、应变分为线应变e和切应变g ;2、线应变为无量纲量;3、若物体的各部分均无变形,则物体内各点的应变均为零;4、若物体内各点的应变均为零,则物体无位移。
现有四种答案:(A) 1、2对(B) 3、4对(C) 1、2、3对(D) 全对5. 铸铁压缩试验破坏由什么应力造成?破坏断面在什么方向?以下结论哪一个是正确的?(A) 切应力造成,破坏断面与轴线大致成45º方向(B) 切应力造成,破坏断面在横截面(C) 正应力造成,破坏断面在横截面(D) 正应力造成,破坏断面与轴线大致夹角成45º方向6. 材料的主要强度指标是哪几个?以下结论哪一个是正确的?(A) σ p 和σ s(B) σ s 和ψ(C) σ b 和δ(D) σ b 和σ s二、判断题(判断正误,共12道小题)7.均匀性假设认为,材料内部各点的应变是相同的。
8.各向同性假设认为,材料沿各个方向具有相同的变形。
9.构件的强度、刚度和稳定性问题均与材料的力学性能有关。
10.构件在载荷作用下发生的变形,包括构件尺寸的改变和形状的改变。
11.外力就是构件所承受的载荷。
12.材料力学主要研究构件弹性范围内的小变形问题。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
超静定系统1. 平面框架受切向分布载荷q ,则截面A 上的弯矩、轴力、剪力分别为:A M = ,A F N = , A F S = 。
答:0;0;qb2. 图示薄圆环C布载荷q 证:0 ,0==C SC M F 。
只有轴力01=∂∂=X U∆ (1))()()(θθθ cos 1 cos1)(11-=∂∂--=R X M R qR X M 解出 qR X =1 于是有:(θM3. 试证明当任意载荷作用于梁A B C 的外伸部分时,若A B 跨内无任何外载荷,则截面A 上的弯矩在数值上等于截面B 上的弯矩之一半。
证:将左端固定端解除一个约束使之变为固定铰支座EIl311=δ,EI l M B6 1F =∆01F 111=+∆δX211F11BM X -=-=δ∆ 即 2B A M M -=4. 刚架的弯曲刚度为EI ,承受力F 后,支座C 有一下陷量∆,试求刚架C 处的反力。
解:以C 处竖直向上反力1X∆∆δ-=+F 1111X EIl l l l l l l EI 34)3221(1311=⨯⨯+⨯⨯⨯=δCEI Fl l l Fl l l Fl EI4829265212213F 1-=⎥⎦⎤⎢⎣⎡⨯⨯-⨯⨯⨯-=∆解得 31 436429l EI F X ∆-=5. 已知刚架的弯曲刚度为EI 。
试求刚架支座B 处的反力By F 。
解:相当系统如图0F 1111=+∆δXEIa q x a a q x x a x q EI a a5] d )6( d )6([1400022011310F 1-=⎰⎰-+-=∆EIa x a x x EI a a 34] d d [13022102111=⎰+⎰=δ解得 )( 20301↑==a q X F By6. 两刚架由C 点铰链连接,已知刚架的弯曲刚度为EI 。
试求铰链C 处的反力。
解:利用对称条件,由C 处切开,可见0S =C F0=C M ,取一半相当系统如图0F 1111=+∆δXEIa x x EI a 32 d )(230211=⎰-=δ()EIqa x x qa EI a 8 d )8(2402F 1=⎰--=∆解得 ()←→-= 1631qa X ,实际方向与假设相反。
7. 已知刚架的弯曲刚度为EI ,试求刚架内最大弯矩及其作用位置。
解:相当系统如图0F 1111=+∆δXa x a x x a x x EI a a a 3002032322121112] d )( d d [1=⎰⎰⎰-++=δEIFa x x Fx EI a 3 d 130F 1-=⎰⋅-=∆解得:)( 61↑==F X F Ey8. 已知刚架的弯曲刚度为EI 。
试求刚架支座A 的反力和最大弯矩及其作用位置。
解:相当系统如图0F 1111=+∆δXEI l x l x x EI l l 34] d d [13022102111=⎰+⎰=δEI ql x l ql EI l 2 d 21402F 1-=⎰⋅-=∆解得 )( 831↓==ql F X Ay 最大弯矩在B 右截面max M9. 图示两跨刚架,已知kN 60=F ,m 6 =l25m kN 103⋅⨯=EI ,试以C 处竖直反力作为多余约束求解此刚架。
解:相当系统如图0F 1111=+∆δX()EIFlx l x x F x x F EI l l 16] d 2 d 2[13222F 1-=⎰-+⎰-=∆EIl x x EI l 32 d 230211=⎰=δ解得 kN 63.51=X10. 已知结构的弯曲刚度为EI ,试求对称轴上的内力。
解:根据双对称条件,从A 处切开0S =A F ,N F A 0F 1111=+∆δX EIFa x x F EI a 4 d 2120F 1-=⎰-=∆EIax EI a 2 d 1 2011=⎰⋅=δ 解得 81Fa M X A ==,2,0N S FF F A A ==11. 已知刚架的弯曲刚度为EI 。
试求截面A 处弯矩A M 。
解:相当系统如图0F 1111=+∆δXEIax EI a 2 d 12011=⎰⋅=δ EI qax qx qax qa x qx EI a a 300222221211F ]d )2121( d 21[1-=-++-=∆⎰⎰ 解得 ) ( 2121qa X =法二:利用对称性如图2, 22qa M qa F A S ==12. 已知桁架各杆的拉压刚度为EA解:0F 1111=+ΔX δ解得 ααα3331N3sin cos 1)cos 1(+++==FX F αααα332N1sin cos 1 cos sin ++-=FF ,ααα332N2sin cos 1 sin ++=FF13. 图示平面桁架,已知各杆的拉q压刚度为EA,其中杆1、2、3横截面面积为30 cm2,其余各杆面积为15 cm2,m6=a,kN130=F。
试求杆2轴力。
解:0解得)287(3)2118(1N5++==FXFkN8.8221311N2-=--=XFF14. 已知桁架各杆的拉压刚度为EA解:0F 1111=+ΔX δEA EA a a a a EA )322(2]2)21(2)21(2)21[(222211+=+-+-+=δ EA Fa a F a F a F EA Δ-=-+--+-=]2)21(22)21)(2(2)21)(2[(2F 1 解得 拉)( )223(1F X -=压)( )22( N N F F F CH AD -== 压)( )222( N N F F F BH DB -== 拉)( )12( N N F F F BC AB -==15. 已知图示桁架各杆的拉压刚度为EA ,试求各杆轴力。
解: 0F 1111=+ΔX δEAEA 1F 11解得 F F F F F F X F 212, 2N4N3N2N11N5-======, F F 2226N --=注:将杆6看成多余约束时求解将更方便!!!16. 已知图示半圆曲杆的弯曲刚度为EI ,试求曲杆支座A 处垂直反力F Ay 。
A C R F /2X 1A C R F /2θA C R θ1解: 0F 1111=+∆δXEIR EI R 4π d sin 32π2311=⎰=θθδEIFR EI FR 4 d sin ) cos -(1232π3F 1-=⎰-=θθθ∆解得 )( π1↓==FX F Ay17. 已知桁架各杆的拉压刚度为EA ,试求各杆的轴力。
解: 以杆6的轴力X 1为多余反力0F 1111=+ΔX δ解得 3321+-=FX 3325N 6N+-==F F F ,333N 1N +==F F F , 3334N 2N +-==F F F 注:本题最好以杆1(或杆3)的轴力X 1为多余反力,这样才不破坏对称性。
18. 已知桁架各杆的拉压刚度为EA解: 0F 1111=+ΔX δ l解得 F F F X F Ax 495.0 , 65.01N 1-===, 3.0, 335.03N 2N F F F F -=-= 335.0, 495.05N 4N F F F F -=-=注:本题若以杆3的轴力X 1为多余反力,求轴力将更方便。
19. 已知图示桁架各杆的拉压刚度为EA ,试求各杆轴力。
解: 0F 1111=+ΔX δEAEA 1F 11解得 N6N5N4N2N11N3 31F F F F F FX F =====+== 20. 已知桁架各杆的长度均为a ,各杆的拉压刚度为EA ,试求各杆轴力。
解: 0F 1111=+ΔX δ 静定基各杆轴力0N6N5N4N3N2N1======F F F F F F F F F F F F F ======N12N11N10N9N8N7单位力下各杆轴力1N6N5N4N3N2N1======F F F F F F1N12N11N10N9N8N7-======F F F F F FEAFaΔEA a 6, 121F 11-==δ 解得 2, 2N 1N1F F F X F i ===各杆轴力均为21. 已知桁架各杆的长度均为a ,拉压刚度为EA 。
试求各杆轴力。
解: 0F 1111=+ΔX δ0, 11F 11==ΔEAδ 解得 01N8==X FN12N11N10N9N6N5N4N3N2N1==========F F F F F F F F F FF F F ==N10N722. 已知图示结构各杆的拉压刚度为EA ,横梁AD 的弯曲刚度为EI 。
试求杆BC 的轴力。
解:0F 1111=+ΔX δEAa EI a aEA a EA a EA x EI a x EI x a a a)243(351)1(2)2()2(2 d )( d )(2322220211++=+-++-+-=⎰⎰δEIFa x a EI Fax x EI Fx Δa a a 35 d )( d )(2320F 1-=⎰-+⎰-=解得 )243(355221N AIa Fa X F BC ++== 23. 已知图示圆环的弯曲刚度为EI ,求支座B解:qR F By =3)-π( d ] cos cos )sin -2(1-)sin -[(132π022311EIR EIR =+=⎰ϕϕϕϕϕδ 3)-π( d ) cos -sin -[(142π24F 1EIqR EI qR -=⎰-=ϕϕϕ∆ 解得=X F Bx24. 已知图示半圆曲杆的弯曲刚度为EI ,试求曲杆支座A 处垂直反力F Ay 。
A C R F /2X 1A C R F /2θA C R θ1解: 0F 1111=+∆δXEI R EI R 4π d sin 32π2311=⎰=θθδ EIFR EI FR 4 d sin ) cos -(1232π03F 1-=⎰-=θθθ∆解得 )( π1↓==F X F Ay25. 已知梁的弯曲刚度为EI解:⎩⎨⎧=∆++=∆++00F 2222121F 1212111X X X X δδδδ⎰+-=+-=a EI b a Fa x b x Fx EI 021F 6)32( d))((1∆ ⎰=--=a EI Fa x Fx EI 022F 2 d )1)((1∆EI l x x EI l 3 d 130211=⎰=δ EIlx xEI l 2 d 1)(1202112-=⎰⋅⋅-==δδ EIlx EI l =⎰=022 d 1δ 解得 )( )3(321↑+==b a l Fa X F By , 222lbFa X M B == (顺时针))( )3(32↑+=b a l Fb F Ay , 22lFab M A = (逆时针)2x1。
