全等三角形的判定(HL)练习题
11 三角形全等的判定(四)HL

11 三角形全等的判定(四)HL基础题训练1.判定两直角三角形全等的方法有__________(填简写)SSS ,SAS ,ASA ,AAS ,HL2.如图,若PB ⊥AB 于B ,PC ⊥AC 于C ,且PB =PC ,则AB = __________,理由是__________(填全等三角形及三角形全等的理由)AC △ABP ≌△ACP (HL )A3.如图,△ABC 中,AB =AC ,若AD ⊥BC ,则BD =CD ,其判定三角形全等的方法是( )DA .SASB .ASAC .SSSD .HLB C4.如图,∠A =∠D =90°,AC =DB ,欲证OB =OC ,可以先利用“HL ”说明__________得到AB =DC ,再利用__________证明△AOB ≌__________得到OB =O C .△ABC ≌△DCB “AAS ” △DOCC5.已知:如图∠B =∠E =90°,AC =DF ,FB =E C .求证:AB =DE .FEC B证:△ABC ≌△DEF (HL )6.如图,四边形ABDC 中,∠ABD =∠ACD =90°,BD =CD ,求证:AD ⊥B C .C AB证:△ABD ≌△ACD (HL ) △BDE ≌△CDE (SAS )7.如图,已知∠A =90°,AB =BD ,ED ⊥BC 于D ,求证:DE +CE =A C .D证:连BE . △ABE ≌△DBE (HL ),DE =AE .8.如图,∠ACB =∠BDA =90°,,若要使△ACB ≌△BDA ,还需添加一个什么条件?把它们写出来(不再添加字母)⑴__________ ,理由__________;AC =BD HL⑵__________ ,理由__________;BC =AD HL⑶__________ ,理由__________;∠ABC =∠BAD AAS⑷__________ ,理由__________;∠BAC =∠ABD AAS中组题训练9.如图,AC ⊥BC ,BD ⊥AD ,AC 、BD 相交于O ,如果AC =BD ,那么下列结论中: ①AD =BC ;②∠DAC =∠CBD ;③OC =OD ,其中正确的有( )AA .①②③B . ①②C . ①D .③10.如图,已知AE ⊥BC 于E ,DF ⊥BC 于F ,AE =DF ,AB =DC ,AC 与BD 有怎样的关系?你能进行证明吗?E F证:△ABE≌△DCF(HL),∠ABE=∠DCF,△ABC≌△DCB(SAS)11.在△ABC中,D是BC的中点,DE⊥AB,DF⊥AC,垂足分别是E、F,且DE=DF,求证:AB=A C.DB证:连AD,△BDE≌△CDF(HL).BE=CF.证:△ADE≌△ADF(HL),AE=AF,AE+BE=AF+CF,故AB=A C.12.如图,AB=AE,BC=DE,AF⊥CD于,∠B=∠E,求证:AF平分∠BAE.F EBA证:连AC、AD,△ABC≌△AED(SAS) △ACF≌△ADF(HL)13.如图,在平面直角坐标系中,将直角三角形的直角顶点放在点(4,4)处,两直角边与坐标轴交于点A和点B.⑴求OA+OB的值;P⑵将直角三角形绕点逆时针旋转,两直角边与坐标轴交于点A和点B,求OA-OB的值.解:⑴作PM⊥x轴于M,PN⊥y轴于N,证∠P AM=∠PBN,△P AM≌△PBN AB=BN,OM=ON,∴OA+OB=OM+ON=8.⑵作PM⊥x轴于M,PN⊥y轴于N,证∠P AM=∠PBO,△P AM≌△PBNAM=BN,OM=ON,∴OA-OB=OM+ON=8.。
(完整版)全等三角形的判定综合练习题
1
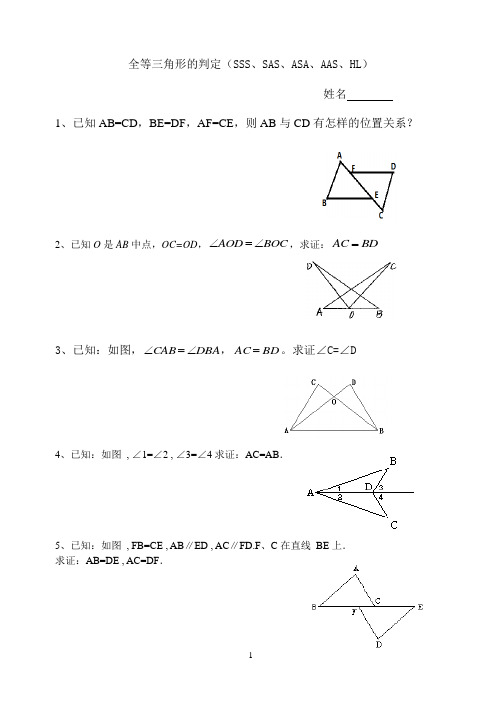
全等三角形的判定(SSS 、SAS 、ASA 、AAS 、HL )
姓名
1、已知AB=CD ,BE=DF ,AF=CE ,则AB 与CD 有怎样的位置关系?
2、已知O 是AB 中点,OC=OD ,AOD BOC ∠=∠,求证:AC BD =
3、已知:如图,DBA CAB ∠=∠,BD AC =。
求证∠C=∠D
4、已知:如图 , ∠1=∠2 , ∠3=∠4求证:AC=AB .
5、已知:如图 , FB=CE , AB ∥ED , AC ∥FD.F 、C 在直线 BE 上. 求证:AB=DE , AC=DF .
2
6、 已知:如图 , E 、D 、B 、F 在同一条直线上 , AD ∥CB , ∠BAD=∠BCD , DE=BF .
求证:AE ∥CF.
7、如图,△ABC 中,D 是BC 上一点,DE⊥AB,DF⊥AC,E 、F 分别为垂足, 且AE=AF ,试说明:DE=DF ,AD 平分∠BAC.
8、如图,CD ⊥AB ,BE ⊥AC ,垂足分别为D 、E ,BE 交CD 于F ,且AD=DF ,求证:AC= BF 。
B
A
E
F
C
D
9、如图,AB=CD ,DF ⊥AC 于F ,BE ⊥AC 于E ,DF=BE ,求证:AF=CE.
10、如图,△ABC 中,∠C=90°,AB=2AC ,M 是AB 的中点,点N 在BC 上,MN ⊥AB 。
求证:AN 平分∠BAC 。
A
D
C
B F E
B A
2
1N M
C。
八年级数学全等三角形的判定(HL)(人教版)(基础)(含答案)

全等三角形的判定(HL)(人教版)(基础)一、单选题(共6道,每道12分)1.如图,已知AC⊥BD,垂足为O,AO=CO,AB=CD,则可得到△AOB≌△COD,理由是( )A.HLB.SASC.ASAD.AAS答案:A解题思路:由题意可得,在Rt△AOB和Rt△COD中∴Rt△AOB≌Rt△COD(HL)故选A试题难度:三颗星知识点:略2.如图,DE⊥AC,BF⊥AC,垂足分别是E,F,且DE=BF,若利用“HL”证明△DEC≌△BFA,则需添加的条件是( )A.EC=FAB.DC=BAC.∠D=∠BD.∠DCE=∠BAF答案:B解题思路:由题意可得,△DEC和△BFA为直角三角形,DE=BF要用“HL”证明△DEC≌△BFA,则需要添加的条件为DC=BA故选B试题难度:三颗星知识点:略3.如图,BE,CD是△ABC的高,且BD=EC,判定△BCD≌△CBE的依据是( )A.SASB.AASC.ASAD.HL答案:D解题思路:由题意可得,∠CDB=∠BEC=90°在Rt△BCD和Rt△CBE中∴Rt△BCD≌Rt△CBE(HL)所以判定△BCD≌△CBE的依据是HL故选D试题难度:三颗星知识点:略4.能使两个直角三角形全等的条件是( )A.一个锐角对应相等B.两个锐角对应相等C.一条边对应相等D.两条边对应相等答案:D解题思路:选项A:一个锐角对应相等,利用已知的直角相等,可得出另一组锐角相等,缺乏边的条件,不能证明两个三角形全等,故选项错误;选项B:两个锐角相等,那么也就是三组对应角相等,缺乏边的条件,不能证明两个三角形全等,故选项错误;选项C:一条边对应相等,再加一组直角相等,不能得出两个三角形全等,故选项错误;选项D:两条边对应相等,若是两条直角边相等,可利用SAS证全等;若一直角边对应相等,一斜边对应相等,可利用HL证全等,故选项正确.故选D试题难度:三颗星知识点:略5.下列说法中,正确的有( )①斜边和一直角边对应相等的两个直角三角形全等;②有两边和它们的夹角对应相等的两个三角形全等;③一锐角和斜边对应相等的两个直角三角形全等;④两组锐角对应相等的两个直角三角形全等.A.1个B.2个C.3个D.4个答案:C解题思路:①斜边和一直角边对应相等,可用HL证全等,正确;②有两边和它们的夹角对应相等,可用SAS证全等,正确;③一锐角和斜边对应相等,则两锐角和斜边对应相等,可用ASA证全等,正确;④两组锐角对应相等的两个直角三角形,缺乏边的条件,不能证全等,错误.故选C试题难度:三颗星知识点:略6.如图是标准跷跷板的示意图,横板AB的中点过支撑点O,且绕点O只能上下转动.如果∠OCA=90°,∠CAO=15°,则小孩玩耍时,跷跷板可以转动的最大角度为( )A.15°B.20°C.30°D.40°答案:C解题思路:如图,∵O为AB的中点,∴OA=OB=在△AOC和△中∴△AOC≌△(HL)∴.故选C试题难度:三颗星知识点:略二、填空题(共2道,每道14分)7.如图,∠AOB=70°,QC⊥OA于点C,QD⊥OB于点D,若QC=QD,则∠CQO=____°.答案:55解题思路:由题意可得,在Rt△OCQ和Rt△ODQ中∴Rt△OCQ≌Rt△ODQ(HL)∴∠COQ=∠DOQ==35°∴∠CQO=90°-35°=55°故应填55试题难度:知识点:略8.如图,在Rt△ABC与Rt△DEF中,∠B=∠E=90°,AC=DF,AB=DE,∠A=50°,∠DFE=____°.答案:40解题思路:由题意可得,在Rt△ABC和Rt△DEF中∴Rt△ABC≌Rt△DEF(HL)∴∠A=∠D=50°∴∠DFE=90°-50°=40°故应填40试题难度:一颗星知识点:略。
数学人教版八年级上册三角形全等的判定(HL)课后作业

三角形全等的判定(HL )课后作业1. 如图1,∠B=∠D=90°,BC=CD ,∠1=30°,则∠2的度数为( )A. 30°B. 60°C. 30°和60°之间D. 以上都不对12A B C D(图1) (图2) (图3)2. 如果两个直角三角形的两条直角边对应相等,那么两个直角三角形全等的 依据是( )A. AASB.SASC.HLD.SSS3. 已知在△ABC 和△DEF 中,∠A=∠D=90°,则下列条件中不能判定△ABC 和 △DEF 全等的是( )A.AB=D E,AC=DFB.AC=EF,BC=DFC.AB=DE,BC=EFD.∠C=∠F,BC=EF4. 如图2,已知AD 是△ABC 的BC 边上的高,下列能使△ABD≌△ACD 的条件是5.如图3,在Rt △ABC 中,∠BAC=90°,AB=AC ,分别过点B ,C 作过点A 的直线的垂线BD ,CE ,若BD=4cm ,CE=3cm ,则DE=________cm .6.如图4,在Rt △ABC 和Rt △DCB 中,AB=DC ,∠A=∠D=90°,AC 与BD 交于点O ,则有△________≌△________,其判定依据是________,还有△________≌△________,其判定依据是________.(图4) (图5)7.如图5,南京路与八一街垂直,西安路也与八一街垂直,曙光路与环城路垂直.如果小明站在南京路与八一街的交叉口,准备去书店,按图中的街道行走,最近的路程为__________m.8.在△ABC中,AB=CB,∠ABC=90º,F为AB延长线上一点,点E在BC上,且AE=CF.(1)求证: Rt△AB E≌Rt△CBF;(2)若∠CAE=30º,求∠ACF度数.9. 已知如图,AB=AC,∠BAC=90°,AE是过A点的一条直线,且B、C在DE的异侧,BD⊥AE于D,CE⊥AE于E,求证:BD=DE+CE.B AC D。
12-2-5 三角形全等的判定HL(原卷版)

12.2.5三角形全等的判定HL用HL判定三角形全等概念题型一:判定使用HL证明全等【例题1】(2020·广东期末)如图,OD AB⊥于D,OP AC⊥于P,且OD OP=,则AOD与AOP 全等的理由是()A.SSS B.ASA C.SSA D.HL【点睛】本题考查三角形全等的判定方法HL.根据已知结合图形,找到已经有的条件,然后结合判定方法选择条件是正确解答本题的关键.特别注意题目要求利用HL判定全等,需要的是两个直角三角形的斜边和一直角边对应相等.变式训练【变式1-1】(2021·四川期末)如图,AB BD⊥,CD BD⊥,AD BC=,则能直接判断Rt RtABD CDB△△≌的理由是()A.HL B.ASA C.SAS D.SSS知识点管理归类探究在两个直角三角形中,有斜边和一条直角边对应相等的两个直角三角形全等(可以简写成“斜边、直角边”或“HL”).应用“斜边、直角边”判定两个直角三角形全等的过程中要突出直角三角形这个条件,书写时必须在两个三角形前加上“Rt”【变式1-2】(2021·全国八年级)如图,AB BC ⊥,CD BC ⊥,AC BD =,则能证明ABC DCB ≅的判定法是( )A .SASB .AASC .SSSD .HL【变式1-3】(2020·东莞市东莞中学初中部八年级期中)如图,CE AB ⊥,DF AB ⊥,垂足分别为点E ,F ,且CE DF =,AC BD =,那么Rt Rt AEC BFD △≌△的理由是( ).A .HLB .SSSC .SASD .AAS题型二:通过添加条件利用SSS ,判定三角形全等【例题2】(2020·河南期末)如图,ABC 中,AD BC ⊥于D ,要使ABD ACD △≌△,若根据“HL ”判定,还需要加条件__________【点睛】本题考查选条件补齐使用HL 证明三角形全等.注意要两个直角三角形+斜边+一直角边. 变式训练【变式2-1】(2020·东莞期中)如图,已知AB⊥CD ,垂足为B ,BC=BE ,若直接应用“HL”判定⊥ABC ⊥⊥DBE ,则需要添加的一个条件是__________.【变式2-2】(2021·江苏期末)结合如图,用符号语言表达定理“斜边和一条直角边分别相等的两个直角三角形全等”的推理形式:在Rt ABC ∆和Rt DEF ∆中,90C F ∠=∠=︒,AC DF =,_______Rt ABC Rt DEF ∴∆≅∆.【变式2-3】(2020·永善县墨翰中学八年级月考)如图,要用“HL ”判定Rt ABC 和Rt A B C '''全等的条件是( )A .AC AC ''=,BCBC ''= B .A A '∠=∠,AB A B ''=C .AC AC ''=,AB A B ''=D .B B '∠=∠,BC B C ''= 题型三:直接利用SSS 证明三角形全等【例题3】(2020·沭阳县修远中学七年级期末)已知:BE⊥CD ,BE =DE ,BC =DA ,求证:⊥BEC⊥⊥DAE【点睛】HL 证明全等需要两个直角三角形+两个条件,在此类简单的证明题中往往题目中给出两个明显的条件,第三个条件可能隐藏在公共边或者线段的和差得到;此外还可能需要寻找题目中已知条件或者图形中隐含条件通过等量代换达到证明全等的目的.变式训练【变式3-1】(2021·湖北武汉市·八年级期中)如图,已知AB =CD ,CE =BF ,AE ⊥BC ,DF ⊥BC ,垂足分别为E ,F ,求证:CD ⊥AB .【变式3-2】(2020·云南红河哈尼族彝族自治州·九年级学业考试)已知:如图,AB=CD ,DE⊥AC ,BF⊥AC ,E ,F 是垂足,AE=CF .求证:⊥ABF⊥⊥CDE【变式3-3】(2020·荣县留佳初级中学校八年级期中)已知:如图,DE⊥AC ,BF⊥AC ,AD=BC ,DE=BF ,求证:AD⊥BCHL 证明全等的应用题型四:全等三角形性质与HL 判定的综合运用【例题4】(2021·全国八年级专题练习)如图,Rt ABC 与Rt DEF △的顶点A ,F ,C ,D 共线,AB 与EF 交于点G ,BC 与DE 相交于点H ,90B E ∠=∠=︒,AF CD =,AB DE =.(1)求证:Rt ABC Rt DEF ≌;(2)若1GF =,求线段HC 的长.【点睛】方法总结:证明线段相等或角相等可以通过证明三角形全等而得到,所以可以根据题目给出的已知条件,考虑证明三角形全等,还需要什么条件这些条件怎样可以得到.由对应边角相等的条件边得到三角形全等,这是全等三角形的判定;由三角形全等得到对应的边角相等,这是全等三角形的性质.变式训练【变式4-1】 (2019·江苏苏州市·七年级期末)已知:如图,AB BC ⊥,CD DA ⊥,AB CD =.求证:OB OD =.【变式4-2】(2019·河南开封市·八年级月考)在ABC 中,,90AB CB ABC ︒=∠=,F 为AB 延长线上一点,点E 在BC 上,且AE CF =.(1)求证:Rt ABE Rt CBF ≅△△(2)若30EAB ︒∠=,求BFC ∠度数.【变式4-3】(2020·贵州省施秉县第二中学八年级期末)如图所示,C 、D 分别位于路段A 、B 两点的正北处与正南处,现有两车分别从E 、F 两处出发,以相同的速度直线行驶,相同时间后分别到达C 、D 两地,休整一段时间后又以原来的速度直线行驶,最终同时到达A 、B 两点,那么CE 与DF 平行吗?为什么?题型五:角平分线与HL 的综合【例题5】(2019·江苏南通市·南通第一初中七年级月考)如图,PD ⊥AB ,PE ⊥AC ,垂足分别为D 、E ,且PD =PE ,则⊥APD 与⊥APE 全等的理由是( )A .SASB .AAAC .SSSD .HL【点睛】此题型考查全等三角形的判定和性质,角平分线的性质与判定,熟练掌握HL 全等三角形的判定和性质是解题的关键.注意灵活使用角平分线上的点到角两边距离相等.变式训练【变式5-1】(2019·浙江台州市·八年级期末)用三角尺画角平分线:如图,先在AOB ∠的两边分别取OM ON =,再分别过点M ,N 作OA ,OB 的垂线,交点为P .得到OP 平分AOB ∠的依据是( )A .HLB .SSS B .C .SASD .ASA 【变式5-2】(2020·吉林市亚桥第一九年制学校八年级期中)如图,四边形ABCD 中,90D ∠=︒,AB AC =,BEAC ⊥于点E ,=AE AD .求证:AC 平分DAB ∠.3.(2018·郴州市第五中学八年级期末)如图,AC平分⊥BAD,CE⊥AB于E,CF⊥AD的延长线于F,且BC=DC.求证:BE=DF.【真题1】(2014·江苏南京市)(问题提出)学习了三角形全等的判定方法(即“SAS”、“ASA”、“AAS”、“SSS”)和直角三角形全等的判定方法(即“HL”)后,我们继续对“两个三角形满足两边和其中一边的对角对应相等”的情形进行研究.(初步思考)我们不妨将问题用符号语言表示为:在⊥ABC和⊥DEF中,AC=DF,BC=EF,⊥B=⊥E,然后,对⊥B进行分类,可分为“⊥B是直角、钝角、锐角”三种情况进行探究.(深入探究)第一种情况:当⊥B是直角时,⊥ABC⊥⊥DEF.(1)如图⊥,在⊥ABC和⊥DEF,AC=DF,BC=EF,⊥B=⊥E=90°,根据,可以知道Rt⊥ABC⊥Rt⊥DEF.第二种情况:当⊥B是钝角时,⊥ABC⊥⊥DEF.(2)如图⊥,在⊥ABC和⊥DEF,AC=DF,BC=EF,⊥B=⊥E,且⊥B、⊥E都是钝角,求证:⊥ABC⊥⊥DEF.第三种情况:当⊥B是锐角时,⊥ABC和⊥DEF不一定全等.(3)在⊥ABC和⊥DEF,AC=DF,BC=EF,⊥B=⊥E,且⊥B、⊥E都是锐角,请你用尺规在图⊥中作出⊥DEF,使⊥DEF和⊥ABC不全等.(不写作法,保留作图痕迹)(4)⊥B还要满足什么条件,就可以使⊥ABC⊥⊥DEF?请直接写出结论:在⊥ABC和⊥DEF中,AC=DF,链接中考BC=EF,⊥B=⊥E,且⊥B、⊥E都是锐角,若,则⊥ABC⊥⊥DEF.【拓展1】(2019·辽宁大连市·八年级月考)阅读下面材料,完成(1)-(3)题数学课上,老师出示了这样一道题:如图,⊥ABD和⊥ACE中,AB=AD,AC=AE,⊥DAB=⊥CAE=α,连接DC、BE交于点F,过A作AG⊥DC于点G,探究线段FG、FE、FC之间的数量关系,并证明.同学们经过思考后,交流了自己的想法:小明:“通过观察和度量,发现线段BE与线段DC相等.”小伟:“通过观察发现,⊥AFE与α存在某种数量关系.”老师:“通过构造全等三角形,从而可以探究出线段FG、FE、FC之间的数量关系.”(1)求证:BE=CD;(2)求⊥AFE的度数(用含α的式子表示);(3)探究线段FG、FE、FC之间的数量关系,并证明.【拓展2】(2020·湖北黄石市·黄石八中八年级期中)如图1,AB=12,AC⊥AB,BD⊥AB,AC=BD=8.点P在线段AB上以每秒2个单位的速度由点A向点B运动,同时,点Q在线段BD上由B点向点D运动.它们的运动时间为t(s).(1)若点Q的运动速度与点P的运动速度相等,当t=2时,⊥ACP与⊥BPQ是否全等,请说明理由,并判断此时线段PC和线段PQ的位置关系;(2)如图2,将图1中的“AC⊥AB,BD⊥AB”改为“⊥CAB=⊥DBA=60°”,其他条件不变.设点Q的运动速度为每秒x个单位,是否存在实数x,使得⊥ACP与⊥BPQ全等?若存在,求出相应的x,t的值;若不存在,满分冲刺请说明理由.。
直角三角形全等的判定(HL)(分层作业)(解析版)docx

12.2.4直角三角形全等的判定(HL)夯实基础篇一、单选题:1.在Rt△ABC和Rt△A′B′C′中,∠C=∠C′=90°,下列条件中不能判定Rt△ABC≌Rt△A′B′C′的是()A.AC=A′C′,∠B=∠B′B.∠A=∠A′,∠B=∠B′C.AB=A′B′,AC=A′C′D.AB=A′B′,∠A=∠A′【答案】B【知识点】直角三角形全等的判定(HL)【解析】【解答】解:A、根据全等三角形的判定定理AAS可以判定△ABC≌△A′B′C′.故本选项不符合题意;B、根据AAA不能判定Rt△ABC≌Rt△A′B′C′.故本选项符合题意;C、根据全等三角形的判定定理可以判定Rt△ABC≌Rt△A′B′C′.故本选项不符合题意;D、根据全等三角形的判定定理AAS可以判定Rt△ABC≌Rt△A′B′C′.故本选项不符合题意;故选B.【分析】根据三角形全等的判定方法,SSS、SAS、ASA、AAS,HL等逐一检验.2.下面说法不正确的是()A.有一角和一边对应相等的两个直角三角形全等B.有两边对应相等的两个直角三角形全等C.有两角对应相等的两个直角三角形全等D.有两角和一边对应相等的两个直角三角形全等【答案】C【知识点】直角三角形全等的判定(HL)【解析】【解答】A、∵直角三角形的斜边和一锐角对应相等,所以另一锐角必然相等,∴符合ASA定理,不符合题意;B、两边对应相等的两个直角三角形全等,若是两条直角边,可以根据SAS判定全等,若是直角边与斜边,可根据HL判定全等.不符合题意;C、有两个锐角相等的两个直角三角形相似,符合题意;D、有一直角边和一锐角对应相等的两个直角三角形符合ASA定理,可判定相等,不符合题意.故答案为:C【分析】直角三角形中已经有一个直角对应相等,需要它们全等的话,只需要再有一个角和一组边对应相等,利用AAS或者ASA判断出它们全等;或者只需要两组边对应相等,利用HL或者SAS就可判定出它们全等;根据判定方法即可一一判断出答案。
11.2 三角形全等的判定(HL)(含答案)

11.2 三角形全等的判定(HL)题号一1 二2 三3 四4 五5 六6 七7 八8 得分度的反复训练才能取得跟多的收获,我们设计的试卷主要就是从这点出发,所以从你下载这张试卷开始,就与知识接近了一步。
◆课堂测控测试点斜边,直角边1.如图,△ABC中,AB=AC,AD⊥BC于D,由_______可证明△ABD≌△ACD,从而有BD=______,∠B=________.2.下列命题中,正确的是()A.有两条边分别相等的两个直角三角形全等B.有一条边相等的两个等腰直角三角形全等C.有两条直角边分别相等的两个直角三角形全等D.有两边和其中一边上的高对应相等的两个三角形全等3.如图,已知AB=CD,DE⊥AC,BF⊥AC,DE=BF,求证:AB∥CD.4.(研讨题)“有两边相等的两个直角三角形全等”这个命题对吗?下面是小松、小强、小红三位同学的看法.小松:正确.因为如果两边都为直角边,则夹角是直角,用SAS可以证明它们全等.小强:正确,因为如果其中一边是直角边,另一边是斜边,则可用HL证明它们全等.小红:不正确,如果一个三角形的较长的直角边与较长的直角边相等,•则显而易见两个三角形不全等.请发表你的看法.◆课后测控5.下面说法不正确的是()A.有一角和一边相等的两个直角三角形全等B.有两直角边对应相等的两个直角三角形全等C.有两角对应相等的两个直角三角形全等D.有一锐角和其对边对应相等的两个直角三角形全等6.如图,AB=AC,AF⊥BC于F,D,E分别为BF,CF的中点,•则图中全等三角形共有()A.1对 B.2对 C.3对 D.4对(第6题) (第7题) (第8题)7.如图,AC⊥BC,BD⊥AD,AC,BD交于点O,如果AC=BD,那么下列结论中:①AD=BC;②∠ABC=∠BAD;③∠DAC=∠CBD;④OC=OD,其中正确的有()A.①②③④ B.①②③ C.①② D.②③8.如图,在Rt△ABC的斜边BC上截取CD=CA,过点D作DE⊥BC交AB于E,则有()A.DE=DB B.DE=AE C.AE=BE D.AE=BD9.如图,AC=AD,∠C和∠D是直角,将上述条件标注在图中,线段BC和BD相等吗?请说明理由.10.如图,∠BAC=90°,AB=AC,D在AC上,E在BA的延长线上,•BD=CE,BD延长线交CE 于F,求证:BF⊥CE.[注明:图中标注的∠1,∠2能不能给你启发呢?]11.如图,△ABC中,∠B=90°,AD为∠BAC的平分线,DF⊥AC于F,E为AB上一点,且DE=DC.求证:BE=CF.◆拓展测控12.如图,AD,A′D′分别是△ABC和△A′B′C′的高,•且AB=A′B′,AD=A′D′,请你补充一个条件使△ABC≌△A′B′C′.答案:1.HL CD ∠C (点拨:AD 为公共的直角边) 2.C (点拨:两条直角边的夹角为直角) 3.证明:在Rt △ABF 和Rt △CDE 中, ,,AB CD BF DE =⎧⎨=⎩∴Rt △ABF ≌Rt △CDE (HL ),∴∠A=∠C ,∴AB ∥CD .4.小松、小强两学生的回答都片面地理解成这两边是对应的,•即直角边与直角边对应,斜边与斜边对应,故得出了错误的结论,•恰恰命题中漏掉了两个关键字“对应”,就会出现小红同学的分析结果,故小红是正确的,•所以我们一定要重视全等三角形中的“对应”二字.[总结反思]有斜边和一条直角边对应相等的两个直角三角形全等. 5.C (点拨:C 选项中没有边对应相等)6.D (点拨:图中有△ABF ≌△ACF ,△ABD ≌△ACE ,△ADF ≌△AEF ,△ABE ≌△ACD ) 7.A (点拨:易证:△ABD ≌△BAC ,△AOD ≌△BOC ) 8.B (点拨:连结CE ,则Rt △ACE ≌Rt △DCE ) 9.解:BC=BD .理由如下: 在Rt △ABC 和Rt △ABD 中,,.AC AD AB AB =⎧⎨=⎩∴Rt △ABC ≌Rt △ABD (HL ),∴BC=BD .[解题规律]充分利用公共斜边或直角边证明两直角三角形全等.10.证明:∵∠BAC=90°,∴在Rt △ABD 和Rt △ACE 中,,,AB AC BD CE =⎧⎨=⎩∴Rt △ABD ≌Rt △ACE (HL ).∴∠1=∠2.∵∠2+∠E=90°,∴∠1+∠E=90°,∴∠BFE=90°,即BF⊥CE.[解题方法]结合图形,分析已知条件发现直角三角形全等,得∠1=∠2,再充分利用图中∠2+∠E=90°,从而得到∠1+∠E=90°,这类题目要关注构图的规律.11.证明:∵AD平分∠BAC,∴∠BAD=∠FAD.在△ABD和△AFD中,,90,,BAD FADB AFDAD AD∠=∠⎧⎪∠=∠=︒⎨⎪=⎩∴△ABD≌△AFD(AAS),∴BD=DF.在Rt△BDE和Rt△FDC中,,, BD DF DE DC=⎧⎨=⎩∴Rt△BDE≌Rt△FDC(HL),∴BE=CF.[解题方法]分析结论须证△BDE≌△FDC,但还差一条件,为此先证△ABD≌△AFD得到BD=FD,一般地一次三角形全等不能解决问题时,要细致分析,证两次或两次以上的三角形全等.而第一次全等的目的是为证第二次全等服务的.12.可供选择的条件可从以下几条中任选其一:①∠C=∠C′②BC=B′C′③∠BAC=∠B′A′C′④AC=A′C′⑤∠DAC=∠D′A′C′⑥DC=D′C′[解题技巧]这是一道探究题,题目探究△ABC≌△A′B′C′的条件,解题时应先分析已具备什么条件,还缺什么条件,同时联系三角形全等的各种证明方法,•选择出多种满足结论的条件.可以编辑的试卷(可以删除)。
全等三角形的判定HL及角平分线练习

直角三角形全等HL例1 如图,B 、E 、F 、C 在同一直线上,AE ⊥BC ,DF ⊥BC ,AB=DC ,BE=CF ,试判断AB 与CD 的位置关系. 例2 已知 如图,AB ⊥BD ,CD ⊥BD ,AB=DC ,求证:AD ∥BC.例3 公路上A 、B 两站(视为直线上的两点)相距26km ,C 、D 为两村庄(视为两个点),DA ⊥AB 于点A ,CB ⊥AB 于点B ,已知DA=16km ,BC=10km ,现要在公路AB 上建一个土特产收购站E ,使CD 两村庄到E 站的距离相等,那么E 站应建在距A 站多远才合理?例4 如图,AD 是△ABC 的高,E 为AC 上一点,BE 交AD 于F ,具有BF=AC ,FD=CD ,试探究BE 与AC 的位置关系.例5 如图,A 、E 、F 、B 四点共线,AC ⊥CE 、BD ⊥DF 、AE=BF 、AC=BD ,求证:△ACF ≌△BDE.【经典练习】1.在Rt △ABC 和Rt △DEF 中,∠ACB=∠DFE= 90,AB=DE ,AC=DF ,那么Rt △ABC 与Rt △DEF (填全等或不全等)2.如图,点C 在∠DAB 的内部,CD ⊥AD 于D ,CB ⊥AB 于B ,CD=CB 那么Rt △ADC≌Rt △ABC 的理由是( )A .SSS B. ASAC. SASD. HL3.如图,CE ⊥AB ,DF ⊥AB ,垂足分别为E 、F ,AC ∥DB ,且AC=BD ,那么Rt △AEC≌Rt △BFC 的理由是( ). ABADBCA EBC D ┐ ┎ ABEDFCAC D BBCF┎ ┘AE CD F ┐┘E ABDCEFA .SSS B. AAS C. SAS D. HL4.下列说法正确的个数有( ).①有一角和一边对应相等的的两个直角三角形全等; ②有两边对应相等的两个直角三角形全等; ③有两边和一角对应相等的两个直角三角形全等; ④有两角和一边对应相等的两个直角三角形全等. A .1个B. 2个C. 3个D. 4个5.过等腰△ABC 的顶点A 作底面的垂线,就得到两个全等三角形,其理由是 . 6.如图,△ABC 中,∠C=︒90,AM 平分∠CAB ,CM=20cm ,那么M 到AB 的距离是( )cm.7.在△ABC 和△C B A '''中,如果AB=B A '',∠B=∠B ',AC=C A '',那么这两个三角形( ). A .全等B. 不一定全等C. 不全等D. 面积相等,但不全等8.如图,∠B=∠D=︒90,要证明△ABC 与△ADC 全等,还需要补充的条件是.9.如图,在△ABC 中,∠ACB=︒90,AC=BC ,直线MN 经过点C ,且AD ⊥MN 于D ,BE ⊥MN 于E ,求证:DE=AD+BE.10.如图,已知AC ⊥BC ,AD ⊥BD ,AD=BC ,CE ⊥AB ,DF ⊥AB ,垂足分别为E 、F ,那么,CE=DF 吗?谈谈你的理由!┐ A BMCA CDBADBE NCABCDE F角平分线的性质1作已知角的平分线一、选择题1.如图,OP 平分∠AOB ,PC ⊥OA ,PD ⊥OB ,垂足分别是C 、D .下列结论中错误的是 ( ) A .PC = PD B .OC = ODC .∠CPO = ∠DPOD .OC = PC 2.如图,△ABC 中,∠C = 90°,AC = BC ,AD 是∠BAC 的平分线,D E ⊥AB 于E , 若AC = 10cm ,则△DBE 的周长等于( ) A .10cm B .8cmC .6cmD .9cm二、填空题3.角平分线的性质定理:角平分线上的点_____________________________. 4.⑴如图,已知∠1 =∠2,DE ⊥AB ,DF ⊥AC ,垂足分别为E 、F ,则DE ____DF . ⑵已知DE ⊥AB ,DF ⊥AC ,垂足分别 为E 、F ,且DE = DF ,则∠1_____∠2.三、解答题5.如图,点D 、B 分别在∠A 的两边上,C 是∠A 内一点,AB = AD ,BC = CD ,CE ⊥AD 于E ,CF ⊥AF 于F . 求证:CE = CF6.已知:如图,在△ABC 中,∠A =90°,AB = AC , BD 平分∠ABC . 求证:BC = AB + AD一、选择题ABC DO PEDCBA 21ABCDEFF A B EC DD B A C1.到三角形三条边的距离都相等的点是这个三角形的( ) A .三条中线的交点B .三条高的交点C .三条边的垂直平分线的交点D .三条角平分线的交点2. 如图所示,表示三条相互交叉的公路,现要建一个货物中转站,要求它到三条公路的距离相等,则可供选择的地址有( ) A.1处 B.2处 C.3处 D.4处二、填空题3.角的内部_____________________________的点,在这个角的平分线上. 4.如图, 点 P 到∠AOB 两边的距离相等,若∠POB =30°, 则 ∠AOB =_____度.5.已知:有一块三角形空地,若想在空地中找到一个点,使这个点到三边的距离相等,试找出该点.(保留画图痕迹)6.已知,如图,BP 是△ABC 的外角平分线,点P 在∠BAC 的角平分线上.求证:CP 是△ABC 的外角平分线.7.如图2,△ABC 中,∠C=900,AD 平分∠BAC ,BD=4,BC=7,则D 到AB 的距离是 .④①②③BD ACE 图2。
