数字逻辑_习题四_答案
数字逻辑-习题以及习题答案

AD
F的卡诺图
ACD
G的卡诺图
根据F和G的卡诺图,得到:F G
湖南理工学院计算机与信息工程系通信教研室 陈进制作
第3章习题 3.4 在数字电路中,晶体三极管一般工作在什么状态?
答:在数字电路中,晶体三极管一般工作在饱和导通状态 或者截止状态。
湖南理工学院计算机与信息工程系通信教研室 陈进制作
第3章习题
111110
1100110
⊕ ⊕⊕⊕ ⊕
10 000 1
⊕ ⊕⊕⊕ ⊕⊕
10 101 01
⑵ (1100110)2 = 64+32+4+2 = (102)10 = (0001 0000 0010)8421码
(1100110)2 =( 101?0101 )格雷码
湖南理工学院计算机与信息工程系通信教研室 陈进制作
第2章习题
2.2 用逻辑代数的公理、定理和规则证明下列表达式:
⑴ AB AC AB AC
⑵ AB AB AB AB 1
⑶ AABC ABC ABC ABC
证⑴:AB AC
AB AC
A B A C
AA AC BA BC
证⑶:AABC
A A B C
AB AC
第1章习题 1.3 数字逻辑电路可分为哪两种类型?主要区别是什么?
答:数字逻辑电路可分为组合逻辑电路、时序逻辑电路两 种类型。 主要区别:组合逻辑电路无记忆功能, 时序逻辑电路有记忆功能。
湖南理工学院计算机与信息工程系通信教研室 陈进制作
第1章习题 1.6 将下列二进制数转换成十进制数、八进制数和十六进制数。
第2章习题 2.8 ⑴ ②求出最简或-与表达式。
两次取反法
圈0,求F 最简与或式。
数字逻辑(白中英)课后习题答案
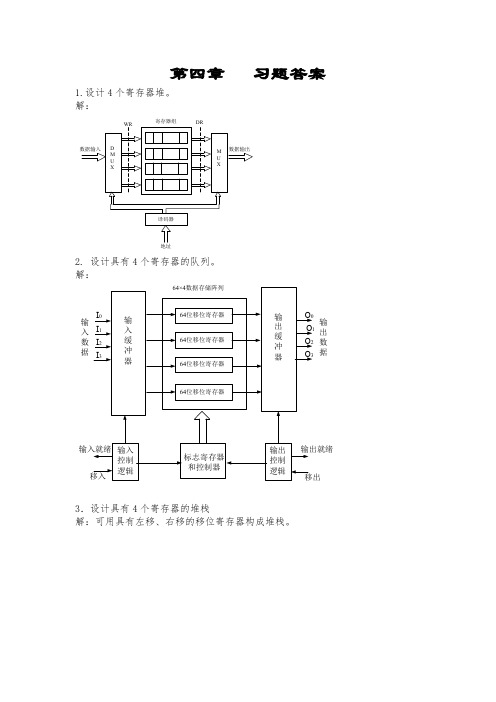
第四章习题答案1.设计4个寄存器堆。
解:寄存器组2. 设计具有4个寄存器的队列。
解:输入数据输出数据3.设计具有4个寄存器的堆栈解:可用具有左移、右移的移位寄存器构成堆栈。
栈顶SR 1SR 2SR 3输入数据输出数据压入弹出4.SRAM 、DRAM 的区别解:DRAM 表示动态随机存取存储器,其基本存储单元是一个晶体管和一个电容器,是一种以电荷形式进行存储的半导体存储器,充满电荷的电容器代表逻辑“1”,“空”的电容器代表逻辑“0”。
数据存储在电容器中,电容存储的电荷一般是会慢慢泄漏的,因此内存需要不时地刷新。
电容需要电流进行充电,而电流充电的过程也是需要一定时间的,一般是0.2-0.18微秒(由于内存工作环境所限制,不可能无限制的提高电流的强度),在这个充电的过程中内存是不能被访问的。
DRAM 拥有更高的密度,常常用于PC 中的主存储器。
SRAM 是静态的,存储单元由4个晶体管和两个电阻器构成,只要供电它就会保持一个值,没有刷新周期,因此SRAM 比DRAM 要快。
SRAM 常常用于高速缓冲存储器,因为它有更高的速率;5. 为什么DRAM 采用行选通和列选通解:DRAM 存储器读/写周期时,在行选通信号RAS 有效下输入行地址,在列选通信号CAS 有效下输入列地址。
如果是读周期,此位组内容被读出;如果是写周期,将总线上数据写入此位组。
由于DRAM 需要不断刷新,最常用的是“只有行地址有效”的方法,按照这种方法,刷新时,是在RAS 有效下输入刷新地址,存储体的列地址无效,一次选中存储体中的一行进行刷新。
每当一个行地址信号RAS 有效选中某一行时,该行的所有存储体单元进行刷新。
6. 用ROM 实现二进制码到余3码转换 解: 真值表如下:8421码 余三码B3B2 B1 B0G3G2 G1G00 0 0 00 0 0 10 0 1 00 0 1 10 1 0 00 1 0 10 1 1 00 1 1 11 0 0 01 0 0 10 1 1 01 0 0 01 0 1 01 1 0 01 1 1 10 0 0 10 0 1 10 1 0 10 1 1 110 0最小项表达式为:G 3=∑)9,8,7,6,5( G 2=∑)9,4,3,2,1( G 1=∑)8,7,4,3,0( G 0=∑)8,6,4,2,0( 阵列图为:G 3G 2G 1GB 3B 2B 1B B 07. 用ROM 实现8位二进制码到8421码转换解:输入为8位二进制数,输出为3位BCD 码,12位二进制数,所以,所需ROM 的容量为:28*12=30728.ROM、EPROM和EEPROM的区别解:ROM 指的是“只读存储器”,即Read-Only Memory。
数字逻辑第四版课后练习题含答案

数字逻辑第四版课后练习题含答案1. 第一章1.1 课后习题1. 将十进制数22转换为二进制数。
答:22 = 101102. 将二进制数1101.11转换为十进制数。
答:1101.11 = 1 x 2^3 + 1 x 2^2 + 0 x 2^1 + 1 x 2^0 + 1 x 2^(-1) + 1 x 2^(-2) = 13.753. 将二进制数1101.01101转换为十进制数。
答:1101.01101 = 1 x 2^3 + 1 x 2^2 + 0 x 2^1 + 1 x 2^0 + 0 x 2^(-1)+ 1 x 2^(-2) + 1 x 2^(-4) + 0 x 2^(-5) + 1 x 2^(-6) = 13.406251.2 实验习题1. 合成与门电路设计一个合成与门电路,使得它的输入A,B和C,只有当A=B=C=1时输出为1,其他情况输出为0。
答:下面是一个合成与门电路的示意图。
合成与门电路示意图其中,S1和S2是两个开关,当它们都被打开时,电路才会输出1。
2. 第二章2.1 课后习题1. 将十进制数168转换为八进制数和二进制数。
答:168 = 2 x 8^3 + 1 x 8^2 + 0 x 8^1 + 0 x 8^0 = 250(八进制)。
168 = 10101000(二进制)。
2. 将八进制数237转换为十进制数和二进制数。
答:237 = 2 x 8^2 + 3 x 8^1 + 7 x 8^0 = 159(十进制)。
237 = 010111111(二进制)。
2.2 实验习题1. 全加器电路设计一个全加器电路,它有三个输入A,B和C_in,两个输出S和C_out。
答:下面是一个全加器电路的示意图。
C_in|/ \\/ \\/ \\/ \\/ \\A|________ \\| | AND Gate______| |B|__| XOR |_| S\\\\ /\\ /\\ /\\ /| | OR Gate| ||_| C_out其中,AND Gate表示与门,XOR Gate表示异或门,OR Gate表示或门。
数字逻辑课后习题答案(科学出版社_第五版)

第一章开关理论基础1.将下列十进制数化为二进制数和八进制数十进制二进制八进制49 110001 6153 110101 65127 1111111 177635 1001111011 11737.493 111.1111 7.7479.43 10011001.0110111 231.3342.将下列二进制数转换成十进制数和八进制数二进制十进制八进制1010 10 12111101 61 751011100 92 1340.10011 0.59375 0.46101111 47 5701101 13 153.将下列十进制数转换成8421BCD码1997=0001 1001 1001 011165.312=0110 0101.0011 0001 00103.1416=0011.0001 0100 0001 01100.9475=0.1001 0100 0111 01014.列出真值表,写出X的真值表达式A B C X0 0 0 00 0 1 00 1 0 00 1 1 11 0 0 01 0 1 11 1 0 11 1 1 1 X=A BC+A B C+AB C+ABC5.求下列函数的值当A,B,C为0,1,0时:A B+BC=1(A+B+C)(A+B+C)=1(A B+A C)B=1当A,B,C为1,1,0时:A B+BC=0(A+B+C)(A+B+C)=1(A B+A C)B=1当A,B,C为1,0,1时:A B+BC=0(A+B+C)(A+B+C)=1(A B+A C)B=06.用真值表证明下列恒等式(1) (A⊕B)⊕C=A⊕(B⊕C)A B C (A⊕B)⊕C A⊕(B⊕C)0 0 0 0 00 0 1 1 10 1 0 1 10 1 1 0 01 0 0 1 11 0 1 0 01 1 0 0 01 1 1 1 1所以由真值表得证。
(2)A⊕B⊕C=A⊕B⊕CA B C A⊕B⊕C A⊕B⊕C0 0 0 1 10 0 1 0 00 1 0 0 00 1 1 1 11 0 0 0 01 0 1 1 11 1 0 1 11 1 1 0 07.证明下列等式(1)A+A B=A+B证明:左边= A+A B=A(B+B)+A B=AB+A B+A B=AB+A B+AB+A B=A+B=右边(2)ABC+A B C+AB C=AB+AC证明:左边= ABC+A B C+AB C= ABC+A B C+AB C+ABC=AC(B+B)+AB(C+C)=AB+AC=右边(3)EDCCDACBAA)(++++=A+CD+E 证明:左边=EDCCDACBAA)(++++=A+CD+A B C+CD E=A+CD+CD E=A+CD+E=右边(4) C B A C B A B A ++=C B C A B A ++ 证明:左边=C B A C B A B A ++=C B A C AB C B A B A +++)( =C B C A B A ++=右边8.用布尔代数化简下列各逻辑函数表达式9.将下列函数展开为最小项表达式 (1) F(A,B,C) = Σ(1,4,5,6,7)(2) F(A,B,C,D) = Σ(4,5,6,7,9,12,14) 10.用卡诺图化简下列各式(1)C AB C B BC A AC F +++=化简得F=C(2)C B A D A B A D C AB CD B A F++++=F=D A B A +(3) F(A,B,C,D)=∑m (0,1,2,5,6,7,8,9,13,14)化简得F=D BC D C A BC A C B D C ++++(4) F(A,B,C,D)=∑m (0,13,14,15)+∑ϕ(1,2,3,9,10,11)化简得F=AC AD B A ++11.利用与非门实现下列函数,并画出逻辑图。
数字逻辑_习题四_答案

习题四部分习题参考答案4.1 将下列函数简化,并用与非门和或非门画出逻辑电路图。
& (3)C B C A D C A B A D C B A F +++=),,,( 解:化简得F=C B C A B A ++F 的与非式为:F=C B C A B A •• ,逻辑电路图如图1所示。
F 的或非式为:F=C B A C B A C B A ABC F +++++=+=,逻辑电路图如图2所示。
图1 图2 4.3分析图4.59所示的逻辑电路图,并说明其逻辑功能。
解:(1)由逻辑电路图写出逻辑表达式并化简可得:DC D B D C D B F D BC D C B D C A D BC D C B D C A F CDABD CD ABD F +=⋅=++=⋅⋅=+=⋅=012(2)根据逻辑表达式,其逻辑功能如表所示。
1 C1&1&&&& &&ABF≥1 0 ≥1≥1≥1ACB ≥1≥1F由真值表可知,DCBA 表示的二进制数,当该值小于等于5,F0=1,当当该值小于等于10,大于5,F1=1,当该值小于等于15,大于10,F2=1。
4.4 试分析图4.60 所示的码制转换电路的工作原理答:①写出逻辑表达式001G B B =⊕ 112G B B =⊕ 223G B B =⊕ 33G B =D C B A F2 F1 F0 输 入 输 出0 00 0 0 1 0 0 0 1 0 0 1 0 0 1 0 0 0 1 0 0 1 1 0 0 1 0 1 0 0 0 0 1 0 1 0 1 0 0 1 0 1 1 0 0 1 0 0 1 1 1 0 1 0 1 0 0 0 0 1 0 1 0 0 1 0 1 0 1 0 1 0 0 1 0 1 0 1 1 1 0 0 1 1 0 0 1 0 0 1 1 0 1 1 0 0 1 1 1 0 1 0 0 1 1 1 1 1 0 0③由真值表可以发现,任意相邻的两个代码之间只有一位不同,而其余各位均相同。
《数字逻辑》第四版部分习题答案_khdaw

⑴真值表:
⑵真值表:
∴Y3=AB,Y2= AB ,Y1=0,Y0= AB + AB =B,逻辑电路为:
⑵ Y = X 3 ,(Y 也用二进制数表示)
因为一个两位二进制正整数的立方的二进制数最多有五位,故输入端用A、B两个变量, 输出端用Y4、Y3、Y2、Y1、Y0五个变量。可列出真值表⑵
∴Y4=AB,Y3= AB + AB= A ,Y2=0,Y1= AB ,Y0= AB + AB =B,逻辑电路如上图。
F3
(
A,B,C , D
)
=
A⋅
BC
+
ABC
⋅
D+
ABCD
第8页
《数字逻辑》习题解答
习题三
3.1 将下列函数简化,并用“与非”门和“或非”门画出逻辑电路。 ⑴ F ( A, B,C ) = ∑m(0,2,3,7)= A ⋅ C + BC = A ⋅ C ⋅ BC Q F = AC + BC ∴ F = A + C + B + C
2.9 用卡诺图判断函数 F ( A, B,C , D ) 和 G( A, B,C , D ) 有何关系。 F( A,B,C , D ) =
= B ⋅ D + A ⋅ D + C ⋅ D + AC D G( A,B,C , D ) =
= BD + CD + A ⋅ + ABD 可见, F = G
= ∏M(5,6,7,8,9,10,11,12,13,14,15) (如下卡诺图 3)
第6页
《数字逻辑》习题解答
2.8 用卡诺图化简下列函数,并写出最简“与-或”表达式和最简“或-与”表达式: ⑴ F ( A, B,C ) = ( A + B )( AB + C ) = AC + BC = C( A + B )
数字逻辑设计习题参考答案(第4章)
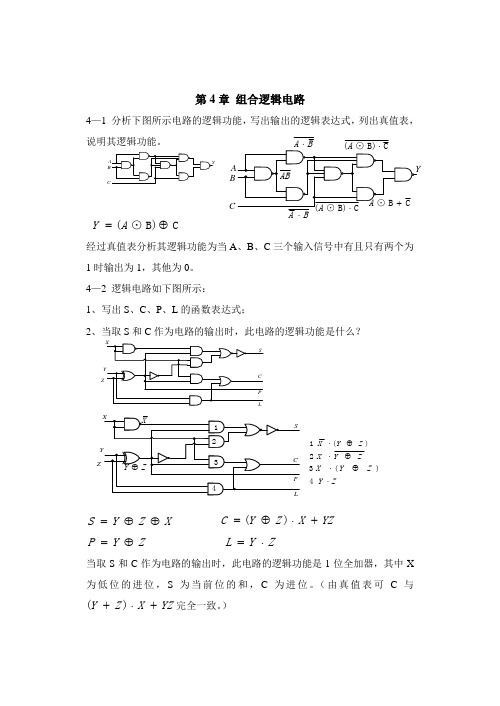
第4章 组合逻辑电路4—1 分析下图所示电路的逻辑功能,写出输出的逻辑表达式,列出真值表,说明其逻辑功能。
C B)⊙(⊕=A Y经过真值表分析其逻辑功能为当A 、B 、C 三个输入信号中有且只有两个为1时输出为1,其他为0。
4—2 逻辑电路如下图所示: 1、写出S 、C 、P 、L 的函数表达式;2、当取S 和C 作为电路的输出时,此电路的逻辑功能是什么?X Z Y S ⊕⊕= YZ X Z Y C +⋅⊕=)(Z Y P ⊕= Z Y L ⋅=当取S 和C 作为电路的输出时,此电路的逻辑功能是1位全加器,其中X 为低位的进位,S 为当前位的和,C 为进位。
(由真值表可C 与YZ X Z Y +⋅+)(完全一致。
)ZB CBA ⋅CB)⊙(⋅A Z)(Z Y X ⊕⋅ZY X ⊕⋅)(Z Y X ⊕⋅ZY ⋅12344—3 下图是由三个全加器构成的电路,试写出其输出1F ,2F ,3F ,4F 的表达式。
Z Y X F ⊕⊕=1 Z Y X F ⋅⊕=)(2Z XY Z XY F +⋅=3 XYZ F =44—4 下图是由3线/8线译码器74LS138和与非门构成的电路,试写出1P 和2P 的表达式,列出真值表,说明其逻辑功能。
ABC C B A m m m m Y Y P +⋅⋅=+=⋅=⋅=70707016543216543212m m m m m m Y Y Y Y Y Y P +++++=⋅⋅+⋅⋅=C B C A B A ++=P1的逻辑功能为当三个输入信号完全一致时输出为1。
P2的逻辑功能为当上输入信号不完全一致时输出为1。
4—5使用74LS138 译码器及少量门电路对三台设备状态进行监控,由不同指示灯进行指示。
当设备正常工作时,指示灯绿灯亮;当有一台设备出故障时,指示灯红灯亮;当有两台设备出故障时,指示灯黄灯亮;当有三台设备出故障时,指示灯红灯和黄灯都亮。
1234解:设输入变量A 、B 、C 分别对应三台设备的状态,0表示故障,1表示正常;输出变量X 、Y 、Z 表示绿、黄、红三个灯的亮灭,0表示灭,1表示亮,根据题意可得真值表如下:设ABC 分别连入74LS138的A 2A 1A 0 由真值表得 42104210Y Y Y Y m m m m Y ⋅⋅⋅=+++=6530Y Y Y Y Z ⋅⋅⋅=4—6 下图3.6是由八选一数据选择器构成的电路,试写出当1G 0G 为各种不同的取值时的输出Y 的表达式。
数字逻辑-第四章习题-759

4-1 试分析图题4-1中各电路的逻辑功能。
图题4 - 1
4-2 试分析图题4-2中各电路的逻辑功能。
图题4 - 2
4-3 分析图题4-3所示逻辑电路,写出其简化的逻辑表达 式,并用与非门改进设计。
图题4 - 3
4-4 分析图题4-4所示逻辑电路,写出其简化的逻辑表 达式。
图题4 - 4
4-5 分析图题4-5所示逻辑电路的逻辑功能,写出函数 的逻辑表达式,并用最简线路实现它。
4-16 举重比赛有3个裁判,一个是主裁判A,2个是辅 裁判B和C,杠铃完全举上的裁决由每个裁判按一下自己 面前的按钮来决定。只有2个基本点以上裁判(其中必须 有主裁判)判明成功时,表示成功的灯才亮。试设计此逻 辑电路。
4-17 试用与非门设计一个无反变量输入的最简三级 线路,以实现下列函数。
(1)F(A ,B,C)= Σ m(3,5,6) (2)F(A ,B,C,D)= Σm(1,4,5,8,12)+
Σd(3,6,9,15) (3)F(A ,B,C,D)= Σ m(0,6,10,11,14) (4)F(A ,B,C)= AB + AC + AB 4-18 试用8选1多路选择器组成64选1多路选择器。 4-19 试用中规模集成4位二进制比较器组成18位二 进制数字比较器。 4-20 试用中规模集成4位二进制比较器组成20位二 进制数字比较器。
4-10 设二进制补码[x]补= x0. x1 x2 x3 x4 ,分别写出下 列要求的判断条件:
(1)(1/2≤ x)或(x < - 1/2) (2)(1/4≤ x <1/2)或(- 1/2≤ x < - 1/4) (3)(1/8≤ x <1/4)或(- 1/4≤ x < - 1/8) (4)(0≤ x <1/8)或(- 1/8≤ x <0) 4-11 设输入ABCD是按余3码编码的二进制数码,其相 应的十进制数路如图题4-6 所示,其中A和B为输入变量 ,F为输出函数。试说明当S3 、S2 、S1 、S0 作为控制信 号时,F 与A、B 的逻辑关系。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
习题四部分习题参考答案
4.1 将下列函数简化,并用与非门和或非门画出逻辑电路图。
& (3)C B C A D C A B A D C B A F +++=),,,( 解:化简得F=C B C A B A ++
F 的与非式为:F=C B C A B A •• ,逻辑电路图如图1所示。
F 的或非式为:F=C B A C B A C B A ABC F +++++=+=,逻辑电路
图如图2所示。
图1 图2 4.3分析图4.59所示的逻辑电路图,并说明其逻辑功能。
解:(1)由逻辑电路图写出逻辑表达式并化简可得:
D
C D B D C D B F D BC D C B D C A D BC D C B D C A F CD
ABD CD ABD F +=⋅=++=⋅⋅=+=⋅=012
(2)根据逻辑表达式,其逻辑功能如表所示。
1 C
1
&
1
&
&
&
& &
&
A
B
F
≥1 0 ≥1
≥1
≥1
A
C
B ≥1
≥1
F
由真值表可知,DCBA 表示的二进制数,当该值小于等于5,F0=1,当当该值小于等于10,大于5,F1=1,当该值小于等于15,大于10,F2=1。
4.4 试分析图4.60 所示的码制转换电路的工作原理
答:①写出逻辑表达式
001G B B =⊕ 112G B B =⊕ 223G B B =⊕ 33G B =
D C B A F2 F1 F0 输 入 输 出
0 0
0 0 0 1 0 0 0 1 0 0 1 0 0 1 0 0 0 1 0 0 1 1 0 0 1 0 1 0 0 0 0 1 0 1 0 1 0 0 1 0 1 1 0 0 1 0 0 1 1 1 0 1 0 1 0 0 0 0 1 0 1 0 0 1 0 1 0 1 0 1 0 0 1 0 1 0 1 1 1 0 0 1 1 0 0 1 0 0 1 1 0 1 1 0 0 1 1 1 0 1 0 0 1 1 1 1 1 0 0
③由真值表可以发现,任意相邻的两个代码之间只有一位不同,而其余各位均相同。
因此,上述逻辑电路的功能是把一个四位二进制数转换成了Gray 码。
4.5当输入变量为何值时,图4.61中各逻辑电路图等效。
解:根据逻辑电路图可知:
2
1321F F B A B A F B
A B A F B
A F +=+==+==
则可知当输入A=B=0时,F 1=F 2=F 3=0,等效;当输入A=B=1时,F1=F2=F3=0,
等效。
4.7 设二进制补码 [x]补=x 0x 1x 2x 3x 4,写出下列要求的判断条件:
(1)
1122x x ≤<-或 (2)11114224x x ≤<-≤<-或
(3)11118448
x x ≤<-≤<-或
(4)11
0088
x x ≤<-≤<或
答:根据补码定义,若x>y 且x 、y 同号,则[x]补>[y]补。
x 0符号位,小数点在x 0后。
因此: (1)
1122
x x ≤<-或 (x 0=0,x 1=1) 或
(x 0=1且x 0.x 1x 2x 3x 4<1.1即x 0=1且x 1=0)
因此,F= x 0⊕x 1。
(2)
11114224
x x ≤<-≤<-或 (0.01≤[x]补<0.1,所以x 0=0 ∧ x 1=0 ∧ x 2=1)
或
(1.1≤[x]补<1.11,所以x 0=1 ∧ x 1=1 ∧ x 2=0)
因此,012012F x x x x x x =+
(3)
11118448
x x ≤<-≤<-或 (0.001≤[x]补<0.01,所以x 0=0 ∧ x 1=0 ∧ x 2=0 ∧ x 3=1) 或
(1.11≤[x]补<1.111,所以x 0=1 ∧ x 1=1 ∧ x 2=1 ∧ x 3=0)
因此,01230123F
x x x x x x x x =+
(4)11008
8
x x ≤<-≤<或
(0.0000≤[x]补<0.001,所以x 0=0 ∧ x 1=0 ∧ x 2=0 ∧ x 3=0) 或
(1.111≤[x]补<2,所以x 0=1 ∧ x 1=1 ∧ x 2=1 ∧ x 3=1) 因此,01230123F
x x x x x x x x =+
4.8假定X=AB 代表一个两位二制正整数,用与非门设计满足如下要求的逻辑电路。
(2)Y=X 3
解:由题意,确定真值表如下:
可得:Y4=Y1=AB=1⋅AB Y3=A Y2=0 Y0=B
4.12 设计一个能接收两位二进制数Y=y 1y 0,X=x 1x 0,并输出Z=z 1z 0的逻辑电路。
当Y=X
时,Z=11;当Y>X 时,Z=10
;当Y <X 时,Z=01。
用与非门实现该逻辑电路。
A B Y4 Y3 Y2 Y1 Y0 0 0 0 0 0 0 0 0 1 0 0 0 0 1 1 0 0 1 0 0 0 1 1 1 1 0 1 1
②画出z 0、z 1对应的卡诺图,进行化简。
由此可得,010********z y y x x y x y x y x =++++。
由此可得,11010011110z x x y y y x y x y x =++++。
③根据要求的逻辑门类型,进行转换并画出逻辑电路图。
010101011011010101101z y y x x y x y x y x y y x x y x y x y x =++++=
110100111101010011110z x x y y y x y x y x x x y y y x y x y x =++++=
根据上述与非形式,可以用与非门实现该逻辑电路。
(图略)
4.13 已知[x]原=x 0x 1x 2,试设计一个逻辑电路,以原码作为输入,要求:当AB=01时,输出反码;当AB=10时,输出补码。
②画出y 0 、y 1 、y 2对应的卡诺图,进行化简。
所以,000201()()()y AB x AB x x x x =++
1y 和2y 的处理方法同上。
所以,1010112012()()()()y AB x x AB x x x x x x x =+++
所以,202022()()()()y AB x x x x AB x =++
根据上述y 0 、y 1 、y 2的函数表达式,可画出相应的逻辑电路图(略)。
4.14 设计一个8421BCD 码十进制数对9的变补电路。
要求:写出真值表;给出最简逻辑表达式;画出电路图。
②画出F 1 、F 2 、F 3和F 4对应的卡诺图,进行化简。
所以,1
F ABC =。
所以,2
F BC BC B C =+=⊕
所以,3
F C =。
所以,4
F D =。
电路图略。
4.17 设计一个组合逻辑电路,其输入为三位二进制数A=A 2 A 1 A 0,输出也为一个三位二进
制数Y=Y 2Y 1Y 0。
当A 的值小于2时,Y=0;当2≤A <5时,Y=A+3;当A >5时,Y=A-3。
要求用与非门实现该电路。
答:①根据逻辑要求,建立真值表。
②画出Y 0、Y 1 、Y 2对应的卡诺图,进行化简。
所以,2212110212110212110Y A A A A A A A A A A A A A A A A A A =++=++=。
所以1
210202121020212102021Y A A A A A A A A A A A A A A A A A A A A A =++=++=。
所以0
102110211021Y A A A A A A A A A A A A =+=+=。
上述表达式已经进行了适当的转换,可以很方便地用与非门来实现。
电路图略。
4.18一组合电路有4个输入A 、B 、C 和D (表示4位二进制数,A 为最高位,D 为最低位),
两个输出为X 和Y 。
当且仅当该数被3整除时,X=1;当且仅当该数被4整除时,Y=1。
求出X 和Y 的逻辑函数,画出最简逻辑电路。
答:①根据逻辑要求,建立真值表。
②画出X 、Y 对应的卡诺图,进行化简。
所以,(0,3,6,9,12,15)X
m =∑。
所以,Y C D =。
逻辑电路图略。
