自动控制原理课后习题答案第四章教学教材
自动控制原理课后习题第四章答案

G(s)H(s)=
Kr s(s+1)(s+3)
σ根 s=3-K+ω轨r4-3-迹+p4s132ω1-3的+~3ω32分p===s2-离+001K点.p-3r=3:KK~0θrr===012+ωω6021,o=3,=0+±1810.7o
8
jω
1.7
s1
A(s)B'系(s)统=根A'轨(s迹)B(s)
s3 p3
s=sK2±r没=j24有.8.6位×于2K.r根6=×4轨80.迹6=上7,. 舍去。
2
第四章习题课 (4-9)
4-9 已知系统的开环传递函数,(1) 试绘制出
根轨迹图。
G(s)H与(s虚)=轴s交(0点.01s+1K)(系0.统02根s+轨1迹)
jω
70.7
解: GKK(rr=s=)10H5(0s)=ωω2s1,(3=s=0+±17000K.7)r(s+50)
s1
A(s)B'(系s)统=A根'(轨s)迹B(s)
s3 p3
p2
p1
-4
-2
0
((24))ζ阻=尼03.振5s2荡+1响2应s+s的81==K-r0值0.7范+围j1.2
s=s-s10=3=.-80-56.8+50K.7r×=20=s.82-=54×-.631..1155×3.15=3.1
-2.8
450
1080
360
0σ
0σ
第四章习题课 (4-2)
4-2 已知开环传递函数,试用解析法绘制出系
统的根轨迹,并判断点(-2+j0),(0+j1),
自动控制原理 第四章习题集配套答案
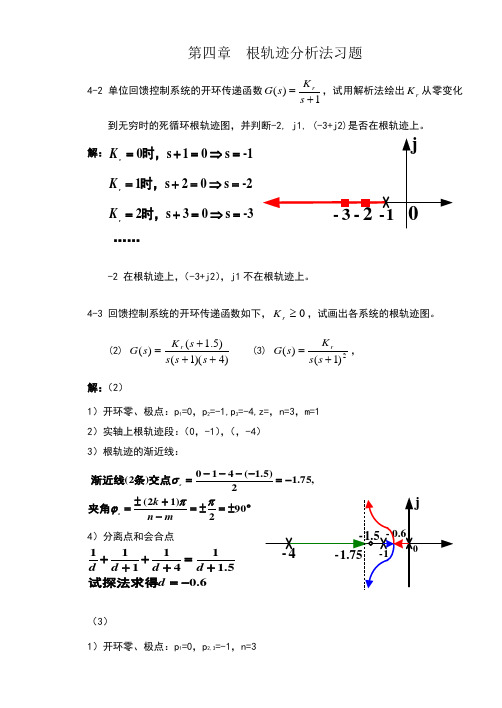
第四章 根轨迹分析法习题4-2 单位回馈控制系统的开环传递函数1)(+=s K s G r,试用解析法绘出r K 从零变化到无穷时的死循环根轨迹图,并判断-2, j1, (-3+j2)是否在根轨迹上。
解:1-s 01s 0r=⇒=+=时,K2-s 02s 1r=⇒=+=时,K3-s 03s 2r=⇒=+=时,K……-2 在根轨迹上,(-3+j2),j1不在根轨迹上。
4-3 回馈控制系统的开环传递函数如下,0≥r K ,试画出各系统的根轨迹图。
(2) )4)(1()5.1()(+++=s s s s K s G r (3) 2)1()(+=s s K s G r , 解:(2)1)开环零、极点:p 1=0,p 2=-1,p 3=-4,z=,n=3,m=1 2)实轴上根轨迹段:(0,-1),(,-4) 3)根轨迹的渐近线:︒±=±=-+±=-=----=902)12(,75.12)5.1(410)2( ππϕσm n k aa夹角交点条渐近线4)分离点和会合点6.05.1141111-=+=++++d d d d d 试探法求得(3)2)实轴上根轨迹段:(0,-1),(-1,-∞) 3)根轨迹的渐近线:±=-+±=-=--=3)12(,323110)3( ππϕσm n k aa夹角交点条渐近线4)分离点和会合点310121-=⇒=++d d d 5)与虚轴交点:223++s s4-5 系统的开环传递函数为)1()2()(++=s s s K s G r ,(1) 画出系统的根轨迹,标出分离点和会合点;(2) 当增益r K 为何值时,复数特征根的实部为-2求出此根。
解: (1)1)开环零、极点:p 1=0,p 22)实轴上根轨迹段:(0,-13)分离点和会合点.3,586.02111121-=-=⇒+=++d d d d d123ss s s r2K-r211K rKj,202rr±==⇒=-s K K(2)系统特征方程为02)1(rr2=+++K s K s2j 2322122,1rr±-==-=+-=-s K Ka b ,,得:由4-6 单位回馈系统的前向信道函数为)3)(1()(++=s s s K s G r,为使死循环主导极点具有阻尼比5.0=ξ,试确定r K 的值。
国防《自动控制原理》教学资料包 课后习题答案 第四章

第4章课后习题参考答案4-1(a)(b)(c)(d)4-2(1)(2)4-3(1)(2)(j 24.20 ),K=10.14 4-4 (1)(2)(3)4-5(1)0>K (2)2>K 4-6(1)(2) 闭环极点(j 7.597.0±-),K=34.77 4-7 (1)110222-=+++s s s a(2)130202-=+ss a4-8正反馈 负反馈表明K>0对于正反馈系统不稳定,负反馈系统稳定。
4-90.707ξ=,系统开环传递函数为)4(8)(+=s s s G ,系统的单位阶跃响应为)(t h =)452sin(5.012 +--t e t4-10σωj 007.17-93.2-5-10-(1) K=5;(2)不含有衰减振荡分量的K 值范围为86.00<<K 或29>K 。
4-11 系统的开环极点为0和-p ,开环零点为-z 。
由根轨迹的幅角条件, 得π)12()()(+=+∠-∠-+∠q p s s z s 。
将ωσj s +=代入,整理有pz++︒=-+---σωσωσω111tan 180tan tan取上述方程两端的正切,并利用下列关系yx yx y x tan tan 1tan tan )tan( ±=±有p z z +=++-σωωσσω2)(,则zp z z -=++222)(ωσ,这是一个圆的方程,圆心位于(-z ,j 0)处,而半径等于zp z -2(注意,圆心位于开环传递函数的零点上)。
证毕。
4-12(1)分离点-0.465,对应K=0.88;虚轴的交点j 2± (2)88.00<<K ,阶跃响应不出现超调。
4-13(1)(2)70MAX K =4-14负反馈稳定K 值范围为0<K<73.8,正反馈稳定K 值范围为0<K<35,所以确定根轨迹增益K 的范围为0<K<35。
自动控制原理 胡寿松 第二版 课后答案 第四章答案汇编

自动控制原理胡寿松第二版课后答案
:系统的开环传递函数为
根轨迹如图所示
4-2 解:
4-3 解:
(1)系统的开环传递函数为
概略的根轨迹如下图所示:
(2)系统的开环传递函数为
根轨迹如下图所示
4-4 解:
(1)系统的开环传递函数为
(2)系统的开环传递函数为
有三个极点
一个零点:(-20,j0)。
起始角:
根轨迹如下图
4-5 (1)
(2)
(3)解:系统的开环传递函数
起始角:
根轨迹如下图所示
4-6解
根轨迹图如下:
4-8解:
所以系统闭环不稳定。
(2)若H(S)=2S+1,系统的开环传递函数为:
根轨迹如下:
自动控制原理吴怀宇 课后习题 第四章

第四章4-1已知单位反馈系统的开环传递函数为()(1)(2)KG s s s s =++ 试绘制该系统在正、负反馈情况下的根轨迹图。
解:(1)负反馈情况令(1)(2)=0s s s ++,解得 3个开环极点1230,1,2p p p ==-=-根轨迹分支数为3,起点分别为(0,0),(1,0),(2,0)j j j -- 终点均为无穷远处。
在实轴上的根轨迹为(][],2,1,0-∞--两段。
由n=3,m=0得轨迹有3条渐近线,它们在实轴上的交点坐标111n mi ji j a p zn mσ==-==--∑∑渐近线与实轴正方向的夹角为2121=3a k k n m ππϕ++=-()(),(k=0,1,2)当k=0,1,2时,计算得a ϕ分别为60°,180°,-60° 确定分离点,由111++=012d d d ++解得120.42, 1.58d d =-=-由于2d 不是根轨迹上的点,故不是分离点,分离点坐标为1d确定根轨迹与虚轴的交点:控制系统特征方程3232=0s s s K +++令=s j ω 代入上式得3232=0j j K ωωω--++ 写出实部和虚部方程233=020K ωωω⎧-⎪⎨-=⎪⎩可求得=006K K ωω⎧⎧=⎪⎨⎨==⎪⎩⎩因此,根轨迹在ω=6K =;另外实轴上的根轨迹分支在0ω=处与虚轴相交。
负反馈系统根轨迹如下图所示(2)正反馈情况令(1)(2)=0s s s ++,解得 3个开环极点1230,1,2p p p ==-=-根轨迹分支数为3,起点分别为(0,0),(1,0),(2,0)j j j -- 终点均为无穷远处。
在实轴上的根轨迹为[](]2,1,0,--+∞两段。
由n=3,m=0得轨迹有3条渐近线,它们在实轴上的交点坐标111n mi ji j a p zn mσ==-==--∑∑渐近线与实轴正方向的夹角为2=3a k πϕ,(k=0,1,2)当k=0,1,2时,计算得a ϕ分别为0°,120°,-120° 确定分离点,由111++=012d d d ++解得120.42, 1.58d d =-=-由于1d 不是根轨迹上的点,故不是分离点,分离点坐标为2d确定根轨迹与虚轴的交点:控制系统特征方程3232-=0s s s K ++将=s j ω 代入上式得3232-=0j j K ωωω--+ 写出实部和虚部方程23-3=020K ωωω⎧-⎪⎨-=⎪⎩可求得=00-6K K ωω⎧⎧=⎪⎨⎨==⎪⎩⎩ 因此,根轨迹在0ω=处与虚轴相交。
自动控制原理第二版第四章课后答案

自动控制原理第二版第四章课后答案【篇一:《自动控制原理》第四章习题答案】4-1 系统的开环传递函数为g(s)h(s)?k*(s?1)(s?2)(s?4) 试证明点s1??1?j3在根轨迹上,并求出相应的根轨迹增益k*和开环增益k。
解若点s1在根轨迹上,则点s1应满足相角条件?g(s)h(s)??(2k?1)?,如图解4-1所示。
对于s1= -1+j3,由相角条件?g(s1)h(s1)?0??(?1?j3?1)??(?1?j3?2)??(?1?j3?4)? 0??2??3??6???满足相角条件,因此s1= -1+j3在根轨迹上。
将s1代入幅值条件: g(s1)h(s1?k*?1?1?j3?1??1?j3?2??1?j3?4k8*解出: k=12 ,k=*?324-2 已知开环零、极点如图4-2 所示,试绘制相应的根轨迹。
解根轨如图解4-2所示:4-3 单位反馈系统的开环传递函数如下,试概略绘出系统根轨迹。
⑴ g(s)?ks(0.2s?1)(0.5s?1)k(s?5)s(s?2)(s?3)* ⑵ g(s)?⑶ g(s)?k(s?1)s(2s?1)解⑴ g(s)?ks(0.2s?1)(0.5s?1)=10ks(s?5)(s?2)系统有三个开环极点:p1?0,p2= -2,p3 = -5①实轴上的根轨迹:???,?5?, ??2,0?0?2?57?????a??33②渐近线: ????(2k?1)????,?a?33?③分离点:1d?1d?5?1d?2?0解之得:d1??0.88,d2?3.7863(舍去)。
④与虚轴的交点:特征方程为 d(s)=s3?7s2?10s?10k?0?re[d(j?)]??7?2?10k?0令 ? 3im[d(j?)]????10??0?解得?????k?7。
根轨迹如图解4-3(a)所j)与虚轴的交点(0,?示。
⑵根轨迹绘制如下:①实轴上的根轨迹:??5,?3?, ??2,0?0?2?3?(?5)????0a??2②渐近线: ????(2k?1)????a?22?③分离点: 1d?1d?2?1d?3?1d?5用试探法可得 d??0.886。
自动控制原理第4章课后习题答案

第4章4-1 已知系统的开环传函如下,试绘制系统参数K 从0→∞时系统的根轨迹图,对特殊点要加以简单说明. (1) ()()(4)(1)(2)K s G s H s s s s +=++ (2) ()()2(4)(420)KG s H s s s s s =+++ 解:(1)有3个开环几点,1个开环零点,固有3条根轨迹分别始于0,-1,-2; 1条根轨迹终于-4,另外2条根轨迹趋于无穷远处 实轴上的根轨迹分布在-1~0之间及-4~-2之间 渐近线条数为n-m=3-1=2 渐进线的交点12041312σ++-=-=-渐近线的倾角90θ︒=±分离点22[()()]02152480d G s H s s s s ds =⇒+++= 解得: 12s =- 其它舍去求与虚轴交点:令s j ω=代入特征方程(1)(2)(4)0s s s K s ++++=中得(1)(2)(4)0j j j K j ωωωω++++= 令上式两边实部和虚部分别相等,有226430(2)0 2.83K K K ωωωω⎧=⎧-=⎪⎪⇒⎨⎨+-==±=±⎪⎪⎩⎩绘制系统根轨迹,如图4-1(1)(2)有4个开环几点,无开环零点,有4条根轨迹,分别起始于0,-4, 24j -±终于无穷远处 实轴上的根轨迹分布在-4~0之间; 渐近线条数为n-m=4-0=4 渐进线的交点04242424j j σ++++-=-=-渐近线的倾角45,135θ︒︒=±±分离点22[()()]042472800d G s H s s s s ds=⇒+++=解得: 2s =-由()()1G s H s =得21224(2)4220K=--+--⨯+, K=64绘制系统根轨迹,如图4-1(2)图4-1(1)图4-1(2)4-2 已知系统的开环传函为(2)(3)()()(1)K s s G s H s s s ++=+(1) 试绘制系统参数K 从0→∞时系统的根轨迹图,求取分离点和会和点 (2) 试证明系统的轨迹为圆的一部分解:有2个开环极点,2个开环零点,有2条根轨迹,分别起始于0,-1; 终于-2,-3;实轴上的根轨迹分布在-3~-2之间及-1~0之间分离会和点2221,2,321[()()]02401,12123(2)()()()[()()]0[2(6)4]0203602,18()()[()()]00020,d G s H s s ds KK K s G s H s s s a d G s H s s s a s a dsa a a a s KG s H s sd G s H s s ds a s s =⇒+===-+⨯-++=+=⇒+++=⇒-+≥⇒≤≥===⇒=≤≤=23s ==解得:当10.634s =-时 由()()1G s H s =得(0.6342)(0.6343)10.070.6340.6341K K -+-+=⇒=-⨯-+当2 2.366s =-时 同理 K=13.9 绘制系统根轨迹 如图4-2证明:如果用s j αβ=+代入特征方程1()()0G s H s +=中,并经整理可得到以下方程式:2233()24αβ++=(注:实部虚部相等后消K 可得)显然,这是个圆的方程式,其圆心坐标为3(,0)2-,半径为2图4-24-3 已知系统的开环传函()()(1)(3)KG s H s s s =++(1) 试绘制系统参数K 从0→∞时系统的根轨迹图(2) 为了使系统的阶跃响应呈现衰减振荡形式,试确定K 的范围 解:有2个开环极点,无开环零点,有2条根轨迹,分别起始于-1,-3; 终于无穷远处;实轴上的根轨迹分布-3~-1之间; 渐近线条数2; 渐近线的交点13022σ+-=-=- 渐近线的倾角90θ︒=± 分离会和点[()()]0240d G s H s s ds=⇒+=解:S=-2由()()1G s H s =得1,12123KK ==-+⨯-+绘制系统根轨迹图4-3由图知 当1<K<+∞时系统的响应呈现衰减振荡形式4-4 设负反馈控制系统的开环传函为2(2)()()()K s G s H s s s a +=+试分别确定使系统根轨迹有一个,两个和三个实数分离点的a 值,分别画出图形 解:求分离点2[()()]0[2(6)4]0d G s H s s s a s a ds=⇒+++=解得s=0,或分离点为实数2203602a a a ⇒-+≥⇒≤或18a ≥当a=18时 实数分离点只有s=0 如图4-4(1)当a>18时 实数分离点有三个,分别为1,2,3(6)0,4a s -+=如图4-4(2)当a=2时2()()K G s H s s =分离点[()()]00d G s H s s ds=⇒= 即分离点只有一个s=0 如图4-4(3) 当02a ≤≤分离点有一个s=0 如图4-4(4) 当a<0时 分离点有1230,s s s ===(舍去)如图4-4(5)综上所述:当a=18,0≤a ≤2时,系统有一个分离点 当a >18时,系统有三个实数分离点 当a <0时,系统有两个分离点a=18图4-4(1) a=2图4-4(2)图4-4(3) a=1图4-4(4)图4-4(5)4-65 已知系统的开环传递函数为3(1)(3)()()K S S G S H S S++=(1)绘制系统的根轨迹。
自动控制原理课后习题第四章答案

然后,根据闭环传递函数的定义,闭环传递函数F(s)=G(s)/(1+G(s)H(s))。
解析3
将G(s)H(s)代入闭环传递函数的定义中,得到F(s)=100/((s+1)^2+3)/(1+100/((s+1)^2+4)((s+1)^2+3))。
解析4
化简得到F(s)=100/((s+1)^2+3)(4((s+1)^2+3))=400/(4(s^2+2s+3))。
1)(s + 2)/(s^2 + 3s + 2)。
04
题目四答案
题目内容
• 题目四:已知系统的开环传递函数为 G(s)H(s)=K/(s^2+2s+2),其中K>0,试 求系统的闭环极点和稳定性。
答案解析
闭环极点
根据开环传递函数,我们可以求出闭环传递函数为 G(s)H(s)/(1+G(s)H(s)),然后求出闭环极点。由于开环传递函 数为K/(s^2+2s+2),所以闭环极点为-1±√2i。
标准形式,即 G(s)H(s) = (s + 1)(s + 2)/(s^2 + 3s + 2)。
02
解析二
根据开环传递函数的分子和分母,可以得出系统的开环传递函数为
G(s)H(s) = (s + 1)(s + 2)/(s^2 + 3s + 2)。
03
解析三
根据开环传递函数,可以求出系统的闭环传递函数为 G(s)H(s) = (s +
自动控制原理课后习题第四章 答案
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
自动控制原理课后习题答案第四章
第四章
4-4 设单位反馈控制系统开环传递函数如下,试概略绘出相应的闭环根轨迹图(要求确定分离点坐标d):
(1)
)1
5.0
)(1
2.0(
)
(
+
+
=
s
s
s
K
s
G
(2)
)1
2(
)1
(
)
(
+
+
=
s
s
s
K
s
G
解:(1)
)5
)(
2
(
)1
5.0
)(1
2.0(
)
(
*
+
+
=
+
+
=
s
s
s
K
s
s
s
K
s
G
,K
K10
*=
①n=3,根轨迹有3条分支;
②起点:p1=0,p2=-2,p3=-5;没有零点,终点:3条根轨迹趋向于无穷远处。
③实轴上的根轨迹:[-2,0],(
5
,-
∞
-];
④渐进线:3
7
3
5
2
-
=
-
-
=
a
σ
,
π
π
π
ϕ,
3
3
)1
2(
±
=
+
=
K
a
;
⑤分离点:
5
1
2
1
1
=
+
+
+
+
d
d
d
求解得:
79
.3
1
-
=
d(舍去),88
.0
2
-
=
d;
作出根轨迹如图所示:
(2)
*
(1)(1)
()
(21)(0.5)
K s K s
G s
s s s s
++
==
++,*0.5
K K
=
①n=2,根轨迹有2条分支;
②起点:p1=0,p2=-0.5,;终点:1
1
z=-
,1
n m
-=条根轨迹趋向于无穷远处。
③实轴上的根轨迹:[-0.5,0],(
,1
-∞-];
④分离点:
111
0.51
d d d
+=
++
求解得:1
0.29
d=-
,2
1.707
d=-
;
作出根轨迹如图所示:
4-6 设单位反馈控制系统的开环传递函数如下,要求:
确定
)20)(10()()(2+++=*s s s z s K s G 产生纯虚根为±j1的z值和*K 值。
解:
020030)()20)(10()(**234*2=++++=++++=z K s K s s s z s K s s s s D 令j s =代入0)(=s D ,并令其实部、虚部分别为零,即:
02001)]1(Re[*=+-=z K j D ,030)]1(Im[*=+-=K j D
解得:63.6,30*==z K
画出根轨迹如图所示:
4-10 设单位反馈控制系统的开环传递函数
)102.0)(101.0()(++=
s s s K s G
要求:
(1) 画出准确根轨迹(至少校验三点);
(2) 确定系统的临界稳定开环增益K c; (3) 确定与系统临界阻尼比相应的开环增益K 。
分析:利用解析法,采用逐个描点的方法画出系统闭环根轨迹。
然后将s j ω=代入特征方程中,求解纯虚根的开环增益,或是利用劳斯判据求解临界
稳定的开环增益。
对于临界阻尼比相应的开环增益即为实轴上的分离点对应的开环增益。
解:(1)
5000
()
(50)(100)
K
G s
s s s
=
++
①n=3,根轨迹有3条分支,且均趋于无穷远处;
②实轴上的根轨迹:[-50,0],(
,1
-∞-00];
③渐进线:
50100
50
3
a
σ
--
==-
,
(21)
,
33
a
kππ
ϕπ
+
==±
;
④分离点:
111
50100
d d d
+=
++
求解得:1
21.3
d=-
,2
78.8
d=-
(舍去);
作出根轨迹如图所示:
(2)临界开环增益c K为根轨迹与虚轴交点对应的开环增益。
32
()150********
D s s s s K
=+++
令s jω
=,代入()0
D s=,并令其实部、虚部分别为零,即
2
Re[()]15050000
D j K
ωω
=-+=,3
Im[()]50000
D jωωω
=-+=
解得:1,23
500070.71,0
ωω
=±=±=
(舍去)150
c
K=
(3)系统处于临界阻尼比1
ζ=,相应闭环根位于分离点处,即要求分离点d 对应的K值。
将s=d=-21.3代入幅值条件:
0.0110.0219.622
K s s s
=++=
4-14 设系统开环传递函数如下,试画出b从零变到无穷时的根轨迹图。
(1)
)
)(
4
(
20
)
(
b
s
s
s
G
+
+
=
(2)
)
10
(
)
(
30
)
(
+
+
=
s
s
b
s
s
G
解:(1)22
()4420420(4)0
D s s s bs b s s b s
=++++=++++=
做等效开环传递函数
*
2
(4)(4)
()
420(24)(24)
b s b s
G s
s s s j s j
++
==
+++++-
①n=2,有2条根轨迹分支,n-m=1条趋于无穷远处;
②实轴上的根轨迹:(,4
-∞-];
③分离点
111
24244
d j d j d
+=
+++-+
整理得
2
1
2
840
8.47
0.47()
d d
d
d
+-=
=-
=舍去
出射角:1
000
180arctan290135
p
θ=+-=
根轨迹如图所示:
(2)2
()(10)30()40300
D s s s s b s s b
=+++=++=
做等效开环传递函数
*
2
3030
()
40(40)
b b
G s
s s s s
==
++
①n=2,有2条根轨迹分支,且均趋于无穷远处;
②实轴上的根轨迹:[40,0
-];
③分离点
11
40
d d
+=
+
整理得20
d=-
根轨迹如图所示:。
