统计学实验作业

合集下载

统计学实训综合实验报告

一、实验目的通过本次统计学实训综合实验，旨在使学生熟练掌握统计学的基本理论和方法，提高学生运用统计学知识解决实际问题的能力。

实验内容主要包括数据收集、整理、描述、推断和分析等环节，通过实际操作，加深对统计学理论的理解，培养学生的统计学素养。

二、实验内容1. 数据收集本次实验以某地区居民消费水平为研究对象，通过查阅相关资料，收集了该地区居民在食品、衣着、居住、生活用品及服务、交通和通信、教育文化娱乐、医疗保健等方面的消费数据。

2. 数据整理对收集到的数据进行整理，将其分为食品、衣着、居住、生活用品及服务、交通和通信、教育文化娱乐、医疗保健七个类别。

3. 描述性统计（1）计算各类别消费的平均值、中位数、众数等集中趋势指标。

（2）计算各类别消费的标准差、极差等离散趋势指标。

（3）绘制各类别消费的直方图、饼图等图形，直观展示消费结构。

4. 推断性统计（1）对居民消费水平进行假设检验，判断各类别消费是否存在显著差异。

（2）运用方差分析等方法，探究各类别消费之间的相关性。

5. 相关性分析（1）运用相关系数分析各类别消费之间的线性关系。

（2）运用因子分析等方法，提取影响居民消费水平的关键因素。

6. 交叉分析（1）根据性别、年龄、收入等变量，分析不同群体在消费结构上的差异。

（2）运用卡方检验等方法，探究不同群体在消费结构上的显著差异。

三、实验结果与分析1. 描述性统计结果根据计算，该地区居民在食品、衣着、居住、生活用品及服务、交通和通信、教育文化娱乐、医疗保健等方面的消费平均分别为：3000元、1500元、2000元、1000元、1000元、500元、500元。

2. 推断性统计结果通过对居民消费水平的假设检验，发现食品、衣着、居住、生活用品及服务、交通和通信、教育文化娱乐、医疗保健等方面的消费存在显著差异。

3. 相关性分析结果运用相关系数分析，发现食品、衣着、居住、生活用品及服务等方面的消费与居民收入呈正相关，而交通和通信、教育文化娱乐、医疗保健等方面的消费与居民收入呈负相关。

统计学作业

统计学作业
将抗生素注入人体会产生抗生素与血浆蛋白质结合现象，以致减少了药性，下表列出5种常用的抗生素注入牛的体内时，抗生素与血浆蛋白质结合的百分比
抗生素青霉素四环素链霉素红霉素氯霉素
1 29.6 27.3 5.8 21.6 29.2
2 24.
3 32.6 6.2 17.
4 32.8
3 28.5 30.8 11.0 18.3 25.0
4 32.0 34.8 8.3 19.0 24.2
试在显著性水平a=0.05下检验这些百分比的均值有无显著性差异。

解：以u1，u2，u3，u4，u5依次表示青霉素，四环素，链霉素，红霉素，氯霉素与血浆蛋白质结合的百分比均值，本题需假设检验
Ho：u1=u2=u3=u4=u5，
H1：u1，u2，u3，u4，u5不全相等。

折线散点图：
SUMMARY
组观测数求和平均方差
青霉素 4 114.4 28.6 10.35333
四环素 4 125.5 31.375 10.05583
链霉素 4 31.3 7.825 5.6825
红霉素 4 76.3 19.075 3.2625
氯霉素 4 111.2 27.8 15.92
方差分析
差异源SS df MS F P-value F crit 组间1480.823 4 370.2058 40.88488 6.73978E-08 3.055568 组内135.8225 15 9.054833
总计1616.646 19
Fa(4,15)=3.06 <F=40.88488 所以接受H0，认为这些均值无显著性差异。

统计学例题作业

35
36
32
35
37
36
28
35
35
36
33
38
27
35
37
38
30
26
36
37
32
33
30
33
32
34
33
34
37
35
32
34
32
35
36
35
35
35
34
32
30
36
30
36
35
38
36
31
33
32
33
36
34
第三章习题3.6：
试分别算出以下两个玉米品种的10个果穗长度(cm)的标准差及
变异系数，并解释所得结果。
3．做出第40页图3.3和图3.4。
第三章习题3.2：
100个小区水稻产量的资料如下(小区面积1m2，单位10g)
37
36
39
36
34
35
33
31
38
34
46
35
39
33
41
33
32
34
41
32
38
38
42
33
39
39
30
38
39
33
38
34
33
35
41
31
34
35
39
30
39
35
36
34
36
35
37
总结分析：从上折线表可以看出，100个小区水稻产量呈正态分布，由此可看出水稻产量是比较稳定的
BS24：

实验统计学实验(仅供参考)

实验统计学实验报告学院：班级：学号：姓名：实验数据的计算机分析综合性实验一、目的本综合性实验包括试验数据的整理、描述性统计分析、方差分析、回归分析及SAS的编程。

做完本实验可使学生系统掌握数据分析技术及常用的统计分析软。

二、实验内容1.用EXCEL对数据进行整理和描述性统计分析1）用EXCEL对下表数据进行分组，列出次数分布表并作次数分布图。

17721519797123159245119119131149152167104 16121412517521911819217617595136199116165 2149515883137801381511871261961342061379897129143179174159165136108101141148168 16317610219414517375130149150161155111158 13118991142140154152163123205149155131209 18397119181149187131215111186118150155197 116254239160172179151198124179135184168169 173181188211197175122151171166175143190213 1922311631591581591771471942271411691241592）分别用分组数据和未分组数据计算平均数、方差、标准差等统计数，在EXCEL中所用到的函数分别为：A VERAGE（）、V AR（）和STDEV（）等。

未分组数据：2.用EXCEL进行常用统计分析如用EXCEL可用加载宏功能，把“分析工具库”模块加载便可进行有关分析。

1）成对数据（相关样品）和成组数据（独立样品）的假设测验用下表数据分别作成对数据和成组数据的T测验，并分析其结果的异同。

1234567891011121314153.74.25.36.4 2.8 3.4 3.8 5.4 3.3 4.7 4.1 3.2 4.6 3.3 2.94.35.2 4.1 5.5 3.4 5.7 4.2 5.1 4.6 3.7 5.5 4.6 3.7 5.4 3.3-0.6 -1 1.2 0.9 -0.6 -2.3 -0.4 0.3 -1.3 1 -1.4 -1.4 0.9 -2.1 -0.4 双样本的成对法分析：根据上表可知，可以认为A、B两组数据的方差相同，故采用t-检验: 双样本等方差假设进行成组法分析。

统计学作业

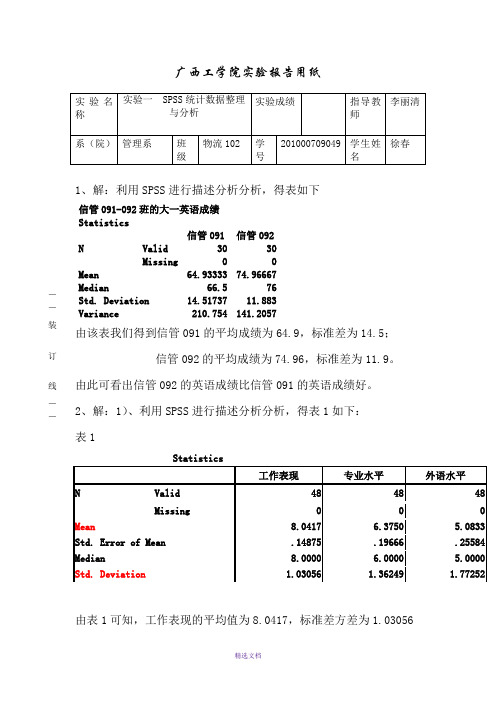
广西工学院实验报告用纸1、解：利用SPSS 进行描述分析分析，得表如下信管091-092班的大一英语成绩 Statistics信管091 信管092N Valid 30 30 Missing 0 0Mean 64.93333 74.96667Median 66.5 76 Std. Deviation 14.51737 11.883 Variance 210.754141.2057由该表我们得到信管091的平均成绩为64.9，标准差为14.5；信管092的平均成绩为74.96，标准差为11.9。

由此可看出信管092的英语成绩比信管091的英语成绩好。

2、解：1）、利用SPSS 进行描述分析分析，得表1如下：表1由表1可知，工作表现的平均值为8.0417，标准差方差为1.03056— — 装订线— —专业水平的平均值为6.3750，标准差方差为 1.36249外语水平的平均值为5.0833，标准差方差为1.77252由此可见，用人单位对该校毕业生工作表现方面最为满意。

外语水平方面最不满意。

应在外语水平方面作出教学改革。

措施：1、在入学前就针对性的对英语成绩进行筛选2、入学后分班进行上课3、加强对英语课程的教育4、开展一些有关英语互动的活动5、要求每个班每天早上用一定时间读英语2）、由表1可知，工作表现的标准误差为0.14875，全距为4专业水平的标准误差为0.19666，全距为5外语水平的标准误差为0.25584，全距为7由此可见，用人单位对该校毕业生外语水平方面的满意程度差别最大。

产生的原因是：从抽取的样本看来，学生的外语水平参差不齐，有的学生外语水平很高，而有的学生水平非常低，同时大多数学生的外语水平都较低。

所以使得用人单位对该校毕业生外语水平方面的满意程度差别较大。

3）、利用SPSS进行，得表1、表2和表3如下：商学院表1Statistics工作表现专业水平外语水平N Valid 17 17 17Missing 0 0 0Mean 8 5.823529 4.764706Std. Deviation 1.118034 0.951006 1.601929Variance 1.25 0.904412 2.566176生物学院表2Statistics工作表现专业水平外语水平N Valid 17 17 17Missing 0 0 0Mean 8 6.647059 5.294118Std. Deviation 1.06066 1.271868 1.611083Variance 1.125 1.617647 2.595588医学院表3Statistics工作表现专业水平外语水平N Valid 14 14 14Missing 0 0 0Mean 8.142857 7.214286 3.714286Std. Deviation 0.949262 1.368805 1.489893Variance 0.901099 1.873626 2.21978由以上三个表对比可知社会对三个学院的毕业生工作表现方面的满意程度近于一致。

统计学实验作业

1、一家大型商业银行在多种地区设有分行，其业务重要是进行基础设施建设、国家重点项目建设、固定资产投资等项目旳贷款。

近年来,该银行旳贷款额平稳增长，但不良贷款额也有较大比例旳增长，这给银行业务旳发展带来较大压力。

为弄清晰不良贷款形成旳因素，管理者但愿运用银行业务旳有关数据做些定量分析,以便找出控制不良贷款旳措施。

该银行所属旳２５家分行旳有关业务数据是“例11.6.x ｌs”。

（1）试绘制散点图，并分析不良贷款与贷款余额、合计应收贷款、贷款项目个数、固定资产投资额之间旳关系；２计算不良贷款、贷款余额、合计应收贷款、贷款项目个数、固定资产投资额之间旳有关系数（2）求不良贷款对贷款余额旳估计方程;从表系数可以看出常量、应收贷款、项目个数、固定资产投资额,都接受原假设，只有贷款余额回绝原假设，因此只有贷款余额对不良贷款起作用。

系数ａ模型非原则化系数原则系数 t S ｉg. B 原则误差试用版1(常量) －1.022.７82－1．306 ．2０6 各项贷款余额 (亿元).040.010．8913.83７.001本年合计应收贷款 (亿元) .１48.079.2601.879．075贷款项目个数 (个）.０1５.083.03４.１7５.8６３本年固定资产投资额 (亿元)-．0２9.０15-．325-1.９37.067ａ. 因变量: 不良贷款 (亿元）从共线性可以看出，第五个特性值对贷款余额解释87%,相应收账款解释度为12%、对贷款个数解释度为63%、对固定资产投资解释度为5%。

因此不是太共线。

、线性方程为Y＝0．01X Y为不良贷款,X为贷款余额。

4 检查不良贷款与贷款余额之间线性关系旳明显性（α=0.0５);回归系数旳明显性（α＝0．0５)；通过对上表分析得出：贷款余额线性关系通过明显性检查,回归系数2．练习《记录学》教材P33０练习题11.1、1１.6、11.7、11.8、11．1５，相应旳数据文献为“习题11.１．xls”、“习题11.６.xls”、“习题11.7.xlｓ”、“习题1１.８．xlｓ”、“习题１1.15.xls”。

统计学实验

统计学实验内容一、频数统计1．A公司在招聘时采用了综合能力测试（满分为100分），由于应聘的人数较多，现随机抽取了157名应聘者的测试成绩，其测试分数的数据如book1所示。

（1）根据上面的资料，进行分组，并确定组数和组距。

根据资料判断，进行分组，分为六组，组距为10。

（2）编制频率分布表上限成绩频数频率19 10～20 16 0.10191129 20～30 27 0.17197539 30～40 56 0.35668849 40～50 39 0.24840858 50～60 14 0.08917268 60～70 5 0.031847合计157接收频率累积 %19 16 10.19%29 27 27.39%39 56 63.06%49 39 87.90%59 14 96.82%69 5 100.00%其他0 100.00%（3）画出直方图。

2. 为评价家电行业售后服务的质量，随机抽取了由100家庭构成的一个样本。

服务质量的等级分别表示为：A.好；B.较好；C.一般；D.差；E.较差。

调查结果见book2。

(1) 指出表中的数据属于什么类型？定序型(2) 制作一张频数分布表；服务质量等级频数频率1 A 14 0.142 B 21 0.213 C 32 0.324 D 18 0.185 E 15 0.15合计100(3)绘制一张条形图，反映服务质量的分布。

等量质计数项:服务质量等级服务质量等级汇总A 14B 21C 32D 18E 15总计100二、参数估计1．已知灯管使用寿命服从正态分布，其标准差为50小时。

现从一批产品中抽取25个作为样本，测得其平均使用寿命为1600小时，要求在95%的概率保证下估计该批产品平均使用寿命的置信区间。

（运用CONFIDENCE函数）标准差50置信度0.95样本容量25平均值1600极限误差19.59964置信区间1580.4 1619.6抽样平均误差 19.59964，置信区间即（1580.4003~1619.59964）2．在一篇关于“通货紧缩”的文章中，作者考察了各种各样投资的收益情况。

统计学四篇实验报告

《统计学》四篇实验报告实验一:用Excel构建指数分布、绘制指数分布图图1-2：指数分布在日常生活中极为常见，一般的电子产品寿命均服从指数分布。

在一些可靠性研究中指数分布显得尤为重要。

所以我们应该学会利用计算机分析指数分布、掌握EXPONDIST函数的应用技巧。

指数函数还有一个重要特征是无记忆性。

在此次实验中我们还学会了产生“填充数组原理”。

这对我们今后的工作学习中快捷地生成一组有规律的数组有很大的帮助。

实验二：用Excel计算置信区间一、实验目的及要求1、掌握总体均值的区间估计2、学习CONFIDENCE函数的应用技巧二、实验设备（环境）及要求1、实验软件：Excel 20072、实验数据：自选某市卫生监督部门对当地企业进行检查，随机抽取当地100家企业，平均得分95，已知当地卫生情况的标准差是30，置信水平0.5，试求当地企业得分的置信区间及置信上下限。

三、实验内容与步骤某市卫生监督部门对当地企业进行检查，随机抽取当地100家企业，平均得分95，已知当地卫生情况的标准差是30，置信水平0.5，试求当地企业得分的置信区间及置信上下限。

第1步：打开Excel2007新建一张新的Excel表；第2步：分别在A1、A2、A3、A4、A6、A7、A8输入“样本均值”“总体标准差”“样本容量”“显著性水平”“置信区间”“置信上限”“置信下限”；在B1、B2、B3、B4输入“90”“30”“100”“0.5”第3步：在B6单元格中输入“=CONFIDENCE(B4,B2,B3)”，然后按Enter键；第4步：在B7单元格中输入“=B1+B6”，然后按Enter键；第5步：同样在B8单元格中输入“=B1-B6”，然后按Enter键；计算结果如图2-1四、实验结果或数据处理图2-1：实验二：用Excel产生随机数见图3-1实验二：正态分布第1步：同均匀分布的第1步；第2步：在弹出“随机数发生器”对话框，首先在“分布”下拉列表框中选择“正态”选项，并设置“变量个数”数值为1，设置“随机数个数”数值为20，在“参数”选区中平均值、标准差分别设置数值为30和20，在“输出选项”选区中单击“输出区域”单选按钮，并设置为D2 单元格，单击“确定”按钮完成设置。

统计学实验报告及答案

统计学实验课第一次作业数据整理案例管理报告:现金个人支票信用卡平均8.84 平均42.732 平均40.87682 标准误差0.856497 标准误差 2.470033 标准误差 3.171108 中位数7.405 中位数41.34 中位数45.33 众数#N/A 众数#N/A 众数#N/A标准差 5.2798 标准差15.62186 标准差14.87382 方差27.87629 方差244.0425 方差221.2304 峰度-0.85908 峰度0.266625 峰度-1.00003 偏度0.435257 偏度-0.03301 偏度-0.11736 区域19.39 区域75.49 区域55.33 最小值 1.09 最小值 2.67 最小值14.44 最大值20.48 最大值78.16 最大值69.77 求和335.92 求和1709.28 求和899.29 观测数38 观测数40 观测数22置信度(95.0%) 1.735427置信度(95.0%)4.996113 置信度(95.0%)6.5946811）平均数：现金（8.84），个人支票（42.732），信用卡（40.87682），由上可知，支付金额越大，人们首先会选择用个人支票支付，其次是信用卡，再来是现金。

众数：现金（7.405），个人支票（41.34），信用卡（45.33），由上可知，支付金额越大，人们首先会选择用信用卡支付，其次是个人支票，再来是现金。

2）极差=最大值-最小值，现金（19.39），个人支票（75.49），信用卡（55.33）,由上可知，支付金额越大，人们首先会选择用个人支票支付，其次是信用卡，再来是现金。

标准差（由表可知）,现金（5.2798），个人支票（15.62186），信用卡（14.87382）由上可知，用现金支付的代表性最大，其次是信用卡，再来是个人支票。

标准差系数=标准差/平均数*100%，现金（59.73%），个人支票（36.56%），信用卡（36.387%），由上可知，用信用卡支付的代表性最大，其次是个人支票，再来是现金。

统计学大作业调查实验报告

统计学大作业调查实验报告《统计学调查实验报告》一、引言统计学是应用数学的一门重要学科，其通过收集、分类、整理、分析和解释数据，为决策提供有效的依据。

为了深入理解统计学的应用，我们进行了一项调查实验，并撰写本报告，以总结实验过程和结果。

本报告的目的是通过实际调查实验的结果，来阐述统计学在实践中的重要性。

二、实验方法我们选择了一个高校的学生群体作为调查对象。

通过发放调查问卷，我们收集了与学生相关的各种数据，包括年龄、性别、学习成绩、兴趣爱好等。

为了控制变量，我们要求被调查者按照实验设计自愿参与，并确保调查过程的随机性和代表性。

三、数据分析在数据收集完成后，我们使用了统计学方法对数据进行了分析。

首先，我们计算了平均值、标准差和频数分布等基本统计量，并得出了数据的基本统计特征。

然后，我们使用图表展示了不同变量之间的关系，例如年龄与性别、学习成绩与兴趣爱好等。

此外，我们还进行了假设检验、方差分析和回归分析等进一步的统计分析。

四、实验结果通过数据分析，我们得出了一些有意义的结果。

首先，我们发现男女学生在兴趣爱好上存在差异：男生更倾向于体育和游戏，而女生更倾向于文学和音乐。

其次，我们发现年龄对学习成绩的影响不显著，但是性别对学习成绩有明显的差异，女生的平均分高于男生。

此外，我们还发现学习成绩与父母的教育程度和家庭背景密切相关。

这些结果对于学校教育和家庭教育有着重要的启示。

五、讨论与结论本次调查实验结果表明统计学在实践中的重要性。

通过收集和分析大量的数据，我们能够找出数据中隐藏的规律和关系。

这对于做出准确的决策非常重要，无论是在教育、医疗还是商业等领域。

同时，本实验还暴露了一些问题，例如个别数据的异常值和样本容量的局限性，这些都需要在未来的调查实验中加以改进。

综上所述，统计学调查实验是一项有益的实践活动。

通过实际操作和数据分析，我们深入了解了统计学的应用和局限性。

在今后的学习和工作中，我们将更加重视统计学的知识和方法，以提高自己的决策能力和分析能力。

统计学上机实验题目

A.1. 要求筛选出（1）统计学成绩等于75分的学生；（2）数学成绩高的前3名学生；（3）4门课程成绩都大于70分的学生。

2. 要求筛选出（1）数学成绩等于60分的学生；（2）经济学成绩高的前4名学生；（3）4门课3. 要求筛选出（1）英语成绩等于85分的学生；（2）统计学成绩高的前4名学生；（3）4门课4. 要求筛选出（1）统计学成绩等于90分的学生；（2）经济学成绩高的前3名学生；（3）4门5. 要求筛选出（1）数学成绩等于85分的学生；（2）英语成绩高的前3名学生；（3）4门课程B.1. 为评价家电行业售后服务的质量，随机抽取了由100个家庭构成的一个样本。

服务质量的等级分别表示为：A.好；B．较好；C.一般；D.较差；E．差。

调查结果如下所示；B EC C AD C B AE D A C B C D E C E E A D B C C A E D C B B A C D E A B D D C C B C E D B C C B C D A C B C D E C E B B E C C A D C B A E B A C D E A B D D C A D B C C A E D C B C B C E D B C C B C要求编制品质数列，列出频率、频数，并选用适当的统计图如：圆形图、条形图等形象地显示资料整理的结果。

（要求展现整理过程）2. 为评价家电行业售后服务的质量，随机抽取了由100个家庭构成的一个样本。

服务质量的等级分别表示为： A.好；B．较好；C.一般；D.较差；E．差。

调查结果如下所示；A E C DB DC B A ED B D B C DE C E D A D B C C A E D B B B A C D E A B D D B C B C E C B C B B C D A C A C D E C E B B E C C A D D B A E B A C D E A B D E C A D B C C A E D B B C B C E D B D C A B要求编制品质数列，列出频率、频数，并选用适当的统计图如：圆形图、条形图等形象地显示资料整理的结果。

统计学实验报告作业

统计学实验报告作业统计学实验报告实验一：数据数量特征的描述时间；1个学时。

实验内容：描述数据有关的特征，如，中位数，众数，均值，方差，峰度等。

实验目的：掌握利用有关电子工具对数据的数量特征进行描述的操作方法。

二、演示过程：EXCEL中用于计算描述统计量的方法有两种，函数方法和描述统计工具的方法。

常用的描述统计量有众数、中位数、算术平均数、调和平均数、几何平均数、极差、四分位差、标准差、方差、标准差系数等。

（一）运用函数法进行统计描述函数名称 Average Geomean Harmean Median Mode Max Min Quartile Stdev Stdevp Var Varp常用的统计函数函数功能计算指定序列算数平均数计算数据区域的几何平均数计算数据区域的调和平均数计算给定数据集合的中位数计算给定数据集合的众数计算最大值计算最小值计算四分位点计算样本的标准差计算总体的标准差计算样本的方差计算总体的方差在Excel中有一组求标准差的函数，一个是求样本标准差的函数Stdev，另一个是求总体标准差的函数Stdevp。

Stdev与Stdevp的不同是：其根号下的分式的分母不是N，而是N-1。

此外，还有两个对包含逻辑值和字符串的数列样本标准差和总体标准差的函数，分别是Stdeva和Stdevpa。

实验材料：50名学生的英语考试成绩如下：59 61 61 62 63 64 84 74 74 74 85 86 65 66 70 71 72 6768 69 69 72 72 73 75 75 91 91 95 75 75 76 77 78 79 80 81 82 83 84 86 87 88 90 97 99 50 51 54 58步骤：第一步：打开一个EXCEL工作表并在A列中输入变量数列数据，并排序。

在B单元列列中输入各组的分组上限，一般取“10”的倍数减1，下限则默认为“10”的倍数。

并且在第一个数值上方的单元格中键入有关的标志名称，以便在输出图表的分析结果中定义数据的名称。

统计学实验大作业

统计学实验大作业基于中国各主要省市气候状况的分析与比较一．案例背景中国国土面积广阔，东西南北地区在各个方面都有很大的差异，我们能够适应家乡的气候环境，但是换个地方生活呢？情况就会不同了，拿学生选择大学来说，最好是选择与自己的家乡的气候差异不大的地方的学校，所以，为了能更好地了解各地区的气候差异，我选择了2010年底中国各省市的关于年平均气温，年极端最高气温，年极端最低气温，年平均相对湿度，全年日照时间，全年降水量的数据，进行统计分析。

比较各个省市之间的气候状况，并对造成这种差异的原因进行分析。

二．数据来源及说明使用的数据来源于国家统计局，关于中国各个主要省市2010年底年平均气温，年极端最高气温，年极端最低气温，年平均相对湿度，全年日照时间，全年降水量六个指标的数据。

三．分析方法及要求用聚类分析的方法将各个省市按照不同的尺度分类，用多元回归分析的方法研究年平均相对湿度，全年日照时间，全年降水量，年极端最高气温，年极端最低气温对年平均气温的影响极其多远回归方程。

四．实验内容聚类分析* * * * * * * * * * * * * * * * * * * H I E R A R C H I C A L C L U S T E R A N A L Y S I S * * * * * * * * * * * * * * * * * * *Dendrogram using Ward MethodRescaled Distance Cluster CombineC A S E 0 5 10 15 20 25Label Num +---------+---------+---------+---------+---------+南京 12 -+合肥 14 -+武汉 20 -+南宁 23 -+-----+上海 11 -+ |杭州 13 -+ |望城 21 -+ +-+福州 15 -+ | |沙坪坝 26 -+ | |贵阳 28 -+-----+ +---------------------------------------+温江 27 -+ | |南昌 16 -+ | |海口 24 -+-------+ |广州 22 -+ |济南 17 -+ |昆明 29 -+ |沈阳 7 -+ |长春 8 -+-----+ |哈尔滨 9 -+ | |泾河 32 -+ | |天津 2 -+ | |郑州 19 -+ +-----------------------------------------+石家庄 3 -+ |太原 4 -+ |北京 1 -+ |呼和浩特 5 -+ |银川 35 -+-----+乌鲁木齐 36 -+皋兰 33 -+西宁 34 -+拉萨 30 -+聚类结果：以上是层次聚类的树状图，根据此图我们可以看出南宁，上海，杭州，广州，等省市的气候基本类似，而长春，哈尔滨，天津，郑州，石家庄，太原，北京，呼和浩特，银川的气候也是基本类似的。

《统计学》上机实验例题(一)

• •
2010年
生成频数分布表
(列联表—Excel)
不同类型饮料和顾客性别的频数分布
绿色健康饮品
2010年
分类数据的图示—条形图
(bar Chart)
2010年
分类数据的图示—复式条形图
(bar Chart)
• 饮料类型和顾客性别的条形图
2010年
分类数据的图示—帕累托图
(pareto chart)
(a)向上累积
非常不满意一般满意不满意 (b)向下累积
甲城市家庭对住房状况评价的累积频数分布
环形图
(例题分析)
13% 10% 7% 8% 非常不满意
15%
21% 36% 33% 不满意
一般
31% 26% 甲乙两城市家庭对住房状况的评价满意非常满意
用Excel制作图形
2.3 数值型数据的整理与展示 2.3.1 2.3.2 数据分组数值型数据的图示
温度 / 0C 6 8 降雨量 /mm 25 40 产量/ （ kg/hm2 ） 2250 3450
位面积产量与降雨量和温度等有一定关系。为了解它们之间的关系形态，收集数据如表。试绘制小麦产量与降雨量的散点图，并分析它们之间的关系。
10
13 14 16 21
58
68 110 98 120
一、数值型数据：用数据分析中的直方图编制频数分布表；绘制直方图折线图
【例 2.5】（
见教材38～ 42页）表中
是某电脑公司 2002 年前四个月各天的销售量数据(单位：台) 。试对数据进行分组
等距分组表
(上下组限重叠)
分组数据的图示
(直方图的绘制)

统计学实验作业

1、一家大型商业银行在多个地区设有分行，其业务主要是进行基础设施建设、国家重点项目建设、固定资产投资等项目的贷款。

近年来，该银行的贷款额平稳增长，但不良贷款额也有较大比例的增长，这给银行业务的发展带来较大压力。

为弄清楚不良贷款形成的原因，管理者希望利用银行业务的有关数据做些定量分析，以便找出控制不良贷款的办法。

该银行所属的25家分行2002年的有关业务数据是“例11.6.xls”。

（1）试绘制散点图，并分析不良贷款与贷款余额、累计应收贷款、贷款项目个数、固定资产投资额之间的关系；2计算不良贷款、贷款余额、累计应收贷款、贷款项目个数、固定资产投资额之间的相关系数（2）求不良贷款对贷款余额的估计方程；从表系数可以看出常量、应收贷款、项目个数、固定资产投资额，都接受原假设，只有贷款余额拒绝原假设，所以只有贷款余额对不良贷款起作用。

从共线性可以看出，第五个特征值对贷款余额解释87%，对应收账款解释度为12%、对贷款个数解释度为63%、对固定资产投资解释度为5%。

所以不是太共线。

、线性方程为Y=0.01X Y为不良贷款,X为贷款余额。

4 检验不良贷款与贷款余额之间线性关系的显著性（α=0.05）；回归系数的显著性（α=0.05）；共线性诊断a模型维数特征值条件索引方差比例(常量)各项贷款余额(亿元)1 1 1.837 1.000 .08 .082 .163 3.354 .92 .92a. 因变量: 不良贷款(亿元）通过对上表分析得出：贷款余额线性关系通过显著性检验，回归系数通过显著性检验。

5绘制不良贷款与贷款余额回归的残差图。

2.练习《统计学》教材P330 练习题11.1、11.6、11.7、11.8、11.15，对应的数据文件为“习题11.1.xls”、“习题11.6.xls”、“习题11.7.xls”、“习题11.8.xls”、“习题11.15.xls”。

(任选两题)11.1（1）绘制产量与生产费用之间的散点图，判断二者之间的关系形态.正向相关（2）计算产量与生产费用之间的线性相关系数相关性产量（台）生产费用（万元）产量（台）Pearson 相关性 1 .920**显著性（双侧）.000N 12 12 生产费用（万元）Pearson 相关性.920** 1显著性（双侧）.000N 12 12 **. 在 .01 水平（双侧）上显著相关。

统计实验作业

《农村经济统计》实验学院专业年级学号姓名农村经济统计学实验实验一统计调查方案设计实验目的：通过调查了解农村社会经济问题的主要状况，掌握调查方案的设计。

实验资料：选择自己感兴趣的农村社会经济问题，在理论教学的基础上，通过互联网等途径收集资料或者模拟资料。

实验要求：1.方案设计要求：1）调查目的要做到有的放矢，要根据实际需要来确定；2）要准确把握方案的调查对象和调查单位，即方案要体现搜集谁的资料或者由谁提供资料；3）拟订的调查项目（即调查内容），应根据需要和可能确定；4）确定调查时间（即资料所属时间），若农村社会经济现象是时期现象，则应明确反映调查对象从何年何月何日起到何年何月何日止的资料;瑞是时点现象，就要明确规定统一的标准调查时点；5）要确定调查地点；6）要设计调查工作的组织计划：包括调查的组织领导机构和调查人员的组织；人员配备与培训、文件印刷；调查资料的报送办法；经费预算和开支等等。

2.实验作业要求：1）每人根据调查课题，设计一份完整周密的调查方案；2）在此基础上写出2000字以上的统计调查报告，要求根据处理后的数据信息，分析存在的问题、提出有效的解决方案等。

实验步骤：根据调查方案的内容及统计调查方案设计要求展开。

实验二指标体系的设计实验目的：通过对本班同学的生活消费状况研究，进行认真细致的指标设计，使学生将理论知识应用到实践中去，加深学生对教学内容的理解和掌握，提高学生分析问题和解决问题的能力。

即要掌握指标体系的设计方法和操作过程，运用统计指标及方法分析和研究现实中的经济问题。

实验资料：包括学习、餐饮、衣着、日用品、社会交往、文体活动等方面的消费。

实验要求：在初步了解同学们生活消费的基本情况的基础上设计一个“学生生活消费指标体系”。

1.指标体系应规范：先从几个大的方面来设计，即从生活消费品支出、非商品支出。

再设计分指标体系，如生活消费品支出可分为衣、食、住、行、用等方面的消费资料支出。

最后针对分指标体系设计子指标体系；2.要说明指标分类的主要根据，指标选择的主要原则；3.要明确每个指标的名称及其内涵外延、相关的计算公式和统计方法，以及其他应的注意事项。

统计学实验报告

《统计学》实验一一、实验名称：数据的图表处理二、实验日期：三、实验地点：管理学院实验室四、实验目的和要求目的：培养学生处理数据的基本能力。

通过本实验，熟练掌握利用Excel，完成对数据进行输入、定义、数据的分类与整理。

要求：就本专业相关问题收集一定数量的数据（ 30），利用EXCEL进行如下操作：1.进行数据排序2.进行数据分组3.制作频数分布图、直方图和帕累托图，并进行简要解释4. 制作饼图和雷达图，并进行简要解释五、实验仪器、设备和材料：个人电脑（人/台），EXCEL 软件六、实验过程（一）问题与数据在福州市有一家灯泡工厂，厂家为了确定灯泡的使用寿命，在一批灯泡中随机抽取100个进行测试，所得结果如下：700716728719685709691684705718 706715712722691708690692707701 708729694681695685706661735665 668710693697674658698666696698 706692691747699682698700710722 694690736689696651673749708727 688689683685702741698713676702 701671718707683717733712683692 693697664681721720677679695691 713699725726704729703696717688（二）实验步骤1、将上表数据复制到EXCEL中；2、将上述数据调整成一列的形式；3、选择“数据-排序“得到由小到到的一列数据4、选择“插入-函数（fx）-数学与三角函数-LOG10”计算lg100/lg2=6.7,从而确定组数为K=1+ lg100/lg2=8,这里为了方便取为10组；确定组距为：（max-min）/K=(749-651)/10=9.8 取为10；5、确定接受界限为 659 669 679 689 699 709 719 729 739 749，分别键入EXCEL 表格中，形成一列接受区域；6、选“工具——数据分析——直方图”得到如下频数分布图和直方图表1 灯泡使用寿命的频数分布表图1 灯泡使用寿命的直方图（帕累托图）7、将其他这行删除，将表格调整为：表2 灯泡使用寿命的新频数分布表8、选择“插入——图表——柱图——子图标类型1”，在数据区域选入接收与频率两列，在数据显示值前打钩，标题处键入图的名称图2 带组限的灯泡使用寿命直方图9、双击上述直方图的任一根柱子，将分类间距改为0，得到新的图图2 带组限的灯泡使用寿命直方图图3 分类间距为0的灯泡使用寿命直方图10、选择“插入——图表——饼图”，得到：图4 灯泡使用寿命分组饼图11、选择“插入——图表——雷达图”，得到（三）实验结果分析：从以上直方图可以发现灯泡使用寿命近似呈对称分布，690-700出现的频次最多，690-700的数量最多，说明大多数处于从饼图和饼图也能够清晰地看出结果。

统计学大作业

宁波大红鹰学院工商管理分院《应用统计学》实验(践)报告专业：工商管理专业班级：学生姓名：同组人员：无任课老师：黄涛2017年6月12日目录实验（一） SPSS安装 (2)实验（二）统计数据的搜集与整理 (6)实验（三）统计数据的图表描述 (9)实验四统计数据的度量 (16)实验五统计抽样与参数估计 (19)实验六相关与回归分析 (24)实验七统计数据的动态分析 (33)实验八统计指数分析 (35)实验（一） SPSS安装一、实验名称：SPSS安装二、实验目的：学会安装spss软件及有关操作三、实验步骤：SPSS的安装和启动在启动SPSS软件之前，需要先在计算机上进行安装。

其安装方法主要有两种：一是直接使用SPSS安装光盘进行安装；二是通过网络下载SPSS安装程序进行安装。

本小节使用第二种方法详细介绍SPSS的安装步骤（以IBM SPSS 19.0为例）。

1.打开计算机，找到已经下载到计算机上的SPSS安装程序。

如图一图一2.单击该图标，按照顺序下去，直到出现如下界面，单击“下一步”，则弹出对话框；个人用户选择第一个“单个用户许可证”，如果图二所示。

图二3.单击“下一步”，切换到用户协议对话框。

在该对话框中接受用户协议，然后单击“下一步”，如图三所示。

图三4.单击“下一步”，显示客户信息。

在该对话框中填写好用户姓名与单位，然后单击“下一步”，如图四所示。

图四5.单击“下一步”，语言选择。

选择“英语”，然后单击“下一步”，如图五所示。

图五6.在弹出的对话框中是选择文件安装位置，如图六所示。

在该对话框中单击“更改”，可调整软件的安装位置。

图七7.在选择文件安装对话框中单击“下一步”，在弹出的对话框中单击“安装”即可，如图七所示。

图七8.此时则弹出正在安装的界面，如图八所示。

图八9.在以上安装程序完后，则弹出授权许可证的对话框。

把框中的勾去掉，单击“确定”，如图九所示。

图九10.此时则弹出产品授权对话框，选择“启用以用于临时使用”按钮，单击“下一步”，如图十所示。

统计学实验一作业1

新疆财经大学实验报告
课程名称：统计学
实验项目名称：变量描述统计分析
姓名：阿不都合力力.阿吾提
学号： 2010100598
班级：统计10-2班
指导教师：阿迪力〃努尔
2010年 10月24日
新疆财经大学实验报告
1、用两种方法分析性别、学历的频数和频率，饼图和条形图
2、对工资按下列分组，1500以下，1500-2000，2000-2500,2500—3000，3000以上，画出频数分布表和直方图。

写出实验步骤、分析说明实验结果
第一题
表1 某公司职员性别分布表
图1 某公司职员性别分布图
图2 某公司的性别分组条形图
表2 某公司职员学历分布表
图3 某公司职员的学历饼图
图4 某公司职员的学历条形图
第二题
表3 某公司职员工资分布表
图5 某公司职员的工资柱形图
实验的步骤
第一题；
步骤一：原始数据复制到EXCEL的工作表里面。

二：选择职员编号和性别（或学历）画出该公司的性别（或学历）分布表。

三：在分布表里面选择选择性别（或学历）和频数（不能选择总计）。

四：选择图表向导然后选择里面的饼图（或条形图）画出饼图（或条形图）。

第二题；
步骤一：在EXCEL的工作表里面制定好工资的下线和上线画出工资的分布表。

二：计算出每一个组距间拿该组距间工资的人数。

三：选择工资和频数（不能选择总计）。

四：选择图表向导，里面选择柱形图画出柱形图。

spss统计学第一次实验作业答案

实验作业1.为评价家电行业售后服务的质量，随机抽取了由100家庭构成的一个样本。

服务质量的等级分别表示为：A.好；B.较好；C.一般；D. 较差；E.差。

调查结果见book3.01.xls。

要求：（1）根据Excel文件中提供的数据，建立SPSS数据文件，简述操作步骤。

（2）指出上述数据属于什么类型？（3）制作一张频数分布表；（4）绘制一张条形图，反映评价等级的分布。

解：（1）、①【文件】—【打开】—【数据】②将【文件类型】改为“所有文件”,找到【文件】book3.01.xls -【打开】③取消“从第一行数据读取变量名”。

----单击【确定】（2）、字符型数据。

（4）、见数据实验2．某行业管理局所属40个企业20XX年的产品销售收入数据（单位：万元）见book3.02.xls。

要求：（1）根据Excel文件中提供的数据，建立SPSS数据文件。

（2）根据上面的数据进行适当的分组，编制频数分布表，并计算出累积频数和累积频率；（3）如果按规定：销售收入在125万元以上为先进企业，115～125万元为良好企业，105～115万元为一般企业，105万元以下为落后企业，按先进企业、良好企业、一般企业、落后企业进行分组。

解：（1）、见文件夹book3.02.sav（2）、理论分组数目：K= 1+ln(40)/ln(2)=6.32≈6组距=（最大值-最小值）/组数=（152-87）/6≈10.83≈11（3）按题目要求分组并进行统计，得到分组表如下：某管理局下属40个企分组表按销售收入分组（万元）企业数（个）频率（%）先进企业良好企业一般企业落后企业11119927.527.522.522.5合计40 100.03．为了确定灯泡的使用寿命（小时），在一批灯泡中随机抽取100只进行测试，所得结果见book3.04.xls。

（1）根据Excel文件中提供的数据，建立SPSS数据文件。

（2）利用计算机对上面的数据进行排序；（3）以组距为10进行等距分组，整理成频数分布表，并绘制直方图。

统计学实验作业

统计学实训综合实验报告

统计学作业

统计学例题作业

实验统计学实验(仅供参考)

统计学作业

统计学实验作业

统计学实验

统计学四篇实验报告

统计学实验报告及答案

统计学大作业调查实验报告

统计学上机实验题目

统计学实验报告作业

统计学实验大作业

《统计学》上机实验例题(一)

统计学实验作业

统计实验作业

统计学实验报告

统计学大作业

统计学实验一 作业1

spss统计学第一次实验作业答案

统计学实验一作业1