第0章-弹性力学、变分原理与有限元法2014
弹性力学边值问题及有限元法(PPT)
（3）在边界上部分给定面力，部分给定位移——混合边界条件
基本解法
弹性力学边值问题——基本方程+边界条件
给定作用在物体全部边界或内部的外界作用(包括温度影响、 外力等)，求解物体内由此产生的应力场和位移场。
具体地说，对物体内每一点，当它处在弹性阶段，其应力分 量、应变分量、位移分量等15个未知函数要满足平衡方程、几 何力程、本构方程这15个泛定方程，在边界上并要满足给定的 全部边界条件。
通过与原问题基本方程及边界条件等效的变分原理，建立求 解的代数方程组，求解有限个节点上的场变量值
用有限个节点场变量值插值得到全求解域任意位置的场变量
单元内近似函程形式必须一样 单元内近似函数一般取Lagrange多项式
单元位移函数
对三角形单元，假定单元内的位移分量是坐标的线性函数
x
x
xy
y
xz
z
Fbx
0
yx
x
y
y
yz
z
Fby
0
zx
x
zy
y
z
z
Fbz
0
平衡方程的意义
受力而平衡的弹性体内 各应力之间（及其与体 力之间）的相互制约关 系
几何方程
x
u x
y
v y
z
w z
xy
u y
v x
xy
v z
w y
xy
w x
u z
应变与位移之间的关系， 以及应变之间的关系
物理方程
也叫本构方程
应力应变之间的关系
x
E(1 ) (1 )(1 2)
( x
1
y
弹性力学的广义变分原理
弹性力学的广义变分原理摘要：研究了在弹性力学的三类变量广义变分原理中，变量三个变量是否独立，是否包含了应力应变关系。
指出了在应用广义变分原理时应满足下列条件：泛函中的应变能用应变表示、应变余能用应力表示：在用广义变分原理求实际问题的近似解时。
三类变量的试探函数可以独立选择，但各类变量之间应不违背力学基本关系。
为了解除应力应变关系的变分约束，我们提出了一个高阶拉格朗日乘子法。
用这个高阶拉氏乘子法，我们从胡鹭原理和海赖原理分别导出了前所未知的更普遍的广义变分原理。
我们也证明了在这两类变分原理之间，有等价定理和相关的等价关系存在。
关键词：弹性力学；广义变分原理前言：弹性力学广义变分原理是弹性力学最小势能原理和弹性力学最小余能原理的推广，其特点是，变分式中各量都可有独立的变分，并且事前不受任何限制。
1.广义变分原理Ⅰ1.1广义函数及其构造。
弹性力学最小势能原理和弹性力学最小余能原理的推广，其特点是，变分式中各量都可有独立的变分，并且事前不受任何限制。
在弹性力学空间问题中，最一般的广义变分原理可叙述为：弹性力学空间问题的解必须满足弹性体的广义势能变分为零的条件，该条件又称为驻值条件，即方程，包括应变-位移关系，应力-应变关系、平衡方程和边界条件。
上述变分原理的独立变量有位移、应变、应力三类，因此称为三类变量广义变分原理。
它是中国力学家胡海昌于1954年首先提出的，日本的鹫津久一郎于1955年也独立地得到这一原理，所以又称胡-鹫津原理。
弹性力学广义变分原理有一种稍弱的形式，即二类变量广义变分原理，又称为赫林格-瑞斯纳原理。
它由E．赫林格于1914年和E．瑞斯纳于1950年分别独立提出，其数学表达式为：在有限元法和工程弹性理论中，广义变分原理有广泛的应用。
例如，在板壳弯曲的有限元计算中，用它处理变形的不协调性，可得到较好的结果。
对于解决几何非线性问题，胡-鹫津原理是一个有力的工具。
在工程弹性理论中，广义变分原理可用于推导各种近似理论；在弹性振动和稳定理论中，可用于求固有频率和临界载荷，并能获得较好的结果。
有限元基本理论
2、虚应力原理
第1章 预备知识
1.4.4 线弹性力学的变分原理
1、最小位能原理
第1章 预备知识
设：
第1章 预备知识
2、最小余能原理
第1章 预备知识
第1章 预备知识
第2章 弹性力学有限元
2.1 平面问题3结点三角形单元
第2章 弹性力学有限元
2.1.1 单元位移模式及插值函数
第2章 弹性力学有限元
取：
则：
2.3.3 3结点环状单元的等效结点荷载
第2章 弹性力学有限元
例：计算3结点环状单元自重荷载
由面积坐标
第2章 弹性力学有限元
积分
则：
2.4 空间问题有限元
2.4.1 4结点四面体单元
第2章 弹性力学有限元
1、位移函数
第2章 弹性力学有限元
其中：
代入结点坐标得：
有限元基本理论
目 录
第1章 预备知识 第2章 弹性力学有限元 第3章 单元插值函数的构造 第4章 杆件结构力学问题 第5章 平板弯曲问题 第6章 应用中的若干问题 第7章 材料非线性问题
第1章 预备知识
1.1 引言
数值分析方法
有限差分法
微分方程近似解法
有限单元法
几何形状规则
几何形状规则
则两项近似解为：
力矩法
一项近似解，取W1=1（0≤x≤1）
则一项近似解为：
由
第1章 预备知识
两项近似解，取W1=1，W2=x
由
则两项近似解为：
伽辽金法
第1章 预备知识
一项近似解，取W1= N1 = x(1-x)
由
则一项近似解为：
两项近似解，取W1= N1= x(1-x) ，W2= N2 = x2(1-x)
(同济大学)第1讲_弹性力学及有限元方法概述
有限元分析
的一般规律物体在空间的位置随时间的改变
对象内容
任务
对象内容
任务
概述
ANSYS 静力分析z起重机械有限元应用
整机模态分析
车辆安全性
工件淬火3.06 min 时的温度、组织分布(NSHT3D)
同济大学
同济大学
金属反挤压成型：温度分布和变化铸造成型：温度变化和气泡
速度
压力导流管分析
超音速飞行压力分布汽车气动分析
高速导弹气动
同济大学
两根热膨胀系数不同的棒焊接在一起，加热后的变形情况
子结构方法分析大型结构的早期应用法
梁单元
建模时充分利用重复性。
有限元法的基本原理
第二章有限单元法的基本原理作为一种比较成熟的数值计算方法，有限元的数学基础是变分原理。
经过半个过世纪的发展，它的数学基础已经比较完善。
从数学角度分析，有限元法是以变分原理和剖分插值为基础的数值计算方法。
它广泛的应用于解算各种类型的偏微分方程，特别对椭圆型方程，因为椭圆型方程的边值问题等价于适当的变分问题，即能量积分的级值问题。
通过变分，导出相应的泛涵，再把作用域从几何上剖分为足够小的单元，这样就能够用简单的图形去拟合复杂的边界，用简单的初等函数去模拟单元的性质。
在解算中先对每个单元进行分析，后在通过连接单元的节点对作用域的整体进行分析，就是对泛涵求极值，从而把一个复杂的偏微分方程求解问题，变成解线形代数方程组的问题。
尽管这样会出现大量的未知数，由于采用了矩阵分析的方法，总体上很有规律，适合编制程序用计算机完成。
通常的数学考虑包括这些：1）从古典变分方法原理去定义微分方程边值问题的广义解以及在古典变分方法的框架对有限元进行理论分析。
2）保证偏微分方程边值问题的提法正确，即要求解存在、唯一和稳定，即保证数值解法是可靠的。
3）有限元中重要的一点是采用了分块多项式插值函数，因此，有限元的误差估计转化为插值逼近的误差估计问题。
4）有限元的收敛性和误差估计。
由于本文是应用有限元的理论解决大地测量中的问题，因此，这里将不讨论上叙问题，而是从固体力学的基本方程出发，通过虚功原理建立起离散化的有限元方程。
另外，还以八节点六面体单元为例，简要叙述了实际中最常用的等参单元的概念及其数值变化的一些公式。
§2.1 弹性力学基本方程有限元法中经常要用到弹性力学的基本方程，这里写出这些方程的矩阵表达式。
2-1-1、平衡方程对任意一点的受力情况分析，沿坐标轴方向x, y ,z分解得到平衡方程0*00000000=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎣⎡∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂z y xxz yz xy z y x F F F z yzz x y z y x τττσσσ 记为： 0=+F A σ其中A 是微分算子，F 是体积力向量。
弹性力学的变分法
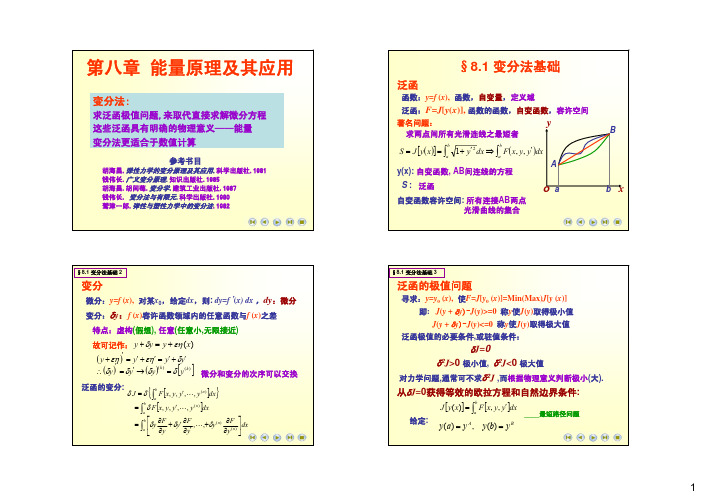
F (i) j
=
0
j=1 i=1
i =1
n：质点总数，mj：第j个质点上作用的外力的数量
虚位移原理与牛顿定理完全等价
质点系→弹性体
§8.2 虚位移原理、总位能最小原理3
证明充分性:
∫∫∫ − σ ijδε ij dV + ∫∫∫ X iδui dV ∫∫ + X Viδui dΣ = 0
Ω
Ω
Σ
∫∫∫ ∫∫∫ ∫∫∫ ( ) ∫∫∫ σ ijδε ij dV = σ ijδui, j dV =
S : 泛函
自变函数容许空间: 所有连接AB两点 光滑曲线的集合
oa
B
bx
§8.1 变分法基础 3
泛函的极值问题
寻求：y=y0 (x), 使F=J[y0 (x)]=Min(Max)J[y (x)] 即: J(y + δy)-J(y)>=0 称y使J(y)取得极小值 J(y + δy)-J(y)<=0 称y使J(y)取得极大值
∴
⎧δ ⎩⎨δ
X X
i Vi
=0 =0
Q
⎪⎧σ ⎪⎩⎨σ
ij ij
,j
n
+ Xi j−X
=
Vi
0 =
0
∴
⎪⎧δσ ⎪⎩⎨δσ
ij ij
,j
n
=0 j =0
引入本构关系，对于上述满足平衡方程的应变状态，显然：
δX i = 0, 但 δXVi ≠ 0 即δσij引入约束反力δXvi
虚应力原理可写作：
∫∫∫ − δσ ijε ij (σ )dV + ∫∫ δX Vi (σ )uidΣ = 0
U* U
第3讲—弹性力学问题的有限单元法
1 T U d Kd 2
u1 d u 2 u 3
有限单元法
崔向阳
Step 3: 单元集成
单元集成——外力功
整体节点 位移列阵
整体等效节 点力列阵
u1 d u2 u 3
f1 R1 f f 2 0 f F 3
有限单元法
崔向阳
Step 2.单元特征分析
xi
单元节点位移列阵： 单元节点坐标列阵： 单元等效节点力列阵：
II＝0
有限单元法 崔向阳
真实位移
6
最小势能原理
1 II ij ij dV bi ui dV pi ui dA 2 Sp 1 II Dijkl ij kl dV bi ui dV pi ui dA Sp 2
ij
ij
dV biui dV piui dA
Sp
弹性问题中等价于最小势能原理！
有限单元法 崔向阳
比较：虚功原理和能量变分原理
虚功原理是理论力学上的一个根本性原理，可以用于
一切非线性力学问题。
最小势能原理只是虚功原理对弹性体导出的一种表述
形式，但是对于线弹性问题，最小势能原理的应用非 常方便。
ij ui ij ui Dijkl ij kl dV bi ui dV pi ui dA Sp ij ij dV bi ui dV pi ui dA Sp
V= – W
弹性势能—弹性体变形后，产生弹性内力，这种力也具有对外作 功的能力，称为弹性势能，或弹性应变能。
弹性力学与有限元法1ppt课件
➢ 瞬态分析 确定以时间为函数的温度等。 可模拟相变（融化及凝固）。
熨斗的瞬态热分析
28
本课程涉及到的高等数学及线性代数知识
1、泰勒级数
如果函数 f(x) 在点x0的某邻域内具有各阶导数 f ' (x), f '' (x),L , f (n) (x),L ，则可以将 f(x) 按照 泰勒级数展开为
应力种类
一次局部薄膜应 力
薄膜加弯曲应力
应力水平/MPa 限制值/MPa
41.12
167×1.5＝250.5
73.81
167×3.0＝511
评定结果 通过 通过
路径2
一次局部薄膜应 力
薄膜加弯曲应力
48.43 163.5
167×1.5＝250.5 167×3.0＝511
通过 通过
路径3
一次局部薄膜应 力
个坐标轴上的投影u、v、w来表示。以沿坐
标轴正方向的为正，沿坐标轴负方向的为负。
B
y
40
第一章 绪论
弹性力学的基本方法
从取微元体入手，综合考虑静力（或运动）、几 何、物理三方面条件，得出其基本微分方程，再进行求 解，最后利用边界条件确定解中的常数。
按照方程中保留的未知量，求解方法可分为 应力法（以应力为未知量） 位移法（以位移为未知量） 混合法（同时以应力和位移为未知量）
zy x
b
xxyz zx
yz
y yx
B
o
A PA dx, PBz dy, PC dz y
x
同样，可以列出另两个力矩平衡方程。得出
yz zy , zx xz , xy yx
38
第一章 绪论
弹性力学总结与复习全文
4
2 r 2
1 r
r
1 r2
2
2
2
0
（2） 由式（4－5）求出相应的应力分量： r , , r
（4－6）
r
1 r
r
1 r2
2 2
2
r 2
r
r
1 r
（4－5）
（3） 将上述应力分量 r , , r 满足问题的边界条件：
位移边界条件： ur s ur , u s u 应力边界条件： l r s m r s kr （位移单值条件） l r s m s k
y
叠加法的应用
第七章 平面问题的差分解
（1）了解差分法的基本思想； （2）了解应力函数差分解中，应力分量的差分公式；应力函数
Q分别为梁截面上弯矩与剪力。
结合应力分量与应力函数的关系确定 应力函数：
2
r 2
f (r) f (r)sin f (r) cos
4. 半平面问题 P
O
y
r
rf ( ) x
q
O
r
y
r2 f ( )
M O
y
r
( ) x
q(x)
O
x
x
r
q aa
y r3 f ( )
O
x
r
y 0
y f ( y)
y xf ( y)
O
x
O
b
x
xl
g
gy
y
y 0
习题：3 -1，3 –2，3 –3，3 -4
g
y
(x, y)
ax3 bx2 y cxy2 dy3
第四章 平面问题的极坐标解答
（1）极坐标解答适用的问题结构的几何形状？ （圆环、圆筒、圆弧形曲杆、楔形体、半无限平面体等）
总结材料力学、弹性力学、有限元三门课程解决问题的思路和步骤,指出其异同点
总结材料力学、弹性力学、有限元三门课程解决问题的思路和步骤，指出其异同点航天航空学院1334班艾松学号：4113006012杆件在多种外力共同作用下的变形(或力)，可先分别求出各外力单独作用下杆件的变形(或力)，然后将这些变形（或力）叠加，从而得到最终结果。
②几何非线性问题。
若杆件变形较大，就不能在原有几何形状的基础上分析力的平衡，而应在变形后的几何形状的基础上进行分析。
这样，力和变形之间就会出现非线性关系，这类问题称为几何非线性问题。
③物理非线性问题。
在这类问题中，材料的变形和力之间（如应变和应力之间）不满足线性关系，即材料不服从胡克定律。
在几何非线性问题和物理非线性问题中，叠加原理失效。
解决这类问题可利用卡氏第一定理、克罗蒂－恩盖塞定理或采用单位载荷法解。
直角坐标系下的弹性力学的基本方程为：平衡微分方程（1）几何方程（2）物理方程（3）(1)式中的σx、σy、σz、τyz=τzy、τxz=τzx、τxy=τyx为应力分量，X、Y、函数的插值点，将微分方程中的变量改写成由各变量或其导数的节点值与所选用的插值函数组成的线性表达式，借助于变分原理或加权余量法，将微分方程离散求解。
采用不同的权函数和插值函数形式，便构成不同的有限元方法。
有限元方法最早应用于结构力学，后来随着计算机的发展慢慢用于流体力学的数值模拟。
在有限元方法中，把计算域离散剖分为有限个互不重叠且相互连接的单元，在每个单元选择基函数，用单元基函数的线形组合来逼近单元中的真解，整个计算域上总体的基函数可以看为由每个单二、变形及刚度条件 拉压：∑⎰===∆LEAxx N EAL N EANLL d )(ii 扭转：()⎰=∑==Φpp i i p GI dx x T GI L T GI TLπφ0180⋅=Φ=p GI T L弯曲：(1)积分法：)()(''x M x EIy =C x x M x EI x EIy +==⎰d )()()('θD Cx x x x M x EIy ++=⎰⎰d ]d )([)((2)叠加法：()21,P P f …=()()21P f P f ++…()21,P P θ=()()++21P P θθ…三、应力状态与强度理论 二向应力状态斜截面应力：ατασσσσσα2sin 2cos 22xy yx yx --++=ατασστα2cos 2sin 2xy yx +-=二向应力状态极值正应力及所在截面方位角：到。
有限元法和变分原理
带入试函数：
2 2 ⎧⎛ ⎫ ∂ψ i ⎞ ⎛ ∂ψ i ⎞ ⎪ ⎪ ∏(φ ) = ∫∫ ⎨⎜ ∑ Ci + ⎜ ∑ Ci − 2∑ Ciψ i f ⎬ dxdy ⎟ ⎟ ∂x ⎠ ⎝ ∂y ⎠ ⎪⎝ ⎪ ⎩ ⎭
⎧⎛ ∂ψ ⎞2 ⎛ ∂ψ ⎞2 ⎫ ⎪ ⎪ = ∑ Ci 2 ∫∫ ⎨⎜ i ⎟ + ⎜ i ⎟ ⎬ dxdy ⎪⎝ ∂x ⎠ ⎝ ∂y ⎠ ⎪ ⎩ ⎭ ⎛ ∂ψ i ∂ψ j ∂ψ i ∂ψ j +2∑ CiC j ∫∫ ⎜ + ∂y ∂y i≠ j ⎝ ∂x ∂x
第二章 连续体问题的离散化方法
1
应力场、温度场、电磁场等
数学
偏微分方程或微分方程＋边条 件＋初始条件，即边值问题
等价（若存在对应的泛函）
变分法（泛函求极值）
经典变分法 （整个求解域）
有限元法 （把求解域离散 许多子区域）
2
要点
微分方程的等效积分形式 加权余值法 变分原理和里兹法 有限元法 弹性力学变分原理
9
(3) 最小二乘法：
⎧ ∂ ⎫ ⎪ ⎪ {w j } = ⎨ ∂a A ( Na ) ⎬ ⎪ j ⎪ ⎩ ⎭ ∂ ⎡ A Na 等价于 ⎢ ∫Ω ( ) ∂a j ⎣
{
} {A ( Na )}d Ω⎤ = 0 ⎥ ⎦
弹性力学的变分原理
(
f y '
)
0
f
y '
xa 0
f y '
xb 0
( •)
（•）称为自然边界条件
自变函数事先满足旳边界条件称为本质边 界条件。 实例
本章学习要点：建立力学概念
本章包括了非常多旳力学概念，这些概念是有限 元及其他力学分支中普遍用到旳，需对其内涵有 一定了解
公式推导较多、较繁，但
公式旳推导、证明过程了解思绪即可
注意到：
( y) y(x) y(x)
与(*)式比较，可见：
( y) (y)'
即：
（ddyx） ddx（y）
结论：导数旳变分等于变分旳导数，或变分
记号与求导记号能够互换。
三、泛函旳变分
一般情况下，泛函可写为：
b
I a f (x, y, y)dx
1、按照泰勒级数展开法则，被积函数 f 旳增 量能够写成
vε vc ijij
对于线弹性体
vε
vc
1 2
ijij
允 许 位 移
允 许 应 变
允 许 应 力
虚 位 移
虚 应 变
虚 应 力
§11-3 广义虚功原理
虚
虚
功
位
应
互
移
力
等
原
原
原
理
理
理
§11-3 广义虚功原理
一、真实位移、真实应力和真实应变
ui 真实位移，满足：
ij
1 2
(ui,
j
u j,i )
j
u
k j ,i
)
uik ui
x V x Su
k ij
弹性力学变分原理培训课件
弹性力学的基本方程
描述物体的物理性质与外 力的关系。
描述物体在变形过程中形 状的变化。
描述物体在力系作用下的 平衡状态。
平衡方程
几何方程
物理方程
02
变分原理概述
变分法的概念
最小作用量原理
在给定的约束条件下，物理系统的真实运动是使得作用量取极值的路径。
极值条件
在最小作用量原理中，物理系统的真实运动应满足欧拉方程和边界条件。
泛函与变分问题
泛函
泛函是一个函数，其值是另一个函数 在某个特定点上的值。
变分问题
变分问题是指求泛函的极值问题，即 在给定约束条件下，求泛函的极值。
欧拉方程与极值条件
欧拉方程
欧拉方程是变分问题的基本方程，它 描述了物理系统的运动规律。
极值条件
在求解欧拉方程时，需要满足极值条 件，即物理系统的运动应使得泛函取 极值。
实例解析
以有限元软件ANSYS为例，介绍如何使用有限元方法对弹 性问题进行建模、分析和求解。通过具体的实例操作，展 示如何将实际问题转化为有限元模型，并进行求解得到结 构的位移和应力分布。
THANKS
感谢观看
弹性力学变分原理培训课 件
• 弹性力学基础 • 变分原理概述 • 弹性力学中的变分原理 • 变分原理的应用 • 弹性力学变分原理的实例解析
01
弹性力学基础
弹性力学简介
弹性力学
一门研究弹性物体在外力作用下变形和内力的 学科。
弹性力学的重要性
为工程结构的设计、分析和优化提供理论基础。
弹性力学的发展历程
04
变分原理的应用
弹性力学问题的变分形式
弹性力学中的应力、应变和位移等物理量可以通过变分原理转换为对应的泛函极值 问题。
弹性直梁问题的变分原理及有限元素法
第二章弹性直梁问题的变分原理及有限元素法讨论的问题：一变剖面的梁，一端 （x =0 ）固支，另一端（x = l ）简支。
承受轴向拉 在 x= l 处：w = W |称谓：把满足方程及全部边界条件的挠度叫真实挠度，精确解；把满足基本边界条 件但不满足微分方程和自然边界条件的挠度叫（变形）可能挠度。
i ） 最小势能原理（变分原理）把载荷看作是不变的已知函数， 整个系统的势能包括三部分:（1）梁的应变能：f . 2 ¥d w—r I dx I dx 丿（3）横向载荷势能:力N ，分布横向载荷q （x ）以及端点弯矩M i 的作用。
4J控制微分方程及边界条件（以梁的挠度 w 表示）叮 EjdV dx 2 Idx 2丿.2M d w -Ny^q udx 2丿=q在x= 0处：w = w 0,也 dxN o＞基本边界条件（广义固支）.2d w — -EJ —- M | dx自然边界条件（M + M i ） = O21 l □厂Jo EJ（2）轴向应变能:□N1 i rON 2w \dx、2dxdxgs 气㈣+1十丄dx Vl dx 丿2把挠度看作是可变的自变函数。
I w+dwOT 11(w ^^f lf EJ d 2wd^w.dx 2 dx 2 +N 叢詈-计严+恥心在 X =0处，人w=0, i w ' = 0 在X =丨处，A w = 0与W k 相应的总势能:=口(w k )= n(w + A w )= ri(w )+z n 11(w, A w )中n 2(A w )其中:Ij P = —[qwdx +M |W '(I )后项取加号，是为着能够得到自然边界条件的结果⑷系统总势能口:n/g EJ(d 2w )2 1 X 厂㊁々w V一——I-qw>dx + M i w '(l )I dx 丿*除w 为可变外，其余变量假定为已知的不变量。
最小势能原理：在所有变形可能的挠度中，精确解使系统的总势能取最小值 。
第0章-弹性力学、变分原理与有限元法2014
1 1 E 2 2 2
PS
PC
（如 x 轴沿杆轴向：可记
1 x x ） 2
B
4. 一般三维均质弹性体
z
M x, y , z
0
y
x
弹性体 中任一点 M x, y, z 处有微元体 B
x, y, z
UB U lim B VB VB 0 VB
0
0 x 0 y , 1 xy 2
x 1 1 y E 0 xy
1 0
x 0 y 21 xy 0
弹性力学平衡问题 微分方程边值问题（15 个方程求解 15 个未知量，在 u ， ） 解法： （1）位移法； （2）应力法； （3）混合法 弹性力学位移法定解问题：物体表面 u 取未知函数 u ，经变换
: E DE T u f 0
: u : u u ； : P E ν DE T u
为梯度矢
ε E T u
（几何线性）
在单连通域中： ε u 一一对应，但多连通域中未必一一对应
§0.2 应力分析（Stress Analysis）
取 P 点处一微平行六面体与 xyz 平行，决定 P 点应力状态的 6 个分量为
σ x
y z yz zx xy T
3
体力（外力, N m ） ： f fx
fy
fz
T
一、平衡方程： （由微六面体平衡所致）
x xy xz fx 0 y z x y xy yz fy 0 x z y yz z xz fz 0 x y z
弹性力学弹性力学的变分原理
静力可能的应力 弹性体的功能关系 功的互等定理 弹性体的总势能 虚应力 应变余能函数 应力变分方程 最小余能原理的近似解法 扭转问题最小余能近似解 有限元原理与变分原理 有限元原理的基本概念 有限元整体分析 第十一章 弹性力学的变分原理几何可能的位移虚位移虚功原理最小势能原理瑞利-里茨 (Rayleigh-Ritz) 法 伽辽金(『anQpKUH )法 最小余能原理 平面问题最小余能近似解 基于最小势能原理的近似计算方法 基于最小余能原理的近似计算方法 有限元单元分析一、内容介绍由于偏微分方程边值问题的求解在数学上的困难，因此对于弹性力学问题， 只能采用半逆解方法得到个别问题解答。
一般问题的求解是十分困难的， 甚至是 不可能的。
因此，开发弹性力学的数值或者近似解法就具有极为重要的作用。
变分原理就是一种最有成效的近似解法，就其本质而言，是把弹性力学的基 本方程的定解问题， 转换为求解泛函的极值或者驻值问题， 这样就将基本方程由 偏微分方程的边值问题转换为线性代数方程组。
变分原理不仅是弹性力学近似解 法的基础，而且也是数值计算方法，例如有限元方法等的理论基础。
本章将系统地介绍最小势能原理和最小余能原理， 并且应用变分原理求解弹 性力学问题。
最后，将介绍有限元方法的基本概念。
本章内容要求学习变分法数学基础知识，如果你没有学过上述课程，请学习 附录3或者查阅参考资料。
知识点、重点1几何可能的位移和静力可能的应力；2、弹性体的虚功原理；3、最小势能原理及其应用；4、最小余能原理及其应用；5、有限元原理的基本概念。
§11.1弹性变形体的功能原理学习思路：本节讨论弹性体的功能原理。
能量原理为弹性力学开拓了新的求解思路，使得基本方程由数学上求解困难的偏微分方程边值问题转化为代数方程组。
而功能关系是能量原理的基础。
首先建立静力可能的应力「：，和几何可能的位移’概念；静力可能的应力和几何可能的位移；可以是同一弹性体中的两种不同的受力状态和变形状态，二者彼此独立而且无任何关系。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
引入算子
x E 0 0
其中 i
0 y 0
0 0 z
0 z y
z 0 x
y x 0
j k ( x y z x
y
T ) z
定义：单位体积中具有的应变能称为（应变）比能，记为 对杆：
U P d d V 0A L 0
上式适用于非线性应力应变关系。特别： P , 即 为线性关系（Hooke 定律）
E
（5-6） (与路径无关) （5-7）
E d
x, y, z
因此， 为一般坐标 M x, y, z 的场函数，又应力、应变也是坐标 M x, y, z 的场函数。
8
空间问题均质弹性体的应力和应变张量 σ x, y , z ， ε x, y, z 分别为六个独立分量函数：
σ ( x, y, z ) x y z yz zx xy ( x, y , z ) ε ( x, y, z ) x
x 1 y E z
1 1 0 0
0 x 0 y 2 xy
§0.5 弹性力学变分原理（Variational Principle of Elastic Mechanics） 一、弹性体的形变势能
T
y z yz zx xy ( x, y , z )
T
如何计算三维弹性体的应变比能 ？先通过事例介绍二维弹性体的应变比能计算。 例题 4-1：受轴向力的线弹性直杆，见前图。应变比能有
A 1 F外力 dr F 弹力 dr k 02 2 A0 A0 2 A
3. 弹性杆的形变势能（应变能） 例：A 为杆截面积，L——杆长
6
P L
P
(N / m ) 合力记为N , 则N P
2
P
P 1
一般为非线性关系
0
d
1
w Pd
材料试件单向拉伸 P 曲线
V
注： w 0
k 2 02 （外力功） 2 1 k 02 2 （弹性力的功） 2
(5-3)
特别：以弹簧的自然位置为零势点，则弹性能
V
外力的功） 弹性能=外力做功
V
1 2 k 2
其中矩阵
Py
Pz
Px
l 0 0 0 n m E ν 0 m 0 n 0 l 0 0 n m l 0
§0.3 本构方程（应力、应变关系）Relation of Stress and Strain
对均质各向同性线弹性体有广义 Hooke 定律
σ Dε ,
对平面应力问题有
z 0, z
x y , kk x y , xy u x u y E y x
4
应力应变关系：
x E y 2 1 xy
1 0
1
3
体力（外力, N m ） ： f fx
fy
fz
T
一、平衡方程： （由微六面体平衡所致）
x xy xz fx 0 y z x y xy yz fy 0 x z y yz z xz fz 0 x y z
§0.4 弹性力学平衡问题的微分方程提法
方程（15 个） 边界条件 未知函数（15 个） 类型 静力平衡
E σ f 0
P E ν σ (应力型，
自由边， )
σ
ε E T u
σ Dε
或 ε D 1σ
u u（位移型，u ）
ε，u
几何连续性 物理性
P x, y , z
x
z
1
二、应变：P 点处在 xyz 轴的三个微段的变化，得到变状态的 6 个分量
ε x
y
z
yz
zx
xy T
几何方程（6 个） ：位移、应变之关系
x
v w v u v u w u w ， y ， z ， yz ， xz ， xy x y z y z z x y x
0
1 1 E 2 2 2
PS
PC
（如 x 轴沿杆轴向：可记
1 x x ） 2
B
4. 一般三维均质弹性体
z
M x, y , z
0
y
x
弹性体 中任一点 M x, y, z 处有微元体 B
x, y, z
UB U lim B VB VB 0 VB
由上解出 （位移表示的应力边界条件）
uε σ。
1 1 fx 0 1 2 x G 1 1 2v fy 0 1 2 y G 1 1 2w fz 0 1 2 z G 2u
显式：
式中
u v w 2 2 2 2 ， ， u， x y z x 2 y 2 z 2
0
0 x 0 y , 1 xy 2
x 1 1 y E 0 xy
1 0
x 0 y 21 xy 0
对平面应变问题有
z 0, z x y
1 1 2 x E y 1 1 xy 0
1 2 1 1 2
0
0 x 0 y ； 1 xy 2
第0章
弹性力学基本方程
弹性力学的任务：寻求弹性体在外力作用下，物体的变形、内力分布规律 外力 变形(位移)、内力（应力）
§0.1 应变分析（Strain Analysis）
取笛卡尔坐标轴 oxyz，对空间上任一点处的任一方向用矢量 表示 其单位方向矢量为 ν li mj nk
1 0 0 0
0 0 0 0 0 0 0 0 0 21 0 0 0 21 0 0 0 21
3
物理量： ——Lame 常数，G——剪切模量，E——弹性模量， ——泊松比
G
E E , 1 1 2 21
引子： 1. 弹性力做功 一弹簧支于 O 点，弹簧原长为 l0 ，见 图 5-1。在受外力 P 作用，其弹簧（性）力
F k r l0 er k r l0
r r
（5-1）
式中 k —弹簧刚度系数 N/m ，N/mm 。弹性力大小 F k ，方向 er r / r ，r 表示 OA ，
A2
(5-2)
性质：
1 弹性力做功： w12 仅与弹簧初、末变形量 1 、 2 有关，与路径无关； 2 w12 可正、可否；
1 1 3 特别 1 0 时， w12 k 22 ，注：外力做功 w w12 k 22 。 2 2
2. 弹性力场中的势能：弹簧力做功的负值 以变形量为 0 处为势能零点，则在 处，弹簧力的势能 V 为
弹性力学平衡问题 微分方程边值问题（15 个方程求解 15 个未知量，在 u ， ） 解法： （1）位移法； （2）应力法； （3）混合法 弹性力学位移法定解问题：物体表面 u 取未知函数 u ，经变换
: E DE T u f 0
: u : u u ； : P E ν DE T u
ε D 1σ
物理线性
D 称为弹性矩阵
1 1 E 1 1 D 1 1 2 0 0 0
1
1
1 1
1 0 0 0
0 0 0 1 2 21 0 0
0 0 0 0 1 2 21 0
1
0 0 0
0 0 0 0 1 2 21 0
D 1
1 1 E 0 0 0
1 0 0 0
为梯度矢
ε E T u
（几何线性）
在单连通域中： ε u 一一对应，但多连通域中未必一一对应
§0.2 应力分析（Stress Analysis）
取 P 点处一微平行六面体与 xyz 平行，决定 P 点应力状态的 6 个分量为
σ x
y z yz zx xy T
弹性杆在轴向力 P 作用下，产生均匀的轴向应力 ，轴向应变
N A,
L
(5-4)
假定：弹性体在受力的过程中始终保持平衡 外力 P 做功:
w Pd
0
（5-5）
外力功 w 以弹性应变能储存于杆中。 杆的应变能 U 等于外力功 W （例：射箭）
U W Pd
0
7
《有限元法》课程讲稿
合肥工业大学土木与水利学院工程力学系
牛忠荣
1987-2011 年制作, 2014 年 2 月新修改
参考书：
1. 王元汉、李丽娟、李银平《有限元法基础与程序设计》 ，华南理工大学出版社，2002 年， 第一版 2. 王勖成，邵敏《有限单元法基本原理和数值方法》 ，清华大学出版社，1997 年，第二版 3. 何福保,丁皓江编《弹性和塑性力学中的有限单元法》 ，机械工业出版社， 1989-年，第 二版 4.