中考数学专题知识梳理:尺规作图、视图与投影、空间图形、圆
2011年中考考点复习策略(4)——“尺规作图、视图与投影”

2011年中考考点复习策略(4)——“尺规作图、视图与投影”“视图”以“视”的基础上的“对应”为特征,建立起三维(空间)的基本几何体及简单物体与二维(平面)图形表示方法间的对应关系如:几何体与展开图之间的关系;“投影”以画图和相关的计算为特征,研究光线下实物与其影子的对应关系。
视图与投影可以视为研究同一问题的两种策略。
通过了解近几年各地中考试题和中考课外复习资料,这一类的知识点例析、习题甚少,考查的分值不多,从而常常也会被疏忽,但这类题型考查学生的操作能力和空间想象能力,属于易得分题目。
考试中我们不能采用模型实验操作,更不想浪费太多时间思考。
因此我们就必须在复习中理解、归纳其规律,掌握注意要点就显得非常重要了。
一、“尺规作图、视图与投影”的中考内容要求1.会作基本作图:作一条线段等于已知线段,作一个角等于已知角,作角的平分线,作线段的垂直平分线,利用基本作图作三角形。
2.会画基本几何体的三视图,判断简单物体的三视图,了解几何体的侧面展开图,几何体与其三视图、展开图之间的关系,视点、视角在简单的平面和立体图中表示。
二、“尺规作图、视图与投影”的考点特点1. 试卷中一般以操作探究的形式对这部分知识进行重点考查;2.试题类型主要以三视图、展开与折叠和有实际背景的平行投影、中心投影作为问题情景,重点考查空间观念的掌握情况.三、典型试题分析(一)理解几何体与展开图的关系1、从展开图中找相对面之间的关系例1.(2010年福建省德化县中考题)如图1,是正方体的展开图, 则原正方体相对两个面上的数字和最小的是( ).A. 4B. 6C. 7D.8分析:面2与面6相对间隔着面5,面3与面4相对间隔着单面一排面2、5、6,面1与面5相对间隔着单面一排面2、4,因此,面2与面6,面3与面4,面1与面5是对面。
所以面1与面5的数字和为6是最小的。
故答案选B点评:正方体的任何一个面都会和4个面相邻和唯一个面相对,对面的中间总是相间隔着一个面或单面一排。
考点25 视图与投影 、尺规作图 、命题(精讲)(解析版)

考点25.视图与投影、尺规作图、命题(精讲)【命题趋势】本专题以考查几何体的三视图和正方体的展开图、尺规作图和真假命题为主,年年都会考查,是广大考生的得分点,分值为10分左右,预计2024年各地中考还将出现,视图与投影和命题在选填题出现的可能性较大,一般只考查基础应用,所以考生在复习时要多注重该考点的概念以及应用.而尺规作图的考查涉及多种形式,不再是单一的对作图技法操作进行考查,而是把作图与计算、证明、分析、判断等数学思维活动有效融合,既体现了动手实践的数学思维活动,也考查了学生运用数学思考解决问题的能力。
【知识清单】1:图形的投影(☆☆)1)投影:在光线的照射下,空间中的物体落在平面内的影子能够反映出该物体的形状和大小,这种现象叫做投影现象.影子所在的平面称为投影面。
2)平行投影、中心投影、正投影(1)中心投影:在点光源下形成的物体的投影叫做中心投影,点光源叫做投影中心。
(2)平行投影:投射线相互平行的投影称为平行投影。
(3)正投影:投射线与投影面垂直时的平行投影,叫做正投影。
2:几何体的三视图(☆☆☆)1)视图:由于可以用视线代替投影线,所以物体的正投影通常也称为物体的视图。
2)三视图:(1)主视图:从正面看得到的视图叫做主视图;(2)左视图:从左面看得到的视图叫做左视图;(3)俯视图:从上面看得到的视图叫做俯视图。
3)三视图的画法(1)画三视图要注意三要素:主视图与俯视图长度相等;主视图与左视图高度相等;左视图与俯视图宽度相等.简记为“主俯长对正,主左高平齐,左俯宽相等”。
(2)注意实线与虚线的区别:能看到的线用实线,看不到的线用虚线。
4)常见几何体的展开图几何体立体图形表面展开图侧面展开图圆柱圆锥三棱柱5)正方体的展开图正方体有11种展开图,分为四类:第一类,中间四连方,两侧各有一个,共6种,如下图:第二类,中间三连方,两侧各有一、二个,共3种,如下图:第三类,中间二连方,两侧各有二个,只有1种,如图10;第四类,两排各有三个,也只有1种,如图11。
2024年中考数学考点必备知识必备10 视图与投影、尺规作图(原卷版)
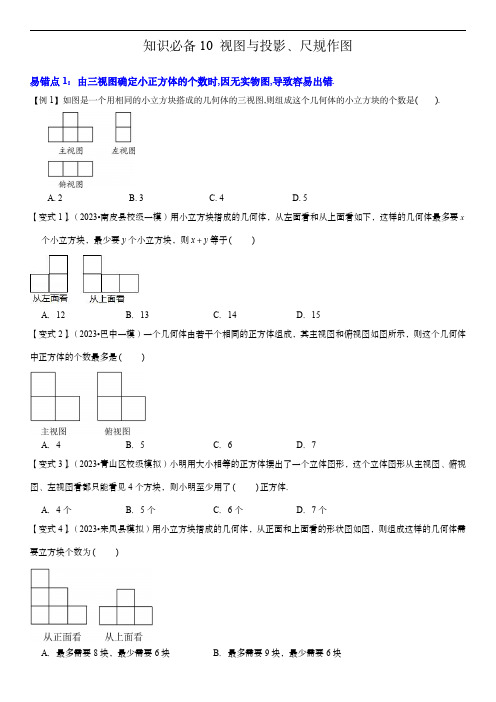
知识必备10视图与投影、尺规作图易错点1:由三视图确定小正方体的个数时,因无实物图,导致容易出错.【例1】如图是一个用相同的小立方块搭成的几何体的三视图,则组成这个几何体的小立方块的个数是().A.2B.3C.4D.5【变式1】.(2023•南皮县校级一模)用小立方块搭成的几何体,从左面看和从上面看如下,这样的几何体最多要x 个小立方块,最少要y个小立方块,则x y等于()A.12B.13C.14D.15【变式2】.(2023•巴中一模)一个几何体由若干个相同的正方体组成,其主视图和俯视图如图所示,则这个几何体中正方体的个数最多是()A.4B.5C.6D.7【变式3】.(2023•青山区校级模拟)小明用大小相等的正方体摆出了一个立体图形,这个立体图形从主视图、俯视图、左视图看都只能看见4个方块,则小明至少用了()正方体.A.4个B.5个C.6个D.7个【变式4】.(2023•来凤县模拟)用小立方块搭成的几何体,从正面和上面看的形状图如图,则组成这样的几何体需要立方块个数为()A.最多需要8块,最少需要6块B.最多需要9块,最少需要6块C.最多需要8块,最少需要7块D.最多需要9块,最少需要7块【变式5】.(2023·河北·统考中考真题)如图1,一个2×2的平台上已经放了一个棱长为1的正方体,要得到一个几何体,其主视图和左视图如图2,平台上至还需再放这样的正方体()A.1个B.2个C.3个D.4个【变式6】.(2023·四川眉山·统考中考真题)由相同的小正方体搭成的立体图形的部分视图如图所示,则搭成该立体图形的小正方体的最少个数为()A.6B.9C.10D.14【变式7】.(2023·黑龙江牡丹江·统考中考真题)由若干个完全相同的小正方体搭成的几何体的主视图和左视图如图所示,则搭成该几何体所用的小正方体的个数最多是()A.6B.7C.8D.9【变式8】.(2023·湖北黄石·统考中考真题)如图,根据三视图,它是由()个正方体组合而成的几何体A.3B.4C.5D.6【变式9】.(2022·黑龙江牡丹江·统考中考真题)由一些大小相同的小正方体搭成的几何体的三视图如图所示,则搭成这个几何体的小正方体的个数是()A.3B.4【变式10】.(2023·四川成都·统考中考真题)一个几何体由几个大小相同的小立方块搭成,它的主视图和俯视图如【变式11】.(2022·几何体的小正方体的个数是易错点2:根据视图求几何图形的表面积和体积,因缺乏合理的方法而出错.【例2】如图所示,,则这个几何体的侧面积是().A.18cm2B.20cm222cm D cm.(18【变式1】.(2023·黑龙江齐齐哈尔·统考中考真题)如图,若几何体是由六个棱长为1的正方体组合而成的,则该几何体左视图的面积是()表示面积,A.48πcm2【变式8】.(2020·四川是()A.20πB.18π【变式9】.(2020·湖南永州·中考真题)如图,这是一个底面为等边三角形的正三棱柱和它的主视图、俯视图,则它的左视图的面积是()A.1B.2【变式11】.(2021·山东菏泽积为()A.12 B.18【变式13】.(2021·江苏扬州cm.面积为2【变式14】.(2021·云南一.作图—基本作图(共9小题)1.(2023•福建)阅读以下作图步骤:①在OA和OB上分别截取OC,OD,使OC OD;②分别以C,D为圆心,以大于12CD的长为半径作弧,两弧在AOB内交于点M;③作射线OM,连接CM,DM,如图所示.根据以上作图,一定可以推得的结论是()A.12且CM DMB.13且CM DMC.12且OD DMD.23且OD DM2.(2023•长春)如图,用直尺和圆规作MAN的角平分线,根据作图痕迹,下列结论不一定正确的是() A.AD AEB.AD DFC.DF EFD.AF DE3.(2023•湖北)如图,矩形ABCD中,3AB ,4BC ,以点B为圆心,适当长为半径画弧,分别交BC,BD于点E,F,再分别以点E,F为圆心,大于12EF长为半径画弧交于点P,作射线BP,过点C作BP的垂线分别交BD,AD于点M,N,则CN的长为()A .10B .11C .23D .44.(2023•随州)如图,在ABCD 中,分别以B ,D 为圆心,大于12BD 的长为半径画弧,两弧相交于点M ,N ,过M ,N 两点作直线交BD 于点O ,交AD ,BC 于点E ,F ,下列结论不正确的是()A .AE CF B .DE BF C .OE OF D .DE DC5.(2023•山西)如图,在ABCD 中,60D .以点B 为圆心,以BA 的长为半径作弧交边BC 于点E ,连接AE .分别以点A ,E 为圆心,以大于12AE 的长为半径作弧,两弧交于点P ,作射线BP 交AE 于点O ,交边AD 于点F ,则OF OE 的值为.6.(2023•成都)如图,在ABC 中,D 是边AB 上一点,按以下步骤作图:①以点A 为圆心,以适当长为半径作弧,分别交AB ,AC 于点M ,N ;②以点D 为圆心,以AM 长为半径作弧,交DB 于点M ;③以点M 为圆心,以MN 长为半径作弧,在BAC 内部交前面的弧于点N ;④过点N 作射线DN 交BC 于点E .若BDE 与四边形ACED 的面积比为4:21,则BE CE 的值为.7.(2023•益阳)如图,在ABCD中,6AB ,4AD ,以A为圆心,AD的长为半径画弧交AB于点E,连接DE,分别以D,E为圆心,以大于12DE的长为半径画弧,两弧交于点F,作射线AF,交DE于点M,过点M作//MN AB交BC于点N.则MN的长为.8.(2023•河南)如图,ABC中,点D在边AC上,且AD AB.(1)请用无刻度的直尺和圆规作出A的平分线(保留作图痕迹,不写作法);(2)若(1)中所作的角平分线与边BC交于点E,连接DE.求证:DE BE.9.(2023•鄂州)如图,点E是矩形ABCD的边BC上的一点,且AE AD.(1)尺规作图(请用2B铅笔):作DAE的平分线AF,交BC的延长线于点F,连接DF.(保留作图痕迹,不写作法);(2)试判断四边形AEFD的形状,并说明理由.二.作图—复杂作图(共3小题)10.(2023•陕西)如图,已知四边形ABCD,//AD BC.请用尺规作图法,在边AD上求作一点E,在边BC上求作一点F,使四边形BFDE为菱形.(保留作图痕迹,不写作法)11.(2023•无锡)如图,已知APB,点M是PB上的一个定点.(1)尺规作图:请在图1中作O与射线PB相切于点M,同时与PA相切,切点记为N;,使得OMN与PM、PN所围成图形的面积是.(2)在(1)的条件下,若60的劣弧APB,3PM ,则所作的O12.(2023•陕西)如图.已知锐角ABC内部求作一点P.使PB PC.且B,请用尺规作图法,在ABC,48.(保留作图痕迹,不写作法)24PBC三.作图—应用与设计作图(共1小题)13.(2023•广安)如图,将边长为2的正方形剪成四个全等的直角三角形,用这四个直角三角形拼成符合要求的四边形,请在下列网格中画出你拼成的四边形(注:①网格中每个小正方形的边长为1;②所拼的图形不得与原图形相同;③四边形的各顶点都在格点上).四.简单几何体的三视图(共4小题)14.(2023•河南)北宋时期的汝官窑天蓝釉刻花鹅颈瓶是河南博物院九大镇院之宝之一,具有极高的历史价值、文化价值.如图所示,关于它的三视图,下列说法正确的是()A.主视图与左视图相同B.主视图与俯视图相同C.左视图与俯视图相同D.三种视图都相同15.(2023•济南)下列几何体中,主视图是三角形的为()A.B.C.D.16.(2023•淄博)在如图所示的几何体中,其主视图、左视图和俯视图完全相同的是()A.B.C.D.17.(2023•辽宁)如图所示,该几何体的俯视图是()A.B.C.D.五.简单组合体的三视图(共6小题)18.(2023•襄阳)先贤孔子曾说过“鼓之舞之”,这是“鼓舞”一词最早的起源,如图是喜庆集会时击鼓瞬间的情景及鼓的立体图形,该立体图形的主视图是()A.B.C.D.19.(2023•海南)如图是由5个完全相同的小正方体摆成的几何体,则这个几何体的俯视图是()A.B.C.D.20.(2023•枣庄)榫卯是古代中国建筑、家具及其他器械的主要结构方式,是我国工艺文化精神的传承,凸出部分叫榫,凹进部分叫卯.如图是某个部件“卯”的实物图,它的主视图是()A.B.C.D.21.(2023•青岛)一个正方体截去四分之一,得到如图所示的几何体,其左视图是()A.B.C.D.22.(2023•十堰)下列几何体中,三视图的三个视图完全相同的几何体是()A.B.C.D.23.(2023•重庆)四个大小相同的正方体搭成的几何体如图所示,从正面得到的视图是()A.B.C.D.六.由三视图判断几何体(共1小题)24.(2023•陕西)陕西饮食文化源远流长,“老碗面”是陕西地方特色美食之一.图②是从正面看到的一个“老碗”的一部分,D是 AB的中点,连接OD,与弦AB交于点C,连接OA,OB.已(图①)的形状示意图. AB是O知24,则O的半径OA为()CD cm,碗深8AB cmA.13cm B.16cm C.17cm D.26cm。
中考数学复习方案 第七单元 图形的变化 第30课时 视图与投影、尺规作图课件

D.正方体
图30-4
( A )
4.[2018·河北]尺规作图要求:Ⅰ.过直线外一点作这条直线的垂线;Ⅱ.作线段的
垂直平分线;Ⅲ.过直线上一点作这条直线的垂线;Ⅳ.作角的平分线.
图30-5是按上述要求排乱顺序的尺规作图:
则正确的配对是 (
)
A.①—Ⅳ,②—Ⅱ,③—Ⅰ,④—Ⅲ
B.①—Ⅳ,②—Ⅲ,③—Ⅱ,④—Ⅰ
(续表)
定义
类型
用无刻度的直尺和圆规作图叫尺规作图
步骤:
(1)以点O为圆心,任意长为半径作弧,交直线于
5.过直线上
A,B两点;
一点作已知
(2)分别以点 A,B 为圆心,以大于 AB 长为半径向
直线的垂线
直线上方作弧,交点为 M;
1
2
(3)作直线 MO,MO 即为所求
对点演练
题组一
必会题
1.下列四个图形是三棱柱的表面展开图的是( A )
D.5π
图30-18
| 考向精练 |
[2019·甘肃]已知某几何体的三视图如图30-19所示,其中俯视图为等边三角形,
则该几何体的左视图的面积为
.
图30-19
[答案] 3 3 cm2
[解析]该几何体是一个三棱柱,
底面等边三角形边长为 2 cm,
高为 3cm,
三棱柱的高为 3 cm,
所以其左视图的面积为 3 3 cm2,
定义
类型
用无刻度的直尺和圆规作图叫尺规作图
步骤:
1.作一条线段等
(1)作射线OP;
于已知线段
(2)在OP上截取⑬ OA=a
OA即为所求线段
,
(续表)
定义
类型
用无刻度的直尺和圆规作图叫尺规作图
中考数学复习 第1部分 第七章 图形与变换 第一节 投影、视图与尺规作图课件

【自主解答】 对于正方体的平面展开图中相对的面一定相隔
一个小正方形,由图形可知,与“值”字相对的字是“记”. 故选A.
第十四页,共二十九页。
正方体展开图口诀 正方体展有规律,十一种类看仔细; 中间四个成一行,两 边各一无规矩;二三紧连错一个,三一相连一随意;两两相 连各错一,三个两排一对齐;一条线上不过(bùguò)四,田七和凹要 放弃;相间之端是对面,间二拐角面相邻.
室外的阳光下观察向日葵影子的变化情况,他发现(fāxiàn)这四个
时
A
刻向日葵影子的长度各不相同,那么影子最长的时刻为( )
A.2时
第二十一页,共二十九页。
考点五 尺规作图 (5年2考) 例5 (2018·潍坊中考)如图,木工师傅在板材边角处作直角
时,往往使用“三弧法”,其作法是:
第二十九页,共二十九页。
30°,
3 2 3 ∴BD= AB,∴S△ABD= AB2. 3 ∵AC=CD,∴S△BDC= AB2.
1
∠ACB=
2
故A,B,C正确.故选D. 4
第二十五页,共二十九页。
尺规作图的依据
常见的尺规作图一般有五种,在复习时,要掌握每一种尺规
作图的基本步骤,并理解其中(qízhōng)的作图依据,往往会因为不理
【自主解答】 如图,∵DE∥BC,∴△ADE∽△ABC,
∴
解得BC=18.故答案为18.
第十九页,共二十九页。
9.如图,夜晚路灯下有一排同样高的旗杆,离路灯越近,
旗杆的影子( B )
A.越长(yuè chánɡ)
B.越短
C.一样长 D.随时间变化而变化
第二十页,共二十九页。
10.小华在上午8时,上午9时,上午10时,上午12时四次到
最新中考数学_图形的认识第2讲:尺规作图、视图与投影

于
点M;4.以点M为圆心,PQ
已
长为半径作弧,交前弧于点
知
N;5.过点N作射线O′B,
角
∠BO′A即为所求角
过直 过一
线外 点作
一点 已知
作已 直线
知直 的垂
线的 线
垂线
步骤:1.在直线另一 侧取点M;2.以P为圆 心,以PM为半径画弧, 交直线于A、B两点; 3.分别以A、B为圆心, 以大于12AB长为半径 画弧,交M同侧于点N; 4. 连接PN,则直线PN 即为所求垂线
由一些小正方体组合而成的,则这个几何体 的俯视图是( D )
【解析】本题考查了小正方体组合体的 俯视图.俯视图是从物体上面向下看所得到 的图形,从组合体上面看到的平面图形共有 两行,第一行是三个正方形,第二行是左右 两边各一个正方形,中间空一个正方形.
【方法指导】小正方块组成几何体的三 视图判断方法:
2
【思维方式】解决此题应清楚题中的作 图过程为作角的平分线,然后在图中找到所 求角度,即可得到∠MAB为∠CAB的一半, 再结合已知条件,可利用平行线的性质求得 ∠CAB,从而此题即可得解.
【方法指导】解决此类问题应熟练掌握两点 内容:①掌握五种基本尺规作图,一般考查3种, 即作角的平分线、线段的垂直平分线和高线;② 掌握等腰三角形的性质、角平分线的性质、平行 线性质和直角三角形的性质及定理.解决问题时, 先通过分析作法,得出相应的作图,再结合作图 以及已知图形性质,利用三角形内角和,直角三 角形或等腰三角形三线合一求解.
②“一三二”型:
【温馨提示】“1”与“5”相对;“2”与“4” 相对;“3”与“6”相对.
③“二二二”型:
【温馨提示】“1”与“4”相对;“2”与“5” 相对;“3”与“6”相对.
中考数学真题专项汇编解析—投影与视图、命题、尺规作图
中考数学真题专项汇编解析—投影与视图、命题、尺规作图一.选择题1.(2022·新疆·中考真题)如图是某几何体的展开图,该几何体是()A.长方体B.正方体C.圆锥D.圆柱【答案】C【分析】观察所给图形可知展开图由一个扇形和一个圆构成,由此可以判断该几何体是圆锥.【详解】解:∵展开图由一个扇形和一个圆构成,∵该几何体是圆锥.故选C.【点睛】本题考查圆锥的展开图,熟记圆锥展开图的形状是解题的关键.2.(2022·江苏宿迁·中考真题)下列展开图中,是正方体展开图的是()A.B.C.D.【答案】C【分析】根据正方体的表面展开图共有11种情况,A,D是“田”型,对折不能折成正方体,B是“凹”型,不能围成正方体,由此可进行选择.【详解】解:根据正方体展开图特点可得C答案可以围成正方体,故选:C.【点睛】此题考查了正方体的平面展开图.关键是掌握正方体展开图特点.3.(2022·浙江金华·中考真题)如图,圆柱的底面直径为AB,高为AC,一只蚂蚁在C处,沿圆柱的侧面爬到B处,现将圆柱侧面沿AC“剪开”,在侧面展开图上画出蚂蚁爬行的最近路线,正确的是()A.B.C.D.【答案】C【分析】根据圆柱的侧面展开特征,两点之间线段最短判断即可;【详解】解:∵AB为底面直径,∵将圆柱侧面沿AC“剪开”后,B点在长方形上面那条边的中间,∵两点之间线段最短,故选:C.【点睛】本题考查了圆柱的侧面展开,掌握两点之间线段最短是解题关键.4.(2022·四川遂宁·中考真题)如图是正方体的一种展开图,那么在原正方体中与“我”字所在面相对的面上的汉字是()A.大B.美C.遂D.宁【答案】B【分析】正方体的表面展开图,相对的面之间一定相隔一个正方形,根据这一特点作答.【详解】解:正方体的表面展开图,相对的面之间一定相隔一个正方形,“我”与“美”是相对面.故选:B.【点睛】本题主要考查了正方体相对两个面上的文字,注意正方体的空间图形,从相对面入手.5.(2022·四川自贡·中考真题)如图,将矩形纸片ABCD绕边CD所在的直线旋转一周,得到的立体图形是()A.B.C.D.【答案】A【分析】根据矩形绕一边旋转一周得到圆柱体示来解答.【详解】解:矩形纸片ABCD绕边CD所在的直线旋转一周,得到的立体图形是圆柱体.故选:A.【点睛】本题考查了点、线、面、体,熟练掌握“面动成体”得到的几何体的形状是解题的关键.6.(2022·湖南衡阳·中考真题)石鼓广场供游客休息的石板凳如图所示,它的主视图是()A.B.C.D.【答案】A【分析】根据主视图的定义和画法进行判断即可.【详解】解:从正面看过去,看到上下共三个矩形,所以主视图是:故选A【点睛】本题考查简单几何体的主视图,主视图就是从正面看物体所得到的图形.7.(2022·云南·中考真题)下列图形是某几何体的三视图(其中主视图也称正视图,左视图也称侧视图),则这个几何体是()A.三棱柱B.三棱锥C.四棱柱D.圆柱【答案】D【分析】根据三视图逆向即可得.【详解】解:此几何体为一个圆柱.故选:D.【点睛】此题考查由三视图还原几何体,既要考虑各视图的形状,还要把各视图的情况综合考虑才能得到几何体的形状.8.(2022·天津·中考真题)下图是一个由5个相同的正方体组成的立体图形,它的主视图是()A.B.C.D.【答案】A【分析】画出从正面看到的图形即可得到它的主视图.【详解】解:几何体的主视图为:故选:A【点睛】本题考查了简单组合体的三视图:画简单组合体的三视图要循序渐进,通过仔细观察和想象,再画它的三视图.9.(2022·江西·中考真题)如图是四个完全相同的小正方体搭成的几何体,它的俯视图为()A.B.C.D.【答案】A【分析】从上面观察该几何体得到一个“T”字形的平面图形,横着两个正方形,中间有一个正方形,且有两条垂直的虚线,下方有半个正方形.画出图形即可.【详解】俯视图如图所示.故选:A.【点睛】本题主要考查了几何体的三视图,俯视图是从上面观察几何体得出的平面图形..注意:能看到的线用实线,看不到而存在的线用虚线.10.(2022·浙江温州·中考真题)某物体如图所示,它的主视图是()A.B.C.D.【答案】D【分析】根据主视图的定义和画法进行判断即可.【详解】解:某物体如图所示,它的主视图是:故选:D.【点睛】本题考查简单几何体的主视图,主视图就是从正面看物体所得到的图形.11.(2022·浙江宁波·中考真题)如图所示几何体是由一个球体和一个圆柱组成的,它的俯视图是()A.B.C.D.【答案】C【分析】根据俯视图的意义和画法可以得出答案.【详解】根据俯视图的意义可知,从上面看物体所得到的图形,选项C符合题意,故答案选:C.【点睛】本题主要考查组合体的三视图,注意虚线、实线的区别,掌握俯视图是从物体的上面看得到的视图是解题的关键.12.(2022·江苏扬州·中考真题)如图是某一几何体的主视图、左视图、俯视图,该几何体是()A.四棱柱B.四棱锥C.三棱柱D.三棱锥【答案】B【分析】根据各个几何体三视图的特点进行求解即可.【详解】解:∵该几何体的主视图与左视图都是三角形,俯视图是一个矩形,而且两条对角线是实线,∵该几何体是四棱锥,故选B.【点睛】本题主要考查了由三视图还原几何体,熟知常见几何体的三视图是解题的关键.13.(2022·浙江绍兴·中考真题)由七个相同的小立方块搭成的几何体如图所示,则它的主视图是()A.B.C.D.【答案】B【分析】根据题目中的图形,可以画出主视图,本题得以解决.【详解】解:由图可得,题目中图形的主视图是,故选:B.【点睛】本题考查简单组合体的三视图,解题的关键是画出相应的图形.14.(2022·浙江嘉兴·中考真题)如图是由四个相同的小立方体搭成的几何体,它的主视图是()A.B.C.D.【答案】B【分析】主视图有3列,每列小正方形数目分别为2,1,1.【详解】如图所示:它的主视图是:.故选:B.【点睛】此题主要考查了简单组合体的三视图,正确把握观察角度是解题关键.15.(2022·浙江丽水·中考真题)如图是运动会领奖台,它的主视图是()A.B.C.D.【答案】A【分析】根据从正面看得到的图形是主视图,可得答案.【详解】解:领奖台的主视图是:故选:A.【点睛】本题考查了简单几何体的三视图,从正面看得到的图形是主视图.16.(2022·安徽·中考真题)一个由长方体截去一部分后得到的几何体如图水平放置,其俯视图是()A.B.C.D.【答案】A【分析】找到从上面看所得到的图形即可,注意所有的看到的棱都应表现在俯视图中.【详解】解:该几何体的俯视图为:,故选:A【点睛】本题考查了三视图的知识,俯视图是从物体的上面看得到的视图.17.(2022·浙江舟山·中考真题)用尺规作一个角的角平分线,下列作法中错误的是( )A .B .C .D .【答案】D【分析】根据作图轨迹及角平分线的定义判断即可得出答案.【详解】A 、如图,由作图可知:,OA OC AB BC ==,又∵OB OB =,∵OAB OCB ≅,∵AOB COB ∠=∠,∵OB 平分AOC ∠.故A 选项是在作角平分线,不符合题意;B 、如图,由作图可知:,OA OB OC OD ==,又∵COB AOD ∠=∠,∵OBC OAD ≅,∵OA OB OAD OBC OCB ODA =∠=∠∠=∠,,,∵AC BD =,∵CEA BED ∠=∠,ECA EDB ∠=∠,∵AEC BED ≅△△,∵AE BE =,∵,EAO EBO OA OB ∠=∠=,∵AOE BOE ∠=∠,∵OE 平分AOB ∠.故B 选项是在作角平分线,不符合题意;C 、如图,由作图可知:,AOB MCN OC CD ∠=∠=,∵CD OB ∥,COD CDO =∠∠,∵DOB CDO ∠=∠,∵COD DOB ∠=∠,∵OD 平分AOB ∠.故C 选项是在作角平分线,不符合题意;D 、如图,由作图可知:,OA BC OC AB ==,又∵OB OB =,∵AOB CBO ≅,∵,,AOB OBC COB ABO ∠=∠∠=∠故D 选项不是在作角平分线,符合题意;故选:D【点睛】本题考查了角平分线的作图,全等三角形的性质与判定,掌握以上知识是解题的关键.18.(2022·山东泰安·中考真题)某种零件模型如图所示,该几何体(空心圆柱)的俯视图是( )A .B .C .D .【答案】C【详解】找到从上面看所得到的图形即可:空心圆柱由上向下看,看到的是一个圆环.故选C19.(2022·湖北十堰·中考真题)如图,工人砌墙时,先在两个墙脚的位置分别插一根木桩,再拉一条直的参照线,就能使砌的砖在一条直线上.这样做应用的数学知识是()A.两点之间,线段最短B.两点确定一条直线C.垂线段最短D.三角形两边之和大于第三边【答案】B【分析】由直线公理可直接得出答案.【详解】解:建筑工人砌墙时,经常在两个墙脚的位置分别插一根木桩,然后拉一条直的参照线,这种做法用几何知识解释应是:两点确定一条直线.故选:B.【点睛】此题主要考查了直线的性质,要想确定一条直线,至少要知道两点.20.(2022·四川达州·中考真题)下列命题是真命题的是()A.相等的两个角是对顶角B.相等的圆周角所对的弧相等C.若a b<,则22ac bc<D.在一个不透明的箱子里放有1个白球和2个红球,它们除颜色外其余都相同,从箱子里任意摸出1个球,摸到白球的概率是1 3【答案】D【分析】分别根据对顶角的定义,圆周角定理,不等式的基本性质及概率公式进行判断即可得到答案.【详解】有公共顶点且两条边互为反向延长线的两个角是对顶角,故A选项错误,不符合题意;在同圆或等圆中,相等的圆周角所对的弧相等,故B选项错误,不符合题意;若a b<,则22ac bc≤,故C选项错误,不符合题意;在一个不透明的箱子里放有1个白球和2个红球,它们除颜色外其余都相同,从箱子里任意摸出1个球,摸到白球的概率是13,故D选项正确,符合题意;故选:D.【点睛】本题考查了命题的真假,涉及对顶角的定义,圆周角定理,不等式的基本性质及概率公式,熟练掌握知识点是解题的关键.21.(2022·湖北随州·中考真题)如图是一个放在水平桌面上的半球体,该几何体的三视图中完全相同的是()A.主视图和左视图B.主视图和俯视图C.左视图和俯视图D.三个视图均相同【答案】A【分析】根据三视图的形成,从正面、左面和上面三个方向看立体图形得到的平面图形,注意所有的看到的或看不到的棱都应表现在三视图中,看得见的用实线,看不见的用虚线,虚实重合用实线.【详解】解:从正面和左面看,得到的平面图形均是半圆,而从上面看是一个圆,因此该几何体主视图与左视图一致,故选:A.【点睛】本题考查了三视图的知识,准确把握从正面、左面和上面三个方向看立体图形得到的平面图形是解决问题的关键.22.(2022·湖北黄冈·中考真题)某几何体的三视图如图所示,则该几何体是()A.圆锥B.三棱锥C.三棱柱D.四棱柱【答案】C【分析】由主视图和左视图得出该几何体是柱体,再结合俯视图可得答案.【详解】解:由三视图知,该几何体是三棱柱,故选:C.【点睛】本题主要考查由三视图判断几何体,由三视图想象几何体的形状,首先,应分别根据主视图、俯视图和左视图想象几何体的前面、上面和左侧面的形状,然后综合起来考虑整体形状.23.(2022·广西梧州·中考真题)下列命题中,假命题...是()A.2-的绝对值是2-B.对顶角相等C.平行四边形是中心对称图形D.如果直线,∥∥,那么直线a ba cb c∥【答案】A【分析】根据绝对值的意义,对顶角的性质,平行四边形的性质,平行线的判定逐一判断即可.【详解】解:A.2-的绝对值是2,故原命题是假命题,符合题意;B.对顶角相等,故原命题是真命题,不符合题意;C.平行四边形是中心对称图形,故原命题是真命题,不符合题意;D.如果直线,a cb c∥∥,那么直线a b∥,故原命题是真命题,不符合题意;故选:A.【点睛】本题考查了命题真假的判断,属于基础题.根据定义:符合事实真理的判断是真命题,不符合事实真理的判断是假命题,不难选出正确项.24.(2022·内蒙古包头·中考真题)几个大小相同,且棱长为1的小正方体所搭成几何体的俯视图如图所示,图中小正方形中的数字表示在该位置小正方体的个数,则这个几何体的左视图的面积为()A.3B.4C.6D.9【答案】B【分析】根据该几何体的俯视图以及该位置小正方体的个数,可以画出左视图,从而求出左视图的面积;【详解】由俯视图以及该位置小正方体的个数,左视图共有两列,第一列两个小正方体,第二列两个小正方体,可以画出左视图如图,所以这个几何体的左视图的面积为4故选:B【点睛】本题考查了物体的三视图,解题饿到关键是根据俯视图,以及该位置小正方体的个数,正确作出左视图.25.(2022·湖北武汉·中考真题)如图是一个立体图形的三视图,该立体图形是()A.长方体B.正方体C.三棱柱D.圆柱【答案】A【分析】根据题意可得这个几何体的三视图为长方形和正方形,即可求解.【详解】解:根据题意得:该几何体的三视图为长方形和正方形,∵该几何体是长方体.故选:A【点睛】本题考查由三视图确定几何体的名称,熟记常见几何体的三视图的特征是解题的关键.26.(2022·黑龙江齐齐哈尔·中考真题)由一些大小相同的小正方体搭成的几何体的主视图、左视图和俯视图都是如图所示的“田”字形,则搭成该几何体的小正方体的个数最少为()A.4个B.5个C.6个D.7个【答案】C【分析】从俯视图中可以看出最底层小正方体的个数及形状,从左视图可以看出第二层的个数,从而算出总的个数.【详解】解:由题中所给出的左视图知物体共两层,每一层都是两个小正方体;从俯视图可以可以看出最底层的个数所以图中的小正方体最少2+4=6.故选:C.【点睛】本题主要考查学生对三视图掌握程度和灵活运用能力,同时也体现了对空间想象能力方面的考查.如果掌握口诀“俯视图打地基,正视图疯狂盖,左视图拆违章”就更容易得到答案.27.(2022·黑龙江绥化·中考真题)下列图形中,正方体展开图错误的是()A.B.C.D.【答案】D【分析】利用正方体及其表面展开图的特点解题.【详解】D选项出现了“田字形”,折叠后有一行两个面无法折起来,从而缺少面,不能折成正方体,A、B、C选项是一个正方体的表面展开图.故选:D.【点睛】此题考查了几何体的展开图,只要有“田”“凹”字的展开图都不是正方体的表面展开图.28.(2022·广西贺州·中考真题)下面四个几何体中,主视图为矩形的是()A.B.C.D.【答案】A【分析】依次分析每个选项中的主视图,找出符合题意的选项即可.【详解】解:A选项图形的主视图为矩形,符合题意;B选项图形的主视图为三角形,中间由一条实线,不符合题意;C选项图形的主视图为三角形,不符合题意;D选项图形的主视图为梯形,不符合题意;故选:A.【点睛】本题考查了几何体的主视图,解题关键是理解主视图的定义.29.(2022·湖南永州·中考真题)我市江华县有“神州摇都”的美涨,每逢“盘王节”会表演长鼓舞,长鼓舞中使用的“长鼓”内腔挖空,两端相通,两端鼓口为圆形,中间鼓腰较为细小.如图为类似“长鼓”的几何体,其俯视图的大致形状是()A.B.C.D.【答案】B【分析】根据题目描述,判断几何体的俯视图即可;【详解】解:根据长鼓舞中使用的“长鼓”内腔挖空,两端相通,可知俯视图中空,两端鼓口为圆形可知俯视图是圆形,鼓腰也是圆形,且是不能直接看见,所以中间是虚圆;故选:B.【点睛】本题主要考查几何体的三视图中的俯视图,解本题的关键在于需学生具备一定的空间想象能力.30.(2022·湖南岳阳·中考真题)某个立体图形的侧面展开图如图所示,它的底面是正三角形,那么这个立体图形是()A.圆柱B.圆锥C.三棱柱D.四棱柱【答案】C【分析】根据常见立体图形的底面和侧面即可得出答案.【详解】解:A选项,圆柱的底面是圆,故该选项不符合题意;B选项,圆锥的底面是圆,故该选项不符合题意;C选项,三棱柱的底面是三角形,侧面是三个长方形,故该选项符合题意;D选项,四棱柱的底面是四边形,故该选项不符合题意;故选:C.【点睛】本题考查了几何体的展开图,掌握n棱柱的底面是n边形是解题的关键.31.(2022·河南·中考真题)2022年北京冬奥会的奖牌“同心”表达了“天地合·人心同”的中华文化内涵,将这六个汉字分别写在某正方体的表面上,如图是它的一种展开图,则在原正方体中,与“地”字所在面相对的面上的汉字是()A.合B.同C.心D.人【答案】D【分析】根据正方体的展开图进行判断即可;【详解】解:由正方体的展开图可知“地”字所在面相对的面上的汉字是“人”;故选:D.【点睛】本题主要考查正方体的展开图相对两个面上的文字,注意正方体的空间图形,从相对面入手是解题的关键.32.(2022·湖南湘潭·中考真题)如图,小明在学了尺规作图后,作了一个图形,其作图步骤是:∵作线段2AB ,分别以点A、B为圆心,以AB长为半径画弧,两弧相交于点C、D;∵连接AC、BC,作直线CD,且CD与AB相交于点H.则下列说法不正确的是()A.ABC是等边三角形B.AB CD⊥C.AH BH=D.45∠=︒ACD【答案】D【分析】根据等边三角形的判定和性质,线段垂直平分线的性质一一判断即可.【详解】解:由作图可知:AB=BC=AC,∵∵ABC是等边三角形,故A选项正确∵等边三角形三线合一,由作图知,CD是线段AB的垂直平分线,∵AB CD⊥,故B选项正确,∵AH BH=,30∠=︒,故C选项正确,D选项错误.故选:D.ACD【点睛】此题考查了作图-基本作图,等边三角形的判定和性质,线段垂直平分线的性质,解题的关键是理解题意,灵活运用所学知识解决问题.33.(2022·四川广元·中考真题)如图,在∵ABC中,BC=6,AC=8,∵C=90°,以点B为圆心,BC长为半径画弧,与AB交于点D,再分别以A、D为圆心,AD的长为半径画弧,两弧交于点M、N,作直线MN,分别交AC、AB于大于12点E 、F ,则AE 的长度为( )A .52B .3C .D .103【答案】A【分析】由题意易得MN 垂直平分AD ,AB =10,则有AD =4,AF =2,然后可得4cos 5AC A AB ∠==, 进而问题可求解.【详解】解:由题意得:MN 垂直平分AD ,6BD BC ==,∵1,902AF AD AFE =∠=︒,∵BC =6,AC =8,∵C =90°,∵10AB ,∵AD =4,AF =2,4cos 5AC A AB ∠==,∵5cos 2AF AE A ==∠;故选A . 【点睛】本题主要考查勾股定理、垂直平分线的性质及三角函数,熟练掌握勾股定理、垂直平分线的性质及三角函数是解题的关键.34.(2022·河北·中考真题)∵~∵是由相同的小正方体粘在一起的几何体,若组合其中的两个,恰是由6个小正方体构成的长方体,则应选择( )A.∵∵B.∵∵C.∵∵D.∵∵【答案】D【解析】【分析】观察图形可知,∵~∵的小正方体的个数分别为4,3,3,2,其中∵∵组合不能构成长方体,∵∵组合符合题意【详解】解:观察图形可知,∵~∵的小正方体的个数分别为4,3,3,2,其中∵∵组合不能构成长方体,∵∵组合符合题意故选D【点睛】本题考查了立体图形,应用空间想象能力是解题的关键.二、填空题35.(2022·江苏无锡·中考真题)请写出命题“如果a b>,那么0-<”的逆命题:b a________.【答案】如果0-<,那么a b>b a【分析】根据逆命题的概念解答即可.【详解】解:命题“如果a b>,那么0b a-<,那么a b>”,-<”的逆命题是“如果0b a故答案为:如果0-<,那么a b>.b a【点睛】此题考查了互逆命题的知识,两个命题中,如果第一个命题的条件是第二个命题的结论,而第一个命题的结论又是第二个命题的条件,那么这两个命题叫做互逆命题.其中一个命题称为另一个命题的逆命题.36.(2022·湖南常德·中考真题)如图是一个正方体的展开图,将它拼成正方体后,“神”字对面的字是________.【答案】月【分析】正方体的表面展开图,相对的面之间一定相隔一个正方形,根据这一特点作答.【详解】解:由正方体的展开图特点可得:“神”字对面的字是“月”.故答案为:月.【点睛】此题考查了正方体相对两个面上的文字的知识;掌握常见类型展开图相对面上的两个字的特点是解决本题的关键.37.(2022·浙江湖州·中考真题)“如果a b =,那么a b =”的逆命题是___________.【答案】如果a b =,那么a b =【分析】把一个命题的条件和结论互换就得到它的逆命题,从而得出答案.【详解】解:“如果a b =,那么a b =”的逆命题是:“如果a b =,那么a b =”,故答案为:如果a b =,那么a b =.【点睛】本题考查命题与定理,解题的关键是理解题意,掌握逆命题的定义. 38.(2022·浙江温州·中考真题)如图是某风车示意图,其相同的四个叶片均匀分布,水平地面上的点M 在旋转中心O 的正下方.某一时刻,太阳光线恰好垂直照射叶片,OA OB ,此时各叶片影子在点M 右侧成线段CD ,测得8.5m,13mMC CD==,垂直于地面的木棒EF与影子FG的比为2∵3,则点O,M之间的距离等于___________米.转动时,叶片外端离地面的最大高度等于___________米.【答案】1010【分析】过点O作AC、BD的平行线,交CD于H,过点O作水平线OJ交BD 于点J,过点B作BI∵OJ,垂足为I,延长MO,使得OK=OB,求出CH的长度,根据23EF OMFG MH==,求出OM的长度,证明BIO JIB∽,得出23BI IJ=,49OI IJ=,求出IJ、BI、OI的长度,用勾股定理求出OB的长,即可算出所求长度.【详解】如图,过点O作AC、BD的平行线,交CD于H,过点O作水平线OJ 交BD于点J,过点B作BI∵OJ,垂足为I,延长MO,使得OK=OB,由题意可知,点O是AB的中点,∵OH AC BD,∵点H是CD的中点,∵13m CD=,∵16.5m2CH HD CD===,∵8.5 6.515m MH MC CH=+=+=,又∵由题意可知:23EF OMFG MH==,∵2153OM=,解得10m=OM,∵点O、M之间的距离等于10m,∵BI∵OJ,∵90BIO BIJ∠=∠=︒,∵由题意可知:90OBJ OBI JBI ∠=∠+∠=︒,又∵90BOI OBI ∠+∠=︒,∵BOI JBI ∠=∠,∵BIO JIB ∽,∵23BI OI IJ BI ==,∵23BI IJ =,49OI IJ =, ∵,OJ CD OH DJ ,∵四边形IHDJ 是平行四边形,∵ 6.5m OJ HD ==, ∵46.5m 9OJ OI IJ IJ IJ =+=+=,∵ 4.5m IJ =,3m BI =,2m OI =,∵在Rt OBI △中,由勾股定理得:222OB OI BI =+,∵OB ,∵OB OK ==,∵(10m MK MO OK =+=,∵叶片外端离地面的最大高度等于(10m,故答案为:10,10+【点睛】本题主要考查了投影和相似的应用,及勾股定理和平行四边形的判定与性质,正确作出辅助线是解答本题的关键.39.(2022·浙江杭州·中考真题)某项目学习小组为了测量直立在水平地面上的旗杆AB 的高度,把标杆DE 直立在同一水平地面上(如图).同一时刻测得旗杆和标杆在太阳光下的影长分别是BC =8.72m ,EF =2.18m .已知B ,C ,E ,F 在同一直线上,AB ∵BC ,DE ∵EF ,DE =2.47m ,则AB =_________m .【答案】9.88【分析】根据平行投影得AC ∵DE ,可得∵ACB =∵DFE ,证明Rt ∵ABC ∵∵Rt ∵DEF ,然后利用相似三角形的性质即可求解.【详解】解:∵同一时刻测得旗杆和标杆在太阳光下的影长分别是BC =8.72m ,EF =2.18m .∵AC ∵DE ,∵∵ACB =∵DFE ,∵AB ∵BC ,DE ∵EF ,∵∵ABC =∵DEF =90°,∵Rt ∵ABC ∵∵Rt ∵DEF , ∵AB BC DE EF =,即8.722.47 2.18AB =,解得AB =9.88, ∵旗杆的高度为9.88m .故答案为:9.88.【点睛】本题考查了相似三角形的判定与性质,平行投影:由平行光线形成的投影是平行投影,如物体在太阳光的照射下形成的影子就是平行投影.证明Rt ∵ABC ∵∵Rt ∵DEF 是解题的关键.40.(2022·湖南衡阳·中考真题)如图,在ABC 中,分别以点A 和点B 为圆心,大于12AB 的长为半径作圆弧,两弧相交于点M 和点N ,作直线MN 交CB 于点D ,连接AD .若8AC =,15BC =,则ACD △的周长为_________.【答案】23【分析】由作图可得:MN 是AB 的垂直平分线,可得,DA DB =再利用三角形的周长公式进行计算即可.【详解】解:由作图可得:MN 是AB 的垂直平分线,,DA DB ∴=8AC =,15BC =,81523,ACD CAC CD AD AC CD BD AC BC 故答案为:23【点睛】本题考查的是线段的垂直平分线的作图,线段的垂直平分线的性质,掌握“线段的垂直平分线的性质”是解本题的关键.三.解答题41.(2022·陕西·中考真题)小明和小华利用阳光下的影子来测量一建筑物顶部旗杆的高.如图所示,在某一时刻,他们在阳光下,分别测得该建筑物OB 的影长OC 为16米,OA 的影长OD 为20米,小明的影长FG 为2.4米,其中O 、C 、D 、F 、G 五点在同一直线上,A 、B 、O 三点在同一直线上,且AO ∵OD ,EF ∵FG .已知小明的身高EF 为1.8米,求旗杆的高AB .【答案】旗杆的高AB 为3米.【分析】证明∵AOD ∵∵EFG ,利用相似比计算出AO 的长,再证明∵BOC ∵∵AOD ,然后利用相似比计算OB 的长,进一步计算即可求解. 【详解】解:∵AD ∵EG ,∵∵ADO =∵EGF . 又∵∵AOD =∵EFG =90°,∵∵AOD ∵∵EFG . ∵AO ODEF FG =.∵ 1.820152.4EF OD AO FG ⋅⨯===. 同理,∵BOC ∵∵AOD .∵BO OCAO OD =.∵15161220AO OC BO OD ⋅⨯===. ∵AB =OA −OB =3(米).∵旗杆的高AB 为3米.【点睛】本题考查了平行投影:由平行光线形成的投影是平行投影,如物体在太阳光的照射下形成的影子就是平行投影.平行投影中物体与投影面平行时的投影是全等的.42.(2022·陕西·中考真题)如图,已知,,ABC CA CB ACD =∠△是ABC 的一个外角.请用尺规作图法,求作射线CP ,使CP AB ∥.(保留作图痕迹,不写作法)。
中考数学尺规作图和视图和投影

A
C
30º
B
h
23
祝同学们:金榜题名!
愿我们:心想事成!
h
24
申博 申博官网 申博 申博官网
xqj674qox
我那时的第一个老师——陈教师,缘于】给女性们们拿书,所骑轮椅与一辆货车相碰撞,没有以后继而不要在那所高二教书了。 感到高兴的是,陈教师如今已无大碍。平时,对咱们一帮小鬼不了解顽皮到随意地步,给陈教师起的外号是“小李”。到如今, 我还是照样我还记得尤其清楚分明,但对咱们实际上未去口碑不等量的事了,讲起“小李”,有特别多说不出的跟高二的幸福记 忆。在路过三四年级的最近,又来了一位教师,他姓何,因此对咱们给何教师的外号为“老何“。 销售村,缘于刚下过几天的雨,路并非是好走。虽然说如此,也干预不上我那时的活动。使用的时候,经过了好多块麦地,麦 子平时始出泛黄,收割的时节行将到达。对我来讲,那一条路再熟习不过了。上高二的最近,遗憾整天来回走。走在那一条熟 习的学校,非常多的种种的点滴涌上了我那时的心头,我那时的思绪始出感觉会有些没序。但我很明显,如今不是认真思考不 等量的事的最近,接着我又立马很快苏醒了过来。我了解,我也坚信,在将来的某一日,我就该每月去想一下和回想那么多的 平时与种种,我就该让我本人有富足的精力和时间去回味和感受。
⑥了解视点、视角及盲区的涵义,并能在 简单的平面图和立体图中表示。
⑦通过实例了解中心h 投影和平行投影。 5
一、基本作图及其数学语言
1.尺规作图限定作图工具只有圆规和没有
刻度的直尺.
2.基本作图
⑴作一条线段等于已知线段;
作线段AB=a.
⑵作一个角等于已知角;
作∠ABC=∠α.
⑶作已知角的平分线;
作∠ABC的平分线BP.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
中考数学专题知识梳理:尺规作图、视图与投影、空间图形、圆
河北省馆陶县路桥中学 万永霞 057751
一、尺规作图
1.在几何里把限定用直尺和圆规来画图,称为尺规作图,最基本最常用的尺规作图,称基本作图.
2.基本作图包括:作一条线段等于已知线段,作一个角等于已知角,作已知角的平分线,作已知线段的垂直平分线.
3.利用基本作图作三角形:已知三边作三角形;已知两边及其夹角作三角形;已知两角及其夹边作三角形;已知边底
及边底上的高作等腰三角形.
4.平面内,过一点可以作无数个圆;过两点可以做无数个圆,圆心在以这两点为端点的线段的中垂线上;过不在同一
直线上的三点有且只有一个圆,圆心是以这三点为顶点的三角形的外心,即边的中垂线的交点.
5.对于尺规作图题,会写已知、求作和作法(不要求证明).
二、视图与投影
1.三视图:当我们从某一个角度观察一个物体时,所看到的图像叫做物体的一个视图,从正面得到的视图叫做主视图,
从上面得到的视图叫做俯视图,从左边得到的视图叫做左视图.主视图反映它的长和高,俯视图反映物体的长和宽,左视
图反映它的宽和高.
2.几何体的表面展开图:同一个几何体,由于剪开的方式不同,展开的平面图形也就不同,无论是哪种形式的表面展
开图,只要能将其围成一个相应的立体图形,它就是该立体图形的表面展开图.
3.投影
(1)平行投影:物体在光线照射下,在某个平面上得到的影子叫做投影.太阳光线可看作平行的,平行光线形成的投
影为平行投影.平行投影有以下两条性质:两个直立于地面的物体在阳光下的投影,或平行或在同一条直线上,两个物体、
它们的平行投影及过物体顶端的投影线,分别组成直角三角形,这两个三角形相似;同一时刻,物体的高度与影长成比例.
(2)中心投影:由同一点(点光源)发出的光线形成的投影叫做中心投影.中心投影有:点光源、物体边缘的点以及
它在影子上的对应点在同一直线上;物体的影长与物体的高度不一定成比例.
3.视点、视线、盲区:眼睛所在的位置叫做视点;由视点发出的线叫做视线,视线都是直线;眼睛看不到的地方即为
盲区.
三、空间图形
1.几何图形包括立体图形(几何体)和平面图形.在我们的生活的空间中,能够由实物的形状想象出几何图形,所看到
或接触到的物体中存在大量的立体图形,概括起来可分下面几类:正方体、正方体、圆柱、圆锥、棱柱、球体等.
2.用一平面去截一几何体,得到一个平面图形,这个平面图形就是截面.截不同的几何体可得到不同的截面,同一几何体
沿不同的方向截,得到的截面可能不同.如沿不同的方向截一正方体,可以得到的截面有:三角形、正方形、长方形、梯形、
五边形、六边形.
四、圆
1.圆的有关概念:圆、圆心、半径、弧、优弧、劣弧、弦、直径、圆心角、圆周角.
2.圆的有关性质:
(1)圆是轴对称图形也是中心对称图形.
(2)垂径定理:垂直于弦的直径平分这条弦,并且平分弦所对的弧.推论:平分弦(不是直径)的直径垂直于弦,并
且平分弦所对的弧.
(3)弧、弦、圆心角的关系:在同圆或等圆中,如果两个圆心角,两条弧,两条弦中有一组量相等,那么它们所对
应的其余各组量都分别相等.
(4)圆周角定理:同弧所对的圆周角等于圆心角的一半.推论:在同圆或等圆中,同弧或等弧所对的圆周角相等;直
径所对的圆周角是直角;90”的圆周角所对的弦是直径.
3.三角形的内心和外心:三角形的外心是三角形外接圆的圆心,三角形三边的垂直平分线的交点;三角形的内心是三
角形的内切圆的圆心,三角形三条角平分线的交点.
4.点和圆的位置关系有三种:点在圆外,点在圆上,点在圆内,设圆的半径为r,点到圆心的距离为d,则点在圆外d
>r.点在圆上d=r.点在圆内d<r.
5.直线和圆的位置关系有三种:相交、相切、相离.设圆的半径为r,圆心到直线的距离为d,则直线与圆相交d
<r,直线与圆相切d=r,直线与圆相离d>r
6.圆与圆的位置关系:设两圆的圆心距为d,两圆的半径分别为R和r,则
⑴ 两圆外离d>R+r;
⑵ 两圆外切d=R+r;
⑶ 两圆相交R-r<d<R+r(R≥r)
⑷ 两圆内切d=R-r(R>r);
⑸ 两圆内含d<R—r(R>r).(注意:两国内含时,如果d为0,则两圆为同心圆)
7.切线的性质和判定定理:圆的切线垂直于过切点的直径;经过半径的外端,并且垂直于这条半径的直线是圆的切线.
8.有关计算
(1)弧长公式:180nRl(n为圆心角的度数,R为圆的半径)
(2)扇形的面积公式S=213602nRlR(n为圆心角的度数,R为圆的半径).
(3)圆锥的侧面积S=πRl ,(l为母线长,r为底面圆的半径),圆锥的侧面积与底面积之和称为圆锥的全面积.
