一元一次方程的等积变形问题
一元一次方程的应用等积变化问题

一元一次方程的应用等积变化问题等积变化问题是一元一次方程应用题中的一种常见题型,其基本特点是涉及到体积、面积、长度等量的变化,而这种变化是等积的,即变化前后的量是相等的。
解决等积变化问题的关键在于理解“等积”的含义,即体积、面积、长度等量在变化过程中保持不变。
因此,我们需要根据题目描述,建立等量关系,然后列出方程求解。
下面是一个具体的例子:题目:有一个长方体,它的长增加了2cm,宽和高不变,体积增加了40立方厘米;宽增加了2cm,长和高不变,体积增加了60立方厘米;高增加了2cm,长和宽不变,体积增加了48立方厘米。
求原来长方体的体积是多少?解:设原长方体的长为l cm,宽为w cm,高为h cm。
根据题目描述,我们可以建立以下方程:1. 长增加2cm后,体积增加了40立方厘米:(l + 2) × w × h - l × w × h = 402. 宽增加2cm后,体积增加了60立方厘米:l × (w + 2) × h - l ×w × h = 603. 高增加2cm后,体积增加了48立方厘米:l × w × (h + 2) - l × w × h = 48将以上三个方程整理为一元一次方程组:1) (l + 2) × w × h - l × w × h = 402) l × (w + 2) × h - l × w × h = 603) l × w × (h + 2) - l × w × h = 48通过解这个方程组,我们可以得到原长方体的长、宽、高分别为:l = 5 cm, w = 4 cm, h = 3 cm。
因此,原来长方体的体积是:l × w × h = 5 × 4 × 3 = 60 立方厘米。
一元一次方程的等积变形问题课件

长为:x+10=20+10=30米
答:该长方形的长为 30米,宽为20米.
.
示图分析
100 米
篱笆材料的长度=围成的三面墙的长度和
.
解:设仓库的宽X米. 根据题意得:
2x+x+100 3x=90 X=30
所以仓库的长为:x+10=30+10=40 米 答:该仓库的长为40米,宽为30米。
5dm 1. 5m
3dm 0. 5m
.
分析: 根据以上演示我们知道了它们的等量关系: 水位上升部分的体积 =小圆柱形铁块的体积 圆柱形体积公式是 _____?_r_2h, 水升高后的体积 小铁块的体积 (_____0_._5_2_?_x) (______0._3_2_×)0.5 ?
解:设水面将升高 x米, 根据题意得 方程为: _____0_._5_2_?_x_=__0_.3_2_×__0_.5 ? 解这个方程: _____x__=_0_.1_8 答:____容__器__内__水__面__将__升__高_. _0_.1_8m 。
.
等面积的变形
把一块梯形空地(如图)改成宽为30m的长 方形运动场地,要求面积不变,则应将原梯 形的上下底边作怎样的调整?
解:将下底缩短 Xm,则长方形的长
30m
是(60 -X),
由题意得:
30m
(30+60) ×30 ÷2=1350
60m
30(60 —x)=1350
解得: x=15
经检验:x=15是方程的解,且符合题意。
解:水的底面积、高度发生了变化,水的体积和 质量都保持不变 2、用一根 15cm 长的铁丝围成一个三角形,然后把它围 成长方形;
一元一次方程实际应用题之等积变形问题
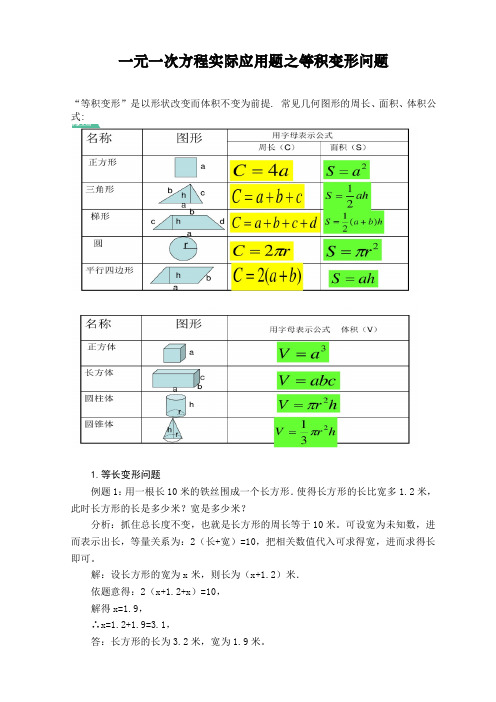
一元一次方程实际应用题之等积变形问题“等积变形”是以形状改变而体积不变为前提. 常见几何图形的周长、面积、体积公式:1.等长变形问题例题1:用一根长10米的铁丝围成一个长方形.使得长方形的长比宽多1.2米,此时长方形的长是多少米?宽是多少米?分析:抓住总长度不变,也就是长方形的周长等于10米。
可设宽为未知数,进而表示出长,等量关系为:2(长+宽)=10,把相关数值代入可求得宽,进而求得长即可。
解:设长方形的宽为x米,则长为(x+1.2)米.依题意得:2(x+1.2+x)=10,解得x=1.9,∴x=1.2+1.9=3.1,答:长方形的长为3.2米,宽为1.9米。
2.等体积变形问题例题2:要锻造直径为60mm,高为30mm的圆柱形毛坯,需截取直径为40mm的圆钢长是多少毫米?分析:抓住锻造前后的体积不变,此题的等量关系为:锻造前的体积=锻造后的体积.据此列方程求解。
要注意的是,题目中已知直径,需要转化为半径。
解:设需截取直径为40mm的圆钢长xmm,60÷2=30(mm)、40÷2=20(mm);依题意得:π×30^2×30=π×20^2×x解得:x=67.5例题3:有一段钢材可作一个底面直径 8 厘米,高 9 厘米的圆柱形零件。
如果把它改制成高是 12 厘米的圆锥形零件,零件的底面积是多少平方厘米?分析:根据“底面直径8厘米,高9厘米的圆柱形零件”,利用圆柱体积公式,可以求出圆柱的体积,又因为把圆柱形的零件改制成圆锥形零件时,此段钢的体积不变,根据体积不变列出方程求解。
解:零件的底面积是x平方厘米。
8÷2=4(厘米)依题意得:3×π×4^2×9=x×12解得:x=36π答:零件的底面积是36π平方厘米。
3.等面积变形问题例题4:如图,某小学将一块梯形空地改成宽为30m的长方形运动场地,要求面积不变.若在改造后的运动场地,小王、小李两人同时从点A出发,小李沿着长方形边顺时针跑,小王则是逆时针跑,并且小王每秒比小李多跑2m,经过10秒钟他们相遇.(1)求长方形的长;(2)求小王、小李两人的速度分析:(1)求得原梯形的面积,利用面积不变和长方形的面积求得长方形的长即可;(2)设小李的速度是xm/s,则小王的速度是(x+2)m/s,利用10秒钟他们相遇所走的路程为长方形的周长列出方程解决问题。
一元一次方程的等积变形问题

方程两边同乘或同除一个含有未知数的式子,可以消去分母,使方程化为一元一次方程。
通过这种方式,可以将方程中的某些项消去,简化方程。
方程两边同乘或同除一个含有未知数的式子
等积变形的步骤与技巧
#O3
识别等积变形的机会
观察方程 在解一元一次方程时,要时刻观察方程的形式,判断是否可以通过等积变形简化问题。 寻找等式两边的共同因子 如果等式两边有共同因子,可以通过提取共同因子简化方程。 寻找等式两边的同类项 如果等式两边有同类项,可以通过合并同类项简化方程。
03
重量不变问题
在称重过程中,当两个物体质量相等时,可以通过等积变形来求解相关问题。
01
体积不变问题
在容器中装有一定体积的水,将水倒入另一个容器,保持水的体积不变,可以通过等积变形来求解相关问题。
02
面积不变问题
在平面几何中,当两个相似图形面积相等时,可以通过等积变形来求解相关问题。
数学题目中的等积变形ຫໍສະໝຸດ 在解代数方程时,可以通过等积变形将方程转化为更易于解决的形式。
在几何图形中,可以通过等积变形将图形转化为更易于计算面积或体积的形式。
几何图形的等积变形
代数方程的等积变形
等积变形在解题中的应用
简化计算过程
通过等积变形可以将复杂的问题转化为简单的问题,从而简化计算过程。
寻找未知数
在某些问题中,可以通过等积变形来寻找未知数,从而解决问题。
解决实际问题
在解决实际问题时,等积变形可以帮助我们更好地理解问题,并找到合适的解决方案。
等积变形的注意事项与挑战
#O5
等积变形的适用范围
等积变形适用于解一元一次方程时,当方程的解为分数或根号形式时,需要进行等积变形。
一元一次方程经典讲义之等积变形

第四讲等积变形数字问题【基本数量关系】原料体积=成品体积数的表示方法:一个三位数的百位数字为a,十位数字是b,个位数字为c(其中a、b、c 均为整数,且1≤a≤9, 0≤b≤9, 0≤c≤9)则这个三位数表示为:100a+10b+c。
【典型例题】1.用直径为4厘米的圆钢,铸造三个直径为2厘米,高为16厘米的圆柱形零件,问需要截取多长的圆钢?2.某工厂锻造直径为60毫米,高20毫米的圆柱形瓶内装满水,再将瓶内的水倒入一个底面直径6厘米、高10厘米的圆柱形玻璃杯中,能否完全装下?若装不下,那么瓶内水面还有多高?若未能装满,求杯内水面离杯口的距离。
3.一个长、宽、高分别是9厘米、7厘米、3厘米的长方体铁块和一个棱长为5厘米的正方体铁块,熔化成一个圆柱体,其底面直径为20厘米,请求圆柱体的高(π不需化成3.14)4.一个两位数,十位上的数字比个位上的数字大1,十位与个位上的数字和是这个两位数的1/6,这两个数是多少?5.有一个三位数,其各数位的数字之和是16,十位数字是个位数字与百位数字的和,若把百位数字与个位数字对调,那么新数比原数大594,求原数。
【课堂精练】1.要锻造一个半径为5厘米,高为8厘米的圆柱形毛胚,应截取半径为4厘米的圆钢多长?2.某机器加工厂要锻造一个毛胚,上面是一个直径为20毫米,高为40毫米的圆柱,下面也是一个圆柱,直径为60毫米,高为20毫米,问需要直径为40毫米的圆钢多长?3.将一罐满水的直径为40厘米,高为60厘米的圆柱形水桶里的水全部灌于另一半径为30厘米的圆柱形水桶里,问这时水的高度是多少?4.一个直径为1.2米高为1.5米的圆柱形水桶,已装满水,向一个底面边长为1米的正方形铁盒倒水,当铁盒装满水时,水桶中的水高度下降了多少米?5.有一块棱长为4厘米的正方体铜块,要将它熔化后铸成长2厘米、宽4厘米的长方体铜块,铸成后的铜块的高是多少厘米(不计损耗)?6.有一个圆柱形铁块,底面直径为20厘米,高为26厘米,把它锻造成长方体毛胚,若使长方体的长为10π厘米,宽为13厘米,求长方体的高。
3.4_实际问题与一元一次方程-等积变形问题

_ _x厘米 30厘米 15厘米 可列方程:π×32x-π22(18-15)=π×22×15
3厘米
等量关系2:水的体积+水中金属柱的体积=水加柱的体积
可列方程:π×32×15+π×22×18=π×32(15+x)
解:设容器内放入金属圆柱后水面升高x厘米
(1)容器内的水面升高后没有淹没金属圆柱,那么由题
一元一次方程的应用
等积变形问题
要想求出某个同学的体积是多少?你怎么测量呢?
升高的水的 体积恰好等 于人的体积。
R h
你还能举出相类似的事例吗? (古代:曹冲称象)
例题7
2厘米
设水面升高了x厘米
18厘米
2厘米
3厘米
3厘米 x 厘 米
厘 米 30厘米 15厘米
x
18厘米 15厘米
金属柱没有被淹没的情况:
(或:π×32×15+π×22×18=π×32(15+x)) 解得:x=8 经检验x=8符合题意 所以,容器内水面升高8厘米
练习
一个盛有水的圆柱形容器里的内半径为 10cm,容器内水的高度为12cm, 把一根半径为2cm,高2厘米的玻璃柱放 入水中,问容器内水将升高多少厘米 。
意得
π×32x+π22(18-15)=π×22×15
(或π×32×15+π×22×(15+x)=π×32(15+x))
解得:x=12
因为12+15=27>18,所以此时容器内的水面已经淹没了金属柱, 不符合假定,应舍去 (2)如果容器内的水面升高后淹没放入的金属圆柱,那么由题意得
π×32x+π22(18-15)=π×22×15
华师版七年级下册数学精品教学课件 第6章 一元一次方程 第1课时 等积变形问题

解这个方程,得 x = 25.
答:这一支牙膏能用 25 次.
思考:你认为列一元一次方程解应用题的主要步骤 有哪些?关键是什么?
1. 审——通过审题找出等量关系. 2. 设——设出合理的未知数(直接或间接),注意单位名称. 3. 列——依据找到的等量关系,列出方程. 4. 解——求出方程的解(对间接设的未知数切忌继续求解). 5. 检——检验求出的值是否为方程的解,并检验是否符
1. 一个长方形的周长是 40 cm,若将长减少 8 cm,
宽增加 2 cm,长方形就变成了正方形,则正方
形的边长为 ( B )
A. 6 cm
B. 7 cm
C. 8 cm
D. 9 cm
2. 一个梯形的面积是 60 cm2,高为 5 cm,它的上底比 下底短 2 cm,求这个梯形上底和下底的长度.设下底长 为 x cm,则下面所列方程正确的是 ( C )
合实际问题. 6. 答——注意单位名称.
做一做 1. 要锻造一个直径为 8 厘米、高为 4 厘 米的圆柱形毛坯,则至少应截取直径为 4 厘米 的圆钢___1_6__厘米.
2. 钢锭的截面是正方形,其边长是 20 厘米,要 锻造成长、宽、高分别为 40 厘米、30 厘米、10 厘米的长方体,则应截取这种钢锭多长? 答:应截取这种钢锭 30 厘米.
2.9×2.1 = 6.09 (m2),(1) 中长方形的面积为 3.2×1.8 =
5.76 (m2). 此时长方形的面积比 (1) 中长方形的面积增大 6.09-
5.76 = 0.33 (m2).
(3) 若该长方形的长与宽相等,即围成一 个正方形,则正方形的边长是多少?它围成的 正方形的面积与 (2) 中相比,又有什么变化?
4-3一元一次方程的应用(二) 等积变形问题2022-2023学年鲁教版(五四制)六年级上册

变式训练
1.两个圆柱体容器如图所示,它们的直径分别为4cm 和8cm,高分别为39cm和10cm。我们先在第二个容 器中倒满水,然后将其倒入第一个容器中。问:倒 完以后,第一个容器中的水面离瓶口有多少厘米?
容器1
容器2
变式训练
2. 如图所示,小明将一张正方形纸片剪去一个宽为
4cm的长条后,再从剩下的长方形纸片上剪去一个宽
方形的面积比(1)中长方形的面积增大了0.33㎡。
(3)设正方形的边长为xm。根据题意,得,
4x=10
解这个方程,得 x=2.5 2.5×2.5=6.25(㎡) 6.25-6.09=0.16(㎡)
这个正方形的边长为 2.5 m,它的面积比 (2)中长方形的面积增大了0.16㎡。
点拨
5.76
6.09
谢谢
9cm 20cm
X cm 10cm
合作交流
• 题设已经给出了等量关系:锻压过程中圆 柱体积不变,几变形后的体积等于变形前 的体积。
• 未知量是? 已知量是?
例1:
用一根长为10m的铁丝围成一个长方形。
(1)使得这个长方形的长比宽多1.4m,此时长方形的 长、宽各为多少米? (2)使得这个长方形的长比宽多0.8m,此时长方形的 长、宽各为多少米?这个长方形(1)中的长方形相比, 面积有什么变化? (3)使得这个长方形的长与宽相等,即围成一个正方 形,此时正方形的边长是多少米?它的面积与(2)中 的长方形的面积相比又有什么变化?
分析:由题意知,长方形的周长始终是不变的,即
长方形的周长=10m
在解决这个问题的过程中,要抓住这个等量关系。
解:(1)设此时长方形的宽为xm,则它的长为(x+1.4)m。
根据题意,得
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2 ×0.5 0.3 (_________)
r2h
解:设水面将升高x米, 根据题意得
2 x = 0.32 ×0.5 0.5 方程为:___________________
x =0.18 解这个方程:__________
容器内水面将升高0.18m。 答:______________________
例1:用直径为200毫米的圆柱体钢,锻造一个长、 宽、高分别为300毫米、300毫米和90毫米的长方 体毛坯,应截取多少毫米长的圆柱体钢?(计算 时取3.14.要求结果误差不超过1毫米)
200
x
90
300
300
圆柱体钢
长方体毛坯
分析题意,找出等量关系 : 圆柱体钢体积 = 长方体毛坯体积 解:设应截取圆柱体钢长为x毫米,根据题意 可得:
练
习
2.已知一圆柱形容器底面半径为0.5m,高为1.5m,里
面盛有1m深的水,将底面半径为0.3m,高为0.5m的
圆柱形铁块沉入水中,问容器内水面将升高多少?
5dm 1. 5m
3dm
0. 5m
分析: 根据以上演示我们知道了它们的等量关系: 水位上升部分的体积=小圆柱形铁块的体积 圆柱形体积公式是_______, 水升高后的体积 小铁块的体积 (__________)
22cm 10cm
A
B
200 3.14 x 300 300 90 2 x 258 解得:
答:应截取圆柱体钢的长约为258毫米。
2
练
习
1.将一个底面直径为10厘米,高为36厘米的“瘦
长”形圆柱锻压成底面直径是20厘米的“矮胖”
形圆柱,高变成了多少? 锻压 等量关系:变形前的体积=变形后的体积
一元一次方程的应用
——等积变形问题
常见图形周长及面积公式
名称
正方形 三角形 梯形 圆 平行四边形
图形
用字母表示公式
周长(C) a 面积(S)
C 4a
c
S a
2
b
h a b a r
C abc
d
1 S ah 2
S 1 ( a b) h 2
c
h
C abcd
C 2r
示图分析
100米
(X+10)米
x米
有什么等量关系呢?
长方形的周长=原铁丝的长度.
等长变形:
2、有100米长的篱笆材料,想围成一长
方形仓库,在场地的北面有一堵足够长的
旧墙,其它三面用篱笆围成,若与墙平行
的一面为长,且长比宽长10米,求这个仓
库的长和宽?
示图分析
100 米
篱笆材料的长度=围成的三面墙的长度和
30m
30m
(30+60) ×30 ÷2=1350
30(60 —x)=1350
解得:x=15
60m
答:将下底由60m缩小到45m.将上底30m放大到45m.
要想求出某个同学的体积是多少?你怎么测量呢?
R h
你还能举出相类似的事例吗? (古代:曹冲称象)
想一想:请指出下列过程中,哪些量发生了变化,
小结:列方程解应用题的一般步骤:
列一元一次方程解应用题的一般步骤:
1、审题:分析题意,找出题中数量及其关系; 2、设元:选择一个适当的未知数用字母表示; 3、列方程:根据等量关系列出方程. 4、解方程:求出未知数的值. 5、检验:检验求得的值是否正确和符合实际情形, 并写出答案.
合作讨论
如图,有A,B两个圆柱形容器,A容器的底面 积是B容器底面积的2倍,B容器的壁高为 22cm。已知A容器内装水的高度为10cm,若 把这些水倒入B容器,水会溢出吗?
解:设仓库的宽X米. 根据题意得:
2x+x+10=100 3x=90 X=30
所以仓库的长为:x+10=30+10=40米
答:该仓库的长为40米,宽为30米。
等面积的变形
把一块梯形空地(如图)改成宽为30m的长 方形运动场地,要求面积不变,则应将原梯 形的上下底边作怎样的调整?
解:将下底缩短Xm,则长方形的长 是(60 -X), 由题意得:
哪些量保持不变?
1、把一小杯水倒入另一只大杯中; 解:水的底面积、高度发生了变化,水的体积和 质量都保持不变 2、用一根15cm长的铁丝围成一个三角形,然后把它围 成长方形;
解:围成的图形的面积发生了变化,但铁丝的长度不变 3、用一块橡皮泥先做成一个立方体,再把它改变成球。
解:形状改变,体积不变
例题学习
C 2a b
S r
2
h a
b
S ah
常见图形的体积公式
名称 图形 用字母表示公式 体积(V)
正方体
a
V a
c b
3
长方体
2
圆柱体
h
r
圆锥体
h r
1 2 V r h 3
等长变形
1、用一根长为100米的铁丝围成一个
长比宽长10米的长方形,问这个长方形的 长和宽各是多少米?
