平面图形的几何性质
平面解析几何

平面解析几何解析几何是数学中的一个分支,通过使用代数方法和几何方法相结合的方式来研究图形和方程的关系。
在解析几何中,平面是一个重要的概念。
本文将对平面在解析几何中的应用进行介绍。
一、平面的定义与性质在解析几何中,平面可以被定义为一个无限大的二维空间,其中的点满足一定的条件。
平面可以用方程或参数方程的形式表示。
平面有一些重要的性质,包括与平面相关的坐标系、平面上的直线、平面的方程等等。
二、平面上的点与直线在平面上,点是最基本的元素。
点在平面上的位置可以用坐标表示。
平面上的直线可以有不同的表示形式,包括斜截式、点斜式、一般式等。
通过点和直线的关系,我们可以研究平面上的几何图形以及它们之间的性质。
三、平面曲线与方程在解析几何中,平面曲线是指在平面上由给定方程或参数方程描述的图形。
常见的平面曲线包括直线、抛物线、椭圆、双曲线等等。
解析几何中,研究平面曲线的方法主要是通过代数方程的分析来获得几何信息。
四、平面的变换在解析几何中,平面的变换是指将平面上的点按照一定规则进行转换的操作。
常见的平面变换包括平移、旋转、镜像、放缩等等。
通过平面变换,我们可以研究平面上的对称性、相似性等几何性质。
五、平面解析几何的应用平面解析几何在实际中有广泛的应用。
它可以用来描述物体在平面上的运动轨迹,例如抛物线可以用来描述抛体的运动。
平面解析几何也常被应用于物理学、工程学、计算机图形学等领域。
例如,在计算机图形学中,平面解析几何可以用来描述二维图形的形状和变换。
六、总结解析几何是数学中的一个重要分支,平面是解析几何的基本概念之一。
通过使用代数方法和几何方法相结合,我们可以研究平面上的点、直线、曲线以及它们之间的关系和性质。
平面解析几何在实际中有广泛的应用,可以用来描述物体的运动轨迹以及在各个领域的应用。
通过学习和应用平面解析几何,我们可以更好地理解和应用数学知识。
惯性矩
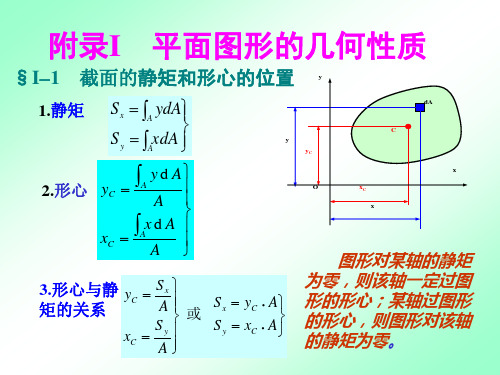
x0
x IIII 10
120
10
C
70
I y I Iy I IIy I IIIy 1.84106 mm 4
5.08106 mm 4
I xy I Ixy I IIxy I IIIxy -2.31106 mm 4
附录I 平面图形的几何性质
§I-1 截面的静矩和形心的位置
1.静矩
S x A ydA S y AxdA
y yC x O xC y dA C
y d A 2.形心 yC A A xd A A xC A
x
3.形心与静 yC S x S x yC A A 矩的关系 或 Sy S y xC A
yC O
dy
S x 2r 3 / 3 4r yC 2 A r / 2 3
C r
y x
例I-2 求图示图形的形心。 解:将此图形分别为I、II、III三 部分,以图形的铅垂对称轴为y轴, 过II、III的形心且与y轴垂直的轴线 取为x轴,则
yC Ay A
i Ci
10
y y1
200
10 I II O III
300
C y 150 C
x1
x
i
(20010) (5 150) 2 (10 300) 0 20010 2 (10 300) 38.8 mm
由于对称知: xC=0
§I-2 极惯性矩 惯性矩 惯性积
1.极惯性矩: I p A 2 dA 为图形对一点的极惯性矩;
[I z C 1 ( y C - y 1 ) 2 A 1 ][ I z C 2 ( y C - y 2 ) 2 A 2 ] 34530mm 4
任务七平面图形的几何性质
任务七 平面图形的几何性质一、填空题1. 图示B H ⨯的矩形中挖掉一个b h ⨯的矩形,则此平面图形的z W =( 2366z BH bh W H=- )。
2. 对图示矩形,若已知x I 、y I 、b 、h ,则11x y I I +=( 1122()/12y z y z I I I I bh b h +=+=+ )。
3. 任意平面图形至少有( 1 )对形心主惯性轴,等边三角形有( 无穷多 )对形心主惯性轴。
4.在边长为2a 的正方形的中心部挖去一个边长为a 的 正方形,则该图形对y 轴的惯性矩为( 454a )。
5.图形对所有平行轴的惯性矩中,图形对形心轴的惯性矩为( 最小 )。
6.对直径为d 的圆形截面,它的惯性半径为( i=d/4 )。
二、选择题1.在下列关于平面图形的结论中,( D )是错误的。
A.图形的对称轴必定通过形心;B.图形两个对称轴的交点必为形心;C.图形对对称轴的静矩为零;D.使静矩为零的轴为对称轴。
2.在平面图形的几何性质中,( D )的值可正、可负、也可为零。
A.静矩和惯性矩B.极惯性矩和惯性矩C.惯性矩和惯性积D.静矩和惯性积。
3.设矩形对其一对称轴z 的惯性矩为I ,则当其长宽比保持不变。
而面积增加1倍时,该矩形对z 的惯性矩将变为( D )。
A. 2IB. 4IC. 8ID. 16I 4.若截面图形有对称轴,则该图形对其对称轴的( A )。
A.静矩为零,惯性矩不为零B.静矩不为零,惯性矩为零C.静矩和惯性矩均为零D.静矩和惯性矩均不为零 5.若截面有一个对称轴,则下列说法中( D )是错误的。
A. 截面对对称轴的静矩为零;B. 对称轴两侧的两部分截面,对对称轴的惯性矩相等;C. 截面对包含对称轴的正交坐标系的惯性积一定为零;D. 截面对包含对称轴的正交坐标系的惯性积不一定为零。
6.任意图形,若对某一对正交坐标轴的惯性积为零,则这一对坐标轴一定是该图形的( B )。
6.3平行移轴公式

第6章 平面图形的几何性质6.3 惯性矩和惯性积的平行移轴公式 主轴和主惯性矩6.3.1 惯性矩和惯性积的平行移轴公式任一平面图形如图6.9所示,其面积为A ,形心为C ,坐标轴y c 和z c 为形心轴。
正交坐标轴y 、z 与形心轴y c 、z c 平行,两对平行轴之间的间距分别为a 和b 。
截面对y c 轴、z c 轴的惯性矩I y c、I z c 及惯性积I y z c c 为已知,现求图形对y 、z 轴的惯性矩和惯性积。
图中任一点在两坐标系下的坐标关系为=+z z a c =+y y b c由式(6.5)⎰⎰⎰⎰==+=++I z A z a A z A a z A a AAAAy c c c d ()d d 2d 2222其中⎰=z A I Ac y cd 2,⎰=A A Ad ,⎰=z A S Ac y cd 。
因y c 为形心轴,所以=S y c 0,于是可得同理 ⎭⎪=+⎪⎬=+⎪⎪=+⎫I I abA I I b A I I a A yz y z z z y y c c c 22c (6.9)上式即为惯性矩和惯性积的平行移轴公式(parallel-axis theorem )。
因为a A 2和b A 2均为正,所以在所有相互平行的轴中,同一图形对形心轴的惯性矩最小。
在应用公式(6.9)时需注意,a 、b 是图形的形心C 在yOz 坐标下的坐标,有正、负之分。
同时,y c 、z c 轴一定是形心轴。
6.3.2 主轴和主惯性矩由式(6.6)可知,同一图形对不同的一对直角坐标轴的惯性积是不同的,若图形对某一对直角坐标轴的惯性积等于零,则该直角坐标轴称为主惯性轴,或简称为主轴(principal axes )。
图形对主轴的惯性矩称为主惯性矩(principal moment of inertia )。
通过图形形心的主轴称为形心主轴(centroidal axis ),图形对形心主轴的惯性矩称为形心主惯性矩(principal moment of inertia for an area )。
平面图形的认识(ppt)

学习立体几 何
学习图形的 变换
图形的组合是研究如何将多个图形组合在一起形成更 复杂图形的方法,通过学习图形的组合,可以更深入
地理解图形的构造和应用。
学习图形的 组合
图形的变换是研究图形在平面上如何移动和变换的方 法,通过学习图形的变换,可以更深入地理解图形的 几何性质和应用。
THANKS
感谢观看
边长关系
平面图形中的边长关系是指图形中各 边之间的长度关系。例如,等边三角 形的三条边长度相等,而等腰梯形的 两条腰长度相等。
面积和周长的计算
面积计算
面积是指平面图形所占的面积大小。不同形状的平面图形有不同的面积计算公 式。例如,正方形的面积是边长的平方,而圆的面积是π乘以半径的平方。
周长计算
周长是指平面图形的边界长度。不同形状的平面图形有不同的周长计算公式。 例如,正方形的周长是4乘以边长,而圆的周长是2π乘以半径。
转不变性。
圆形在几何学中具有重要的地位, 是许多定理和公式的核心。
圆形可以用于表示钟表、方向盘、 车轮等物体的外轮廓。
其他平面图形
其他常见的平面图形还包括五边形、六边形、扇形、椭圆等 。
这些图形在日常生活和科学研究中都有广泛的应用,如五角 星、蜂巢等。
03
平面图形的性质和特点
对称性
第一季度
第二季度
平面图形的认识
• 引言 • 平面图形的分类 • 平面图形的性质和特点 • 平面图形在实际生活中的应用 • 总结与展望
01
引言
主题简介
01
平面图形是数学和几何学中的基 本概念,是指二维空间中的图形 。
02
平面图形通常由直线、曲线、多 边形等基本元素构成,具有多种 属性和特征。
《材料力学》课程讲解课件附录I平面图形几何性质

解:
y
d
S x
yd A
A
2 yb( y) d y
0
b(y)
C
xc
yc
d
2 y2
R2 y2 d y d3
0
12
x
d
yc
Sx A
d3 12 πd 2 8
2d 3π
b( y) 2 R2 y2
29
yc
Sx A
d3 12 πd 2 8
2d 3π
y
2、求对形心轴 xc 的惯性矩
Ix
πd 4 64 2
3、惯性积是对轴而言。
y
z
dA
4、惯性积的取值为正值、负值、零。
y
5、规律:
o
z
20
5、规律:
Izy
zydA
A
0
y
dA z z dA
y
y
z
o
两坐标轴中,只要有一个轴为图形的对称轴,则 图形这一对坐标轴的惯性积为零。
21
对比记忆 静矩、形心;惯矩和惯性半径;它们都是反映截
面面积关于坐标轴分布情况的物理量。 静矩=(面积)(形心坐标) 惯矩=(面积)(惯性半径)2
z
o
dA y
z
全面积对z轴的惯性矩: I z y2dA,
2 z2 y2
全面积对y轴的惯性矩: I y A z2dA
A
15
Iz y2dA, I y z2dA
A
A
y
z
dA
y
o
z
2、量纲:[长度]4;单位:m4、cm4、mm4。 2 z2 y2
3、惯性矩是对轴而言(轴惯性矩)。
A
《生活中平面图形》课件

CATALOG
DATE
ANALYSIS
SUMMARY
《生活中平面图形》 ppt课件
目录
CONTENTS
• 平面图形的基本概念 • 生活中的常见平面图形 • 平面图形的设计与创意 • 平面图形与生活的关系
REPORT
CATALOG
DATE
ANALYSIS
SUMMAR Y
01
平面图形的基本概念
文化内涵
平面图形可以融入文化元素, 展现地域特色和民族风情。
REPORT
CATALOG
DATE
ANALYSIS
SUMMAR Y
04
平面图形与生活的关系
生活中的平面图形元素
交通工具
如汽车、飞机、火 车的车身和座椅设 计。
服饰
如衣服、鞋子、包 包的图案和款式设 计。
家居装饰
如墙纸、地毯、窗 帘等图案设计。
02
生活中的常见平面图形
圆形
总结词
完美的对称,流畅的弧线
详细描述
圆形在生活中无处不在,如太阳、盘子、轮胎等。它具有完美的对称性,给人一 种完整、和谐的感觉。圆形还具有流畅的弧线,使得它成为一种优雅的图形。
三角形
总结词
稳定、力量和方向
详细描述
三角形是一种具有稳定性的图形,常用于需要支撑或稳定的结构,如桥梁、建筑等。它还给人一种力量和方向感 ,常用于代表进取、积极向上的意象。
平面图形的基本性质
总结词
平面图形具有一些基本的几何性质,如对称性、角度、边长等。
详细描述
平面图形可能具有对称性,即图形沿某一直线折叠后两部分能够重合;平面图 形由线段构成,具有角度和边长等基本属性,这些属性可用于描述图形的形状 和大小。
平面几何形的平移性质

平面几何形的平移性质在我们的日常生活和数学世界中,平面几何形的平移是一个常见且重要的概念。
平移,简单来说,就是将一个图形沿着某个方向移动一定的距离,而图形的形状、大小和方向都保持不变。
让我们先来直观地感受一下平移。
想象一下,你在一张纸上画了一个正方形,然后你把这张纸沿着水平方向向右移动了一段距离,纸上的正方形也跟着移动了相同的距离,这个正方形的形状和大小没有发生任何变化,这就是一个简单的平移过程。
平移具有一些非常重要的性质。
首先,平移前后的图形是全等的。
这意味着平移不会改变图形的边长、角度、面积等几何量。
比如,一个三角形经过平移后,它的三条边长度、三个角的大小以及面积都和原来的三角形完全相同。
其次,平移具有保向性。
也就是说,平移前后图形的方向不变。
例如,一个箭头形状的图形在平移后,箭头所指的方向依然保持不变。
再来看平移在坐标系中的表现。
在平面直角坐标系中,如果一个点(x, y) 向右平移 a 个单位,向上平移 b 个单位,那么它平移后的坐标就变成了(x + a, y + b) 。
这个规律对于直线、曲线等图形同样适用。
比如,对于直线 y = 2x + 1 ,如果将其向右平移 3 个单位,向上平移2 个单位,那么新的直线方程就是 y 2 = 2(x 3) + 1 ,整理后得到 y= 2x 3 。
平移在解决实际问题中也有广泛的应用。
比如在建筑设计中,设计师们常常需要将一个房间的布局或者一个建筑物的某个部分进行平移,以达到更好的空间利用效果。
在计算机图形学中,平移操作是实现图像移动和动画效果的基础。
在数学证明中,平移也能发挥很大的作用。
有时候,通过巧妙地运用平移,可以将复杂的图形关系变得简单明了,从而更容易得出证明。
举个例子,假设有两个平行四边形 ABCD 和 A'B'C'D' ,如果我们将平行四边形 A'B'C'D' 平移,使其与平行四边形 ABCD 重合,那么我们就可以更直观地发现它们之间的对应边和对应角的关系,从而证明这两个平行四边形是全等的。
