定弦定角最值问题(教师版)

合集下载

线段最值系列之（一）——定弦定角，定最值

线段最值系列之（一）——定弦定角，定最值一条线段的两个端点和该线段外一动点构成的角（动点是角的顶点），不随点的运动而变化，即该动角的度数恒定不变，称为“定弦定角”问题。

该线段称“定弦”，该运动的定值角称“定角”。

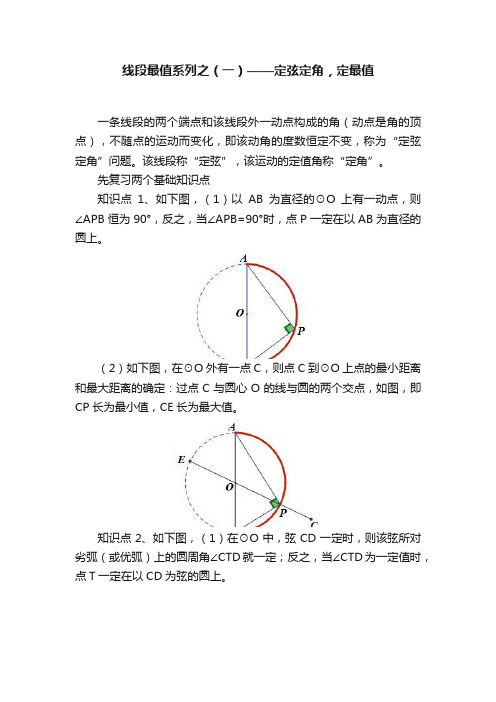
先复习两个基础知识点知识点1、如下图，（1）以AB为直径的⊙O上有一动点，则∠APB恒为90°，反之，当∠APB=90°时，点P一定在以AB为直径的圆上。

（2）如下图，在⊙O外有一点C，则点C到⊙O上点的最小距离和最大距离的确定：过点C与圆心O的线与圆的两个交点，如图，即CP长为最小值，CE长为最大值。

知识点2、如下图，（1）在⊙O中，弦CD一定时，则该弦所对劣弧（或优弧）上的圆周角∠CTD就一定；反之，当∠CTD为一定值时，点T一定在以CD为弦的圆上。

（2）如下图，在⊙O外有一点A，射线AO与圆的交点分别为点T和点E，则点A到圆的最小距离是AT的长，最大距离是AE的长。

下面，以两道典型例题来说明定弦定角在解一类线段最值题目中的应用。

例1：如图，在Rt△ABC ,∠ABC=90° ，AB=4, BC=6 ,P是△ABC 内部的一个动点，且满足∠PAB=∠PBC , 则线段CP的长度的最小值是 .(您的点赞，就是给予作者一份信心，别忘了，给作者一个鼓励，点个赞哦！)下面还有，继续……变式练习：如图，在Rt△ABC ,∠ABC=90° ，AB=4,BC=6, P是△ABC所在平面上的一个动点，且满足∠APB=90° , 则线段CP长度的取值范围是 .例2：如图，已知点E , F为等边△ABC边AB 、AC上的两动点，且AF=BE ,:连接CE , BF交于点T, 若等边△ABC的边长为6 ，则AT的长度的最小值是 .。

(完整版)定弦定角最值问题(教师版)

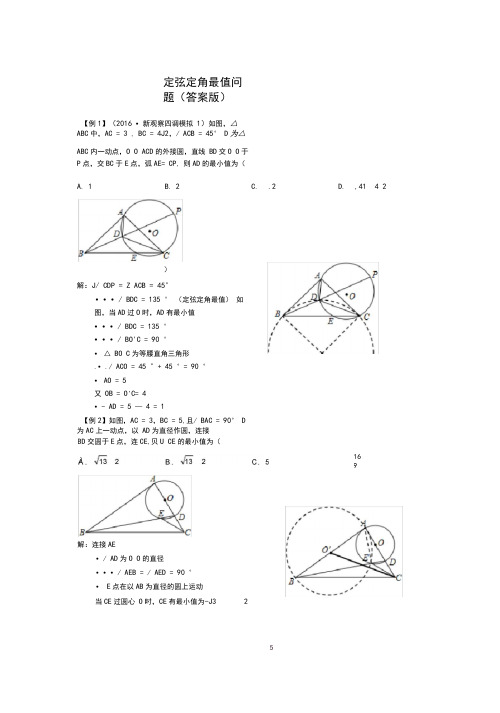
定弦定角最值问题（答案版）【例1】（2016 •新观察四调模拟1）如图，△ABC中，AC = 3 , BC = 4J2，/ ACB = 45° D为△ABC内一动点，O O ACD的外接圆，直线BD交O O于P点，交BC于E点，弧AE= CP, 则AD的最小值为（）解：J/ CDP = Z ACB = 45°•••/ BDC = 135 ° （定弦定角最值）如图，当AD过O时，AD有最小值•••/ BDC = 135 °•••/ BO'C = 90 °•△ BO C为等腰直角三角形.•./ ACO = 45 °+ 45 °= 90 °•AO = 5又OB = O'C= 4•- AD = 5 —4 = 1【例2】如图，AC = 3，BC = 5,且/ BAC = 90° D为AC上一动点，以AD为直径作圆，连接当CE过圆心O时，CE有最小值为-J3 2BD交圆于E点，连CE,贝U CE的最小值为（）169解：连接AE•/ AD为O O的直径•••/ AEB = / AED = 90 °•E点在以AB为直径的圆上运动C. .2D. ,414 2A. 1B. 21）如图，在△ ABC 中，AC = 3，BC = 4 . 2，/ ACB = 45° AM IIBC ，点P 在射线AM 上运动，连 BP 交厶APC 的外接圆于 D ，则AD 的最小值为（）A . 1 ■_W【练】（2015 •江汉中考模拟-.oAB4..3c交aB 223 *0CD2B . 6 33 A . 12 6,3C . 12 3.3D . 6 A.-啕诂目隹丹丘it 按丿E 易汞丄片虾・圧戸二上*虾・宴罠厶乂肚的叢丸丽希则点芒駆腼閉壯\ AB=1^, ^ACB=XT,R^AMB =<M *・当^c^t^jsfn 中屯肘* 点闭肋睡琥大.此01氐册?两梅三甸肪CV2樁+玄皿L*X2括X （2』J"・&+M ，放说3,【练】（2014 •洪山区中考模拟 1）如图，O O 的半径为1,弦AB = 1,点P 为优弧AB 上一动点,••• AD 的最小值为 5 — 4= 1 % /■…/【例3】（2016 •勤学早四调模拟 1）如图，O O 的半径为2,弦AB 的长为2... 3，点P 为优弧上一动点，AC 丄AP 交直线PB 于点C ,则△ ABC 的面积的最大值是（.⑼M 救学早呵H 權H n »）才闻，®。

完整版定弦定角最值问题教师版

定弦定角最值问题（答案版）△45°＝【例1】(2016·新观察四调模拟1)如图，△ABC中，AC3，BC为＝＝，∠，ACBD24，CP于E点，弧AE＝△ACD的外接圆，直线BD交⊙O于P点，交BCABC内一动点，⊙O为的最小值为（）则AD．B．2CD．A．12241?4＝45°：∵∠CDP＝∠ACB解135°（定弦定角最值）∴∠BDC＝AD有最小值过O′时，如图，当AD 135°∵∠BDC＝＝BO90°′C∴∠BO′C∴△为等腰直角三角形∴∠ACO′＝45°＋45°＝90°∴AO′＝5又O′B＝O′C＝4∴AD＝5－4＝1【例2】如图，AC＝3，BC＝5，且∠BAC＝90°，D为AC上一动点，以AD为直径作圆，连接BD交圆于E点，连CE，则CE的最小值为（）162?21313?．D．B．5A．C 9解：连接AE∵AD为⊙O的直径∴∠AEB＝∠AED＝90°∴E点在以AB为直径的圆上运动13?2 CE有最小值为CE过圆心O′时，当42，∠ACB＝45°，3，BC＝AM∥BC，AC如图，在(2015【练】·江汉中考模拟1)△ABC中，＝点P在射线AM上运动，连BP交△APC的外接圆于D，则AD的最小值为（）A．1B．2242?3 ．D ．CCD解：连接＝∠ACB＝45°∴∠PAC＝∠PDC135°BDC＝∴∠AD有最小值如图，当AD过圆心O′时，135°∵∠BDC＝90°∴∠BO′C＝4 B′＝O′C＝∴O又∠＝90°ACO′5′＝∴AO1＝5－4∴AD的最小值为32AB例【3】(2016·勤学早四调模拟1)如图，的长为P，点的半径为2，弦AB为优弧⊙O ABC的面积的最大值是（）C上一动点，AC⊥AP交直线PB于点，则△3633?12312?66?334?．．AC．B ． D·洪山区中考模拟1)如图，⊙O的半径为1，弦AB＝1，点P为优弧【练】(2014AB上一动点，AC⊥AP交直线PB于点C，则△ABC的最大面积是（）12．A． B 2233．．C D 24为弧于E、F两点，CAB(3，0)，以为直径作⊙M，射线OF交⊙M，【例5】如图，A(10)、B__________的中点．当射线绕O点旋转时，CD的最小值为AB的中点，D为EF解：连接DM的中点D是弦EF∵EF∴DM⊥为直径的圆上运动为圆心的，OM∴点D在以A有最小值时，CD当CD过圆心A连接CM AB 的中点∵C为弧⊥AB∴CM CD的最小值为∴12?的中点，连接AP是60°，P是上一动点，D，∠AB【练】如图，是⊙O的直径，AB＝2ABC＝__________ 的最小值为CD，则CDOD解：连接D为弦AP的中点∵OD⊥AP∴在以AO为直径的圆上运动∴点D CD有最小值′当CD过圆心O时，过点C作CM⊥AB于M∵OB＝OC，∠ABC＝60°∴△OBC为等边三角形13，CM＝∴OM＝22．7＝C∴O′417的最小值为CD∴?24练习：如图，在动点C与定长线段AB组成的△ABC中，AB＝6，AD⊥BC于点D，BE⊥AC于点E，DE2 _________AB 的距离的最大值是到CDE连接．当点在运动过程中，始终有，则点C?AB2。

高一数学《三角函数的最值问题》苏教版

y 1 a s in x a c o s x a 2 s in x c o s x
令 tsinxcosx,
则sinxcosx1t2 2
t [ 2, 2]
所以y1ata21t2
2
即 ya2t2 at1a2
2
2
ppt课件
返回
1求值函数yy2sisnin 四x x、 3co 课asxc在后os区练x间＋习4 0， 2上的最小
三角函数中的几种最值问题
ppt课件
一、典型例题
例1 已知函数，f(x ) 2 s in 2x 3 a c o sx a (a 是常数 ) x [ 0 , ], 求其最大值；
2 例题小结：例1是把三角函数的问题转换为二次型函数来处理的。
ppt课件
一、典型例题
变1 已知函数，f(x ) 2 s in 2x 23 ac o s 2x a (a 是常数 )
例题小结：
例2及变3都是利用对三角公式的应用，都把三角函数式中的
y a s in x b c o s x 结构，化为 y a 2 b 2 s in (x )
来处理。
ppt课件
探究：能否用我二们已、经探复习索的研求究最值的方法，解
探决以究下1：求问函题数？y [1 c o s(3 x )](1 c o sx )的最小值。
ppt课件
三、课堂小结
三角函数中几个求最值的方法：
（1）把三角函数转换为二次型函数处理。
（2）把三角函数转换为y a2b2sin(x)处
理。（3）三角函数中固定的结构关系特征，如sinx+cosx,sinxcosx , 通过换元来处理。
ppt课件
探究1解：y(1 sinx)(1 co sx)

定弦定角最值问题

定弦定角最值问题【定弦定角题型的识别】有一个定弦，一个主动点，一个从动点，定弦所对的张角固定不变。

【题目类型】图形中一般求一个从动点到一个定点线段长度最值问题，一般涉及定弦定角最值问题【解题原理】同弧所对的圆周角相等，定弦的同侧两个圆周角相等，则四点共圆，因此动点的轨迹是圆。

（线段同侧的两点对线段的张角相等，则这两点以及线段的两个端点共圆。

）【一般解题步骤】①让主动点动一下，观察从动点的运动轨迹，发现从动点的运动轨迹是一段弧。

②寻找不变的张角（这个时候一般是找出张角的补角，这个补角一般为45°、60°或者一个确定的三角函数的对角等）③找张角所对的定弦，根据三点确定隐形圆。

④确定圆心位置，计算隐形圆半径。

⑤求出隐形圆圆心至所求线段定点的距离。

⑥计算最值：在此基础上，根据点到圆的距离求最值（最大值或最小值）。

【例1】(2016·新观察四调模拟1)如图，△ABC 中，AC ＝3，BC ＝24，∠ACB ＝45°，D 为△ABC 内一动点，⊙O 为△ACD 的外接圆，直线BD 交⊙O 于P 点，交BC 于E 点，弧AE ＝CP ，则AD 的最小值为（）A ．1B ．2C ．2D ．2441-解：∵∠CDP ＝∠ACB ＝45°∴∠BDC ＝135°（定弦定角最值）如图，当AD 过O ′时，AD 有最小值∵∠BDC ＝135°∴∠BO ′C ＝90°∴△BO ′C 为等腰直角三角形∴∠ACO ′＝45°＋45°＝90°∴AO ′＝5又O ′B ＝O ′C ＝4∴AD ＝5－4＝1【例2】如图，AC ＝3，BC ＝5，且∠BAC ＝90°，D 为AC 上一动点，以AD 为直径作圆，连接BD 交圆于E 点，连CE ，则CE 的最小值为（）A ．213-B ．213+C ．5D ．916解：连接AE∵AD 为⊙O 的直径∴∠AEB ＝∠AED ＝90°∴E 点在以AB 为直径的圆上运动当CE 过圆心O ′时，CE 有最小值为213-【练】(2015·江汉中考模拟1)如图，在△ABC 中，AC ＝3，BC ＝24，∠ACB ＝45°，AM ∥BC ，点P 在射线AM 上运动，连BP 交△APC 的外接圆于D ，则AD 的最小值为（）A ．1B ．2C ．2D ．324-解：连接CD ∴∠PAC ＝∠PDC ＝∠ACB ＝45°∴∠BDC ＝135°如图，当AD 过圆心O ′时，AD 有最小值∵∠BDC ＝135°∴∠BO ′C ＝90°∴O ′B ＝O ′C ＝4又∠ACO ′＝90°∴AO ′＝5∴AD 的最小值为5－4＝1【例3】(2016·勤学早四调模拟1)如图，⊙O 的半径为2，弦AB 的长为32，点P 为优弧AB 上一动点，AC ⊥AP 交直线PB 于点C ，则△ABC 的面积的最大值是（）A ．3612+B ．336+C ．3312+D ．346+【练】(2014·洪山区中考模拟1)如图，⊙O 的半径为1，弦AB ＝1，点P 为优弧AB 上一动点，AC ⊥AP 交直线PB 于点C ，则△ABC 的最大面积是（）A ．21 B ．22 C ．23 D ．43【例5】如图，A (1，0)、B (3，0)，以AB 为直径作⊙M ，射线OF 交⊙M 于E 、F 两点，C 为弧AB 的中点，D 为EF 的中点．当射线绕O 点旋转时，CD 的最小值为__________解：连接DM∵D 是弦EF 的中点∴DM ⊥EF∴点D 在以A 为圆心的，OM 为直径的圆上运动当CD 过圆心A 时，CD 有最小值连接CM∵C 为弧AB 的中点∴CM ⊥AB∴CD 的最小值为12-【练】如图，AB 是⊙O 的直径，AB ＝2，∠ABC ＝60°，P 是上一动点，D 是AP 的中点，连接CD ，则CD 的最小值为__________解：连接OD∵D 为弦AP 的中点∴OD ⊥AP∴点D 在以AO 为直径的圆上运动当CD 过圆心O ′时，CD 有最小值过点C 作CM ⊥AB 于M∵OB ＝OC ，∠ABC ＝60°∴△OBC 为等边三角形∴OM ＝21，CM ＝23∴O ′C ＝47 ∴CD 的最小值为2147。

定弦定角问题

定弦定角问题
定弦定角问题是指在数学圆中，半径相等的圆内，长度相等的弦所对应的圆心角相等，与圆心同旁的圆周角相等，与圆心易侧的圆周角相等。

这些问题通常涉及到弦的长度、圆心角的大小、圆周角的大小等方面的计算和比较。

下面是一些相关的例题和解决方法:
- 例 1:在三角形 abc 中，ac=bc=2，角 ac=90o，则角 bc 的度数为多少？
解决方法：根据定弦定角问题，可知弦 ac 的长度是 bc 的一半，即弦 ac=√3/2 bc，又因为角 ac=90o，所以角 bc=45o。

- 例 2:在三角形 abc 中，ac=2bc=4，则角 bc 的度数为多少？
解决方法：同样根据定弦定角问题，可知弦 ac 的长度是 bc 的一半，即弦 ac=√3/2 bc，因为角 ac=90o，所以角 bc=45o。

- 例 3:在圆 o 中，弦 ab 的长度为 2，圆心角 ab 的大小为360o/2=180o,则弦 ab 所对的圆心角为多少？
解决方法：根据定弦定角问题，可知弦 ab 的长度是圆心角 ab 的大小的一半，即弦 ab=√3/2 圆心角 ab，因为圆心角 ab=180o，所以弦 ab 所对的圆心角为 360o/2=180o。

- 例 4:在三角形 abc 中，ac=2bc=4，则角 bc 的度数为多少？
解决方法：同样根据定弦定角问题，可知弦 ac 的长度是 bc 的一半，即弦 ac=√3/2 bc，因为角 ac=90o，所以角 bc=45o。

总之，定弦定角问题是数学圆中比较基础的问题，熟练掌握这些问题的解决方法对于圆的学习和应用都是非常重要的。

定弦定角最值问题

定弦定角最值问题（教师版）work Information Technology Company.2020YEAR定弦定角最值问题（答案版）【例1] （2016 •新观察四调模拟1）如图，△ABC 中，AC=3, BC= 4迈,ZACB = 45\ D 为厶 ABC 内•动点，OO 为△ACD 的外接圆，直线BD 交00于P 点，交BC 于E 点,弧AE=CP.则 AD 的最小值为（〉B ・2解：VZCDP=Z^CB = 45°:丄BDC= 135° （定弦定角最值）如图，当AD过时，AD 有最小值・・•乙BDC= 135°・・.乙BOQ 90。

为等腰直角三角形・・・ ZACO r = 45° + 45° = 90°・・.AO' = 5又 O ，B = OU4/.AD = 5-4= 1【例2】如图，AC = 3, BC = 5,且乙B4C = 90。

，D 为AC 上一动点，以AD 为直径作圆，连接 BD 交圆于E 点，连竺，则CK 的杲小值为（）A . V13-2 /AD 为（DO 的直径・・・乙AEB=乙AED = 90°•••E 点在以他为直径的圆上运动当CE 过圆心O 时，C£有最小值为加-2A ・1 9【练】（2015江汉中考模拟1）如图，在△ABC 中，AC = 3. BC= 4^2 f AACB = 45\ AM// BC,点P 在射线AM 上运动，连BP 交△APC 的外接圆于0则AD 的杲小值为（）C . V2D . 4佢-3 ---- M解「连接CD・・.ZPAC=乙PDC= ZACB = 45°・・・乙BDC= 135°如图，当AD 过圆心O 时，4D 有最小值V ZBDC= 135°・・・乙BO'C = 90°・・.O I B = O ,C = 4又乙 ACO' = 90°.\AO f = 5・・.AQ 的最小值为5-4=1 \/'、 __________ /【例3】（2016動学早四调模拟1）如图，OO 的半径为2,弦血的长为2羽、点P 为优弧AB 上一动点，AC 丄AP 交直线皿于点C,贝IJAABC 的面积的杲大值是（） C . 12 + 3JJ故选 B.D . 6 + 4“ ・（2016劫学早四H 模拟一TlO ）如图，©O 篱龜\^5=2 C 到曲的更樹證丸此时ZUBC 为［练】(2014P 为优弧A 〃上一动--2V32 • ・A C A/2-2V3-4 ••B D /BC 点，C 为弧【练1如图，加是【例5】如图，A(l, 0)、8(3, 0).以AB 为直径作OM,射线OF 交乜AB 的中点，》为£尸的中点•当射线绕。

定弦定角最值问题(教师版)

定弦定角最值问题（答案版）【例1】(2016·新观察四调模拟1)如图，△ABC 中，AC ＝3，BC ＝24，∠ACB ＝45°，D 为△ABC 内一动点，⊙O 为△ACD 的外接圆，直线BD 交⊙O 于P 点，交BC 于E 点，弧AE ＝CP ，则AD 的最小值为（）A ．1B ．2C ．2D ．2441-解：∵∠CDP ＝∠ACB ＝45°∴∠BDC ＝135°（定弦定角最值）如图，当AD 过O ′时，AD 有最小值∵∠BDC ＝135°∴∠BO ′C ＝90°∴△BO ′C 为等腰直角三角形∴∠ACO ′＝45°＋45°＝90°∴AO ′＝5又O ′B ＝O ′C ＝4∴AD ＝5－4＝1【例2】如图，AC ＝3，BC ＝5，且∠BAC ＝90°，D 为AC 上一动点，以AD 为直径作圆，连接BD 交圆于E 点，连CE ，则CE 的最小值为（）A ．213-B ．213+C ．5D ．916解：连接AE∵AD 为⊙O 的直径∴∠AEB ＝∠AED ＝90°∴E 点在以AB 为直径的圆上运动当CE 过圆心O ′时，CE 有最小值为213-【练】(2015·江汉中考模拟1)如图，在△ABC 中，AC ＝3，BC ＝24，∠ACB ＝45°，AM ∥BC ，点P 在射线AM 上运动，连BP 交△APC 的外接圆于D ，则AD 的最小值为（）A ．1B ．2C ．2D ．324-解：连接CD∴∠P AC ＝∠PDC ＝∠ACB ＝45°∴∠BDC ＝135°如图，当AD 过圆心O ′时，AD 有最小值∵∠BDC ＝135°∴∠BO ′C ＝90°∴O ′B ＝O ′C ＝4又∠ACO ′＝90°∴AO ′＝5 ∴AD 的最小值为5－4＝1【例3】(2016·勤学早四调模拟1)如图，⊙O 的半径为2，弦AB 的长为32，点P 为优弧AB 上一动点，AC ⊥AP 交直线PB 于点C ，则△ABC 的面积的最大值是（）A ．3612+B ．336+C ．3312+D ．346+【练】(2014·洪山区中考模拟1)如图，⊙O 的半径为1，弦AB ＝1，点P 为优弧AB 上一动点，AC ⊥AP 交直线PB 于点C ，则△ABC 的最大面积是（）A ．21 B ．22 C ．23 D ．43【例5】如图，A (1，0)、B (3，0)，以AB 为直径作⊙M ，射线OF 交⊙M 于E 、F 两点，C 为弧AB 的中点，D 为EF 的中点．当射线绕O 点旋转时，CD 的最小值为__________解：连接DM∵D 是弦EF 的中点∴DM ⊥EF∴点D 在以A 为圆心的，OM 为直径的圆上运动当CD 过圆心A 时，CD 有最小值连接CM∵C 为弧AB 的中点∴CM ⊥AB∴CD 的最小值为12【练】如图，AB 是⊙O 的直径，AB ＝2，∠ABC ＝60°，P 是上一动点，D 是AP 的中点，连接CD ，则CD 的最小值为__________解：连接OD∵D 为弦AP 的中点∴OD ⊥AP∴点D 在以AO 为直径的圆上运动当CD 过圆心O ′时，CD 有最小值过点C 作CM ⊥AB 于M∵OB ＝OC ，∠ABC ＝60°∴△OBC 为等边三角形∴OM ＝21，CM ＝23∴O ′C ＝47 ∴CD 的最小值为2147-练习：如图，在动点C 与定长线段AB 组成的△ABC 中，AB ＝6，AD ⊥BC 于点D ，BE ⊥AC 于点E ，连接DE ．当点C 在运动过程中，始终有22=AB DE ，则点C 到AB 的距离的最大值是_________。

几何中最值定值问题教师版精编版

【2013年中考攻略】专题8:几何最值问题解法探讨在平面几何的动态问题中，当某几何元素在给定条件变动时，求某几何量（如线段的长度、图形的周长或面积、角的度数以及它们的和与差）的最大值或最小值问题，称为最值问题。

解决平面几何最值问题的常用的方法有：（1）应用两点间线段最短的公理（含应用三角形的三边关系）求最值；（2）应用垂线段最短的性质求最值；（3）应用轴对称的性质求最值；（4）应用二次函数求最值；（5）应用其它知识求最值。

下面通过近年全国各地中考的实例探讨其解法。

一、应用两点间线段最短的公理（含应用三角形的三边关系）求最值：典型例题：例1.如图，/ MON=9°，矩形ABCD勺顶点A B分别在边OM ON上，当B在边ON上运动时，A随之在边OM上运动，矩形ABCD勺形状保持不变，其中AB=2 BC=1运动过程中，点D到点O的最大距离为【】A 、.21 C.平5 D 撐【答案】Ao【考点】矩【分析】如图，取AB 的中点E ,连接OE DE OD••• ODC OE+DE•••当OD E 三点共线时，点D 到点O 的距离最大, 1此时AB=2 BC=1 • OE=AE= AB=t2 DE= AD 2 AE 2 二 12 12 二 2，• OD 的最例2.在锐角三角形 ABC 中, BC=4V2，/ ABC=45，BD 平分/ ABC M ・N 分别是BD BC 上的动点，则CM+MI ®最小值是 _________M垃【分析】如图，在BA 上截取BE=BN 连接EM 【答案】【考点】【分析】 245动点问题，垂直线段的性质，勾股定理。

如图，根据垂直线段最短的性质，当 BP 丄AC 时, 得最小值。

【答案】4【考点】最短路线问题，全等三角形的判定和性质，三角形三边关系，垂直线段的性质，锐角三角函数定义，特殊角的三角函数值。

vZ ABC 的平分线交 AC 于点 D,A Z EBM M NBM在厶AME W^AMN^，v BE=BN ，Z EBM Z NBM BM=B ， •••△ BME^ BMN( SAS 。

几何中最值定值问题教师版精编版

【2013年中考攻略】专题8：几何最值问题解法探讨在平面几何的动态问题中，当某几何元素在给定条件变动时，求某几何量（如线段的长度、图形的周长或面积、角的度数以及它们的和与差）的最大值或最小值问题，称为最值问题。

下面通过近年全国各地中考的实例探讨其解法。

一、应用两点间线段最短的公理（含应用三角形的三边关系）求最值：典型例题：例1. 如图，∠MON=90°，矩形ABCD 的顶点A 、B 分别在边OM ，ON 上，当B 在边ON 上运动时，A 随之在边OM 上运动，矩形ABCD 的形状保持不变，其中AB=2，BC=1，运动过程中，点D 到点O 的最大距离为【】A ．21+B ．5C ．1455 5D ．52【答案】A 。

【考点】矩形的性质，直角三角形斜边上的中线性质，三角形三边关系，勾股定理。

【分析】如图，取AB 的中点E ，连接OE 、DE 、OD ，∵OD ≤OE+DE ，∴当O 、D 、E 三点共线时，点D 到点O 的距离最大，此时，∵AB=2，BC=1，∴OE=AE=12AB=1。

DE=2222AD AE 112=+=+=， ∴OD 的最大值为：21+。

故选A 。

例2.在锐角三角形ABC 中，BC=24，∠ABC=45°，BD 平分∠ABC ，M 、N 分别是BD 、BC 上的动点，则CM+MN 的最小值是。

【答案】4。

【考点】最短路线问题，全等三角形的判定和性质，三角形三边关系，垂直线段的性质，锐角三角函数定义，特殊角的三角函数值。

【分析】如图，在BA 上截取BE=BN ，连接EM 。

∵∠ABC 的平分线交AC 于点D ，∴∠EBM=∠NBM 。

在△AME 与△AMN 中，∵BE=BN ，∠EBM=∠NBM ，BM=BM ， ∴△BME ≌△BMN （SAS ）。

几何中最值定值问题教师版

For personal use only in study and research; not for commercial useFor personal use only in study and research; not for commercial use【2013年中考攻略】专题8：几何最值问题解法探讨在平面几何的动态问题中，当某几何元素在给定条件变动时，求某几何量（如线段的长度、图形的周长或面积、角的度数以及它们的和与差）的最大值或最小值问题，称为最值问题。

下面通过近年全国各地中考的实例探讨其解法。

【考点】矩形的性质，直角三角形斜边上的中线性质，三角形三边关系，勾股定理。

【分析】如图，取AB 的中点E ，连接OE 、DE 、OD ，∵OD ≤OE+DE ，∴当O 、D 、E 三点共线时，点D 到点O 的距离最大，此时，∵AB=2，BC=1，∴OE=AE=12AB=1。

DE=2222AD AE 112=+=+=，∴OD 的最大值为：21 。

故选A 。

例2.在锐角三角形ABC 中，BC=24，∠ABC=45°，BD 平分∠ABC ，M 、N 分别是BD 、BC 上的动点，则CM+MN 的最小值是。

中考数学几何模型重点突破讲练专题28 圆中的定弦定角和最大张角模型(教师版)

②如图②， BC BD
深入思考
（3）如图③，在 ABC 中，ห้องสมุดไป่ตู้ A 、 Ð B 、 C 均小于 120 ，用直尺和圆规作它的强等角点 Q .（不写作法，保
留作图痕迹）
（4）下列关于“等角点”、“强等角点”的说法：
①直角三角形的内心是它的等角点；
②等腰三角形的内心和外心都是它的等角点；
③正三角形的中心是它的强等角点；
故答案为：100、130 或 160．
（2）选择①：
连接 PB, PC
∵ DB DC
= DC

∴ DB
∴ BPD CPD
∵ APB BPD 180 ， APC CPD 180
∴ APB APC
∴ P 是 ABC 的等角点．
选择②
连接 PB, PC
根据垂直平分线的性质和作图方法可得：BD=CD=BC
最大。
当 AQB 的外接圆与边 PE 相切于点 Q 时， AQB 最大。
'
'
'
'
【证明】如图 28-6，作 AQB 的外接圆⊙O，设点 Q 为 PE 上不同与 Q 点的任意一点，连接 Q A 、Q B ，Q A
与⊙O 交于点 D，连接 BD，
ADB AQ ' B, AQB ADB
专题 28 圆中的定弦定角和最大张角模型
【模型 1】定弦定角模型
如图 28-1，在 ABC 中，BC 的长为定值 a ， A 为定角度，
（1）确定点 A 的运动轨迹，有 3 种情况：
①如图 28-2，当 90 时，点 A 的运动轨迹为优弧��（不与 B、C 点重合）；
②如图 28-3，当 90 时，点 A 的运动轨迹为⊙O（不与点 B、C 重合）；

(完整word版)定弦定角最值问题

定弦定角最值问题【定弦定角题型的识别】有一个定弦，一个主动点，一个从动点，定弦所对的张角固定不变。

（线段同侧的两点对线段的张角相等，则这两点以及线段的两个端点共圆。

）【一般解题步骤】①让主动点动一下，观察从动点的运动轨迹，发现从动点的运动轨迹是一段弧。

④确定圆心位置，计算隐形圆半径。

⑤求出隐形圆圆心至所求线段定点的距离。

⑥计算最值：在此基础上，根据点到圆的距离求最值（最大值或最小值）。

【例1】（2016 •新观察四调模拟 1）如图，△ ABC 中，AC = 3 , BC = 4J2，/ ACB = 45° D 为△ ABC 内一动点，O O 为厶ACD 的外接圆，直线 BD 交O O 于P 点，交BC 于E 点，弧AE = CP , 则AD 的最小值为（）•••/ BDC = 135 ° （定弦定角最值）如图，当AD 过O 时，AD 有最小值 •••/ BDC = 135 ° •••/ BO'C = 90 °• △ BO C 为等腰直角三角形:丄 ACO = 45 °+ 45 °= 90 °• AO = 5又 OB = O 'C = 4 •- AD = 5 — 4 = 1【例 2】如图，AC = 3，BC = 5,且/ BAC = 90° D BD 交圆于E 点，连CE ,贝U CE 的最小值为（A . 1B . 2解：•••/ CDP = Z ACB = 45 D . . 41 4.2B .13 2C . 5169•••/ AEB = Z AED = 90 °• E 点在以AB 为直径的圆上运动当CE 过圆心O 时，CE 有最小值为-132解：连接AE•/ AD 为O O 的直径【练】（2015 •江汉中考模拟1）如图，在△ ABC 中，AC = 3，BC = 4： 2，/ ACB = 45° AM II BC ，）:丄 BDC = 135 °如图，当AD 过圆心0时，AD 有最小值 •••/ BDC = 135° •••/ BO 'C = 90° 二 O 'B = O C = 4 又/ ACO = 90°• AO = 5• AD 的最小值为 5 — 4= 1【例3】（2016 •勤学早四调模拟 1）如图，O O 的半径为2,弦AB 的长为2... 3，点P 为优弧AB 上一动点，AC 丄AP 交直线PB 于点C ,则△ ABC 的面积的最大值是（.⑼M 鞋学早呵H 權®L TU 】如图，◎◎的平栓为b 范屈的凰育2再'点尸为优那M 上一玫钛丄ULAP 交宜线刊干点:G 刖用I 面理的舉丈值杲：划:占臼二.y*AGG = — E .宴匣乙肋i •川匚*扎怡离最九叮抽=7N/U 片3W 代蛊（？在①財丄.且£月血二抄,当点＜?划次胡眄中点时.自E 利肋餡夏咼烧大.此01卫肿（?两梅三肃希CW ・2希+玄皿尸据XQJJ+为・6+3的，【练】（2014 •洪山区中考模拟 1）如图，OO 的半径为1, 则△ ABC 的最大面积是（22■■；■ 34C . 12 3.3D . 6 4. 3A. I2+6J3C L2+3 7JD. 6+4^/3PB 于点C ， AC 丄AP 交直线【例5】如图，A(1 , 0)、B(3, 0)，以AB为直径作O M,射线OF交O M于E、F两点，C为弧AB的中点，D为EF的中点•当射线绕O点旋转时，CD的最小值为 _________________J4'01//解：连接DM••• D是弦EF的中点• DM 丄EF1•点D在以A为圆心的，OM为直径的圆上运动C当CD过圆心A时，CD有最小值连接CM x__ ••• C为弧AB的中点0'、A\阿• CM 丄AB\ V /『/••• CD的最小值为.2 1【练】如图，AB是O O的直径，AB = 2,/ ABC = 60° P是上一动点,CD，贝U CD的最小值为__________•/ D为弦AP的中点• OD 丄AP•••点D在以AO为直径的圆上运动当CD过圆心O时，CD有最小值过点C作CM丄AB于M •/ OB = OC，/ ABC = 60°• △ OBC为等边三角形1•OM = -，CM2•O，c= —74练习：如图，在动点C与定长线段AB组成的△ ABC中，AB= 6 ,D是AP的中点，连接• CD的最小值为■■ 7 1解：连接ODAD丄BC于点D , BE丄AC于点E , 连接DE •当点C在运动过程中，始终有匹至，则点C到AB的距离的最大值是________________________________________________________________________________AB 22.如图，已知以BC为直径的。

初中九年级数学教案-定弦定角模型的最值问题-优秀奖

课题：定弦定角模型的最值问题
准
备
教学过程设计
（设计意图：这道题综合性很强，包含三大类型问题：定弦定角问题，双动点最值问题，点圆之间距离最值问题，通过这道题的分析让学生掌握定弦定角模型的最值问题）
教学反思
1、本节课是九年级总复习中的“定弦定角模型的最值问题”专题，综合性很强，通过这道题的分析，让学生了解定弦定角模型，并从中找到隐形圆，这是重点和难点，也是解决这类题的关键入口
2、学生对双动点问题不熟悉，学生可以从这道题当中体验转化的思想把不熟悉的双动点问题转化为我们熟悉的单动点问题最终转化点圆距离问题
3、定弦定角模型有关问题是一个难点，学生们要学会从题目中构造出模型，以后也还要多加练习。

定弦定角最值问题(教师版)

线段最值系列之（一）——定弦定角，定最值

(完整版)定弦定角最值问题(教师版)

完整版定弦定角最值问题教师版

高一数学《三角函数的最值问题》 苏教版

定弦定角最值问题

最新九年级讲义定弦定角最值问题秘籍

定弦定角问题

定弦定角最值问题

定弦定角最值问题(教师版)

几何中最值定值问题教师版精编版

几何中最值定值问题教师版精编版

几何中最值定值问题教师版

中考数学几何模型重点突破讲练专题28 圆中的定弦定角和最大张角模型(教师版)

(完整word版)定弦定角最值问题

初中九年级数学教案-定弦定角模型的最值问题-优秀奖

高一数学《三角函数的最值问题》苏教版