2019-2020年全国版2017版高考数学一轮复习第九章算法初步统计统计案例9.1算法与程序框图基本算法语句课件理
全国版2017版高考数学一轮复习第九章算法初步统计统计案例9.2随机抽样课件理

由差异明显的几部分组成
【特别提醒】 1.随机数法编号要求:应保证各号数的位数相同,而抽
签法则无限制.
2.不论哪种抽样方法,总体中的每一个个体入样的概率 是相同的.
3.系统抽样是等距抽样,入样个体的编号相差 N 的整 n 数倍.
4.分层抽样是按比例抽样,每一层入样的个体数为该层
的个体数乘以抽样比.
10 D. 27
【解析】选C.根据题意,
9 1 解得n=28.故每个 , n 1 3
个体被抽到的概率为
10 5 . 28 14
【加固训练】
1.下面的抽样方法是简单随机抽样的是(
)
A.在某年明信片销售活动中,规定每100万张为一个开
奖组,通过随机抽取的方式确定号码的后四位为2709的
【解析】选D.总体是指这箱1000袋方便面的质量;个体 是一袋方便面的质量;样本为20袋方便面的质量;样本
容量为20.
2.(必修3P100A组T2(2)改编)某工厂生产A,B,C三种不 同型号的产品,产品的数量之比依次为3∶4∶7,现在用
分层抽样的方法抽出容量为n的样本,样本中A型号产品
有15件,那么样本容量n为 A.50 B.60 ( ) D.80
【规律方法】
1.简单随机抽样的特点
(1)抽取的个体数较少.(2)是逐个抽取.(3)是不放回抽
取.(4)是等可能抽取.只有四个特点都满足的抽样才是
简单随机抽样.
2.抽签法与随机数法的适用情况
(1)抽签法适用于总体中个体数较少的情况,随机数法
适用于总体中个体数较多的情况.
(2)一个抽样试验能否用抽签法,关键看两点:
一是抽签是否方便;二是号签是否易搅匀.一般地,当总 体容量和样本容量都较小时可用抽签法.
全国版2017版高考数学一轮复习第九章算法初步统计统计案例91算法与程序框图基本算法语句课件理

4.执行如图所示的程序框图,若输出的结果是8,则输入的数是________.
x822;
【解析】由a≥b得x2≥x3,解得x≤1,所以当x≤1时,
输出a=x2;当x>1时,输出b=x3.
当x≤1时,由a=x2=8,解得
当x>1时,b=x3=8,解得x=2.
所以输入的数为2或
答案:2或
2
2.
3 和 2, 23
程序框图,运行相应的程序后,输出i的
值为 ( )
A.3
B.4
C.5
D.6
【解析】选B.运行程序a=1,i=0,i=1,a=1×1+1=2, 因为2>50不满足,所以执行循环体,i=2,a=5, 因为5>50不满足,所以执行循环体,i=3,a=16, 因为16>50不满足,所以执行循环体,i=4,a=65, 因为65>50满足,输出i=4.
_____
WEND
__D_O 循环体
____________条件
LOOP UNTIL
【特别提醒】 1.当型循环与直到型循环的区别 直到型循环是“先循环,后判断,条件满足时终止循环”;而当型循环则是“先判断,后循环,条件满足时执行循 环”;两者的判断框内的条件表述在解决同一问题时是不同的,它们恰好相反.
A.24
B.25
C.30
D.40
【解析】选D.a=32-1=8,b=8-3=5,y=8×5=40.
3.(2016·成都模拟)如图所示的程序框图的输入值x∈[-1,3],则输出值y的取值范围为 ( ) A.[1,2] B.[0,2] C.[0,1] D.[-1,2]
【解析】选B.当0≤x≤3时,1≤x+1≤4, 所以,0≤log2(x+1)≤2, 当-1≤x<0时,0<-x≤1⇒1<2-x≤2, 所以,0<2-x-1≤1,所以,y的取值范围为[0,2].
2020版高考数学一轮复习第九章算法初步、统计、统计案例第一节算法初步学案理(含解析)新人教A版
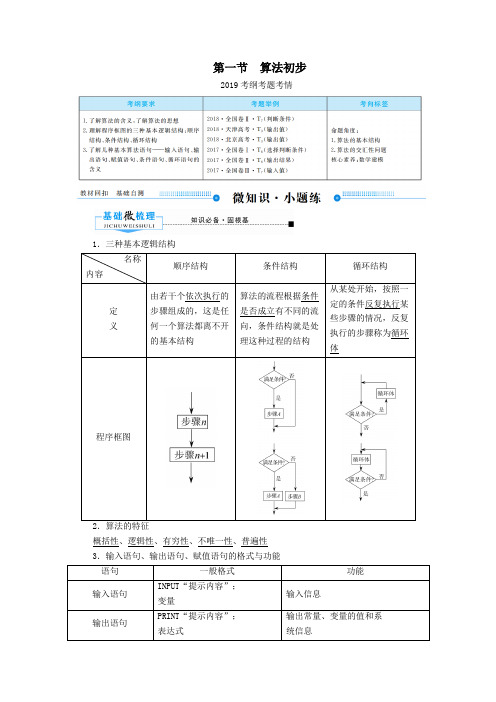
第一节 算法初步2019考纲考题考情1.三种基本逻辑结构概括性、逻辑性、有穷性、不唯一性、普遍性 3.输入语句、输出语句、赋值语句的格式与功能(1)算法中的条件结构与条件语句相对应。
(2)条件语句的格式及框图。
①IF—THEN格式:②IF—THEN—ELSE格式:5.循环语句(1)算法中的循环结构与循环语句相对应。
(2)循环语句的格式及框图。
①UNTIL语句:②WHILE语句:1.赋值号左边只能是变量(不能是表达式),在一个赋值语句中只能给一个变量赋值。
2.直到型循环是“先循环,后判断,条件满足时终止循环”;当型循环则是“先判断,后循环,条件满足时执行循环”;两者的判断框内的条件表述在解决同一问题时是不同的,它们恰好相反。
一、走进教材1.(必修3P25例5改编)如图为计算y=|x|函数值的程序框图,则此程序框图中的判断框内应填________。
解析输入x应判断x是否大于等于零,由图知判断框应填x<0?。
答案x<0?2.(必修3P30例8改编)执行如图所示的程序框图,则输出S的值为( )A .-32B .32C .-12D .12解析 按照程序框图依次循环运算,当k =5时,停止循环,当k =5时,S =sin 5π6=12。
答案 D 二、走近高考3.(2018·北京高考)执行如图所示的程序框图,输出的s 的值为( )A .12B .56C .76D .712解析 运行程序框图,k =1,s =1;s =1+(-1)1×12=12,k =2;s =12+(-1)2×13=56,k =3;满足条件,跳出循环,输出的s =56。
故选B 。
答案 B4.(2017·全国卷Ⅰ)如图所示程序框图是为了求出满足3n-2n>1 000的最小偶数n ,那么在和 两个空白框中,可以分别填入( )A .A >1 000和n =n +1B .A >1 000和n =n +2C .A ≤1 000和n =n +1D .A ≤1 000和n =n +2解析 因为输出的n 为偶数,所以 中应填n =n +2。
全国版2017版高考数学一轮复习第九章算法初步统计统计案例9.3用样本估计总体课件理

【母题变式】
1.若本例题(2)中条件不变,求年龄在[30,40)的频率?
【解析】年龄在[30,40)的工人有16人,因此年龄在
[30,40)的频率是
16 4 . 36 9
2.若本例题(2)中条件不变,求工人年龄的中位数.
【解析】将工人年龄按由小到大排序得:
27,31,33,34,34,36,36,37,37,37,38,38,38,39,39,
(3)平均数、方差的公式推广
①若数据x1,x2,…,xn的平均数为
x mx2+a,mx3+a,…,mxn+a的平均数是m +a.
②数据x1,x2,…,xn 的方差为s2.
,那么mx1+a,
x
(ⅰ)数据x1+a,x2+a,…,xn+a的方差也为s2; (ⅱ)数据ax1,ax2,…,axn的方差为a2s2.
7
8
45
42
16
17
39
38
25
26
37
44
34
35
37
49
9
43
18
36
27
42
36
39
①用系统抽样法从36名工人中抽取容量为9的样本,且
在第一分段里用随机抽样法抽到的年龄数据为44,列
出样本的年龄数据;
②计算①中样本的平均值和方差;
③36名工人中年龄在 -s与 +s之间有多少人?所占
的百分比是多少(精确到 x 0.01%)? x
A.甲
(
B.乙
)
C.丙 D.丁
【解析】选C.由题目表格中数据可知,丙平均环数最高,
且方差最小,说明技术稳定,且成绩好.
全国版2017版高考数学一轮复习第九章算法初步统计统计案例9.2随机抽样课时提升作业理

随机抽样(25分钟50分)一、选择题(每小题5分,共35分)1.现要完成下列3项抽样调查:①从10盒酸奶中抽取3盒进行食品卫生检查.②科技报告厅有32排,每排有40个座位,有一次报告会恰好坐满了听众,报告会结束后,为了听取意见,需要请32名听众进行座谈.较为合理的抽样方法是( )A.①简单随机抽样,②系统抽样,③分层抽样B.①简单随机抽样,②分层抽样,③系统抽样C.①系统抽样,②简单随机抽样,③分层抽样D.①分层抽样,②系统抽样,③简单随机抽样【解析】选A.对于①,个体没有差异且总数不多可用简单随机抽样法;对于②,将总体分成均衡的若干部分指的是将总体分段,在第1段内采用简单随机抽样确定一个起始编号,在此编号的基础上加上分段间隔的整数倍即为抽样编号,是系统抽样;对于③,个体有明显的差异,所以选用分层抽样法.A.简单随机抽样B.按性别分层抽样C.按学段分层抽样D.系统抽样2.(2016·长沙模拟)为了检查某超市货架上的饮料是否含有塑化剂,要从编号依次为1到50的塑料瓶装饮料中抽取5瓶进行检验,用选取的号码间隔一样的系统抽样方法确定所选取的5瓶饮料的编号可能是( )【解析】选D.利用系统抽样,把编号分为5段,每段10个,每段抽取一个,号码间隔为10.3.(2016·洛阳模拟)系统抽样是从N个个体中抽取n个个体为样本,先确定抽样间隔,即抽样距k=错误!未找到引用源。
(取整数部分),从第一段1,2,…,k个号码中随机抽取一个入样号码i0,则i0,i0+k,…,i0+(n-1)k号码均入样构成样本,所以每个个体的入样可能性是( )A.相等的B.不相等的C.与i0有关D.与编号有关【解析】选A.因为每个个体都是随机编号,每一段利用简单随机抽样,因此,每个个体入样的可能性是相等的.4.(2016·洛阳模拟)某单位有840名职工,现采用系统抽样方法抽取42人做问卷调查,将840人按A.11B.12C.13D.14【解析】选B.方法一:按照系统抽样的规则,将840名职工分成42组,每组抽取1人,其中编号481在第25组,方法二:840÷42=20,把1,2,…,840分成42段,不妨设第1段抽取的号码为l,则第k段抽取的号码为l+(k-1)·20,1≤l≤20,1≤k<42.令481≤l+(k-1)·20≤720,得25+错误!未找到引用源。
2019年高考数学一轮复习(文理通用) 第9章 算法初步、统计、统计案例 第1讲

• 知识点二 三种基本逻辑结构及相应语句 • 1.三种基本逻辑结构 从上到下 • (1)顺序结构是按 ____________的顺序进行,这是任何一 个算法都离不开的基本结构.
其结构形式为:
• (2)条件结构是指算法的流程根据条件是否成立而选择执行 不同的流向的结构形式. • 其结构形式为:
• (3)循环结构是指从某处开始,按照一定的条件反复执行某 些步骤.反复执行的步骤称为 ________. 循环体 • 其结构形式为:
• [解析] (1)正确,(2)(3)(4)(5)不正确,故选B.
2.下列图形符号属于判断框的是 导学号 58533366 ( C )
3.下列给变量赋值的语句正确的是 导学号 58533367 ( D ) A.5=a C.a=b=4 B.a+2=a D.a=2]
4.(2017· 课标全国Ⅱ,10,5 分)执行如图所示的程序框图,如果输入的 a=- 1,则输出的 S= 导学号 58533368 ( B ) A.2 C.4 B.3 D.5
• [解析] 分两种情况,当x,y满足 x≥0,y≥0,x+y≤1时,运用线性规 划知识先画出可行域(图略),再将直 线2x+y=0平移至过点(1,0),得到S 的最大值为2;当x,y不满足x≥0, y≥0,x+y≤1时,S等于1,综合两种
• 考点2 循环结构
• 角度1 由程序框图求输出结果
(2016· 全国卷Ⅱ,5 分)中国古代有计算多项式值的 秦九韶算法,如图是实现该算法的程序框图.执行该程序框图, 若输入的 x=2,n=2,依次输入的 a 为 2,2,5,则输出的 s= 导学号 58533372 ( C ) A.7 C.17 B.12 D.34
5 . (2017· 衡水中学调研)已知函数 y= -1x>0, 0x=0, 1x<0,
(新课标)2017高考数学一轮复习 第九章 算法初步、统计、.

(2)频率分布折线图
各小长方形上端的中点 ,就 顺次连接频率分布直方图中 _____________________ 得到频率分布折线图. (3)总体密度曲线 总体密度曲线反映了总体在各个范围内取值的百分比,它
能提供更加精细的信息.
(4)茎叶图
中间 的一列数,叶是从茎的 ________ 茎叶图中茎是指 _______ 旁边 生长出来的数.
④甲地该月 14 时的气温的标准差大于乙地该月 14 时的气 温的标准差. 其中根据茎叶图能得到的统计结论的编号为 导学号 25402250 ( A.①③ C.②③
(2)(2015· 安徽)若样本数据 x1,x2,…,x10 的标准差为 8, 则数据 2x1-1,2x2-1, …, 2x10-1 的标准差为 导学号 25402246 ( ) A.8 C.16 B.15 D.32
(1) 由平均数的定义,可知每个个体增加 C ,则平
[答案] (1)B (2)C
[解析 ] 均数也增加C,方差不变,故选B.
2.用样本的数字特征估计总体的数字特征 (1)众数:一组数据中出现次数最多的数. (2)中位数:将数据从小到大排列,若有奇数个数,则最中 间的数是中位数;若有偶数个数,则中间两数的平均数是中位 数.
x1+x2+…+xn n (3)平均数:x =_________________ ,反映了一组数据的平
[规律总结] 茎叶图的优缺点 优点:一是所有的信息都可以从这个茎叶图中得到;二是 茎叶图便于记录和表示,能够展示数据的分布情况. 缺点:样本数据较多或数据位数较多时,不方便表示数
据.
(1)为了了解某校教师使用多媒体进行教学的情况,现采用 简单随机抽样的方法, 从该校 400 名授课教师中抽取 20 名, 调 查了他们上学期使用多媒体进行教学的次数,结果用茎叶图表 示,如图所示.据此可估计上学期该校 400 名教师中,使用多 媒体进行教学的依次在 [16,30) 内的人数为 导学号 25402249 ( )
2017版高考数学一轮总复习 第九章 算法初步、统计与统计案例 第一节 算法与程序框图练习 理

第一节算法与程序框图【最新考纲】 1.了解算法的含义,了解算法的思想.2.理解程序框图的三种基本逻辑结构:顺序、条件、循环.3.理解几种基本算法语句——输入语句、输出语句、赋值语句、条件语句、循环语句的含义.1.算法(1)算法通常是指按照一定规则解决某一类问题的明确和有限的步骤.(2)应用:算法通常可以编成计算机程序,让计算机执行并解决问题.2.程序框图定义:程序框图又称流程图,是一种用程序框、流程线及文字说明来表示算法的图形.3.三种基本逻辑结构4.基本算法语句1.(质疑夯基)判断下列结论的正误.(正确的打“√”,错误的打“×”)(1)程序框图中的图形符号可以由个人来确定.( )(2)一个程序框图一定包含顺序结构,但不一定包含条件结构和循环结构.( )(3)“当型”循环与“直到型”循环退出循环的条件不同.( )(4)在算法语句中,X=X+1是错误的.( )答案:(1)×(2)√(3)√(4)×2.根据给出的程序框图,计算f(-1)+f(2)=( )A.0 B.1 C.2 D.4解析:输入-1,满足x≤0,所以f(-1)=4×(-1)=-4;输入2,不满足x≤0,所以f(2)=22=4,即f(-1)+f(2)=0.答案:A3.(2015·陕西卷)根据右边框图,当输入x为2 006时,输出的y=( )A.2B.4C.10D.28解析:x每执行一次循环减少2,当x变为-2时跳出循环,y=3-x+1=32+1=10. 答案:C4.某程序框图如图所示,若输出的S=57,则判断框内为( )A.k>4?B.k>5?C.k>6?D.k>7?解析:由程序框图可知,k=1时,S=1;k=2时,S=2×1+2=4;k=3时,S=2×4+3=11;k=4时,S=2×11+4=26;k=5时,S=2×26+5=57.答案:A5.阅读如图所示的程序框图,运行相应的程序,输出的S的值等于________.解析:第1次循环:S=0+21+1,此时S=3<15;第2次循环:S=3+22+2,此时S=9<15;第3次循环:S=9+23+3,此时S=20>15;终止循环,输出S=20.答案:20每个算法结构都含有顺序结构,循环结构中必定包含一个条件结构,用于确定何时终止循环体,循环结构和条件结构都含有顺序结构.一种区别当型循环与直到型循环的区别直到型循环是“先循环,后判断,条件满足时终止循环”;而当型循环则是“先判断,后循环,条件满足时执行循环”;两者的判断框内的条件表述在解决同一问题时是不同的,它们恰好相反.两点注意1.赋值号左边只能是变量(不是表达式),在一个赋值语句中只能给一个变量赋值.2.利用循环结构表示算法,要明确是利用当型循环结构,还是直到型循环结构.要注意:(1)选择好累计变量;(2)弄清在哪一步开始循环,满足什么条件不再执行循环体.A 级 基础巩固一、选择题1.(2015·四川卷)执行如图所示的程序框图,输出S 的值( )A .-32 B.32 C .-12 D.12解析:当k =5时,输出S =sin 5π6=sin ⎝ ⎛⎭⎪⎫π-π6=sin π6=12.答案:D2.(2016·西安调研)根据框图(如图所示),对大于2的整数N ,输出的数列的通项公式是( )A.a n=2nB.a n=2(n-1)C.a n=2nD.a n=2n-1解析:第一次运行:i=1,a1=2×1=2,S=a1=2第二次运行:i=2,a2=2×2=22,S=a2=22.第三次运行:i=3,a3=2×22=23,S=a3=23.第四次运行:i=4,a4=2×23=24,S=a4=24.……∴a n=2n.答案:C3.(2015·北京卷)执行如图所示的程序框图,输出的结果为( )A.(-2,2) B.(-4,0)C.(-4,-4) D.(0,-8)解析:第一次循环:S=1-1=0,t=1+1=2,x=0,y=2,k=1.第二次循环:S=0-2=-2,t=0+2=2,x=-2,y=2,k=2;第三次循环:S=-2-2=-4,t=-2+2=0,x=-4,y=0,k=3.因此输出的点为(-4,0).答案:B4.(2014·课标全国Ⅰ卷)执行下面的程序框图,若输入的a,b,k分别为1,2,3,则输出的M=( )A.203 B.72 C.165 D.158解析:第一次执行循环后:M =1+12=32,a =2,b =32,n =2;第二次执行循环后:M =2+23=83,a =32,b =83,n =3.第三次执行循环后:M =32+38=158,a =83,b =158,n =4.这时n =4,跳出循环,输出M 的值158.答案:D5.(2016·唐山质检)所示的程序框图,若输出k 的值为6,则判断框内可填入的条件是( )A .S>12?B .S>35?C .S>710?D .S>45?解析:第一次执行循环:s =1×910=910,k =8,s =910应满足条件;第二次执行循环:s =910×89=810,k =7,s =810应满足条件,排除选项D ;第三次执行循环:s =810×78=710,k =6,不再满足条件,结束循环.因此判断框中的条件为S>710.答案:C6.(2016·郑州质量预测)利用如图所示算法在平面直角坐标系上打印一系列点,则打印的点在圆x 2+y 2=10内的个数为( )A.2B.3C.4D.5解析:执行题中的程序框图,打印的点的坐标依次为(-3,6),(-2,5),(-1,4),(0,3),(1,2),(2,1),其中点(0,3),(1,2),(2,1)位于圆x2+y2=10内,因此打印的点位于圆x2+y2=10内的共有3个.答案:B二、填空题7.运行下列程序,当输入a,b分别为2,3时,最后输出的m的值为________.解析:∵a=2,b =3,满足a<b , ∴应把b 值赋给m ,∴m 的值为3. 答案:38.(2015·山东卷)执行如图所示的程序框图,输出的T 的值为________.解析:当n =1时,T =1+∫10x 1dx =1+12x 2|10=1+12=32;当n =2时,T =32+∫10x 2dx =32+13x 3|10=32+13=116;当n =3时,结束循环,输出T =116.答案:1169.(2015·安徽卷)执行如图所示的程序框图(算法流程图),输出的n 为________.解析:执行第一次判断:|a -1.414|=0.414>0.005, a =32,n =2; 执行第二次判断:|a -1.414|=0.086>0.005,a =75,n =3;执行第三次判断:|a -1.414|=0.014>0.005,a =1712,n =4;执行第四次判断:|a -1.414|<0.005,输出n =4. 答案:4 三、解答题10.某篮球队6名主力队员在最近三场比赛中投进的三分球个数如表格所示:统计该6名队员在最近三场比赛中投进的三分球总数的程序框图如图所示.(1)试在判断框内填上条件;(2)求输出的s的值.解:(1)依题意,程序框图是统计6名队员投进的三分球的总数.∴判断框内应填条件“i≤6?”.(2)6名队员投进的三分球数分别为a1,a2,a3,a4,a5,a6.故输出的s=a1+a2+…+a6.B级能力提升1.(2015·课标全国Ⅰ卷)执行如图的程序框图,如果输入的t=0.01,则输出的n=( )A.5 B.6 C.7 D.8解析:运行第一次:S=1-12=12=0.5,m=0.25,n=1,S>0.01;运行第二次:S=0.5-0.25=0.25,m=0.125,n=2,S>0.01;运行第三次:S=0.25-0.125=0.125,m=0.062 5,n=3,S>0.01;运行第四次:S=0.125-0.062 5=0.062 5,m=0.031 25,n=4,S>0.01;运行第五次:S=0.031 25,m=0.015 625,n=5,S>0.01;运行第六次:S=0.015 625,m=0.007 812 5,n=6,S>0.01;运行第七次:S=0.007 812 5,m=0.003 906 25,n=7,S<0.01.结束循环,输出n=7.答案:C2.(2016·济南模拟)执行如图所示的程序框图,若输入的x的值为1,则输出的n的值为________.解析:按照程序框图逐一执行.由x2-4x+3≤0,解得1≤x≤3.当x=1时,满足1≤x≤3,所以x=1+1=2,n=0+1=1;当x=2时,满足1≤x≤3,所以x=2+1=3,n=1+1=2;当x=3时,满足1≤x≤3,所以x=3+1=4,n=2+1=3;当x=4时,不满足1≤x≤3,所以输出n=3.答案:33.已知数列{a n}的各项均为正数,观察程序框图如图所示,若k=5,k=10时,分别有S=511和S=1021,试求数列{a n}的通项公式.解:由程序框图可知,数列{a n }是等差数列,首项为a 1,公差为d. S i =1a 1a 2+1a 2a 3+…+1a i a i +1=1d (1a 1-1a 2+1a 2-1a 3+…+1a i -1a i +1) =1d ⎝ ⎛⎭⎪⎫1a 1-1a i +1 当k =5时,S =⎝ ⎛⎭⎪⎫1a 1-1a 61d =5a 1a 6=511.∴a 1a 6=11,即a 1(a 1+5d)=11;①当k =10时,S =⎝ ⎛⎭⎪⎫1a 1-1a 111d =10a 1a 11=1021,∴a 1a 11=21,即a 1(a 1+10d)=21,② 由①②联立,得a 1=1,d =2, 因此a n =a 1+(n -1)d =2n -1.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
B.求b-a的值
C.求|a-b|的值
D.以上都不对
【解析】选C.当a≥b时,输出结果为a-b;当a<b时,输出
结果为b-a,故其功能是求|a-b|的值.
2.(必修3P20习题1.1A组T2改编)设计一个程序框图,求 满足12+22+32+…+n2≥10000的最小n值.
【解析】程序框图如图:
感悟考题 试一试 3.(2015·四川高考)执行如图所示的程序 框图,输出S的值为 ( )
_____ WEND ___ DO 循环体 ____________ 条LO件OP UNTIL
【特别提醒】 1.当型循环与直到型循环的区别 直到型循环是“先循环,后判断,条件满足时终止循 环”;而当型循环则是“先判断,后循环,条件满足时执 行循环”;两者的判断框内的条件表述在解决同一问题 时是不同的,它们恰好相反.
【变式训练】(2015·福建高考)阅读 如图所示的程序框图,运行相应的程 序,若输入x的值为1,则输出y的值为
() A.2 B.7 C.8 D.128 【解析】选C.x=1→x≥2?(否)→代入y=9-x→y=8.
【加固训练】 1.给出一个如图所示的程序框图, 若要使输入的x值与输出的y值相 等,则这样的x值的个数是( ) A.1 B.2 C.3 D.4
s11111, 执行第四次循环时,k=8, 2 4 6 12 此时结束循环,故判断框中s应12填入14的16条18件为2245,
s 1 1 ?. 12
【技法感悟】 1.求程序运行结果的思路 (1)要明确程序框图的顺序结构、条件结构和循环结构. (2)要识别运行程序框图,理解框图所解决的实际问题. (3)按照题目的要求完成解答并验证.
A .3 B .3 C . 1 D .1
2
2
22
【解析】选D.按照程序框图依次循环运算,当k=5时, 停止循环,当k=5时, Ssin5 1.
62
4.(2015·安徽高考)执行如图所示的程序框图(算法流 程图),输出的n为________.
【解析】执行第一次循环体a= 3 , n=2; 2
=0.5,S=S-m=0.5,m= =0.25,
1
m
n2 =1,S=0.5>t=0.01,是2 ,执行循环;
执行第二次,S=S-m=0.25,mm = =0.125,n=2, 2
S=0.25>t=0.01,是,执行循环;
执行第三次,S=S-m=0.125,mm = =0.0625,n=3, S=0.125>t=0.01,是,执行循环2 ;
5.(2015·山东高考)执行如图所示的程序框图,若输入 的x的值为1,则输出的y的值为________.
【解析】执行程序框图为x=1→x=2,y=3×22+1=13. 答案:13
考向一 顺序结构与条件结构
【典例1】(1)(2016·郑州模拟)如图所示
的程序框图的运行结果是 ( )
A.2
B.2.5
第九章 算法初步、统计、统计案例 第一节 算法与程序框图、 基本算法语句
【知识梳理】 1.常用程序 框及其功能
起始和结束 输入和输出的信息
赋值、计算 成立与否 先后顺序
2.三种基本逻辑结构及相应语句
名称
顺序结 构
示意图
相应语句
①输入语句: INPUT “提示内容”;变量 ②输出语句: PRINT “提示内容”;表达式 ③赋值语句: 变量=表达式
执行第四次,S=S-m=0.0625,m= =0.03125,n=4, S=0.0625>t=0.01,是,执行循环m ;
2
执行第五次,S=S-m=0.03125,mm = =0.015625, 2
n=5,S=0.03125>t=0.01,是,执行循环;
执行第六次,S=S-m=0.015625, mm = =0.0078125, n=6,S=0.015625>t=0.01,是,执行2 循环;
C.s 11? 12
B.s 5 ? 6
D.s 25 ? 24
【解题导引】根据循环结构中输出k的值以及循环结束 时s的值,结合各选项可以判断出判断框中的条件.
【规范解答】选C.执行第一次循环时,k=2, s 1 , 2
执行第二次循环时,k=4, s 1 1 3, 执行第三次循环时,k=6, 2 4 4
若输入x为3,则输出的y的值为 ( )
A.24
B.25
C.30
D.40
【解析】选D.a=32-1=8,b=8-3=5,y=8×5=40.
3.(2016·成都模拟)如图所示的程序框图的输入值 x∈[-1,3],则输出值y的取值范围为 ( ) A.[1,2] B.[0,2] C.[0,1] D.[-1,2]
【解析】选C.由程序框图知
x2,x 2,
y
ห้องสมุดไป่ตู้
2x
3,
2<
x
5,
由 解已 得 x知1x =, 得x0>或5,xxx2=21x,或或x22=< x3x,35x,或x1x>5x,.
这样的x值的个数是3.
2.(2016·安庆模拟)阅读如图所示程序框图.
2.(2016·天津模拟)如果执行如图 所示的程序框图,输入N=5,则输出的 数等于 ( )
A .5 B .4 C .6 D .5 4556
【解析】选D.根据程序框图可知,该程序框图的功能是
计算S=1 1221 33 14 现N 在输1 N 入1的, N=5,
所以不满足条件k<N的结果为S= 111
【一题多解】解答本例题(2),你知道几种解法? 解答本题,还有以下解法: 不妨设a,b,c的值分别为8,5,6,运行程序框图: 因为a>b成立,故将b的值赋给a得a=5,又a>c不成立, 故直接输出a的值为5,再结合选项知B成立.
【母题变式】 1.若本例题(2)条件“是与否”互换 位置如图,其他条件不变,试解答本题. 【解析】选A.两个条件结构都是挑选 较大的值.故输出a的值是三个数中的 最大值.
考向三 基本算法语句 【典例4】(1)下面程序运行的结果是 ( )
A.5,8
B.8,5
C.8,13 D.5,13
(2)(2015·江苏高考改编)根据如图所示的算法语句, 可知输出的结果s为________.
【解题导引】(1)赋值语句的功能是将后面的值赋给前 面的变量,根据赋值语句的功能求解. (2)由已知中的算法语句,可得程序的功能是利用循环计 算变量s的值,模拟程序的运行过程,即可得到答案.
【规范解答】(1)选C.此程序先将A的值赋给X,故X=5; 再将B的值赋给A,故A=8;再将X+A的值赋给B,即将原 来的A与B的和赋给B,故B=5+8=13. (2)由已知中的算法语句,模拟程序的运行过程可得: i=1时,i<8,s增大为3,i增大为4; 当i=4时,i<8,s增大为5,i增大为7;
12 23 34 11 ( 1 1 ) (1 1 ) (1 1 ) 5 .
4 55 6 223 566
3.(2016·衡阳模拟)执行如图所示的
程序框图,若输出的S=88,则判断框内
应填入的条件是 ( )
A.k>7?
B.k>6?
C.k>5?
D.k>4?
【解析】选C.第一次循环:k=1+1=2,S=2×0+2=2; 第二次循环:k=2+1=3,S=2×2+3=7; 第三次循环:k=3+1=4,S=2×7+4=18; 第四次循环:k=4+1=5,S=2×18+5=41; 第五次循环:k=5+1=6,S=2×41+6=88,满足条件,则输出 S的值,而此时k=6,故判断框内应填入的条件是“k>5?”.
名称
条件 结构
示意图
相应语句
_I_F___条__件____T_H_E_N_ 语句体 ________ _E_N_D___I_F________ 语IF句体条1件 THEN _____ 语EL句SE体2 END IF
名称
当型 循环 循 结构 环 结 直到 构 型循 环结
构
示意图
相应语句
_W_H_I_L_E_ 条件 循环体
此时|a-1.414|=|1.5-1.414|=0.086>0.005;
执 此行 时第 |a-二1.次41循4环|=体|1a.4=-175 ,.n4=134;|=0.014>0.005;
执行第三次循环体a= n=4;此时|a-1.414|<0.005, 此时不满足判断条件,输1 7 出, n=4.
12 答案:4
程序框图,运行相应的程序后,输出i的
值为 ( )
A.3
B.4
C.5
D.6
【解析】选B.运行程序a=1,i=0,i=1,a=1×1+1=2, 因为2>50不满足,所以执行循环体,i=2,a=5, 因为5>50不满足,所以执行循环体,i=3,a=16, 因为16>50不满足,所以执行循环体,i=4,a=65, 因为65>50满足,输出i=4.
2.解决程序框图问题要注意几个常用变量 (1)计数变量:用来记录某个事件发生的次数,如i=i+1. (2)累加变量:用来计算数据之和,如S=S+i. (3)累乘变量:用来计算数据之积,如p=p×i.
【小题快练】 链接教材 练一练 1.(必修3P25例5改编)给出如图程序框图,其功能是
()
A.求a-b的值
【解析】选B.当0≤x≤3时,1≤x+1≤4, 所以,0≤log2(x+1)≤2, 当-1≤x<0时,0<-x≤1⇒1<2-x≤2, 所以,0<2-x-1≤1,所以,y的取值范围为[0,2].
