导数练习题基础题数学小丸子讲义
高中数学导数练习题

高中数学导数练习题一、基础题1. 求函数 $f(x) = x^3 3x$ 的导数。
2. 求函数 $f(x) = \sqrt{1+x^2}$ 的导数。
3. 求函数 $f(x) = \frac{1}{x^2}$ 的导数。
4. 求函数 $f(x) = \ln(x^2 + 1)$ 的导数。
5. 求函数 $f(x) = e^{2x}$ 的导数。
二、应用题1. 已知函数 $f(x) = ax^2 + bx + c$,求 $f'(x)$ 并说明其几何意义。
2. 某物体做直线运动,其位移 $s$ 与时间 $t$ 的关系为 $s =t^2 2t + 1$,求物体在 $t=2$ 时的瞬时速度。
3. 已知函数 $f(x) = \frac{1}{\sqrt{x}}$,求曲线在$x=4$ 处的切线方程。
4. 求函数 $f(x) = \sin(x)$ 在区间 $[0, \pi]$ 上的最大值和最小值。
5. 已知函数 $f(x) = \ln(x 1)$,求 $f(x)$ 的单调区间。
三、综合题1. 设函数 $f(x) = (x^2 1)^3$,求 $f'(x)$。
2. 已知函数 $f(x) = \frac{2x + 3}{x 1}$,求 $f'(x)$。
3. 求函数 $f(x) = \sqrt{1 + \sqrt{1 + x^2}}$ 的导数。
4. 已知函数 $f(x) = e^{x^2}$,求曲线在 $x=0$ 处的切线方程。
5. 设函数 $f(x) = \ln(\sin^2 x)$,求 $f'(x)$。
四、拓展题1. 已知函数 $f(x) = \frac{1}{x^2 + 1}$,求 $f''(x)$。
2. 设函数 $f(x) = (x^3 + 1)^4$,求 $f'''(x)$。
3. 已知函数 $f(x) = \arctan(x)$,求 $f'(x)$。
导数基本试题及解析答案

导数基本试题及解析答案1. 求函数 \( f(x) = 3x^2 + 2x - 5 \) 在 \( x = 1 \) 处的导数。
解析:首先求出函数 \( f(x) \) 的导数 \( f'(x) \)。
根据导数的定义,我们有:\[ f'(x) = \frac{d}{dx}(3x^2 + 2x - 5) = 6x + 2 \]然后将 \( x = 1 \) 代入 \( f'(x) \) 中,得到:\[ f'(1) = 6(1) + 2 = 8 \]答案:\( f'(1) = 8 \)。
2. 计算函数 \( g(x) = \sin(x) \) 的导数。
解析:根据三角函数的导数规则,我们知道 \( \sin(x) \) 的导数是\( \cos(x) \)。
因此:\[ g'(x) = \cos(x) \]答案:\( g'(x) = \cos(x) \)。
3. 求复合函数 \( h(x) = \sqrt{x^3 + 2x} \) 的导数。
解析:对于复合函数,我们使用链式法则。
设 \( u(x) = x^3 + 2x \),则 \( h(x) = \sqrt{u(x)} \)。
首先求 \( u(x) \) 的导数:\[ u'(x) = 3x^2 + 2 \]然后求 \( h(x) \) 的导数:\[ h'(x) = \frac{1}{2\sqrt{u(x)}} \cdot u'(x) =\frac{1}{2\sqrt{x^3 + 2x}} \cdot (3x^2 + 2) \]答案:\( h'(x) = \frac{3x^2 + 2}{2\sqrt{x^3 + 2x}} \)。
4. 已知 \( y = e^{2x} \),求 \( \frac{dy}{dx} \)。
解析:对于指数函数 \( e^{kx} \),其导数是 \( ke^{kx} \)。
高中数学《导数》讲义(全)

高中数学导数讲义完整版第一部分 导数的背景一、导入新课 1. 瞬时速度问题1:一个小球自由下落,它在下落3秒时的速度是多少? (221gt s =,其中g 是重力加速度).2. 切线的斜率问题2:P (1,1)是曲线2x y =上的一点,Q 是曲线上点P 附近的一个点,当点Q 沿曲线逐渐向点P 趋近时割线PQ 的斜率的变化情况.3. 边际成本问题3:设成本为C ,产量为q ,成本与产量的函数关系式为103)(2+=q q C ,我们来研究当q =50时,产量变化q ∆对成本的影响. 二、小结:瞬时速度是平均速度ts∆∆当t ∆趋近于0时的极限;切线是割线的极限位置,切线的斜率是割线斜率xy∆∆当x ∆趋近于0时的极限;边际成本是平均成本q C ∆∆当q ∆趋近于0时的极限.三、练习与作业:1. 某物体的运动方程为25)(t t s =(位移单位:m ,时间单位:s )求它在t =2s 时的速度. 2. 判断曲线22x y =在点P (1,2)处是否有切线,如果有,求出切线的方程. 3. 已知成本C 与产量q 的函数关系式为522+=q C ,求当产量q =80时的边际成本. 4. 一球沿某一斜面自由滚下,测得滚下的垂直距离h (单位:m )与时间t (单位:s )之间的函数关系为2t h =,求t =4s 时此球在垂直方向的瞬时速度. 5. 判断曲线221x y =在(1,21)处是否有切线,如果有,求出切线的方程.6. 已知成本C 与产量q 的函数关系为742+=q C ,求当产量q =30时的边际成本.第二部分 导数的概念一、新课:1.设函数)(x f y =在0x x =处附近有定义,当自变量在0x x =处有增量x ∆时,则函数()y f x =相应地有增量)()(00x f x x f y -∆+=∆,如果0→∆x 时,y ∆与x ∆的比xy∆∆(也叫函数的平均变化率)有极限(即xy∆∆无限趋近于某个常数),我们把这个极限值叫做函数)(x f y =在0x x →处的导数,记作0/x x y =,即xx f x x f x f x ∆-∆+=→∆)()(lim)(0000/。
导数基础练习题高中

导数基础练习题高中一. 概念回顾在开始解答导数基础练习题之前,我们先回顾一下导数的基本概念。
导数的定义如下:设函数y = f(x)在点x₀处可导,则它在该点的导数记作f'(x₀),定义为:f'(x₀) = lim┬(△x→0)(f(x₀+△x)-f(x₀))/△x二. 导数基本运算法则在求解导数的过程中,我们需要熟悉导数的基本运算法则,包括常数法则、幂函数法则、和差法则、积法则和商法则。
接下来,我们通过练习题来巩固对这些法则的理解。
1. 设y = 2x² + 3x - 5,求y'。
解:根据幂函数法则和和差法则,我们有:y' = (2·2x^(2-1)) + (3·1x^(1-1)) + (0·(-5)^(0-1))= 4x + 32. 设y = √x + 1/x,求y'。
解:根据幂函数法则、和差法则和商法则,我们有:y' = (1/2)·(x^(-1/2)) + (-1/x^2)= 1/(2√x) - 1/x²三. 求导法则的应用在实际问题中,我们经常需要利用求导法则来解决相关的数学问题。
下面我们通过一些例题来应用求导法则,加深对其应用的理解。
1. 曲线y = x³ - 3x² + 2x的切线方程在x = 2处的斜率为多少?解:首先,我们先求出函数y = x³ - 3x² + 2x的导数:y' = 3x² - 6x + 2然后,代入x = 2,得到切线斜率:y'(2) = 3(2)² - 6(2) + 2 = 102. 曲线y = e^x在点x = 0处的切线方程为y = 2x + 1,求e的值。
解:根据切线方程的斜率和点的定义,我们有:y'(0) = 2而y = e^x的导数为:y' = e^x将x = 0代入导数表达式,得到y'(0) = e^0 = 1因此,根据等式2 = 1,我们得到e = 2。
(完整)高中数学导数基础练习题
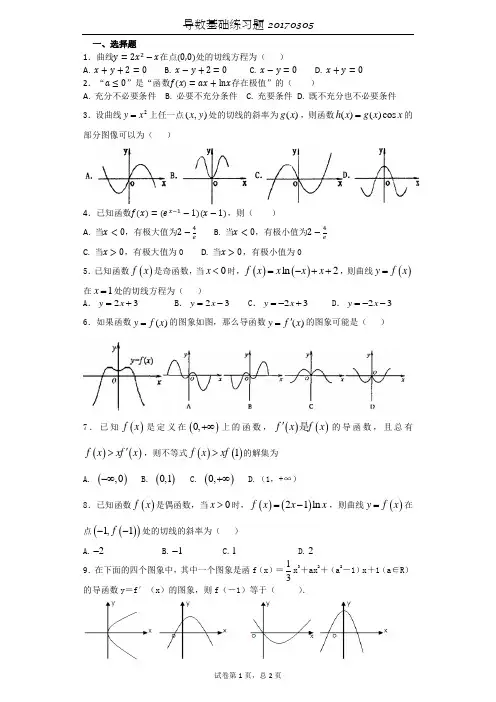
导数基础练习题20170305一、选择题1.曲线y =2x 2−x 在点(0,0)处的切线方程为( )A. x +y +2=0B. x −y +2=0C. x −y =0D. x +y =0 2.“a ≤0”是“函数f(x)=ax +lnx 存在极值”的( )A. 充分不必要条件B. 必要不充分条件C. 充要条件D. 既不充分也不必要条件 3.设曲线2y x =上任一点(,)x y 处的切线的斜率为()g x ,则函数()()cos h x g x x =的部分图像可以为( )4.已知函数f(x)=(ex−1−1)(x −1),则( )A. 当x <0,有极大值为2−4eB. 当x <0,有极小值为2−4eC. 当x >0,有极大值为0D. 当x >0,有极小值为05.已知函数()f x 是奇函数,当0x <时,()()ln 2f x x x x =-++,则曲线()y f x =在1x =处的切线方程为( )A .23y x =+B .23y x =-C .23y x =-+D .23y x =-- 6.如果函数()y f x =的图象如图,那么导函数()y f x '=的图象可能是( )7.已知()f x 是定义在()0,+∞上的函数,()()f x f x '是的导函数,且总有()()f x xf x '>,则不等式()()1f x xf >的解集为A. (),0-∞B. ()0,1C. ()0,+∞D.(1,+∞)8.已知函数()f x 是偶函数,当0x >时,()()21ln f x x x =-,则曲线()y f x =在点()()1,1f --处的切线的斜率为( )A.2-B.1-C.1D.2 9.在下面的四个图象中,其中一个图象是函f (x )=13x 3+ax 2+(a 2-1)x +1(a ∈R )的导函数y =f ′(x )的图象,则f (-1)等于( ).A二、填空题10.定义在R 上的偶函数f(x)满足:当x <0时,f(x)=xx−1,则曲线y =f(x)在点(2,f(2))处的切线的斜率为__________. 11,(0,3]x ∈,其图象上任意一点00(,)P x y 处的切线的斜恒成立,则实数a 的取值范围是 . 12.设函数f(x)=x 3−3x +1,x ∈[−2,2]的最大值为M ,最小值为m ,则M +m =__________.13.在平面直角坐标系xoy 中,若曲线y =ax 2+bx (a,b 为常数)过点P(2,−5),且该曲线在点P 处的切线与直线7x +2y +3=0平行,则a +b = .14.过函数 ()32325f x x x x =-++图像上一个动点作函数的切线,则切线倾斜角的取值范围是 __________. 15,若0'()1f x =,则 16.已知定义域为R 的奇函数()y f x =的导函数为()'y f x =,当0x ≠时,,则 a b c ,,的大小关系是 .17,直线l 与函数()(),f x g x 的图像都相切于点(1,0).(1)求直线l 的方程及函数()g x 的解析式;(2)若()()()h x f x g x '=-(其中()g x '是()g x 的导函数),求函数()h x 的极大值. 18.已知函数f(x)=x 2−2x ,g(x)=ax −1,若∀x 1∈[−1,2],∃x 2∈[−1,2],使得f(x 1)=g(x 219 (1)若3x =是()f x 的极值点,求()f x 的极大值; (2)求a 的范围,使得()1f x ≥恒成立.本卷由系统自动生成,请仔细校对后使用,答案仅供参考。
导数基础练习题

导数基础练习题在数学学科中,导数是一个非常基础且重要的概念。
它是微积分的核心内容之一,也是解决许多实际问题的关键步骤。
为了帮助大家更好地理解和掌握导数的相关知识,下面将给出一些导数基础的练习题。
一、基本导数1. 对于函数f(x)=2x,求f'(x)。
2. 对于函数f(x)=-3x^2,求f'(x)。
3. 对于函数f(x)=5,求f'(x)。
二、常见函数导数1. 对于函数f(x)=sin(x),求f'(x)。
2. 对于函数f(x)=cos(x),求f'(x)。
3. 对于函数f(x)=e^x,求f'(x)。
4. 对于函数f(x)=ln(x),求f'(x)。
三、求导法则1. 对于函数f(x)=3x^2-2x+1,求f'(x)。
2. 对于函数f(x)=4x^3+2x^2-3x,求f'(x)。
3. 对于函数f(x)=2sqrt(x)+3/x,求f'(x)。
4. 对于函数f(x)=ln(x^2+1),求f'(x)。
四、链式法则1. 对于函数f(x)=(2x+1)^3,求f'(x)。
2. 对于函数f(x)=sin(2x+1),求f'(x)。
3. 对于函数f(x)=e^(2x+1),求f'(x)。
4. 对于函数f(x)=ln(2x+1),求f'(x)。
五、高阶导数1. 对于函数f(x)=x^4-2x^3+3x^2-4x,求f''(x)和f'''(x)。
2. 对于函数f(x)=sin(x),求f''(x)和f'''(x)。
3. 对于函数f(x)=e^x,求f''(x)和f'''(x)。
六、隐函数求导1. 已知函数方程x^3+y^3=9xy,求dy/dx。
2. 已知函数方程x^2+y^2=4,求dy/dx。
导数基础训练试题及答案
导数基础训练试题及答案一、单项选择题(每题3分,共30分)1. 函数f(x)=x^2在x=1处的导数是()。
A. 0B. 1C. 2D. 32. 函数f(x)=3x^3+2x^2+5的导数是()。
A. 9x^2+4xB. 9x^2+4x+5C. 3x^2+4xD. 3x^2+4x+53. 函数f(x)=sin(x)的导数是()。
A. cos(x)B. sin(x)C. -cos(x)D. -sin(x)4. 如果函数f(x)的导数为f'(x)=6x,那么f(x)可能是()。
A. 3x^2+CB. 2x^3+CC. x^3+CD. x^2+C5. 函数f(x)=e^x的导数是()。
A. e^xC. -e^xD. -e^(-x)6. 函数f(x)=ln(x)的导数是()。
A. 1/xB. xC. ln(x)D. 17. 函数f(x)=x^(1/3)的导数是()。
A. 1/3x^(-2/3)B. 1/3x^(1/3)C. x^(-2/3)D. x^(2/3)8. 函数f(x)=sqrt(x)的导数是()。
A. 1/(2sqrt(x))B. 1/2sqrt(x)C. 2/sqrt(x)D. 2sqrt(x)9. 函数f(x)=x^5-5x^3+x的导数是()。
A. 5x^4-15x^2+1B. 5x^4-15x^2+xC. 5x^4-15x^2+1+xD. 5x^4-15x^210. 函数f(x)=cos(x)的导数是()。
A. -sin(x)B. sin(x)D. cos(x)二、填空题(每题4分,共20分)1. 函数f(x)=x^3的导数是______。
2. 函数f(x)=1/x的导数是______。
3. 函数f(x)=tan(x)的导数是______。
4. 函数f(x)=x^2-6x+10的导数是______。
5. 函数f(x)=ln(x)+x的导数是______。
三、解答题(每题10分,共50分)1. 求函数f(x)=x^2+3x-5在x=2处的导数值。
导数基础运算基础练习题
导数基础运算基础练习题导数作为微积分的重要概念,是描述函数变化率的工具。
在学习导数的过程中,理解并掌握导数的基础运算是非常重要的。
下面我们来进行一些基础练习题,巩固对导数的运算规则的理解和运用。
一、求函数f(x) = x^2在点x=3处的导数。
解答:函数f(x) = x^2的导数即为函数的斜率,我们可以通过求导公式来计算。
对于幂函数来说,求导的公式为f'(x) = nx^(n-1)。
将函数f(x) = x^2代入公式中,我们可以得到f'(x) = 2x^(2-1) = 2x。
因此,函数f(x) = x^2在点x=3处的导数为f'(3) = 2 * 3 = 6。
二、求函数g(x) = 2x^3 + 3x^2 - 4x在点x=2处的导数。
解答:函数g(x) = 2x^3 + 3x^2 - 4x的导数即为函数的斜率,我们可以通过求导公式来计算。
对于多项式函数来说,求导的公式为f'(x) = n * a_n * x^(n-1),其中n为幂次,a_n为对应幂次的系数。
将函数g(x) = 2x^3 + 3x^2 - 4x代入公式中,我们可以得到g'(x) = 3* 2 * x^(3-1) + 2 * 3 * x^(2-1) - 1 * 4 * x^(1-1) = 6x^2 + 6x - 4。
因此,函数g(x) = 2x^3 + 3x^2 - 4x在点x=2处的导数为g'(2) = 6 *2^2 + 6 * 2 - 4 = 32。
三、求函数h(x) = e^x在点x=1处的导数。
解答:函数h(x) = e^x的导数即为函数的斜率,我们可以使用指数函数的导数公式来计算。
对于指数函数e^x来说,它的导数仍然是e^x。
因此,函数h(x) = e^x在点x=1处的导数为h'(1) = e^1 = e。
通过以上的练习题,我们可以发现,对于基础的函数形式,求导运算并不复杂。
2.7导数的应用(讲义+典型例题+小练)(原卷版)
2.7导数的应用(讲义+典型例题+小练)1. 基本方法:(1)函数的导数与函数的单调性的关系:设函数y =f (x )在某个区间内有导数,如果在这个区间内/y >0,那么函数y =f (x )为这个区间内的增函数;如果在这个区间内/y <0,那么函数y =f (x )为这个区间内的减函数.(2)用导数求函数单调区间的步骤:①求函数f (x )的导数f ′(x ). ②令f ′(x )>0解不等式,得x 的范围就是递增区间. ③令f ′(x )<0解不等式,得x 的范围,就是递减区间.(3)判别f (x 0)是极大、极小值的方法:若0x 满足0)(0='x f ,且在0x 的两侧)(x f 的导数异号,则0x 是)(x f 的极值点,)(0x f 是极值,并且如果)(x f '在0x 两侧满足“左正右负”,则0x 是)(x f 的极大值点,)(0x f 是极大值;如果)(x f '在0x 两侧满足“左负右正”,则0x 是)(x f 的极小值点,)(0x f 是极小值.(4)求函数f (x )的极值的步骤:①确定函数的定义区间,求导数f ′(x ). ②求方程f '(x )=0的根. ③用函数的导数为0的点,顺次将函数的定义区间分成若干小开区间,并列成表格. 检查f '(x )在方程根左右的值的符号,如果左正右负,那么f (x )在这个根处取得极大值;如果左负右正,那么f (x )在这个根处取得极小值;如果左右不改变符号,即都为正或都为负,则f (x )在这个根处无极值.2、基本思想:学习的目的,就是要会实际应用,本讲主要是培养学生运用导数知识解决实际问题的意识,思想方法以及能力.解决实际应用问题关键在于建立数学模型和目标函数. 把“问题情景”译为数学语言,找出问题的主要关系,并把问题的主要关系近似化,形式化,抽象成数学问题,再化为常规问题,选择合适的数学方法求解.根据题设条件作出图形,分析各已知条件之间的关系,借助图形的特征,合理选择这些条件间的联系方式,适当选定变化区间,构造相应的函数关系,是这部分的主要技巧.知识当回归于生活,在现实生活中,有很多时候我们需要用到最大、最小。
(完整word版)导数基础练习题(word文档良心出品)
导数基础练习题1 若曲线 y x 4的一条切线 l 与直线 x 4 y 8 0垂直,则 l 的方程为( A )A . 4x y 3 0B . x 4 y 5 0C . 4x y 3 0D . x 4 y 3 0 2 曲线 y = x 3-3x 2+ 1 在点 (1 ,- 1) 处的切线方程为 BA . =3 -4 B. =- 3 x +2 C. =-4 +3 D.y =4 -5y xyy xx3 函数 y (x 1) 2 ( x 1) 在 x 1处的导数等于( D)A . 1B . 2C . 3D . 44 若函数 f(x) =x 2+b x +c 的图象的极点在第四象限,则函数 f/(x) 的图象是( A )yyyyox ox ox o xABCDx35 曲线 y 2x 4 在点 (13), 处的切线的倾斜角为(B)A . 30°B . 45°C . 60°D . 120°6 设曲线 y ax 2 在点( 1, a )处的切线与直线 2xy 60 平行,则 a ( A)A . 1B .1C .1 D . 1227 已知曲线 yx 23lnx 的一条切线的斜率为1, 则切点的横坐标为( A)42B.2C. 1D.12x8 曲线 y2x 1 A.x y2在点 1,1 处的切线方程为 B (B )B.x y 2 0C.x 4 y 5 0 D. x 4 y 5 09. 设曲线 y x n 1 (n N * ) 在点( 1,1)处的切线与 x 轴的交点的横坐标为 x n , 则 x 1 x 2x n的值为 (B)(A)1 (B)1 n (D) 1n(C)n 1n 110 设 f(x) 、g(x) 分别是定义在 R 上的奇函数和偶函数 , 当 x <0 时 , f ( x) g( x) f ( x) g (x)>0. 且 g 3 0 , . 则不等式 f(x)g(x) < 0 的解集是( D )A ( 3,0) (3, )B . ( 3,0) (0,3)C . ( ,3) (3, )D . (, 3)(0,3)12 已知函数 y xf (x) 的图像如右图所示(此中f ( x) 是函数 f ( x)的导函数 ) ,下边四个图象中 y f ( x) 的图象大概是 ( C)yyyyyy=xf ' (x)2244 11122-1 o 1 2 x-2 -1 o1 2 3 x-1o1xo1x-2-2-2-2o2 x-113 设函数 f x x 3 bx 2 cx( x R) ,已知 g (x)f ( x) f ( x) 是奇函数,则函数f(x) 的解析式为 _____ fxx 3 3x 2 ( x R)14. 函 数 y = f (x )x 3 ax 2bx a 2 在 x 1 时 ,有极值 10,那 么 a, b 的 值a 4 为.b1115.已知函数f (x) x 3 12x 8 在区间 [ 3, 3]上的最大值与最小值分别为M , m ,则M m ____ .3216.已知函数 f ( x) 1 x 31 ax2 6 x( x R) ,若它的导函数 y f ( x)在[2,)上是32单一递加函数,则实数 a 的取值范围是 _____ ( ,4]17. 确立以下函数的单一区间(1) y =x 3-9x 2+24x (2) y =x -x 318. (满分 10 分) 设函数 f (x ) x 31 x2 2x 5, 若对于随意 x [ 1,2] 都有 f (x ) m 建立 , 务实数 m2的取值范围 .解: f (x ) 3x 2x 2, 令 f ( x)0, 得 x 2或 x 1 .3∵当 x在( 2, 3极大值为21 时 , f ( x)0, ∴ yf (x ) 在 ( ,2) 上为增函数 ,或 x)和 (1,3231) 上为减函数 , ∴ f (x ) 在 x在 x 1 处有极小值 .处有极大值 ,2 223而 f (2)7 , ∴ f ( x) 在 [ 1, 2] 上的最大值为 7.f ( )5 , 327若对于随意 x [ 1, 2] 都有 f (x ) m 建立 , 得 m 的范围 m 7 .19 已 知 x1 是 函 数 f (x ) mx 3 3( m 1) x2 nx 1 的 一 个 极 值 点 ,其 中m, n R , m0,(1) 求 m 与 n 的关系式 ; (2)求 f ( x) 的单一区间 ;(3) 当 x [ 1,1] 时, 函数 y f ( x) 的图象上随意一点的切线斜率恒大于3m, 求 m 的取值范围 .解:(1) f ( x ) 3mx 26(m 1) xn 由于 x1是函数 f ( x) 的一个极值点 , 因此 f (1) 0 ,即 3m 6(m 1) n 0, 因此 n 3m 6(2) 由 (1) 知 , f (x)3mx 26(m 1)x 3m 6 3m( x 1)[ x (12)]2,当 x 变化时, f (x ) 与 f (x ) 的变化以下表 :m当 m0 时, 有 11m故有上表知 , 当 m0 时 , f (x ) 在 (,1 2 ) 单一递减 , 在 (1 2 ,1) 单一递加 , 在(1, )m m上单一递减 .(3) 由已知得 f (x ) 3m , 即 mx 2 2(m 1)x 2又 m0 因此 x22(m 1)x2 0 , 即 x22( m 1) x 2 0, x[ 1,1] ①m mmm设g( x ) x22(11)x 2 , 其函数张口向上 , 由题意知①式恒建立 ,mmg( 1) 012 2 2 0 44,0)因此m mm0 , 即 m 的取值范围为 (g(1) 013320.( 满分 12分 ) 设函数 f ( x)x 3 3x 2 分别在 x 1 、 x 2 处获得极小值、极大值 . xoy 平面上点 A 、 B 的坐标分别为 ( x 1 , f ( x 1 )) 、 ( x 2 , f ( x 2 )) , 该平面上动点 P 知足 PA PB 4 ,点 Q 是点 P 对于直线 y 2(x 4) 的对称点 . 求 ( Ⅰ ) 点 A 、 B 的坐标 ;( Ⅱ ) 动点 Q 的轨迹方程解: ( Ⅰ ) 令 f ( x) ( x 33x 2)3x 23 0解得 x 1或 x 1当 x1 时 , f ( x)0 , 当 1 x 1时, f ( x) 0 , 当 x 1时 , f ( x)因此 , 函数在 x 1 处获得极小值 , 在 x 1获得极大值 , 故x 1 1, x 2 1, f ( 1) 0, f (1) 4因此 , 点 A 、 B 的坐标为 A( 1,0), B(1,4) .( Ⅱ ) 设 p( m,n) ,Q ( x, y) ,PA PB1 m, n 1 m,4 nm21 n24n 4k PQ 1,因此yn1,又 PQ的中点在y 2( x 4) 上,因此y m2 x n 4 2 x m 2 2 2消去 m, n 得x 8 2 y 2 2 9。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高考导数考点复习讲义
考点1:导数切线问题求法
曲线ylnkxx在点1,k处的切线平行于x轴,则求k
2
56lnfxaxx
,aR,曲线yfx在点1,1f处的切线与y轴相交于点0,6。确定a值
已知函数2()(2)lnfxxaxax,aR.若曲线()yfx在点(2,(2))f处的切线的斜率为1,求a
已知函数()fx,mmxx.当2m时,求曲线)(xfy在点))1(,1(f处的切线方程;
已知函数()ln()fxxaxaR当2a时,求曲线()yfx在点(1,(1))Af处的切线方程。
设l为曲线C:lnxyx在点(1,0)处的切线。求l的方程。
已知函数()fx=2xaxb,()gx=()xecxd,若曲线()yfx和曲线()ygx都过点P(0,2),且在点P
处有相同的切线42yx,求a,b,c,d的值
考点2:导数极值单调问题
已知函数()fx21(1)ln2xxaxa.若a32,求函数f()x的极值
设2156ln2fxxx,其中aR,求函数fx的单调区间与极值。
设函数21xfxxekx(其中kR).当1k时,求函数fx的单调区间
已知f(x)=ax-lnx,x∈(0,e],g(x)=,
讨论a=1时,f(x)的单调性、极值;
函数Raxaxnxxxf21)(.若函数)(xf在1x处取得极值,求a的值;
设函数1()(01)1fxxxxnx>且求函数()fx的单调区间。
设函数2lnfxxaxx.若1a,试求函数fx的单调区间
考点3:导数范围最值问题
已知函数()fxlnaxx,其中a为常数,e为自然对数的底数.当1a时,求()fx的最大值;
若0a,且()fx在区间0,e上的最大值为3,求a的值;
设函数ln fxxax,xgxeax,其中a为实数.若fx在1,上是单调减函数,且
gx
在1,上有最小值,求a的范围
考点4:导数的恒成立问题
已知函数xaxxfln1)(()aR.
若函数)(xf在1x处取得极值,对x),0(,2)(bxxf恒成立,求实数b的取值范
围
已知函数aaxxxxfln)1(21)(2.若对任意的)3,1(x,都有0)(xf成立,求a的取值范围.
已知函数22()fxxx,1()2xgxm.若1[1,2]x,2[1,1]x使12()()fxgx求m取值范围
已知函数2()ln2afxxx,若1()2fx恒成立,求a的取值范围.
设函数1()(01)1fxxxxnx>且,已知1121nanxx>对任意(0,1)x成立,求实数a的取值范围.
考点5:导数分类讨论问题
已知函数xaxxfln1)(()aR.讨论函数)(xf在定义域内的极值点的个数;
已知函数2()(2)lnfxxaxax,其中aR.求函数()fx的单调区间.
设21xf(x)e(axx).若0a,讨论f(x)的单调性;
已知函数()ln,fxaxx.当0a时,求()fx的单调区间
已知函数xxaxfln)1()(2.讨论函数)(xf的单调性
已知f(x)=ax-lnx,x∈(0,e],是否存在实数a,使f(x)的最小值是3,若存在,求出a的值;若不存
在,说明理由
已知函数()ln()fxxaxaR,求函数()fx的极值.
考点6:导数零点讨论问题
已知函数()xgxe.若不等式()gxxmx有解,求实数m的取值菹围;
已知函数()e,xfxxR.设x>0,讨论曲线y=f(x)与曲线2(0)ymxm公共点的个数.
设函数ln fxxax,xgxeax,其中a为实数.若gx在1,上是单调增函
数,试求fx的零点个数,并证明你的结论.
已知函数()fx,()2lnmmxgxxx.当1m时,判断方程)()(xgxf在区间1,上有
无实根.
函数2()(2.71828xxfxceeL是自然对数的底数,)cR.讨论关于x的方程
|ln|()xfx
根的个数.
已知函数()fxlnaxx,其中a为常数,当1a时,判断方程|()|fxln12xx是否有
实根?若无实根请说明理由,若有实根请给出根的个数.
考点7:导数与不等式问题
设l为曲线C:lnxyx在点(1,0)处的切线。证明:除切点(1,0)之外,曲线C在直线l的下
方
函数Raxaxnxxxf21)(.若函数)(xf的图象在直线xy图象的下方,求a的取值范围
已知函数()fx2(1)lnaxx.讨论函数)(xf的单调性;若对任意)2,4(a及]3,1[x时,恒
2
axfma
成立,求实数m的取值范围.
已知函数()ln,()xfxaxxgxe。证明:当a=0时,()()2fxgx。
已知函数()fx,()2lnmmxgxxx。若ex,1时,不等式2)()(xgxf恒成立,求实数m的取值
范围.
已知f(x)=ax-lnx,x∈(0,e],g(x)=,证明a=1时f(x)>g(x)+;
