一种改进的种子填充算法
案例10 扫描线种子填充算法

程序代码
PointTemp.x=xleft;PointTemp.y=PointTemp.y-2; //处理下一条扫描线 while(PointTemp.x<xright) { bSpanFill=FALSE; while(pDC->GetPixel(Round(PointTemp.x),Round(PointTemp.y))!=BoundaryClr && pDC->GetPixel(Round(PointTemp.x),Round(PointTemp.y))!=SeedClr) { bSpanFill=TRUE; PointTemp.x++; } if(bSpanFill) { if(PointTemp.x==xright && pDC->GetPixel(Round(PointTemp.x), Round(PointTemp.y))!=BoundaryClr && pDC->GetPixel(Round(PointTemp.x),Round(PointTemp.y))!=SeedClr) PopPoint=PointTemp; else PopPoint.x=PointTemp.x-1;PopPoint.y=PointTemp.y; Push(PopPoint); bSpanFill=FALSE; } while((pDC->GetPixel(Round(PointTemp.x),Round(PointTemp.y))==BoundaryClr && PointTemp.x<xright) || (pDC->GetPixel(Round(PointTemp.x),Round(PointTemp.y)) ==SeedClr && PointTemp.x<xright)) PointTemp.x++; } }
一种基于位存储的种子填充算法

第2 4卷第 2 期
20 0 8年 4月
呵 方学院学 (然 学 ) ' 自 科 版
J u n l f He e r h Un v r i ( t r l ce c iin o r a b i o No t i e st y Na u a in e Edto ) S
Vo . 4 No 2 12 .
Apr 0 .2 08
一
种 基 于 位存 储 的种 子 填 充 算 法
胡 云
( 锡市广播电视大学,江苏 无锡 241) 无 1 0 1
摘 要 :为 了提 高 利 用 种 子 填 充 算 法 对 区 域 填 充 的效 率 .主要 方 法 是 改 进 基 本 的算 法 思 想 。改 变 像 素 点 简单
着 色 和 入栈 的顺 序 ,从 而 像 素 点 入 栈 的次 数 ,达 到 降低 算法 执 行 时所 占空 间 的 目的 .在 具 体 的程 序 实 现 时 减少
对 像 素 点 坐标 的存 储 采 用 占用 空间较多 的整型 ,没有考虑到像素点 坐标取 值的实际情况 ,消耗空间较多.改进 、
区域 填充 是计算 机 图形学 的基本 问题 之一 ,它是 用一 种颜色 或 图案来填 充一 个 二维 区域 ,该 区域 卜 可 以是带 孔 的 ,也 可 以是 不带 孔 的 ,它 主要 用来 实现 绘制 二维平 面及 三维 物体 的 中一个 面. 种子填 充算法
Ab t a t I r r t m p ov t e e fce c o r a iln u i i s r c : n o de o i r e h fii n y f a e fli g sng smpl e d ilng a go ihm , t e s e fli l rt he ma n m e ho st n v t a i l o ihm h gh , c a i he o de i e h d ng a s i g a e i t d i o i no a e b sc a g rt t ou t h ng ng t r rofp x ls a i nd pu h n r a it tc n o s a k, t e e y r d i he t t lnu b r o u h ng a e nt t c h r b e ucng t a a m e f p s i r a i o s a k. Thu he g a f r du i he s t o lo e cng t s a eu e p c s d whe m p e n i he l o ihm s a hiv d. Ho v r t e m e n i l me tng t a g rt i c e e we e , h mor o pi e i oo d — y t x lpont c r i na e a s mo e oc u n y s c urn he p ro o r t o e r t s t ke r . c pa c pa e d i g t e i d ofc nc e epr c du e。 a d t e a t a iu to fC — n h c u ls t a i n o O or i a e f t oi t v u s S o t ke i o on i r to d n t s o he p n al e i n t a n nt c sde a i n, a hu nd t s, m o e s a e S a n. The i r p c i t ke m— p o e e d fli g a g r t r v d s e iln l o ihm s u e o e r s oo d na e n t o m fpo ii o ntd i g t e c r e i s d t xp e s c r i t s i he f r o ston p i urn h ou s o mplme tn he pr c du e, t n f r he e c h c u e l c . An he e e i n a e u t h s fi e n ig t o e r he u t r r du e t e o c pi d p a e d t xp rme t lr s l a a s r v d t e vai t ft sm e ho . lo p o e h ldiy o hi t d Ke r s: s e ilng; b tme r y wo d e d fli i mo y; a e ilng; s a k r a fli tc
区域填充算法

区域填充算法⼀、区域填充概念区域:指已经表⽰成点阵形式的填充图形,是象素的集合。
区域填充:将区域内的⼀点(常称种⼦点)赋予给定颜⾊,然后将这种颜⾊扩展到整个区域内的过程。
区域填充算法要求区域是连通的,因为只有在连通区域中,才可能将种⼦点的颜⾊扩展到区域内的其它点。
1、区域有两种表⽰形式1. 内点表⽰:枚举出区域内部的所有象素内部所有象素着同⼀个颜⾊边界像素着与内部象素不同的颜⾊。
2. 边界表⽰:枚举出区域外部的所有象素边界上的所有象素着同⼀个颜⾊内部像素着与边界象素不同的颜⾊。
2、区域连通1. 四向连通区域:从区域上⼀点出发可通过上、下、左、右四个⽅向移动的组合,在不越出区域的前提下,到达区域内的任意象素。
2. ⼋向连通区域:从区域上⼀点出发可通过上、下、左、右、左上、右上、左下、右下⼋个⽅向移动的组合,在不越出区域的前提下,到达区域内的任意象素。
3. 四连通与⼋连通区域的区别连通性:四连通可以看作⼋连通的⾃⼰,但是对边界有要求⼆、简单种⼦填充算法1、基本思想给定区域G⼀种⼦点(x, y),⾸先判断该点是否是区域内的⼀点,如果是,则将该点填充为新的颜⾊,然后将该点周围的四个点(四连通)或⼋个点(⼋连通)作为新的种⼦点进⾏同样的处理,通过这种扩散完成对整个区域的填充。
这⾥给出⼀个四连通的种⼦填充算法(区域填充递归算法),使⽤【栈结构】来实现原理算法原理如下:种⼦像素⼊栈,当【栈⾮空】时重复如下三步:2、算法代码这⾥给出⼋连通的种⼦填充算法的代码:void flood_fill_8(int[] pixels, int x, int y, int old_color, int new_color) { if (x < w && x > 0 && y < h && y > 0) {// 如果是旧的颜⾊⽽且还没有给他填充过if (pixels[y * w + x] == old_color) {// 填充为新的颜⾊pixels[y * w + x]== new_color);// 递归flood_fill_8(pixels, x, y + 1, old_color, new_color);flood_fill_8(pixels, x, y - 1, old_color, new_color);flood_fill_8(pixels, x - 1, y, old_color, new_color);flood_fill_8(pixels, x + 1, y, old_color, new_color);flood_fill_8(pixels, x + 1, y + 1, old_color, new_color);flood_fill_8(pixels, x + 1, y - 1, old_color, new_color);flood_fill_8(pixels, x - 1, y + 1, old_color, new_color);flood_fill_8(pixels, x - 1, y - 1, old_color, new_color);}}}3、OpenCV实现import cv2def seed_fill(img):ret, img = cv2.threshold(img, 128, 255, cv2.THRESH_BINARY_INV) label = 100stack_list = []h, w = img.shapefor i in range(1, h-1, 1):for j in range(1, w-1, 1):if (img[i][j] == 255):img[i][j] = labelstack_list.append((i, j))while len(stack_list) != 0:cur_i = stack_list[-1][0]cur_j = stack_list[-1][1]img[cur_i][cur_j] = labelstack_list.remove(stack_list[-1])# 四邻域,可改为⼋邻域if (img[cur_i-1][cur_j] == 255):stack_list.append((cur_i-1, cur_j))if (img[cur_i][cur_j-1] == 255):stack_list.append((cur_i, cur_j-1))if (img[cur_i+1][cur_j] == 255):stack_list.append((cur_i+1, cur_j))if (img[cur_i][cur_j+1] == 255):stack_list.append((cur_i, cur_j+1))cv2.imwrite('./result.jpg', img)cv2.imshow('img', img)cv2.waitKey()if __name__ == '__main__':img = cv2.imread('./test.jpeg', 0)seed_fill(img)4、简单种⼦填充算法的优点和缺点优点:1. 该算法也可以填充有孔区域缺点:1. 有些像素会多次⼊栈,降低算法效率,栈结构占空间2. 递归执⾏,算法简单,但效率不⾼,区域内每⼀像素都要进/出栈,费时费内存3. 改进算法,减少递归次数,提⾼效率三、扫描线种⼦填充算法⽬标:减少递归层次适⽤于边界表⽰的4连通区间1、基本思想在任意不间断区间中只取⼀个种⼦像素(不间断区间指在⼀条扫描线上⼀组相邻元素),填充当前扫描线上的该段区间;然后确定与这⼀区段相邻的上下两条扫描线上位于区域内的区段,并依次把它们保存起来,反复进⾏这个过程,直到所保存的各个区段都填充完毕。
射线填充——种子填充算法的改进

a )栈 顶像 素 出栈 ; b )将 出栈像 素设 置成 填充 色 ; c )检 查 出栈像 素 的 8 一邻 接点 ,若 其 中某 个像 ( 3 ) 检 查 栈 是 否 为 空 ,若 栈 非 空 重 复 步 骤 ( 2 ) , 该填 充 算 法 过程 是 很 简 单 的 ,可 以在 用 户 先
关 键词 : 区域 填 充 ;种 子点 ;八连 通 ;射 线 ;不规 则 区域
中图分 类号:T P 3 9 1 . 4 1
文献 标识码 :A
文 字标 号:粤 内登 字。 一1 0 2 6 7 ( 2 0 1 3 ) 0 1 — 0 0 7 0 — 0 3
常 用 的填 充算 法可分 为 两大类 :扫描 转换 和种 区域边 界颜 色范 围 内的所有像 素 为止 。算法 步骤如
本 原理 为 : 只要 在某 个 区域 内有一 个 已知像 素 , 就
能 从此 像 素 出发找 到 区域 内所 有其 他像 素 , 并 对它 素不 是边界 色且 未置 成填充 色 ,则把该 像 素人栈 。
们进行填充 。根据区域的特性 , 种子填充法可分为
出发 。 可 以通 过 上 、下 、左 、右 四个方 向或者 上 、
l 1 . 子填 充 。前者着 重解 决 由多边形 轮廓 线所 围 的区域 下 【
的填色问题 。后者适用于任意形状轮廓线所围成的
区域 ,但 缺点是 要求 区域 必须 闭合且 一次 只能 填充
一
( 1 ) 种子 像素 人栈 ;
( 2 ) 执行 如下 三步 :
个单 连 通 区域 。 种 子填 充法 是 区域 填充 的一种基 本 方法 , 其 基
内 的任 意像 素 。传统 的种 子填充 法存在 着 占用空 间 色和图案 ,用途比较广泛 。然而该算法需要很大的
《计算机图形学》试题-A卷及参考答案

7、对于由P 0 P 1 P 2 三点所决定的二次B样条曲线,下列叙述中错误的是( D )
A)起始点位于(P 0 +P 1 )/2 处; B)终止点位于(P 2 +P 1 )/2 处; C)若P 0 P 1 P 2 三点共线时,该曲线是一条线段; D)起始点的切矢为:2(P 1 -P 0 )。 8、下列不属于计算机图形学中三维形体表示模型的是:( C )。 A 线条模型 B 表面模型 C 粒子模型 D 实体模型
X(t)=3t 2 3 Y(t)=3t-9t +6t 2 3 Z(t)= 3t-9t +6t 将 t 分别等于 0,1/3, 2/3,1 代入上述参数曲线,得 P(0)=(0,0,0) P(1/3)=(1,2/9,2/9) P(1/2)=(3/2,0,0) P(2/3)=(2,-2/9,-2/9) P(1)=(3,0,0)
计算机图形学试题
一、选择题(20 分) 1、种子填充算法中,正确的叙述是( C ) A)按扫描线的顺序进行象素点的填充; B)四连接算法可以填充八连接区域;
A
C)四连接区域内的每一象素可以通过上下左右四个方向组合到达; D)八连接算法不能填充四连通区域。 2、在多边形的逐边裁剪法中,对于某条多边形的边(方向为从端点 S 到端点 P)与 某条裁剪线(窗口的某一边)的比较结果共有以下四种情况,分别需输出一些顶点. 请问哪种情况下输出的顶点是错误的? ( A ) A) S 和 P 均在可见的一侧,则输出 S 和 P. B) S 和 P 均在不可见的一侧,则输出 0 个顶点. C) S 在可见一侧,P 在不可见一侧,则输出线段 SP 与裁剪线的交点. D) S 在不可见的一侧,P 在可见的一侧,则输出线段 SP 与裁剪线的交点和 P. 3、透视投影中主灭点最多可以有几个?( D ) A)0 B)1 C)2 D)3
第3章 填充
3.5.2 多边形域填充 常用的填充方法是按扫描线顺序,计算扫描线 与多边形的相交区间,再用要求的颜色显示这些区 间的像素,即完成填充工作,简称为扫描线填充算 法。区间的端点可以通过计算扫描线与多边形边界 线的交点获得,该方法适用于自动填充。
1.多边形域的填充步骤 一般多边形的填充过程,对于一条扫描线,可以分为 4个步骤: (1) 求交:计算扫描线与多边形各边的交点。 (2) 排序:把所有交点按x递增顺序进行排序。 (3) 交点配对:第1个与第2个,第3个与第4个等两两配对, 每对交点就代表扫描线与多边形的一个相交区间。 (4) 区间填色:把这些相交区间内的像素置成多边形颜色。
对例3.4重新使用改进后的简单种子填充算法步骤如下。 解: (1) 种子像素(3, 2)入栈并着色。 (2) 出栈(3, 2)。入栈(2, 2)、(3, 3)、(4, 2)、(3, 1)并着色。 (3) 出栈(3, 1)。入栈(2, 1)、(4, 1)并着色。 (4) 出栈(4, 1)。 (5) 出栈(2, 1)。 (6) 出栈(4, 2)。 (7) 出栈(3, 3)。入栈(2, 3)并着色。 (8) 出栈(2, 3)。 (9) 出栈(2, 2)。入栈(1, 2)并着色。 (10) 出栈(1, 2),栈空结束。
3.5 区域填充
3.5.1 种子填充算法
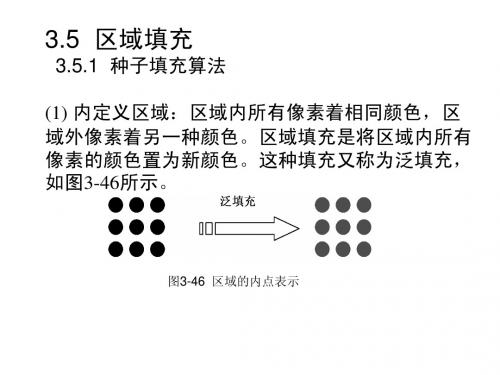
(1) 内定义区域:区域内所有像素着相同颜色,区 域外像素着另一种颜色。区域填充是将区域内所有 像素的颜色置为新颜色。这种填充又称为泛填充, 如图3-46所示。
图3-46 区域的内点表示
(2) 边界定义区域:区域边界像素着特定颜色,区 域内像素不取特定颜色。区域填充是将区域内所有 像素的颜色置为边界像素颜色或新颜色。这种填充 称为边界填充,如图3-47所示。
基于三角面网格细化策略的改进种子填充算法

2 . E d u c a t i o n a l T e c h n o l o g y C e n t e r , P L A G e n e r a l H o s p i t a l , B e i j i n g 1 0 0 8 5 3 , C h i n a ) [ A b s t r a c t ]A i mi n g a t t h e p r o b l e m t h a t t h e g e n e r a l b o u n d a r y — f i l 1 a p p r o a c h c a n n o t w o r k e f f e c t i v e l y f o r s p a c e s u r f a c e s . t h i s p a p e r p r o p o s e s
i n t he a r e a o f bo t h e ic f i e n c y , a n d il f l s e f f e c t of a l go r i t h m p r o p os e d .
[ K e y wo r d s ]b o u n d a y- r f i N ; s e e d 一 1 1 a l g o r i t h m; t r i a n g u l a r s u r f a c e me s h ; t r i a n g l e s u b d i v i s i o n ; c o n v e x h u l l ; v i r t u a l s u r g e r y
a s e e d— f i l l a l g o r i t h m wh i c h i s a v a i l a b l e f or t he t r i a n g ul a r me s he s . By c h a n gi n g t h e wa y t o de t e r mi ne a s e e d i t ma k e s t h e a l go r i t h m a v a i l a bl e f o r t h e 3 D me s h e s . Th i s s u bd i vi s i on a l go r i t h m i s g u i de d b y t h e c o nt o u r , a nd il f t e r s t he s u bd i v i s i o n p oi n t b y s o me f e a t u r e o f t h e c o n v e x hu l 1 . Exp e r i me nt a l r e s ul t s h o ws t ha t t h i s a l g o r i t h m c a n d o b o u nd a y— r f i I 1 o n t r i a n g ul a r me s he s we l 1 . h a s pr a c t i c a l v a l ue .s a t i s ie f s t h e pr a c t i c a l n e e d
大学mooc计算机图形学章节测验期末考试答案

解忧书店 JieYouBookshop
青春须早为,岂能长少年。
第二讲测验
1
单选 (2 分)
种子填充算法中,正确的论述是 A.四连通算法的数据结构采用的是队列结构 B.四连通算法可以填充八连通区域 C.它是按扫描线的顺序进行像素点的填充 D.四连通区域内的每一象素可以通过上下左右四个方向组合到达
正确答案:A、B 你没选择任何选项
3
判断 (1 分)
使用齐次坐标可以将 n 维空间的一个点向量唯一的映射到 n+1 维空间中
©解忧书店,严禁转载,违者必究!
4 / 16
正确答案:×
青春须早为,岂能长少年。
第六讲测验
1
单选 (2 分)
透视投影中主灭点最多可以有几个? A.3 B.1 C.2 D.0
A 正确答案: 你没选择任何选项
正确答案:C、D 你没选择任何选项
2
多选 (2 分)
在区域分割(Warnack)消隐算法中,窗口与多边形的关系包括哪些? A.包围 B.内含 C.相交 D.分离
©解忧书店,严禁转载,违者必究!
3 / 16
正确答案:A、B、C、D 你错选为 D
青春须早为,岂能长少年。
第五讲测验
1
多选 (2 分) 下述对坐标系的描述哪些是正确的?
2
单选 (2 分)
有关平面几何投影的叙述,错误的是 A.斜投影又可分为斜等测、斜二测 B.正轴测又可分为正一测、正二测 C.透视投影又可分为一点透视、二点透视、三点透视 D.三视图又可分为主视图、侧视图、俯视图
B 正确答案: 你没选择任何选项
3
多选 (2 分)
在下列对投影的描述里,正确的论述为 A.太阳光线产生的投影为平行投影 B.物体经过透视投影后可产生缩放的效果 C.三视图属于透视投影 D.透视投影与平行投影相比,视觉效果更有真实感,而且能真实地反映物体的精确的尺 寸和形状
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
3 算法描述
改进算法的算法语言描述 (采用类 C 语言描述 )如下 :
seed(x1,y1)是最初给定的种子像素点,point 表示一个像素点 , 由 x1,y1 坐标组成 ; seed(x2,y2)是由种子 seed(x1,y1)产生的种子 , 由 x2,y2 坐标组成 ; InitStack()初始化栈 , 并使它为空 ; Push()是将一个像素点入栈 ; Pop()是出栈 , 返回类型为像素点 ; StackEmpty()是栈的判空函数 ; getpixel()返回指定像素点的颜色值; putpixel()设定指定像素点的颜色值为给定的颜色值; // 程序从下面开始 InitStack(); putpixel(seed(x1,y1)) ; putpixel(seed(x2,y2)) ; Push (seed(x1,y1)) ; Push (seed(x2,y2)) ; while(! StackEmpty()) { point=Pop(); if(point 的左上一点不为填充色也不为边界色) { putpixel(point 的左上一点 );Push(point 的左上一点 );} if(point 的左下一点不为填充色也不为边界色) { putpixel(point 的左下一点 ); Push (point 的左下一点 );} !"# !" if(point 的右上一点不为填充色也不为边界色) 50 { putpixel(point 的右上一点 ); Push (point 的右上一点 );} 100 150 if(point 的右下一点不为填充色也不为边界色) 200 { putpixel(point 的右下一点 ); Push (point 的右下一点 );} } 4 算法比较
One Impr oved Seed- filling Algor ithm
HU Yun, LI Pan- rong
(Wuxi Radio & TV University,Wuxi 214021,China) Abstr act: After the analysis and discussion of the tranditional seed- filling algorilms,tha authors put forword an improved seed - filling algorilm , which is superior to the old ones in increasing the efficiency of time or space. Key wor ds: seed filling algorithm; region filling;stack
表1
!"#$% !"#$ !"#$ 7651 1588 31015 6327 70088 14329 124843 25469 !"#$% !"#$ !"#$ 30978 15690 124866 62834 281522 141362 500914 251258
收稿日期 : 2005- 07- 12 作者简介 : 胡云( 1978- ) , 男 , 江苏盐城人 , 无锡市广播电视大学教师 , 主要研究算法设计与数据库技术。
・ 56 ・
安庆师范学院学报 ( 自然科学版 )
2006 年
子是给定的 , 另外一个是根据给定的种子产生的。 如图 2 , 假定像素 ① 是给定的种子 , 则另外一个种子可 以取像素 ② 、 ③、 ④、 ⑤ 中的任何一个 , 当然要保证其在填充区域之内。 ( 3 ) 传统的四向连通区域填充取上、 下、 左、 右四个方向 , 而本文四向连通区域填充取左上、 左下、 右 上、 右下四个方向 , 如图 3 所示 , 种子 ① 填充 ○ 标识区域 , 种子 ② 填充 ● 标识区域。
! 1 !"#$%&’()*
2 算法的实现思想
传统种子填充算法不足之处主要有两点 : ( 1 ) 像素存在重复入栈 , ( 2 ) 栈所占空间很大。 其中像素的重复 入栈也是栈空间所占空间很大的一个重要原因。本文针对上述两点对算法进行改进。 ( 1 ) 在递归种子填充算法中 , 采用的是先入栈 , 出栈后再填充 , 即当 填充某点 时 , 不管它的 四连通点 是否已被填充 , 都要进入堆栈 , 这会导致很多的冗余像素点入栈。而本文算法采用的是先填充再入栈 , 在入栈之前要判断像素点是否已被填充 , 若已被填充才入栈 , 否则不予考虑。 这样将会减少入栈的冗余 像素 , 即每一个像素点只入栈一次。 ( 2 ) 传统种子填充算法采用的是用一个种子进行填充 , 而本文算法采用两个种子进行填充。 其中一个种
214021 )
( 无锡市广播电视大学 , 江苏 无锡
摘
要 : 在对种子填充算法进行分析和讨论的基础上 , 提出了一种改进的种子填 充算法 , 该改进的 种 子
填充算法无论是时间还是空间效率都优于传统算法。 关键词 : 种子填充算法 ; 区域填充 ; 栈 中图分类号 : TP391 文献标识码 : A 文章编号 : 1007- 4260 ( 2006 ) 01- 0055- 02
2006 年 2 月
第 12 卷第 1 期
安庆师范学院学报 (
自然科学版 )
Feb.2006 Vol.12 No.1
பைடு நூலகம்
J ourna l of Anqing Te a che rs Colle ge ( Na tura l S cie nce Edition )
一种改进的种子填充算法
胡 云1 , 李盘荣 2
! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! !
[参考文献 ]
[1]
陈元琰 , 陈洪波 . 一种基于链队列的种子填充法 [J]. 广西师范大学学报 : 自然科学版 , 2003 , 21 ( 3 ) : 30- 33. 计算机图形学的算法基础 (第 2 版 )[M]﹒ 北京 : 机械工业出版社 , 2002 : ﹒ [2] (美 )David F.Rogers. ﹒ 99- 105.
1 问题的提出
区域填充是 计算机图形 学的基本问 题之一 , 种子 填充算法是 区域填充 的一种重要 算法 , 它 广 泛 应 用于交互式绘图系统和数字图像处理中。递归种子填充算法是从填充区域内部的一点开始 , 并由此出 发找到区域内的所有像素。算法从给定种子 (x,y)开始 , 先检测该点的颜色 , 如果它与边界色和填充色都 不相同 , 就用填充色来填充该点 , 然后检测相邻位置 , 以确定它们是否是边界色 和填充色 , 若 不是 , 就采 用递归算法填充该相邻点。这个过程运行到检测完区域边界范围内的所有像素为止。有两种方法检测 , 本文采用四向连通区域填充。 相邻像素 : 四向连通区域填充和八向连通区域填充 递归种子填 充算法的优 点是算法简 单 , 易 于 实 现 , 也 可 以 填 充 带 有内孔的平 面区域。但是 这种算法需 要很大的存 储 空 间 以 实 现 栈 结 构 , 这是因为当 某一像素出 栈时 , 其周围 的所有 4 个像 素 不 管 是 否 已 被填充 , 都必须入栈。这样会导致一个像素要入栈多次。如图 1 所示 , 像素 ⑤ 周围有 8 个像素 , 当像素 ② 出栈时 , 按照四连通填充算法 , 要将 同理 , 当像素 ④ , ⑥ , ⑧ 出栈时也分别要把 ⑤ 压入堆栈 , 不 ⑤ 压入堆栈。 管它是否已在堆栈中 , 不管它是否已被填充 , 也不管它是否是边界 , 这 也就意味着入栈总数是所有像素个数总和的 4 倍。 由于栈中有如此多 的“ 冗余” 信息 , 所以采用这种算法进行填充时 , 所需要的栈空间很大 , 而且对同一个像素如此反复入栈和出栈 , 所花费的时间也很多。
为了验证以上改进算法在栈所用空间大小和进出栈次数方面的改进 , 我们在微机上进行了实验 , 该 实验是在 Pentium4 1.4GHz/256MB/Windows2000/VC++6.0 的环境下完成的。具体实验数据见表 1 , 由此 可以看出 : ( 1 ) 在栈所用空间大小上 , 改进算法的栈空间大小大概是传统种子填充算法的栈空间大小的 这说明改进算 20% 左右 ; ( 2 ) 从进出栈的次数来看 , 传统种子填充算法的进出栈次数是改进算法的 2 倍。 法无论在时间还是在空间上都优于原算法。 在改进的算法中 , 能够节约空间 , 尽量减少了像素点的检测 次数和入栈的总次数 , 同时可以加快填充速度 , 当填充区域很大时这种差别更明显。
