(完整版)关于数值计算过程说明
第1章 数值计算导论

5. 1957 年,美国 IBM 公司的 J. Backus 领导开发的 Fortran 最优编译器算法; 6. 1959-1961 年,英国伦敦 Ferranti 公司的 J. Francis 发现的计算矩阵特征值的稳定算法,
纯数学
纯科学
经过发展、融合,形成“数值计算”方向 的过程. 为了突出数值计算在各种科学
应用数学 实验/工程科学
与工程问题中的应用,以及它作为计算机
学科一部分的重要性,近年来也将它称为 科学计算(scientific computing).
计算数学 计算科学与工程
与数值计算联系紧密的一个研究方
向是高性能计算,它的研究对象包括高性 能的计算机硬件体系结构及其应用,包括
2. 1947 年,美国兰德(RAND)公司的 G. Dantzig 创造的解线性规划问题的单纯型算法 (Simplex 算法);
3. 1950 年,美国国家标准局数值分析研究所的 M. Hestenes, E. Stiefel 和 C. Lanczos 开创 的 Krylov(克雷洛夫)子空间迭代法;
名称 CMLIB
FMM
HSL
IMSL
NAG NAPACK
Netlib NR NUMERALGO MATLAB PORT SLATEC SOL
TOMS
表 1-1 重要的数值计算软件、程序包的网络资源
内容说明
商业/免费
网址
美国国家标准技术协会(NIST)的数学与 免费
1.1.2 数值计算的问题与策略
数值计算的问题来自各个科学和工程分支,可归纳为下述三种情况: 1. 没有解析解的数学问题. 一个简单的例子是五次或更高次一元代数方程的求解,如:
数值分析2-3(牛顿插值法)

二阶差商
f [ xi , x j , xk ]
一般的k阶差商定义为
f [ x0 , x1 ,..., x k ] f [ x0 ,..., x k 2 , x k ] f [ x0 , x1 ,..., x k 1 ] x k x k 1
特别地,f(x)关于一个点xi的零阶 差商定义为函数值本身,即
§3
差 商 与 牛 顿 插 值
一、差商及其性质 二、差商的计算
三、牛顿插值公式 四、牛顿插值法举例
一、差商及其性质
1. 差商的定义 函数关于 xi, xj 一阶差商
f [ xi , x j ] fห้องสมุดไป่ตู้( x j ) f ( xi ) x j xi
f [ x j , xk ] f [ xi , x j ] xk xi
∶ ∶ ∶
f[x0,x1,x2] f[x1,x2,x3]
∶ ∶ ∶
f[x0,x1,x2,x3]
∶ ∶ ∶
例 已知函数y= f (x)的观测数据如下, 试构造差商表,并求 f [2,4,5,6]的值
x 0 2 f(x) 1 5
4 5 6 9 -4 13
解 构造差商表如下
xi f(xi) 一阶 二阶 三阶 0 1 2 5 2 4 9 2 0 5 -4 -13 -5 -1 6 13 17 15 5 四阶
4 3 2
用二次插值求f (3)时,取
x0=2, x1=4, x2=5, 得 f ( 3) f ( 2) f [2,4]( 3 2)
f [2,4,5]( 3 2)( 3 4) 7 5( 3 2)( 3 4) 12 思考:若本题只给出前三个点,结果 如何?请你总结牛顿插值法何时停止?
数值计算方法

数值计算方法在数学中,数值计算是解决实际问题常用的重要方法。
解决这类问题时,只要按照由简单到复杂、由特殊到一般的思维顺序进行逐步分析和研究,总能得到正确的结果。
下面,就有关数值计算方法和运算的规则及要求,进行分析讨论,并举例说明。
当数列或函数的各项中,如果出现加减乘除以外的运算,一定要首先考虑通过“分解”、“凑整”等数值运算的办法来解决,而不能直接运算。
具体来说,可采用以下方法:在运算过程中,为了省略乘方或开方运算,需将原式写成分子、分母都是较大数字的形式;为了使相乘的积尽量不变号,也可以把分母化成整数,再相乘;为了使被除数尽可能多地乘上除数所以位数较多的数,应把除数扩大成被除数的许多倍,然后用乘法分配律进行简便运算;为了把小数化成整数,需将小数点向右移动若干位,使小数的小数部分全部转换成整数的形式;为了保证每一位乘得的结果不变号,还可以对乘法和除法同时进行一次因式分解,使分子、分母同时除以较大的数字,从而在计算时,把小数化成整数,最后按照前面说的分配律,用简便方法进行简便运算。
对于分数值的计算,要先根据分数的意义计算出结果,再将得到的整数写成分数的形式,最后按照分数的运算法则进行运算。
计算方法不但要考虑数字本身的特征,而且还要注意分数与整数之间的互化问题。
一般地,分数的分子和分母都乘以同一个整数后,分数值发生了变化,所以必须进行同分母分数的加减运算;一般地,分数的分子和分母同时乘以较大的整数时,其值仍然不变,故不需要进行同分子分数的加减运算。
例如: 12*10=12(10)=2×3= 6(后一步不需要进行运算); 2*4=8(后一步不需要进行运算); 15*5=45(后一步不需要进行运算)。
关于约分,不仅要看被分数的整数部分和分数部分是否互质,而且要考虑两部分的大小是否适合分子、分母互质,是否有公因数等情况。
例如: 6*2/3=2/3(大小合适); 14/18=4/9(大小不合适)。
(完整版)Mathematica数值分析和数值计算

第五章 数值分析和数值计算1. 如何求插值多项式给定n 个点( x i ,y i ),(i=1,2,…,n),构造一个次数不超过n-1的多项式函数f(x),使得f(x i )=y i ,则称f(x)为拉格朗日插值多项式。
可以证明该多项式函数由公式))...()(())...()((...))...()(())...()(())...()(())...()((1211212321231113121321--------++------+------=n n n n n n n n n n x x x x x x x x x x x x y x x x x x x x x x x x x y x x x x x x x x x x x x y y唯一给定。
Mathematica 提供了根据插值点数据计算拉格朗日插值多项式的函数InterpolatingPolynomial ,下面是其调用格式:InterpolatingPolynomial[data,var]作出以data 为插值点数据,以var 为变量名的插值多项式。
例:在多数情况下,我们构造插值函数的目的在于计算函数f(x)的值,而并不在意插值多项式的具体表示形式。
对于拉格朗日插值多项式,当n 较大时,得到的高次插值多项式由于截断误差和舍入误差的影响,往往误差较大。
此时在实际应用中,一般采用分段插值。
Mathematica 提供了分段插值函数Interpolation ,其使用格式为:Interpolation[data,InterpolationOrder->n]这里InterpolationOrder->n 指定插值多项式的次数,默认值为3。
此外数据data 中还可以包括插值点处的导数,格式为:{{x1,{y1,dy1}},{x2,{y2,dy2}},…}例:已知f(0)=0,f(1)=2,f’(0)=1,f’(1)=1,求3次插值多项式f(x),并计算f(0.72)和画出函数f(x)在[0,1]区间上的图形。
数值计算方法和算法课程设计

数值计算方法和算法课程设计一、简介数值计算方法和算法课程是计算机科学与技术专业中重要的课程之一,其内容主要包含了数值计算方法和基本算法的理论、思想、原理和应用,培养了我们在计算机运算中提高算法效率和准确度的能力。
本文档是数值计算方法和算法课程设计的撰写指南,旨在帮助大家完成课程设计的撰写,以完成课程的要求。
二、数值计算方法数值计算方法是对数值问题进行数学解法的研究。
数值计算方法涉及的问题包括:求解方程、插值和逼近、数值积分和数值微分、常微分方程、偏微分方程等。
在数值计算方法中,我们需要了解一些常见的算法,例如:二分法、牛顿迭代法、高斯-塞德尔迭代法、龙格-库塔法等。
课程设计要求学生能够对各种数值方法进行学习、比较、分析和综合使用,完成一定的数值计算问题。
三、算法设计算法设计是在具体的问题基础上,根据规则和原则选择合适的计算流程和方法,得到满足计算要求的算法过程。
计算机算法是在计算机程序设计过程中所采用的一些指导模式,其目的在于使计算机能够依据事先给定的任务说明和数据,精细地指导其运算。
算法设计需要学生具备深厚的数学功底和良好的编程能力,同时,还需要学生掌握常见的算法设计原则和技巧。
四、课程设计要求本门课程设计要求学生独立完成一个数值计算问题的解法的完整过程。
具体要求:1.选择适合的数值计算问题并设计算法实现;2.实现程序并进行测试;3.通过测试数据的分析和效果评价,进行算法设计的改进;4.撰写设计报告并提交。
五、设计报告内容设计报告应该包括以下内容:1.问题的阐述与分析,明确所需要解决的数值计算问题,并说明具体的解法;2.算法实现流程,详细说明算法中所使用的思想、原理和过程;3.程序编写内容,对程序进行详细的讲解和分析,并附上程序代码;4.程序测试过程,对测试数据和效果进行分析和说明,并展示输出结果;5.算法改进,对算法的不足之处和改进方向进行分析;6.总结,对设计过程中的感受和体会进行总结并对未来方向进行展望和思考。
数值计算方法

1.题目造倒数表,并例求 18 的倒数。
(精度为2.算法原理牛顿迭代法牛顿迭代法是通过非线性方程线性化得到迭代序列的一种方法。
对于非线性方程f x() = 0 ,若已知根x* 的一个近似值x k ,将f (x) 在x k 处展成一阶泰勒公式后忽略高次项可得:f (x) ≈ f x( k ) + f '(x k )(x −x k )右端是直线方程,用这个直线方程来近似非线性方程f (x) 。
将非线性方程fx( ) = 0的根x*代入f x( *) = 0 ,即f x( k ) + f '(x k )(x* −x k ) ≈ 0* x k−f (x k ) 解出x ≈f '(x k )将右端取为x k+1 ,则x k+1 是比x k 更接近于x* 的近似值,即f (x)x≈ x−f '(x k ) 这就是牛顿迭代公式,相应的迭代函数是f (x)ϕ(x) = x −f '(x)牛顿迭代法的应用1 1计算是求cx− =1 0的解,解出x,即得到。
取c c 有牛顿迭代公式cx−1 1x= x−= c c 这样就失去了迭代的意义,达不到迭代的效果。
1f (x) = cx−1, f '(x)= c,故重新构造方程:cx2 −x = 0 ,也是该式的解。
故取f (x) = cx2 −x ,cf '(x) = 2cx −1,则有牛顿迭代公式x= x−cx2 −x= cx, k = 0,1,...2cx k −1 2c k −11 1的值在~ 之间,取初值x0 = 。
20 103.流程图,,Nxε读入1k⇒()0xf′=x输出1k kx x⇒+⇒()()f xx xf x⇒−′x xε−<≠=<=≥≠4.输出结果5.结果分析当k= 3时,得 5 位有效数字 564。
此时,x3 −x4 = 000 < 005,故取x* = x3 = 564 ≈ 。
数值计算方法实验大纲
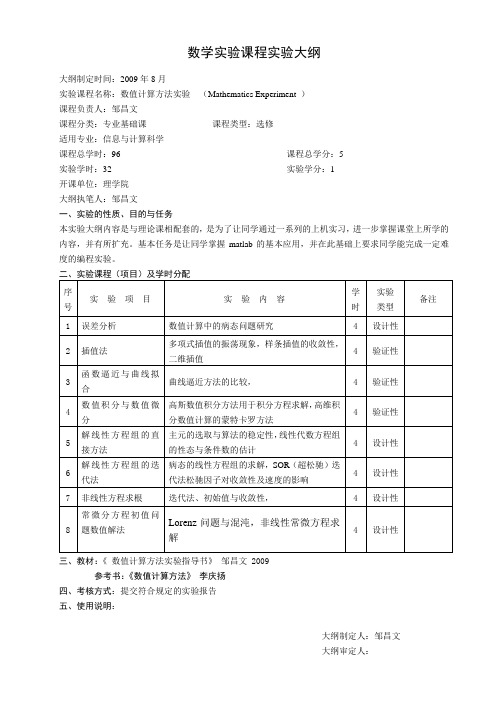
数学实验课程实验大纲
大纲制定时间:2009年8月
实验课程名称:数值计算方法实验(Mathematics Experiment )
课程负责人:邹昌文
课程分类:专业基础课课程类型:选修
适用专业:信息与计算科学
课程总学时:96 课程总学分:5
实验学时:32 实验学分:1
开课单位:理学院
大纲执笔人:邹昌文
一、实验的性质、目的与任务
本实验大纲内容是与理论课相配套的,是为了让同学通过一系列的上机实习,进一步掌握课堂上所学的内容,并有所扩充。
基本任务是让同学掌握matlab的基本应用,并在此基础上要求同学能完成一定难度的编程实验。
三、教材:《数值计算方法实验指导书》邹昌文 2009
参考书:《数值计算方法》李庆扬
四、考核方式:提交符合规定的实验报告
五、使用说明:
大纲制定人:邹昌文
大纲审定人:。
数值分析 迭代法 二分法和迭代法原理

lim | xk x* | 0
k
即 lim xk x *.
k
(b) | xk1 x*| L | xk x*|
| xk 1 xk | | ( xk 1 x*) ( xk x*) | xk x * xk 1 x * (1 L) xk x * 1 xk x * xk 1 xk 1 L 又 | xk1 xk | ( xk ) ( xk1 ) | '( ) | | xk xk1 | L | xk xk1 |
等价变换
x = (x) 称为迭代函数
(x) 的不动点x*
不动点迭代
具体做法:
从一个给定的初值 x0 出发,计算 x1 = (x0), x2 = (x1), … x 若 k k 0 收敛,即存在 x* 使得 lim x k x *,则由 的连续
k
xk 1 lim xk 可得 x* = (x*),即 x* 是 的不 性和 lim k k
根的估计
引理3.1(连续函数的介值定理) 设f(x)在 [a,b]上连续,且f(a) f(b)<0,则存在x*(a,b) 使f(x*)=0。 例3.1 证明x33x1 = 0 有且仅有3个实根,并 确定根的大致位置使误差不超过 =0.5。 解:
单调性分析和解的位置 选步长h=2, 扫描节点函数值 异号区间内有根
ek 1 xk 1 x* ( xk ) ( x*) '( )ek e 取极限得 lim k 1 '( x*) 0 线性收敛. k e k
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(完整版)关于数值计算过程说明
本文档旨在提供数值计算过程的详细说明,以帮助读者更好地理解和应用数值计算方法。
1. 引言
数值计算是一种通过使用数字近似值来解决数学问题的方法。
它在科学和工程领域中得到广泛应用,并且在很多情况下,数值计算是解决问题的唯一可行方法。
2. 数值计算过程概述
数值计算过程通常可分为以下几个步骤:
1. 问题建模:首先,将实际问题转化为可计算的数学模型。
这包括确定需要计算的量,规定适用的数学公式和方程。
问题建模:首先,将实际问题转化为可计算的数学模型。
这包括确定需要计算的量,规定适用的数学公式和方程。
2. 数值方法选择:选择适当的数值方法来解决问题。
不同的问
题可能需要使用不同的数值方法,如迭代法、插值法、数值积分等。
数值方法选择:选择适当的数值方法来解决问题。
不同的问题可能
需要使用不同的数值方法,如迭代法、插值法、数值积分等。
3. 数值算法实现:根据选定的数值方法,编写计算机程序来实
现算法。
这包括编写数值计算代码和处理可能出现的误差或异常情
况的代码。
数值算法实现:根据选定的数值方法,编写计算机程序
来实现算法。
这包括编写数值计算代码和处理可能出现的误差或异
常情况的代码。
4. 输入数据准备:为计算过程提供所需的输入数据。
这可以是
初始条件、样本数据或用户输入的参数。
输入数据准备:为计算过
程提供所需的输入数据。
这可以是初始条件、样本数据或用户输入
的参数。
5. 计算过程运行:运行数值计算程序来执行所选的数值方法。
这将使用输入数据作为计算的基础,并生成相应的计算结果。
计算
过程运行:运行数值计算程序来执行所选的数值方法。
这将使用输
入数据作为计算的基础,并生成相应的计算结果。
6. 结果评估:评估计算结果的准确性和可靠性。
这可能包括与已知解析解或实验数据的比较,或者通过使用数值稳定性和误差分析方法进行评估。
结果评估:评估计算结果的准确性和可靠性。
这可能包括与已知解析解或实验数据的比较,或者通过使用数值稳定性和误差分析方法进行评估。
7. 结果解释和应用:根据计算结果解释问题的答案,并根据需要应用结果进行进一步的决策或分析。
结果解释和应用:根据计算结果解释问题的答案,并根据需要应用结果进行进一步的决策或分析。
3. 数值计算过程中的注意事项
在进行数值计算过程时应注意以下事项:
- 数值稳定性:某些数值方法可能对输入数据的微小变化非常敏感,导致计算结果不稳定。
在这种情况下,通常需要采取适当的数值稳定性技术来保证计算的准确性和可靠性。
数值稳定性:某些数值方法可能对输入数据的微小变化非常敏感,导致计算结果不稳
定。
在这种情况下,通常需要采取适当的数值稳定性技术来保证计算的准确性和可靠性。
- 误差控制:数值计算过程中常常伴随着各种误差,如舍入误差、截断误差等。
为了控制误差并提高计算结果的准确性,可以采用数值误差分析技术和优化算法。
误差控制:数值计算过程中常常伴随着各种误差,如舍入误差、截断误差等。
为了控制误差并提高计算结果的准确性,可以采用数值误差分析技术和优化算法。
- 计算效率:在进行大规模数值计算时,对计算效率的考虑变得尤为重要。
可以采用并行计算、优化算法和近似计算等技术以提高计算效率。
计算效率:在进行大规模数值计算时,对计算效率的考虑变得尤为重要。
可以采用并行计算、优化算法和近似计算等技术以提高计算效率。
4. 结论
数值计算过程是解决许多实际问题的重要工具。
通过选择适当的数值方法和实施正确的数值算法,结合合理的输入数据和准确的
结果评估,我们可以得到满意的数值计算结果,并用于科学研究、工程设计和决策分析等领域。
希望本文档能够使读者对数值计算过程有更深入的理解,并能够在实践中应用数值计算方法,解决各种数学问题。
