量子化学习题
基础量子化学练习

2010基础量子化学练习(1)一、 判断正误( )1、 一个态函数总是等于时间的函数乘以坐标的函数。
( )2、 态函数总是Hamiltonian 算符的本征函数。
( )3、 Hamiltonian 算符的本征函数的任意线性组合是Hamiltonian 算符的本征函数。
( )4、 如果态函数不是算符ˆA的本征函数,则性质A 的一次测量可给出一个不是ˆA的本征值的值。
( )5、 几率密度与时间无关。
( )6、 如果两个算符具有共同的本征函数,那么这两个算符可对易。
( )7、 算符ˆx 与d i dx-可对易。
( )8、 氢原子Hamiltonian 算符的束缚态的本征函数构成完备集。
( )9、 厄米算符的本征函数是正交的。
( )10、 描述电子轨道运动的波函数必须是奇函数。
二、已知:2ˆˆˆ,A d dx B x ==,计算2ˆˆˆˆ,()A B A B ⎡⎤+⎣⎦及 三、已知:11223344ˆˆˆˆ,,,,A a A b A a A d ϕϕϕϕϕϕϕϕ====如果任意状态可以表示为12343253,ψϕϕϕϕ=+++那么当我们对该状态进行测量时,获得a 和d的几率各是多少?求任意状态? 的性质A 的平均值。
2010基础量子化学练习(2)一、 判断正误( )11、 算符ˆˆˆ,,A B C 满足ˆˆˆˆ,0,,0A B A C ⎡⎤⎡⎤==⎣⎦⎣⎦,则三个算符存在共同的本征函数集。
( )12、 不能对易的算符不可能具有共同的本征函数。
( )13、 当对本征态的性质A 进行测量时,能够得到的唯一仅有的值是算符ˆA的本征值。
( )14、 如果一个算符的平方等于单位算符,那么这个算符的本征值等于+1或者-1。
( )15、 所有品优的奇函数和偶函数都是宇称算符的本征函数。
( )16、 满足[]1212ˆˆˆ()()()()A c f x c g x c Af x c Ag x +=+的算符称为线性算符。
量子化学期末考试及答案

量子化学期末考试及答案量子化学期末考试一、选择题(每题2分,共20分)1. 量子化学的基本概念是:A. 原子的能量状态B. 原子的电子结构C. 原子的结构D. 原子的电荷2. 在量子化学中,电子的状态可以用:A. 原子轨道表示B. 原子能量表示C. 原子电荷表示D. 原子结构表示3. 在量子化学中,电子的状态可以用:A. 原子轨道表示B. 原子能量表示C. 原子电荷表示D. 原子结构表示4. 在量子化学中,电子的状态可以用:A. 原子轨道表示B. 原子能量表示C. 原子电荷表示D. 原子结构表示5. 在量子化学中,电子的状态可以用:A. 原子轨道表示B. 原子能量表示C. 原子电荷表示D. 原子结构表示二、填空题(每题2分,共20分)1. 量子化学的基本原理是____________。
答:量子力学。
2. 量子化学中,电子的状态可以用____________表示。
答:原子轨道。
3. 量子化学中,电子的能量可以用____________表示。
答:原子能量。
4. 量子化学中,电子的电荷可以用____________表示。
答:原子电荷。
5. 量子化学中,电子的结构可以用____________表示。
答:原子结构。
三、论述题(每题10分,共30分)1. 请简要介绍量子化学的基本原理。
答:量子化学是一门研究原子和分子的科学,它基于量子力学的原理,用来描述原子和分子的结构和性质。
量子力学的基本原理是,电子的运动是由量子态决定的,而不是由经典物理学的运动方程决定的。
量子力学的基本原理是,电子的运动是由量子态决定的,而不是由经典物理学的运动方程决定的。
量子力学还提出了一种新的概念,即电子的状态可以用原子轨道、原子能量、原子电荷和原子结构等表示。
量子力学的基本原理是,电子的运动是由量子态决定的,而不是由经典物理学的运动方程决定的。
2. 请简要介绍量子化学的应用。
答:量子化学的应用非常广泛,它可以用来研究原子和分子的结构和性质,以及它们之间的相互作用。
应化所量子化学考试题库及其答案详解

Principles Of Quantum Chemistry——Kwong.S.T名词解释1.测不准关系:()()41M L 22≥∆⋅∆{∫ψ*i[L ,M ]ψdx}22.酉矩阵:S +=S -13.厄米算符:算符L 满足∫u 1*(x)L u 2(x)dx=∫u 2(x)L *u 1*(x)dx,其中u 1(x)和u 2(x)是任意两个平方可积函数,积分遍于自变量全部区域。
则称L 是厄米算符。
4.等价表示:矩阵群M 和M’所包含的每一个对应矩阵之间只差一个同样的相似变换,就说M’和M 是等价表示。
5.可约表示:如果一个矩阵表示可以表示成子矩阵的直和,那么这个矩阵表示是可约表示。
6.不可约表示特征标:不可约表示矩阵群的对角元素之和称为这个不可约表示的特征标。
7.投影算符:P R R hl k j Rj j k*∑Γ=λλ)()()(,其中R 为群元素,*Γk j R λ)()(是第j 个不可约表示操作R 的第λ行第k 列的矩阵元,l j 是第j 个不可约表示的维数,h 为群的阶。
8.轨道近似:认为各个电子的运动是彼此独立的,每个电子都在核与其它电子所形成的稳定的平均场中运动,从而每个电子的状态可以用一个单电子波函数来描写。
9.定域分子轨道:认为成键电子只是集中在相邻两原子间的键轴区域内。
10.正则分子轨道:由HFR 方程解出的分子轨道。
11.Slater 行列式:描述多电子体系满足保里原理的波函数。
12.ab initio :严格的按HFR 方程进行计算称为从头计算。
13.NDO :假设原子轨道在空间任何地方都不重叠。
DO :对所有不同原子轨道的乘积都采用忽略微分重叠近似。
15.NDDO :对属于同一原子各对轨道重叠的排斥积分全部予以保留。
16.INDO :只保留单中心积分中同一原子对各轨道的微分重叠。
17.EHMO :整个分子不在一个平面上,则σ,π分离就不可能,于是就必须对分子中所有原子的所有价电子进行计算,若这种计算不是基于自洽场分子轨道理论,就称之为推广的休克尔分子轨道法。
量子化学习题及答案

量子化学习题及答案1.1998及2013年度诺贝尔化学奖分别授予了量子化学以及分子模拟领域的杰出贡献者,谈谈你的了解及认识。
答:1998年诺贝尔化学奖得主:瓦尔特·科恩和约翰·波普尔。
1964-1965年瓦尔特·科恩提出:一个量子力学体系的能量仅由其电子密度所决定,这个量比薛定谔方程中复杂的波函数更容易处理得多。
他同时还提供一种方法来建立方程,从其解可以得到体系的电子密度和能量,这种方法称为密度泛函理论,已经在化学中得到广泛应用,因为方法简单,可以应用于较大的分子。
沃尔特·库恩的密度泛函理论对化学作出了巨大的贡献。
约翰·波普尔发展了化学中的计算方法,这些方法是基于对薛定谔方程中的波函数作不同的描述。
他创建了一个理论模型化学,其中用一系列越来越精确的近似值,系统地促进量子化学方程的正确解析,从而可以控制计算的精度,这些技术是通过高斯计算机程序向研究人员提供的。
今天这个程序在所有化学领域中都用来作量子化学的计算。
2013年诺贝尔化学奖得主:马丁·卡普拉斯、迈克尔·莱维特、阿里耶·瓦谢勒。
他们为复杂化学系统创立了多尺度模型。
为研发了解和预测化学过程的强有力的计算机程序奠定了基础。
对于今天的化学家来说,计算机就像试管一样重要。
模拟过程是如此的真实以至于传统实验的结果也能被计算机预测出来。
多尺度复杂化学系统模型的出现无疑翻开了化学史的“新篇章”。
化学反应发生的速度堪比光速。
刹那间,电子就从一个原子核跳到另一个原子核,以前,对化学反应的每个步骤进行追踪几乎是不可能完成的任务。
而在由这三位科学家研发出的多尺度模型的辅助下,化学家们让计算机做“做帮手”来揭示化学过程。
20世纪70年代,这三位科学家设计出这种多尺度模型,让传统的化学实验走上了信息化的快车道。
2.谈谈你对量子化学中两种流派(VBT,MOT)的认识。
答:1926年,奥地利物理学家薛定谔(Schrodinger)建立了描述电子运动规律的波动方程。
量子化学习题附答案_

Py基础量子化学习题1.为什么微观粒子的运动状态要使用量子力学来描述,而不能用经典力学来描述?答:以牛顿三大定律为中心内容的经典力学适用于宏观物体的机械运动,当经典力学的应用范围推广到高速运动和小线度范围时,实验表明经典力学遇到了不可克服的困难。
对微观体系的研究导致了量子力学的诞生。
因为许多微观粒子都具有波粒二象性。
而在观察之前,我们得不到一个粒子的确切位置,它是一道弥散的波。
可以通过波函数来表示它们在每一区域出现的概率。
所以,描述描述微观粒子的运动状态要用量子力学。
2. 原子 A 和原子 B 在 y 轴上,指出 A 原子的 Px, Py, Pz 原子轨道与 B 原子的 dxy, dyz, dz 2 原子轨道间分别可形成什么分子轨道?①原子 A 的 Px 原子轨道与原子 B 的任意原子轨道无法形成分子轨道②原子 A 的 Py 原子轨道与原子 B 的 dyz 原子轨道形成π分子轨道(如图 1)图(1)③原子 A 的 Pz 原子轨道与原子 B 的 dyz 原子轨道形成σ 型分子轨道(如图 2)图(2)3. 原子 A 和原子 B 在 y 轴上,指出 A 原子的 px, py, pz 原子轨道与 B 原子的 dxy, dyz, dz2 原子轨道间分别可形成什么分子轨道?①原子 A 的 Px 原子轨道与原子 B 的 dxy 原子轨道形成π型分子轨道(如图 3)。
②原子 A 的 Py 原子轨道与原子 B 的任意原子轨道都无法形成分子轨道。
③原子 A 的 Pz 原子轨道与原子 B 的 dyz 原子轨道形成σ 型分子轨道(如图 4)。
∑ ∑ 10∑ ∑ 10 R )0 14. 写出任意一个原子的能量算符。
写出 Na+和 F-的薛定谔方程算符表达式。
ˆ h 22e 2H 原子的能量算符: H = -8π 2μ∇ - 4πε rNa +的薛定谔方程H ˆ = - h 10102i 11e 2+ ∑∑ e 8π 2 m i =1 i =1 4πε 0 r ii =1 i > j 4πε 0 r ijH ˆ ψ = E ψF -的薛定谔方程: H ˆ = - h10 10 2 i 9e 2 + ∑∑ e 8π 2 m i =1 i =1 4πε0 r ii =1 i ≠ j 4πε0 r ijH ˆ ψ = E ψ5. 写出任意一个分子的能量算符。
量子化学习题集

(7)
ex2 ;(8)
1
x 0
2
1 x 1 x 1 or x 1
1.21 下面那些算符是线性的 (1) Â=;(2) Â=*;(3) Â=2;(4) Â=d/dx;
第二章 量子力学简单体系
2.1 对于简并能级,任意波函数的线性组合都是Hˆ 的具有同意本征值的本征函数,
因此对于任何简并能级,可写出无限多个不同的本征函数。实际上我们只关
(4) [Â, [Bˆ , Ĉ]]+ [Bˆ , [Ĉ, Â]]+ [Ĉ, [Â, Bˆ ]]=0 1.9 Hˆ pˆ x2 2m V (x) ,分别计算(1)当 V(x)=V(常数),(2)当 V(x)=kx2/2,(3)当 V(x)
V(r)=e2/40r 时的对易子[Hˆ , pˆ x ] 与[Hˆ , x]
量子化学习题集
第一章 量子力学基础
1.1 如果 g= Âf 对每一组 Â 与 f 求 g。 (1) Â=d/dx, f=cos(x2+1); (2) Â=5, f=sinx; (3) Â=( )2, f=sinx; (4) Â=exp , f=lnx; (5) Â=d2/dx2, f=ln3x; (6) Â=d2/dx2+3xd/dx, f=4x3;
(t0)=Nx(lx) (0 x l)。如果在 t0 时刻我们测量粒子的能量,此时测量的 可能结果是什么,每个结果的概率是多少?
1.20 下面那些函数哪些是品优的? 对于不是品优的那些函数, 要说明理由 (1) = x;(2) = x2;(3) = e|x|;(4) = ex;(5) = cosx;(6) = sin|x|;
心线性独立的本征函数,所谓线性独立,是指如果 c1 1c2 2 cn n 0 只在 c1, c2, ..., cn 均为零时才成立,那么1, 2, ..., n 称为线性独立,能级的
量子化学试题及答案

6-31G*=6-31G(d)6:代表每个内层轨道由六个高斯型基函数拟合而成;价层轨道劈裂成两个Salter型基函数,内层轨道不发生劈裂,其中一个Salter型基函数由一个Gauss型基函数拟合而成,另一个Salter型基函数由一个Gauss型基函数拟合而成;d:表示要对出氢以外的原子都要加d轨道Salter型基函数:2*4+(1+2+2*3+6)*2=38Gauss型基函数:4*4+(6+4+4*3+1*6)*2=722、解:第一种方法:CH,1, 1.08290068H,1, 1.08290068,2, 109.47122063H,1, 1.08290068,2, 109.47122063,3,120.0,0H,1, 1.08290068,2, 109.47122063,3,-120.0,0第二种方法:CH 1 B1H 1 B2 2 A1H 1 B3 2 A2 3 D1 0H 1 B4 2 A3 3 D2 0B1 1.08290068B2 1.08290068B3 1.08290068B4 1.08290068A1 109.47122063A2 109.47122063A3 109.47122063D1 120.00000000D2 -120.000000003、解:在分子势能面上有五类极值点,分别如下:整体极小点、局部极小点、整体极大点、局部极大点及鞍点。
整体极小点:整个势能面上的最低点,代表了能量最低也就是最稳定的结构;局部极小点:势能面某个区域内的最低点,代表了局部区域内能量最低的点;整体极大点:整个势能面上的最高点,代表了能量最高的点;局部极大点:势能面某个区域内的最高点,代表了局部区域内的能量最高的点;鞍点:在一个方向上是极小点,其他方向上都是极大点,代表了体系的过渡态。
判断某一极值点是否为过度态:首先,是否有且只有一个虚频(数值为负值,足够大,一般上百);其次,看虚频的震动模式是不是朝着反应物和产物的方向震动;再次,进行IRC计算,看看是不是总想了反应物和产物。
《量子化学基础》习题课
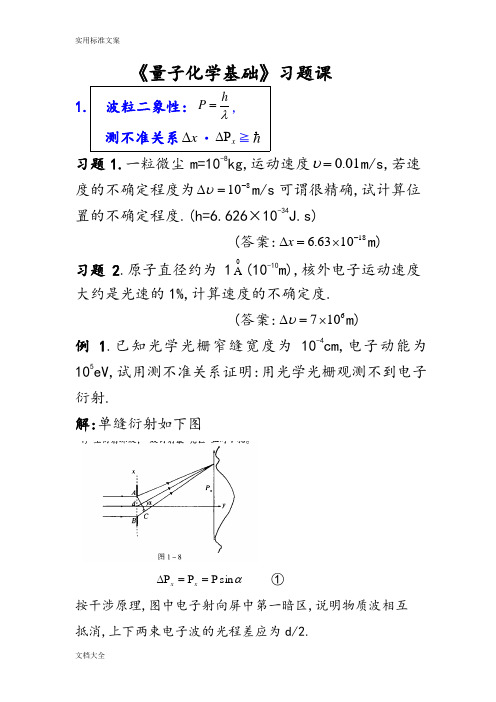
《量子化学基础》习题课 1. 波粒二象性: λhP =,测不准关系x ∆·x ∆P ≧习题1.一粒微尘m=10-8kg,运动速度01.0=υm/s,若速度的不确定程度为810-=∆υm/s 可谓很精确,试计算位置的不确定程度.(h=6.626×10-34J.s)(答案:181063.6-⨯=∆x m)习题2.原子直径约为10A (10-10m),核外电子运动速度大约是光速的1%,计算速度的不确定度.(答案:6107⨯=∆υm)例1.已知光学光栅窄缝宽度为10-4cm,电子动能为105eV,试用测不准关系证明:用光学光栅观测不到电子衍射.解:单缝衍射如下图αsin P =P =∆P x x ①按干涉原理,图中电子射向屏中第一暗区,说明物质波相互抵消,上下两束电子波的光程差应为d/2.λαα=⋅∆=⋅=sin sin x d BC ②这里410-=∆=x d cm,meV h mE h h 22==P =λ (=m 9.11×10-31kg ;=e 1.602×10-19C) 51025.1225.12==V λ=3.87×10-12m 661210101087.3sin ---=⨯==m m d λα 0≈α 证毕. 习题3.计算动能为3000eV 的电子的de Brogle 波长(1eV=1.602×10-19J, V 3000C10602.1J 10602.130001919=⨯⨯⨯=--V ) (答案: 0A 2237.0300025.1225.12===V λ.) 2 .一维势箱: 2228ml h n E =,),2,1( =nx ln C x πsin )(2=ψ 习题4.计算箱宽为5×10-10m 的一维势箱中粒子n=1、2时的能量.及粒子从n=2跃迁到n=1时辐射的波长. (答案:E 1=2.41×10-19J,E 2=9.64×10-19J191023.7-⨯=∆E J 71075.2-⨯=λm) 习题 5.可将原子中的电子粗略的模拟为一维箱中粒子,箱的宽度为原子的尺度.计算在长度10A 的箱中电子两个最低能级之差(eV)和在此两能级间跃迁的光子波长(cm). (答案:21013.1⨯=∆E eV, 8101.1-⨯=λm)例2. 丁二烯(H 2C=CH-CH=CH 2)4个π电子(P z 电子),可以近似地看作长度为大Π键键长(已知:双键长035.1A 、单键长054.1A )的一维势箱中的4个粒子的运动.体系的基态向第一激发态的跃迁为:_______1_______2___________3___________4↑↓=↑↓===n n n n 1_______2________3________4___________=↑↓=↑=↑=n n n n求:体系基态向第一激发态的跃迁能(cm -1).解.箱长:m A A l 10001078.554.1235.12-⨯=⨯+⨯=.)23(888222222222223-=-=∆l m h l m h n l m h n E e e e 21031234)1078.5(1011.985)10626.6(m kg s J ---⨯⨯⨯⨯⨯⋅⨯=J 191002.9-⨯=.14834191054.4/10310626.61002.9----⨯=⨯⨯⋅⨯⨯=∆=cm s m s J J hc E ν 例3.有一个量子数为n 在长度为l 的一维箱中运动的粒子(1)计算在箱的左端41区内找到粒子的几率.(2)n 为何值时该几率最大?(3)计算当n →∞时该几率的极限?解: 2sin 2141)sin 2(2410πππn n dx x l n l P -==⎰⎪⎩⎪⎨⎧==-==8,6,4,2,015,11,7,3,113,9,5,1,12sin n n n n 当当当π 即,n=3时,P 最大.π6141max +=P . 41)2sin 2141(lim =-∞→ππn n n (该式说明:当n →∞时量子力学问题还原为经典(力学)问题,因为经典力学处理一维箱问题在左端1/4处的几率正是1/4.)习题6.有一质量为1g 的小球,在长为10cm 的一维箱中运动小球速度0.1cm/s,试求小球的量子数n 是多少 ? (答案:n=3.018×1026) 3. 一位谐振子:m k πν21=)21(+=υνh E ( 3,2,1,0=υ) 习题7.HI 近红外光谱的基本振动频率22300=-ν.1cm -1,求HI 键的弹力常数k . (答案:k =2.93×105 D.cm -1) 习题8.已知H 2和Cl 2的基本振动频率分别为24.4395)(20=H νcm -1,9.564)(20=Cl νcm -1,求它们的零点能. (答案:E 0(H 2)=6.28kg/mol, E 0(Cl 2)=0.807kg/mol) 例 4.利用简谐振动公式:)sin()(φω+=t C t x ,证明一维谐振子的总能量是常数:221kC E =解:)(sin 21)(cos 2122222φωφωω+++=+=t kC t C m V T E m k =2ω ,带入上式,得: 221kC E =. 习题9.若H 35Cl 基本振动频率13010667.8⨯=νs -1,试求H 37Cl 的基本振动频率,设它们键的力常数相同.(答案:8.660×1013s -1) 4. 刚性转子:)1(22+=l l IE ( 3,2,1,0=l ) )1(2)(+=l B l ν (式中Ic hB 28π=) 例5.由HCl 的远红外光谱数据得知HCl 的转动能级相邻谱线间距为20.74cm -1,求HCl 分子的键长r.解: c r hIc h B 222442μππν===∆24231063.11002.6)45.35008.1(45.35008.1-⨯=⨯+⨯=+⋅=Cl H Cl H m m m m μg/mol 211024227212)2/74.20(1031063.1)1416.3(810626.6)8(][⨯⨯⨯⨯⨯⨯==--cB h r μπ =1.287×10-8cm=1.2870A习题10.从CN 的微波谱知道一系列谱线的间距皆为3.7978cm -1,求该分子的核间距r.(答案:r=1.172×10-10m)习题11.已知CN +的键长是1.290A ,指出CN +微波谱的第一到第四条线的位置.(答案:3.134cm -1,6.268cm -1,9.402cm -1,12.536cm -1 5.算符:),,(t q P F ∧∧其中q i ∂∂-=P ∧与本征函数:∧A )(x f =k )(x f习题12.写出下列物理量的算符:(1)动量P,(2)动量3y p ,(3)x y yp xp -,(4)动能T( 答案(1))(z k y j x i i P ∂∂+∂∂+∂∂-=∧,(2)3333y i P y ∂∂=∧(3))()(x y y x i p y p x L x y z ∂∂-∂∂-=-=∧∧∧ (4) )(22222222z y x m T ∂∂+∂∂+∂∂-=∧) 13.计算算符222kx dx d A -=∧的本征函数2x e α-的本征值(答案:22)24()(222222x x e kx x e kx dx d αααα----=- )14.利用[∧D ,∧x ]=1,(1)计算2)(x D +∧,(2)))((x D x D -+∧∧ (答案:(1)2)(x D +∧1222+++=∧x D x D (2)1))((22--=-+∧∧∧x D x D x D )15.三维箱中粒子的波函数是下列那些算符的本征函数(1)∧x p ,(2)∧2x p ,(3)∧2z p ,(4)∧2x .(答案(2),(3) )6.对易计算以下对易恒等式可方便对易运算:①.],[],[∧∧∧∧-=A B B A②.0],[=∧∧n A A (n=1,2,3…)③.],[],[],[∧∧∧∧∧∧==B A k kB A B kA④],[],[],[∧∧∧∧∧∧∧+=+C A B A C B A⑤ ],[],[],[∧∧∧∧∧∧∧∧∧+=C A B C B A C B A 例6.计算对易子:],[∧x P x ,],[2∧x P x ,],[∧H x ,],[∧∧H P x .解: i i x x i x x i x i x P x x =-=∂∂-=∂∂=∂∂=∧],[],[],[],[ ],[],[],[2∧∧∧∧∧+=x x x x x P x P P P x P xx i i x i i ∂∂⋅+∂∂⋅= x ∂∂=22)](21,[],[)],,(,[],[222∧∧∧∧∧∧++==+=z y x P P P m x T x z y x V T x H x ∧∧=∂∂==x x P mi x m P x m 22],[21 ],[)](,[21],[222V P P P P P m H P x z y x x x ∧∧∧∧∧∧∧+++= x V i V x i V P x ∂∂-=∂∂-==∧],[],[(式中x V f x f V x Vf f x V V x f V x ∂∂=∂∂-∂∂=∂∂-∂∂=∂∂)()(],[)16.计算:],[222c bx ax dx d ++ (答案: ],[222c bx ax dx d ++=dxd b ax a )24(2++. ) 例7.证明:222)(〉〈-〉〈=∆A A A解: 〉〉〈-〈≡≡∆∧222)()(A A A A στψψd A A ⎰〉〈-=∧*2)( τψψτψψτψψτψψd A d A A d A A d A ⎰⎰⎰⎰〉〈+〉〈-〉〈-=*∧*∧*∧*22τψψτψψτψψd A d A A d A A A ⎰⎰⎰*∧*∧*〉〈+〉〈-〉〈-〉〈=22 2222〉〈+〉〈-〉〈-〉〈=A A A A 22〉〈-〉〈=A A 证毕 7. H 原子薛定谔方程的解222204118n R n h e E n -=-=εμ (n=1,2,…),其中22048h e R εμ-=. )()()(,,,θϕθϕψm l l n m l n Y r R r =)()()(,,ϕθm m l l n r R ΦΘ= ϕθim ml na Zr i l l n i i e P e a Zr c C )(cos })({0101--+-=∑= 氢原子波函数受控于三个量子数(m l n ,,)∞=,,2,1 n1,,2,1,0-=n ll m ±±±=,,2,1,0习题17.下列函数(1)2P z ,(2)2P x ,(3)2P 1分别是算符∧H 、∧2L 、∧z L 中哪个的本征函数. (答案:(1)、(3)全是,(2)是∧H 、∧2L 的本征函数) 习题18.对H 原子P 态,测量L Z 的可能值为h 、0、-h,问在下列函数中测量L Z 得到各可能值的几率.(1)Pz 2ψ,(2) Px 2ψ,(3) 12P ψ(答案:(1) 121211210200-⋅+⋅+=ψψψψPz得0值几率为1,得h 、-h 几率为0. (2) 121211*********-++⋅=ψψψψPx 得h 、-h 几率各为21,得0值几率为0.(3) 12P ψ=211ψ,得h 几率为1,其余为0) 例8.已知H 原子)(ϕΦ方程复数解:ϕπϕim m e 21)(=Φ,(1)验证)(ϕm Φ是归一化的.(2)证明)(ϕm Φ是算符ϕ∂∂-=∧ i L z 的本征函数.而)(ϕm Φ线性组合的实函数: ⎪⎪⎩⎪⎪⎨⎧=Φ=Φϕπϕϕπϕm m m msin 1)(cos 1)('`不是∧z L 的本征函数.解:(1)121212020202===ΦΦ=Φ⎰⎰⎰⎰-*ππϕϕπϕπϕπϕϕd d e e d d im im (2) )(21)(ϕπϕϕϕm im m z m e i L Φ±=∂∂-=Φ±∧而 ϕπϕπϕϕm m i m i L m z sin cos 1)( =∂∂-=Φ∧不构成本征方程: )()(ϕϕm m z c L Φ≠Φ∧.例如n=2,l =1的H 原子波函数是p 轨道,有三个状态(m=1,0,-1),其复函数形式为:θθϕψcos )()(0,1,2r r f r = (即:z p p 也是0)ϕθθϕψi e r r f r ±±=sin )()('1,1,2 (即:11-p p 和)其中复函数z p p 等于实函数0,复函数11-p p 和线性组合为实函数y x p p ,,即ϕθθϕϕcos sin )()(sin )(11r R N e e r R N p i i x =+=- ϕθθϕϕsin sin )()(sin )(11r R N e e r R N p i i y =-=- 因此,z p p 和0都是∧z L 的本征函数. 11-p p 和也是∧z L 的本征函数.只有y x p p ,不是∧z L 的本征函数.P 轨道的实函数与复函数形式都是体系的状态函数,但表示图形不一样:例9.对H 原子基态,(1)求2倍玻耳半径之外的电子几率.(2)玻耳半径之内的电子几率. 解:H 原子基态,n=1,0=l ,m=0301,,,1)()()(a r s ml l n m l n eaY r R r -=→=πψθϕθϕψ(1)设P 2为02a 之外的电子几率 ϕθθπτψππd drd re a d P a r a s sin 1122200203021200-⎰⎰⎰⎰==-⎰⎰⎰-=ππϕθθπ2022023sin 10d d dr e r a a r adr e r a a ra 002202304-⎰=ππ利用积分公式][0203020022302)82422(41a a r ara a r ea P ---=--)22(3222b b x b x e dx e x bx bx +-=⎰]4)44448([430303030430a a a a e a +---=- 4131e -= 即: 24.01342==e P(2)设1P 是玻耳半径0a 之内的电子几率,则dr e r a P a r a 02023014-⎰=][00302002230)82422(4a a r a ra a r e a ---=-]4)44242([430303030230a a a a e a +---=-32.0512=-=e例10.已知类氢离子基态波函数 03031a zr s ea z-=πψ,(1) 求半径r 的平均值.(2)r 的最可几值.解:(1)ϕθθπτψψππd drd r ea zd r r a zr ssin 32002030310-∞*⎰⎰⎰⎰==〉〈dr er a za zr 02033034-∞⎰⋅=ππ利用广义积分公式:10!+∞-=⎰n qxn qn dx ex (0,1>->q n )z a a z a z dr e r a z r a zr23)2(!344040303023330=⋅==〉〈⎰∞-(2)径向分布函数: 0223032214)(a zr ser a z r r R D -=⋅=求最可几半径就是求最大径向分布函数时r,0)22(4)(40202230322303=-==---a zr a zr a zr ea z r rea zer dr d a z dr dD020=-r r a z 即, z a r 0=为最可几半径.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1、求处于基态的一维箱中的粒子出现在0.250.75a x a ≤≤内的几率。
a 是一维箱的长。
解:基态波函数为:1()xx aπψ=几率:dx a xa xdx a a p a a a a ⎰⎰-==75.025.075.025.0222cos12sin 2ππ dx ax a dx a aa a a ⎰⎰-=75.025.075.025.02cos 1212π aaa x a a a a 75.025.02sin 21)25.075.0(2⎥⎦⎤⎢⎣⎡⨯--=ππ )2sin 23(sin 215.0πππ--=π15.0+=818.0=2、一电子在长为0.6 nm 的一维箱中运动,由能级n =5跃迁到n =4所发出的光子的波长是多少?解:2228e n h E m a= 2225422225169888e e e h h h E m a m a m a -∆=-=λνhch E ==∆-4534873425431926.62610310 1.32010 m 132.0 nm 9(6.62610)89.11010(0.610)hc E λ------⨯⨯⨯===⨯=⨯⨯∆⨯⨯⨯⨯ 3、 证明如果ˆF和ˆG 是线性算符,则a ˆF +b ˆG 和G F ˆˆ也是线性算符。
式中a ,b 为常数。
证明:(1) 如果ˆF和ˆG 是线性算符,则有: ˆˆ)(ˆ2121u F u F u u F +=+ (1) ˆˆ)(ˆ2121u F a u F a u u Fa +=+ (2) 2121ˆˆ)(ˆu G u G u u G +=+ (3) 2121ˆˆ)(ˆu G b u G b u u Gb +=+ (4) (2)+(4)得:ˆˆˆˆ)(ˆ)(ˆ21212121u G b u G b u F a u F a u u G b u u F a +++=+++ 2121)ˆˆ()ˆˆ())(ˆˆ(u G b F a u G b F a u u G b Fa +++=++ 所以a ˆF+b ˆG 是线性算符。
(2) 212121ˆˆˆˆ)ˆˆ(ˆ)(ˆˆu G F u G F u G u G F u u G F +=+=+所以G Fˆˆ也是线性算符。
4、 证明若ˆF和ˆG 是厄米算符,则ˆF +ˆG 和F G G F ˆˆˆˆ+也是厄米算符。
证明:若ˆF和ˆG 是厄米算符,则有: vdu G F d v u G vd u F d v G u d Fv ud Gv Fv u vd G F u ⎰⎰⎰⎰⎰⎰⎰∧∧∧∧∧∧∧∧∧∧+=+=+=+=+*******])[( )()( )()(ττττττ所以,ˆF +ˆG 是厄米算符。
τττvd FG u vd G F u vd F G G F u )ˆˆ()ˆˆ()ˆˆˆˆ(***⎰⎰⎰+=+ ττvd Fu G vd G u F ˆ)ˆ(ˆ)ˆ(**⎰⎰+= =ττvd u G F vd u F G⎰⎰+**)ˆˆ()ˆˆ( τvd u F G G F⎰+=*])ˆˆˆˆ[( 所以,F G G F ˆˆˆˆ+是厄米算符。
5、 函数)21exp(2x -和)21exp(2x x -是否算符)(222x dxd +-的本征函数?若是,其本征值是多少?证明:)21exp()]21exp([)21exp()(2222222x x x x dx d x x dxd -+---=-+-=)21exp()]21exp([)21exp(2222x x x x x x -+--+-)21exp(2x -=即:函数)21exp(2x -是算符)(222x dxd +-的本征函数,其本征值为1.)21exp()]21exp([)]21exp()[(232222222x x x x dxd x x x dx d -+--=-+-)21exp()]21exp()21[exp(23222x x x x x dx d -+----=)21exp()21exp()21exp(2)21exp(232322x x x x x x x x -+---+-=)21exp(32x x -=即:函数)21exp(2x x -是算符)(222x dxd +-的本征函数,其本征值为3.6、证明23cos 1θ-是算符222cos ()sin θθθθ∂∂-+∂∂的本征函数,并求其本征值。
证明:222cos ()sin θθθθ∂∂-+∂∂(23cos 1θ-) )1cos 3(sin cos )1cos 3(222222-∂∂--∂∂-=θθθθθθ)s i n c o s 6(s i n c o s )s i n c o s 6(22θθθθθθθ---∂∂-= )cos 6()cos 6sin 6(22222θθθ +--=θθ2222cos 12sin 6 +-=θθ2222cos 12)cos 1(6 +--= θ222cos 186 +-= )1cos 3(622-=θ所以,函数23cos 1θ-是算符222cos ()sin θθθθ∂∂-+∂∂的本征函数,其本征值为26 .7、设有一个质量为m 的自由粒子(势能V=0),给出下列3种情况的薛定谔方程,并指出描述其状态的波函数各是哪些变量的函数。
(1) 在三维空间中运动;(2) 被束缚在半径为a 的球面上运动(球面上势能为零,球内外势能为无穷大);(3) 被束缚在半径为a 的圆周上运动(圆周上势能为零,圆周内外势能为无穷大)。
解: (1)222E mψψ-∇=),,(z y x ψψ=2222222111()(sin )sin sin r r r r r θθθθθθθ∂∂∂∂∂∇=++⋅∂∂∂∂∂(2)),(φθψψ=, r a =为常数2222211((sin ))2sin sin E ma θψψθθθθφ⎡⎤∂∂∂-+=⎢⎥∂∂∂⎣⎦(3) ),(φθψψ=, r a =,2πθ=为一常数,sin sin 12πθ==2222()2E ma ψψφ∂-=∂ 8、写出平面刚性转子,即被束缚在一圆周上的粒子的薛定谔方程,并求其解。
解: 考虑一围绕相距为 r 的固定点的自由粒子的运动,也就是被束缚在半径为r 的球面上的自由粒子的运动。
由于自由粒子在运动过程中 r 不变,故称为刚性转子。
薛定谔方程 2222()2E ma ψψφ∂-=∂ 整理得:022222=+ψψφEma d d 令:yz),,(z y x 222m a E β=222 E m a =β()()022=+φβψφφψd d薛定谔方程特解: φψE ma ie 22±=根据波函数的单值性: )2()(πφψφψ+=即:)2(2222πφφ+±±=E ma iE ma iee将上式写成复数的三角函数表达式:)2(2sin )2(2cos 2sin 2cos 2222πφπφφφ+±+=±E ma i E ma E ma i E ma 使该方程成立,需要复数的实部与虚部分别相等)2(2c o s 2c o s 22πφφ+=Ema E ma)2(2sin 2sin 22πφφ+=Ema E ma为满足上述两式, 2, 1, 0, ,2222==n n Ema ππ即:n E ma = 222222m an E = 波函数可以写作:,φψin e = (,2,1±±=n )将波函数归一化:,21φπψin e =( ,2,1±±=n )9、若取变分函数为 ,试用变分法求H 原子的基态波函数Ψ1s 和能量E1s 。
解:薛定谔方程为0)]4(2[0222=++∇ψπεμr ze E ()e ar s c r -=ψ因为 ()()r CR Y R n n r ns ===00000ψψ()r ns ψ是r 的函数,所以式中消去ce -ar ,则满足上式,则常数项为0,项系数为0解得:529.042200==me a πε波尔半径0)4(2)(102222=++s s rze E m dr d r dr d r ψπεψ 0)4(2]sin 1)(sin sin 1)(1[0222222222=++∂∂+∂∂∂∂+∂∂∂∂ψπεμψφθθθθθr ze E r r r r r r dr d r dr d dr d r r dr d r r dr d r dr d r 2211)(1222222222+=⋅+=0)4(2202222=+++s s s rze E m dr d r dr d ψπεψψ arsce -=1ψ⎪⎪⎭⎪⎪⎬⎫=-=--ar s ar s ce a dr d ace drd 21221ψψ0)4(2)(20222=++-+---ar arar ce r ze E m ace r ce a πε 0422220222=++- πεmze r mE a r a 0)242(1220222=-++a mze r mE a πε⎪⎪⎩⎪⎪⎨⎧=-=+02420220222a m ze m E a πε020220244a zme z mze a === πεπε10、已知H 3和H 3+均为正三角形构型,用HMO 法估计两者的相对稳定性。
解:久期行列式方程为:0 1- 1-1- 1-1- 1- =xx x展开,x 3-3x -2=0x =2, -1, -1即E 1=α+2β E 2=E 3=α-βE 1=α+2βE 2=α-βαH 3有3个电子,键能-{(2α+4β+α-β)-3α}=-3βH 3+有2个电子,键能-{(2α+4β)-2α}=-4β 所以,H 3+比H 3稳定.这是由于H 3比H 3+多一个电子,位于反键轨道。
11、求三亚甲基甲烷(CH 2)3C 的π电子能级,基组态的多重度2S +1和其最低能级的分子轨道。
解:久期行列式方程为:0 0 0 1-0 0 1-00 1-1- 1- 1- = xx x x展开,得:x 4-3x 2=03 ,0 ,34321-====x x x x(1) π电子能级:βααβα3 , ,34321-===+=E E E E(2) 基组态的多重度: 基态时4个π电子分布在321 , ,E E E 三个轨道中,其中1E 中有2个成对电子,32 , E E 中有2个自旋平行的电子, S =1体系的自旋多重度为3.1231234(3) 最低能级的分子轨道:将31=x 代入久期方程,0 0 0 1-0 0 1-0 0 1-1- 1- 1- 4321=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎪⎪⎭⎫ ⎝⎛c c c c x x x x 得到:⎪⎪⎩⎪⎪⎨⎧===++=41312143213333c c c c c c c c c c即143233c c c c === )(334321111φφφφψ+++=c c 归一化,得)(612143211φφφφψ+++= 12、按环丁二烯是平面正方形构型,用HMO 法求其π电子能级和其最低能级的分子轨道。
