二重积分通俗理解
二重积分的概念及几何意义

D
o x
此时二重积分为
f ( x , y )d f ( x , y )dxdy . D D
( 2)如果函数f ( x , y )在闭区域D上连续, 那么它在D 上的二重积分必定存在.
三、二重积分的几何意义
当被积函数大于零时,二重积分是柱体的体积. 当被积函数小于零时,二重积分是柱体体积的负 值. 二重积分的几何意义 二重积分是各部分区域 上柱体体积的代数和,在xoy 平面上方的取正,在xoy平面 下方取负.
z f ( x, y)
o x
D
n
y
( i ,i )
Di
i 1
f ( i ,i ) 面薄片的质量
设有一平面薄片占 有xOy面上的闭区域 D ,它在 点 ( x , y ) 处的面密度为 ( x , y ), ( x , y ) 0且在D上连 续.计算该薄片的质量 .
D
i 1
f ( x , y )d lim f ( i ,i ) i . 0 i 1 D
积 分 区 域 被 积 函 数
n
积 分 变 量
被面 积积积 表元分 达素和 式
对二重积分(double integral)定义的说明
(1)在定义中, 对闭区域 D的划分 是任意的,面积元素 d表示积分 和中的 i , 在直角坐标系中面 积元素d dxdy ,
y
( i , i )
将薄片分割成若干小块,
取典型小块,将其近似
看作均匀薄片,
所有小块质量之和
Di
O
x
n i 1
近似等于薄片总质量
M lim ( i ,i ) i .
0
二、二重积分的定义
考研二重积分强化笔记

考研二重积分强化笔记二重积分是微积分中的重要概念,它在数学、物理、工程等领域都有广泛的应用。
下面我将从多个角度全面完整地回答你关于考研二重积分的问题。
首先,二重积分的定义是对二元函数在一个有界闭区域上的积分。
它可以看作是将一个平面区域分割成无穷多个小矩形,然后对每个小矩形内的函数值进行求和得到的极限。
二重积分的符号表示为∬f(x,y)dxdy,其中f(x,y)是被积函数,dx和dy分别表示对x和y的积分变量。
在求解二重积分时,可以采用不同的方法,如直角坐标系下的直接计算、极坐标系下的转化等。
对于简单的区域和函数,可以直接按照定义进行计算;对于复杂的区域和函数,可以采用变量代换、对称性等技巧简化计算过程。
在考研中,二重积分的强化主要包括以下几个方面:1. 区域的确定,要求熟练掌握如何确定二重积分的积分区域。
可以通过观察图形、利用对称性、变量代换等方法确定积分区域的边界和限制条件。
2. 计算积分,要熟悉二重积分的计算方法,包括直接计算、极坐标转化、变量代换等。
对于不同类型的函数和区域,需要掌握相应的计算技巧和公式。
3. 应用题,要能够将实际问题转化为二重积分的形式,并进行求解。
这需要对问题进行适当的建模和分析,将问题中的条件和要求转化为积分的限制条件和被积函数。
4. 与其他数学概念的关联,二重积分与其他数学概念有着密切的联系,如面积、体积、质量、质心等。
要能够将二重积分与这些概念进行关联,理解其物理和几何意义。
5. 解题技巧,要掌握一些解题的技巧和方法,如利用对称性简化计算、利用积分的性质化简表达式、合理选择坐标系等。
这些技巧可以帮助我们更快、更准确地求解二重积分。
总之,考研二重积分是一个相对较难的内容,需要对积分的基本概念和计算方法有深入的理解和掌握。
通过大量的练习和实践,加深对二重积分的理解,掌握解题的技巧和方法,相信你能够在考研中取得好的成绩。
希望以上内容能够对你的学习有所帮助!。
二重积分的概念及性质

积分对变量的可加性
定义
如果f(x,y)在平面上是可积的,那么对于任 意的a和b,有 ∫∫Df(x,y)dσ=∫a→bf(x,y)dσ+∫∫Df(x,y)dσ, 其中D是包含在区间[a,b]内的可积区域。
应用
该性质可以用于计算二重积分,特别是当被 积函数与某个变量的关系较为简单时。
04 二重积分的物理应用
个小弧段进行积分,然后将结果相加得到总长度。
平面曲线的曲率与挠率
曲率
曲率是描述曲线弯曲程度的量,可以 通过二重积分计算出曲线的曲率。
挠率
挠率是描述曲线在垂直方向上的弯曲 程度的量,也可以通过二重积分计算 出曲线的挠率。
THANKS FOR WATCHING
感谢您的观看
积分区域的可加性
定义
如果D1和D2是平面上互不相交的可积区域,则它们分别上的二重积分之和等于它们并集上的二重积分。 即,如果D=D1∪D2,则∫∫Df(x,y)dσ=∫∫D1f(x,y)dσ+∫∫D2f(x,y)dσ。
应用
该性质可以用于简化复杂的积分区域,将复杂区域分解为简单区域进行计算。
积分对区域的可加性
转换坐标
将被积函数从直角坐标转换为极坐标形式,即$x = rhocostheta$,$y = rhosintheta$。
分层积分
将极坐标下的二重积分拆分成两个累次积分,即先对角度积分再对极径积分。
逐个计算
对每个角度范围,计算其在极径上的积分值,并求和。
得出结果
将所有角度范围的积分结果相加,得到整个极坐标区域上的二重积分值。
二重积分的概念及性质
目录
• 二重积分的定义 • 二重积分的计算方法 • 二重积分的性质和定理 • 二重积分的物理应用 • 二重积分的数学应用
二重积分

8.6 二重积分二重积分也是由实际问题的需要而产生的。
在一元函数积分学中我们已经知道,定积分是某种特定形式的和的极限,把这种和的极限的概念推广到定义在某个区域上的二元函数的形式,便可得到二重积分的概念。
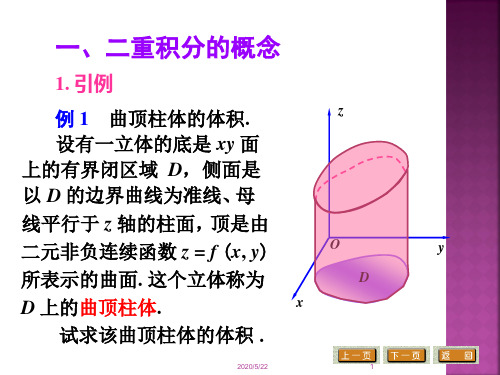
一. 二重积分的概念引例1 曲顶柱体的体积设有一立体,它的底是xoy 平面上的有界闭区域D ,它的侧面是以D 的边界曲线为准线而母线平行于z 轴的柱面,它的顶是曲面),(y x f z =,这里0),(≥y x f ,且在D 上连续(如图所示)。
这种立体称为曲顶柱体。
现在我们来讨论它的体积。
关于曲项柱体,当点),(y x 在区域D 上变动时,高),(y x f 是个变量,因此它的体积不能直接用体积公式来计算。
不难想到,用求曲边梯形面积的方法来解这个问题。
(1) 分割:我们用一曲线网把区域D 任意分成n 个小区域1σ∆,2σ∆,…,n σ∆小区域i σ∆的面积也记作i σ∆。
以这些小区域的边界曲线为准线作母线平行于z 轴的柱面,这些柱面把原来的曲项柱体分为n 个细条的小曲顶柱体。
它们的体积分别记作1V ∆,2V ∆,…,n V ∆(2) 近似代替:对于一个小区域i σ∆,当直径(i σ∆最长两点的距离)很小时,由于),(y x f 连续,),(y x f 在i σ∆中的变化很小,可以近似地看作常数。
即若任意取点∈),(i i ηξi σ∆,则当i y x σ∆∈),(时,有),(y x f ),(i i f ηξ≈,从而以i σ∆为底的细条曲顶柱体可近似地看作以),(i i f ηξ为高的平顶柱体(如图所示)于是≈∆i V ),(i i f ηξi σ∆ ),,3,2,1(n i =(3) 求和:把这些细条曲顶柱体体积的近似值),(i i f ηξi σ∆加起来,就得到所求的曲顶柱体体积V 的近似值,即∑∑==∆≈∆=ni i i i n i i f V V 11),(σηξ(4) 取极限:一般地,如果区域D 分得越细,则上述和式就越接近于曲顶柱体体积V ,当把区域D 无限细分时,即当所有小区域的最大直径0→λ时,则和式的极限就是所求的曲顶柱体的体积V ,即0lim →=λV ∑=∆n i i ii f 1),(σηξ引例2 非均匀平面薄板的质量设薄片的形状为闭区域D(如图所示),其面密度ρ是点),(y x 的函数,即),(y x ρρ=在D 上为正的连续函数.当质量分布是均匀时,即ρ为常数,则质量M 等于面密度乘以薄片的面积。
高中数学(人教版)二重积分的概念与性质课件

取近似 2) 取近似. m i ( i , i ) i Vi f ( i , i ) i 和 ) f ( , 求
i 1 i i
n
3) 求和. V
n
i
( , )
i 1 i i
n
n
i
, i ) i4) 取极限.m lim ( i , i ) i 4) 取极限.V lim f ( i 取极限
o
x
(一)引例
1.曲顶柱体的体积 1) 分割. 用一组曲线网把D分成n个小区域
2.平面薄片的质量
1) 分割. 用一组曲线网把D分成n个小块
1 , 2 , , i , , n
i
几 何 问 题 2) 取近似. V f ( , )
3) 求和. V
1 , 2 , , i , , n
D
f ( x, y) 0
一般情况
曲顶柱体体积的负值
曲顶柱体体积的代数和
例 1
根据二重积分的几何意义,计算下列积分值:
D : x2 y2 R2.
(1)
y
d
D
o
z
x
( 2)
D
R 2 x 2 y 2 d
o
y
x
二重积分的概念与性质
一、二重积分的概念
二、二重积分的性质
二重积分的概念与性质
0
i 1
i , i ) i . f ( f ( x , y )d lim 0
D i 1
n
积 分 区 域
被 积 函 数
积 分 变 量
被面 积积 积 表元 分 达素 和 式
二重积分的概念及几何意义

若函数$f(x,y)$和$g(x,y)$在区域$D$ 上均可积,则有 $iint_{D}[f(x,y)+g(x,y)]dsigma=iint_ {D}f(x,y)dsigma+iint_{D}g(x,y)dsig ma$。
积分区域的可加性
简单区域的叠加
若复杂区域$D$可以划分为有限个简单区域(如矩形、三角形等)的并集,且函数在每个简单区域上 均可积,则二重积分可以通过在这些简单区域上分别进行积分并求和得到。
复杂区域的分解
对于复杂的不规则区域,可以通过引入辅助线将其划分为几个较简单的子区域,然后在每个子区域上 分别进行积分,最后将结果相加。这种方法在处理具有复杂边界或包含多个不同部分的积分区域时特 别有用。
03
二重积分的计算
直角坐标系下的二重积分
积分区域为矩形区域
通过对矩形区域进行划分,将二重积分转化为累次积分进行计算。
对于环形区域,可以通过对内外圆的极径 进行划分,将环形区域划分为若干个小扇 形区域,然后对每个小扇形区域进行积分 ,最后将结果相加得到二重积分的值。
二重积分的换元法
直角坐标与极坐标的互化
通过直角坐标与极坐标之间的互化公式,可以将直角坐标系下的二重积分转化为极坐标 系下的二重积分进行计算。
一般变换
对于一般的二重积分,可以通过变量代换的方法将其转化为更简单的形式进行计算。常 用的变量代换方法有极坐标代换、广义极坐标代换等。
积分的数乘性质
若函数$f(x,y)$在区域$D$上可积,则对于任意常数$k$,有 $iint_{D}kf(x,y)dsigma=kiint_{D}f(x,y)dsigma$。
可加性质
积分区域的可加性
若区域$D$可分成两个不相交的区域$D_1$和 $D_2$,且函数$f(x,y)$在$D_1$和$D_2$上均 可积,则有 $iint_{D}f(x,y)dsigma=iint_{D_1}f(x,y)dsigm a+iint_{D_2}f(x,y)dsigma$。
二重积分和二次积分的关系

二重积分和二次积分的关系在数学中,积分是一种重要的概念,用于求解曲线下的面积、体积、质量等问题。
二重积分和二次积分是积分的两种不同形式,它们之间存在密切的关系。
我们来了解一下什么是二重积分。
二重积分是将一个二元函数在一个有限的区域上进行积分运算,得到的是一个数值。
它的本质是将一个平面区域划分成无限个无穷小的面积元素,然后将这些面积元素相加得到的总面积。
二重积分可以表示为∬f(x,y)dxdy,其中f(x,y)是被积函数,dxdy表示面积元素。
而二次积分则是求解一个函数的积分的过程。
一次积分是对一个函数在一个区间上的积分,而二次积分则是对一个函数在一个二维区域上的积分。
二次积分可以表示为∫∫f(x,y)dA,其中f(x,y)是被积函数,dA表示面积元素。
可以看出,二次积分和二重积分的形式很相似,都是对一个函数在一个平面区域上进行积分运算。
实际上,二次积分可以看作是二重积分的一种特殊情况。
当被积函数f(x,y)为常数函数时,二次积分就等于被积函数f(x,y)乘以区域的面积。
二次积分和二重积分的关系可以通过一个简单的例子来说明。
假设我们要计算一个圆的面积,可以使用二次积分的方法。
我们可以将圆划分成无数个无穷小的扇形面积元素,然后将这些面积元素相加得到总面积。
而利用二重积分的方法,我们可以将圆划分成无数个无穷小的面积元素,然后将这些面积元素相加得到总面积。
可以看出,二次积分和二重积分的结果是一样的。
除了计算面积,二次积分和二重积分还可以用于求解其他问题。
例如,二重积分可以用于求解质心、转动惯量等物理问题,而二次积分可以用于求解电场、电势等电磁问题。
总结来说,二次积分和二重积分是积分的两种不同形式,它们之间存在密切的关系。
二次积分可以看作是二重积分的一种特殊情况,二次积分和二重积分在计算面积等问题时可以得到相同的结果。
二次积分和二重积分在数学和物理中都有广泛的应用,可以用于求解各种问题。
通过对二重积分和二次积分的关系的了解,我们可以更好地理解积分的概念和应用。
二重积分
是这些小区域上的二重积分的和.
2015-1-12
23
例1
两种不同 试将二重积分 f ( x, y ) d 化为
D
次序的累次积分, 其中 D 是由 x = a, x = b, y = c, y = d (a < b, c < d) 所围成的矩形区域 . 解 画出积分区域 D 如图.
如果先积 y 后积 x,则有
D D D
2015-1-12
11
性质 3
如果区域 D 被分成两个子区域 D1 与 D2,
则在 D 上的二重积分 等于各子区域 D1、D2 上的二重
积分之和, 即
f ( x, y) d f ( x, y) d f ( x, y) d .
D D1 D2
这个性质表明二重积分对于积分区域具有可加性 .
2
d x f ( x, y ) d y d x
0 0
2
2- x 0
1
f ( x, y ) d y,
2015-1-12
25
如果先积 x 后积 y , 则为
f ( x, y ) d d y
D 0
1
2- y y
f ( x, y) d x.
2015-1-12
26
f ( x, y) d ≤
D D
f ( x , y ) d .
2015-1-12
13
性质 6 如果 M、m 分别是函数 f( x, y) 在 D 上 的最大值与最小值, 为区域 D 的面积, 则
m ≤
D
f ( x, y ) d ≤ M .
性质 7(二重积分中值定理) 设函数 f( x,y) 在有 界闭区域 D 上连续,记 是 D 的面积,则在 D 上至 少存在一点(, ), 使得
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
二重积分通俗理解
一、什么是二重积分?
1.1 定义
二重积分是微积分中的重要概念之一,用于求解二元函数在有界闭区域上的积分。
它是对一个区域上的函数进行“求和”的操作,可以用来计算该函数在该区域上的平均值、总体积、质心等。
1.2 符号表示
一般来说,用符号∬来表示二重积分。
对于一个函数f(x,y),其在区域D上
的二重积分可以表示为:
∬f
D
(x,y) dx dy,
其中D表示一个有界闭区域,dx dy表示在该区域内按照矩形的面积进行积分。
二、二重积分的计算方法
2.1 直角坐标系中的二重积分计算
在直角坐标系中,我们可以通过将区域D分割成许多小矩形来进行计算。
对于一个小矩形R i,其面积可以表示为ΔA i=Δx iΔy i,其中Δx i和Δy i分别为矩形的
宽度和高度。
然后,我们选取矩形R i中点(x i∗,y i∗),计算函数在该点的值
f(x i∗,y i∗),并乘以该矩形的面积ΔA i。
将所有小矩形的贡献相加,即可得到二重积分的近似值。
当矩形的宽度和高度趋近于零时,即Δx i和Δy i趋近于零,这时我们可以得到准确的二重积分。
用极限的形式表示为:
∬f D (x,y) dx dy=lim
Δx i→0
Δy i→0
∑f
n
i=1
(x i∗,y i∗)ΔA i.
2.2 极坐标系中的二重积分计算
在极坐标系中,二重积分的计算可以更加简化。
对于一个区域D,我们可以使用极坐标的面积元素r dr dθ来进行积分。
其中r表示极径,θ表示极角,dr
和dθ分别表示极径和极角的微小增量。
则二重积分的计算公式为:
$$\iint_D f(x, y) \,dx\,dy = \iint_D f(r\cosθ, r\sinθ)
r\,dr\,d\theta.$$
这种方法适用于具有旋转对称性的问题,通过转换到极坐标系可以简化计算过程。
三、二重积分的应用
3.1 几何意义
二重积分的一个重要应用是求解曲面面积或体积。
对于一个曲面z=f(x,y)在区域D上的投影曲域为D′的情况,可以通过以下公式计算曲面的面积S:
S=∬√1+(∂z
∂x
)
2
+(
∂z
∂y
)
2
D
dx dy.
3.2 质心的计算
另一个常见的应用是计算一个区域D上物体的质心位置。
对于一个均匀物体,其密度函数为常数ρ,则质心的坐标(x‾,y‾)可以用以下公式表示:
x‾=1
M
∬x
D
ρ(x,y) dx dy, y‾=
1
M
∬y
D
ρ(x,y) dx dy,
其中M表示物体的总质量。
3.3 数学物理问题
二重积分在数学物理问题中有着广泛的应用,例如计算物体的质量、质心、力矩等。
通过建立合适的数学模型,并应用二重积分的相关公式,可以解决许多复杂的物理问题。
四、总结
二重积分是微积分中的重要概念,用于求解二元函数在有界闭区域上的积分。
它有直角坐标系和极坐标系两种计算方法,可以应用于几何问题、质心计算以及数学物理问题等。
通过对二重积分的学习和应用,我们可以更好地理解函数的积分性质,解决实际问题,并丰富我们的数学知识。
参考文献
1.Stewart, J. (2007). “Calculus: Early Transcendentals” (6th ed.).
Thomson.
2.Anton, H., Bivens, I., & Davis, S. (2002). “Calculus” (8th ed.).
John Wiley & Sons.。
