六年级数学上册椭圆的周长求阴影部分面积专项训练
第一单元求含圆的阴影部分面积“基础型”专项练习-2023-2024学年六年级数学上册典型例题北师大版

20232024学年六年级数学上册典型例题系列第一单元:求含圆的阴影部分面积“基础型”专项练习Cπd分别求出大圆和小圆的周长,再分别用大圆、小圆,求出大圆和小圆的周长的一半;再用环宽;最后用大圆周长的一半+小圆周长的一半+两个环宽,即可求出左边图【详解】作图:【分析】如图所示,整个图形是一个长方形,空白部分合在一起是一个整圆,阴影部分的周长=空白部分圆的周长+长方形的长×2,阴影部分的面积=长方形的面积-空白部分圆的面积,据此解答。
阴影部分的面积是214cm2。
7.计算阴影部分的面积。
(单位:厘米)【答案】343平方厘米;75.36平方厘米【分析】阴影部分可以看成是一个长方形减去一个半圆的面积,根据长方形的面积=长×宽,圆的面积S=πr2,把数据代入计算即可;阴影部分是一个半圆环,根据圆环的面积S=π(R2-r2),把数据代入公环式,所得结果再除以2即可。
【详解】20×25-(20÷2)2×3.14÷2=500-102×3.14÷2=500-100×3.14÷2=500-314÷2=500-157=343(平方厘米)所以阴影部分的面积为343平方厘米;大圆半径:16÷2=8(厘米)小圆半径:8÷2=4(厘米)3.14×(82-42)÷2=3.14×(64-16)÷2=3.14×48÷2=150.72÷2=75.36(平方厘米)所以阴影部分的面积为75.36平方厘米。
8.求阴影部分的面积。
【答案】107cm 2【分析】观察图形可知,阴影部分的面积=半圆的面积-中间空白三角形的面积,中间的三角形是等腰直角三角形,该三角形的底和高等于圆的半径,根据圆的面积公式:2S r 圆形 ,三角形的面积公式:S ah 2三角形,据此进行计算即可。
北师大版六年级数学上册第一单元:求含圆的阴影部分面积“拓展型”专项练习(原卷版+解析)

2023-2024学年六年级数学上册典型例题系列第一单元:求含圆的阴影部分面积“拓展型”专项练习1.计算阴影部分的周长和面积。
2.求阴影部分面积。
3.大圆半径5厘米,小圆半径3厘米,求两圆中阴影部分的面积差。
4.求阴影部分的面积。
(单位:厘米)5.图中圆的周长是25.12厘米,空白部分是一个正方形,阴影部分的面积是多少平方厘米?6.求阴影部分的面积。
7.计算如图中阴影部分的面积。
8.根据图中的数据求阴影部分的面积。
(单位:米)9.下图中,底边和高都是6厘米的等腰三角形,分别以高的长为直径画圆,以底的一半长为直径画两个半圆,求阴影部分的面积。
(π取3.14)10.图中阴影部分的面积是400平方厘米,环形的面积是多少?( 取3.14)11.求下图阴影部分的面积。
12.求出阴影部分的面积和周长。
13.求图中阴影部分的面积。
(单位:cm)14.求阴影部分的面积。
(1)(2)15.求阴影部分的周长和面积。
16.计算下面图形中阴影部分的面积。
17.求阴影部分的面积。
(单位:厘米)18.如图,阴影部分的面积是25平方米,求圆环面积。
2023-2024学年六年级数学上册典型例题系列 第一单元:求含圆的阴影部分面积“拓展型”专项练习【分析】C 2r π=圆形,C d 圆形π,阴影部分的周长=直径为10厘米圆的周长×12+半径为10厘米圆的周长×14+10厘米;2S r 圆形π,阴影部分的面积=半径为10厘米圆的面积×14-直径为10厘米圆的面积×12,据此解答。
【详解】3.1412rπ”表示出大圆和小圆的面积,再求出它们的差,据此解【分析】1【分析】观察图形可知,如图所示:将左上角的两小块阴影部分移到右下角的空白部分,此时阴影部分的面积即是底为8cm,高为8cm 的三角形的面积,再根据三角形的面积公式:S=ah÷2,据此代入数值进行计算即可。
【详解】8×8÷2=64÷2=32(cm2)14.求阴影部分的面积。
小学数学六年级圆的阴影面积与周长100道经典题型

小学数学六年级圆的阴影面积与周长100道经典题型六年级圆的阴影面积与周长100道经典题型1.求阴影部分的面积。
(单位:厘米)2.正方形面积是7平方厘米,求阴影部分的面积。
(单位:厘米)3.求图中阴影部分的面积。
(单位:厘米)4.求阴影部分的面积。
(单位:厘米)5.求阴影部分的面积。
(单位:厘米)6.如图:已知小圆半径为2厘米,大圆半径是小圆的3倍,问:空白部分甲比乙的面积多多少厘米?7.求阴影部分的面积。
(单位:厘米)8.求阴影部分的面积。
(单位:厘米)9.求阴影部分的面积。
(单位:厘米)10.求阴影部分的面积。
(单位:厘米)11.求阴影部分的面积。
(单位:厘米)12.求阴影部分的面积。
(单位:厘米)13.求阴影部分的面积。
(单位:厘米)14.求阴影部分的面积。
(单位:厘米)15.已知直角三角形面积是12平方厘米,求阴影部分的面积。
16.求阴影部分的面积。
(单位:厘米)17.图中圆的半径为5厘米,求阴影部分的面积。
(单位:厘米)18.求阴影部分的面积。
(单位:厘米)19.正方形边长为2厘米,求阴影部分的面积。
20.如图,正方形ABCD的面积是36平方厘米,求阴影部分的面积。
21.如图,正方形边长为8厘米,求阴影部分的面积。
22.求阴影部分的面积。
23.求阴影部分的周长与面积。
24.求阴影部分的周长与面积。
25.求阴影部分的周长与面积。
26.求阴影部分的周长与面积。
27.求阴影部分的周长与面积。
28.求阴影部分的周长与面积。
29.求阴影部分的面积。
30.求阴影部分的面积。
31.正方形面积是7平方厘米,求阴影部分的面积和周长。
(单位:厘米)32.求图中阴影部分的面积和周长。
(单位:厘米)33.求图中阴影部分的面积和周长。
(单位:厘米)34.求图中阴影部分的面积和周长。
(单位:厘米)35.求图中阴影部分的面积和周长。
(单位:厘米)36.求图中阴影部分的面积和周长。
(单位:厘米)37.求图中阴影部分的面积和周长。
椭圆的练习题(阴影部分的面积周长20题)

椭圆的练习题(阴影部分的面积周长20题)第一题题目:如图所示,已知椭圆的长轴长为6,短轴长为4。
阴影部分是由椭圆及直线段围成的图形,请计算阴影部分的面积和周长。
解答:根据椭圆的性质,长轴为2a,短轴为2b,则该椭圆的长轴长为6,则a=3,短轴长为4,则b=2。
要计算阴影部分的面积和周长,我们可以先计算椭圆的面积和周长,再减去直线段的部分。
椭圆的面积计算公式为:S = π * a * b代入已知的a和b的值,得到:S = π * 3 * 2S = 6π椭圆的周长计算公式为:L = 2π * √((a^2 + b^2) / 2)代入已知的a和b的值,得到:L = 2π * √((3^2 + 2^2) / 2)L = 2π * √(13 / 2)L = π * √26阴影部分的面积为椭圆的面积减去直线段的部分,即6π - 6。
阴影部分的周长为椭圆的周长减去直线段的长度,即π * √26 - 4。
所以,阴影部分的面积为6π - 6,周长为π * √26 - 4。
第二题题目:如图所示,已知椭圆的长轴长为8,短轴长为6。
阴影部分是由椭圆及直线段围成的图形,请计算阴影部分的面积和周长。
解答:根据椭圆的性质,长轴为2a,短轴为2b,则该椭圆的长轴长为8,则a=4,短轴长为6,则b=3。
要计算阴影部分的面积和周长,我们可以先计算椭圆的面积和周长,再减去直线段的部分。
椭圆的面积计算公式为:S = π * a * b代入已知的a和b的值,得到:S = π * 4 * 3S = 12π椭圆的周长计算公式为:L = 2π * √((a^2 + b^2) / 2)代入已知的a和b的值,得到:L = 2π * √((4^2 + 3^2) / 2)L = 2π * √(25 / 2)L = 5π * √2阴影部分的面积为椭圆的面积减去直线段的部分,即12π - 12。
阴影部分的周长为椭圆的周长减去直线段的长度,即5π * √2 - 8。
六年级圆的阴影面积和周长100道经典题型
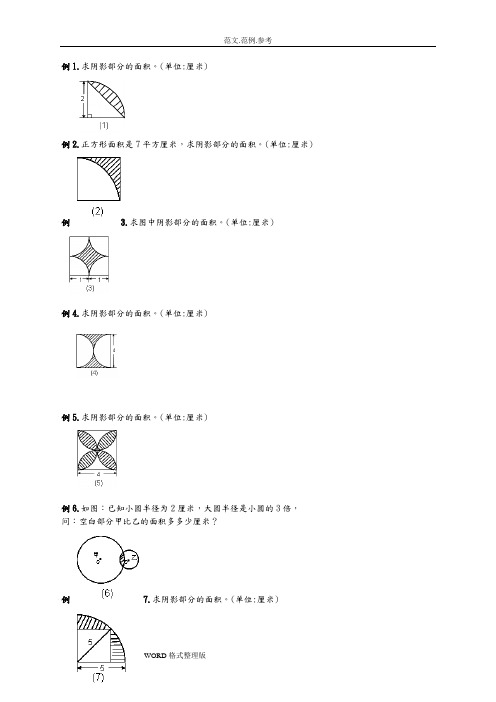
例1.求阴影部分的面积。
(单位:厘米)例2.正方形面积是7平方厘米,求阴影部分的面积。
(单位:厘米)例 3.求图中阴影部分的面积。
(单位:厘米)例4.求阴影部分的面积。
(单位:厘米)例5.求阴影部分的面积。
(单位:厘米)例6.如图:已知小圆半径为2厘米,大圆半径是小圆的3倍,问:空白部分甲比乙的面积多多少厘米?例7.求阴影部分的面积。
(单位:厘米)例8.求阴影部分的面积。
(单位:厘米)例9.求阴影部分的面积。
(单位:厘米)例10.求阴影部分的面积。
(单位:厘米)例11.求阴影部分的面积。
(单位:厘米)例12.求阴影部分的面积。
(单位:厘米)例13.求阴影部分的面积。
(单位:厘米)例14.求阴影部分的面积。
(单位:厘米)例15.已知直角三角形面积是12平方厘米,求阴影部分的面积。
例16.求阴影部分的面积。
(单位:厘米)例17.图中圆的半径为5厘米,求阴影部分的面积。
(单位:厘米)例18.求阴影部分的面积。
(单位:厘米)例19.正方形边长为2厘米,求阴影部分的面积。
例20.如图,正方形ABCD的面积是36平方厘米,求阴影部分的面积。
例21.如图,正方形边长为8厘米,求阴影部分的面积。
例21.如图,三角形ABC是直角三角形,阴影部分甲比阴影部分乙面积大28平方厘米,AB=40厘米。
求BC的长度。
.例22求阴影部分的面积例23求阴影部分的周长与面积例24求阴影部分的周长与面积例25求阴影部分的周长与面积例26求阴影部分的周长与面积例27求阴影部分的周长与面积例28求阴影部分的周长与面积例29求阴影部分的面积例30求阴影部分的面积例31正方形面积是7平方厘米,求阴影部分的面积和周长。
(单位:厘米)例32求图中阴影部分的面积和周长。
(单位:厘米)例33求图中阴影部分的面积和周长。
(单位:厘米)例34求图中阴影部分的面积和周长。
(单位:厘米)例35求图中阴影部分的面积和周长。
(单位:厘米)例36求图中阴影部分的面积和周长。
椭圆的周长及面积练习题

椭圆的周长及面积练习题题目一一个椭圆的长轴长12cm,短轴长8cm,请计算其周长和面积。
解答椭圆的周长可以根据公式计算:C = π × (a + b),其中a和b分别为长轴和短轴的一半。
长轴的一半为6cm,短轴的一半为4cm,代入公式得到周长:C = π × (6 + 4) = 20π cm。
椭圆的面积可以根据公式计算:A = π × a × b,其中a和b分别为长轴和短轴的一半。
代入长轴和短轴的一半得到面积:A = π × 6 × 4 = 24π cm²。
题目二一个椭圆的周长是16π cm,长轴和短轴的比例为3:2,请计算其长轴和短轴的长度。
解答设长轴的一半为3x,短轴的一半为2x。
根据椭圆的周长公式:16π = π × (3x + 2x)。
化简得到:16 = 5x。
解方程得到:x = 3.2。
长轴的一半为3x,即3 × 3.2 = 9.6,长轴的长度为19.2 cm。
短轴的一半为2x,即2 × 3.2 = 6.4,短轴的长度为12.8 cm。
题目三一个椭圆的面积是36π cm²,长轴和短轴的比例为4:3,请计算其长轴和短轴的长度。
解答设长轴的一半为4x,短轴的一半为3x。
根据椭圆的面积公式:36π = π × 4x × 3x。
化简得到:36 = 12x²。
解方程得到:x² = 3。
解得:x ≈ 1.732。
长轴的一半为4x,即4 × 1.732 ≈ 6.928,长轴的长度为13.856 cm。
短轴的一半为3x,即3 × 1.732 ≈ 5.196,短轴的长度为10.392 cm。
人教版六年级上册数学期末求阴影部分面积及周长专题训练
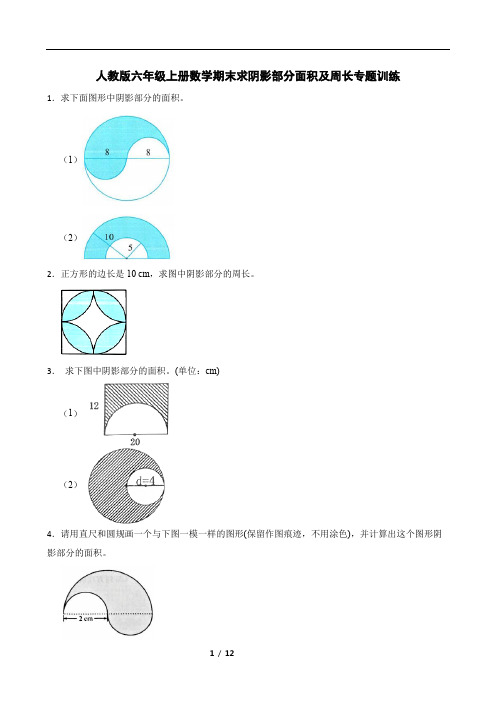
人教版六年级上册数学期末求阴影部分面积及周长专题训练1.求下面图形中阴影部分的面积。
(1)(2)2.正方形的边长是10 cm,求图中阴影部分的周长。
3.求下图中阴影部分的面积。
(单位:cm)(1)(2)4.请用直尺和圆规画一个与下图一模一样的图形(保留作图痕迹,不用涂色),并计算出这个图形阴影部分的面积。
5.求出下面图形中的阴影部分的面积。
6.求阴影部分面积(单位cm)7.求下面图形的周长和面积。
8.求下图阴影部分的周长。
(单位:厘米)9.求下图中阴影部分的面积(单位:cm)(1)(2)10.求下面各图形中阴影部分的面积。
(单位:cm)(1)(2)11.求下面各图中阴影部分的面积(1)(2)12.求阴影部分的面积。
13.计算图中阴影部分的面积。
(单位:cm)14.计算阴影部分的周长和面积。
15.求下图阴影部分的面积是多少平方分米.(结果用小数表示)16.计算下面阴影部分的周长和面积。
(1)(2)17.求下图中阴影部分的面积。
18.求下面图形中阴影部分的周长和面积。
(1)19.求阴影部分的面积。
20.如图中圆的半径为4分米,求图中阴影部分的面积。
答案解析部分1.【答案】(1)解:3.14×82÷2=200.96÷2=100.48(cm2)(2)解:3.14×(102-52)÷2=3.14×75÷2=235.5÷2=117.75(cm2)【解析】【分析】(1)可以将阴影部分的下面小半圆移到上面空白部分,这样阴影部分面积就是外面大圆面积的一半,圆的面积=圆周率×半径的平方。
(2)阴影部分是圆环面积的一半,圆环的面积=圆周率×(大圆半径的平方-小圆半径的平方)。
2.【答案】解:正方形的边长就是圆的直径,图中阴影部分的周长就是2个圆的周长;3.14×10 ×2 =62.8(cm)答:图中阴影部分的周长是62.8厘米。
六年级圆的阴影面积及周长100道经典题型

例1.求阴影部分的面积。
(单位:厘米)例2.正方形面积是7平方厘米,求阴影部分的面积。
(单位:厘米)例 3.求图中阴影部分的面积。
(单位:厘米)例4.求阴影部分的面积。
(单位:厘米)例5.求阴影部分的面积。
(单位:厘米)例6.如图:已知小圆半径为2厘米,大圆半径是小圆的3倍,问:空白部分甲比乙的面积多多少厘米?例7.求阴影部分的面积。
(单位:厘米)例8.求阴影部分的面积。
(单位:厘米) 例9.求阴影部分的面积。
(单位:厘米) 例10.求阴影部分的面积。
(单位:厘米) 例11.求阴影部分的面积。
(单位:厘米) 例12.求阴影部分的面积。
(单位:厘米)例13.求阴影部分的面积。
(单位:厘米)例14.求阴影部分的面积。
(单位:厘米)例15.已知直角三角形面积是12平方厘米,求阴影部分的面积。
例16.求阴影部分的面积。
(单位:厘米)例17.图中圆的半径为5厘米,求阴影部分的面积。
(单位:厘米)例18.求阴影部分的面积。
(单位:厘米)例19.正方形边长为2厘米,求阴影部分的面积。
例20.如图,正方形ABCD的面积是36平方厘米,求阴影部分的面积。
例21.如图,正方形边长为8厘米,求阴影部分的面积。
例21.如图,三角形ABC是直角三角形,阴影部分甲比阴影部分乙面积大28平方厘米,AB=40厘米。
求BC的长度。
.例22求阴影部分的面积例23求阴影部分的周长与面积例24求阴影部分的周长与面积例25求阴影部分的周长与面积例26求阴影部分的周长与面积例27求阴影部分的周长与面积例28求阴影部分的周长与面积例29求阴影部分的面积例30求阴影部分的面积例31正方形面积是7平方厘米,求阴影部分的面积和周长。
(单位:厘米)例32求图中阴影部分的面积和周长。
(单位:厘米)例33求图中阴影部分的面积和周长。
(单位:厘米)例34求图中阴影部分的面积和周长。
(单位:厘米)例35求图中阴影部分的面积和周长。
(单位:厘米)例36求图中阴影部分的面积和周长。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
六年级数学上册椭圆的周长求阴影部分面
积专项训练
介绍
本次专项训练旨在帮助六年级学生掌握椭圆的周长求阴影部分面积的方法。
周长求解步骤
1. 首先,了解椭圆的定义和性质。
椭圆是一个平面上的图形,其形状类似于拉伸的圆形。
它有两个焦点和一个长轴和短轴。
2. 掌握椭圆的周长计算公式。
椭圆的周长公式为:C = 2π * sqrt((a^2 + b^2) / 2),其中a为长轴的长度,b为短轴的长度。
3. 根据给定的椭圆,确定要求解的阴影部分。
此部分可能是椭圆内的一段或多段弧。
4. 根据给定的弧段长度,使用比例关系来计算弧长所对应的椭圆的弧度。
5. 将弧长转化为角度,并利用角度和椭圆的周长公式来计算阴影部分的面积。
例题训练
现在我们来做几个例题,以巩固对周长求解和阴影部分面积计算的理解。
例题1:
已知椭圆的长轴长度为12cm,短轴长度为8cm,求椭圆内一段弧长为3π cm的阴影部分的面积。
解答:
步骤一:根据椭圆的长轴长度和短轴长度,计算椭圆的周长:- 长轴a = 12cm
- 短轴b = 8cm
- 椭圆的周长C = 2π * sqrt((12^2 + 8^2) / 2) ≈ 31.83cm
步骤二:根据弧长和周长的比例关系,计算对应的弧度:
- 弧长L = 3π cm
- 弧长L / 椭圆周长C = 弧度θ / 360°
- 弧度θ ≈ (3π cm / 31.83cm) * 360° ≈ 107.46°
步骤三:使用角度和周长公式计算阴影部分的面积:
- 阴影部分的面积= (θ / 360°) * 椭圆的面积
- 椭圆的面积= π * a * b = π * 12cm * 8cm ≈ 301.59cm²
- 阴影部分的面积≈ (107.46° / 360°) * 301.59cm² ≈ 89.48cm²
综上所述,椭圆内一段弧长为3π cm的阴影部分的面积约为89.48cm²。
...
总结
通过这次专项训练,希望学生们能掌握椭圆的周长求解和阴影部分面积计算的方法。
继续多做练习题,加深理解,提高对数学问题的解决能力。
