高中数学回归课本(三角函数)
2024年度高中数学必修四三角函数PPT课件
建筑设计
在建筑设计中，利用三角函数计算建筑物的角度、高度和距离等 参数，确保设计的准确性和美观性。
机械设计
在机械设计中，三角函数用于计算齿轮、轴承等机械元件的尺寸和 角度，保证机械传动的精确性和稳定性。
航空航天工程
在航空航天工程中，利用三角函数分析飞行器的姿态、航向和速度 等参数，确保飞行安全。
21
2024/3/24
32
THANKS
感谢观看
2024/3/24
33
周期性、奇偶性、单调性等
解三角形
正弦定理、余弦定理及应用
29
常见题型解析及技巧点拨
01
三角函数求值问题：利 用同角关系式、诱导公 式等求解
2024/3/24
02
三角函数的图像与性质 应用：判断单调性、周 期性等
03
04
三角恒等变换的应用： 证明等式、化简表达式 等
30
解三角形问题：利用正 弦定理、余弦定理求解 边或角
易错知识点剖析及防范措施
混淆三角函数定义域和值域
注意定义域和值域的区别，避免混淆
忽视三角函数的周期性
在解题时要考虑周期性，避免漏解或 多解
2024/3/24
错误使用三角恒等变换公式
注意公式的适用条件和变形方式，避 免误用
忽视解三角形的限制条件
在解三角形时要注意边和角的限制条 件，避免得出不符合题意的解
第三象限
正弦、余弦均为负、正切为正 。
第四象限
正弦为负、余弦为正、正切为 负。
2024/3/24
7
02 三角函数诱导公 式与变换
2024/3/24
8
诱导公式及其应用
2024/3/24
诱导公式的基本形式
2020高考数学冲刺 回归教材 3 三角函数、三角恒等变换与解三角形
解析 取CD的中点O，连接ON，EO，因为△ECD为正三角形，所以EO⊥CD， 又平面ECD⊥平面ABCD，平面ECD∩平面ABCD＝CD，所以EO⊥平面ABCD.
设正方形 ABCD 的边长为 2，则 EO＝ 3，ON＝1，
所以EN2＝EO2＋ON2＝4，得EN＝2. 过M作CD的垂线，垂足为P，连接BP，
板块四 回归教材 赢得高考
内容索引
NEIRONGSUOYIN
回归教材 易错提醒
1 回归教材
PART ONE
1.终边相同角的表示 所有与角α终边相同的角，连同角α在内，可构成一个集合S＝_{_β_|_β_＝__α_＋__k_·3_6_0_°_，___ k∈Z} ，即任一与角α终边相同的角，都可以表示成角α与整数个周角的和.
解析 当－1<x≤0 时，0<x＋1≤1，则 f(x)＝12 f(x＋1)＝12(x＋1)x； 当1<x≤2时，0<x－1≤1，则f(x)＝2f(x－1)＝2(x－1)(x－2)； 当2<x≤3时，0<x－2≤1，则f(x)＝2f(x－1)＝22f(x－2)＝22(x－2)(x－3)，…，
…， 12x＋1x，－1<x≤0， 由此可得 f(x)＝xx－1，0<x≤1， 2x－1x－2，1<x≤2， 22x－2x－3，2<x≤3，
10.函数y＝Asin(ωx＋φ)(ω>0，A>0)的图象 (1)“五点法”作图 设 z＝ωx＋φ，令 z＝0，π2，π，32π，2π，求出相应的 x 的值与 y 的值，描点、连线可得. (2)由三角函数的图象确定解析式时，一般利用五点中的零点或最值点作为解题突破口. (3)图象变换 y＝sin x―向―平左―移―φ―|>φ―0|个―或―单― 向位―右―长― φ度―<→0y＝sin(x＋φ) ―横―坐――标―变―纵 ―为―坐原―― 标来―不的―― 变1ω――ω―>―0―倍→y＝sin(ωx＋φ)
高考数学回归课本 三角函数
练习3--三角函数1．函数)652tan(3π-=x y 的最小正周期是________ 2．函数)4πtan(-=x y 的定义域是________ 3．下列函数中，同时满足：①在（0，2π）上是增函数；②为奇函数；③以π为最小正周期的函数是( )A ．y =tan xB ．y =cos xC ．y =tan 2xD ．y =|sin x |4．函数)4π3cos(2-=x y 的对称中心和对称轴分别是________ 5．函数y=sin(2x+π6)的图象可看成是把函数y=sin2x 的图象向_______平移_____单位得到 6．已知)sin(ϕω+=x A y 在同一周期内，9π=x 时有最大值21，94π=x 时有最小值21-，则函数的解析式为________ 7．函数221cos 21sin ++=x x y 在区间]2,2[ππ-的最小值是________ 8．函数)cos (sin sin 2x x x y +=的最大值是________9．已知θ为第二象限角，225sinsin 240,θθ+-=则cos 2θ的值为________ 10．已知==-∈x x x 2tan ,54cos ),0,2(则π________ 11．函数)33sin(51π-=x y 的定义域是____ _____，值域是________，周期是______，振幅是______，频率是________，相位是 ，初相是________。
12．函数的2cos 3cos 2y x x =-+最小值为 。
13．=0330sin 。
14．若角α的终边经过点(12)P -，，则tan 2α的值为 。
15．化简：cos sin 36ππαα⎛⎫⎛⎫+++= ⎪ ⎪⎝⎭⎝⎭。
16．1)6cos()(--=πωx x f 的最小正周期为5π，其中0>ω，则=ω 。
17．方程2cos 14x π⎛⎫-= ⎪⎝⎭在区间(0,)π内的解是 。
高三数学回归课本复习材料：三角函数基本概念(二)
三角函数基本概念回归课本复习材料21象限角的概念： 已知α为第三象限角，则2α所在的象限是 D （A ）第一或第二象限 （B ）第二或第三象限 （C ）第一或第三象限 （D ）第二或第四象限 2.弧长公式已知球O 的半径为1，A 、B 、C 三点都在球面上，且每两点间的球面距离均为2π，则球心O 到平面ABC 的距离为（B ） A31 B 33 C 32 D 36 4、任意角的三角函数的定义：已知角α的终边经过点P(5，－12)，则ααcos sin +的值为＿＿。
（答：713-）； 5.三角函数线（1）已知sin α＞sin β，那么下列命题成立的是（ D ） A.若α、β是第一象限角，则cos α＞cos β B.若α、β是第二象限角，则tan α＞tan β C.若α、β是第三象限角，则cos α＞cos β D.若α、β是第四象限角，则tan α＞tan β（2）若α为锐角，则,sin ,tan ααα的大小关系为_______ （答：sin tan ααα<<）； 6.特殊角的三角函数值：7. 同角三角函数的基本关系式：8.三角函数诱导公式97costan()sin 2146πππ+-+的值为 （答：2323-）； 9、两角和与差的正弦、余弦、正切公式及倍角公式：(2) 函数4()cos f x x =2sin cos x x -4sin x -的最小正周期为____（答：π）；10. 三角函数的恒等变形 （1）巧变角已知,αβ为锐角，sin ,cos x y αβ==，3cos()5αβ+=-，则y 与x 的函数关系为___（答：23431(1)555y x x x =--+<<） (2)三角函数名互化(切割化弦)， 求值sin50(13tan10)+ （答：1）； (3)公式变形使用tan 20tan 403tan 20tan 40++⋅ 的值为3为sin cos y x x =-得到的图象，只要把函数sin cos y x x =+的图象按向量a 平移，则a等于A ．π(,0)2B ．π(-,0)2C ．4π(,0) D ．π(-,0)4(4)三角函数次数的降升，(5)式子结构的转化(对角、函数名、式子结构化同)。
高考冲刺回归课本篇(二)
高考冲刺回归课本篇（二）一、基本知识篇 （四）三角函数1.三角函数符号规律记忆口诀：一全正，二正弦，三是切，四余弦；2.对于诱导公式，可用“奇变偶不变，符号看象限”概括；3.记住同角三角函数的基本关系，熟练掌握三角函数的定义、图像、性质；4.熟知正弦、余弦、正切的和、差、倍公式，正余弦定理，处理三角形内的三角函数问题勿忘三内角和等于1800，一般用正余弦定理实施边角互化；5.正(余)弦型函数的对称轴为过最高点或最低点且垂直于x 轴的直线，对称中心为图象与x 轴的交点；正(余)切型函数的对称中心是图象和渐近线分别与x 轴的交点，但没有对称轴。
6.（1）正弦平方差公式：sin 2A －sin 2B=sin(A+B)sin(A －B);（2）三角形的内切圆半径r=cb a S ABC ++∆2；（3）三角形的外接圆直径2R=;sin sin sin Cc B b A a == （五）平面向量1.两个向量平行的充要条件,设a=(x 1,y 1),b=(x 2,y 2),λ为实数。
（1）向量式：a ∥b(b ≠0)⇔a=λb;（2）坐标式：a ∥b(b ≠0)⇔x 1y 2－x 2y 1=0;2.两个向量垂直的充要条件, 设a=(x 1,y 1),b=(x 2,y 2), （1）向量式：a ⊥b(b ≠0)⇔a ∙b=0; （2）坐标式：a ⊥b ⇔x 1x 2+y 1y 2=0;3.设a=(x 1,y 1),b=(x 2,y 2),则a ∙θ=x 1x 2+y 1y 2;其几何意义是a ∙b 等于a 的长度与b 在a 的方向上的投影的乘积； 4.设A （x 1,x 2）、B(x 2,y 2)，则S ⊿AOB ＝122121y x y x -； 5.平面向量数量积的坐标表示：（1）若a=(x 1,y 1),b=(x 2,y 2),则a ∙b=x 1x 2+y 1y 2221221)()(y y x x -+-=;（2）若a=(x,y),则a 2=a ∙a=x 2+y 2,22y x a +=;二、回归课本篇：1、下列各式能否成立？为什么？(A) cos 2x = 2 (B) sinx －cosx = 32 (C) tanx + 1tanx = 2(D) sin 3x = －π42、求函数y = lgcos (2x －π3)tanx －1的定义域。
新课标回归教材三角函数
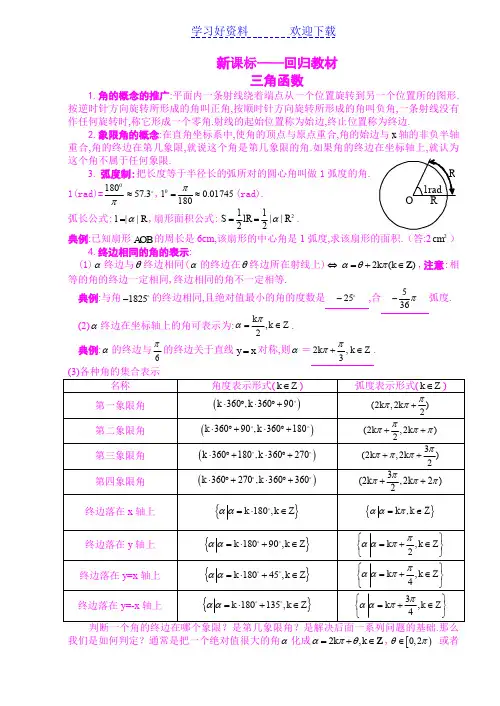
新课标——回归教材三角函数1.角的概念的推广:平面内一条射线绕着端点从一个位置旋转到另一个位置所的图形.按逆时针方向旋转所形成的角叫正角,按顺时针方向旋转所形成的角叫负角,一条射线没有作任何旋转时,称它形成一个零角.射线的起始位置称为始边,终止位置称为终边.2.象限角的概念:在直角坐标系中,使角的顶点与原点重合,角的始边与x 轴的非负半轴重合,角的终边在第几象限,就说这个角是第几象限的角.如果角的终边在坐标轴上,就认为这个角不属于任何象限.3. 弧度制:把长度等于半径长的弧所对的圆心角叫做1弧度的角1(rad)=0180π57.3≈,010.01745180π=≈(rad). 弧长公式:||l R α=,扇形面积公式:211||22S lR R α==.典例:已知扇形AOB 的周长是6cm,该扇形的中心角是1弧度,求该扇形的面积.（答:22cm ）4.终边相同的角的表示:(1)α终边与θ终边相同(α的终边在θ终边所在射线上)⇔2()k k αθπ=+∈Z ,注意:相等的角的终边一定相同,终边相同的角不一定相等. 典例:与角1825-的终边相同,且绝对值最小的角的度数是25-,合536π-弧度.(2)α终边在坐标轴上的角可表示为:,2k k Z πα=∈. 典例:α的终边与6π的终边关于直线y x =对称,则α＝2,3k k Z ππ+∈. )) ) )}}}我们是如何判定？通常是把一个绝对值很大的角α化成2,k k απθ=+∈Z ,[)0,2θπ∈ 或者是化成)360,,0,360k k Z αθθ⎡=⋅+∈∈⎣,这样只要判定θ是第几象限角就可以了.典例: (1)291033πππ-=-+,因为3π是第一象限角,所以293π-的终边也在第一象限; (2) 790236070=⨯+,因为70是第一象限角,所以790的终边也在第一象限. 5.α与2α的终边关系:由“两等分各象限、一二三四”确定. 如图,若角α终边在第一(二、三、四)象限,则角2α的终边位于右图中标有数字1(2、3、4)区域.这个方法叫做等分象限法.典例:若α是第二象限角,则2α是第 一、三 象限角.6.任意角的三角函数的定义:设α是任意一个角,P (,)x y 是α的终边上的任意一点(异于原点),它与原点的距离是0r =,那么sin ,cos y x r r αα==,()tan 0yx xα=≠.三角函数值只与角的大小有关,而与终边上点P 的位置无关.典例:(1)已知角α的终边经过点P(5,－12),则sin cos αα+的值为713-(2)设α是第三、四象限角,23sin 4m mα-=-,则m 的取值范围是32(1,)-; (3)若|sin |cos 0sin |cos |αααα+=,试判断cot(sin )tan(cos )αα⋅的符号（答:负）7.三角函数线的特征是:正弦线MP “站在x 轴上(起点在x 轴上)余弦线OM “躺在x 轴上(起点是原点)”、正切线AT “与圆O 切在点(1,0)A 处(起点是A )”.三角函数线的重要应用是比较三角函数值的大小和解三角不等式.典例:(1)若08πθ-<<,则sin ,cos ,tan θθθ的大小关系为tan sin cos θθθ<<;(2)若α为锐角,则,sin ,tan ααα的大小关系为sin tan ααα<<;(3)函数lg(2sin y x =的定义域是2(2,2]()33k k k Z ππππ-+∈(1)平方关系:22sin cos 1αα+=;(2)商数关系:sin tan cos ααα=. 同角三角函数的基本关系式的主要应用是,已知一个角的三角函数值,求此角的其它三角函数值.在运用平方关系解题时,要根据已知角的范围和三角函数的取值,尽可能地压缩角的范围,以便进行定号;在具体求三角函数值时,一般不需用同角三角函数的基本关系式,而是先根据角的范围确定三角函数值的符号,再利用解直角三角形求出此三角函数值的绝对值.解题方法总结(1)已知一弦值,求正切.通常是利用sin α=cos α=,然后利用sin tan cos ααα=求正切.要注意α的象限,分象限定符号.(2)已知正切,求正弦、余弦值.方法一是解方程组.方法二是利用一个推导公式直接求,公式221cos 1tan αα=+,222tan sin 1tan ααα=+,不过还是要注意开根号时的正负的确定.(3)解题中常用的三种技巧:一、切化弦;二、1的代换;三、分子分母同时除以cos α或者2cos α. (4)解题中常用的两组公式:222(sin cos )sin cos 2sin cos 12sin cos αααααααα+=++=+;222(sin cos )sin cos 2sin cos 12sin cos αααααααα-=+-=-.典例:(1)函数sin tan cos cot y αααα+=+的值的符号为大于0;(2)若022x π≤≤,cos2x 成立的x 的取值范围是3[0,][,]44πππ;(3)已知3sin 5m m θ-=+,42cos ()52m m πθθπ-=<<+,则tan θ＝512-; (4)已知tan 1tan 1αα=--,则sin 3cos sin cos αααα-+＝53-;2sin sin cos 2ααα++＝135;(5)已知sin200a =,则tan160等于 B A.C.;(6)已知(cos )cos3f x x =,则(sin30)f 的值为 －1 .10.三角函数诱导公式(2kπα+)的本质是:奇变偶不变(对k 而言,指k 取奇数或偶数),符号看象限(看原函数,同时可把α看成是锐角).诱导公式的应用是求任意角的三角函数值,其一般步骤:“负化正,大化小,化成锐角再查表”即:(1)负角变正角,再写成2k π+α,02απ≤<;(2)转化为锐角三角函数.典例:(1)97cos tan()sin 2146πππ+-+的值为; (2)已知4sin(540)5α+=-,则cos(270)α-=45-,若α为第二象限角,则2[sin(180)cos(360)]tan(180)ααα-+-=+3100-. 11.两角和与差的正弦、余弦、正切公式及倍角公式:正:()sin sin cos cos sin αβαβαβ±=±;逆:sin cos )a b αααφ±=±,其中tan b a φ=.正:()cos cos cos sin sin αβαβαβ±=;逆:cos sin )a b αααφ±=,其中tan baφ=.正:()tan tan tan 1tan tan αβαβαβ±±=;变:tan tan tan()(1tan tan )αβαβαβ±=±.正:22tan sin 22sin cos 1tan ααααα==+;变:21sin 2(sin cos )ααα±=± 正:2222221tan cos22cos 112sin cos sin 1tan ααααααα-=-=-=-=+;变:221cos22cos ,1cos22sin αααα+=-=(降角升幂公式),逆:221+cos21cos2cos ,sin 22αααα-＝＝(降幂升角公式);sin 1cos tan 21cos sin ααααα-==+(半角正切) 典例:(1)下列各式中,值为12的是 CA.sin15cos15B.22cos sin1212ππ- C.2tan 22.51tan 22.5- (2)命题P:tan()0A B +=,命题Q:tan tan 0A B +=,则P 是Q 的 C 条件.A 、充要B 、充分不必要C 、必要不充分D 、既不充分也不必要; (3)已知3sin()cos cos()sin 5αβααβα---=,那么cos2β的值为725;(4)1sin10的值是 4 ;(5)已知0tan110a =,求0tan50的值(用a 表示)甲求得的结果是,乙求得的结果是212a a-,对甲、乙求得的结果的正确性你的判断是 甲、乙都对 . 12.三角函数的化简、计算、证明的恒等变形的基本思路是:一角二名三结构.即首先观察角与角之间的关系,注意角的一些常用变式,角的变换是三角函数变换的核心！第二看函数名称之间的关系,通常“切化弦”;第三观察代数式的结构特点通常是分式要因式分解、通分后约分、根号下配方后开方.基本的技巧有:★★★(1)巧变角（已知角与特殊角的变换、已知角与目标角的变换、角与其倍角的变换、两角与其和差角的变换.如:()()ααββαββ=+-=-+,2()()ααβαβ=++-,2()()αβαβα=+--,22αβαβ++=⋅,222αββααβ+=---⎛⎫⎛⎫ ⎪ ⎪⎝⎭⎝⎭等. 典例:(1)已知2tan()5αβ+=,1tan()44πβ-=,那么tan()4πα+的值是322;(2)已知02πβαπ<<<<,且1cos()29βα-=-,2sin()23αβ-=,求cos()αβ+的值239729-;(3)若,αβ为锐角,3sin ,cos ,cos()5x y αβαβ==+=-,则y 与x 的函数关系为43(1)55y x x =<<. (2)三角函数名互化(切化弦),典例:(1)求值sin50(13tan10)+= 1 ;(2)已知sin cos 21,tan()1cos23αααβα=-=--,求tan(2)βα-的值18(3)公式变形使用（tan tan αβ±()()tan 1tan tan αβαβ=±.典例:(1)已知A 、B 为锐角,且满足tan tan tan tan 1A B A B =++,则cos()A B +＝; (2)ABC ∆中,tan tan tan A B A B +=,sin cos A A =则此三角形是 等边 三角形. (4)三角函数次数的降升(降幂公式:21cos 2cos 2αα+=,21cos 2sin 2αα-=与升幂公式:21cos22cos αα+=,21cos22sin αα-=).典例:(1)若3(,)2αππ∈,sin2α;(2)2()5sin cos f x x x x =-)x R ∈的单调递增区间为5[,]()1212k k k Z ππππ-+∈. (5)式子结构的转化(对角、函数名、式子结构化同). 典例:(1)tan (cos sin )ααα-sin tan cot csc αααα+++= sin α;(2)求证:21tan 1sin 212sin 1tan 22αααα++=--; (3)化简:42212cos 2cos 22tan()sin ()44x x x x ππ-+-+= 1cos 22x . (6)常值变换主要指“1”的变换（221sin cos x x =+tan sin 42ππ===等）典例:已知tan 2α=,求22sin sin cos 3cos αααα+-=35.(7)正余弦“三兄妹—sin cos sin cos x x x x ±、”的内存联系—“知一求二”.典例:(1)若 sin cos x x t ±=,则sin cos x x =212t -±,特别提醒:这里[t ∈;(2)若1(0,),sin cos 2απαα∈+=,求tan α的值.（答: ）; (3)已知2sin22sin 1tan k ααα+=+()42ππα<<,试用k 表示sin cos αα-的值（答）.(2)当函数2cos 3sin y x x =-取得最大值时,tan x 的值是2-;(3)如果()()sin 2cos()f x x x ϕϕ=+++是奇函数,则tan ϕ= －2 ; (4)求值:2223164sin 20sin 20cos 20-+︒=︒︒32 . 14.正弦函数和余弦函数的图象:正弦函数sin y x =和余弦函数cos y x =图象的作图方法:五点法:先取横坐标分别为0,,2π3,,22πππ的五点,再用光滑的曲线把这五点连 接起来,就得到正弦曲线和余弦曲线在一个周 期内的图象.如右图所示:15.正弦函数sin ()y x x R =∈、余弦函数 cos ()y x x R =∈性质:(1)定义域R.(2)值域[]1,1-.对sin y x =,当()22x k k Z ππ=+∈时,y 取最大值1;当()322x k k Z ππ=+∈时,y 取最小值－1;对cos y x =,当()2x k k Z π=∈时,y 取最大值1,当()2x k k Z ππ=+∈时,y 取最小值－1.典例:(1)若函数sin(3)6y a b x π=-+的最大值为32,最小值为12-,则a =12,b =1±;(2)函数()sin f x x x =（[,]22x ππ∈-）的值域是 [－1, 2] ;(3)若2αβπ+=,则cos 6sin y βα=-的最大值和最小值分别是 7 、 -5 ;(4)2()2cos sin()3f x x x x π=+sin cos x x +的最小值是 2 ,此时x =()12k k Z ππ+∈;(5)己知1sin cos 2αβ=,则sin cos t βα=的取值范围11[,]22-;(6)若22sin 2sin 2cos αβα+=,则22sin sin y αβ=+的最大值 1 、最小值2. 特别提醒 :在解含有正余弦函数的问题时,你深入挖掘正余弦函数的有界性了吗?例如前面的关于求值域的一个运用！(3)周期性:①sin y x =、cos y x =的最小正周期都是2π;②()sin()f x A x ωϕ=+和()cos()f x A x ωϕ=+的最小正周期都是2||T πω=.典例:(1)若()sin 3xf x π=,则(1)(2)(3)(2003)f f f f ++++＝ 0 ;(2)函数4()cos f x x =2sin cos x x -4sin x -的最小正周期为π;(3)设()2sin()25f x x ππ=+,若12()()()()f x f x f x x R ≤≤∈恒成立,则12min ||x x -= 2 .(4)奇偶性与对称性:①函数sin ()y x x R =∈是奇函数,对称中心是()(),0k k Z π∈,对称轴是直线()2x k k Z ππ=+∈;②函数cos ()y x x R =∈是偶函数,对称中心是(),02k k Z ππ⎛⎫+∈ ⎪⎝⎭,对称轴是直线()x k k Z π=∈（正(余)弦型函数的对称轴为过最值点且垂直于x 轴的直线,对称中心为图象零点所在点.）典例:(1)函数5sin 22y x π⎛⎫=- ⎪⎝⎭的奇偶性是 偶函数 ;(2)已知函数3()sin 1(,f x ax b x a b =++为常数）,且(5)7f =,则(5)f -= －5 ;(3)2cos (sin cos )y x x x =+的对称中心和对称轴分别是(,1)()28k k Z ππ-∈、()28k x k Z ππ=+∈;(4)已知()sin())f x x x θθ=++为偶函数,求θ的值.（答:()6k k Z πθπ=+∈）(5)单调性:()sin 2,222y x k k k Z ππππ⎡⎤=-+∈⎢⎥⎣⎦在上单调递增,在()32,222k k k Z ππππ⎡⎤++∈⎢⎥⎣⎦单调递减;cos y x =在[]()2,2k k k Z πππ+∈上单调递减,在[]()2,22k k k Z ππππ++∈上单调递增.16.形如sin()y A x ωϕ=+的函数:(1)几个物理量:A ―振幅;1f T=―频率（周期的倒数）;x ωϕ+―相位;φ―初相; (2)求sin()y A x ωϕ=+表达式:A 由最值确定;ω由周期确定;ϕ由图象上的特殊点确定.(3)函数sin()y A x ωϕ=+图象的画法:①“五点法”—设X x ωϕ=+,令X ＝0,3,,,222ππππ求出相应的x 值,计算得出五点的坐标,描点后得出图象;②图象变换法:这是作函数简图常用方法.(4)函数sin()y A x k ωϕ=++的图象与sin y x =图象间的关系:①sin y x =的图象上各点向左(φ>0)或向右(φ<0)平移||ϕ个单位得()sin y x ϕ=+的图象;②()sin y x ϕ=+图象的纵坐标不变,横坐标变为原来的1ω,得到函数()sin y x ωϕ=+的图象; ③()sin y x ωϕ=+图象上各点横坐标不变,纵坐标变为原来的A 倍,得sin()y A x ωϕ=+图象;④sin()y A x ωϕ=+图象上各点向上(0k >)或向下(0k <),得到()sin y A x k ωϕ=++的图象.特别注意 :由()sin y x ω=得到()sin y x ωϕ=+的图象,则向左或向右平移应平移||ϕω单位.典例:(1)函数2sin(2)14y x π=--的图象经过怎样的变换才能得到sin y x =的图象？（答:2sin(2)14y x π=--向上平移1个单位得2sin(2)4y x π=-的图象,再向左平移8π个单位得2sin2y x =的图象,横坐标扩大到原来的2倍得2sin y x =的图象,最后将纵坐标缩小到原来的12即得sin y x =的图象）;(2)要得到函数cos()24x y π=-的图象,只需把函数sin 2xy =的图象向 左 平移2π个单位;(3)(现在考纲不作要求)将函数72sin(2)13y x π=-+图像,按向量a 平移后得到的函数图像关于原点对称,这样的向量是否唯一？若唯一,求出a ;若不唯一,求出模最小的向量(答:存在但不唯一,模最小的向量(,1)6a π=--);(4)若函数()[]()cos sin 0,2f x x x x π=+∈的图象与直线y k =有且仅有四个不同的交点,则k的取值范围是.(5)研究函数sin()y A x ωϕ=+性质的方法:类比于研究sin y x =的性质,只需将sin()y A x ωϕ=+中的x ωϕ+看成sin y x =中的x ,但在求sin()y A x ωϕ=+的单调区间时,要特别注意A 和ω的符号,通过诱导公式先将ω化正.典例:(1)函数sin(2)3y x π=-+的递减区间是5[,]()1212k k k Z ππππ-+∈;(2)12log cos()34x y π=+的递减区间是33[6,6]()44k k k Z ππππ-+∈;(3)设函数()sin()(0,0,)22f x A x A ππωφωφ=+≠>-<<的图象关于直线23x π=对称,它的周期是π,则( C )A 、1()(0,)2f x 的图象过点 B 、()f x 在区间52[,]123ππ上是减函数 C 、5()(,0)12f x π的图象的一个对称中心是 D 、()f x 的最大值是A; (4)对于函数()2sin 23f x x π⎛⎫=+ ⎪⎝⎭给出下列结论, 其中正确结论是 ②④ .①图象关于原点成中心对称; ②图象关于直线12x π=成轴对称;③图象可由函数2sin2y x =的图像向左平移3π个单位得到; ④图像向左平移12π个单位,即得到函数2cos2y x =的图像. (5)已知函数()2sin()f x x ωϕ=+图象与直线1y =的交点中,距离最近两点间的距离为3π,那么此函数的周期是π 17.正切函数tan y x =的图象和性质:(1)定义域:{|,}2x x k k Z ππ≠+∈.有关正切函数问题时,你注意到正切函数的定义域了吗？(2)值域是R,在上面定义域上无最大值也无最小值;(3)周期性:π,它与直线y a =的两个相邻交点之间的距离是一个周期π.绝对值或平方对三角函数周期性的影响:一般说来,某一周期函数解析式加绝对值或平方,其周期性是:弦减半、切不变.既为周期函数又是偶函数的函数自变量加绝对值,其周期性不变,其它不定.(只作了解即可)典例:(1)2sin ,sin y x y x ==,|tan |y x =的周期都是π.(2)sin y x =cos x +的周期为2π.(3)1|2sin(3)|,|2sin(3)2|626y x y x ππ=-+=-+的周期都是2π;(4)tan y x =奇偶性与对称性:是奇函数,对称中心是,02k π⎛⎫⎪⎝⎭()k Z ∈.特别提醒 :正切型函数的对称中心有两类:一类是图象与x 轴的交点,另一类是渐近线与x 轴的交点,但无对称轴,这是与正弦、余弦函数的不同之处.(5)单调性:正切函数在开区间()(,)22k k k Z ππππ-++∈内都是增函数.但要注意在整个定义域上不具有单调性.18.三角形中的有关公式:(1)内角和定理:三角形三角和为π,这是三角形中三角函数问题的特殊性,解题可不能忘记！任意两角和与第三个角总互补,任意两半角和与第三个角的半角总互余.锐角三角形⇔三内角都是锐角⇔三内角的余弦值为正值⇔任两角和都是钝角⇔任意两边的平方和大于第三边的平方.(2)正弦定理:2sin sin sin a b cR A B C===(R 为三角形外接圆的半径). 注意:①正弦定理的一些变式:()sin sin sin i a b c A B C ::=::;()sin ,sin ,sin 22a b ii A B C R R== 2c R=;()2sin ,2sin ,2sin iii a R A b R B b R C ===;②已知三角形两边一对角,求解三角形时,若运用正弦定理,则务必注意可能有两解.(3)余弦定理:2222222cos ,cos 2b c a a b c bc A A bc+-=+-=等,常选用余弦定理鉴定三角形形状.(4)面积公式:111sin ()222a S ah ab C r a bc ===++(其中r 为三角形内切圆半径).海伦-秦九韶公式 S 其中2a b cp ++=.典例:ABC ∆中,若22222sin cos cos sin sin A B A B C -=,判断ABC ∆的形状（答:直角三角形）.特别提醒 :(1)求解三角形中的问题时,一定要注意A B C π++=这个特殊性:所以有,,sin()sin ,sin cos 22A B CA B C A B C π++=-+==;(2)求解三角形中含有边角混合关系的问题时,常运用正弦定理、余弦定理实现边角互化.典例:(1)ABC ∆中,A 、B 的对边分别是 a b 、,且A=60, 4a b =,那么满足条件的ABC ∆A 、 有一个解B 、有两个解C 、无解D 、不能确定（答:C ）; (2)在ABC ∆中,A ＞B 是sin sin A B >成立的 充要 条件;(3)在ABC ∆中,(1tan )(1tan )2A B ++=,则2log sin C ＝12-;(4)在ABC ∆中,若()(sin sin a b c A B +++sin )3sin C a B -=,则C ∠＝60; (5)在ABC ∆中,若其面积222S =则C ∠=30;(6)在ABC ∆中,60, 1A b ==,,则ABC ∆;(7)在△ABC 中,21,cos 32B C a A +=则=13,22b c +的最大值为92; (8)在△ABC 中AB=1,BC=2,则角C 的取值范围是06C π<≤;(9)设O 是锐角三角形ABC 的外心,若75C ∠=,且,,AOB BOC COA ∆∆∆的面积满足关系式AOB BOC COA S S ∆∆∆+=,求A ∠（答:45）．19.求角的方法:先确定角的范围,再求出关于此角的某一个三角函数（要注意选择,其标准有二:一是此三角函数在角的范围内具有单调性;二是根据条件易求出此三角函数值）.特别提示:要尽量利用已知条件精确地确定角所在的范围.典例:(1)若,(0,)αβπ∈,且tan α、tan β是方程2560x x -+=的两根,则求αβ+的值34π;(2)ABC ∆中,3sin 4cos 6,4sin 3cos 1A B B A +=+=,则C ∠＝3π; (3)若02αβγπ≤<<<且sin sin sin 0αβγ++=,cos cos cos 0αβγ++=,求βα-的值（答:23π）.。
高考数学回归课本基础总复习三角函数
三角函数一、基础知识定义1 角，一条射线绕着它的端点旋转得到的图形叫做角。
若旋转方向为逆时针方向，则角为正角，若旋转方向为顺时针方向，则角为负角，若不旋转则为零角。
角的大小是任意的。
定义2 角度制，把一周角360等分，每一等价为一度，弧度制：把等于半径长的圆弧所对的圆心角叫做一弧度。
360度=2π弧度。
若圆心角的弧长为L ，则其弧度数的绝对值|α|=rL ,其中r 是圆的半径。
定义3 三角函数，在直角坐标平面内，把角α的顶点放在原点，始边与x 轴的正半轴重合，在角的终边上任意取一个不同于原点的点P ，设它的坐标为（x ,y ），到原点的距离为r,则正弦函数s in α=r y ,余弦函数co s α=r x ,正切函数tan α=x y ，余切函数cot α=y x，正割函数se c α=xr ,余割函数c s c α=.yr定理1 同角三角函数的基本关系式，倒数关系：tan α=αcot 1,s in α=αcsc 1，co s α=αsec 1；商数关系：tan α=αααααsin cos cot ,cos sin =；乘积关系：tan α×co s α=s in α,cot α×s in α=co sα；平方关系：s in 2α+co s 2α=1, tan 2α+1=se c 2α, cot 2α+1=c s c 2α.定理2 诱导公式（Ⅰ）s in (α+π)=-s in α, co s(π+α)=-co s α, tan (π+α)=tan α, cot (π+α)=cot α;（Ⅱ）s in (-α)=-s in α, co s(-α)=co s α, tan (-α)=-tan α, cot (-α)=cot α; （Ⅲ）s in (π-α)=s inα, co s(π-α)=-co s α, tan =(π-α)=-tan α, cot (π-α)=-cot α; （Ⅳ）s in ⎪⎭⎫⎝⎛-απ2=co s α,co s ⎪⎭⎫⎝⎛-απ2=s in α, tan ⎪⎭⎫⎝⎛-απ2=cot α（奇变偶不变，符号看象限）。
三角函数教材回归
高考数学概念、方法、题型、易误点及应试技巧总结四、三角函数1、角的概念的推广：平面内一条射线绕着端点从一个位置旋转到另一个位置所的图形。
按逆时针方向旋转所形成的角叫正角，按顺时针方向旋转所形成的角叫负角，一条射线没有作任何旋转时，称它形成一个零角。
射线的起始位置称为始边，终止位置称为终边。
2、象限角的概念：在直角坐标系中，使角的顶点与原点重合，角的始边与x轴的非负半轴重合，角的终边在第几象限，就说这个角是第几象限的角。
如果角的终边在坐标轴上，就认为这个角不属于任何象限。
3. 终边相同的角的表示：（1）α终边与θ终边相同(α的终边在θ终边所在射线上)⇔2()k kαθπ=+∈Z，注意：相等的角的终边一定相同，终边相同的角不一定相等.如与角1825-的终边相同，且绝对值最小的角的度数是＿＿＿，合＿＿＿弧度。
（答：25- ；536π-）（2）α终边与θ终边共线(α的终边在θ终边所在直线上) ⇔()k kαθπ=+∈Z.（3）α终边与θ终边关于x轴对称⇔2()k kαθπ=-+∈Z.（4）α终边与θ终边关于y轴对称⇔2()k kαπθπ=-+∈Z.（5）α终边与θ终边关于原点对称⇔2()k kαπθπ=++∈Z.（6）α终边在x轴上的角可表示为：,k k Zαπ=∈；α终边在y轴上的角可表示为：,2k k Zπαπ=+∈；α终边在坐标轴上的角可表示为：,2kk Zπα=∈.如α的终边与6π的终边关于直线xy=对称，则α＝____________。
（答：Zkk∈+,32ππ）4、α与2α的终边关系：由“两等分各象限、一二三四”确定.如若α是第二象限角，则2α是第_____象限角（答：一、三）5.弧长公式：||l Rα=，扇形面积公式：211||22S lR Rα==，1弧度(1rad)57.3≈ .如已知扇形AOB的周长是6cm，该扇形的中心角是1弧度，求该扇形的面积。
（答：22cm）6、任意角的三角函数的定义：设α是任意一个角，P(,)x y是α的终边上的任意一点（异于原点），它与原点的距离是0r=>，那么s i n,c o sy xr rαα==，()tan,0yxxα=≠，cotxyα=(0)y≠，secrxα=()0x≠，()csc0ryyα=≠。
2024春新教材高中数学5.2.1三角函数的概念教案新人教A版必修第一册
在解决实际问题时，可以运用三角函数的性质和周期性进行计算。例如，已知一个角的大小为π/3，可以通过查表或计算得到其正弦值为√3/2，余弦值为1/2，正切值为√3。
（4）在线课程：国内外知名大学开设的三角函数相关在线课程，如麻省理工学院的《线性代数与几何》、斯坦福大学的《数学分析》等，学生可以在线观看视频讲座、完成练习题，拓展知识视野。
2.拓展建议：
（1）阅读数学杂志：鼓励学生阅读数学杂志，了解三角函数的研究现状和发展趋势，提高学术素养。
（2）利用网络资源：引导学生利用学术网站资源，查阅三角函数相关论文和著作，加深对知识点的理解。
核心素养目标
本节课旨在培养学生的数学抽象和数学建模的核心素养。通过学习三角函数的概念，使学生能够理解从具体情境中抽象出三角函数的基本思想，提升数学抽象能力。同时，通过分析三角函数的性质和图像，使学生能够运用数学语言描述三角函数的性质，培养学生的数学建模能力。此外，通过小组讨论和自主探究的学习方式，提升学生的逻辑推理和数据分析能力，培养学生的合作交流和自主学习的能力。
三、实践活动（用时10分钟）
1.分组讨论：学生们将分成若干小组，每组讨论一个与三角函数相关的实际问题。
2.实验操作：为了加深理解，我们将进行一个简单的实验操作。这个操作将演示三角函数的基本原理。
3.成果展示：每个小组将向全班展示他们的讨论成果和实验操作的结果。
四、学生小组讨论（用时10分钟）
1.讨论主题：学生将围绕“三角函数在实际生活中的应用”这一主题展开讨论。他们将被鼓励提出自己的观点和想法，并与其他小组成员进行交流。
高三数学回归教材：第4章 三角函数、解三角形
第四章 三角函数、解三角形一、知识梳理（一）角的相关概念1、任意角：正角、负角、零角；2、象限角： （1）定义；（2）象限角集合表示：第一象限角、第二象限角、第三象限角、第四象限角； （3）终边在x 轴上、y 轴上、坐标轴上的角的集合的表示； （4）与角α终边相同的角的集合的表示； 3、弧度制（1）长度等于半径长的弧所对的圆心角叫做1弧度；（2）半径为r 的圆的圆心角α所对弧的长为l ，则角α的弧度数的绝对值是lrα=；（3）弧度制与角度制的换算公式：2360π=，1180π=，1801()57.3π=≈；（4）若扇形的圆心角为α（弧度制）、半径为r ，则弧长l r α=、周长2C r l =+C 、面积21122S lr r α==；（二）三角函数 1、三角函数定义（1）设α终边上一点(,)P x y 到原点距离是(r r =，则sin y rα=，cos x r α=，tan (0)yx x α=≠；（2）三角函数符号：第一象限全为正，第二象限正弦为正，第三象限正切为正，第四象限余弦为正；2、三角函数线：sin α=MP ，cos α=OM ，tan α=AT ；sin tan x x x <<（限制？）；|sin ||cos |1x x +≥．3、同角三角函数基本关系：（1）22sin cos 1αα+=2222(sin 1cos ,cos 1sin )αααα=-=-； （2）sin tan cos ααα=sin (sin tan cos ,cos )tan αααααα==； 4、诱导公式：奇变偶不变，符号看象限；5、正弦函数、余弦函数、正切函数的图象与性质 （1）图象、五点法； （2）定义域； （3）值域； （4）最值； （5）周期性； （6）奇偶性； （7）对称性； （8）单调性；6、函数sin()(0,0)y x ωϕω=A +A >>的性质（1）平移变换、伸缩变换； （2）基本概念：振幅A 、周期2πωT =、频率12f ωπ==T 、相位x ωϕ+、初相ϕ； （3）最值与单调区间的求解； （三）三角恒等变换1、两角和差的正弦、余弦、正切公式：C αβ±、S αβ±、T αβ±；2、二倍角的正弦、余弦、正切公式、升幂公式、降幂公式；3、半角公式：sin 1cos sintan 2221cos sin ααααααα-=====+； 4、辅助角公式：sin cos )αααϕA +B =+，其中tan ϕB=A； 5、三倍角公式：（1）3sin33sin 4sin 4sin sin()sin()33ππθθθθθθ=-=-+；（2）3cos34cos 3cos 4cos cos()cos()33ππθθθθθθ=-=-+；（3）323tan tan tan3tan tan()tan()13tan 33θθππθθθθθ-==-+-； 6、积化和差与和差化积： （1）积化和差cos()cos()sin sin 2αβαβαβ--+=；cos()cos()cos cos 2αβαβαβ-++=；sin()sin()sin cos 2αβαβαβ-++=；sin()sin()cos sin 2αβαβαβ+--=；（2）和差化积sin sin 2sincos22αβαβαβ+-+=⋅；sin sin 2cossin22αβαβαβ+--=⋅； cos cos 2coscos22αβαβαβ+-+=⋅；cos cos 2sinsin22αβαβαβ+--=-⋅；7、万能公式：22tan2sin 1tan 2ααα=+，221tan 2cos 1tan 2ααα-=+，22tan2tan 1tan 2ααα=-；8、三角变换常用思想方法技巧：（1）常见的角变换：①2α是α的二倍；4α是2α的二倍；α是2α的二倍；2α是4α的二倍； ②()ααβα=+-、2()()()()44ππααβαβαα=++-=+--、()424πππαα+=--等；（2）名称变换：如在三角函数中正余弦是基础，通常化切为弦，变异名为同名； （3）常数代换：如常数“1”的代换变形有221sin cos sin90tan 45αα=+==；（4）幂的变换：次数较高的三角函数式，一般采用降幂处理（常用降幂公式有那些？）；；（5）公式变形：应熟练掌握三角公式的顺用、逆用、变形用； （6）化简运算通常从“角、名、形、幂”四方面入手如：切化弦、化同角、化单角、化同名、高次化低次、无理化有理、特殊值与特殊角互化；（四）解三角形 1、正弦定理及变形公式 （1）2sin sin sin a b cR C===A B ； （2）2sin a R =A ，2sin b R =B ，2sin c R C =； （3）sin 2a R A =，sin 2b R B =，sin 2c C R=；（4）::sin :sin :sin a b c C =A B ； 2、三角形面积公式（1）1111sin sin sin ()22242ABC abc S bc A ab C ac B r a b c R ∆=====++；（2）2S 正△； （3）若12(,)CA a a =，12(,)CB b b =，则2212211(||||)()||2ABC S CA CB CA CB a b a b ∆⋅-⋅=-； 3、余弦定理及变形公式（1）2222cos a b c bc A =+-；2222cos b a c ac B =+-；2222cos c a b bc C =+-；（2）222cos 2b c a A bc +-=；222cos 2a c b B ac +-=；222cos 2a b c C ab+-=；（3）边角关系：22290a b c A >+⇔>︒；22290a b c A =+⇔=︒；22290a b c A <+⇔<︒； （五）三角形的四心与平面向量 1、重心的向量表示（1）重心：三角形三条中线的交点；（2）0GA GB GC ++=⇔G 是ABC ∆的重心； （3）1()3PG PA PB PC =++⇔G 为ABC ∆的重心；（4）()(0)OP OA AB AC λλ=++>⇔点P 的轨迹通过ABC ∆的重心； （5）()(0)||sin ||sin AB ACOP OA AB B AC Cλλ=++>⇔点P 的轨迹通过ABC ∆的重心；（6）若G 是ABC ∆的重心，则13BGC AGC AGB ABC S S S S ∆∆∆∆===；2、内心的向量表示（1）内心：三角形三条内角平分线的交点、内切圆的圆心；（2）0sin sin sin 0a OA b OB c OC A OA B OB C OC ⋅+⋅+⋅=⇔⋅+⋅+⋅=⇔O 是ABC ∆的内心； （3）()(0)||||AB ACOP OA AB AC λλ=++>⇔点P 的轨迹通过ABC ∆的内心； （4）()()()0||||||||||||AB AC BA BC CA CBOA OB OC AB AC BA BC CA CB ⋅-=⋅-=⋅-=⇔O 是ABC ∆的内心； （5）若I 是ABC ∆的内心，则::::BIC AIC AIB S S S a b c ∆∆∆=； 3、垂心的向量表示（1）垂心：三角形三条高的交点；（2）tan tan tan 0HA HB HB HC HC A HA B HB C H HC A ⋅⋅+⋅+=⋅=⋅⋅⇔=⇔H 是ABC ∆的垂心； （3）()(0)||cos ||cos AB ACOP OA AB B AC Cλλ=++>⇔点P 的轨迹通过ABC ∆的垂心；（4）若H 是ABC ∆（非直角三角形）的垂心，则::tan :tan :tan BHC AHC AHB S S S A B C ∆∆∆=；4、外心的向量表示（1）外心：三角形三边垂直平分线的交点、外接圆的圆心；（2）sin 2sin 2sin 20||||||A OA OA B OB C B O C O C O ⋅+⋅+=⋅==⇔⇔O 是ABC ∆的外心； （3）()()()0OA OB AB OB OC BC OC OA CA +⋅=+⋅=+⋅=⇔O 是ABC ∆的外心；（4）1()()(0)2||cos ||cos AB ACOP OB OC AB B AC Cλλ=+++>⇔点P 的轨迹通过ABC ∆的外心； （5）若O 是ABC ∆的外心，则::sin :sin :sin sin 2:sin 2:sin 2BOC AOC AOB S S S BOC AOC AOB A B C ∆∆∆=∠∠∠=； 5、（1）设ABC ∆的外心为O ，则点P 为垂心⇔OH OA OB OC =++；（2）设ABC ∆的外心、重心、垂心分别为O G H 、、，则O G H 、、共线（欧拉线），且2OG GH =； （六）奔驰定理1、已知O 为ABC ∆内一点，则0BOC AOC AOB S OA S OB S OC ∆∆∆⋅+⋅+⋅=，称此结论为平面向量的“奔驰定理”；2、三个定理：设123::::BOC AOC AOB S S S k k k ∆∆∆=（1）定理1：设O 为ABC ∆内一点，则1230k OA k OB k OC ⋅+⋅+⋅=；（2）定理2：设O 为ABC ∆外一点，不妨设A 、O 位于直线BC 同侧，则1230k OA k OB k OC ⋅+⋅+⋅=； （3）定理3：设O 为ABC ∆外一点，不妨设A 、O 位于直线BC 两侧，则1230k OA k OB k OC -⋅+⋅+⋅=； （七）平面几何补充知识1、正三角形：中心（四心合一）、2ABC S ∆=、h =、R 、r =、::3:2:1h R r =；2、直角三角形：2b c ar +-=、射影定理（2AB BD BC =⋅、2AC CD CB =⋅、2AD BD CD =⋅）； 3、内（外）角平分线定理：AB BDAC CD=； 4、切线长定理：切线长相等、圆心与该点连线平分两切线夹角；5、切割线定理：2PT PA PB =⋅；6、相交弦定理：EA EB EC ED ⋅=⋅；7、弦长公式：222()2AB r d -=； 二、考前必看。
回归教材( 三角函数、解三角形、平面向量)
解析
1
2
3
4
5
6
7
8
9
10 11 12
π 3.将函数 y＝sin(2x＋φ)(φ>0)的图象沿 x 轴向左平移8个单位后，得到一个 偶函数的图象，则 φ 的最小值为( 3π A. 4 3π B. 8 ) π D.8
π 解析 将函数 y＝sin(2x＋φ)(φ>0)的图象沿 x 轴向左平移8个单位后， π π 得到一个偶函数 y＝sin[2(x＋8)＋φ]＝sin(2x＋4＋φ)的图象，
第四篇 回归教材，纠错例析，帮你减少高考失分点
3. 三角函数、解三角形、平面向量
栏目索引
1
要点回扣 易错警示
查缺补漏
2
3
要点回扣
1.α终边与θ终边相同(α的终边在θ终边所在的射线上)⇔α＝θ＋2kπ(k∈Z)， 注意：相等的角的终边一定相同，终边相同的角不一定相等.
任意角的三角函数的定义：设 α 是任意一个角，P(x，y)是 α 的终边上的 y 任意一点(异于原点)，它与原点的距离是 r＝ x ＋y >0，那么 sin α＝ r ，
解析 由θ为锐角，有0<cos θ<1. 2 λ＋ 1 2λ＋1 a· b 又∵cos θ＝ ＝ ，∴0< <1 ， 2 2 |a||b| 5× λ ＋1 5× λ ＋1
1 λ>－ ， 2λ＋1>0， 1 2 ∴ 解得 . 2 λ | λ > － 且 λ ≠ 2 ∴ λ 的取值范围是 2 2λ＋1< 5× λ ＋1， λ ≠ 2.
[问题 8]
在△ABC 中，D 是 AB 的中点，E 是 AC 的中点，CD 与 BE 交 )
高中数学回归课本(三角函数)
回归课本(五)三角函数一．考试内容：角的概念的推广.弧度制.任意角的三角函数.单位圆中的三角函数线. 同角三角函数的基本关系式.正弦、余弦的诱导公式.两角和与差的正弦、余弦、正切.二倍角的正弦、余弦、正切. 正弦函数、余弦函数的图像和性质.周期函数.函数sin()y x ωϕ=+的图像.正切函数的图像和性质. 已知三角函数值求角.正弦定理.余弦定理.斜三角形解法.二．考试要求：(1)理解任意角的概念、弧度的意义.能正确地进行弧度与角度的换算.(2)掌握任意角的正弦、余弦、正切的定义.了解余切、正割、余割的定义.掌握同角三角函数的基本关系式.掌握正弦、余弦的诱导公式.了解周期函数与最小正周期的意义.(3)掌握两角和与两角差的正弦、余弦、正切公式.掌握二倍角的正弦、余弦、正切公式.(4)能正确运用三角公式，进行简单三角函数式的化简、求值和恒等式证明. (5)理解正弦函数、余弦函数、正切函数的图像和性质，会用“五点法”画正弦函数、余弦函数和函数y=Asin(鵻+)的简图，理解A, ,的物理意义. (6)会由已知三角函数值求角，并会用符号arcsin x 、arccos x 、arctanx 表示. (7)掌握正弦定理、余弦定理，并能初步运用它们解斜三角 【注意】近年的高考题中，三角函数主要考查基础知识、基本技能、基本方 法，一般都在选择题与填空题中考查，多为容易或中等难度的题目.其中，同角三角函数的 基本公式和诱导公式，三角函数的图像和性质，求三角函数式的值等为考查热点.三．基础知识:1．常见三角不等式 （1）若(0,)2x π∈，则sin tan x x x <<.(2) 若(0,)2x π∈，则1sin cos x x <+≤(3) |sin ||cos |1x x +≥.2.同角三角函数的基本关系式22sin cos 1θθ+=，tan θ=θθcos sin ，tan 1cot θθ⋅=.3.正弦、余弦的诱导公式212(1)sin ,sin ()2(1)s ,nn n co απαα-⎧-⎪+=⎨⎪-⎩212(1)s ,s ()2(1)s i n ,nn co n co απαα+⎧-⎪+=⎨⎪-⎩ 4.和角与差角公式sin()sin cos cos sin αβαβαβ±=±;cos()cos cos sin sin αβαβαβ±= ; tan tan tan ()1tan tan αβαβαβ±±=.22sin()sin()sin sin αβαβαβ+-=-(平方正弦公式); 22cos()cos()cos sin αβαβαβ+-=-. sin cos a b αα+()αϕ+(辅助角ϕ所在象限由点(,)a b 的象限决定,tan b aϕ=).5.二倍角公式sin 2sin cos ααα=.2222cos 2cos sin 2cos 112sin ααααα=-=-=-.22tan tan 21tan ααα=-.6. 三倍角公式3sin 33sin 4sin 4sin sin ()sin ()33ππθθθθθθ=-=-+.3co s 34co s 3co s 4co s co s()co s()33ππθθθθθθ=-=-+.323tan tan tan 3tan tan ()tan ()13tan 33θθππθθθθθ-==-+-.7.三角函数的周期公式 函数sin()y x ωϕ=+，x ∈R 及函数cos()y x ωϕ=+，x ∈R(A,ω,ϕ为常数，且A ≠0，ω＞0)的周期2T πω=；函数t a n()y x ωϕ=+，,x k k Z ππ≠+∈(A,ω,ϕ为常数，且A ≠0，ω＞0)的周期T π=.8.正弦定理2sin sin sin a b c R ABC===.9.余弦定理2222cos a b c bc A =+-;2222cos b c a ca B =+-; 2222cos c a b ab C =+-.10.面积定理 （1）111222a b c S a h b h ch ===（a b c h h h 、、分别表示a 、b 、c 边上的高）.（2）111sin sin sin 222S a b C b c A ca B ===.(3)O A B S ∆=11.三角形内角和定理在△ABC 中，有()A B C C A B ππ++=⇔=-+222C A B π+⇔=-222()C A B π⇔=-+.四．基本方法和数学思想1.三角函数符号规律记忆口诀：一全正，二正弦，三是切，四余弦；2.对于诱导公式，可用“奇变偶不变，符号看象限”概括；3.记住同角三角函数的基本关系，熟练掌握三角函数的定义、图像、性质；4.熟知正弦、余弦、正切的和、差、倍公式，正余弦定理，处理三角形内的三角函数问题勿忘三内角和等于1800，一般用正余弦定理实施边角互化；5.正弦型函数)sin(φω+=x A y 的对称轴为)(2Z k k x ∈-+=ωφππ；对称中心为))(0,(Z k k ∈-ωφπ；类似可得余弦函数型的对称轴和对称中心；6.（1）正弦平方差公式：sin 2A －sin 2B=sin(A+B)sin(A －B);（2）三角形的内切圆半径r=cb a S ABC ++∆2；（3）三角形的外接圆直径2R=;sin sin sin C cB b A a ==五．高考题回顾1.（天津卷）函数),2,0)(sin(R x x A y ∈π<ϕ>ωϕ+ω=的部分图象如图所示，则函数表达式为（ ） （A ）)48sin(4π+π-=x y（B ）)48sin(4π-π=x y （C ）)48sin(4π-π-=x y （D ）)48sin(4π+π=x y2. （江西卷）设函数)(|,3sin |3sin )(x f x x x f 则+=为A ．周期函数，最小正周期为32π B ．周期函数，最小正周期为3πC ．周期函数，数小正周期为π2D ．非周期函数3.（04年天津卷.理9）函数]),0[()26sin(2ππ∈-=x x y为增函数的区间是A. ]3,0[πB. ]127,12[ππC. ]65,3[ππD. ],65[ππ4. （山东卷）已知函数)12cos()12sin(π-π-=x x y，则下列判断正确的是（A ）此函数的最小正周期为π2，其图象的一个对称中心是)0,12(π（B ）此函数的最小正周期为π，其图象的一个对称中心是)0,12(π （C ）此函数的最小正周期为π2，其图象的一个对称中心是)0,6(π（D ）此函数的最小正周期为π，其图象的一个对称中心是)0,6(π5. (天津卷）要得到函数x y c o s 2=的图象，只需将函数)42sin(2π+=x y 的图象上所有的点的(A)横坐标缩短到原来的21倍（纵坐标不变）,再向左平行移动8π个单位长度 (B)横坐标缩短到原来的21倍（纵坐标不变），再向右平行移动4π个单位长度 (C)横坐标伸长到原来的2倍（纵坐标不变），再向左平行移动4π个单位长度 (D)横坐标伸长到原来的2倍（纵坐标不变），再向右平行移动8π个单位长度6. .（江西卷）在△OAB 中，O 为坐标原点，]2,0(),1,(sin ),cos ,1(πθθθ∈B A ，则当△OAB 的面积达最大值时，=θA ．6πB ．4πC ．3πD ．2π7.（全国卷Ⅰ）当2π<<x 时，函数xxx x f 2sin sin82cos 1)(2++=的最小值为 （A ）2（B ）32 （C ）4（D ）348. 锐角三角形的内角A 、B 满足tan A - A2sin 1 = tan B,则有 （A ）sin 2A–cos B = 0 (B)sin 2A + cos B = 0(C)sin 2A – sin B = 0 (D) sin 2A+ sin B = 09. 设02x π≤≤,sin cos x x =-,则(A) 0x π≤≤ (B)744x ππ≤≤(C)544x ππ≤≤(D)322x ππ≤≤10. 若∈<<=+απαααα则),20(tan cos sinA ．)6,0(πB ．)4,6(ππC ．)3,4(ππD ．)2,3(ππ 11. (湖南卷）设函数f (x )的图象与直线x =a ，x =b 及x 轴所围成图形的面积称为函数f (x )在[a ，b]上的面积，已知函数y ＝sinn x 在[0，nπ]上的面积为n2（n ∈N * ），（i ）y ＝sin3x 在[0,32π]上的面积为 ；（ii ）y ＝sin （3x －π）＋1在[3π，34π]上的面积为六.课本中习题归纳一、任意角的三角函数1 已知α是锐角,则2α是 ( )A,第一象限角 B, 第二象限角 C,小于0180的正角 D,不大于直角的正角 2 已知α是钝角,则2α是 ( )A, 第四象限角 B, 第二象限角 C, 第一、三象限角 D, 锐角 3 已知α是第二象限角, 则2α是 ( )A, 第一象限角 B, 第一、三象限角 C, 第二、四象限角 D, 锐角4 设()f x 为偶函数,且(0,1)x ∈时,()2f x x =-+,则列说法正确的是 A,0(0.5)(30)f f < B,0(sin 0.5)(sin 30)f f < C,(sin 1)(cos 1)f f < D,(sin 2)(cos 2)f f >5 角θ为第一或第二象限角的充要条件是 ( )A,sin 0θ> B,|sin |sin θθ= C,cos tan 0θθ> D,θ为锐角或钝角 6 已知4sin =5α,则cos α= ,tan α= ,cot α= ,sec α= ,7 已知8co s 17α=-,则sin =α ,tan α= . 8 已知t a n 3α=,则sin =α , cos α= ,cot α= ,9 下列等式不正确的是 ( )A,co s 1sin 1sin co s αααα+=- B,4222sin sin cos cos 1αααα++=C,2222tan sin tan sin αααα-= D,1sin co s tan1co s sin 2ααααα+-=++10 已知tan 2α=，则sin co s sin co s αααα+- 。
回归课本专题四三角函数与平面向量
回归课本专题四 三角函数与平面向量 第1 页回归课本专题四： 三角函数、平面向量一．三角函数：1.终边相同(2,k k Z βπα=+∈)；弧长公式：||l R α=，扇形面积公式：211||22S lR R α==， 1弧度(1rad)57.3≈.例1：（1）θ是第一象限角，试探究：（1）2θ一定不是第几象限角？（2）3θ是第几象限角？(2)当角,αβ满足什么条件时，有sin sin αβ=？cos cos ?αβ= (3)若α为锐角（单位为弧度），试利用单位圆及三角函数线比较：,sin ,tan ααα之间的大小. (4)设O 为坐标原点，111(,)P x y 和222(,)P x y 为单位圆上两点，且12POP θ∠=，求证：1212cos x x y y θ+=. (5).已知扇形AOB 的周长是6cm ，该扇形的中心角是1弧度，求该扇形的面积.2、函数sin(),(0,0)y A x A ωϕω=+>>①五点法作图；②振幅?相位?初相?周期T=ωπ2,频率?③,k k Z ϕπ=∈时奇函数；,2k k Z πϕπ=+∈时偶函数.例2（1）函数522y sin x π⎛⎫=-⎪⎝⎭的奇偶性是______； （2）已知函数31f (x )ax bsin x (a,b =++为常数），且57f ()=，则5f ()-=______；（3）函数)c o s (s i n c o s2x x x y +=的图象的对称中心和对称轴分别是__________、____________；（4）已知f (x )sin(x )x )θθ=++为偶函数，求θ的值.④变换:1||sin sin()sin()y x y x y x ϕωϕωϕ=−−−−−→=+−−−−−−−→=+横坐标伸缩到原来的倍左或右平移1||sin sin sin()y x y x y x ϕωωωωϕ=−−−−−−−→=−−−−−→=+横坐标伸缩到原来的倍左或右平移||sin()sin()A b y A x y A x b ωϕωϕ−−−−−−−→=+−−−−−→=++纵坐标伸缩到原来的倍上或下平移.例3.把函数sin(2)3y x π=+的图像向右平移6π个单位,所得到的图像的函数的解析表达式为 ,在将图像上的所有点的横坐标变为原来的一半(纵坐标不变),则所得到的图像的函数表达式为 .3、正弦定理:2sin a R A ==B b sin =C c sin ；内切圆半径2ABCS r a b c∆=++；余弦定理：2222cos a b c bc A =+-,bca cb A 2cos 222-+=；111sin sin sin 222S ab C bc A ca B ===例4. 在ABC ∆中,已知cos cos ,a b c B c A -=⋅-⋅则ABC ∆的形状是 . 4、同角基本关系： 例5：已知11tan tan -=-αα，则ααααcos sin cos 3sin +-＝____；2cos sin sin 2++ααα＝_________；5、诱导公式简记:奇变偶不变．．．．．,．符号看象限．．．．．．(注意：公式中始终视．．．α．为锐角．．．)．6、重要公式：两角和与差的三角函数：sin()sin cos cos sin αβαβαβ±=⋅±⋅；cos()cos cos sin sin αβαβαβ±=⋅⋅ ； tan tan tan()1tan tan αβαβαβ±±=⋅ ；二倍角公式：sin 22sin cos ααα=⋅；2222cos 2cos sin 2cos 112sin ααααα=-=-=-；22tan tan 21tan ααα=-； 升、降幂公式：21cos 22cos αα+=；21cos 22sin αα-=；例6.(1)函数25f (x )sin xcos x x =-x R )∈的单调递增区间为___________ ⑵已知ABC ∆中，三内角为,,A B C，满足112,cos cos A C B A C +=+=，求cos 2A C -的值.巧变角：如()()ααββαββ=+-=-+，2()()ααβαβ=++-，2()()αβαβα=+--，22αβαβ++=⋅，()()222αββααβ+=---等， 例6（3）已知2tan()5αβ+=，1tan()44πβ-=，那么tan()4πα+的值是_____；（4）已知,αβ为锐角，sin ,cos x y αβ==，3cos()5αβ+=-，则y 与x 的函数关系为______（5）求证：①1sin 2cos 2tan 1sin 2cos 2θθθθθ+-=++；②sin50(1)1︒⋅+︒=； （6）已知sin sin(2)m βαβ=+，且(),(),122k k k Z k Z m ππαβπα+≠+∈≠∈≠. 求证：1tan()tan 1mmαβα++=-. 7、辅助角公式中辅助角的确定：()sin cos a x b x x θ+=+(其中tan b aθ=)如：（1）当函数23y cos x sin x =-取得最大值时，tan x 的值是______；（2）如果()()sin 2cos()f x x x ϕϕ=+++是奇函数，则tan ϕ= ；二、平面向量：8、向量定义、向量模、零向量、单位向量、相反向量(长度相等方向相反的向量叫做相反向量.回归课本专题四 三角函数与平面向量 第2 页的相反向量是－a .)、共线向量、相等向量注意:不能说向量就是有向线段，为什么？（向量可以平移）9、加、减法的平行四边形与三角形法则:AC BC AB =+;CB AC AB =-,+≤±≤-,10、向量数量积的性质：设两个非零向量，，其夹角为θ，则：①0a b a b ⊥⇔⋅=；②当a ，b 同向时，a ⋅b ＝a b，特别地，22,a a a a a =⋅==当a 与b 反向时，a ⋅b ＝－a b；当θ为锐角时，a ⋅b ＞0，且 a b 、不同向，0a b ⋅>是θ为锐角的必要非充分条件；当θ为钝角时，a ⋅b ＜0，且 a b 、不反向，0a b ⋅<是θ为钝角的必要非充分条件；③||||||a b a b ⋅≤.如（1）已知)2,(λλ=→a ，)2,3(λ=→b ，如果→a 与→b 的夹角为锐角，则λ的取值范围是______；11、向量b 在方向上的投影︱b ︱cos θ12、 →1e 和→2e 是平面一组基底,则该平面任一向量→→→+=2211e e a λλ(21,λλ唯一)特别：＝12OA OB λλ+，则121λλ+=是三点P 、A 、B 共线的充要条件如：平面直角坐标系中，O 为坐标原点，已知两点)1,3(A ,)3,1(-B ,若点C 满足=−→−OC −→−−→−+OB OA 21λλ,其中R ∈21,λλ且121=+λλ,则点C 的轨迹方程是_______13、在ABC ∆中，①1()3PG PA PB PC =++⇔G 为ABC ∆的重心，特别地0PA PB PC P ++=⇔ 为ABC ∆的重心；②PA PB PB PC PC PA P ⋅=⋅=⋅⇔为ABC ∆的垂心；③向量()(0)||||AC AB AB AC λλ+≠所在直线过ABC ∆的内心(是BAC ∠的角平分线所在直线)；如：（1）若O 是ABC 所在平面内一点，且满足2OB OC OB OC OA -=+-，则ABC的形状为____；（2）若D 为ABC ∆的边BC 的中点，ABC ∆所在平面内有一点P ，满足0P A B P C P ++= ，设||||AP PD λ=，则λ的值为___； （3）若点O 是ABC △的外心，且0OA OB CO ++=，则ABC △的内角C 为____；14、重心⎪⎪⎩⎪⎪⎨⎧++=++=.3y y y y ,3x x x x 32132115、点),(y x P 按),(k h a = 平移得),(y x P ''',则PP ' ＝a 或⎩⎨⎧+='+='ky y h x x 函数)(x f y =按),(k h a =平移得函数方程为：)(h x f k y -=-如（1）按向量a 把(2,3)-平移到(1,2)-，则按向量a把点(7,2)-平移到点______；（2）函数x y 2sin =的图象按向量→a 平移后，所得函数的解析式是12cos +=x y ，则→a ＝________（3）设,a b 是两个非零向量，如果()()375a b a b +⊥- ，且()()472a b a b -⊥-，求a b与的夹角.（4）设ABC ∆中，,,AB c BC a CA b ===，且a b b c c a ⋅=⋅=⋅ ，判断ABC ∆的形状.（5）已知向量,,OA OB OC 满足条件0OA OB OC ++= ，且1OA OB OC ===，求证：ABC ∆为正三角形.三、练习：1.（必修4P24.9（2）改编）设1tan 2α=-，则23cos 2sin 21αα=++ . 2.（必修4P24.10）若α可化简为 . 3.（必修4P24.15）已知1sin()64x π+=，则25sin()sin ()63x x -+-= . 4.（必修4P24.3改编）若函数()sin()5f x kx π=+的最小正周期为23π，则k= .5.（必修4P42.2）把函数sin(2)3y x π=+的图像向右平移6π个单位，所得到的图像的解析式为 ，再将图像上的所有点的横坐标变为原来的12倍（纵坐标不变），则所得到的图像的解析式为 .6.（必修4P49.7= .7.（必修4P11.5（2））已知sin cos cos A B Ca b c==，则ABC ∆的形状为 . （必修4P17.10）在ABC ∆中，已知22,sin sin sin a b c A B C =+=，则ABC ∆的形状为 . （必修4P24.2（2））已知sin sin sin cos cos A BC A B+=+,则ABC ∆的形状为 .回归课本专题四 三角函数与平面向量 第3 页8.（必修4P16.例6）AM 是ABC ∆中BC 边上的中线，则AM 可用三边AB,AC,BC 表示为 .9.（必修4P84.例1改编）已知向量,,a b c ，满足0a b c ++= ，且a b 与的夹角为135，c b与的夹角为1202c =，，则a b ⋅= . 10.（必修4P77.11）已知O 为坐标原点，A （3，1），B （-1，3）.若点C 满足OC OA OB αβ=+其中1R αβαβ∈+=，，且，则点C 的轨迹方程为 .11.（必修4P83.10改编）设(,3),(2,1)a x b ==-.①若a b 与的夹角为锐角，则x 的取值范围为 ；②若a b与的夹角为钝角，则x 的取值范围为 ；③当x=4时，a 在b方向上的投影为 .12.（必修4P99.例4）︒︒︒-20cos 20sin 10cos 2= .（必修4P105.4）︒++︒︒︒︒81tan 39tan 240tan 81tan 39tan = ； （必修4P109例4）()︒︒+10tan 3150sin = . （必修4P118.15（2））()()()︒︒︒+++45tan 12tan 11tan 1 = .13. （必修4P117.12改编）24cos 3sin 2++=-m m αα，则m 的取值范围是 . 14. （必修4P115.2改编） ︒︒-15sin 75sin = ；︒︒-15cos 75cos = ；︒︒+15sin 75sin = ；=+︒︒15cos 75cos .（必修4P114.1改编）︒︒15cos 75sin = ；︒︒15cos 75cos = .︒︒15sin 75cos = ；sin ︒75︒15sin = .15.如图，设P,Q 为ABC ∆内的两点，且2155AP AB AC =+ ，2134AQ AB AC =+，则ABP ∆的面积与ABQ ∆的面积之比为.16. （必修4P83.13）已知1,a b a b ==+=则a b a b +- 与 的夹角为 .17. 设P 是椭圆1162522=+y x 上任意一点，A 和F 分别是椭圆的左顶点和右焦点， 则14PA PF PA AF ⋅+⋅的最小值为 .18.在ABC ∆中,︒===60,8,5C b a ,则⋅的值为 .19. O 为平面上的定点，A 、B 、C 是平面上不共线的三点，若( -)·(+-2)=0，则∆ABC 是 三角形.20. O 是平面上一定点,A,B,C 是平面上不共线的三个点,动点P 满足),0[+∞∈++=λλOA OP ,则P 的轨迹一定通过△ABC 的 心.21.已知向量M={ | =(1,2)+λ(3,4) λ∈R}， N={|=(-2,2)+ λ(4,5) λ∈R }，则M ⋂N= . 22. 过△ABC 的重心作一直线分别交AB,AC 于D,E,若x = y =,(0≠xy ),则yx 11+的值为 . 23.要得到函数的图像，x y sin =只需将函数⎪⎭⎫ ⎝⎛-=3cos πx y 的图像 . 24. 已知()()()⎪⎭⎫⎝⎛⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛>⎪⎭⎫ ⎝⎛+=36,36,03sin ππππϖπϖ，在区间且x f f f x x f 有最小值，无最大值，则=ϖ .四、品味经典1. （必修4P117.14）如图，在半径为R ，圆心角为60︒的扇形AB 弧上任取一点P ，作扇形的内接矩形PMNQ,使点Q 在OA 上，点M,N 在OB 上，求这个矩形面积的最大值及相应的AOP ∠的值.MNB回归课本专题四 三角函数与平面向量 第4 页2.已知函数2()4sin sin ()cos242xf x x x π=++ （1）设0ω>为常数，若()y f x ω=在区间2,23ππ⎡⎤-⎢⎥⎣⎦上是增函数，求w 的取值范围 （2）设集合{}2;()263A xx B x f x m ππ⎧⎫=≤≤=-<⎨⎬⎩⎭，若A B ⊆，求实数m 的取值范围.3.在ABC ∆中，角A,B,C 分别对应边为,,,cos a b c b a C =，判断ABC ∆的形状.4. 在ABC ∆中，已知角A 、B 、C 所对的三边分别是,,a b c ,且ac b =2（1）求证：30π≤<B ；（2）求函数BB By cos sin 2sin 1++=的值域.。
高一期末复习回归课本之三角函数、解三角形
回归课本三角函数、解三角形一、填空题：1．（必修4P23习题11）（1）设tan 2a =，则sin cos sin cos a a a a +-=___________.（2）设1tan 2a =-，则221sin sin cos 2cos a a a a--=______.2．（必修4P23习题18）若角θ的终边经过点_____sin )0)(3,4(=≠-θ，则a a a P .3．（必修4P23习题17）已知,416sin(=+πx 则)3(sin )65sin(2x x -+-ππ=_______.4．（必修4P40练习3）把函数)32sin(π+=x y 的图像向右平移6π个单位长度，再将所得图像上的所有点的横坐标变为原来的21倍（纵坐标不变），则所得的图像的函数解析式为___________.5．(必修4P110，例题5)2cos10sin 20cos 20-=________.6.(必修4P121，例题4)sin 50(1)+= ________.7.(必修4P131，习题14)在△ABC 中，已知tan tan tan tan 1A B A B ++=，求角C =____.8.（必修5P11习题5）在△ABC 中，cC b B a A cos cos sin ==，则△ABC 是_____三角形.9.(必修5P15习题5)在△ABC 中，已知()()a b c a b c ac ++-+=，则B =_______.10.(必修5P17习题6)在△ABC 中，已知2cos c a B =，则△ABC 是_______三角形.11.(必修5P17习题10)在△ABC 中，已知C =60°，,BC a AC b ==,且,a b 是方程213400x x x -+=的两个根，则AB 的长为_______.12.(必修5P21习题6)如图，在△ABC 中，已知45B =，D BC 是边上一点，10,14,6AD AC DC ===，则AB 的长为_______.二、解答题：13.(必修5P24习题7)如图，已知∠A 为定角，P ,Q 分别在∠A 的两边上，PQ 为定长.当P ,Q 处于什么位置时，△APQ 的面积最大？14.(必修4P121，习题17)已知函数22sin 2sin cos 3cos ,y x x x x x R =+-∈.（1）求函数的最小正周期；（2）求函数的最大值.15.（必修4P46习题13）如图，摩天轮的半径为40m ，点O 距地面的高度为50m ，摩天轮做匀速转动，每3min 转一圈，摩天轮上点P 的起始位置在最低点处.（1）试确定在时刻t （min ）时点P 距离地面的高度；（2）在摩天轮转动的一圈内，有多长时间点P 距离地面超过70m?16.(必修4P132，习题18)如图，在半径为R 、圆心角为60°的扇形AB 弧上任取一点P ，做扇形的内接矩形PNMQ ，使点Q 在OA 上，点M ,N 在OB 上，求这个矩形面积的最大值及相应的∠AOP 的值.17.(必修5P17习题13)如图，已知圆内接四边形ABCD 中，2,6,4,AB BC AD CD ====如何求四边形ABCD 的面积？18.(必修5P27习题14)如图，已知△ABC 中，5,2AB CD ==∠ABC =45°，∠ACB =60°，求AD 的长.。
高考数学-函数 返璞归真 回归课本(五)
返璞归真回归课本（五）主题：三角函数1.（1）已知1cos()5αβ+=，3cos()5αβ-=，求tan tan αβ的值；（2）已知1cos cos 2αβ+=，1sin sin 3αβ+=，求cos()αβ-的值．【详解】（1） 13cos(),cos()55αβαβ+=-=，∴1cos()cos cos sin sin ,53cos()cos cos sin sin ,5αβαβαβαβαβαβ⎧+=-=⎪⎪⎨⎪-=+=⎪⎩∴1sin sin ,52cos cos ,5αβαβ⎧=⎪⎪⎨⎪=⎪⎩∴1tan tan 2αβ= ．（2）因为1cos cos 2αβ+=，1sin sin 3αβ+=，所以()21cos cos 4αβ+=，()291sin sin αβ+=，上述两式相加得222211cos 2cos cos cos sin 2sin sin sin 94ααββααββ+++++=+即()1322cos 36αβ+-=解得()59cos 72αβ-=-2.证明（1）4cos 44cos 238cos ααα++=；（2）21sin 211tan 2cos sin 222αααα+=++；（3）sin(2)sin 2cos()sin sin αββαβαα+-+=；（4）434cos 2cos 4tan 34cos 2cos 4A AA A A-+=++.【详解】证明：（1）左边22cos 214cos 23αα=-++()()222242cos 22cos 212(cos 21)22cos 8cosααααα=++=+===右边（2）左边2222sin cos 2sin cos (sin cos )sin cos 11tan 2cos 2sin cos 2cos (cos sin )2cos 22αααααααααααααααα++++====+=++右边.（3）左边sin(2)2cos()sin sin αβαβαα+-+=sin[()]2cos()sin sin αβααβαα++-+=sin()cos cos()sin sin sin sin αβααβαβαα+-+===右边（4）左边()()22222cos 22cos 2134cos 22cos 2134cos 22cos 212cos 22cos 21A A A A A A A A -+-+-==++-++()()22242222sin (1cos 2)tan (1cos 2)2cos A A A A A -====+右边.3.已知1sin cos 5αα-=，0απ≤≤，sin 24πα⎛⎫- ⎪⎝⎭的值．【详解】将1sin cos 5αα-=平方得112sin cos 25αα-=，所以242sin cos 25αα=，所以0,2πα⎛⎫∈ ⎪⎝⎭.所以22449(sin cos )12sin cos 12525αααα+=+=+=，从而7sin cos 5αα+=.联立1sin cos 57sin cos 5αααα⎧-=⎪⎪⎨⎪+=⎪⎩，得4sin 53cos 5αα⎧=⎪⎪⎨⎪=⎪⎩.所以24sin 22sin cos 25ααα==，2222347cos 2cos sin 5525ααα⎛⎫⎛⎫=-=-=- ⎪ ⎪⎝⎭⎝⎭.故()22247312sin 2sin 2cos 2422252550πααα⎡⎤⎛⎫⎛⎫-=-=--= ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦.4.已知3cos 45x π⎛⎫+= ⎪⎝⎭，177124x ππ<<，求2sin 22sin 1tan x x x+-的值．【详解】 22sin 22sin 2sin cos 2sin 1tan 1cos x x x x sin x x x x++=--2sin cos (cos sin )cos sin x x x x x x +=-2sin cos sin()4cos()4x x x x ππ+=+3cos()45x π+= ，177124x ππ<<，4sin()45x π∴+=-，72sin cos 25x x ∴=．∴2sin cos sin()28475cos()4x x x x ππ+=-+，∴2sin 22sin 281tan 75x x x +=--．5.已知2sin cos 2sin ,sin cos sin θθαθθβ+==，求证224cos 2cos 2αβ=.【详解】证明：22sin cos 1θθ+= ，2(sin cos )12sin cos θθθθ∴+=+，把sin cos 2sin θθα+=，2sin cos sin θθβ= 代入得：224sin 12sin αβ=+，即224(1cos )12(1cos )αβ-=+-，整理得：224cos 12cos αβ=+．224cos 212cos αβ-=-+．2cos 2cos 2αβ=，两边平方可得：224cos 2cos 2αβ=．6.已知函数44()cos 2sin cos sin f x x x x x =--．（1）求()f x 的最小正周期；（2）当0,2x π⎡⎤∈⎢⎥⎣⎦时，求()f x 的最小值以及取得最小值时x 的集合．【详解】解：（1）44()cos 2sin cos sin f x x x x x =-- ，2222(cos sin )(cos sin )sin 2x x x x x =-+-，cos 2sin 2x x =-，)4x π=+，故()f x 的最小正周期T π=；（2）由[0,]2x π∈可得2[44x ππ+∈，5]4π，当得24x ππ+=即38x π=时，函数取得最小值．所以38x π⎧⎫∈⎨⎩⎭，时()min f x =7.已知函数()sin sin cos 66f x x x x a ππ⎛⎫⎛⎫=++-++ ⎪ ⎪⎝⎭⎝⎭的最大值为1，（1）求常数a 的值；（2）求函数()f x 的单调递减区间；（3）求使()0f x 成立的x 的取值集合.【详解】（1）由题意：函数()sin()sin(cos 66f x x x x a ππ=++-++，化简得：()sin coscos sin sin cos cos sin cos 6666f x x x x x x a ππππ=++-++cos x x a =++2sin()6x a π=++，sin()6x π+ 的最大值为1，()211f x a ∴=⨯+=，解得：1a =-．（2） 由（1）可知()2sin()16f x x π=+-．根据三角函数的性质可得：[262x k πππ+∈+，32]()2k k Z ππ+∈．即322262k x k πππππ+++ ，()k ∈Z 解得：42233k x k ππππ++ ，()k ∈Z ，()f x ∴的单调递减区间为42,2,33k k k ππππ⎡⎤++∈⎢⎥⎣⎦Z ；（3） 由题意：()0f x ，即2sin()106x π+- ，可得：1sin()62x π+ ．522666k x k πππππ∴+++ ，()k ∈Z ．解得：2223k x k πππ+ ．()k ∈Z ()0f x ∴ 成立的x 的取值范围是2|22,3x k x k k πππ⎧⎫+∈⎨⎬⎩⎭Z．8.已知函数2()22cos f x x x m =++在区间0,2π⎡⎤⎢⎥⎣⎦上的最大值为6，（1）求常数m 的值；（2）当x ∈R 时，求函数()f x 的最小值，以及相应x 的集合.【详解】解：2()22cos f x x x m =++21cos 2x x m=+++2sin 216x m π⎛⎫=+++ ⎪⎝⎭，0,2x π⎡⎤∈⎢⎥⎣⎦ ，72,666x πππ⎡⎤∴+∈⎢⎥⎣⎦，1sin 2126x π⎛⎫-+ ⎪⎝⎭ ，所以函数()f x 的最大值为3m +，36m ∴+=，3m =，（2）由（1）得()2sin 246f x x π⎛⎫=++ ⎪⎝⎭，当x ∈R 时，函数()f x 的最小值为2，此时32262x k πππ+=+，解得2()3x k k Z ππ=+∈即2|,3x x k k Z ππ⎧⎫=+∈⎨⎬⎩⎭时取最小值．9.如图正方形ABCD 的边长为1,,P Q 分别为边,AB DA 上的点,当APQ ∆的周长为2时,求PCQ ∠的大小.【详解】设,,PCB QCD αβ∠=∠=则tan ,tan PB DQ αβ==,则1tan ,1tan AP AQ αβ=-=-21tan 1tan PQ αβ=∴=-+-tan tan tan tan αβαβαβ+=∴+=-⋅即tan()1,4παβαβ+=∴+=4PCQ π∴∠=10.已知1sin cos ,(0,)5βββπ+=∈，（1）求tan β的值；（2）你能根据所给的条件，自己构造出一些求值问题吗？【详解】解：（1）将已知等式1sin cos 5ββ+=①，两边平方得：21(sin cos )12sin cos 25ββββ+=+=，即242sin cos 025ββ=-<，249(sin cos )12sin cos 25ββββ∴-=-=，(0,)βπ∈ ，sin 0β∴>，cos 0β<，即sin cos 0ββ->，7sin cos 5ββ∴-=②，联立①②得：4sin 5β=，3cos 5β=-，则sin 4tan cos 3βββ==-；（2）根据所给条件，可求得仅由sin ,cos ,tan βββ表示的三角函数式的值，例如，sin cos sin cos sin ,cos 2,,32tan 3sin 2cos πβββββββββ--⎛⎫+ ⎪+⎝⎭等.如4sin 5β=，3cos 5β=-，229167cos 2cos sin 252525βββ∴=-=-=-．11.如图，已知直线12l l //，A 是12,l l 之间的一定点并且点A 到12,l l 的距离分别为12,h h ，B 是直线2l 上一动点，作AC AB ⊥，且使AC 与直线1l 交于点C.设ABD α∠=.（1）写出ABC 面积S 关于角α的函数解析式()S α.；（2）画出上述函数的图象；（3）由（2）中的图象求()S α的最小值.【详解】解：（1）1AE l ⊥ ，2AD l ⊥，AC AB ⊥，90ABD BAD ∴∠+∠=︒，90CAE BAD ∠+∠=︒，CAE ABD α∴∠=∠=，2sin h AB α∴=，1cos hAC α=，12121()022sin cos sin 22h h h h S AB AC πααααα⎛⎫∴===<< ⎪⎝⎭．（2）作出函数的图象如图：（3）由（2）中图象可知：当4πα=，即22πα=时，()S α取最小值，()S α的最小值为124S h h π⎛⎫= ⎪⎝⎭.12.英国数学家泰勒发现了如下公式：357246sin ,cos 13!5!7!2!4!6!x x x x x x x x x =-+-+=-+-+ ，其中!12345n n =⨯⨯⨯⨯⨯⨯ .这些公式被编入计算工具，计算工具计算足够多的项就可以确保显示值的精确性.比如，用前三项计算cos0.3，就得到240.30.3cos 0.310.95533752!4!≈-+=.试用你的计算工具计算cos0.3，并与上述结果比较.【详解】解：依题意，用前5项计算，即24680.30.30.30.3cos0.312!4!6!8!≈-+-+10.0450.00033750.00000101250.000000001630.95533648≈-+-+≈．与用前三项计算cos0.3的结果比较可以发现，用前5项计算的结果精确度更高，同时可知，当取的项数足够多时，可以达到更高的精确度，甚至达到任意精确度的要求．13.在地球公转过程中，太阳直射点的纬度随时间周而复始不断变化.（1）如图，设地球表面某地正午太阳高度角为,θδ为此时太阳直射点的纬度，ϕ为当地的纬度值，那么这三个量满足90||θϕδ︒=--.某科技小组以某年春分（太阳直射赤道且随后太阳直射点逐渐北移的时间）为初始时间，统计了连续400天太阳直射点的纬度平均值（太阳直射北半球时取正值，太阳直射南半球时取负值）.下面是该科技小组的三处观测站成员在春分后第45天测得的当地太阳高度角数据，请根据数据完成下面的表格（计算结果精确到0.0001）；观测站AB C 观测站所在纬度ϕ/度40.000023.43930.0000观测站正午太阳高度角θ/度66.387082.946473.6141太阳直射点的纬度δ/度太阳直射点的纬度平均值/度（2）设第x 天时太阳直射点的纬度平均值为y ,该科技小组通过对数据的整理和分析，推断y 与x 近似满足函数sin y A x ω=，其中A 为北回归线的纬度值，约为23.4392911，试利用（1）中的数据，估计ω的值（精确到810-）；（3）定义从某年春分到次年春分所经历的时间为一个回归年，求一个回归年对应的天数（精确到00001）；（4）利用（3）的结果，估计每400年中，应设定多少个闰年，可使这400年与400个回归年所含的天数最为接近（精确到1）.【详解】解：（1）由90||θϕδ︒=--，且第观测站AB C 观测站所在纬度ϕ/度40.000023.43930.0000观测站正午太阳高度角θ/度66.387082.946473.6141太阳直射点的纬度δ/度16.387016.385716.3859太阳直射点的纬度平均值/度16.3862（2）在sin y A x ω=中，23.4392911A =，且过点()45,16.386223.4392911sin 4516.3862ω∴=16.3862sin 4523.4392911ω∴=16.386245arcsin0.7574432023.4392911ω∴=≈0.01720280ω∴≈（3）2T πω= 2365.24220.01720280T π∴=≈（4）设应设定x 个闰年，则平年有400x -个，()366365400365.2422400x x +-=⨯解得97x ≈。
三角函数与解三角形---回归教材
§4-1任意角及任意角的三角函数基础练习1．0570- = 弧度，是第___ _象限的角；=π53 度. 2．3tan 2cos 1sin ⋅⋅的结果的符号为 .3．已知角α的终边过点)3,4(-P ,则a sin =_______,a cos =_______,a tan =_______. 4．已知扇形的周长是6cm ，面积是22cm ，则扇形的中心角θ的弧度数是 . 5．若点P 在32π的终边上，且OP=2，则点P 的坐标是（ ， ）. 6．已知角α的终边上一点的坐标为（32cos,32sinππ）,则角α的最小正值为 7．若,cos sin θθ>且,0cos sin <⋅θθ则θ是第 象限的角.8．已知角α的终边上一点的坐标为（－4，3），则ααcos sin 2+的值为 . 9．已知角α的终边上有一点)0)(3,4(≠-t t t A , 求：ααcos sin 2+的值.10. 已知直线21y x =+与圆224x y +=交于点,A B 两点，以x 轴为始边，分别以,OA OB 为终边的角,αβ，则sin() αβ+=§4-2 同角三角函数的基本关系1、 同角三角函数关系的基本关系式：（1）平方关系： （α∈ ）； （2）商数关系： （α≠ ）； 基础练习1．若2cos sin =+θθ，则=θθcos sin .2．已知,51cos =α且0tan <α，则αsin 的值是 . 3．已知1sin cos (0)5αααπ+=-≤≤，则tan α= . 4．已知5sin cos ,sin cos 4αααα-=-⋅=则 . 5. 已知1cos()44πα-=，则sin 2 α= 6．已知,2tan =θ求下列各式的值： (1)θθθθcos 9sin 4cos 3sin 2--； (2) θθcos sin ； （3）2θθθθ22cos 4cos sin 3sin --.§4-3 正弦、余弦的诱导公式基础练习1．（1）sin 2( π3 －x )＋sin 2( π6 ＋x )＝ . （2）化简＋5()()66sin x sin x ππ-=2．已知cos(π＋θ)＝－45 ，θ是第一象限角，则sin （π＋θ）= ， tan θ= .3．若1sin()4πα-=，则=-)2sin(απ . 4．已知32,cos(9)5παπαπ<<-=-，求：αtan 的值． 4．已知32,cos(9)5παπαπ<<-=-，求：αtan 的值． 5．求值 252525sincos tan()634πππ++-= 6．已知角02πα<<，则经过点12(sin ,0),(0,cos )P αP α的直线的倾斜角为7．化简：（1）3sin ()cos(2)tan()απααπ-+--； （2）2tan(360)cos ()sin()ααα+---o .§4- 4 三角函数的图象基础练习1．“五点法”画正弦函数[]sin ,0,2y x x π=∈的简图； 2． 由函数sin y x =的图象到函数2sin(2)23y x π=++的图象的变换方法为；3．函数)92sin(21π-=x y 的振幅是______,；频率是______,,初相是______； 4．用“五点法”画函数3(2)3πy cos x =-的图象； 5．函数)2tan(ϕ+=x y 的图象过点),0,12(π则ϕ 的一个值是 .6．若函数()sin()f x A x ωϕ=+（0,0,02A ωϕπ>><<）的最小值为2-，周期为23π，且它的图象过点(0,，求函数解析式.7．已知函数sin()y A x ωϕ=+（0,||A ϕπ><）的一段图象如下图所示，求函数的解析式．8．解不等式：sin )x x R ≥∈.§4-5 三角函数的性质1. 函数62cos(π+=x y 的周期为______; 2. 函数)43tan(π-=x y 的周期是 ______;3. 函数3sin y x = 的周期为_______. 3．不等式1tan -<x 的解集是 .4. 函数4tan(π+=x y 的对称中心是___________,函数)32sin(π-=x y 的对称轴方程是__________. 5．若)(x f 是奇函数，当0>x 时，,sin )(2x x x f -=则0<x 时，=)(x f . 6. 若函数)sin(3)(ϕω+=x x f 对任意实数x 都有=+)6(x f π),6(x f -π则________)6(=πf .7. 设函数),52sin(2)(ππ+=x x f 若对任意R x ∈，都有)()()(21x f x f x f ≤≤成立，则21x x -的最小值是 .8. 设函数)(),0)(2sin()(x f y x x f =<<-+=ϕπϕ图象的一条对称轴是直线,8π=x)1(求ϕ； )2(求：函数)(x f y =的单调减区间.§4-6 两角和与差的三角函数公式1．sin17cos47sin73cos43鞍-鞍= ； 2．1tan151tan15-?=+?.3．(1tan 26)(1tan19)+?? .4．若tan 3α=，4tan 3β=，则tan()αβ-等于 . 5．sin62cos28cos118sin152鞍-鞍= ； 6.sin15cos15sin15cos15??=??.7．在ABC ∆中,若,135cos ,54cos ==B A 则C cos 的值是 . 8．设71cos =α,1411)cos(-=+βα，)2,0(πα∈，),2(ππβα∈+，求：β.§4-7 二倍角的正弦、余弦、正切公式1. 若0cos 2sin 3=+x x ，则x 2tan = ；2. 若316sin =⎪⎭⎫⎝⎛-απ，则⎪⎭⎫⎝⎛+απ232cos = . 3．求值： 8sincoscoscos48482412ππππ=4．设02x π≤≤,sin cos x x =-，则（ ） A ． 0x π≤≤ B ．744x ππ≤≤C ． 544x ππ≤≤D ．322x ππ≤≤5．33sin 2 ()542ππαα=-<<-已知,，求的值cos α.336.cos(),()cos(2).45224ππππααα 已知， 求的值-=-<<--7．若tan 3θ=，求sin 2cos2θθ-的值.§4-8 三角函数的最值问题基础练习1．函数x x y cos sin 4=在区间[0,π32]上的最大值为 ,最小值为 . 2．函数x x y cos sin +=的最大值为___ ____，最小值为_____ __. 3．函数25sin 25sin 2+-=x x y 的最大值为 ，最小值为 . 4．函数2cos 3cos 21y x x =--的最小值为 . 5．函数xx y cos sin 21++=的最大值是 .6．函数)6cos()3sin(2x x y +--=ππ的最小值为 .7. 求函数)40)(sin (cos sin π<<-=x x x x y 的最大值.8. 已知函数x x x x x x f cos sin sin 3)3sin(cos 2)(2+-+=π，求函数)(x f 的最大、最小值.§5-1正 余弦定理基础练习1. 边长为5,7,8的三角形的最大角与最小角的和是2. 在△ABC 中，::1:2:3A B C =，则::a b c 等于 3．在△ABC 中，若B a b sin 2=，则A 等于4．等腰三角形一腰上的高是3，这条高与底边的夹角为060，则底边长为5. 在△ABC 中，已知a 2=b 2+c 2-bc ，则角A 为6. 在△ABC 中，若=++=A c bc b a 则,222.7. 在△ABC 中，若sin A ∶sin B ∶sin C =7∶8∶13，则C = . 8. 设锐角三角形ABC 的内角A ，B ，C 的对边分别为a ，b ，c ，2sin a b A =. （Ⅰ）求B 的大小；（Ⅱ）若a =5c =，求b ．§5-2、§5-3 利用正、余弦定理解三角形基础练习1．在△ABC 中，若030,6,90===B a C ，则b c -等于2．已知△ABC 中，AB ＝6，∠A ＝30°，∠B ＝120°，则△ABC 的面积为 3. 在△ABC 中，sin A ：sin B ：sin C =3：2：4，则cos C = 4．在△ABC 中， 若A=30°，B=60°， 则=c b a ::5．在△ABC 中，角,A B 均为锐角，且,sin cos B A >则△ABC 是 三角形 6．在△ABC 中，若角B 为钝角，则sin sin B A -的值 零 7. 在△ABC 中，若,3))((bc a c b c b a =-+++则A = 8．在△ABC 中，若AB ＝5，AC ＝5，且cos C ＝109，则BC ＝ . 9．在锐角三角形ABC 中，60C =︒，则B A sin sin 的最大值是_______________. 10．在△ABC 中，若02,30b B ==，0135C =，a =则 . 11. 在△ABC 中，若CcB b A a cos cos cos ==，则△ABC 是 .12. 在△ABC 中，已知2a =，b =，030A =，解三角形.13. 在ABC △中，5cos 13B =-，4cos 5C =． （Ⅰ）求sin A 的值； （Ⅱ）设ABC △的面积332ABC S =△，求BC 的长.14. 在△ABC 中，a ，b ，c 分别是角A ，B ，C 的对边，且cos B cos C ＝－b2a ＋c. (1)求B 的大小；(2)若b ＝13，a ＋c ＝4，求△ABC 的面积．15. △ABC 的内角A ，B ，C 的对边分别为a ，b ，c ，已知a ＝b cos C ＋c sin B . (1)求B ；(2)若b ＝2，求△ABC 面积的最大值．16．在△ABC 中，A ＝3π4，AB ＝6，AC ＝32，点D 在BC 边上，AD ＝BD ，求AD 的长．17. 在△ABC 中，角A ，B ，C 所对的边分别为a ，b ，c ，满足a ＋c b ＝sin A －sin Bsin A －sin C .(1) 求角C ； (2) 求a ＋bc 的取值范围．18．设ABC D 的内角,,A B C 的对边分别为,,a b c ,()()a b c a b c ac ++-+=. （Ⅰ）求角B 的大小；（Ⅱ）若sin sin A C =，求角C 的大小.19. 在ABC D 中，22sin cos 212A BC ++=，且ABCD 外接圆半径2R =. (1) 当角C 的大小；(2) 求ABC D 面积的最大值.20．(12分)设△ABC 的内角A ，B ，C 的对边分别为a ，b ，c ，a ＝b tan A ，且B 为钝角． (1)证明：B －A ＝π2；(2)求sin A ＋sin C 的取值范围．21.设f (x )＝sin x cos x －cos 2()4x π+.(1)求f (x )的单调区间；(2)在锐角△ABC 中，角A ,B ,C 的对边分别为a ，b ，c .若()02Af =，a ＝1，求△ABC 面积的最大值．22.向量(,cos 2),(sin 2,),()a m x b x n f x a b ===函数,且()y f x =的图象过点(12π和点2(,2)3π-. (1)求m ，n 的值；(2)将y ＝f (x )的图象向左平移φ(0＜φ＜π)个单位后得到函数y ＝g (x )的图象，若y ＝g (x )图象上各最高点到点(0，3)的距离的最小值为1，求y ＝g (x )的单调递增区间．。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
回归课本(五)三角函数一．考试内容：角的概念的推广.弧度制.任意角的三角函数.单位圆中的三角函数线. 同角三角函数的基本关系式.正弦、余弦的诱导公式.两角和与差的正弦、余弦、正切.二倍角的正弦、余弦、正切. 正弦函数、余弦函数的图像和性质.周期函数.函数sin()y x ωϕ=+的图像.正切函数的图像和性质. 已知三角函数值求角.正弦定理.余弦定理.斜三角形解法.二．考试要求：(1)理解任意角的概念、弧度的意义.能正确地进行弧度与角度的换算.(2)掌握任意角的正弦、余弦、正切的定义.了解余切、正割、余割的定义.掌握同角三角函数的基本关系式.掌握正弦、余弦的诱导公式.了解周期函数与最小正周期的意义.(3)掌握两角和与两角差的正弦、余弦、正切公式.掌握二倍角的正弦、余弦、正切公式.(4)能正确运用三角公式，进行简单三角函数式的化简、求值和恒等式证明. (5)理解正弦函数、余弦函数、正切函数的图像和性质，会用“五点法”画正弦函数、余弦函数和函数y=Asin(鵻+)的简图，理解A, ,的物理意义. (6)会由已知三角函数值求角，并会用符号arcsin x 、arccos x 、arctanx 表示. (7)掌握正弦定理、余弦定理，并能初步运用它们解斜三角 【注意】近年的高考题中，三角函数主要考查基础知识、基本技能、基本方 法，一般都在选择题与填空题中考查，多为容易或中等难度的题目.其中，同角三角函数的 基本公式和诱导公式，三角函数的图像和性质，求三角函数式的值等为考查热点.三．基础知识:1．常见三角不等式 （1）若(0,)2x π∈，则sin tan x x x <<.(2) 若(0,)2x π∈，则1sin cos x x <+≤(3) |sin ||cos |1x x +≥.2.同角三角函数的基本关系式22sin cos 1θθ+=，tan θ=θθcos sin ，tan 1cot θθ⋅=. 3.正弦、余弦的诱导公式212(1)sin ,sin()2(1)s ,nn n co απαα-⎧-⎪+=⎨⎪-⎩212(1)s ,s()2(1)sin ,n n co n co απαα+⎧-⎪+=⎨⎪-⎩4.和角与差角公式sin()sin cos cos sin αβαβαβ±=±;cos()cos cos sin sin αβαβαβ±=;tan tan tan()1tan tan αβαβαβ±±=.22sin()sin()sin sin αβαβαβ+-=-(平方正弦公式); 22cos()cos()cos sin αβαβαβ+-=-.sin cos a b αα+)αϕ+(辅助角ϕ所在象限由点(,)a b 的象限决定,tan baϕ= ).5.二倍角公式sin 2sin cos ααα=.2222cos 2cos sin 2cos 112sin ααααα=-=-=-.22tan tan 21tan ααα=-. 6. 三倍角公式3sin 33sin 4sin 4sin sin()sin()33ππθθθθθθ=-=-+.3cos34cos 3cos 4cos cos()cos()33ππθθθθθθ=-=-+.323tan tan tan 3tan tan()tan()13tan 33θθππθθθθθ-==-+-. 7.三角函数的周期公式 函数sin()y x ωϕ=+，x ∈R 及函数cos()y x ωϕ=+，x ∈R(A,ω,ϕ为常数，且A ≠0，ω＞0)的周期2T πω=；函数tan()y x ωϕ=+，,x k k Z ππ≠+∈(A,ω,ϕ为常数，且A ≠0，ω＞0)的周期T π=.8.正弦定理2sin sin sin a b cR A B C===. 9.余弦定理2222cos a b c bc A =+-;2222cos b c a ca B =+-; 2222cos c a b ab C =+-.10.面积定理（1）111222a b c S ah bh ch ===（a b c h h h 、、分别表示a 、b 、c 边上的高）. （2）111sin sin sin 222S ab C bc A ca B ===.(3)22(||||)()OAB S OA OB OA OB ∆=⋅-⋅.11.三角形内角和定理在△ABC 中，有()A B C C A B ππ++=⇔=-+222C A Bπ+⇔=-222()C A B π⇔=-+. 四．基本方法和数学思想1.三角函数符号规律记忆口诀：一全正，二正弦，三是切，四余弦；2.对于诱导公式，可用“奇变偶不变，符号看象限”概括；3.记住同角三角函数的基本关系，熟练掌握三角函数的定义、图像、性质；4.熟知正弦、余弦、正切的和、差、倍公式，正余弦定理，处理三角形内的三角函数问题勿忘三内角和等于1800，一般用正余弦定理实施边角互化；5.正弦型函数)sin(φω+=x A y 的对称轴为)(2Z k k x ∈-+=ωφππ；对称中心为))(0,(Z k k ∈-ωφπ；类似可得余弦函数型的对称轴和对称中心； 6.（1）正弦平方差公式：sin 2A －sin 2B=sin(A+B)sin(A －B);（2）三角形的内切圆半径r=cb a S ABC ++∆2；（3）三角形的外接圆直径2R=;sin sin sin CcB b A a ==五．高考题回顾1.（天津卷）函数),2,0)(sin(R x x A y ∈π<ϕ>ωϕ+ω=的部分图象如图所示，则函数表达式为（ ）（A ）)48sin(4π+π-=x y （B ）)48sin(4π-π=x y （C ）)48sin(4π-π-=x y （D ）)48sin(4π+π=x y2. （江西卷）设函数)(|,3sin |3sin )(x f x x x f 则+=为A ．周期函数，最小正周期为32πB ．周期函数，最小正周期为3πC ．周期函数，数小正周期为π2D ．非周期函数3.（04年天津卷.理9）函数]),0[()26sin(2ππ∈-=x x y 为增函数的区间是A. ]3,0[πB. ]127,12[ππC. ]65,3[ππ D. ],65[ππ 4. （山东卷）已知函数)12cos()12sin(π-π-=x x y ，则下列判断正确的是 （A ）此函数的最小正周期为π2，其图象的一个对称中心是)0,12(π（B ）此函数的最小正周期为π，其图象的一个对称中心是)0,12(π（C ）此函数的最小正周期为π2，其图象的一个对称中心是)0,6(π（D ）此函数的最小正周期为π，其图象的一个对称中心是)0,6(π5. (天津卷）要得到函数x y cos 2=的图象，只需将函数)42sin(2π+=x y 的图象上所有的点的(A)横坐标缩短到原来的21倍（纵坐标不变）,再向左平行移动8π个单位长度 (B)横坐标缩短到原来的21倍（纵坐标不变），再向右平行移动4π个单位长度(C)横坐标伸长到原来的2倍（纵坐标不变），再向左平行移动4π个单位长度(D)横坐标伸长到原来的2倍（纵坐标不变），再向右平行移动8π个单位长度6. .（江西卷）在△OAB 中，O 为坐标原点，]2,0(),1,(sin ),cos ,1(πθθθ∈B A ，则当△OAB 的面积达最大值时，=θA ．6πB ．4πC ．3π D ．2π7.（全国卷Ⅰ）当20π<<x 时，函数x x x x f 2sin sin 82cos 1)(2++=的最小值为 （A ）2 （B ）32 （C ）4 （D ）348. 锐角三角形的内角A 、B 满足tan A - A2sin 1= tan B,则有 （A ）sin 2A–cos B = 0 (B)sin 2A + cos B = 0(C)sin 2A – sin B = 0 (D) sin 2A+ sin B = 09. 设02x π≤≤,1sin 2sin cos x x x -=-,则(A) 0x π≤≤ (B) 744x ππ≤≤ (C) 544x ππ≤≤ (D) 322x ππ≤≤10. 若∈<<=+απαααα则),20(tan cos sinA ．)6,0(πB ．)4,6(ππC ．)3,4(ππD ．)2,3(ππ 11. (湖南卷）设函数f (x )的图象与直线x =a ，x =b 及x 轴所围成图形的面积称为函数f (x )在[a ，b]上的面积，已知函数y ＝sinn x 在[0，n π]上的面积为n2（n ∈N *），（i ）y ＝sin3x 在[0,32π]上的面积为 ；（ii ）y ＝sin （3x －π）＋1在[3π，34π]上的面积为六.课本中习题归纳一、任意角的三角函数1 已知α是锐角,则2α是 ( )A,第一象限角 B, 第二象限角 C,小于0180的正角 D,不大于直角的正角 2 已知α是钝角,则2α是 ( ) A, 第四象限角 B, 第二象限角 C, 第一、三象限角 D, 锐角 3 已知α是第二象限角, 则2α是 ( ) A, 第一象限角 B, 第一、三象限角 C, 第二、四象限角 D, 锐角4 设()f x 为偶函数,且(0,1)x ∈时,()2f x x =-+,则列说法正确的是 A,0(0.5)(30)f f < B,0(sin 0.5)(sin 30)f f < C,(sin1)(cos1)f f < D,(sin 2)(cos 2)f f >5 角θ为第一或第二象限角的充要条件是 ( )A,sin 0θ> B,|sin |sin θθ= C,cos tan 0θθ> D,θ为锐角或钝角6 已知4sin =5α,则 cos α= ,tan α= ,cot α= ,sec α= ,7 已知8cosα=-,则sin =α ,tan α= .8 已知tan α=,则sin =α , cos α= , cot α= ,9 下列等式不正确的是 ( )A,cos 1sin 1sin cos αααα+=- B,4222sin sin cos cos 1αααα++= C,2222tan sin tan sin αααα-= D,1sin cos tan 1cos sin 2ααααα+-=++ 10 已知tan 2α=，则sincos sin cos αααα+- 。
11 化简（1= ，（2= 。
12 化简:0sin(2)cos()cos(180)sin(3)sin()2παπαπαπαα-+----=二、两角和与差的正弦、余弦、正切。