基本的生物统计方法与试验设计方法
生物统计学实验设计
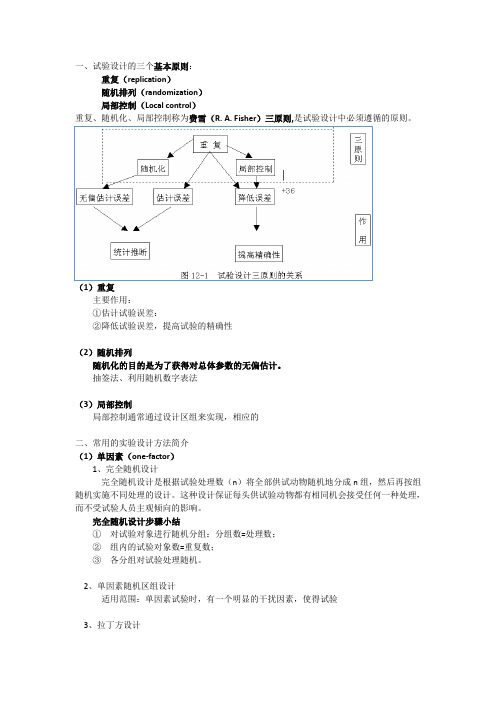
一、试验设计的三个基本原则:
重复(replication)
随机排列(randomization)
局部控制(Local control)
重复、随机化、局部控制称为费雪(R. A. Fisher)三原则,是试验设计中必须遵循的原则。
(1)重复
主要作用:
①估计试验误差:
②降低试验误差,提高试验的精确性
(2)随机排列
随机化的目的是为了获得对总体参数的无偏估计。
抽签法、利用随机数字表法
(3)局部控制
局部控制通常通过设计区组来实现,相应的
二、常用的实验设计方法简介
(1)单因素(one-factor)
1、完全随机设计
完全随机设计是根据试验处理数(n)将全部供试动物随机地分成n组,然后再按组随机实施不同处理的设计。
这种设计保证每头供试验动物都有相同机会接受任何一种处理,而不受试验人员主观倾向的影响。
完全随机设计步骤小结
①对试验对象进行随机分组:分组数=处理数;
②组内的试验对象数=重复数;
③各分组对试验处理随机。
2、单因素随机区组设计
适用范围:单因素试验时,有一个明显的干扰因素,使得试验
3、拉丁方设计
(2)两因素
1、交叉分组设
2、两因素随机区组设计
3、裂区设计
(3)多因素
正交设计。
生物统计与试验设计-试验设计方法

12345 ABCDE1 BCDEA2 CDEAB3 DEABC4 EABCD5
拉丁方设计:是基 于标准拉丁方,进 行一系列行、列和 处理随机化完成的 设计。
拉丁方设计
设计要点: 根据处理数 k 写出一个标准方; 对标准方进行行随机排列; 再进行列向的随机排列。 随机获得处理顺序,并将字母转译。
例 5 处理试验。5个处理分别记为1、2、3、4、5。 处理数k=5。
3.可以将数字依次分配给3种饲料,如表。
完全随机设计
例 一个盆栽试验,2个品种A1和A2,4种短光照B1、B2、 B3和B4,2次重复,共N=8×2=16盆。试设计完全随 机设计。
处理 A1B1 A1B2 A1B3 A1B4
处理 编号
T1
T2
T3
T4
处理 A2B1 A2B2 A2B3 A2B4
处理 编号
随机排列试验设计的分类
随机区组设计
一个方向 局部控制
实行 局部控制
随机排列设计
完全随机设计
不实行 局部控制
完全区组
拉丁方设计
两个方向 局部控制
裂区设计、条区设计
不完全区组
用于 多因素试验
用于 单因素试验
01 完全随机设计 02 随机区组设计 03 拉丁方设计
一、完全随机设计
完全随机设计
设计要点:将试验各处理等概率的随机分配到各供试单元。 1. 将试验单元顺序编号为1、2、3……、N。 2. 获取这N个数字的随机排列。 3. 将N个随机数字顺次分配给各处理,这些数字就是各处理 占有的试验单元。
处理 编号
T1
T2
T3
T4
T5
T6
T7
T8
完全随机设计
生物统计与实验设计

1 [1 (1 u 1)] 1 (1 0.6827) 0.1587 2 2 • 因此正确答案为B。
• 7 、显著性检验中,否定或接受无效假设的依据是 ( )。 • A、中心极限定理 B、小概率原理 原理 D、数学模型 • 解答:正确答案为B • 8 、单因素试验方差分析中 ,试验的总变异就是 ( )的变异。
• 3、t检验、F检验主要应用于数量性状资料 的显著性检验,其理论分布是正态分布;卡 方检验主要应用于质量性状资料的显著性检 验,其理论分布是二项分布或波松分布;
•
t检验主要用于两样本平均数(或一个样 本平均数与总体平均数)间的差异显著性检 验,而F检验主要应用于样本平均数的个数 大于或等于3时的假设检验。
14
C、回归系数
• 解答:正确答案为A、B、C、D
• 4、在下列试验设计方法中,( 部控制原则。 • D、拉丁方设计 • E、随机单位组设计
)应用了局
• A、完全随机设计 B、配对设计 C、非配对设计 解答:根据以上各种试验设计的特点,正确答案为 B、D、E
• 5、下表为某单因素试验四个处理的平均数多重比较 结果,结果表明( )。
)。
• 因此正确答案为C。 • 6、若x~N(10,4),P(x≥12)等于( • A、0.9545 B、0.1587 C、0.0938 D、0.6827 • 解答: x~N(10,4)为一般的正态分布,标准化
8
• 后可得
12 10 P( x 12) P(u ) P(u 1) 2
• 要求:每小题有四个备选答案,从中选出一个正 确答案,并将正确答案的番号填入题干的括号内。 • 举例:
• 1、生物统计中,由样本计算的数称为( 它受抽样变动的影响。
生物统计学与实验设计

生物统计学与实验设计生物统计学是一门研究生物学数据处理和解释的学科,是生物学实验设计和数据分析的重要工具。
合理的实验设计和有效的统计分析可以帮助我们得出可靠的结论和科学的推断。
本文将介绍生物统计学的基本原理和常用方法,以及如何进行合理的实验设计。
一、生物统计学的基本原理生物统计学是应用统计学原理和方法研究生物学数据的科学。
它的基本原理包括以下几个方面:1. 变量类型:生物学实验中通常涉及不同类型的变量,包括定性变量和定量变量。
定性变量是指描述事物属性的变量,如性别、颜色等;定量变量是指可以进行数值计量的变量,如体重、血压等。
2. 数据采集:在生物学实验中,我们需要收集相应的数据来进行分析。
数据采集应该尽量精确、全面和可靠。
采集数据的过程中要严格按照实验设计的要求进行,避免任何干扰因素的影响。
3. 数据整理和清洗:收集到的数据需要进行整理和清洗,包括去除异常值、缺失值的处理等。
数据整理和清洗是保证数据质量和准确性的重要环节。
4. 描述统计分析:描述统计是通过统计指标来描述数据的基本特征。
包括均值、标准差、频数分布等。
描述统计是对数据的第一层次的分析,可以帮助我们对数据有一个直观的认识。
5. 推断统计分析:推断统计是通过样本数据对总体进行推断。
常用的方法包括假设检验、置信区间估计等。
推断统计可以帮助我们从样本数据中得出总体特征的结论。
二、实验设计合理的实验设计是进行科学研究的基础,也是保证实验结果可靠性的重要因素。
一个良好的实验设计应具备以下几个要素:1. 研究目的和假设:明确研究的目的和假设,假设应具备可验证性和明确性。
2. 实验设计:选择适当的实验设计,包括对照组设计、随机分组设计等。
实验设计应遵循科学原理,能够有效控制干扰因素。
3. 样本大小确定:确定合适的样本大小是保证实验结果可靠性的重要环节。
样本大小的确定需要考虑效应大小、显著水平、样本方差等因素。
4. 随机分配:在实验中对实验对象进行随机分配是避免实验结果的偏倚和提高实验效力的重要手段。
「《生物统计附试验设计》教案」

「《生物统计附试验设计》教案」生物统计是生物学的一个重要分支,旨在帮助我们理解和分析生物实验数据。
试验设计是生物统计中的一个重要概念,它指的是和实验相关的一系列决策,包括确定实验的目的、确定实验的因素和水平、随机分配实验单位、以及确定实验的重复次数等等。
本教案将介绍生物统计附试验设计的一些基本概念和方法。
一、教学目标1.了解生物统计在生物学研究中的重要性;2.掌握生物统计附试验设计的基本概念和原则;3.了解一些经典的生物统计附试验设计方法;4.培养学生分析和解读生物实验数据的能力。
二、教学内容1.生物统计的基本原理和方法(200字左右)-介绍生物统计的基本概念和原理,包括总体和样本、统计量和参数、零假设和备择假设等;-介绍生物统计的基本方法,包括描述统计和推断统计。
2.经典的生物统计附试验设计方法(400字左右)-简介完全随机设计、随机区组设计和阻止设计等经典的试验设计方法,包括设计原理和实际应用;-分析和解读生物实验数据的方法,包括方差分析、t检验和卡方检验等。
3.实际案例分析(400字左右)-挑选一些生物学研究中常见的案例,例如药物疗效评价、生长速度比较等;-指导学生对实际数据进行分析和解读,包括数据处理、方差分析和统计推断等。
4.教学方法(100字左右)-以案例教学为主,引导学生主动思考和分析实际问题;-结合实际实验操作,让学生亲自体验生物统计附试验设计的过程;-利用互动教学和小组讨论的方式培养学生的合作和创新能力。
三、教学过程1.生物统计的基本原理和方法(20分钟)-分配教材或电子资料供学生预习;-上课前检查学生对基本概念的理解,并解答疑问;-讲解生物统计的基本原理和方法,引导学生进行思考和讨论。
2.经典的生物统计附试验设计方法(40分钟)-介绍完全随机设计、随机区组设计和阻止设计的原理和应用;-示例实验:设计一个完全随机设计的生物实验,并指导学生进行实际操作;-引导学生对实验结果进行分析和解读,提供帮助和指导。
生物统计-试验设计

一本不错的书:
D.J.格拉斯著, 丛羽生等译. 生命科学实验设计指南.
科学出版社, 2008.
5. 是什么构成了实验问题的合理解释?
实验问题的合理解释(1)
• 对于“天空是什么颜色的”这个问题,运用科学的手段, 能不能找到一个正确、符合事实、又从科学角度可以接受 的答案呢? (1)提出一系列问题,如天空是蓝色的?绿色的?黄色的? 红色的? (2)测量中午时所有可见光的波长。
SSe :试验误差的平方和
SSt=SSA+SSB+SSAB
dfT=dft+dfr+dfe
dft=dfA+dfB+dfAB
二因素随机区组设计试验结果的统计分析(3)
• 各项的方差
s SS / df s SS / df
2 A A 2 B B
A
B
s
2 AB 2 r
SS AB / df
r r
AB
时间进程
• 在时间上进行多次测量叫做时间进程。可以用于了解任何 特定的点上的测量是否具有代表性,以及在不同的条件下 系统是否会发生基础性变化。 • 每5min测量一次。 • 在时间进程实施之前,科学家已对“天空是什么颜色的?” 预言了一个简单的答案。随着时间进程的发展,发现天空 不只是一个颜色;相反,它在时时变化着。因此,科学家 不能仅仅给出一个简单的结论来。而是,需要建立一个适 应这些数据的新模型。
(2)有限的结论:天空在正午是蓝色的。
6. 如何用实验结论来描绘现实?
假设与模型
• 假设与模型的区别 假设先于实验,它仅是一个猜测或推测。相反,模型的建 立是在实验完成之后,因此是以积累的数据为基础的。 • 模型建立是一个基于归纳、联想、从个体到整体对积累的 事实进行理解的过程。
生物统计附试验设计第四版课程设计

生物统计附试验设计第四版课程设计一、课程简介生物统计附试验设计第四版课程设计是一门高等教育课程,旨在帮助学生掌握生物统计分析、实验设计及数据处理等基本技能。
本课程重点介绍生物统计的基本概念、实验设计、统计分析方法和软件应用等内容,并通过实例分析和实验操作掌握实验设计和数据处理的方法。
二、课程目标本课程的主要目标是让学生:•了解生物统计学的基本概念和意义;•熟悉生物实验设计的原则和方法;•掌握生物统计分析的基本方法和软件应用;•能够对生物实验数据进行统计分析和结果解释。
三、课程内容本课程主要包括以下内容:1.生物统计学基础生物统计学的基本概念、生物统计应用领域、概率和假设检验等。
2.生物实验设计生物实验设计原则、生物实验类型、生物实验设计的控制和稳定性分析等。
3.生物统计分析方法t检验、方差分析、卡方检验、回归分析、生存分析等基本方法及其在生物实验中的应用。
4.常用统计软件SPSS、R、Excel等软件的基本操作和分析方法。
5.实验操作与结果解释本课程将通过实验操作,让学生掌握实验设计和数据处理的方法,并学会对实验结果进行统计分析和结果解释。
四、实验设计本课程的实验设计包括以下实验:1.单因素实验设计通过采集不同养分和施肥水平下植物种子的萌发率数据,掌握单因素实验设计、结果分析和生物实验数据处理方法。
2.双因素实验设计通过采集不同肥料类型和施肥方式下植物种子的萌发率和生长速度数据,掌握双因素实验设计、结果分析和生物实验数据处理方法。
五、评分标准本课程的考核主要包括课堂表现、作业评分、实验报告和期末考试。
1.课堂表现(20%)包括出勤、听课和参与课堂讨论等。
2.作业评分(20%)课程中布置的作业,主要包括阅读、计算和分析等。
3.实验报告(30%)课程中操作的实验需要撰写实验报告。
4.期末考试(30%)期末考试主要测试学生对生物统计分析、实验设计及数据处理等的掌握程度。
六、参考资料•《生物统计附试验设计(第四版)》赵光明,张家安,徐瑶,科学出版社。
生物统计附试验设计

第一章绪论1.生物统计学的内容:统计原理、统计方法和试验设计。
2.生物统计的作用:a.科学地整理分析数据;b.判断试验结果的可能性;c.确定事物之间的相互关系;d.提供试验设计的原理。
3.样本容量常记为n,通常把n≤30的样本称为小样本,n.>30的样本称为大样本。
4.名解:(重)①生物统计:生物统计是应用概率论和数据统计的原理和方法来研究生物界数量变化的学科;②总体:是被研究对象的全体,据所含的个体的多少,总体分为有限总体和无限总体。
③样本:是指总体内随机抽取出来若干个体所组成的单位。
④随机误差:由于许多无法控制的内在和外在的偶然因素所造成的误差,内在如个体差异,外在如环境,它影响试验的精确性。
(了)①参数:从总体计算出来的数量特征值,它是一个真值,没有抽样变动的影响,一般用平均数u,标准差s。
②统计量:是从样本计算出来的数量特征值,它是参数的估计值,受样本变动的影响,一般用拉丁字母表示,如平均数。
③系统误差:主要是试验动物的初始条件不同,试验条件相差较大,仪器不准,标准试剂未经校正,药品批次不同,药品用量与种类不符合试验计划要求,以及观察,记录抄案,计算中的错误所引起的误差,它影响试验的准确性。
④准确性:指在试验或调查中某试验指标或形状的观测值与其真值接近的程度。
⑤精确性:指试验或调查中一试验指标或形状的重复观测值彼此接近的程度。
第二章资料的整理1.统计资按性质分为:计量资料、次数资料和半定量资料。
2.计量资料是指用量测方式获得的数量性状资料,即用度、量、衡等计量工具直接测量获得的数量性状资料。
计量资料整理的五步骤如下:(1)求全距,即资料中最大值和最小值之差R=Max(x)—Min(x);(2)确定组数即按样本大小而定;样本含量与组数样本含量组数30~60 6~860~100 8~10100~200 10~12200~500 12~17500以上17~30(3)确定组距,每组最大值与最小值之差记为i ,公式:组距(i)=全距(R)/组数k ;(4)确定组中值及组限,各组的最大值和最小值称为组限,最小值为下限,最大值为上限,每组的中点值称为组中值,组中值=(下限+上限)/2=下限+组距/2=上限-组距/2;(5)归组划线计数,作次数分布表。
