2.雨中行走策略
雨中行走问题模型

数学建模之雨中行走问题模型摘要:由于降雨方向的变化,在跑步过程中尽力快跑不一定是最好的策略。
就淋雨量与跑步快慢这个问题,我们通过建立数学模型来探讨在雨中如何行走才能使淋雨量最少。
在不考虑雨的方向时,当然是跑的越快淋得越少;考虑雨的方向时,那么再分情况讨论,若雨是迎着你前进的方向落下,这时以最大的速度向前跑可使淋雨量最少;若雨是从你的背后落下,那么你应控制在雨中行走的速度,让它刚好等于落雨速度的水平分量。
关键词:淋雨量,数学模型,降雨的方向。
正文1.问题的提出要在雨中从一处沿直线跑到另一处,若雨速为常数且方向不变,试建立数学模型讨论是否跑得越快,淋雨量越少。
将人体简化成一个长方形,高a=1.5(颈部以下),宽b=0.5m,厚c=0.2m,设跑步的距离d=1000m,跑步的最大速度v m=5m/s,雨速u=4m/s,降雨量ω=2cm/h,及跑步速度为v,按以下步骤进行讨论(1)不考虑雨的方向,设降雨淋遍全身,以最大速度跑步估计跑完全程的淋雨量;(2)雨从迎面吹来,雨线与跑步方向在同一平面内,且与人体夹角为 ,问跑步速度v 为多大时可使淋雨量最少。
(3)雨从背面吹来,雨线方向跑步方向在同一平面内,且与人体的夹角为α,如图2.建立总淋雨量与速度v及参数a,b,c,d,u,ω,α之间的关系,问速度v多大,总淋雨量最小。
计算α=30°的总淋雨量.(说明:题目中所涉及的图形为网上提供)2.问题的分析总的淋雨量等于人体的各个面上的淋雨量之和。
每个面上的淋雨量等于单位面积、单位时间的淋雨量与面积以及时间的乘积。
面积由已知各边长乘积得出,时间为总路程与人前行速度的比值。
再由速度分解,合成,相对速度等知识确定各面淋雨量公式,列出总的方程,根据各变量关系,得出最优解。
淋雨量(V )=降雨量(ω)×人体淋雨面积(S )×淋浴时间(t ) ①时间(t )=跑步距离(d )÷人跑步速度(v ) ②由①② 得: 淋雨量(V )=ω×S ×d/v3.合理假设3.1模型的假设(1)人身体的表面非常复杂,为了使问题简单化,假设将人视为一个长方体,并设其高1.5m(颈部以下),宽0.5m,厚0.2m.其前、侧、顶的面积之比为1:b:c, (2)假设降雨量到一定时间时,应为定值; (3)此人在雨中跑步应为直线跑步;(4)、问题中涉及的降雨量应指天空降落到地面的雨,而不是人工,或者流失的水量,因为它可以直观的表示降雨量的多少;(5)设雨速为常速且方向不变,选择适当的空间直角坐标系,使人行走的速度为(u,0,0)设雨的速度为(,,)x y z v v v v =,人行走的距离为d=100米。
微积分的应用雨中行走 药物浓度 水流问题 最速降线

•前表面淋雨量
C2
(v cos
v
u
I )wh(L
/
u)
v cos u I是前面的降雨强度。
v
•总淋雨量(基本模型)
C
C1
C2
wdL [sin
u
h d
(v cos
v
u)]
因为考虑了降雨的方向,淋湿的部位只有顶部和前
面。分两部分计算淋雨量。
取参数v 4m / s, I 2cm / h
第五章 微积分的应用
本章通过用学习过的高等数学知识解决一些简单的问题, 以增加同学们学习数学的兴趣和应用数学的能力。同时,也 通过对其中一些问题的不断深入讨论来体会数学建模没有最 好、只有更好的精神。
1. 雨中行走问题 2. 体内药物浓度的变化 3. 水的流出问题 4. 最速降线问题
1. 雨中行走问题
16
2. 体内药物浓度的变化
医生给病人开处方时必须注明两点:服药的剂量 和服药的时间间隔。超剂量的药物会对患者产生不 良的后果,甚至死亡;剂量不足,则不能达到治疗 的效果。已知患者服药后,随时间推移,药物在体 内被逐渐吸收,发生化学反应,也就是体内药物的 浓度逐渐降低。药物浓度降低的速率与体内当时药 物的浓度成正比。当服药量为A、服药时间间隔为T 时,试分析体内药物的浓度随时间的变化规律。
2)在同样时间内,水从小孔流出的体积为 BS
--- S是从小孔流出的水时在时间段 内流t 经的距离
由质量守恒得
Ah BS
两端同除以 ,t 并令 t取极0 限得
25
可得一阶方程: dh B ds
dt
A dt
由于 ds v, 代入上式得 dt
简单优化模型10雨中行走
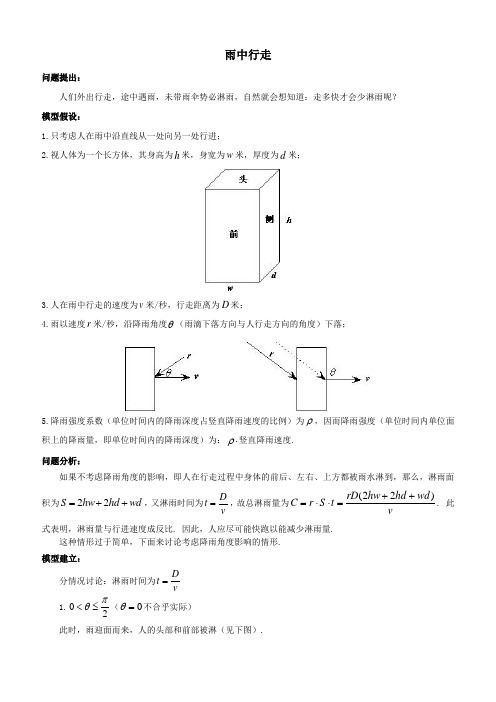
雨中行走问题提出:人们外出行走,途中遇雨,未带雨伞势必淋雨,自然就会想知道:走多快才会少淋雨呢?模型假设:1.只考虑人在雨中沿直线从一处向另一处行进;2.视人体为一个长方体,其身高为h 米,身宽为w 米,厚度为d 米;3.人在雨中行走的速度为v 米/秒,行走距离为D 米;4.雨以速度r 米/秒,沿降雨角度θ(雨滴下落方向与人行走方向的角度)下落;5.降雨强度系数(单位时间内的降雨深度占竖直降雨速度的比例)为ρ,因而降雨强度(单位时间内单位面积上的降雨量,即单位时间内的降雨深度)为:⋅ρ竖直降雨速度.问题分析:如果不考虑降雨角度的影响,即人在行走过程中身体的前后、左右、上方都被雨水淋到,那么,淋雨面积为wd hd hw S ++=22,又淋雨时间为vD t =,故总淋雨量为v wd hd hw rD t S r C )22(++=⋅⋅=. 此式表明,淋雨量与行进速度成反比. 因此,人应尽可能快跑以能减少淋雨量.这种情形过于简单,下面来讨论考虑降雨角度影响的情形.模型建立: 分情况讨论:淋雨时间为v D t =1.20πθ≤<(0=θ不合乎实际)此时,雨迎面而来,人的头部和前部被淋(见下图).头部的淋雨量:头部的面积为dw ,雨在竖直方向上的分速度为θsin r ,降雨强度为θρsin r ⋅,故淋雨量为θρθρsin sin 1dr vwD v D dw r C =⋅⋅=. 前部的淋雨量:前部的面积为wh ,雨在水平方向上的分速度为θcos r ,相对于人的速度为v r +θcos ,降雨强度为)cos (v r +⋅θρ,故淋雨量为)cos ()cos (2v r h vwD v D wh v r C +=⋅⋅+=θρθρ. 于是,总淋雨量为 [])cos (sin )cos (sin 21v r h dr vwD v r h v wD dr v wD C C C ++=++=+=θθρθρθρ. 特别地,当2πθ=(雨竖直下落)时,总淋雨量为)(hv dr vwD C +=ρ. 2.πθπ<<2(πθ=不合乎实际)此时,雨从背后落下,人的头部、后部(或前部)被淋(见下图).v令απθ+=2,则20πα<<.头部的淋雨量:头部的面积为dw ,雨在竖直方向上的分速度为αcos r ,降雨强度为αρcos r ⋅,故淋雨量为αραρcos cos 1dr vwD v D dw r C =⋅⋅=. 水平方向上的淋雨量:后部(或前部)的面积为wh ,雨在水平方向上的分速度为αsin r ,相对于人的速度为|sin |v r -α,降雨强度为|sin |v r -⋅αρ,故淋雨量为|sin ||sin |2v r h vwD v D wh v r C -=⋅⋅-=αραρ. 于是,总淋雨量为 []|sin |cos |sin |cos 21v r h dr v wDv r h v wDdr v wDC C C -+=-+=+=ααραραρ.Case (1):αsin r v ≤此时,人的行进速度不快于雨在水平方向上的分速度(雨从后方赶上人),头部和后部被淋,总淋雨量为[])sin (cos v r h dr v wDC -+=ααρ.特别地,当αsin r v =时,人的行进速度恰好等于雨在水平方向上的分速度(人刚好跟着雨向前走),仅头部被淋,总淋雨量为αρcos dr v wDC =. Case (2):αsin r v >此时,人的行进速度快于雨在水平方向上的分速度(人赶上前方的雨),头部和前部被淋,总淋雨量为[])sin (cos ααρr v h dr v wDC -+=.综上,总淋雨量为[][][]⎪⎪⎪⎩⎪⎪⎪⎨⎧><<-+≤<<-+≤<++=απθπααραπθπααρπθθθρsin ,2,)sin (cos sin ,2,)sin (cos 20,)cos (sin r v r v h dr vwD r v v r h dr vwD v r h dr v wD C 由απθ+=2得[][][]⎪⎪⎪⎩⎪⎪⎪⎨⎧-><<++-≤<<+-≤<++=θπθπθθρθπθπθθρπθθθρcos ,2,)cos (sin cos ,2,)cos (sin 20,)cos (sin r v r v h dr v wD r v v r h dr vwD v r h dr v wD C 即⎪⎪⎪⎩⎪⎪⎪⎨⎧-><<++-≤<<--≤<++=θπθπρθθρθπθπρθθρπθρθθρcos ,2,)cos sin (cos ,2,)cos sin (20,)cos sin ()(r v wDh v h d wDr r v wDh v h d wDr wDh v h d wDr v C 模型求解: 当20πθ≤<和θπθπcos ,2r v -≤<<时,)(v C 均为v 的减函数,故为使)(v C 最小,应使v 尽可能大;当θπθπcos ,2r v -><<时,)(v C 的单调性取决于θθcos sin h d +的正负,应视情况来判断.结论:要使淋雨量最小,(1)若雨迎面而来,则人应以最大可能的速度向前行进;(2)若雨从背后落下,则人应控制行进速度为雨在水平方向上的分速度.模型讨论:如果视人体为一圆柱,如何?。
《雨中行走问题》课件

行人行走的方向
行人行走的速度
雨滴对行人产生的冲击力会影响行人的行走速度和稳定性。
雨滴的冲击力
雨滴的湿度
雨滴的能见度
雨滴的湿度会影响行人的舒适度,进而影响其行走意愿和速度。
雨滴的能见度降低会影响行人的视线和判断力,从而影响其行走安全。
03
02
01
03
CHAPTER
机器学习算法
利用大量的历史数据和实时数据,不断优化和改进系统的行走策略。
数据驱动
适用于数据充足且需要高度智能化的雨中行走问题,如复杂环境、不确定因素等。
适用场景
04
CHAPTER
雨中行走问题的未来研究方向
雨滴对行人的影响
雨滴下落对行人的行走速度、步态和舒适度有何影响?
1
2
3
如何建立一个能够准确描述雨中行走动态过程的数学模型?
在健康和安全领域,研究雨中行走问题可以帮助提高行人的安全意识和行为,减少事故风险。
02
CHAPTER
雨中行走问题的数学模型
雨滴下落的速度取决于风速、重力加速度以及空气阻力等因素。
雨滴下落的速度
雨滴下落的方向与风向、气压等气象条件有关,同时也受到地形、建筑物等因素的影响。
雨滴下落的方向
行人行走的速度取决于其步频、步长以及身体状况等因素。
05
CHAPTER
结论
雨中行走问题涉及到人类日常生活中的实际问题,对解决该问题具有实际意义。
研究雨中行走问题有助于提高人们对于行走行为和环境因素的认知,促进相关领域的发展。
解决雨中行走问题可以为人们提供更加安全、舒适和高效的行走方式,提高生活质量。
通过改进雨具的材料、结构和使用方式,提高雨具的防水性能和舒适度。
雨中行走问题数学模型案例

雨中行走问题数学模型案例
一个常见的数学模型案例是“雨中行走”问题。
在这个问题中,假设有一个人需要从一个地方到另一个地方,但是正在下雨。
人可以以一定的速度行走,但是会因为雨水而放慢速度。
问如何确定最快的路线,使得从起点到终点的时间最短。
为了建立这个数学模型,可以采用以下假设和变量:
1. 假设下雨时,人的行走速度是正常时的百分之多少,这个值称为“减速因子”。
假设减速因子为x%,则雨中行走的速度为正常速度的x%。
2. 假设人在雨中行走时的速度是与雨水的强度相关的。
可以假设速度与雨水强度成正比,即速度v与雨水强度I之间存在关系v = kI (其中k为比例常数)。
3. 假设人在雨中行走的路径是直线。
1
根据上述假设和变量,可以建立以下数学模型:
1. 定义起点和终点的坐标(x1,y1)和(x2,y2)。
2. 定义每个点(x,y)处的雨水强度I。
3. 计算人在一段距离(Δx,Δy)内花费的时间t:t = l / (v * x / 100),其中l是距离,v是速度,x是减速因子。
4. 计算从起点到终点的路线上每个点(x,y)的雨水强度I。
5. 根据模型3计算从起点到终点的每个区间的时间t,并将它们的
和作为总时间T。
6. 通过改变减速因子x,并重新计算总时间T,找到最小的总时间
对应的减速因子x,确定最快的路线。
这样,通过数学模型,可以帮助人们确定在雨中行走时最快的路线。
2。
幼儿园下雨天户外活动方案

幼儿园下雨天户外活动方案一、活动主题。
“雨中的小乐趣”二、活动目标。
1. 让幼儿体验在雨中玩耍的乐趣,培养对自然现象的兴趣。
2. 锻炼幼儿在特殊天气下的适应能力和身体协调性。
3. 通过活动,激发幼儿的观察力、想象力和探索精神。
三、活动时间。
[具体日期],上午[X]点 - [X]点(根据幼儿园作息时间调整)四、活动地点。
幼儿园操场(如果操场排水良好且周边环境安全,若操场不适合可选择有遮雨棚的户外场地)五、活动准备。
1. 雨具准备。
- 为每个幼儿准备适合儿童使用的小雨衣、小雨鞋,确保尺寸合适且质量安全。
- 准备一些大的雨伞,用于教师引导活动和幼儿临时避雨。
2. 活动道具。
- 彩色粉笔若干,用于在湿滑的地面上画画。
- 小水桶若干,幼儿可以收集雨水。
- 一些塑料小动物玩具,让幼儿在水坑里模拟动物的生活场景。
- 自制的小帆船(可以用纸张或塑料片制作),用于在小水洼里航行。
3. 安全准备。
- 提前检查活动场地,清除可能存在的危险因素,如尖锐的石头、破损的排水设施等。
- 准备好急救箱,里面包含常用药品、创可贴、消毒棉球等,以防幼儿滑倒受伤。
六、活动过程。
(一)雨中漫步(10分钟)1. 教师先向幼儿介绍下雨天的特点,如雨滴的声音、雨水的触感等,引起幼儿对雨的兴趣。
2. 教师带领幼儿穿上雨具,在雨中慢慢行走,让幼儿感受雨滴落在雨衣、雨鞋上的声音和感觉,引导幼儿观察雨滴落下形成的小水花。
(二)雨中作画(15分钟)1. 教师将彩色粉笔分给幼儿,鼓励幼儿在操场的地面上(地面有一定积水的地方更好)画画。
2. 引导幼儿发挥想象力,可以画自己喜欢的小动物、花朵或者简单的几何图形。
由于雨水的湿润,粉笔的颜色会更加鲜艳和扩散,幼儿可以感受到与平时不同的作画效果。
(三)雨水收集(15分钟)1. 给每个幼儿发放一个小水桶,让幼儿寻找合适的地方收集雨水。
2. 教师引导幼儿观察雨水的清澈度、颜色等,同时可以提问幼儿,如“雨水是从哪里来的呀?”“雨水可以用来做什么呢?”等,激发幼儿的思考。
雨中行走模型

假设你以6m / s的速度在雨中猛跑,则计算得 C = 11.3 × 10−4 m 3 = 1.13升
-4 6.65 × 10(1.5+(0.4 3+3) ) 2)当 θ = 600时,C= V 结果表明:淋雨量是速度的减函数,当速度尽
可能大时淋雨量达到最小。 假设你以6m / s的速度在雨中猛跑,则计算得 C = 14.7 × 10−4 m 3 = 1.47升
三、模型建立与计算
1、不考虑降雨方向的情况。(你的前后左右和 上方都淋雨) 淋雨面积:S = 2 wh + 2dh + wh(米 2 ) D 雨中行走的时间:t = (秒) V 0.01I 降雨强度:(cm/h)=0.01 I (m / h ) = I ( m / s) 3600
0.01SIt 10DIS 3 (升) 淋雨总量:C= (米 ) = 3600 3600V (模型中 D,I, S为参数,而 V 为变量。) 结论:淋雨量与速度成反比。这也验证 了尽可能快跑能减少淋雨量。 若取D = 1000m,I = 2cm / h, h = 1.5m, w = 0.5m,d = 0.2m,计算 S = 2.2m 2。
你在雨中行走的最大速度v=6米/秒,则计算 得你在雨中行走了167秒,即2分47秒。从而 可以计算被淋的雨水总量为C=2.041升。 经仔细分析,可知你在雨中只跑了2分47秒, 但被淋了2升的雨水,大约有4酒瓶的水量。 这是不可思议的。 表明:用此模型描述雨中行走的淋雨量不符 合实际。
原因是什么呢? 原因是什么呢?
a
= K
2
T
2
a
− Tb = K l
Tb − T d
(1) (2)
Q
'
在雨中应如何行走才能减少淋雨

在雨中应如何行走才能减少淋雨摘要本文通过对人在雨中行走时雨落的四种方式判定怎么行走才能减少淋雨量:(1) 若雨是垂直落下的,应以最大的速度奔跑(2)若人行走的方向是顺风,应以雨速水平分量的速度行走,以便使雨相对于你是垂直下落(3) 若人行走的方向是逆风方向,应以最大的速度向前跑(4) 若人行走的方向是侧边面对雨,应以最大的速度向前跑【关键字】淋雨量行人速度雨速方向奔跑的速度一、问题重述建一模型说明当你在雨中行走又想少淋雨时,应当如下做:(1) 若你行走的方向是顺风且雨的夹角至少为多少,你应以雨速水平分量的速度行走,以便使雨相对于你是垂直下落的(2)在其他情况下,你都应以最快的速度行走二、问题的分析人在雨中行走时可能出现以下四种情形:1、雨垂直下落,人以速度v前行,此时雨只能淋到头上和前面(如图1所示)2、雨背面吹来,雨线与跑步方向在同一平面内,与人的行走速度夹角为θ,此时正面淋不到雨(如图2所示)3、雨从正面吹来,雨线方向与跑步方向在同一平面内,与人的行走速度夹角为θ,此时背面和侧面淋不到雨(如图3所示)4、雨从侧面吹来,雨与跑步的方向不在同一平面,与人行走速度的夹角为θ,此时背面与另一侧面淋不到雨(如图)因为人在雨中前行的时候,人和雨相对地面都是运动的,故知人与雨是相对运动的。
为此我们选择人作为参考系,再考虑雨的相对速度及其与人体方向(即与人体夹角θ)对总淋雨量的影响。
三、基本假设与符号说明1 将人体看成一个长方体。
2 雨速为常数且方向不变,风向与风速不变。
3 降雨量为一定值。
4 人行走的距离是有限的。
四、符号说明:h: 身高b: 厚度a: 宽度r: 雨速Q: 总淋雨量d: 跑步距离v: 跑步速度: 雨与人的夹角s:有效淋雨面积p:雨滴的密度v: 跑步最大速度mI: (cm/h)降雨强度(指单位时间平面上的降下水的厚度 )五、模型的建立与求解1、雨垂直下落,此时人的头部和前面被淋。
淋湿的面积为s=ab+bh(2m)人在雨中行走的时间 t=d/v(s)则淋雨量Q=vbh ab drp )(+结论:由Q=vIsd 知,此时速度越快,淋雨量越少2、雨背面吹来,雨线与跑步方向在同一平面内,与人的速度夹角为θ,若记雨滴下速度为r (米/秒),雨滴的密度为p ,p<=1,则I=rp ,此时的淋雨量为Q=Q1+Q2 顶部的淋雨量Q1=vsin θdabpr背面的淋雨量Q2=vv r dbhp )cos (-θQ=Q1+Q2=vv r h ar dbp ))cos (sin (-+θθ……….(a)(1) 当v<=rcos θ此时对(a )式关于v 求导可得2)cos sin (vhr ar dbp vQ θθ+-=∂∂,可知v 越大,淋雨量Q 越小,又因为v<=rcos θ,故知当v=rcos θ时,Q 最小; (2)当v>=rcos θ即当行走速度快于雨滴的水平速度,你不断地追赶雨滴,雨水将淋湿你的前胸。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
三、模型建立与计算
1、不考虑降雨方向的情况。(你的前后左右和 上方都淋雨) 淋雨面积:S 2 wh 2dh wh(米2 ) D 雨中行走的时间:t (秒) V 0.01I 降雨强度:( I cm/h)=0.01I (m / h ) (m / s) 3600
0.01SIt 10 DIS 3 淋雨总量:C= (米 ) (升) 3600 3600V (模型中D,I,S为参数,而V 为变量。) 结论:淋雨量与速度成反比。这也验证 了尽可能快跑能减少淋雨量。 若取D 1000m,I 2cm / h,h 1.5m, w 0.5m,d 0.2m,计算 S 2.2m 。
2)当d cos r sin 0, v尽可能小时,C才可能小。 而v r sin 时,只有v r sin ,C才可能小。 取v 6m / s, 300时,则淋雨量C=0.77升。 结论:若雨是迎着你前进的方向向你落下,这时 的策略很简单,应以最大的速度向前跑,若雨是 从你的背后落下,你应控制你在雨中的行走速度, 让它刚好等于雨滴速度的水平分量。
0 -4
结果表明:淋雨量是速度的减函数,当速度尽可能 大时淋雨量达到最小。
假设你以6m / s的速度在雨中猛跑,则计算得 C 11.3 10 m 1.13升
3 -4 6.65 10 (1.5+(0.4 3+3) 0 2)当 60 时,C= ) V 结果表明:淋雨量是速度的减函数,当速度尽 4
一、建模准备
建模目标:在给定的降雨条件下,设计一 个雨中行走的策略,使得你被雨水淋湿的 程度最少。 主要因素:淋雨量,降雨的大小,降雨的 方向(风),路程的远近,行走的速度。
二、模型假设及符号说明
1、把人体视为长方体,身高h米,宽度w米, 厚度d米。淋雨总量用C升来记。 2、降雨大小用降雨强度I厘米/时来描述, 降雨强度指单位时间平面上降下雨水的厚度。 在这里可视其为一常量。 3、风速保持不变。 4、你以恒定的速度v米/秒跑完全程D米。
2.雨中行走策略
一个雨天,你有件急事需要从家中到学 校去,学校离家不远,仅一公里,况且事情 紧急,你来不及花时间去翻找雨具,决定碰 一下运气,顶着雨去学校。假设刚刚出发雨 就大了,但你不打算再回去了,一路上,你 将被大雨淋湿。 一个似乎很简单的事情是你应该在雨中 尽可能地快走,以减少雨淋的时间。但如果 考虑到降雨方向的变化,在全部距离上尽力 地快跑是不是最好的策略?试建立数学模型 来探讨如何在雨中行走才能减少淋雨的程度。
原因:不考虑降雨方向的假设,使问题 过于简单化。 2、考虑降雨方向 若记雨滴下落速度为r (m / s ), 雨滴的密度 为p,( p 1), I 表示在一定的时刻在单位体 积的空间内由雨滴所占的空间的比例数, 也称为降雨强度系数,即I rp。
雨滴下落的反方向
d h
w
θ
人前进的方向
因为考虑了降雨的方向,淋雨的部位只有顶部和 前面,分两部分计算淋雨量: Dwdpr sin D 1)顶部的淋雨量C1 ( 表示在雨 v v 中行走的时间,wd 表示顶部面积,r sin 表示雨滴 垂直下落的速度) Dwhp( r cos v ) 2)前表面淋雨量C2 v Dpw(dr sin h( r cos v )) 淋雨总量C=C1 C2 v
Dwdpr cos 2)当v r sin 时,C取最小值C= r sin 4 6.95 10 0.8cos 再次代入数据,得C 4sin 结果表明:当行走速度等于雨滴下落的水平速 特例,若雨滴是以120 的角度落下,即雨滴以
0
度时,淋雨量最小,仅仅被头顶上的雨水淋湿。
可能大时淋雨量达到最小。 假设你以6m / s的速度在雨中猛跑,则计算得 C 14.7 10900 1800 时,雨滴将从后面向你落下。 C=6.95 10 ((0.8sin +6cos)/v+1.5)
-4
令 = +900,则0 900 ,
300的角度从背后落下,你应该以2m / s的速
度行走。
此时,淋雨量为C=0.24升。这意味着你刚 好跟着雨滴前进,前后都没淋雨。 当行走速度快于雨滴的水平运动速度,即
v r sin 时,你不断地追赶雨滴,雨水将 Dpwh(v r sin ) 淋湿你的前胸。淋雨量是C= v d cos r sin h 淋雨总量为C=Dpwr ( ) v v 1)当d cos r sin 0, v尽可能大时,C才可能小。
0 0 -4
0.8sin(90 + )+6cos(90 + ) C=6.95 10 ( +1.5) v =6.95 10-4 ((0.8cos 6sin)/v+1.5)
0
当0 90 时,C可能取负值,这是不可能的。
出现这个矛盾的原因:我们给出的基本模型是针对 雨从你的前面落到你身上的情形,对于这种情况还 需再讨论。 1)当行走的速度慢于雨滴的水平运动速度, 即v r sin ,雨滴将淋在你背上,而淋在背上的雨 Dpwh( r sin v ) 水量是C= v Dpw( dr cos h( r sin v )) 淋雨总量为C v
若取r 4m / s, I 2 3600cm / s, p 1.39 106
4
6.95 10 则C (0.8sin 6cos 1.5v ) v 可以看到:淋雨量与降雨的方向和行走的速度有关。 问题转化为给定,如何选择v,使得C最小。 1)当 90 时,C=6.95 10 (0.8 / v 1.5)
2
你在雨中行走的最大速度v=6米/秒,则计算 得你在雨中行走了167秒,即2分47秒。从而 可以计算被淋的雨水总量为C=2.041升。 经仔细分析,可知你在雨中只跑了2分47秒, 但被淋了2升的雨水,大约有4酒瓶的水量。 这是不可思议的。 表明:用此模型描述雨中行走的淋雨量不符 合实际。
原因是什么呢?
