2014年辽宁省普通高考志愿填报表(新)
2014年沈阳中考填报志愿表格
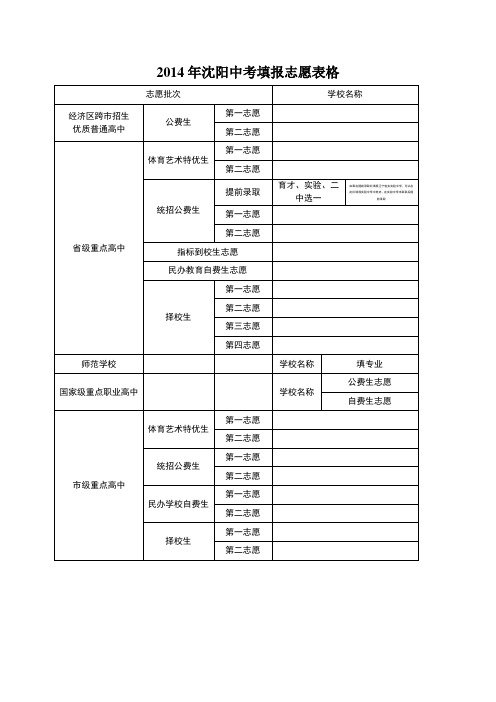
2014年沈阳中考填报志愿表格2014年沈阳市中考考试内容有哪些变化语文、英语、物理、思品四科有调整4月18日,2014年沈阳市中考考试说明新鲜出炉(以下简称中考说明)。
中考说明是学科命题、复习教学的基本依据,每年都会根据课标、教材、教学等实际情况进行合理调整。
今年中考说明都有哪些变化?本报第一时间邀请市教育研究院专家进行权威解读,为考生提供最新、最详尽的考试信息。
各科体例统一调整为五部分第一个变化在体例上。
各学科中考说明体例统一调整为五个部分,即考试性质、命题原则、考试范围及内容要求、考试形式及试卷结构、题型示例。
这种体例的变化更关注与高考考纲说明的对接,更有利于教师、考生和家长对中考说明的阅读和把握。
市教育研究院相关负责人介绍,为了平稳、有序、高效地完成2014年中考命题工作,沈阳市教育研究院对各学科、各层面进行了专项调研,广泛征求意见和建议。
“2014年中考说明”以稳中求变为原则,以《课程标准》为依据,以中高考改革精神为引领,在体例、内容上分别进行了合理调整。
内容调整关注新课程标准的变化和中考改革方案的过渡对比2013年学科考试说明内容,今年数学、化学、历史、俄语、朝语文、汉语文、日语七个学科主体内容没有变化(其中,俄语为小语种考生考试学科,朝语文、汉语文、日语为民族考生考试学科),语文、英语、物理、思想品德四个学科内容有适当调整。
调整内容更关注学科教学的规律,关注学生能力的培养,关注新课程标准的变化,关注中考改革方案的过渡。
语文考查篇目有调整诗文背诵默写及课内文言文阅读的考查篇目有调整。
诗文背诵默写的考查篇目为《语文课程标准》(7—9年级)推荐背诵的50篇优秀诗文及《词两首》(毛泽东)、《乡愁》(余光中)。
文言文课内阅读篇目确定为:鱼我所欲也;生于忧患,死于安乐;曹刿论战;邹忌讽齐王纳谏;出师表;桃花源记:三峡;杂说(四);陋室铭;小石潭记;岳阳楼记;醉翁亭记;爱莲说;记承天寺夜游;送东阳马生序(节选);与朱元思书。
14考生网上录入志愿补充说明

考生网上录入志愿补充说明1)建议考生应下载志愿填报空表,在空表上填好志愿院校及专业编号。
2)登录志愿填报系统,选择报名所在城市,分批次录入院校及专业编号,注意专业服从或不服从一定要选择,否则不能保存。
每批次志愿录入完成后一定要点击‚本次填报(修改)保存‛按钮保存当前志愿信息。
3)艺术类考生专业方向限制,不提示所报专业的专业方向省统考是否通过,只显示该考生艺术省统考合格情况,用来提示考生。
4)艺术特长生、自主招生报名资格在网报系统上不做限制,要求只有通过公示的考生才能报考及录取(东北大学、上海纽约大学综合评价录取志愿除外,填报在自主招生批次)。
5)所有志愿录入完成后,可以点击‚下载当前填报志愿信息‛按钮,下载填报的所有志愿情况表,考生可以离线核对。
发现录入错误或有修改的再登录网报志愿系统进行修改。
6)志愿填报截止时间后,考生可在网报志愿系统上,下载带有加密二维码标识的最终确认的志愿信息表并保存。
重点工作掌握本校未确认志愿考生情况(含首次填报和各批次征集志愿),落实原因,并做好记录备案,填报志愿最后一天上报区招生办。
①考生填报志愿时间如下:(1)6月16日至成绩公布之日,预填报;(2)成绩公布之日至网报系统关闭之日,正式填报。
②考生填报‚征集志愿‛的时间规定如下:(1)7月15日8:00-12:00,填报本科提前批次院校‚征集志愿‛(2)7月20日8:00-12:00,填报本科第一批A段院校‚征集志愿‛(3)7月25日8:00-12:00,填报本科第一批B段院校‚征集志愿‛(4)7月31日8:00-12:00,填报本科第二批院校‚征集志愿‛(5)8月5日8:00-12:00,填报本科第三批院校第一次‚征集志愿‛(6)8月7日8:00-12:00,填报本科第三批院校第二次‚征集志愿‛(7)8月12日8:00-12:00,填报专科(高职)院校第一次‚征集志愿‛(8)8月15日8:00-12:00,填报专科(高职)院校第二次‚征集志愿‛附件:1.高考志愿网报考生须知2.考生填报高考志愿须知的有关政策规定附件1:高考志愿网报考生须知2014年辽宁省普通高考志愿实行网上填报的方式,为顺利完成志愿填报,考生须认真阅读有关高校《招生章程》、《辽宁招生考试》杂志刊登的招生计划、我省有关招生政策和规定,并按照有关要求和规定程序完成高考志愿填报。
辽宁省2011年高考志愿填报表 式样 (1)

考
志
愿
专
科
、
高
职
院
校
1
8
个
平
行
参
考
志
愿
模拟高考志愿填报信息表
考生号
姓名
性别
出生日期
报考科类
毕业中学代码及名称
录取
批次
序号
院校代码及名称
专业代码及名称
服从
志愿
代码
院校名称
专业名称及分数线
专业名称及分数线
专业名称及分数线
专业名称及分数线
提前
本科
1
2
是否愿意录取到其它提前本科院校
提前
专科
1
2
是否愿意录取到其它提前专科院校
第本
设置
代码
院校名称
院校录取线
专业名称及分数
专业名称及分数
专业名称及分数
专业名称及分数
专业名称及分数
专业名称及分数
服从
A
A
一科
批院
录校
取
段
B
C
B
段
A
B
C
第院
二
批
录
取
本பைடு நூலகம்
科校
1
8
个
平
行
参
考
志
愿
设置
代码
院校名称
院校录取线
专业名称及分数
专业名称及分数
专业名称及分数
专业名称及分数
专业名称及分数
专业名称及分数
服从
第院
三
批
录
取
本
科校
1
8
个
平
行
辽宁高校专业大排名
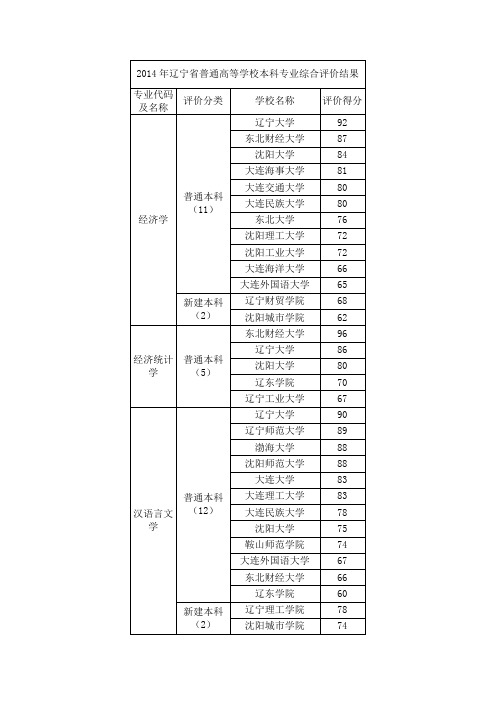
省教育厅将根据本次评价结果,对参评专业布点在5个以上,每种参评专业评价成绩前20%的专业点予以经费支持,促进其进一步加强专业建设,其中,经二次核查、核实确认无效数据总量前20位及存在重复使用教师情况的11个专业点取消奖励资格;对评价成绩后10%,且总分在70分以下的37个专业点的相关高校进行约谈。
对评价成绩在60分以下的13个专业点中的非艺术类专业于2015年起、艺术类专业于2016年起限制招生规模在60人以下。
评分标准评价以学生和教师为重心,选取“生源情况”、“培养模式”、“教学资源”、“本科教学工程”、“教学质量保障”、“培养效果”、“专业特色”等7个有代表性的一级指标,以及“培养模式改革创新”、“在校生综合素质”等14个二级指标,制定通用指标体系框架,并在此基础上,充分考虑不同专业之间的学科特点和同种专业不同院校及其培养类别的特点,研究制定不同院校类别、不同专业种类的38种56个专业评价指标体系,平均每个指标体系有40余个观测点。
3年来,共研制并使用分类分专业的80种133个指标体系开展评价工作。
记者在评价结果中看到,经济统计学专业东北财经大学得分最高,为96分;信息与计算科学专业大连理工大学得分最高,为98分。
多所在连高校的多个专业在评价结果中名列榜首。
高考填报志愿相关信息一、关注度较高的8大工科专业2012年《普通高等学校本科专业目录》一共有专业506种,工学门类专业就有169种,占总数的三分之一。
本次选取的八大工科专业,都是往年受关注度较高、就业率连续三年不低于85%的工科专业。
二、关注度较高的6大艺术类专业这里我们选取了一些报考人数多、开设院校多、受关注度较高的艺术类专业,希望对考生家长选报专业、填报高考志愿有所帮助。
三、毕业人数最多的十个专业根据全国高等学校学生信息咨询与就业指导中心最新的统计数据,2013年国际经济与贸易、法学、汉语言文学等10个普通高校本科专业的毕业生规模最大。
2014年辽宁高考数学理科试卷(带详解)

2014年普通高等学校招生全国统一考试(卷)理科数学第Ⅰ卷(共60分)一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知全集,{|U R A x x ==≤0},{|B x x =≥1},则集合()U A B =U ð( ) A .{|x x ≥0} B .{|x x ≤1} C .{|0x ≤x ≤1} D .{|01}x x <<【测量目标】集合的基本运算. 【考查方式】集合的并集、补集. 【难易程度】容易 【参考答案】D【试题分析】由题意可知,A B U ={|01}x x x ≤或≥,所以()U A B =U ð{|01}x x <<.故选D. 2.设复数z 满足(2i)(2i)5z --=,则z =( ) A .23i + B .23i - C .32i + D .32i - 【测量目标】复数的基本性质和运算.【考查方式】复数的基本运算. 【难易程度】容易 【参考答案】A【试题分析】由(2i)(2i)5z --=,得52i 2iz -=-,故z =23i +.故选A. 3.已知132a -=,21211log ,log 33b c ==,则( ) A .a b c >> B .a c b >> C .c a b >> D .c b a >> 【测量目标】对数的基本运算.【考查方式】对数的大小比较. 【难易程度】容易 【参考答案】C【试题分析】因为13021a -<=<,21log 03b =<,121log 3c =>121log 2c ==1,所以c a b >>.故选C.4.已知m ,n 表示两条不同直线,α表示平面,下列说确的是( ) A .若//,//,m n αα则//m n B .若m α⊥,n α⊂,则m n ⊥ C .若m α⊥,m n ⊥,则//n α D .若//m α,m n ⊥,则n α⊥【测量目标】空间直线与直线,直线与平面的位置关系. 【考查方式】线线平行、垂直,线面平行、垂直的判定. 【难易程度】容易 【参考答案】B【试题分析】由题可知,若//,//,m n αα则m 与n 平行、相交或异面,所以A 错误;若m α⊥,n α⊂,则m n ⊥,故B 正确;若m α⊥,m n ⊥,则//n α或n α⊂,故C 错误.若//m α,m n ⊥,则//n α或n α⊥或n 与α相交,故D 错误.故选B.5.设,,a b c 是非零向量,已知命题P :若0⋅=a b ,0⋅=b c ,则0⋅=a c ;命题q :若//,//a b b c ,则//a c ,则下列命题中真命题是( )A .p q ∨B .p q ∧C .()()p q ⌝⌝∧D .()p q ⌝∨【测量目标】向量的平行与垂直,真假命题的判定. 【考查方式】利用向量之间的位置关系对命题的真假进行判定. 【难易程度】容易 【参考答案】A【试题分析】由向量数量积的几何意义可知,命题p 为假命题;命题q 中,当0≠b 时,,a c 一定共线,故命题q 是真命题.故p q ∨为真命题.故选A.6.6把椅子摆成一排,3人随机就座,任何两人不相邻的做法种数为( ) A .144 B .120 C .72 D .24 【测量目标】排列组合.【考查方式】利用插空法进行排列组合. 【难易程度】容易 【参考答案】D【试题分析】这是一个元素不相邻问题,采用插空法,3334A C 24=.故选D.7.某几何体三视图如图所示,则该几何体的体积为( ) A .82π- B .8π- C .π82-D .π84-第7题图 【测量目标】几何体的体积、三视图.【考查方式】利用三视图对体积的考查. 【难易程度】容易 【参考答案】B【试题分析】根据三视图可知,该几何体是正方体减去两个体积相等的圆柱的一部分(占柱的14)后余下的部分,故该几何体体积为2×2×2-2×14×π×2=8-π.故选B.8.设等差数列{}n a 的公差为d ,若数列1{2}n a a 为递减数列,则( )A .0d <B .0d >C .10a d <D .10a d > 【测量目标】等差数列的基本性质.【考查方式】利用等差数列的性质对首项和公差的正负进行判断. 【难易程度】容易 【参考答案】C 【试题分析】令12n n b a a =,因为数列{}12n a a 为递减数列,所以111111122()212n n n n n nb a a a a a a d b a a +++==-=<,所得10a d <.故选C.9.将函数π3sin(2)3y x =+的图象向右平移π2个单位长度,所得图象对应的函数( ) A .在区间π7π[,]1212上单调递减 B .在区间π7π[,]1212上单调递增 C .在区间ππ[,]63-上单调递减 D .在区间ππ[,]63-上单调递增 【测量目标】三角函数的平移及性质.【考查方式】求正弦型三角函数平移后的单调区间. 【难易程度】容易 【参考答案】B【试题分析】由题可知,将函数π3sin(2)3y x =+的图像向右平移π2个单位长度得到函数2π3sin(2)3y x =-的图像,令π2π2k -+≤2π23x -≤π2π2k +,k ∈Z ,即ππ12k +≤x ≤7ππ12k +,k ∈Z 时,函数单调递增,即函数2π3sin(2)3y x =-的单调递增区间为π7ππ,π1212k k ⎡⎤++⎢⎥⎣⎦,k ∈Z ,可知当0k =时,函数在区间π7π,1212⎡⎤⎢⎥⎣⎦上单调递增.故选B.10.已知点(2,3)A -在抛物线C :22y px =的准线上,过点A 的直线与C 在第一象限相切于点B ,记C 的焦点为F ,则直线BF 的斜率为( ) A .12 B .23 C .34 D .43【测量目标】抛物线的几何性质,直线与抛物线的位置关系.【考查方式】求过抛物线准线并与抛物线相切的直线的斜率. 【难易程度】中等 【参考答案】D【试题分析】因为抛物线C :22y px =的准线为2px =-,且点(2,3)A -在准线上,所以p =4.设直线AB 的方程为2(3)x m y +=-,与抛物线方程28y x =联立得到2824160y my m -++=,由题易知V =0,解得m =12- (舍)或者m =2,这时B 点的坐标为(8,8),而焦点F 的坐标为(2,0),故直线BF 的斜率804823BF k -==-.故选D.11.当[2,1]x ∈-时,不等式3243ax x x -++≥0恒成立,则实数a 的取值围是( ) A .[5,3]-- B .9[6,]8-- C .[6,2]-- D .[4,3]--【测量目标】函数的导函数、单调区间、最值.【考查方式】通过给定函数值的围,利用导函数求函数的单调区间并找出未知量的围. 【难易程度】中等 【参考答案】C【试题分析】当2-≤0x <时,不等式转化为a ≤2343x x x --,令2343()(2x x f x x--=-≤0)x <, 则24489(9)(1)'()x x x x f x x x -++--+==,故()f x 在[-2,-1]上单调递减,在(-1,0)上单调递增,此时有a ≤14321+-=--.当0x =时,()g x 恒成立.当0x <≤1时,a ≥2343x x x --,令2343()(0x x g x x x --=<≤1),则24489(9)(1)'()x x x x g x x x-++--+==, 故()g x 在(0,1]上单调递增,此时有a ≥14361--=-.综上,6-≤a ≤2-.故选C.12.已知定义在[0,1]上的函数()f x 满足: ①(0)(1)0f f ==;②对所有,[0,1]x y ∈,且x y ≠,有1|()()|||2f x f y x y -<-. 若对所有,[0,1]x y ∈,|()()|f x f y k -<,则k 的最小值为( ) A .12 B .14 C .12πD .18【测量目标】函数概念的新定义,不等式的性质.【考查方式】给出新定义的函数,利用给定条件求解未知量的围. 【难易程度】中等 【参考答案】B【试题分析】不妨设0≤y ≤x ≤1.当x y -≤12时,11|()()|||()22f x f y x y x y -<-=-≤14. 12x y ->时,|()()|()(1)(()(0))f x f y f x f f y f -=---≤1()(1)()(0)2f x f f y f -+-< 111110()2224x y x y -+-=--+<.故min 14k =.故选B.第Ⅱ卷(共90分)二、填空题(每题5分,满分20分,将答案填在答题纸上)13.执行右侧的程序框图,若输入9x =,则输出y = .第13题图 【测量目标】程序框图的运算.【考查方式】利用程序框图进行基本运算. 【难易程度】容易 【参考答案】299【试题分析】当9x =时,5y =,则4y x -=;当5x =时,113y =,则43y x -=;当113x =时,299y =,则419y x -=<.故输出299y =.14.正方形的四个顶点(1,1),(1,1),(1,1),(1,1)A B C D ----分别在抛物线2y x =-和2y x =上,如图所示,若将一个质点随机投入正方形ABCD 中,则质点落在阴影区域的概率是 .第14题图 【测量目标】定积分的求解,随机事件的概率.【考查方式】利用定积分求出面积比,进而求出随机事件的概率. 【难易程度】容易 【参考答案】23【试题分析】正方形ABCD 的面积S =2×2=4,阴影部分的面积1231111182(1)d 2()33S x x x x --=-=-=⎰,故质点落在阴影区域的概率82343P ==.15.已知椭圆C :22194x y +=,点M 与C 的焦点不重合,若M 关于C 的焦点的对称点分别为A ,B ,线段MN 的中点在C 上,则||||AN BN += .【测量目标】椭圆的定义及几何性质.【考查方式】椭圆的焦点以及椭圆的几何性质求解相关弧长. 【难易程度】中等 【参考答案】12 【试题分析】取MN 的中点为G ,点G 在椭圆C 上.设点M 关于C 的焦点1F 的对称点为A ,点M 关于C 的焦点2F 的对称点为B ,则有112GF AN =,212GF BN =,所以122()412AN BN GF GF a +=+==.16.对于0c >,当非零实数a ,b 满足224240a ab b c -+-=,且使|2|a b +最大时,345a b c-+的最小值为 .【测量目标】基本不等式的基本应用.【考查方式】利用基本不等式求最值. 【难易程度】较难 【参考答案】-2【试题分析】由题知2222(2)3(43)c a b a b =-+++.221(43)(1)3a b ++≥222(2)43a b a b +⇔+≥23(2)4a b +,即2c ≥25(2)4a b +,当且仅当2243113a b =,即236a b λ==(同号)时, 2a b +240c λ=.223451111(4)288a b c λλλ-+=-=--≥2-, 当且仅当315,,422a b c ===时,345a b c-+取最小值2-.三、解答题 (本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.)17.(本小题满分12分)在△ABC 中,角,,A B C 的对边,,a b c 且a c >,已知2BA BC ⋅=u u u r u u u r ,1cos 3B =,3b =,求:(1)a 和c 的值; (2)cos()B C -的值.【测量目标】两角差的余弦公式、向量的数量积.【考查方式】利用正弦定理和余弦定理解三角形中的边和角. 【难易程度】中等【试题分析】(1)由2BA BC ⋅=u u u r u u u r 得,cos 2c a B ⋅=,又1cos 3B =,所以6ac =.由余弦定理,得2222cos a c b ac B +=+.又3b =,所以2292213ac +=+⨯=.解22613ac a c =⎧⎪⎨+=⎪⎩,得2,33,2a c a c ====或. 因为a c >,3,2a c ∴==. (2)在△ABC中,sin 3B ===由正弦定理,得2sin sin 339c CB b ==⋅=,又因为a b c =>,所以C为锐角,因此7cos 9C ===. 于是cos()cos cos sin sin B C B C B C -=+=1723393927⋅+⋅=. 18. (本小题满分12分)一家面包房根据以往某种面包的销售记录,绘制了日销售量的频率分布直方图,如图所示:第18题图将日销售量落入各组的频率视为概率,并假设每天的销售量相互独立.(1)求在未来连续3天里,有连续2天的日销售量都不低于100个且另一天的日销售量低于50个的概率;(2)用X 表示在未来3天里日销售量不低于100个的天数,求随机变量X 的分布列,期望()E X 及方差()D X .【测量目标】频率分布直方图,随机事件的概率随机变量的期望和方差. 【考查方式】以频率分布直方图为载体计算事件的概率、分布列、期望、方差. 【难易程度】中等 【试题分析】(Ⅰ)设1A 表示事件“日销售量不低于100个”,2A 表示事件“日销售量低于50个”,B 表示事件“在未来连续3天里有连续2天日销售量不低于100个且另一天的日销售量低于50个”.因此1()(0.0060.0040.002)500.6P A =++⨯= , 2()0.003500.15P A =⨯=,()0.60.60.1520.108P B =⨯⨯⨯=.(Ⅱ)X 的可能取值为0,1,2,3.相应的概率为033(0)(10.6)0.064P X C ==⋅-=,123(1)0.6(10.6)0.288P X C ==⋅-=,223(2)0.6(10.6)0.432P X C ==⋅-=,333(3)0.60.216P X C ==⋅=,分布列为X 0 1 2 3 P0.0640.2880.4320.21619. (本小题满分12分)如图,△ABC 和BCD △所在平面互相垂直,且2AB BC BD ===,0120ABC DBC ∠=∠=,E F 、分别为AC 、DC 的中点.(1)求证:EF BC ⊥;(2)求二面角E BF C --的正弦值.第19题图1【测量目标】线线垂直的判定,二面角的正弦值.【考查方式】通过找线、面之间的位置关系,证明线线垂直,求二面角的三角函数值. 【难易程度】中等 【试题分析】(1)证明: (方法一)过E 作EO BC ⊥,垂足为O ,连OF ,第19题图2由△ABC ≌△DBC 可证出△FOC ≌△EOC ,所以π2EOC FOC ∠=∠=,即FO BC ⊥, 又EO BC ⊥,因此BC ⊥平面EFO , 又EF ⊂平面EFO ,所以EF BC ⊥.(方法二)由题意,以B 为坐标原点,在平面DBC 过B 作垂直BC 的直线为x 轴,BC 所在直线为y 轴,在平面ABC 过B 作垂直BC 的直线为z 轴,建立如图所示的空间直角坐标系.第19题图3易得(0,0,0),(0,3)B A -,3,1,0)D -,(0,2,0)C ,因而1331(0,,0)22E F ,所以33((0,2,0)EF BC ==u u u r u u ur ,因此0EF BC ⋅=u u u r u u u r ,从而EF BC ⊥u u u r u u u r ,所以EF BC ⊥.(2)(方法一)在图2中,过O 作OG BF ⊥,垂足为G ,连EG ,由平面ABC ⊥平面BDC ,从而EO ⊥平面BDC ,又OG BF ⊥,由三垂线定理知EG 垂直BF . 因此EGO ∠为二面角E BF C --的平面角; 在△EOC 中,113cos30222EO EC BC ==⋅=o ,由△BGO ∽△BFC知,34BO OG FC BC =⋅=,因此tan 2EOEGO OG∠==,从而sin EGO ∠=255,即二面角E BF C --的正弦值为255. (方法二)在图3中,平面BFC 的一个法向量为1(0,0,1)=n ,设平面BEF 的法向量2(,,)x y z =n ,又3113(,,0),(0,,)22BF BE ==u u u r u u u r ,由220BF BE ⎧⋅=⎪⎨⋅=⎪⎩u u u ru u u r n n 得其中一个2(1,3,1)=-n ,设二面角E BF C --的大小为θ,且由题意知θ为锐角,则121212,cos |cos ,|||||||5θ=<>==⋅n n n n n n ,因sin θ=5=255,即二面角E BF C --的正弦值为255.20. (本小题满分12分)圆224x y +=的切线与x 轴正半轴,y 轴正半轴围成一个三角形,当该三角形面积最小时,切点为P(如图),双曲线22122:1x y C a b-=过点P 且离心率为3.(1)求1C 的方程;(2)椭圆2C 过点P 且与1C 有相同的焦点,直线l 过2C 的右焦点且与2C 交于A ,B 两点,若以线段AB 为直径的圆心过点P ,求l 的方程.第20题图1【测量目标】直线与圆的位置关系,双曲线的标准方程及几何性质,椭圆的几何性质,直线与椭圆的位置关系.【考查方式】利用圆的切线的关系,双曲线的离心率求双曲线方程,通过椭圆与双曲线的的几何性质求解椭圆方程求出直线方程. 【难易程度】较难【试题分析】(1)设切点坐标为0000(,)(0,0)x y x y >>,则切线斜率为0x y -,切线方程为000()x y y x x y -=--,即004x x y y +=,此时,两个坐标轴的正半轴与切线围成的三角形面积为000014482S x y x y =⋅⋅=.由22000042x y x y +=≥知当且仅当00x y =时00x y 有最大值,即S 有最小值,因此点P得坐标为 ,由题意知222222213a ba b a ⎧-=⎪⎨⎪+=⎩解得221,2a b ==,故1C 方程为2212y x -=. (2)由(1)知2C的焦点坐标为(,由此2C 的方程为22221113x y b b +=+,其中10b >.由P 在2C 上,得22112213b b +=+,解得213b =,因此2C 方程为22163x y +=. 显然,l 不是直线0y =.设l的方程为x my =+1122(,),(,)A x y B x y由22163x my x y ⎧=⎪⎨+=⎪⎩得22(2)30m y ++-=,又12,y y 是方程的根,因此122122232y y m y y m ⎧+=-⎪⎪+⎨-⎪=⎪+⎩①②,由1122x my x my ==1212221212122()66()32x x m y y m x x m y y y y m ⎧+=++=⎪⎪⎨-⎪=+++=⎪+⎩③④因1122),)AP x y BP x y ==u u u r u u u r由题意知0AP BP ⋅=u u u r u u u r ,所以12121212))40x x x x y y y y ++++=⑤ ,将①,②,③,④代入⑤式整理得22110m -+=,解得12m =-或12m =-+,因此直线l 的方程为1)0x y --=,或1)0x y +=.21. (本小题满分12分)已知函数8()(cos )(π2)(sin 1)3f x x x x x =-+-+,2()3(π)cos 4(1sin )ln(3)πx g x x x x =--+-. 证明:(1)存在唯一0π(0,)2x ∈,使0()0f x =;(2)存在唯一1π(,π)2x ∈,使1()0g x =,且对(1)中的0x 有01πx x +<. 【测量目标】函数的零点.【考查方式】利用函数导函数的性质求解三角函数中的零点问题. 【难易程度】较难【试题分析】(1)当π(0,)2x ∈时,2'()(1sin )(π2)2cos 03f x x x x x =-++--<,函数()f x 在π(0,)2上为减函数,又28π16(0)π0,()π0323f f =->=--<,所以存在唯一0π(0,)2x ∈,使0()0f x =. (2)考虑函数3(π)cos 2π()4ln(3),[,π]1sin π2x x h x x x x -=--∈+,令πt x =-,则π[,π]2x ∈时,π[0,]2t ∈,记3cos 2()(π)4ln(1)1sin πt t u t h t t t =-=-++,则3()'()(π2)(1sin )f t u t t t =++ , 由(1)得,当0(0,)t x ∈时,'()0u t >,当0π(,)2t x ∈时,'()0u t <.在0(0,)x 上()u t 是增函数,又(0)0u =,从而当0(0,]t x ∈时,()0u t >,所以()u t 在0(0,]x 上无零点.在0π(,)2x 上()u t 是减函数,由0π()0,()4ln 202u x u >=-<,存在唯一的10π(,)2t x ∈ ,使1()0u t =.所以存在唯一的10π(,)2t x ∈使1()0u t =.因此存在唯一的11ππ(,π)2x t =-∈,使111()()()0h x h t u t π=-==.因为当π(,π)2x ∈时,1sin 0x +>,故()(1sin )()g x x h x =+与()h x 有相同的零点,所以存在唯一的1π(,π)2x ∈,使1()0g x =.因1110π,x t t x =->,所以01πx x +<请考生在第22、23、24三题中任选一题作答,如果多做,则按所做的第一题记分,作答时用2B 铅笔在答题卡上把所选题目对应题号下方的方框涂黑.22. (本小题满分10分)选修4-1:几何证明选讲如图,EP 交圆于E 、C 两点,PD 切圆于,D G 为CE 上一点且PG PD =,连接DG 并延长交圆于点A ,作弦AB 垂直EP ,垂足为F . (1)求证:AB 为圆的直径;(2)若AC BD =,求证:AB ED =.第22题图1【测量目标】几何证明选讲.【考查方式】利用圆的性质证明相关结论. 【难易程度】中等 【试题分析】(1)因为PD PG =,所以PDG PGD ∠=∠.由于PD 为切线,故PDA DBA ∠=∠,又由于PGD EGA ∠=∠,故DBA EGA ∠=∠,所以DBA BAD EGA BAD ∠+∠=∠+∠,从而BDA PFA ∠=∠.由于AF 垂直EP ,所以90PFA ∠=o,于是90BDA ∠=o,故AB 是直径. (2)连接BC ,DC .第22题图2由于AB 是直径,故∠BDA =∠ACB =90°,在Rt △BDA 与Rt △ACB 中,AB =BA ,AC =BD , 从而Rt △BDA ≌Rt △ACB ,于是∠DAB =∠CBA .又因为∠DCB =∠DAB ,所以∠DCB =∠CBA ,故DC ∥AB .由于,AB EP ⊥所以,DC EP DCE ⊥∠为直角,于是ED 是直径,由(1)得ED =AB .23. (本小题满分10分)选修4-4:坐标系与参数方程将圆221x y +=上每一点的横坐标保持不变,纵坐标变为原来的2倍,得曲线C . (1)写出C 的参数方程;(2)设直线:220l x y +-=与C 的交点为12,P P ,以坐标原点为极点,x 轴正半轴为极坐标建立极坐标系,求过线段12P P 的中点且与l 垂直的直线的极坐标方程. 【测量目标】坐标系与参数方程.【考查方式】参数方程与极坐标方程转化为普通方程进行求解. 【难易程度】中等【试题分析】(1)设11(,)x y 为圆上的点,在已知变换下位C 上点(x ,y ),依题意,得112x x y y =⎧⎨=⎩ 由22111x y += 得22()12y x +=,即曲线C 的方程为2214y x +=,故C 得参数方程为 cos 2sin x t y t⎧⎨⎩== (t为参数).(2)由2214220y x x y ⎧+=⎪⎨⎪+-=⎩解得10x y =⎧⎨=⎩或02x y =⎧⎨=⎩. 不妨设12(1,0),(0,2)P P ,则线段12P P 的中点坐标为1(,1)2,所求直线的斜率为12k =,于是所求直线方程为111()22y x -=-,化极坐标方程,并整理得 2cos 4sin 3ρθρθ-=-,即34sin 2cos ρθθ=-.24. (本小题满分10分)选修4-5:不等式选讲设函数()2|1|1f x x x =-+-,2()1681g x x x =-+,记()f x ≤1的解集为M ,()g x ≤4的解集为N .(1)求M ;(2)当x M N ∈I 时,证明:22()[()]x f x x f x +≤14. 【测量目标】不等式选讲,集合的简单运算.【考查方式】函数与集合结合证明不等式. 【难易程度】中等 【试题分析】(1)33,[1,)()1,(,1)x x f x x x -∈+∞⎧=⎨-∈-∞⎩当x ≥1时,由()33f x x =-≤1得x ≤43,故1≤x ≤43; 当1x <时,由()1f x x =-≤1得x ≥0,故0≤1x <; 所以()f x ≤1的解集为{|0M x =≤x ≤4}3.(2)由2()1681g x x x =-+≤4得2116()4x -≤4,解得14-≤x ≤34,因此1{|4N x =-≤x ≤3}4,故{|0M N x =I ≤x ≤3}4.当x M N ∈I 时,()1f x x =-,于是22()[()]()[()]x f x x f x xf x x f x +⋅=+211()(1)()42x f x x x x =⋅=-=--≤14.。
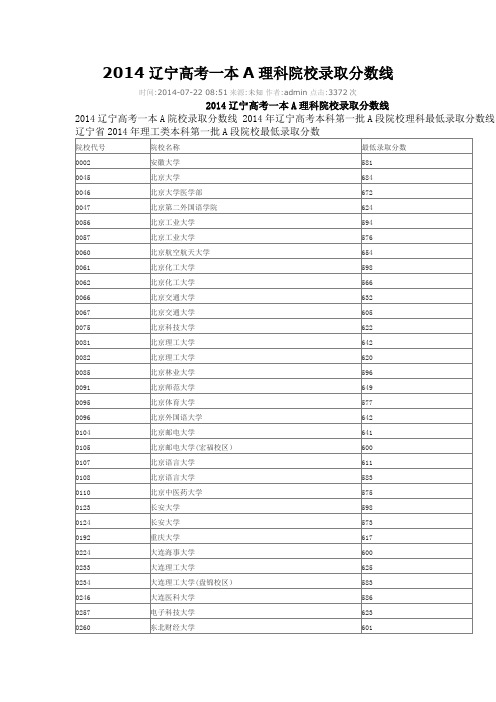
2014辽宁高考一本A理科院校录取分数线
2014辽宁高考一本A理科院校录取分数线
时间:2014-07-22 08:51来源:未知作者:admin 点击:3372次
2014辽宁高考一本A理科院校录取分数线
2014辽宁高考一本A院校录取分数线 2014年辽宁高考本科第一批A段院校理科最低录取分数线
1、分数与本录取最低分相同但未投档的考生,是因为排序分(即考生总分相同时,文科依次按语文、数学、外语单科成绩从高分到低分排序,理科依次按数学、语文、外语单科成绩从高分到低分排序)未达到投档最低排序分;
2、本录取分数不包括保送生、自主招生、艺术特长生、高水平运动员等特殊招生形式;
3、同一院校分列招生代码的均分别公布最低录取分数,包括定向、少数民族预科、民族班、指标到市、联合办学等形式,请在《辽宁省招生考试杂志》所列招生计划中查询对应情况。
2014年辽宁省普通高等学校本科大学生化工设计创业竞赛学生获奖名单名单

王莹 刘莹莹 董金鑫 郭喜超 张雪 王春梅 张鹏寰 高旭 徐黎健 王新建 刘辉 包平 王宝桐 吕雯秀 张乐乐 林山清 蔡陆平 张玉东 李珂 陈晨 李晨榕 施扬威 茹亚霞 兰 兴 侯博谦 黄莹 陈靖伟 付佳 郭锁刚 陆若欣
李博
关珺、何德民、周颖、张述伟
于婧婷 封瑞江、张连红、王海彦、张健 张 强 王璐璐、赵崇峰、李会鹏、封瑞江 赵莹莹 刘红晶 ,赵薇,李素君 周密 王萍 付瑶 何德民、关珺、周颖、郭新闻 黄德智、王大鸷、艾丽梅、谭凤芝 周艳军、齐平、张启俭
李国磊 杨哲(大连工业大学) 艾丽梅,代文双,黄德智,田景丽
张凌烽 宋颖韬、张敏革
孙怀宇、王祝敏、刘东斌、于三三
B-1
张琳琳 曹亚峰、谭凤芝、刘兆丽、李沅
胡婧 蔡景松 曾筱 高策 郭喜军 周立春 王鼎雯 周雪纯 汪磊 王恒 石广强 朱海龙 石博文 牟文庆 丁小东 韩宇 张子鑫 肖扬 张仕强 冯畅 沙慧 原博 蒋芳 朱思尧 沙桐 纵朝阳 邹涵桐 陈英续
三等奖 三等奖 三等奖 三等奖 三等奖 三等奖 三等奖 三等奖 三等奖 三等奖 三等奖 三等奖 三等奖 三等奖 三等奖 三等奖 三等奖 成功参赛奖 成功参赛奖 成功参赛奖 成功参赛奖 成功参赛奖 成功参赛奖 成功参赛奖 成功参赛奖 成功参赛奖 成功参赛奖 成功参赛奖
李震宇 张晓琳、陈理、丁仕强 王冬冬 彭淑静 饶兴未 吴全才、王红梅、刘波、周丽楠 王豪 王景昌、陈理、张晓琳 马成伟 张晓琳, 陈理, 李鸣明 邹湘溢 王卫京 张晓琳 姜宏亚 陈理 欧文琳 陈理,张晓琳 安志刚 李君华、张丹 杨泽清 刘运学 许峰 王丽华 宛彤昕 徐丹 无
名不分先后。
前者获得。
最终得分
I.C.I化工设计 以2,5-二甲基呋喃为原料年产40万吨对二甲苯项目
2014辽宁省高考分数线
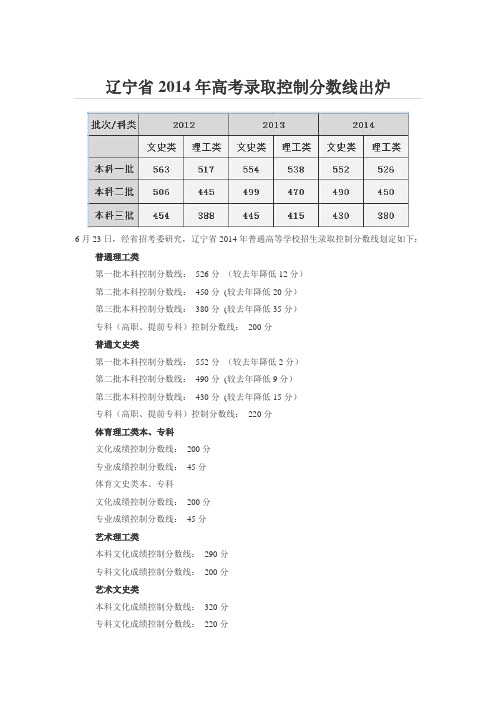
辽宁省2014年高考录取控制分数线出炉
6月23日,经省招考委研究,辽宁省2014年普通高等学校招生录取控制分数线划定如下:普通理工类
第一批本科控制分数线:526分(较去年降低12分)
第二批本科控制分数线:450分(较去年降低20分)
第三批本科控制分数线:380分(较去年降低35分)
专科(高职、提前专科)控制分数线:200分
普通文史类
第一批本科控制分数线:552分(较去年降低2分)
第二批本科控制分数线:490分(较去年降低9分)
第三批本科控制分数线:430分(较去年降低15分)
专科(高职、提前专科)控制分数线:220分
体育理工类本、专科
文化成绩控制分数线:200分
专业成绩控制分数线:45分
体育文史类本、专科
文化成绩控制分数线:200分
专业成绩控制分数线:45分
艺术理工类
本科文化成绩控制分数线:290分
专科文化成绩控制分数线:200分
艺术文史类
本科文化成绩控制分数线:320分
专科文化成绩控制分数线:220分
中职升学(本、专科)
文化基础课控制分数线:80分
专业成绩控制分数线: 85分
附:2013年高考各科类、批次录取控制分数线
文科类:
本科一批554分,本科二批499分,本科三批445分,专科(高职、提前专科)310 分。
理工类:
本科一批538分,本科二批470分;本科三批415分,专科(高职、提前专科)260分。
