高中数学复习课教案新人教版选修22
人教版高中数学含绝对值的不等式教案
人教版高中数学含绝对值的不等式教案一、教学目标1. 知识与技能：（1）理解绝对值不等式的概念；（2）掌握绝对值不等式的解法；（3）能够运用绝对值不等式解决实际问题。
2. 过程与方法：（1）通过实例引导学生认识绝对值不等式；（2）利用数轴分析绝对值不等式的解集；（3）运用转化思想解决含绝对值的不等式问题。
3. 情感态度与价值观：（1）培养学生对数学的兴趣；（2）培养学生勇于探索、积极思考的科学精神；（3）提高学生解决实际问题的能力。
二、教学重点与难点1. 教学重点：（1）绝对值不等式的概念；（2）绝对值不等式的解法；（3）含绝对值的不等式在实际问题中的应用。
2. 教学难点：（1）绝对值不等式的转化；（2）含绝对值的不等式求解过程中的分类讨论。
三、教学过程1. 导入：（1）利用实例引入绝对值不等式的概念；（2）引导学生思考绝对值不等式与普通不等式的区别。
2. 新课讲解：（1）讲解绝对值不等式的定义；（2）通过数轴分析绝对值不等式的解集；（3）介绍绝对值不等式的解法。
3. 案例分析：（1）分析实际问题中的绝对值不等式；（2）引导学生运用转化思想解决含绝对值的不等式问题。
四、课后作业1. 复习本节课所学内容，整理笔记；2. 完成课后练习，巩固知识点；3. 挑选几个实际问题，尝试运用绝对值不等式解决。
五、教学评价1. 课堂表现：观察学生在课堂上的参与程度、提问回答等情况，了解学生的学习状态；2. 课后作业：检查学生的作业完成情况，评估学生对知识的掌握程度；3. 单元测试：进行单元测试，了解学生对含绝对值的不等式知识的运用能力。
六、教学内容与方法1. 教学内容：（1）进一步探究绝对值不等式的性质；（2）学习绝对值不等式的证明方法；（3）解决生活中的实际问题，运用绝对值不等式。
2. 教学方法：（1）采用案例分析法，让学生通过具体例子理解绝对值不等式的性质；（2）运用数形结合法，引导学生利用数轴分析绝对值不等式的解集；（3）采用问题驱动法，激发学生思考，培养学生解决实际问题的能力。
高中数学复习课教学设计
高中数学复习课教学设计一、教学任务及对象1、教学任务本节课的教学任务为高中数学复习课，旨在帮助学生巩固数学基础知识，提高解题能力，培养逻辑思维和抽象思维能力。
通过复习，使学生能够熟练掌握数学公式、定理及解题方法，形成知识体系，为高考数学考试做好充分准备。
2、教学对象本节课的教学对象为高中二年级的学生，他们在之前的学习中已经接触过相关数学知识，具备一定的数学基础。
但由于个体差异，部分学生对某些知识点掌握不够扎实，需要通过复习进行巩固。
此外，学生在这个阶段正处于青春期，思维活跃，求知欲强，但注意力容易分散，需要教师运用多种教学策略激发他们的学习兴趣和积极性。
二、教学目标1、知识与技能（1）掌握高中数学的核心概念、公式、定理及性质，如函数、三角函数、数列、立体几何、解析几何等；（2）熟练运用数学解题方法，如代入法、消元法、归纳法等，解决实际问题；（3）提高数学运算速度和准确性，增强数学推理和论证能力；（4）形成系统的数学知识体系，为高考数学复习奠定坚实基础。
2、过程与方法（1）通过自主探究、小组合作、课堂讨论等多种学习方式，培养学生的自主学习能力和团队合作精神；（2）运用问题驱动、案例教学等方法，引导学生主动发现问题、分析问题、解决问题，提高学生的思维品质；（3）借助信息技术手段，如多媒体教学、网络资源等，丰富教学手段，拓展学习视野；（4）注重数学思想方法的渗透，如化归思想、分类讨论思想等，提高学生的数学素养。
3、情感，态度与价值观（1）激发学生对数学学科的兴趣和热情，培养他们积极向上的学习态度；（2）引导学生认识数学在自然科学、社会科学等领域的重要地位，增强学生的社会责任感和使命感；（3）通过数学学习，培养学生严谨、细致、勤奋、创新的科学精神；（4）培养学生面对困难和挑战时，保持坚持不懈、勇于探索的品质；（5）注重数学美育的渗透，提高学生的审美情趣和人文素养。
三、教学策略1、以退为进在教学过程中，采用“以退为进”的策略，即在教学难点和重点问题上，教师有意识地后退一步，给予学生更多的思考空间和自主学习的机会。
高中数学复习课教案
高中数学复习课教案
课程内容：代数
教学目标：
1. 复习代数中的基本概念和常见方法。
2. 提高学生的代数计算能力和解题技巧。
3. 强化学生对代数知识的掌握和运用能力。
教学重点：
1. 一元一次方程的解法。
2. 一元二次方程的解法。
3. 多项式的加减乘除运算。
教学步骤：
1. 复习一元一次方程的基本概念和解法。
- 回顾一元一次方程的定义和基本形式。
- 讲解如何通过加减乘除等运算求解一元一次方程。
- 练习一元一次方程的解题方法及应用。
2. 复习一元二次方程的基本概念和解法。
- 回顾一元二次方程的定义和基本形式。
- 讲解求解一元二次方程的常见方法，如配方法、公式法等。
- 练习一元二次方程的解题方法及应用。
3. 复习多项式的加减乘除运算。
- 回顾多项式的定义和基本形式。
- 讲解多项式的加减乘除运算规则。
- 练习多项式的运算及应用。
4. 综合练习及作业布置。
- 完成一些综合性的练习题，检验学生对代数知识的掌握情况。
- 布置作业，让学生巩固和提升代数知识的应用能力。
教学反思：
通过这节数学复习课的教学，学生对代数中的基本概念和常见方法有了进一步的了解和掌握。
在未来的学习中，希望学生能够继续努力，提升自己的数学能力，做到熟能生巧，从而取得更优异的成绩。
人教版高中选修(B版)2-22.3数学归纳法教学设计
人教版高中选修(B版)2-22.3数学归纳法教学设计一、教学目标通过本节课的学习，学生应该能够：1.掌握数学归纳法的基本概念和方法；2.熟练掌握数学归纳法的证明过程；3.在实际问题中灵活运用数学归纳法。
二、教学重点1.数学归纳法的基本思想和方法；2.数学归纳法的证明过程。
三、教学难点1.数学归纳法在实际问题中的应用；2.数学归纳法证明过程的严密性和完整性。
四、教学内容1. 数学归纳法的基本概念和方法1.1. 数学归纳法的基本思想和概念1.2. 数学归纳法的基本方法2. 数学归纳法的证明过程2.1. 弱归纳法证明2.2. 强归纳法证明3. 数学归纳法在实际问题中的应用3.1. 例题分析3.2. 综合应用五、教学方法1.讲授法2.例题演练3.自主探究六、教学过程1. 导入（5分钟）1.1. 利用日常生活中的例子引入数学归纳法的概念和思想，如“一只鸟有两只翅膀，两只鸟有四只翅膀……”，“一个人有一个头，两个人有两个头……”。
1.2. 介绍本节课的教学目标和教学重难点。
2. 讲授与演示（20分钟）2.1. 讲授数学归纳法的基本思想和方法，包括弱归纳法和强归纳法的证明过程。
2.2. 进行例题演示，让学生熟悉数学归纳法的证明方法。
3. 实践与探究（25分钟）3.1. 让学生自主探究数学归纳法在实际问题中的应用，例如在排列组合问题、数学归纳法证明等领域的实际应用。
3.2. 带领学生完成一些综合应用的练习，并对练习过程中的问题进行讲解和答疑。
4. 总结与拓展（10分钟）4.1. 对本节课的重点和难点进行总结和回顾。
4.2. 引导学生在课后继续探究数学归纳法的应用和证明过程，拓展数学学科知识和思维能力。
七、教学反思本节课以讲授法为主，通过例题演示和自主探究等教学方法，引导学生全面掌握数学归纳法的基本概念、方法和应用，同时注重培养学生的数学思维能力和创新意识。
但需要注意的是，在引入数学归纳法的应用问题和证明过程时，要让学生理解问题的本质和证明过程的严密性，引导学生养成严谨的数学思维习惯。
高中数学函数复习课教案
高中数学函数复习课教案
一、知识回顾
1. 函数的概念：函数的定义、自变量、因变量、定义域、值域等
2. 函数的表示形式：映射关系、解析式、图象、表格等
3. 基本初等函数：一次函数、二次函数、指数函数、对数函数、幂函数、三角函数等
4. 函数的运算：函数的加减乘除、复合函数、反函数等
二、重点难点解析
1. 函数的复合：给出一个函数和一个变量，求复合函数值
2. 反函数的求法：通过函数的图象求反函数
三、能力训练
1. 练习一：已知函数$f(x)=2x-1$，求$f(f(x))$的解析式。
2. 练习二：已知函数$f(x)=3x+2$，求反函数$f^{-1}(x)$的解析式。
3. 练习三：函数$y=\sqrt{x}$的图象如何与$x$轴交点构成的图形？
4. 练习四：如果$f(x)=\frac{1}{x}$，求$f(2)+f(3)$的值。
四、拓展应用
1. 通过函数的图象，求函数的性质和特点。
2. 通过函数的解析式，构建实际问题，进行解题。
五、任务布置
1. 复习函数的基本概念和运算法则。
2. 练习函数的复合运算和反函数的求法。
3. 拓展思维，思考函数在实际问题中的应用及解法。
六、板书设计
1. 函数的定义和表示形式；
2. 函数的运算规律；
3. 函数的图象和性质。
七、教学反馈
1. 对学生的表现进行评价，引导学生查漏补缺；
2. 学生提出教学反馈意见，以便教师调整教学方式。
高中数学-复习课教案-新人教版选修2-2
宁夏银川贺兰县第四中学2013-2014学年高中数学 复习课教案 新人教版选修2-23．认识数学本质，把握数学本质，增强创新意识，提高创新能力。
二、教学重点：进一步感受和体会常用的思维模式和证明方法，形成对数学的完整认识。
难点：认识数学本质，把握数学本质，增强创新意识，提高创新能力 三、教学过程： 【创设情境】一、知识结构：【探索研究】我们从逻辑上分析归纳、类比、演绎的推理形式及特点；揭示了分析法、综合法、数学归纳法和反证法的思维过程及特点。
通过学习，进一步感受和体会常用的思维模式和证明方法，形成对数学的完整认识。
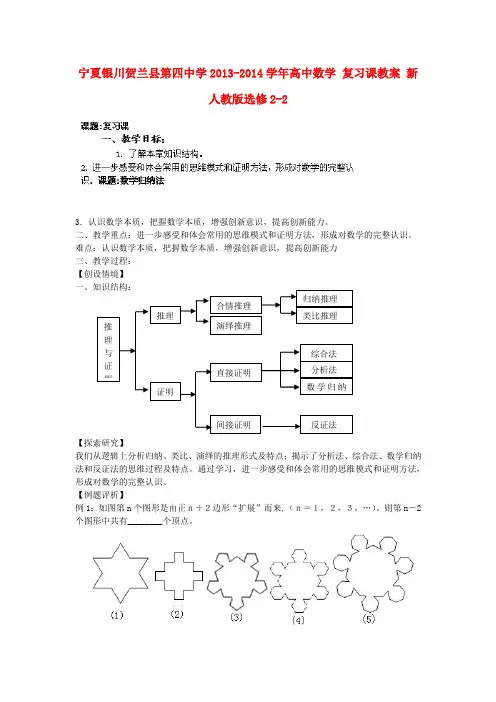
【例题评析】例1：如图第n 个图形是由正ｎ＋２边形“扩展”而来,（ｎ＝１，２，３，…）。
则第n －2个图形中共有________个顶点。
推理与证明推理 证明合情推理演绎推理 直接证明间接证明 类比推理 归纳推理 分析法 综合法 反证法数学归纳变题：黑白两种颜色的正六边形地面砖按如图的规律拼成若干个图案：则第n个图案中有白色地面砖块。
例2：长方形的对角线与过同一个顶点的两边所成的角为,αβ，则22cos sinαβ+=1，将长方形与长方体进行类比，可猜测的结论为：_______________________;变题2：数列}{na的前n项和记为Sn，已知).3,2,1(2,111Λ=+==+nSnnaann证明：（Ⅰ）数列}{nSn是等比数列；（Ⅱ）.41n na S=+例3：设f(x)=ax2+bx+c(a≠0),若函数f(x+1)与函数f(x)的图象关于y轴对称，求证：第1个第2个第3个1()2f x +为偶函数。
例4：设Sn=1+111 (23)+++n (n>1,n ∈N),求证：212n nS >+ （2,n n N ≥∈） 评析：数学归纳法证明不等式时，经常用到“放缩”的技巧。
变题：是否存在a 、b 、c 使得等式1·22+2·32+…+n(n+1)2=12)1(+n n (an2+bn+c) 对于一切正整数n 都成立？证明你的结论。
高中数学选修2-2复习教案2
第4周教学反思：上周的教学内容是选修2-3最后一章《计数原理》.本章的内容较少，但是比较难，本章与前面学习的内容没有任何的联系，主要考查学生的理解能力，从测试的情况来看很不理想。
必须加强对学生的巩固和练习。
教案--选修2-2复习-第5周高中数学选修2-2知识点总结教学目标：1．重点理解导数相关概念及其几何意义； 2．掌握选修2-2的知识点 3．利用选修2-2知识解决简单问题教学重点：利用导数研究与函数有关的简单问题，掌握推理证明的证明方法，会计算与复数有关的简单问题。
教学难点：用所学知识点解决常见问题。
授课类型：复习课 课时安排：4课时第一章、导数1．函数的平均变化率为=∆∆=∆∆x fx y xx f x x f x x x f x f ∆-∆+=--)()()()(111212 注1：其中x ∆是自变量的改变量，平均变化率 可正，可负，可零。
注2：函数的平均变化率可以看作是物体运动的平均速度。
2、导函数的概念:函数)(x f y =在0x x =处的瞬时变化率是xx f x x f x yx x ∆-∆+=∆∆→∆→∆)()(lim lim 0000，则称函数)(x f y =在点0x 处可导，并把这个极限叫做)(x f y =在x 处的导数，记作)(0'x f 或0|'x x y =，即)(0'x f =xx f x x f x yx x ∆-∆+=∆∆→∆→∆)()(lim lim0000.3.函数的平均变化率的几何意义是割线的斜率； 函数的导数的几何意义是切线的斜率。
4导数的背景（1）切线的斜率；（2）瞬时速度； 5、常见的函数导数6、常见的导数和定积分运算公式:若()f x ，()g x 均可导（可积），则有：.用导数求函数单调区间的步骤:①求函数f(x)的导数'()f x②令'()f x>0,解不等式，得x的范围就是递增区间.③令'()f x<0,解不等式，得x的范围，就是递减区间；[注]：求单调区间之前一定要先看原函数的定义域。
高中数学理科人教a版选修2-22.3数学归纳法word学案2
湖南省邵阳市隆回二当选修2-2学案 推理与证明 数学归纳法（2）
【学习目标】
1. 了解数学归纳法的原理，并能以递推思想作指导，理解数学归纳法的操作步骤;
2. 能用数学归纳法证明一些简单的数学命题，并能严格依照数学归纳法证明问题的格式书写;
3. 数学归纳法中递推思想的理解.
【自主学习】
温习1：数学归纳法的大体步骤？
温习2．用数学归纳法证明1 + 2 + 22+…+2
n –1 = 2n – 1(n ∈N *)的进程如下： ①当n = 1时，左侧 = 20 = 1，右边 = 21 – 1 = 1，等式成立；
②假设n = k 时，等式成立，即1 + 2 + 22 +…+2
k –1 = 2k – 1. 则当n = k + 1时，
1 +
2 + 22 +…+2k –1 + 2k =1
1122112k k ++-=--，所以n = k + 1时等式成立. 由此可知对任何自然数n ，等式都成立.
上述证明错在何处
.
【合作探讨】
例1已知数列 1111,,,,1447710(32)(31)
n n ⋅⋅⋅⨯⨯⨯-⨯+，猜想n S 的表达式，并证明.
【目标检测】
1. 给出四个等式: 1=1 1-4=-(1+2) 1-4+9=1+2+3 1-4+9-16=-(1+2+3+4) ……
猜想第n 个等式，并用数学归纳法证明.
2. 用数学归纳法证明:
*11(11)(1)(1)21()3
21
n n N n ++••+>+∈-
【作业布置】任课教师自定。
高中数学新课标人教A版选修2-2教案2
§1.2.2复合函数的求导法则教学目标 理解并掌握复合函数的求导法则．教学重点 复合函数的求导方法：复合函数对自变量的导数，等于已知函数对中间变量的导数乘以中间变量对自变量的导数之积．教学难点 正确分解复合函数的复合过程，做到不漏，不重，熟练，正确．一．创设情景（一）基本初等函数的导数公式表（2）推论：[]''()()cf x cf x =（常数与函数的积的导数，等于常数乘函数的导数）二．新课讲授复合函数的概念 一般地，对于两个函数()y f u =和()u g x =，如果通过变量u ，y 可以表示成x 的函数，那么称这个函数为函数()y f u =和()u g x =的复合函数，记作()()y f g x =。
复合函数的导数 复合函数()()y f g x =的导数和函数()y f u =和()u g x =的导数间的关系为x u x y y u '''=⋅，即y 对x 的导数等于y 对u 的导数与u 对x 的导数的乘积．若()()y f g x =，则()()()()()y f g x f g x g x ''''==⋅⎡⎤⎣⎦三．典例分析例1求y ＝sin （tan x 2）的导数．【点评】求复合函数的导数，关键在于搞清楚复合函数的结构，明确复合次数，由外层向内层逐层求导，直到关于自变量求导，同时应注意不能遗漏求导环节并及时化简计算结果． 例2求y ＝ax x ax 22--的导数．【点评】本题练习商的导数和复合函数的导数．求导数后要予以化简整理．例3求y ＝sin 4x ＋cos 4x 的导数．【解法一】y ＝sin 4x ＋cos 4x ＝(sin 2x ＋cos 2x )2－2sin 2cos 2x ＝1－21sin 22 x ＝1－41（1－cos 4 x ）＝43＋41cos 4 x ．y ′＝－sin 4 x ． 【解法二】y ′＝(sin 4 x )′＋(cos 4 x )′＝4 sin 3 x (sin x )′＋4 cos 3x (cos x )′＝4 sin 3 x cos x ＋4 cos 3 x (－sin x )＝4 sin x cos x (sin 2 x －cos 2 x )＝－2 sin 2 x cos 2 x ＝－sin 4 x【点评】解法一是先化简变形，简化求导数运算，要注意变形准确．解法二是利用复合函数求导数，应注意不漏步．例4曲线y ＝x （x ＋1）（2－x ）有两条平行于直线y ＝x 的切线，求此二切线之间的距离．【解】y ＝－x 3 ＋x 2 ＋2 x y ′＝－3 x 2＋2 x ＋2令y ′＝1即3 x 2－2 x －1＝0，解得 x ＝－31或x ＝1． 于是切点为P （1，2），Q （－31，－2714）， 过点P 的切线方程为，y －2＝x －1即 x －y ＋1＝0．显然两切线间的距离等于点Q 到此切线的距离，故所求距离为2|1271431|++-＝22716．四．课堂练习1．求下列函数的导数 (1) y =sin x 3+sin 33x ；（2）122sin -=x x y ;(3))2(log 2-x a 2.求)132ln(2++x x 的导数五．回顾总结六．布置作业。
人教版高三数学教案5篇
人教版高三数学教案5篇通过对的研究，让学生认识到数学的应用价值，激发学生学习数学的兴趣。
使学生善于从现实生活中数学的发现问题，解决问题，数学是每个学生的必修课，好的教师应当做好对应的数学教案。
通过本节学习，学生应当达到对数学理解有所提高，人教版高三数学教案1一、教材分析1、本节内容在全书及章节的地位：《函数的单调性》是必修1第一章第 3 节，高中数学《函数的单调性》说课稿教案模板是高考的重点考查内容之一，是函数的一个重要性质，在比较几个数的大小、求函数值域、对函数的定性分析以及与其他知识的综合上都有广泛的应用。
通过对这一节课的学习，可以让学生加深对函数的本质认识。
也为今后研究具体函数的性质作了充分准备，起到承上启下的作用。
2、教学目标：根据上述教材结构与内容分析，考虑到学生已有的认知水平我制定如下教学目标：基础知识目标：了解能用文字语言和符号语言正确表述增函数、减函数、单调性、单调区间的概念;明确掌握利用函数单调性定义证明函数单调性的方法与步骤;并能用定义证明某些简单函数的单调性;能力训练目标：培养学生严密的.逻辑思维能力、用运动变化、数形结合、分类讨论的方法去分析和处理问题，情感目标：让学生在民主、和谐的共同活动中感受学习的乐趣。
重点：形成增(减)函数的形式化定义。
难点。
形成增减函数概念的过程中，如何从图像升降的直观认识过渡到函数增减数学符号语言表述;用定义证明函数的单调性。
为了讲清重点、难点，使学生能达到本节设定的教学目标，我再从教法和学法上谈谈：二、教法在教学中我使用启发式教学，在教师的引导下，创设情景，通过开放性问题的设置来启发学生思考，在思考中体会数学概念形成过程中所蕴涵的数学方法，三、学法倡导学生主动参与、乐于探究、勤于动手，培养学生搜集和处理信息的能力、获取新知识的能力、分析和解决问题的能力以及交流与合作的能力”。
数学作为基础教育的核心课程之一，转变学生数学学习方式，不仅有利于提高学生的数学素养，而且有利于促进学生整体学习方式的转变。
高中数学第22课教案
高中数学第22课教案
一、教学目标
1. 知道正弦、余弦、正切三角函数的周期性和奇偶性。
2. 掌握正弦、余弦、正切三角函数的图像特点。
3. 掌握利用三角函数的性质解题。
二、教学重点
1. 正弦、余弦、正切三角函数的周期性和奇偶性。
2. 正弦、余弦、正切三角函数的图像特点。
三、教学难点
1. 利用三角函数的性质解题。
四、教学准备
1. 教材、课件。
2. 黑板、彩色粉笔。
3. 试题纸、学生纸。
五、教学过程
1. 引入：通过一个实际生活中的例子引入三角函数的周期性和奇偶性的概念，引导学生了解三角函数的概念。
2. 讲解：通过讲解正弦、余弦、正切三角函数的周期性和奇偶性，让学生掌握这些函数的基本特点。
3. 练习：让学生分组进行练习，练习解题过程中运用三角函数的性质。
4. 总结：总结本节课的重点难点，强调三角函数的性质在解题中的应用。
5. 作业：布置相关作业，督促学生掌握三角函数的性质及解题方法。
六、板书设计
1. 正弦函数：周期性、奇函数。
2. 余弦函数：周期性、偶函数。
3. 正切函数：周期性。
七、教学反思
本节课主要针对三角函数的性质展开教学，通过实际例子引入，让学生了解三角函数的概念；通过讲解和练习，让学生掌握正弦、余弦、正切函数的周期性和奇偶性，以及运用这些性质解题的方法。
通过板书设计和总结，加深学生对本课内容的理解和记忆。
希望学生能在课后认真完成作业，巩固所学知识。
高中数学教案：二面角复习课doc
二面角复习课一、教学目标：1．使学生进一步掌握好二面角及二面角的平面角的概念；2．使学生掌握求二面角平面角的基本方法，不断提高分析问题和解决问题的能力．二、重点和难点：使学生能够作出二面角的平面角；根据题目的条件，作出二面角的平面角．三、教学过程1．复习二面角的平面角的定义．空间图形的位置关系是立体几何的重要内容．解决立体几何问题的关键在于做好：定性分析，定位作图，定量计算，其中定性是定位、定量的基础，而定量则是定位，定性的深化．在面面关系中，二面角是其中的重要概念之一，它的度量归结为平面上角的度量，一般说来，对其平面角的定位是问题解决的关键一步．可是学生往往把握不住其定位的基本思路而导致思维混乱，甚至错误地定位，使问题的解决徒劳无益．看右图．如图1：α，β是由l出发的两个半平面，O是l上任意一点，OC α，且OC⊥l；OD β，且OD⊥l．这就是二面角的平面角的环境背景，即∠COD是二面角α-l-β的平面角．从中我们可以得到下列特征：（1）过棱上任意一点，其平面角是唯一的；（2）其平面角所在平面与其两个半平面均垂直；另外，如果在OC上任取一点A，作AB⊥OD，垂足为B，那么由特征（2）可知AB⊥β．突出l，OC，OD，AB，这便是另一特征．（3）体现出一完整的三垂线定理（或逆定理）的条件背景．特征（1）表明，其平面角的定位可先在棱上取一“点”．耐人寻味的是这一点可以随便取，但又总是不随便取定的，它必须与问题的条件背景互相沟通，给计算提供方便．例1 已知：如图2，四面体V-ABC中，VA=VB=VC=a，AB=BC=CA=b，VH⊥面ABC，垂足为H，求侧面与底面所成的角的大小．分析：由已知条件可知，顶点V在底面ABC上的射影H是底面的中心，所以连结CH交AB 于O，且OC⊥AB，由三垂线定理可知，VO⊥AB，则∠VOC为侧面与底面所成二面角的平面角．（图2）正因为此四面体的特性，解决此问题，可以取AB的中点O为其平面角的顶点，而且使得题设背影突出在面VOC上，给进一步定量创造了得天独厚的条件．特征（2）指出，如果二面角α-l-β的棱l垂直某一平面γ，那么l必垂直γ与α，β的交线，而交线所成的角就是α-l-β的平面角．（如图3）由此可见，二面角的平面角的定位可以考虑找“垂平面”．例2 矩形ABCD，AB=3，BC=4，沿对角线BD把△ABD折起，使点A在平面BCD上的射影A′落在BC上，求二面角A-BD-C的大小的余弦值．这是一道由平面图形折叠成立体图形的问题，解决问题的关键在于搞清折叠前后的“变”与“不变”．如果在平面图形中过A作AE⊥BD交BD于O、交BC于E，则折叠后OA，OE与BD的垂直关系不变．但OA与OE此时变成相交两线并确定一平面，此平面必与棱垂直．由特征（2）可知，面AOE与面ABD、面CBD的交线OA与OE所成的角，即为所求二面角的平面角．另外，A在面BCD上的射影必在OE所在的直线上，又题设射影落在BC上，所以E点就是A′，这样的定位给下面的定量提供了可能．在Rt△AA′O中，∠AA′O=90°，通过对例2的定性分析、定位作图和定量计算，特征（2）从另一角度告诉我们：要确定二面角的平面角，我们可以把构成二面角的两个半平面“摆平”，然后，在棱上选取一适当的垂线段，即可确定其平面角．“平面图形”与“立体图形”相映生辉，不仅便于定性、定位，更利于定量．特征（3）显示，如果二面角α-l-β的两个半平面之一，存在垂线段AB，那么过垂足B作l的垂线交l于O，连结AO，由三垂线定理可知OA⊥l；或者由A作l的垂线交l于O，连结OB，由三垂线定理的逆定理可知OB⊥l．此时，∠AOB就是二面角α-l-β的平面角．（如图6），由此可见，二面角的平面角的定位可以找“垂线段”．课堂练习1．在正方体ABCD-A1B1C1D1中，棱长为2，E为BC的中点，求面B1D1E与面BB1C1C所成的二面角的大小的正切值．练习1的条件背景表明，面B1D1E与面BB1C1C构成两个二面角，由特征（2）可知，这两个二面角的大小必定互补．为创造一完整的三垂线定理的环境背景，线段C1D1会让我们眼睛一亮，我们只须由C1（或D1）作B1E的垂线交B1E于O，然后连结OD1（或OC1）即得面D1B1E与面CC1B1E所成二面角的平面角∠C1OD1，2．将棱长为a的正四面体的一个面与棱长为a的正四棱锥的一个侧面吻合，则吻合后的几何体呈现几个面？分析：这道题，学生答“7个面”的占99.9％，少数应服从多数吗？从例题中三个特征提供的思路在解决问题时各具特色，它们的目标分别是找“点”、“垂面”、“垂线段”．事实上，我们只要找到其中一个，另两个就接踵而来．掌握这种关系对提高解题技能和培养空间想象能力非常重要．本题如果能融合三个特征对思维的监控，可有效地克服、抑制思维的消极作用，培养思维的广阔性和批判性．如图9，过两个几何体的高线VP，VQ的垂足P，Q分别作BC的垂线，则垂足重合于O，且O为BC的中点．OP延长过A，OQ延长交ED于R，考虑到三垂线定理的环境背影，∠AOR为二面角A-BC-R的平面角，结合特征（1），（2），可得VAOR为平行四边形，VA∥BE，所以V，A，B，E共面．同理V，A，C，D共面．所以这道题的正确答案应该是5个面．例3 如图10，在正方体ABCD-A1B1C1D1中，E是BC的中点，F在AA1上，且A1F∶FA=1∶2，求平面B1EF与底面A1C1所成的二面角大小的正切值．分析：在给定的平面B1EF与底面A1C1所成的二面角中，没有出现二面角的棱，我们可以设法在二面角的两个面内找出两个面的共点，则这两个公共点的连线即为二面角的棱，最后借助这条棱作出二面角的平面角．略解：如图10．在面BB1CC1内，作EH⊥B1C1于H，连结HA1，显然直线EF在底面A1C1的射影为HA1．延长EF，HA1交于G，过G，B1的直线为所求二面角的棱．在平面A1B1C1D1内，作HK⊥GB1于K，连EK，则∠HKE为所求二面角的平面角．在平面A1B1C1D1内，作B1L⊥GH于L，利用Rt△GLB1∽Rt△GKH，可求得KH．又在Rt△EKH中，设EH=a，容易得到：所求二面角大小的正切值注：我们也可以不直接作出二面角的平面角，而通过等价变换或具体的计算得出其平面角的大小．我们可以使用平移法．由两平面平行的性质可知，若两平行平面同时与第三个平面相交，那么这两个平行平面与第三个平面所成的二面角相等或互补．因而例3中的二面角不易直接作出其平面角时，可利用此结论平移二面角的某一个面到合适的位置，以便等价地作出该二面角的平面角．略解：过F作A′B′的平行线交BB′于G，过G作B′C′的平行线交B′E于H，连FH．显见平面FGH∥平面A′B′C′D′．则二面角B′-FH-G的平面角度数等于所求二面角的度数．过G作GM⊥HF，垂足为M，连B′M，由三垂线定理知B′M⊥HF．所以∠B′MG为二面角B′-FH-G的平面角，其大小等于所求二面角平面角的大小．例4 已知：如图12，P是正方形ABCD所在平面外一点，PA=PB=PC=PD=a，AB=a．求：平面APB与平面CPD相交所成较大的二面角的余弦值．分析：为了找到二面角及其平面角，必须依据题目的条件，找出两个平面的交线．解：因为AB∥CD，CD 平面CPD，AB 平面CPD．所以AB∥平面CPD．又P∈平面APB，且P∈平面CPD，因此平面APB∩平面CPD=l，且P∈l．所以二面角B-l-C就是平面APB和平面CPD相交所得到的一个二面角．因为AB∥平面CPD，AB 平面APB，平面CPD∩平面APB=l，所以AB∥l．过P作PE⊥AB，PE⊥CD．因为l∥AB∥CD，因此PE⊥l，PF⊥l，所以∠EPF是二面角B-l-C的平面角．因为PE是正三角形APB的一条高线，且AB=a，因为E，F分别是AB，CD的中点，所以EF=BC=a．在△EFP中，小结：二面角及其平面角的正确而合理的定位，要在正确理解其定义的基础上，掌握其基本特征，并灵活运用它们考察问题的背景．我们已经看到，定位是为了定量，求角的大小往往要化归到一个三角形中去解，因此寻找“垂线段”，把问题化归是十分重要的．四、作业：1．120°二面角α-l-β内有一点P，若P到两个面α，β的距离分别为3和1，求P到l的距离．2．正方体ABCD-A1B1C1D1中，求以BD1为棱，B1BD1与C1BD1为面的二面角的度数．。
高中数学：22 空间向量及其运算 教案(北师大版选修2-1) 教案
课题：空间向量及其运算(一)教学目的：1．理解空间向量的概念，掌握空间向量的加法、减法和数乘运算2．用空间向量的运算意义和运算律解决立几问题教学重点：空间向量的加法、减法和数乘运算及运算律教学难点：用向量解决立几问题授课类型：新授课课时安排：1课时教具：多媒体、实物投影仪内容分析：本节，空间向量及其运算共有4个知识点：空间向量及其线性运算、共线向量与共面向量、空间向量的分解定理、两个向量的数量积这一节是全章的重点，有了第一大节空间平行概念的基础，我们就很容易把平面向量及其运算推广到空间向量由于本教材学习空间向量的主要目的是，解决一些立体几何问题，所以例习题的编排也主要是立体几何问题本小节首先把平面向量及其线性运算推广到空间向量学生已有了空间的线、面平行和面、面平行概念，这种推广对学生学习已无困难但仍要一步步地进行，学生要时刻牢记，现在研究的X围已由平面扩大到空间一个向量已是空间的一个平移，两个不平行向量确定的平面已不是一个平面，而是互相平行的平行平面集，要让学生在空间上一步步地验证运算法则和运算律这样做，一方面复习了平面向量、学习了空间向量，另一方面可加深学生的空间观念当我们把平面向量推广到空间向量后，很自然地要认识空间向量的两个最基本的子空间：共线向量和共面向量把平行向量基本定理和平面向量基本定理推广到空间然后由这两个定理推出空间直线和平面的向量表达式有了这两个表达式，我们就可以很方便地使用向量工具解决空间的共线和共面问题在学习共线和共面向量定理后，我们学习空间最重要的基础定理：空间向量基本定理，这个定理是空间几何研究数量化的基础有了这个定理空间结构变得简单明了，整个空间被3个不共面的基向量所确定空间—个点或一个向量和实数组(x，y，z)建立起一一对应关系本节的最后一个知识点是，两个向量的数量积由平面两个向量的数量积推广到空间最重要的是让学生建立向量在轴上的投影概念为了减轻教学难度，内积的几个运算性质教材中没有证明学生基础好的学校可在教师的指导下，由学生自己证明 教学过程： 一、复习引入： 1向量的概念(1)向量的基本要素：大小和方向(2)向量的表示：几何表示法 AB ，a；坐标表示法(,)a xi yj x y =+=(3)向量的长度：即向量的大小，记作｜a｜(4)特殊的向量：零向量a ＝0 ⇔｜a｜＝0单位向量0a 为单位向量⇔｜0a｜＝1(5)相等的向量：大小相等，方向相同),(),(2211y x y x =⎩⎨⎧==⇔2121y y x x(6)平行向量(共线向量)：方向相同或相反的向量，称为平行向量记作a ∥b由于向量可以进行任意的平移(即自由向量)，平行向量总可以平移到同一直线上，故平行向量也称为共线向量2向量的运算向量的加减法，数与向量的乘积，向量的数量（内积）及其各运算的坐标表示和性质运算类型 几何方法坐标方法运算性质向 量的加 法1平行四边形法则2三角形法则),(2121y y x x b a ++=+a b b a +=+)()(c b a c b a ++=++ AB BC AC +=向量的减法三角形法则),(2121yyxxba--=-)(baba-+=-AB BA=-OB OA AB-=向量的乘法1aλ是一个向量,满足:2λ>0时,aλ与a同向;λ<0时,aλ与a异向;λ=0时,aλ=0),(yxaλλλ=aa)()(λμμλ=aaaμλμλ+=+)(babaλλλ+=+)(a∥babλ=⇔向量的数量积ba•是一个数10=a或0=b时,ba•=020≠a且0≠b时,),cos(||||bababa=•2121yyxxba+=•abba•=•)()()(bababa•=•=•λλλcbcacba•+•=•+)(22||aa=22||yxa+=||||||baba≤•3重要定理、公式：(1)平面向量基本定理21,ee是同一平面内两个不共线的向量，那么，对于这个平面内任一向量，有且仅有一对实数21,λλ，使2211eeaλλ+=(2)两个向量平行的充要条件a∥b⇔a＝λb⇔01221=-yxyx(3)两个向量垂直的充要条件a⊥b⇔a·b＝O⇔02121=+yyxx(4)线段的定比分点公式设点P 分有向线段⇔所成的比为λ，即1PP ＝λ2PP ，则OP ＝λ+111OP ＋λ+112OP (线段的定比分点的向量公式) ⎪⎪⎩⎪⎪⎨⎧++=++=.1,12121λλλλy y y x x x (线段定比分点的坐标公式)当λ＝1时，得中点公式：OP ＝21（1OP ＋2OP ）或⎪⎪⎩⎪⎪⎨⎧+=+=.2,22121y y y x x x (5)平移公式设点),(y x P 按向量),(k h a = 平移后得到点),(y x P '''，则OP '＝OP +a或⎩⎨⎧+='+='.,k y y h x x ，曲线)(x f y =按向量),(k h a =平移后所得的曲线的函数解析式为：)(h x f k y -=-(6)正、余弦定理 正弦定理：.2sin sin sin R CcB b A a === 余弦定理：A bc c b a cos 2222-+=⇔bca cb A 2cos 222-+=B ac a c b cos 2222-+=⇔cab ac B 2cos 222-+=C ab b a c cos 2222-+=⇔abc b a C 2cos 222-+=二、讲解新课：1．空间向量的概念：在空间，我们把具有大小和方向的量叫做向量 注：⑴空间的一个平移就是一个向量⑵向量一般用有向线段表示同向等长的有向线段表示同一或相等的向量aC'B'A'D'DABC GMC'B'A'D'DAB C ⑶空间的两个向量可用同一平面内的两条有向线段来表示 2．空间向量的运算定义：与平面向量运算一样，空间向量的加法、减法与数乘向量运算如下（如图）OB OA AB a b =+=+ BA OA OB a b =-=- ()OP a R λλ=∈运算律：⑴加法交换律：a b b a+=+ ⑵加法结合律：)()(c b a c b a++=++⑶数乘分配律：b a b aλλλ+=+)(3．平行六面体：平行四边形ABCD 平移向量a到D C B A ''''的轨迹所形成的几何体，叫做平行六面体，并记作：ABCD －D C B A ''''它的六个面都是平行四边形，每个面的边叫做平行六面体的棱 三、讲解X 例：例1已知平行六面体ABCD －D C B A ''''化简下列向量表达式，标出化简结果的向量. ⑴AB BC +；⑵AB AD AA '++； ⑶12AB AD CC '++； ⑷1()3AB AD AA '++ 解：如图：⑴AB BC AC +=；⑵AB AD AA '++=AC AA AC ''+=；⑶设M 是线段C C '的中点，则12AB AD CC AC CM AM '++=+=； ⑷设G 是线段C A '的三等份点，则11()33AB AD AA AC AG ''++==向量,,,AC AC AM AG '如图所示:C B AOb b baa例2 已知空间四边形ABCD ，连结,AC BD ，设,M G 分别是,BC CD 的中点，化简下列各表达式，并标出化简结果向量：（1）AB BC CD ++； （2）1()2AB BD BC ++； （3）1()2AG AB AC -+． 解：如图，（1）AB BC CD AC CD AD ++=+=； （2）111()222AB BD BC AB BC BD ++=++ AB BM MG AG =++=；（3）1()2AG AB AC AG AM MG -+=-=． 四、课堂练习：1．如图，在空间四边形ABCD 中，,E F 分别是AD 与BC 的中点， 求证：1()2EF AB DC =+． 证明：1122EF ED DC CF AD DC CB =++=++ 11()22AB BD DC CB =+++ 11()22AB DC CB BD =+++ 1122AB DC CD =++ 1()2AB DC =+ 2．已知2334x y a b c +=-++，385x y a b c --=-+，把向量,x y 用向量,,a b c 表示 解:∵2334x y a b c +=-++，385x y a b c --=-+ ∴32x a b c =-+-， 2y a b c =-+3．如图，在平行六面体ABCD A B C D ''''-中，设AB a =，,AD b AA c '==，,E F 分别是,AD BD '中点，（1）用向量,,a b c 表示,D B EF '；BCDMGABCDEFAA'BB'CC'DD'EFACD（2）化简：2AB BB BC C D D E ''''++++； 解: （1）D B D A A B B B b a c ''''''=++=-+-1122EF EA AB BF D A a BD '=++=++ 111()()()222b c a a b a c =--++-+=- 五、小结 ：空间向量的相关的概念及空间向量的表示方法；平行六面体的概念； 向量加法、减法和数乘运算六、课后作业：如图设A 是△BCD 所在平面外的一点，G 的重心求证：1()3AG AB AC AD =++七、板书设计（略） 八、课后记：。
高中必修二数学复习课教案
高中必修二数学复习课教案主题：复习基础知识
时间：90分钟
教学目标：
1. 进一步巩固高中必修二数学的基础知识；
2. 帮助学生复习重要概念和公式；
3. 培养学生解决问题和运用数学知识的能力。
教学内容：
1. 复习直线方程和二次函数的概念和性质；
2. 复习直线与圆的关系；
3. 复习集合与概率的基本知识；
4. 复习向量的运算和性质；
5. 复习导数的概念和计算方法。
教学步骤：
一、复习直线方程和二次函数（20分钟）
1. 复习直线的方程、斜率和截距的概念；
2. 复习二次函数的图像、顶点和轴等重要性质。
二、复习直线与圆的关系（15分钟）
1. 复习直线与圆的方程和位置关系；
2. 引导学生解决相关题目。
三、复习集合与概率（15分钟）
1. 复习集合的概念和运算；
2. 复习概率的基本知识和计算方法。
四、复习向量的运算和性质（20分钟）
1. 复习向量的定义、运算规则和性质；
2. 练习相关计算题目。
五、复习导数的概念和计算方法（20分钟）
1. 复习导数的定义和基本性质；
2. 练习导数的计算方法。
六、总结与展望（10分钟）
1. 确认学生掌握情况；
2. 展望下一阶段学习内容。
教学资源：
1. 教材《高中数学必修二》；
2. 习题册；
3. 多媒体课件。
教学反思：
通过本节课的复习，学生能够进一步巩固和理解高中必修二数学的基础知识，为下一阶段学习打下坚实的基础。
同时，教师需要根据学生的学习情况及时调整教学策略，确保每位学生都能够理解和掌握所学知识。
高中数学教案(8篇)
高中数学教案（8篇）高中数学教案篇一1.课题填写课题名称（高中代数类课题）2.教学目标（1）知识与技能：通过本节课的学习，掌握。
.。
.。
.知识，提高学生解决实际问题的能力；（2）过程与方法：通过。
.。
.。
.（讨论、发现、探究），提高。
.。
.。
.（分析、归纳、比较和概括）的能力；（3）情感态度与价值观：通过本节课的学习，增强学生的学习兴趣，将数学应用到实际生活中，增加学生数学学习的乐趣。
3.教学重难点（1）教学重点：本节课的知识重点（2）教学难点：易错点、难以理解的知识点4、教学方法（一般从中选择3个就可以了）（1）讨论法（2）情景教学法（3）问答法（4）发现法（5）讲授法5、教学过程（1）导入简单叙述导入课题的方式和方法（例：复习、类比、情境导出本节课的课题）（2）新授课程（一般分为三个小步骤）①简单讲解本节课基础知识点（例：奇函数的定义）。
②归纳总结该课题中的重点知识内容，尤其对该注意的一些情况设置易错点，进行强调。
可以设计分组讨论环节（分组判断几组函数图像是否为奇函数，并归纳奇函数图像的特点。
设置定义域不关于原点对称的函数是否为奇函数的易错点）。
③拓展延伸，将所学知识拓展延伸到实际题目中，去解决实际生活中的问题。
（在新授课里面一定要表下出讲课的大体流程，但是不必太过详细。
）（3）课堂小结教师提问，学生回答本节课的收获。
（4）作业提高布置作业（尽量与实际生活相联系，有所创新）。
6、教学板书2.高中数学教案格式一．课题（说明本课名称）二．教学目的（或称教学要求，或称教学目标，说明本课所要完成的教学任务）三．课型（说明属新授课，还是复习课）四．课时（说明属第几课时）五．教学重点（说明本课所必须解决的关键性问题）六．教学难点（说明本课的学习时易产生困难和障碍的知识传授与能力培养点）七．教学方法要根据学生实际，注重引导自学，注重启发思维八．教学过程（或称课堂结构，说明教学进行的内容、方法步骤）九．作业处理（说明如何布置书面或口头作业）十．板书设计（说明上课时准备写在黑板上的内容）十一．教具（或称教具准备，说明辅助教学手段使用的工具）十二．教学反思：（教者对该堂课教后的感受及学生的收获、改进方法）3.高中数学教案范文【教学目标】1、知识与技能（1）理解等差数列的定义，会应用定义判断一个数列是否是等差数列：（2）账务等差数列的通项公式及其推导过程：（3）会应用等差数列通项公式解决简单问题。
集合复习课教案
教学目的：巩固集合、子、交、并、补的概念、性质和记号及它们之间的关系
教学重点、难点：会正确应用其概念和性质做题
教学方法：讲练结合法
授课类型：复习课
教学过程：
一、复习准备：
本单元主要介绍了以下三个问题：
1,集合的含义与特征。2,集合的表示与转化。3,集合的基本运算
（一）集合的含义t;10，x∈N+}，若A∩B={3}， ={1，5，7}，
学生分析方法→填写图中各块的元素→小结：列举法表示的数集问题用Venn图示法、观察法。
解：因为 {1，9}，所以1、9
因为 {4，6，7}
所以 {1，4，6，7，9}，从而B ={2，3，5，8}；
又 {1，9}， {3}，所以A ={1，3，9}。
例6：已知A ={x|–2 <x<–1或x> 1}，A∪B ={x|x+ 2 > 0}，A∩B ={x|1 <x≦3}，求集合B。
同学组成集合 ，两项都不及格的同学组成集合
，其中U表示全班同学组成的集合。
设两项都及格的同学为x人，则有40 + 31–x+ 4 = 50，解得x= 25。
说明：本题解出后，应代入验证：50名同学中，只有跳远及格人数为15人，只有铅球及格人数为6人，4 + 15 + 25 + 6 = 50，符号题意。
解法：数轴上表示各集合后，分析得出结果。
分析：因为 ，
所以 ，
因为 ，
，
所以 ，
所以 。
例7：满足关系{1，2} A {1，2，3，4，5}的集合A共有个。
分析：满足条件的集合A可列举如下：
{1，2}，{1，2，3}，{1，2，4}，{1，2，5}，{1，2，3，4}，{1，2，3，5}，{1，2，3，4，5}共8个。
高一数学复习教案通用5篇
高一数学复习教案通用5篇高一数学复习教案通用5篇高一数学教案怎么写。
如果教师有一份明确的说课稿，将会大大提升教学效率，提升课堂活跃性，提升学生学习兴趣。
下面小编给大家带来关于高一数学复习教案，希望会对大家的工作与学习有所帮助。
高一数学复习教案（篇1）高一第一学期是初中向高中的重要转折点，学生能否在短期内快速适应高中英语学习是摆在我们面前的重要任务，特制定高一英语教学计划如下：一、指导思想以学校工作计划为指导思想，全面贯彻落实新课程改革和素质教育的精神，落实学科教学常规，营造良好的教研氛围，不断改革课堂教学，探究科学有效的教学形式。
针对高一新生普遍英语底子差，基础薄的实际，打算在高一起始阶段的英语教学中，本着低起点，爬坡走，抓习惯的原则，长期不懈地抓好学生的学习英语的的兴趣和习惯养成。
在本学期的英语教学中，要坚持以下理念的应用：1、坚定不移地突出学生主体，让学生成为学习的主人。
2、面向全体学生，关注每个学生的情感，激发他们学习英语的兴趣，帮助他们建立学习的成就感和自信心。
3、尊重个体差异，让学生在老师的指导下构建知识，提高技能，磨练意志，活跃思维，展现个性，发展心智和拓展视野；4、让学生在使用英语中学习英语，让他们在使用和学习英语的过程中，体味到轻松和成功的快乐。
二、工作重点全面做好初高中衔接工作初中和高中在教学对象、教学内容、教学要求、教学方式和学习方式方面均存在着一定的差异，因此，帮助高一新生了解这些差异，引导他们尽快适应高中的学习与生活，是摆在新学期高一教师面前的迫在眉睫的任务。
具体来说我们要做好以下工作：知识衔接（词汇补充、语法回顾）。
在开新课之前，拿出一周左右的时间搞好高初中之间的词汇衔接和语法衔接，为开新课做好准备。
1、培养习惯，打好基础。
培养基础与指导学法是一致的，培养习惯的过程也是打下扎实基础的过程。
高一起始教学阶段，除重视基础知识的落实巩固，基本技能的培养训练外，最主要的是培养良好的学习习惯和正确的学习方法。
高中数学优秀教学设计【精选10篇】
高中数学优秀教学设计【精选10篇】高中数学优秀教学设计【篇1】【教学目的】(1)使学生初步理解集合的概念，知道常用数集的概念及记法(2)使学生初步了解“属于”关系的意义(3)使学生初步了解有限集、无限集、空集的意义【重点难点】教学重点：集合的基本概念及表示方法教学难点：运用集合的两种常用表示方法——列举法与描述法，正确表示一些简单的集合授课类型：新授课课时安排：1课时教具：多媒体、实物投影仪【内容分析】1.集合是中学数学的一个重要的基本概念在小学数学中，就渗透了集合的初步概念，到了初中，更进一步应用集合的语言表述一些问题例如，在代数中用到的有数集、解集等;在几何中用到的有点集至于逻辑，可以说，从开始学习数学就离不开对逻辑知识的掌握和运用，基本的逻辑知识在日常生活、学习、工作中，也是认识问题、研究问题不可缺少的工具这些可以帮助学生认识学习本章的意义，也是本章学习的基础把集合的初步知识与简易逻辑知识安排在高中数学的最开始，是因为在高中数学中，这些知识与其他内容有着密切联系，它们是学习、掌握和使用数学语言的基础例如，下一章讲函数的概念与性质，就离不开集合与逻辑本节首先从初中代数与几何涉及的集合实例入手，引出集合与集合的元素的概念，并且结合实例对集合的概念作了说明然后，介绍了集合的常用表示方法，包括列举法、描述法，还给出了画图表示集合的例子这节课主要学习全章的引言和集合的基本概念学习引言是引发学生的学习兴趣，使学生认识学习本章的意义本节课的教学重点是集合的基本概念集合是集合论中的原始的、不定义的概念在开始接触集合的概念时，主要还是通过实例，对概念有一个初步认识教科书给出的“一般地，某些指定的对象集在一起就成为一个集合，也简称集”这句话，只是对集合概念的描述性说明【教学过程】一、复习引入：1.简介数集的发展，复习最大公约数和最小公倍数，质数与和数;2.教材中的章头引言;3.集合论的创始人——康托尔(德国数学家)(见附录);4.“物以类聚”，“人以群分”;5.教材中例子(P4)二、讲解新课：阅读教材第一部分，问题如下：(1)有那些概念?是如何定义的?(2)有那些符号?是如何表示的?(3)集合中元素的特性是什么?(一)集合的有关概念：由一些数、一些点、一些图形、一些整式、一些物体、一些人组成的.我们说，每一组对象的全体形成一个集合，或者说，某些指定的对象集在一起就成为一个集合，也简称集.集合中的每个对象叫做这个集合的元素.定义：一般地，某些指定的对象集在一起就成为一个集合.1、集合的概念(1)集合：某些指定的对象集在一起就形成一个集合(简称集)(2)元素：集合中每个对象叫做这个集合的元素2、常用数集及记法(1)非负整数集(自然数集)：全体非负整数的集合记作N，(2)正整数集：非负整数集内排除0的集记作N__或N+(3)整数集：全体整数的集合记作Z ,(4)有理数集：全体有理数的集合记作Q ,(5)实数集：全体实数的集合记作R注：(1)自然数集与非负整数集是相同的，也就是说，自然数集包括数0 (2)非负整数集内排除0的集记作N__或N+ Q、Z、R等其它数集内排除0的集，也是这样表示，例如，整数集内排除0的集，表示成Z__3、元素对于集合的隶属关系(1)属于：如果a是集合A的元素，就说a属于A，记作a∈A(2)不属于：如果a不是集合A的元素，就说a不属于A，记作4、集合中元素的特性(1)确定性：按照明确的判断标准给定一个元素或者在这个集合里，或者不在，不能模棱两可(2)互异性：集合中的元素没有重复(3)无序性：集合中的元素没有一定的顺序(通常用正常的顺序写出)5、⑴集合通常用大写的拉丁字母表示，如A、B、C、P、Q…… 元素通常用小写的拉丁字母表示，如a、b、c、p、q……⑵“∈”的开口方向，不能把a∈A颠倒过来写三、练习题：1、教材P5练习1、22、下列各组对象能确定一个集合吗?(1)所有很大的实数 (不确定)(2)好心的人 (不确定)(3)1，2，2，3，4，5.(有重复)3、设a,b是非零实数，那么可能取的值组成集合的元素是 -2,0,24、由实数x,-x,|x|, 所组成的集合，最多含( A )(A)2个元素 (B)3个元素 (C)4个元素 (D)5个元素5、设集合G中的元素是所有形如a+b (a∈Z, b∈Z)的数，求证：(1) 当x∈N时, x∈G;(2) 若x∈G，y∈G，则x+y∈G，而不一定属于集合G证明(1)：在a+b (a∈Z, b∈Z)中，令a=x∈N,b=0, 则x= x+0__ = a+b ∈G,即x∈G证明(2)：∵x∈G，y∈G，∴x= a+b (a∈Z, b∈Z),y= c+d (c∈Z, d∈Z)∴x+y=( a+b )+( c+d )=(a+c)+(b+d)∵a∈Z, b∈Z,c∈Z, d∈Z∴(a+c) ∈Z, (b+d) ∈Z∴x+y =(a+c)+(b+d) ∈G，又∵ =且不一定都是整数，∴ = 不一定属于集合G【小结】1.集合的有关概念：(集合、元素、属于、不属于)2.集合元素的性质：确定性，互异性，无序性3.常用数集的定义及记法高中数学优秀教学设计【篇2】学习目标明确排列与组合的联系与区别，能判断一个问题是排列问题还是组合问题;能运用所学的排列组合知识，正确地解决的实际问题.学习过程一、学前准备复习：1.(课本P28A13)填空：(1)有三张参观卷，要在5人中确定3人去参观，不同方法的种数是 ;(2)要从5件不同的礼物中选出3件分送3为同学，不同方法的种数是 ;(3)5名工人要在3天中各自选择1天休息，不同方法的`种数是 ;(4)集合A有个元素，集合B有个元素，从两个集合中各取1个元素，不同方法的种数是 ;二、新课导学探究新知(复习教材P14～P25，找出疑惑之处)问题1：判断下列问题哪个是排列问题，哪个是组合问题：(1)从4个风景点中选出2个安排游览，有多少种不同的方法?(2)从4个风景点中选出2个，并确定这2个风景点的游览顺序，有多少种不同的方法?应用示例例1.从10个不同的文艺节目中选6个编成一个节目单，如果某女演员的独唱节目一定不能排在第二个节目的位置上，则共有多少种不同的排法?例2.7位同学站成一排，分别求出符合下列要求的不同排法的种数.(1) 甲站在中间;(2)甲、乙必须相邻;(3)甲在乙的左边(但不一定相邻);(4)甲、乙必须相邻，且丙不能站在排头和排尾;(5)甲、乙、丙相邻;(6)甲、乙不相邻;(7)甲、乙、丙两两不相邻。
高中数学复习课的教案模板
一、课题（填写具体课题名称，如：“函数性质与图像复习”、“三角函数复习”等）二、教学目标1. 知识与技能：- 通过复习，巩固学生对相关数学概念、性质、公式的理解和掌握。
- 培养学生运用所学知识解决实际问题的能力。
2. 过程与方法：- 通过小组讨论、合作探究等方式，提高学生的分析、归纳、总结能力。
- 通过典型例题、习题训练，提高学生的解题技巧和策略。
3. 情感态度与价值观：- 培养学生对数学学习的兴趣，增强自信心。
- 培养学生严谨、求实的科学态度和团队协作精神。
三、教学重难点1. 教学重点：- 对相关数学概念、性质、公式的理解和掌握。
- 典型例题的解题思路和方法。
2. 教学难点：- 复杂问题的分析和解决。
- 学生在复习过程中可能出现的易错点和误区。
四、教学方法1. 讲授法：讲解相关数学概念、性质、公式等基础知识。
2. 讨论法：组织学生分组讨论，共同探讨问题，培养学生的合作能力。
3. 案例分析法：通过典型例题，引导学生分析解题思路，提高解题能力。
4. 习题训练法：布置适量习题，让学生巩固所学知识，提高解题技巧。
五、教学过程1. 导入新课- 复习上节课所学内容，回顾重点知识点。
- 提出本节课的学习目标和要求。
2. 复习巩固- 讲解相关数学概念、性质、公式等基础知识。
- 通过典型例题，引导学生分析解题思路，提高解题能力。
3. 小组讨论- 将学生分成若干小组，针对某一问题进行讨论，培养学生的合作能力。
- 教师巡视指导，解答学生疑问。
4. 习题训练- 布置适量习题，让学生巩固所学知识，提高解题技巧。
- 教师巡视指导，解答学生疑问。
5. 总结归纳- 对本节课所学内容进行总结，强调重点和难点。
- 鼓励学生课后复习，巩固所学知识。
六、教学评价1. 课堂表现：观察学生参与讨论、提问、回答问题的积极性。
2. 作业完成情况：检查学生课后习题完成情况，了解学生对知识的掌握程度。
3. 课后反馈：收集学生对本节课的评价和建议，不断改进教学方法。
高中数学教案选修22《第3章复习与小结》
Word 文档仅限参照教课目的：1．复习复数的观点 ,表示形式（几何和代数）以及复数的四则运算．2．借助图形及向量形式进一步加深对复数的理解,学会用代数方法解决问题．教课要点：复数的综合应用．教课难点：复数的综合应用．教课过程：一、知识回首1．复数的三种形式：（1）代数形式 __________________；（2）几何形式 _______________；（ 3）向量形式 ______________．2 ．复数相等：当a,b,c,d ∈R时 ,a ＋ bi ＝ c＋ di_________ ,a＋bi＝0_____ ．3．复数的四则运算：特别是除法运算,就是分母 __________化．4．共轭复数、模：（1） z＝a＋bi( a, b∈R) 的共轭复数是 ________________,（2） z 是实数 _____________________．（3）│z│＝__________．（4） z z＝ ________ ＝ ________ ．5．复数的几何意义：│z1－ z2│表示．二、数学应用例 1（1）设a,b,c,d∈ R,则复数（a＋bi）（c＋di）为实数的充要条件是____________ ．Word 文档仅限参照（2）在复平面内 ,复数1＋i对应的点位于第 _______象限． i（3）已知m＝1－ni, 此中 m,n 是实数 ,i 是虚数单位 ,则 m＋ni＝_______．1＋ix＋y5．（ 4）设 x,y 为实数 ,且－－＝,则 x＋y＝1i12i1－3i例 2已知复数 z 知足z z＝4 ,且│z＋1＋ 3 i│＝4,求复数z．解a2＋ b2＝4法一待定系数法设 z＝a＋bi,则由条件( a＋1)2＋(b＋ 3) 2＝16法二利用模的几何意义│z│＝2 表示 z 所对应的点在原点为圆心 ,2 为半径的圆上；│z＋1＋3 i│＝ 4 表示 z 所对应的点在以 (－1,－ 3 )为圆心,4为半径的圆上,故 z 所对应的点为两圆的交点 ,即可求解．练习 1 已知 z1,z2∈C,│z1│＝│z2│＝1,│z1＋z2│＝ 3 ,求│z1－z2│．2．设复数 z＝ x＋yi(x,y∈R),则当 z 知足以下条件时 ,动点 Z（x,y）分别表示什么样的图形？（ 1）│z－i │＋│z＋ i│＝4. （2）│z＋1＋i│＝│z－1－i │.例 3已知z1,z2是两个虚数,而且z1＋z2,z1·z2均为实数,求证：z1,z2是共轭虚数．。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
宁夏银川贺兰县第四中学2013-2014学年高中数学 复习课教案 新
人教版选修2-2
3．认识数学本质，把握数学本质，增强创新意识，提高创新能力。
二、教学重点：进一步感受和体会常用的思维模式和证明方法，形成对数学的完整认识。
难点：认识数学本质，把握数学本质，增强创新意识，提高创新能力 三、教学过程： 【创设情境】
一、知识结构：
【探索研究】
我们从逻辑上分析归纳、类比、演绎的推理形式及特点；揭示了分析法、综合法、数学归纳法和反证法的思维过程及特点。
通过学习，进一步感受和体会常用的思维模式和证明方法，形成对数学的完整认识。
【例题评析】
例1：如图第n 个图形是由正ｎ＋２边形“扩展”而来,（ｎ＝１，２，３，…）。
则第n －2个图形中共有________个顶点。
推理与证
明
推理 证明
合情推理
演绎推理 直接证明
间接证明 类比推理 归纳推理 分析法 综合法 反证法
数学归纳
变题：黑白两种颜色的正六边形地面砖按如图的规律拼成若干个图案：则第n个图案中有白色地面砖块。
例2：长方形的对角线与过同一个顶点的两边所成的角为,αβ，则22
cos sin
αβ
+
=1，将长方形与长方体进行类比，可猜测的结论为：_______________________;
变题2：数列
}
{
n
a
的前n项和记为Sn，已知
).
3,2,1
(
2
,1
1
1
Λ
=
+
=
=
+
n
S
n
n
a
a
n
n
证明：
（Ⅰ）数列
}
{
n
S
n
是等比数列；
（Ⅱ）
.
4
1n n
a S=
+
例3：设f(x)=ax2+bx+c(a≠0),若函数f(x+1)与函数f(x)的图象关于y轴对称，求证：第1个第2个第3个
1()
2f x +
为偶函数。
例4：设Sn=1+111
(23)
+++
n (n>1,n ∈N),求证：212n n S >+ （2,n n N ≥∈） 评析：数学归纳法证明不等式时，经常用到“放缩”的技巧。
变题：是否存在a 、b 、c 使得等式1·22+2·32+…+n(n+1)2=12)
1(+n n (an2+bn+c) 对于一切
正整数n 都成立？证明你的结论。
解 假设存在a 、b 、c 使题设的等式成立，
这时令n=1,2,3,有⎪⎩⎪
⎨⎧===∴⎪
⎪⎪⎩⎪⎪
⎪⎨⎧++=++=++=10
11
3 3970)24(2122)(614c b a c
b a
c b a c b a
于是，对n=1,2,3下面等式成立
1·22+2·32+…+n(n+1)2=)
10113(12)
1(2+++n n n n
记Sn=1·22+2·32+…+n(n+1)2 （1）n=1时，等式以证，成立。
（2）设n=k 时上式成立，即Sk=12)
1(+k k (3k2+11k+10) 那么Sk+1=Sk+(k+1)(k+2)2=2)1(+k k (k+2)(3k+5)+(k+1)(k+2)2
=12)2)(1(++k k (3k2+5k+12k+24)=12)
2)(1(++k k ［3(k+1)2+11(k+1)+10］
也就是说，等式对n=k+1也成立
综上所述，当a=3,b=11,c=10时，题设对一切自然数n 均成立
【课堂小结】
体会常用的思维模式和证明方法。
【反馈练习】
1．在R 上定义运算).1(:y x y x -=⊗⊗若不等式1)()(<+⊗-a x a x 对任意实数x 成立， 则
A ．11<<-a
B ．20<<a
C ．2321<<-
a D ．21
23<
<-a 2．定义A*B ，B*C ，C*D ，D*B 分别对应下列图形
那么下列图形中
可以表示A*D ，A*C 的分别是 ( ) A ．（1）、（2） B ．（2）、（3） C ．（2）、（4） D ．（1）、（4）
3 已知f(n) =(2n+7)·3n+9,存在自然数m,使得对任意n ∈N,都能使m 整除f(n)，则最大的m 的值为( )
A 30
B 26
C 36
D 6 解析 ∵f(1)=36,f(2)=108=3×36,f(3)=360=10×36
∴f(1),f(2),f(3)能被36整除，猜想f(n)能被36整除 证明 n=1,2时，由上得证，设n=k(k ≥2)时， f(k)=(2k+7)·3k+9能被36整除，则n=k+1时，
f(k+1)－f(k)=(2k+9)·3k+1－(2k+7)·3k=(6k+27)·3k －(2k+7)·3k =(4k+20)·3k=36(k+5)·3k －2(k ≥2) ⇒f(k+1)能被36整除 ∵f(1)不能被大于36的数整除，∴所求最大的m 值等于36 4 已知数列{bn}是等差数列，b1=1,b1+b2+…+b10=145 (1)求数列{bn}的通项公式bn;
(2)设数列{an}的通项an=loga(1+
n
b 1)(其中a ＞0且a ≠1)记Sn 是数列{an}的前n 项和，试
比较Sn 与31
logabn+1的大小，并证明你的结论
解 (1) 设数列{bn}的公差为d,
（1） （2） （3） （4） （1） （2） （3） （4）
由题意得⎩⎨⎧==⇒⎪⎩⎪
⎨⎧=-+=311452)
110(10101
111d b d b b ,∴bn=3n －2
(2)证明 由bn=3n －2知Sn=loga(1+1)+loga(1+41)+…+loga(1+231
-n ) =loga ［(1+1)(1+41)…(1+ 231
-n )］
而31logabn+1=loga 3
13+n ,于是，比较Sn 与31
logabn+1的大小
⇔比较(1+1)(1+41)…(1+231
-n )与313+n 的大小
取n=1，有(1+1)=
333
11348+⋅=> 取n=2，有(1+1)(1+333
1
2378)41+⨯=>> 推测 (1+1)(1+41)…(1+231
-n )＞3
13+n (*)
①当n=1时，已验证(*)式成立
②假设n=k(k ≥1)时(*)式成立，即(1+1)(1+41)…(1+231
-k )＞3
13+k
则当n=k+1时，
)
131
1(13)2)1(311)(2311()411)(11(3+++>-++-+++k k k k Λ
3
1
31323+++=
k k k
33
3
332(
31)(34)31k k k k ++-++Q
3222
(32)(34)(31)940(31)(31)
k k k k k k +-+++==>++
3
3331
2)343(1)131k k k k k ++>+=+++31
)1(3)1311)(2311()411)(11(++>-+-+++k k k Λ从而,
即当n=k+1时，(*)式成立
由①②知，(*)式对任意正整数n 都成立
于是，当a ＞1时，Sn ＞31
logabn+1
,当 0＜a ＜1时，Sn ＜31
logabn+1
【课外作业】
《课标检测》。