泡利关于动电子微分散射截面的原始论文-德语文字
冉绍尔汤森效应验证和测量气体原子散射截面与电子能量的关系
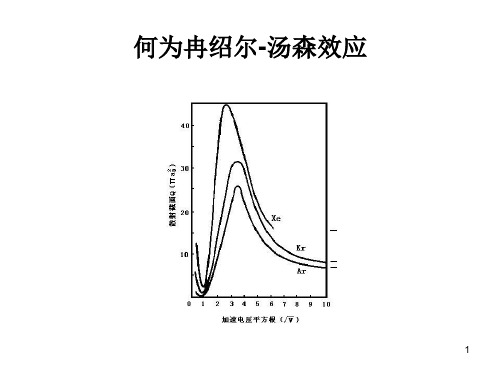
散射截面用以表示A粒子与B粒子发生相互作用而离开入 射束的概率
3
测量原理
冉绍尔-汤森效应实验仪
4
• 测量气体原子总散射截面的原理图
5
• 灯丝被加热,电子自阴极逸出,设阴极电流为Ik,电子在 加速电压的作用下,有一部分电子在到达栅极之前,被屏 极接收,形成电流Is1;有一部分穿越屏极上的矩形孔,形 成电流I0,由于屏极上的矩形孔与板极P之间是一个等势 空间,所以电子穿越矩形孔后就以恒速运动,受到气体原 子散射的电子则到达屏极,形成散射电流Is2;而未受到散 射的电子则到达板极P,形成透射电流Ip
9
• 用测量所得数据作图,分别得到Ea- Is曲线、Ea-Ip曲线、 Ea- Is*曲线、 Ea- Ip*曲线、Ea-f曲线。与交流观察的现象吻 合,各个电流与加速电压的关 系基本成正比例,而Ea-Ip 曲线存在拐角,验证了在交流观察时看到的明显的凹陷。 同时得到的Ea-f曲线,f数值可以低至0.02左右,可视为 f<<1,故关系式(总有效散射截面) Q=-(1/L)*ln[(Ip/Is)*( Is*/ Ip*)]在实验处理时完全可以采用。
10
作出散射几率与电子能量平方根的关系图
Pห้องสมุดไป่ตู้s
0.9
0.8
0.7
0.6
0.5
0.4
0.3
0.2
0.1
0.5
1.0
1.5
2.0
2.5
3.0
3.5
(eV)1/2
11
曲线分析: 有效散射截面与电子的运动速度密切相关。电子能量
降到约6.5eV时,散射截面达到极大值;进一步降低电子 能量,散射截面急剧变小,当电子能量低至约0.9eV,散 射截面出现极小值,此时,气体原子呈现所谓的“透明” 现象,即电子经过原子气体时,几乎不与原子发生碰撞而 径直透过;再降低电子的能量,散射截面将迅速增大。
快中子_64_Zn_n_61_Ni反应微分截面实验测量

快中子64Zn(n,α)61Ni 反应微分截面实验测量张国辉郭利安张家国曹荣太陈金象(北京大学物理学院核物理与核技术国家重点实验室北京100871)Gledenov Yu M Sedysheva M(Frank Laboratory of Neutron Physics, JINR, Dubna, 141980, Russia)Khuukhenkhuu G(Nuclear research Centre, National University of Mongolia, Ulaanbaatar, M ongolia)摘要由于64Zn(n, α)61Ni 反应的剩余核是稳定的,不能用通常的活化法来测量,致使该反应截面实验数据缺乏。
利用双屏栅电离室作为带电粒子探测器,在E n=2.54, 4.00, 5.03, 5.50 与5.95 MeV 5 个能点,对64Zn(n, α)61Ni 反应的微分截面进行了实验测量,并通过微分截面对角度的积分得到了反应截面。
实验在北京大学4.5 MV 静电加速器上进行。
2.54 MeV 的单能中子采用固体氚-钛靶T(p, n)3He 反应产生,其余四种能量的准单能中子通过氘气体靶D(d, n)3He 反应获得。
绝对中子通量采用238U(n, f)反应来确定,实验过程中用BF3 长中子计数器进行相对中子通量监测。
测量结果与已有的实验与评价数据进行了比较。
关键词快中子,64Zn(n, α)61Ni 反应,微分截面,截面中图分类号O571.55,TL811+.1快中子引起的64Zn 出射带电粒子核反应数据,包括64Zn(n,p)64Cu 与64Zn(n,α)61Ni 反应的微分截面与截面等,在核工程应用以及核反应机制的研究中都非常重要。
64Zn(n, p)64Cu 反应已有许多实验测量数据,然而64Zn(n,α)61Ni 反应的测量数据却很少,因为61Ni 是稳定核,不能用通常的活化法测量。
He-H2(D1,T2)碰撞(E=0.2 eV)微分散射截面的理论计算

分截面最大, He - D2 次之, He - T 2 碰撞微分截面 最小。从图 2 中看到, 上述三个碰撞体系的 00 02 转动激发微分截面随角度增加的变化趋势也大 致相同, 即先是减小, 在 10 度角左右为最小, 而后 随角度增加而缓慢增加, 其中 He - D2 碰撞微分截 面有少量起伏, 对一确定散射角 00 - 02 微分截面 数值与 00 - 00 正相反: He - D2 次 He - T 2 最大, 对 He - T 2 碰 之, He - H2 最小。从图 3 中看 到, 撞、 00 - 04 转动激发微分截面随角度增加而比较
本文的目的在于通过对c及其同位素替代碰撞截面的理论计算及理论研究了解在实际原子分子相互作用体系中同位素替代对碰撞截面的影响幅度及规对于比较简单的原子与双原子分子碰撞体系密耦方法被认为是一种非常有效的近似计算方法特别是对于处理像c这类简单的系统由于靶分子转动能级间距较大就一般分子热运动范围内的碰撞问题而言只需选取较少几个初始通道即可获得足够精确的收敛的总截面
动态综述——精选推荐

P:"*,!""!
!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
动态综述
!"# 薄膜紫外受激发射研究的最新进展
吕建国,叶志镇,汪 雷
(浙江大学 硅材料国家重点实验室,浙江 杭州 $%&&’()
关键词: +,- 薄膜;紫外受激发射;光泵浦;自形成谐振腔 中图分类号:23)"4 % !# 文献标识码:5 文章编号:#""# $ 6(’(( !""!)") $ "#64 $ "6
)*+*", -./0"+* 1" )*2*03+4 5" 67,30/157*, 8,19:70,*. ;912215" <53 !"# =1792
/7 89:,.;<=,>0 +?9.@?A,,B53& /A9
(8,0,* >*? @0A530,53? 5< 8171+5" B0,*31072,!4*C10"D 6"1/*321,?,E0"DF45: $%&&’(,GEH)
-A2,30+,: +,- C?9, D9EFG, :G ,=HAE F:CAI9:EG D=I !." GAF9J=,K<JC=IG, ?:HA ALJAEEA,C F9JI=GCI<JC<I:E,=MC9J:E :,K AEAJCI=,9J MI=MAIC9AG % 7ECI:H9=EAC GC9F<E:CAK AF9GG9=, 9G :, =<CGC:,K9,; FAI9C =D +,- C?9, D9EFG % +,- C?9, D9EFG ?:HA ;IA:C M=CA,C9:E :MME9J:C9=,G 9, C?A D9AEKG =D <ECI:H9=EAC KACAJC=IG,/01G :,K /1G C?:,NG C= C?A IA:E9@:C9=, =D C?A =MC9J:EEO M<FMAK <ECI:H9=EAC GC9F<E:CAK AF9GG9=, :,K GAED.:GGAFPEAK IAJ9MI=J:E GCI9MA % QAJA,C :KH:,JAG 9, IAGA:IJ? =, +,- D9EFG D=I <ECI:H9=EAC E:GAIG :IA 9,CI=K<JAK 9, KAC:9E %
南京师范大学QMC6散射理论

1 Aeikz ,
2
f ( , )
eikr r
入射波沿z轴正向传播,散射波是由散 射中心向外传播的:
散射波
1 2 Aeikr
f ( , )
eikr ,
r
入射波
(6.1-8)
对于弹性散射,能量(k)不变。容易证明,解(6.1-8)在r →∞时, 满足 SE (6.1-7).
那么入射波几率流密度JZ 和散射波几率流密度JR分别为:
Ql
4
k2
(2l 1) sin2 l
讨论: 1、由f(θ)的表达式(6.2.-14),振幅f(0)的虚部可 以写为:
1
Im f (0) k l 0
(2l 1) sin2 l
Q
4
k
Im
f
(0)
光学定理
2、用分波法求散射截面,归结为计算相移δl.如 果(6.2-16)式中级数收敛很快,只需要计算前几 个相移即可。
§6.1 碰撞过程,散射截面
★ 散射问题也就是碰撞问题,碰撞实验是研究微观粒子 内部结构的重要实验手段,如卢瑟福的α散射实验、夫兰 克-赫兹实验(电子与原子碰撞)等。
★ 碰撞分弹性碰撞与非弹性碰撞。
★ 散射理论的主要任务是计算散射截面。先猜测未知粒 子的结构,理论计算出其散射截面,然后与实验比较,以 判断原先猜测的粒子结构的正确与否。目前我们还无法用 仪器直接观察分子原子等微观粒子的内部结构,实验上能 做的是测出散射粒子的角分布,即散射截面。
Q q( ,)d
★ 单位时间内散射到各个方向的粒子数与入射总粒子数 之比。
3、散射截面的QM描述
★ 以散射中心为原点,U(r)为散射中心势场,其定 态薛定谔方程为:
2 2 U E 2
量子理论的诞生和发展-从量子论到量子力学

量子理论的诞生和发展-从量子论到量子力学杨树伟;刘国钰【摘要】量子理论的诞生和发展经历了多个阶段,概括起来主要有五个时期:黑体辐射和量子假设、老量子理论的兴与衰、对应原理、波粒二象性、量子力学的初步成长,正是因为这些理论的演变,才逐步的推动着量子理论的进步,论文将结合笔者的研究学习所得,从量子论到量子力学进行简要的分析,为业内研究人士提供一定的参考。
【期刊名称】《电大理工》【年(卷),期】2015(000)001【总页数】2页(P30-31)【关键词】量子理论;量子力学;发展【作者】杨树伟;刘国钰【作者单位】铁岭广播电视大学铁岭112000 辽宁省广播电视大学沈阳 110034;铁岭广播电视大学铁岭112000 辽宁省广播电视大学沈阳 110034【正文语种】中文杨树伟刘国钰铁岭广播电视大学 (铁岭112000) 辽宁省广播电视大学(沈阳 110034)从量子理论到量子力学的发展时间并不长,但其间经历了几次质的突破,推动了量子理论的飞速发展,也为现代量子力学的进步做出了巨大的贡献。
但人类关于量子理论的认识仍然存在很多的未知,因而研究量子理论的演变过程具有积极的意义,文中观点存在不足之处,有待进一步的探讨论证。
1.1 黑体辐射和量子假设量子假设和量子概念是普朗克在1900年基于黑体辐射的谱分析的基础上提出的,黑体可以吸收各个方向射来的频率的辐射,并且吸收率达到了100%。
这种黑体可以由壁周围都处在同一温度下的腔体内部来实现,基尔霍夫在1859年发现腔体内部建立的热辐射和材料无关,只与温度相关,并将之称为黑体辐射或腔辐射。
1879年,斯特潘通过实验证实辐射压力是辐射能量密度的1/3;1893年维恩建立了维恩位移定律,并与1896年提出了半经验公式,但是维恩公式只能与实验的高频部门很好的弥合。
1900年,瑞利根据电磁振动,通过对辐射频率和能量密度的理论函数分析,建立了瑞利公式,但瑞利公式在低频部分比较适用,在高频部分不能用;普朗克则基于维恩公式和瑞利公式,将二者相加得出插值公式,称为普朗克公式,在中间的频率的使用于试验数据很符合,普朗克为了给这种公式一个牢固的支撑,引入了一个崭新的能量量子的概念,假设辐射的能量在发射或吸收时是以不可分割的整个能量量子进行,根据这个假设推导出一个平均能量的量子公式,并与之前的普朗克公式相对应。
电子碰撞Ne和类Ne离子电离的三重微分截面理论研究

电子碰撞Ne和类Ne离子电离的三重微分截面理论研究周丽霞;张燕;燕友果【摘要】采用扭曲波玻恩近似理论计算了共面对称几何条件下类Ne离子2p轨道电子在不同出射电子能量下的(e,2e)反应三重微分截面,出射电子能量分别为3,5,7.5,10,15,20,30和50 eV.计算结果表明,随着出射电子能量的增大和核电荷数Z的增大,三重微分截面的幅度逐渐减小.除Ne以外,对其他离子,在出射电子角度为150?附近出现了一个新的结构,对比不同出射电子能量时的(e,2e)反应三重微分截面,发现这个结构的幅度随着出射电子的能量先增大后减小,文中用一种两次两体碰撞过程对这些现象进行了解释.%Electron impact single ionization of atom or molecule, the so-called (e, 2e) reaction, is one of the basic collision processes between electron and atom or molecule. The triple differential cross section (TDCS) of the collision process can provide important data for gas discharge, celestial bodies, and electron-target interaction. A large number of experimental and theoretical studies of (e, 2e) reactions on atom targets have been carried out under different geometric conditions, such as coplanar symmetric geometry, coplanar asymmetric geometry, non-coplanar symmetric geometry, etc. However, few experimental researches of (e, 2e) reaction on ion target have been reported due to the low target source density. The difference in TDCS between atomic target and ionic target can provide more information about the (e, 2e) reaction. Thus the relevant researches on ionic targets are of significance. In this paper, adopting distorted-wave Born approximation (DWBA), the TDCSs of 2 p orbital for Ne and neon-like ions are calculated at different outgoingelectron energies (3, 5, 7.5, 10, 15, 20, 30, and 50 eV) under the condition of coplanar symmetric geometry. The results indicate that the TDCSs decrease with the increase of outgoing electron energy and nuclear charge number Z. Except Ne, the TDCSs of other ions present a new structure at an outgoing electron angle of about 150?. The intensity of the new structure increases with the increase of the outgoing electron energy in a region of 10–20 eV, while it decreases with the increase of the outgoing electron energy in a region of 20–50 eV. We propose a kind of double-binary collision process to rationalize the new structure. The incident electron ionizes the target atom and the following two outgoing electrons exit in the directions symmetric with respect to the incident electron direction. Then these two outgoing electrons are elastically scattered by the target ions and emitted in the backward directions. In order to confirm this explanation, we compare our calculation results with the previously reported experimental and theoretical results of elastic scattering between electron and Ne. Previous research results show that the elastic scattering cross section has a large intensity at a scattering angle of ~150?, and it reaches the largest intensity at an outgoing electron energy of 20 eV. These structural features are consistent with our calculated results, implying that our proposed process is reasonable.【期刊名称】《物理学报》【年(卷),期】2017(066)020【总页数】7页(P40-46)【关键词】(e,2e)反应;扭曲波玻恩近似;三重微分截面;两次两体碰撞【作者】周丽霞;张燕;燕友果【作者单位】中国石油大学(华东)理学院, 青岛 266580;中国石油大学(华东)理学院, 青岛 266580;中国石油大学(华东)理学院, 青岛 266580【正文语种】中文采用扭曲波玻恩近似理论计算了共面对称几何条件下类Ne离子2p轨道电子在不同出射电子能量下的(e,2e)反应三重微分截面,出射电子能量分别为3,5,7.5,10,15,20,30和50 eV.计算结果表明,随着出射电子能量的增大和核电荷数Z的增大,三重微分截面的幅度逐渐减小.除Ne以外,对其他离子,在出射电子角度为150°附近出现了一个新的结构,对比不同出射电子能量时的(e,2e)反应三重微分截面,发现这个结构的幅度随着出射电子的能量先增大后减小,文中用一种两次两体碰撞过程对这些现象进行了解释.电子碰撞原子分子的单次电离过程即(e,2e)反应是电子与原子分子碰撞最基本的过程之一.实验上通过符合测量被电离电子和散射电子获得(e,2e)反应的三重微分截面(TDCS),这一过程满足能量守恒和动量守恒,所以通过研究不同几何条件下的TDCS 可获得(e,2e)反应中的各种动力学和靶粒子结构的重要信息.(e,2e)反应的TDCS的实验数据能够为研究气体放电及天体的准确物理模型提供重要依据,也能够为理论工作者提供电子和靶粒子碰撞的机理以及碰撞过程中各粒子之间的相互作用的重要信息.早期(e,2e)反应的实验研究主要集中在简单的原子如H和He,对共面对称几何条件、共面不对称几何条件、不共面对称几何条件等各种几何条件下的H和He原子的(e,2e)反应进行了大量研究[1−5],这些实验结果为理论方法的发展提供了重要的数据,理论上发展出了Brauner-Briggs-Klar方法[1,2]、扭曲波玻恩近似理论方法(DWBA)[3]、收敛密耦合理论(CCC方法)等[4,5],这些理论方法的计算结果能够很好地与实验结果相符合.近期对(e,2e)反应的实验研究开始转向更复杂的靶粒子,如Ne,Ar,Kr,Xe,Na,Mg,Ca,K等[6−11],这些实验结果对理论方法提出了新的考验,特别是在低能电子入射的情况下,理论计算与实验结果存在较大差异,研究发现在考虑后碰撞相互作用和极化效应后,理论计算结果能更好地与实验结果相符合.在对Xe 原子的研究中,Panajotovic等[9]和Ren等[10]分别研究了Xe原子5p轨道和4d 轨道的精细结构的(e,2e)反应TDCS,并与DWBA理论计算进行了比较.Panajotovic等[9]发现在反应过程中出射电子与靶原子轨道电子之间的自旋交换扭曲波效应非常明显.Ren等[10]测量了不同入射电子能量下4d5/2与4d3/2的TDCS,发现4d5/2与4d3/2的TDCS比率依赖于p电子动量,这一结果说明反应过程中Xe原子4d轨道的相对论效应十分明显.除了这些较复杂的靶粒子外,离子靶的(e,2e)反应也是一个研究的热点方向,但由于离子靶源密度太低,电子碰撞电离实验难以开展,因此相关理论研究具有重要意义,相关理论研究包括类H离子和若干金属离子(e,2e)反应的TDCS[12−15].Khajuria等[13]和Chen等[14]发现碱金属离子(e,2e)反应TDCS的binary峰在某些条件下会分裂为两个,他们用p电子动量空间密度分布解释了碱金属离子binary峰的分裂.在我们以往的工作中,研究了共面不对称几何条件下电子碰撞类Ne离子(Ne,Na+,Mg2+,Al3+和Si4+)2s轨道[16]和共面对称几何条件下Ag+的4p,4s 轨道的(e,2e)反应三重微分截面[17],均发现了一些新结构,并用电子的多次散射对其进行了解释.本文研究了共面对称几何条件下电子碰撞Ne和类Ne离子2p轨道的(e,2e)反应,采用DWBA理论,并考虑反应过程中的后碰撞相互作用(PCI),出射电子能量为3,5,7.5,10,15,20,30和50 eV.本文提出了一种新的两次两体碰撞过程.能量为E0,动量为k0的入射电子与靶粒子发生碰撞,散射电子和被电离电子的能量和动量分别为E1,k1和E2,k2.DWBA理论计算给出反应的TDCS为[18]其中,表示对末态简并态求和及对初态简并态求平均,ψnl为靶的nl轨道波函数,χ(+)是处于靶原子等效局域基态势下的入射电子扭曲波,χ(−)是处于末态靶离子等效局域基态势下的两出射电子的扭曲波,χ(+)和χ(−)都与ψnl正交.等效的局域基态势为直接势VD和交换势VE之和.直接扭曲势VD[18]为r>是r和r′中的较大者,Nnl是轨道nl的电子数.修正的半经典交换势VE为[19] 其中ρ(r)为电子密度.因此等效的局域基态势(扭曲势)为对(1)式乘以Gamow因子Mee,考虑PCI[20],则(e,2e)反应的TDCS为采用扭曲波玻恩近似理论计算了共面对称几何条件下Ne和类Ne离子2p轨道(e,2e)反应的三重微分截面,如图1所示.图1(a)—图1(e)分别给出了Ne,Na+,Mg2+,Al2+和Si4+的(e,2e)反应的三重微分截面,其2p轨道电离能Ei分别为21.6,47.3,80.1,120.0和166.8 eV[21],采用的出射电子能量分别为3,5,7.5,10,15和20 eV.从图1中可以看出,对所有靶粒子,随着出射电子能量的下降,(e,2e)反应三重微分截面在幅度上逐渐降低.比较不同靶粒子同一出射能量时的(e,2e)反应三重微分截面,发现随着核电荷数Z的增大,三重微分截面的幅度也在逐渐下降.图1(a)中,当出射电子能量为20 eV时,Ne原子的2p轨道(e,2e)反应三重微分截面在θ≈8°附近出现了一个肩膀,Rioualt等[22]对Ne的2p和2s轨道(e,2e)反应三重微分截面的实验和理论研究中也曾经发现过这个结构,他们认为由于入射电子进入Ne原子作用区域后会引起Ne原子的极化,这导致了弹性散射概率的增加,因此入射电子与靶粒子发生了一次弹性散射,然后又与轨道电子碰撞发生(e,2e)反应形成了θ≈8°附近的结构.但这个结构并未在其他类Ne离子的(e,2e)反应三重微分截面中出现,如图1(a)—图1(e)所示,可见对其他类Ne离子,这种两次两体碰撞过程是不易发生的. 除Ne原子外,对于其他离子的(e,2e)反应三重微分截面,另一个结构出现在θ≈150°,如图1(b)—图1(e)所示,在出射电子能量小于7.5 eV时,这个结构尚未出现;但当出射电子能量大于等于7.5 eV时,这个结构开始显现,并且随着能量的增加这个结构变得越来越明显,从一个小肩膀逐渐改变形成峰.这个结构的出现,我们认为是发生了一种新的两次两体碰撞过程,该过程如图2所示,入射电子先与靶粒子中的轨道电子发生(e,2e)反应将轨道电子敲出,同时自己被散射,两个电子沿着与入射电子方向对称的方向出射,然后两个出射电子被靶离子弹性散射,沿着后向散射方向θ出射.为了证实我们对θ≈150°处新结构的解释,将本文中的计算结果与文献[23]对电子碰撞Ne原子弹性散射的实验和理论结果进行了对比分析.图3(a)是Williams等和Fon等[23]的实验和理论结果,他们研究了入射电子能量在20 eV时,不同散射角度下电子碰撞Ne的弹性散射截面.从图中可以看出,弹性散射截面随着散射角度的增加先减小后增大,在散射角度为120°—150°范围内,实验和理论结果均表明弹性散射截面随着出射角度的增加单调上升.这与我们的计算结果相符,类Ne离子(e,2e)反应的TDCS均在出射角度θ≈5°出现了新的结构,即在θ≈5°处敲出电子和散射电子与靶离子发生弹性散射的概率较大.文献[23]中还给出了前人对不同能量的入射电子与Ne原子发生弹性散射的实验和理论研究结果,如图3(b)所示.从图中可以看出,在电子能量小于20 eV时,弹性散射截面随着电子能量的增加而急剧增大,当电子能量大于20 eV时,弹性散射截面开始减小.因此我们又计算了Na+,Mg2+,Al3+和Si4+的2p轨道在出射电子能量为30 eV和50 eV时(e,2e)反应三重微分截面,与出射电子能量为10,15和20 eV时的(e,2e)反应三重微分截面进行比较,如图3(c)—图3(f),均发现当出射电子能量从10 eV增大到20 eV时,θ≈150°处的峰幅度也在增大,当电子能量从20 eV增大到50 eV时,θ≈150°处的峰幅度开始减小了,这与图3(b)中前人的实验和理论结果相符合.以上分析均表明我们对θ≈5°的新结构的解释是合理的.我们采用扭曲波玻恩近似理论计算了共面对称几何条件下类Ne离子2p轨道电子在不同出射电子能量下的(e,2e)反应三重微分截面.发现随着出射电子能量的增大和核电荷数Z的增大,(e,2e)反应三重微分截面在逐渐减小.另外,除Ne以外的其他离子,在出射电子角度θ≈5°处出现了一个新的结构,并且这个结构的幅度随着出射电子的能量先增大后减小,我们用一种两次两体碰撞过程对这些现象进行了解释,即入射电子先与轨道电子发生(e,2e)反应,出射电子再与靶离子发生弹性散射,我们的解释能够很好地与前人电子碰撞Ne原子弹性散射的实验和理论结果相符合.A large number of experimental and theoretical studies of(e,2e)reactions on atom targets have been carried out under different geometric conditions,such as coplanar symmetric geometry,coplanar asymmetric geometry,non-coplanar symmetric geometry,etc.However,few experimental researches of(e,2e)reaction on ion target have been reported due to the low target source density.The di ff erence in TDCS between atomic target and ionic target can provide more information aboutthe(e,2e)reaction.Thus the relevant researches on ionic targets are of signi fi cance.In this paper,adopting distorted-wave Born approximation(DWBA),the TDCSs of 2 p orbital for Ne and neon-like ions are calculated at different outgoing electron energies(3,5,7.5,10,15,20,30,and 50 eV)under the condition of coplanar symmetric geometry.The results indicate that the TDCSs decrease with the increase of outgoing electron energy and nuclearcharge number Z.Except Ne,the TDCSs of other ions present a new structure at an outgoing electron angle of about 150°.The intensity of the new structure increases with the increase of the outgoing electron energy in a region of 10–20 eV,while it decreases with the increase of the outgoing electron energy in a region of 20–50 eV.We propose a kind of double-binary collision process to rationalize the new structure.The incident electron ionizes the target atom and the following two outgoing electrons exit in the directions symmetric with respect to the incident electron direction.Then these two outgoing electrons are elastically scattered by the target ions and emitted in the backward directions.In order to con fi rm this explanation,we compare our calculation results with the previously reported experimental and theoretical results of elastic scattering between electron and Ne.Previous research results show that the elastic scattering cross section has a large intensity at a scattering angle of~150°,and it reaches the largest intensity at an outgoing electron energy of 20 eV.These structural features are consistent with our calculated results,implying that our proposed process is reasonable.PACS:34.80.Dp,34.50.Fa DOI:10.7498/aps.66.203401*Project supported by the Fundamental Research Funds for the Central University,China(Grant No.15CX05059A).†Corresponding author.E-mail:**************.cn【相关文献】[1]Brauner M,Briggs J S,Klar H 1989 J.Phys.B:At.Mol.Opt.Phys.22 2265[2]Chen Z J,Ni Z X,Shi Q C,Xu K Z 1998 J.Phys.B:At.Mol.Opt.Phys.31 3803[3]Roder J,Rasch J,Jung K,Whelan Colm T,Ehrhardt H,Allan R J,Walters H R J 1996 Phys.Rev.A 53 225[4]Bray I,Fursa D V,Kheifets A,Stelbovics A T 2002 J.Phys.B:At.Mol.Opt.Phys.35 R117[5]Bray I,Fursa D V,Roder J,Ehrhardt H 1997 J.Phys.B:At.Mol.Opt.Phys.30 L101[6]Naja A,Staicu Casagrande E M,Lahmam-Bennani A,Nekkab M,Mezdari F,JoulakianB,Chuluunbaatar O,Madison D H J 2007 J.Phys.B:At.Mol.Opt.Phys.40 3775[7]Stevenson M A,Lohmann B 2008 Phys.Rev.A 77 032708[8]Haynes M A,Lohmann B,Prideaux A,Madison D H 2003 J.Phys.B:At.Mol.Opt.Phys.36 811[9]Panajotovic R,Lower J,Weigold E 2006 Phys.Rev.A 73 052701[10]Ren X G,Ning C G,Deng J K,Su G L,Zhang S F,Huang Y R 2006 Phys.Rev.A 73 042714[11]Murray A J 2005 Phys.Rev.A 72 062711[12]Shi Q C,Chen Z J,Chen J,Xu K Z 1997 J.Phys.B:At.Mol.Opt.Phys.30 2859[13]Khajuria Y,Chen L Q,Chen X J,Xu K Z 2002 J.Phys.B:At.Mol.Opt.Phys.35 93[14]Chen L Q,Chen X J,Wu X J,Shan X,Xu K Z 2005 J.Phys.B:At.Mol.Opt.Phys.38 1371[15]Khajuria Y,Tripathi D N 1999 Phys.Rev.A 59 1197[16]Zhou L X,Yan Y G 2014 Chin.Phys.B 23 053402[17]Zhou L X,Yan Y G 2012 Chin.Phys.B 21 093401[18]McCarthy I E 1995 Aust.J.Phys.48 1[19]Gianturco F A,Scialla S 1987 J.Phys.B:At.Mol.Phys.20 3171[20]Ward S J,Macek J H 1994 Phys.Rev.A 49 1049[21]Yin Y J 1988 Physical Chemistry Concise Manuals(Beijing:Higher EducationPress)p364(in Chinese)[印永嘉1988物理化学简明手册(北京:高等教育出版社)第364页] [22]Rioualt S,Pochat A,Gelebart F,Allan R J,Whelan C T,Walters H R J L 1995J.Phys.B:At.Mol.Phys.28 5317[23]Fon W C,Berrington K A 1981 J.Phys.B:At.Mol.Phys.14 323。
微分截面

质子与氧原子的碰撞截面利用MATLAB 模拟更加深入理解类Rutherford 散射实验中截面的概念,同时从截面的概念更加深入地理解整个原子核模型。
在理解质子与氧原子的碰撞截面之后,我们就可以将模型拓展来理解重离子在二氧化硅锥形管中的导向与传输。
第一章 微分截面1.1微分截面的概念在原子核物理学中,截面的概念可以很方便地表达特定事件发生的可能性。
微分截面代表对于单位面积内每个靶核,单位入射离子、单位立体角内的散射粒子数。
微分散射截面具有面积的量纲,它的物理意义是,粒子散射到相应方向单位立体角内的每个原子的有效散射截面。
由于计算是在假定原子核不动的情况下进行的。
所以在实际运用中,必须要把它转到实验室系下。
利用微分散射截面,进行抽样操作,即可得到符合物理事实的粒子出射角度的随机角度分布,利用在二氧化硅锥形管表面原子层以下的弹性碰撞模拟中,可以大大运算提高效率。
1.2 微分截面1.2.1 卢瑟福散射截面22124011()()44sin 2c Z Z e E σθθπε= 此时我们考虑的是用大量粒子去轰击一个单原子的情况,这种情况情况非常特殊,我们在现实的实验过程中往往没办法做到大量粒子只轰击一个中心原子的情况,在这种情况下我们就必须用另外一种公式去计算这个反应截面来达到与我们的实验数据尽可能相符合的情况。
而我们这个时候就找到了的Moliere 势。
1.2.2 Moliere 势更加合理的方案是考虑核外电子屏蔽作用的影响。
我们采用Moliere 势作为研究对象,其形式如下:()26/ 1.2/0.3/120()0.10.550.354r p r p r p Z Z e V r e e e πε---=++其中屏蔽参数2/32/31/21120.885()p a Z Z -=+1a 为波尔第一半径 。
但是,相对于卢瑟福散射截面的应用。
Moliere 势在实际运用有一些实际的困难。
在运用卢瑟福散射截面进行模拟时,由于卢瑟福散射截面有解析形式,所以在实际运用中可以利用卢瑟福散射截面的解析形式进行抽样运算,从而得到散射角。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Über die Intensität der Streustrahlung bewegter Freier Elektronenvon W. Pauli, Zürich(3. VI. 33.)§1. Die ProblemstellungDurch die Formel von Klein und Nishina ist die Intensität der Streustrahlung durch anfangs ruhende freie Elektronen bestimmt. Die vorliegende Arbeit entstand aus der Problemstellung, ob gebundene Elektronen gemäss dieser Klein-Nishina’schen Formel streuen, sobald die einfallende Strahlung eine Frequenz besitzt, die gross ist gegen die Ionisierungsfrequenz des Atoms. Bei der Beantwortung dieser Frage ist zunächst zu beachten, dass bei endlichem Streuwinkel die Frequenz der gestreuten Strahlung bei wachsender Frequenz der einfallenden Strahlung gegen einen festen Grenzwert konvergiert und nicht beliebig anwächst. Schon aus diesem Grunde sind Abweichungen der Intensität der gestreuten Strahlung von dem durch die Klein-Nishina-Formel gegebenen Wert zu erwarten, die prozentual endlich bleiben, wenn beliebig anwächstv v ′v Man kann jedoch den Grenzfall betrachten, dass nicht nur beliebig anwächst, sondern auch , und zwar derart, dass der Quotient gegen einen festen Grenzwert konvergiert. Dies setzt allerdings voraus, dass der Streuwinkel mit wachsendem nach Null konvergiert (und zwar wie ). Wir wollen diesen Grenzfall (Auf die Bedeutung dieses Grenzfalles bin ich von W. Heisenberg aufmerksam gemacht worden.)v v ′/v v ′v 1/2v −v →∞ v ′→∞ /v v 1γ′→< (1)Kurz als “Limes L ” bezeichnen. Man könnte nun vielleicht vermuten, dass wenigstens in diesem Limes L die Intensität der Streustrahlung gleich ist dem für die betreffende Frequenz der Streustrahlung durch die Klein-Nishina-Formel gegebenen Wert . Die Prüfung dieser Frage hat jedoch ergeben, dass diese Vermutung nicht zutrifft . Hier wollen wir dies nur für bewegte freie Elektronen zeigen, während die etwas komplizierteren Verhältnisse bei gebundenen Elektronen in der nachfolgenden Arbeit von CASIMIR behandelt werden.v ′Im Fall der bewegten freien Elektronen zeigt es sich nämlich, dass auch im Limes L die Anfangsgeschwindigkeit der Elektronen in der Formel für die Intensität der Streustrahlung pro Frequenzintervall dv ′ nicht herausfällt, Es kann dies als eine Art Dopplereffekt der Streuintensität betrachtet werden.Im folgenden §2 führen wir allgemein die Lorentz-Transformation der Klein-Nishina-Formel durch, während der §3 den Übergang zum Limes L enthält.§2. Lorentz-Transformation der Klein-Nishina-FormelDer Absorptions- oder Schwächungskoeffizient A der in einer bestimmten Richtung einfallenden Strahlung der Frequenz pro Raumwinkel n v d Ω der gestreuten Strahlung ist folgendermassen definiert. Fällt eine bestimmte Anzahl von Quanten der Frequenz in einer gewissen Zeit auf die ruhende, auf der Einfallsrichtung 1N v t nsenkrechte Fläche mit dem Areal , so werden von diesen Quanten q 211N N Ad q=Ω (2) in den räumlichen Winkel d Ω gestreut. Ist 1E N hv =die während der Zeit einfallende Energie, so ist der Streukoeffizient pro räumlichen Winkel definiert durcht S d Ω1E ESd q′=Ω (3) worin 2E N hv ′′=die aus dem während der Zeit einfallenden Bündel gestreute Energie ist. Es gilt also t v Sd Ad v′Ω=Ω (4) Es ist zu beachten, dass die Zeit während der die Quanten gestreut werden, im Falle, wo sich das Elektron bewegt, eine andere ist, als die Zeit , während welcher die einfallenden Quanten durch die ruhende Fläche hindurchtreten. Und zwar ist t ′t 1t t D′= (5) Wennv 11cos 1(v D c cα=−=−)n i (6) Gesetzt wird, worin v die Anfangsgeschwindigkeit der Elektronen und α der Winkel zwischen ihrer Richtung und derjenigen der einfallenden Strahlung bedeutet. Fragen wir also nach dem Bruchteil Bd ΩDer pro Zeiteinheit in den räumlichen Winkel d Ω gestreuten Quanten zu den pro Zeiteinheit Durch die ruhende Querschnittseinheit einfallenden Quanten, so istt B A DA t ==′(7) Dieser Schwächungskoeffiizent B ist es, der durch die allgemeinen von Waller[1] und Dirac[2] angegebenen Formeln gegeben ist, während wir hier den Schwächungskoeffizient (bzw. den aus ihm folgenden Streukoeffizient ) betrachten wollen. Der letztere liegt auch den Betrachtungen in der ursprünglichen Arbeit von Gordon[3] zu Grunde, Es sei noch bemerkt, dass bei gebundenen Elektronen der Unterschied zwischen den Koeffizienten A S B und fortfällt, da in diesem Fall der Mittelpunkt des Elektronenwellenpaketes sich nicht fortbewegt.A Wir bezeichnen nun mit dem Index 0 alle Grössen, die sich auf das Bezugssystem beziehen, in welchem das Elektron zu Beginn des Prozesses ruht, während mit einem Akzent die Grössen bezeichnet werden, die sich auf den Zustand nach dem Streuprozess beziehen. Im System gilt dann nach Klein und Nishina für unpolarisierte Strahlung0K 0K 220000002000sin (v v v A d C d v v v ϑ′′0)Ω=+−′Ω (8) wenn ϑ den Winkel zwischen der Richtung n des einfallenden Quants und der Richtung desStreuquants bedeutet, sodass giltn ′ cos ()n n ϑ′= i (9) und wenn 42402e C m c= (10) gesetzt ist.Da die Lichtquantenzahlen und in GL(2) Invarianten sind, findet man sofort, dass eine Invariante ist.2N 1N (1/)q Ad Ω00110Ad A d q q Ω=Ω (11) Es lässt sich zeigen, dass selbst eine Invariante ist;q 0q q = (12)Sodass auch gilt0Ad A d 0Ω=Ω (13)Um (12) zu beweisen, bemerken wir zunächst, dass bei dem Ansatzx nct a =+ worin die Wellennormale bedeutet, und der Koordinatenursprung in eine zu betrachtende Wellenfront gelegt wird, folgt n ()2()x n ct a n −= i i 2 2222()x c t a n ct a −=+ iDa die Phase [()]v x n ct − i und 222x c t − Invarianten sind, ergibt sich weiter000()(v a n v a n )= i i 2200002()2()a n ct a a n ct a +=+ i iNun liege der Punkt x auf der Wellenfront, sodass ()a n 0= iDann gilt auch00()a n 0= i Das heisst Weltpunkte der Wellenfront liegen auch im anderen Bezugsystem auf der wellenfront. Ferner folgt dann220a a = d.h. alle räumlichen Abstände, von Punkten der Wellenfront bleiben bei Lorentz- transformationen invariant. Dies hat unmittelbar zur Folge, dass die Querdimensionen eines Lichtbündels sich bei Übergang zu einem anderen Bezugssystem nicht ändern. Die Transformationsformeln für die Frequenzen lauten mit Einführung der Abkürzungenv 11cos 1(v D c cα=−=−)n i (6) v 11cos 1(v D c cα)n ′′=−=−′ i (6’) (α und α′bedeuten die Winkel der einfallenden bzw. gestreuten Strahlung mit derGeschwindigkeitsrichtung des Elektrons vor dem Prozess)0v 1cos v D α−= (14)0v 1cos v v α′−′=′ (14’) Wenn2E =die Energie des Elektrons vor dem Prozess bedeutet. Ferner gilt, dav v ()([]n c ci i bzw.v v ()([]n c ci ′′′ i Die Komponenten je eines Vierervektors bilden, als Folge der Invarianz des skalaren Produktes dieser Vierervektoren000(1cos )(1cos )vv v v ϑϑ′′−=− (15) Wobei mit ϑ und 0ϑ die Streuwinkel im ursprünglichen und im Ruhsystem bezeichnet sind.Führen wir die Abkürzungen ein1cos x ϑ−= 01cos x 0ϑ−= (16)So folgt aus (15) und (14), (14’) die Invarianz von0220x x ()DD E m c =′2 (17) Ferner gilt bekanntlich als Folge des Energie- und Impulssatzes im Ruhsystem2000011x ()m c v v h=−′ (180) Also folgtx ()D D E v v h′=−′ (18) Was man auch durch Anwendung des Energie- und Impulssatzes direkt bestätigen kann. Endlich folgt für den in (8) vorkommenden Wert von 20sin ϑ22222200000001111sin 2x x 2()([]m c m c m c m c h E v D vD h E v D vD ϑ=−=−−−′′′′)0 (19) Für die räumlichen Öffnungswinkel der Lichtbündel des gestreuten Strahles gilt ferner die bekannte Transformationsformel220v d v d ′′Ω=Ω (20) Aus (13), (14), (14’) und (20) folgt schliesslich das Endresultat22220002202sin ()(m c v v vD v D Ad A d C v v ED v D vD)ϑ′′′′Ω=Ω=+−′′ (21) worin 20sin δ aus (19) entnommen werden kann. Für den Streukoeffizient findet man sodann gemäss (4) S 2320032sin ()()m c v vD v D Sd C d v ED v D vDϑ′′′Ω=+−′′Ω (22)§3. Übergang zum Limes LWir wollen jetzt noch den Übergang zum Limesv →∞ v ′→∞ /1v v γ′=<machen. Nach (17) und (18) wird dannx →000x →20sin 0ϑ→und wegencos cos cos sin sin cos ααϑαϑϕ′=+ (23) wenn ϕ das Azimut der Richtung der Streustrahlung in Bezug auf die Ebene durch und v istn cos cos αα′→ /1D D ′→Aus (22) folgt also im Limes L222021()(m c Sd C d EDγγΩ=+Ω (24) Wir wollen nun noch den Streukoeffizient umrechnen auf die Strahlung pro . Hiebei ist zu beachten, dass wegen der Abhängigkeit der Grösse dv ′D ′ von ϑ und ϕ gemäss (18) v nicht nurvon ′ϑ, sondern auch von ϕ abhängt. Und zwar folgt bei festem Azimut ϕ gemäss (18) 211v cos cos sin cos sin ()dv h h Ddk dD dk v E v E v c dk ϑααϕϑ′′−=+=++′ also 21v cos 1sin cos sin ()(ED dv E v h dk hc v v ϕcos αϑαϕϑ′−=++′ Im Limes L ist2112()ED kv v h ϑγ→→− also geht 1v ϑgegen Null wie und es ist im Limes 1/2v −L 2dk ED v dv h′−→′ und dies ist im Limes L unabhängig vom Azimut ϕ. Wegenx v S dv Sd Sd d ϕ′′=Ω=folgt also im Limes L22200212()v m c m c dv S dv C h ED vγπ′′′=+ (25) Es fällt also, wie behauptet. die Geschwindigkeit im Endresultat nicht heraus. Für hat manv v 0=0220002012()v m c dv S dv C h v γ0π′′′=+ (25) Sodass im Faktor 20m c EDin (25) die Anfangsgeschwindigkeit des Elektrons explizite vorkommt.Zürich, Physikal. Institut der E. T. H.[1] J. Waller, ZS. f. Phys. 61, 837, 1930, GL.(23’’).[2] P. M. A. Dirac, Proc. Cambr. Phil. Soc. 26, 361, 1930.[3] W. Gordon, ZS. f. Phys. 40, 117, 1926.。
