一次函数与一元一次方程一元一次不等式的关系PPT课件
一元一次不等式与一次函数

一元一次不等式与一次函数【基础知识精讲】1.一元一次不等式与一次函数的关系。
两个一次函数有时根据需要,要比较其函数值的大小,这时问题就转化为一元一次不等式的问题。
另一方面,利用解不等式的方法也可以求出两个一次函数的值的大小。
事实上,不等式与函数和方程是紧密联系的一个整体。
2.一次函数的图象与一元一次不等式的关系。
一次函数y=kx+b(k≠0)的图像是一条直线,当kx+b>0时,表示图像在x轴上方的部分;当kx+b=0时,表示直线与x轴的交点;当kx+b<0时,表示图像在x轴下方的部分。
【考点聚焦】本章一元一次不等式与一次函数是中考热点,随着素质教育的逐步发展,突出了对创新意识的考查,加大了对“三个一次”(即一元一次方程,一次函数,一元一次不等式)综合应用考查及解决实际问题的考查。
题型有选择题、填空题及解决实际问题(多为压轴题)。
【典例精析】例1作出函数y=x-3的图象如图所示,并观察图象回答下列问题:(1)x取哪些值时,y>0;(2)x取哪些值时,y<0;(3)x取哪些值时,y>3。
思路点拨:首先要认清一次函数的图象是一条直线,两点确定一条直线,所以需要知图象上两点的坐标,可取(3,0)和(0,-3)。
解:由图象可知:(1)当x>3时,y>0;(2)当x<3时,y<0;(3)当x>6时,y>3。
评注:(1)两点确定一条直线。
(2)大于往右看,小于往左看。
【试解相关题】兄弟俩赛跑,哥哥先让弟弟跑9米,然后自己才开始跑。
已知弟弟每秒跑3米,哥哥每秒跑4米,列出函数关系式,画出函数图象,观察图象回答下列问题:(1)何时弟弟跑在哥哥前面?(2)何时哥哥跑在弟弟前面?思路点拨:此题两问均牵扯到不等式问题,但需先列函数关系式。
解:设当时间为x秒时,跑过的路为y米,则y哥哥=4x,y弟弟=3x+9如图所示,由图象知9秒前弟弟跑在哥哥前面;9秒后,哥哥跑在弟弟前面。
评注:通过以上两例,体会:刻画运动变化的规律需要用函数模型;刻画运动变化过程中的某一瞬间需要用方程模型。
沪科版八年级数学上册课件一次函数第六课时一次函数与一元一次方程和一元一次不等式的关系

-2
直线y=mx+n(如图所示),
则方程mx+n=0的解是 x=-2 .
3、对于y1=2x-1, y2=4x-2,下列说法:
①两直线平行; ②两直线交于y轴于同一点;
③两直线交于x轴于同一点; ④方程2x-1 =0与
4x-2=0的解相同; 其中正确的是 ③ ④
⑤当x=1时,y1=y2=1. (填序号)
2x 20
x 10
两个问题实际上是同一个问题.
(3)画出函数y=2x+20的图象,并确定它 与x轴的交点坐标.
y
从“函数图 象”上看
y=2x+20 20
-10
0x
(思考:直线 y=2x+20与x轴交点坐标为(
___-_1,0____0_),这说明方程2χ+20=0的解
是x=_____)
序号 一元一次方程问题 一次函数问题
一次函数与一元一次方程的关系
求ax+b=0(a,b是 常数,a≠0)的解.
从“函数值”看
x为何值时
函数y= ax+b的值 为0.
求ax+b=0(a, b是 常数,a≠0)的解.
从“函数图象”看
求直线y= ax+b
与 x 轴交点的横 坐标.
例1.利用图象解一元一次方程x+3=0
解:作y=x+3图象如下
作出一次函数y=2x-5的图象 x … 0 2.5 …
y=2x-5 … -5 0 …
y
4
y=2x-5
3
2
1
-2 -1-10 1 2 3 4 5 x
-2 -3 -4 -5
视察图象回答下列问题: (1)X取何值时,2x-5=0
一次函数与方程、不等式(共15张PPT)

04 综合练习与提高
综合练习题一
总结词
理解一次函数与方程、不等式之间的 关系
详细描述
通过解决一系列的练习题,理解一次 函数与方程、不等式之间的关系,掌 握将实际问题转化为数学模型的方法 。
综合练习题二
总结词
掌握一次函数的图像和性质
详细描述
通过绘制一次函数的图像,理解函数的增减性、截距等性质,掌握利用图像解决实际问题的技巧。
一次函数与不等式的实际应用
一次函数与不等式在实际生活中有着 广泛的应用。例如,在购物时,我们 可以通过比较商品的价格和折扣率来 选择最划算的购买方案,这需要用到 一元一次不等式的知识。
另外,在生产活动中,我们可以通过 控制生产成本和产量之间的关系来制 定最优的生产计划,这也需要用到一 元一次不等式R。
02 一次函数与方程
一次函数与一元一次方程的关系
一次函数是形如$y = kx + b$的函数,其中$k$和$b$是常数, 且$k neq 0$。一元一次方程是只含有一个变量的方程,其形式 为$ax + b = 0$,其中$a$和$b$是常数,且$a neq 0$。
一次函数与方程、不等式(共15张 ppt)
目录
• 一次函数的基本概念 • 一次函数与方程 • 一次函数与不等式 • 综合练习与提高 • 总结与回顾
01 一次函数的基本概念
一次函数的定义
一次函数
一般形式为y=kx+b(k≠0),其 中x为自变量,y为因变量,b为截 距,k为斜率。
线性函数
特殊的一次函数,形式为y=kx+b (k≠0,b=0)。
一次函数在实际问题中的应用
一次函数可以用于解决实际问题,如路程、速度和时间问题、价格和销售问题等。
第1讲-用一次函数看方程、不等式
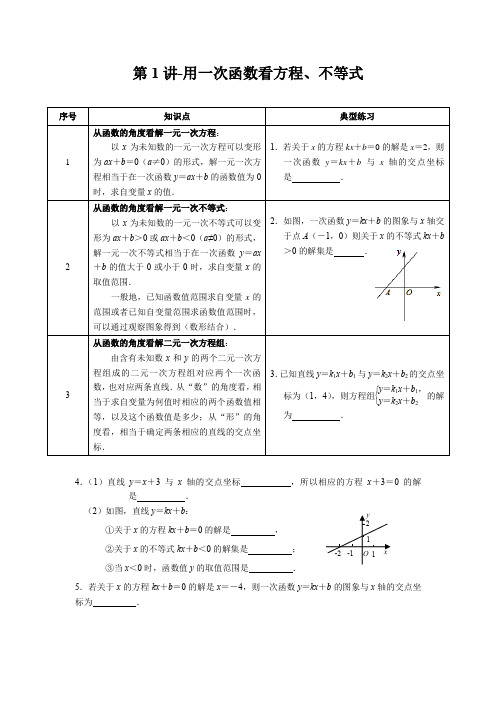
y2 1 1 O -2 -1x第1讲-用一次函数看方程、不等式序号知识点典型练习1从函数的角度看解一元一次方程:以x 为未知数的一元一次方程可以变形为ax +b =0(a ≠0)的形式,解一元一次方程相当于在一次函数y =ax +b 的函数值为0时,求自变量x 的值.1.若关于x 的方程kx +b =0的解是x =2,则一次函数y =kx +b 与x 轴的交点坐标是 .2从函数的角度看解一元一次不等式:以x 为未知数的一元一次不等式可以变形为ax +b >0或ax +b <0(a ≠0)的形式,解一元一次不等式相当于在一次函数y =ax+b 的值大于0或小于0时,求自变量x 的取值范围.一般地,已知函数值范围求自变量x 的范围或者已知自变量范围求函数值范围时,可以通过观察图象得到(数形结合). 2.如图,一次函数y =kx +b 的图象与x 轴交于点A (-1,0)则关于x 的不等式kx +b >0的解集是 .3从函数的角度看解二元一次方程组: 由含有未知数x 和y 的两个二元一次方程组成的二元一次方程组对应两个一次函数,也对应两条直线.从“数”的角度看,相当于求自变量为何值时相应的两个函数值相等,以及这个函数值是多少;从“形”的角度看,相当于确定两条相应的直线的交点坐标. 3.已知直线y =k 1x +b 1与y =k 2x +b 2的交点坐标为(1,4),则方程组⎩⎨⎧y =k 1x +b 1,y =k 2x +b 2的解为 .4.(1)直线y =x +3与x 轴的交点坐标 ,所以相应的方程x +3=0的解是 .(2)如图,直线y =kx +b :①关于x 的方程kx +b =0的解是 , ②关于x 的不等式kx +b <0的解集是 ; ③当x <0时,函数值y 的取值范围是 .5.若关于x 的方程kx +b =0的解是x =-4,则一次函数y =kx +b 的图象与x 轴的交点坐标为 .-21O yx-3Oxy -6 y 1=kx yy 2=ax+bx -2O -4 P6.已知一次函数y =kx +b 的图象,如图所示,当x <0时,y 的取值范围是( ).A .y >0B .y <0C .-2<y <0D .y <-27.如图,已知一次函数图象y =-2x -6,利用图象回答: (1)不等式-2x -6>0解集是 ,不等式-2x -6<0解集是 ;(2)函数图象与坐标轴围成的三角形的面积为 ; (3)当y =-4时,则x = ,当y =2时,则x = ;(4)如果y 的取值范围-4<y ≤2,则x 的取值范围 ;(5)如果x 的取值范围-3≤x ≤3,则y 的最大值是 ,最小值是 ; (6)若直线y =3x +4和直线y =-2x -6交于点A ,则点A 的坐标 .8.如图所示,已知直线y 2=ax +b 和直线y 1=kx 的图象交于点P ,利用图象回答:(1)关于二元一次方程组⎩⎨⎧y =ax+b ,y =kx的解是 ,则两直线的交点坐标是 ;(2)当y 2<y 1时,则x 的取值范围是 ; (3)当ax +b ≥kx 时,则x 的取值范围是 ; (4)当ax ≤kx -b 时,则x 的取值范围是 .9.(15海珠期末)直线y =x +1与直线y =-2x +a 的交点在第一象限,则a 的取值可以是( ). A .2B .1C .0D .-110.(15一中期末)如图,已知函数y1=3x+b和y2=ax-3的图象交于点P(-2,-5),则不等式3x+b>ax-3的解集为.11.(13太原期末改编)如图,直线l1:y1=x+1与直线l2:y2=mx+n相交于点P(1,b),直线y2与x轴交于点A(4,0).(1)求b的值并直接写出关于x,y的方程组1y xy mx n=+⎧⎨=+⎩的解;(2)求直线l2的表达式;(3)判断直线l3:y3=nx+m是否也经过点P?请说明理由.(4)若y3>y2>0,则x的取值范围是________________.12.已知一次函数y =kx+b的图象,如图所示,当y<0时,x的取值范围是().A.x>0B.x<0C.0<x<1D.x<113.(11广州)当实数x的取值使得x-2有意义时,函数y=4x+1中y的取值范围是().A.y≥-7B.y≥9 C.y>9D.y≤9 14.(15海珠期末)如图,直线y1=x+b与y2=kx-1相交于点P,点P的横坐标为-1,则关于x的不等式x+b>kx-1的解集在数轴上表示正确的是().A.B.C.D.15.如图,1l反映了某公司的销售收入与销售量的关系,2l反映了该公司产品的销售成本与销售量的关系,当该公司盈利(收入大于成本)时,销售量().A.小于3t B.大于3t C.小于4t D.大于4t第14题第15题16.(16天河期末)一次函数y1=kx+b与y2=x+a的图象如图,则下列结论①k<0;②a>0;③当x<4时,y1<y2;④b<0.其中正确的结论的个是().A.4个B.3个C.2个D.1个-2yO1x17.(16南充)小朱和爸爸从家步行去公园,爸爸先出发一直匀速前行,小朱后出发.家到公园的距离为2500m,如图是小明和爸爸所走的路程s(m)与步行时间t(min)的函数图象.(1)直接写出小朱所走路程s与时间t的函数关系式;(2)小朱出发多少时间与爸爸第三次相遇?(3)在速度都不变的情况下,小朱希望比爸爸早20min到达公园,则小朱在步行过程中停留的时间需作怎样的调整?18.(15衢州)高铁的开通,给衢州市民出行带来了极大的方便,“五一”期间,小卓卓和小越越相约到杭州市的某游乐园游玩,小卓卓乘私家车从衢州出发1小时后,小越越乘坐高铁从衢州出发,先到杭州火车站,然后再转出租车去游乐园(换车时间忽略不计),两人恰好同时到达游乐园,他们离开衢州的距离y(千米)与乘车时间t(小时)的关系如图所示.请结合图象解决下面问题:(1)高铁的平均速度是每小时多少千米?(2)当小越越达到杭州火车东站时,小卓卓距离游乐园还有多少千米?(3)若小卓卓要提前18分钟到达游乐园,问私家车的速度必须达到多少千米/小时?y (千米)游乐园t(小时)19.(14海珠期末)今年龙舟赛甲乙两队同时出发,其中甲、乙两队在比赛时,路程y (千米)与时间x (小时)的函数关系如图所示.甲队在出发2.5小时到达终点.(假设乙队速度不变)(1)写出比赛全程多少千米?谁先到达终点?乙队花多少时间到达终点? (2)求乙队何时追上甲队?(3)求在比赛过程中,甲乙两队何时相距最远?20.(1)(12恩施州)如图,直线y =kx +b 经过A (3,1)和B (6,0)两点,则不等式组0<kx +b<13x 的解集为 .(1) (2)(2)如图,直线y =kx +b 经过A (2,1),B (-1,-2)两点,则不等式组12x >kx +b >-2的解集为 .21.(15广雅期末)若直线y =-2x +m 与直线y =2x -1的交点在第四象限,则m 的取值范围是( ). A .m >-1 B .m <1C .-1<m <1D .-1≤m ≤1yA 2 1 xB 0 -1 -2 -3 -2-1 1 2 322.依照题意,解答下列问题:(1)如图①,已知直线y =2x +4与x 轴,y 轴分别交于A ,B 两点,请在图①中画出直线y =-12x +4,并探究两函数的图象与x 轴围成的三角形的特点;(2)如图②,已知点M 和点N 的坐标分别为(3,4)和(-2,-1),问在y 轴上是否存在一点P ,使△MNP 是以点M 或点N 为直角顶点的直角三角形?若存在,请求出P 的坐标;若不存在,请说明理由.y xB AO(图①))yx MN O(图②))第一讲-参考答案1.(2,0) 2.x >-13.⎩⎨⎧x =1,y =44.(1)(-3,0),x =-3; (2)①x =-2;②x <-2;③y <1. 5.(-4,0)6.D 7.(1)x <-3,x >-3; (2)9;(3)-1,-4; (4)-4≤x <-1;(5)0,-12;(6)(-2,-2).8.(1)⎩⎨⎧x =-4,y =-2,(-4,-2);(2)x >-4;(3)x ≤-4;(4)x ≥-4.9.A10.x >-211.(1)b =2,12x y =⎧⎨=⎩; (2)2833y x =-+;(3)由(2)可知m =23-,n =83,∴ y =83x -23,当x =1时,y =2.∴直线l 3:y =nx +m 也经过点P . (4)1<x <4.12.D 13.B 14.A 15.D 16.D17.解:(1)s =50(020)1000(2030)50500(3060)t t t t t ⎧⎪⎨⎪-⎩≤≤<≤<≤;(2)设小朱的爸爸所走的路程s 与步行时间t 的函数关系式为:s =kt +b ,则251000250k b b +=⎧⎨=⎩,解得30250k b =⎧⎨=⎩,则小朱的爸爸所走的路程与步行时间的关系式为:s =30t +250, 当50t -500=30t +250,即t =37.5min 时,小朱与爸爸第三次相遇; (3)30t +250=2500,解得,t =75,则小朱的爸爸到达公园需要75min , ∵小朱到达公园需要的时间是60min ,∴小朱希望比爸爸早20min 到达公园,则小朱在步行过程中停留的时间需减少5min .18.解:(1)v =2402-1=240(km/h ).答:高铁的平均速度是每小时240千米; (2)设乘坐高铁时路程与时间的关系式为y =kt +b ,当t =1时,y =0,当t =2时,y =240,得:⎩⎨⎧0=k +b 240=2k +b ,解得:⎩⎨⎧k =240b =-240,故把t =1.5代入y =240t -240,得y =120, 设乘坐私家车时路程与时间的关系式为y =at , 当t =1.5,y =120,得a =80,∴y =80t , 当t =2,y =160,216-160=56(千米), ∴小卓卓距离游乐园还有56千米; (3)把y =216代入y =80t ,得t =2.7,2.7-1860=2.4(小时),216 2.4=90(千米/时).∴小卓卓要提前18分钟到达游乐园,私家车的速度必须达到90千米/小时.19.解:(1)35千米;乙;3516小时; (2)对于乙队,x =1时,y =16,所以y =16x ,对于甲队,出发1小时后,设y 与x 关系为y =kx +b ,把x =1,y =20和x =2.5,y =35代入,得⎩⎨⎧20=k +b35=2.5k +b,则y =10x +10.联立方程组,⎩⎨⎧y =16x y =10x +10,得x =53,即:出发1小时40分钟后,乙队追上甲队; (3)1小时之内,两队相距最远距离是4千米,即当x =3516时,y 甲=10×3516+10=31.875,y 乙=35,y 甲-y 乙=35-31.875=3.125; 当x =1时,y 甲-y 乙=20-16=4;∵3.125<4,所以比赛过程中,甲、乙两队在出发后1小时相距最远.20.(1)3<x <6;(2)-1<x <2. 21.C22.(1)图略;用勾股定理的逆定理可以证明两函数与x 轴围成的三角形是一个直角三角形; (2)设P (0,y ),①当PM为斜边时,PN2+MN2=PM2,即(-2)2+(-1-y)2+25+25=32+(4-y)2,解得:y=-3,即P为(0,-3);②当PN为斜边时,PM2+MN2=PN2,即32+(4-y)2+25+25=(-2)2+(-1-y)2,解得:y=7,即P为(0,7);综上所述,在y轴上存在一点P,使△MNP是直角三角形,P为(0,-3)或(0,7).。
一次函数与一元一次方程、不等式

8、人们常用“心有余而力不足”来为自 己不愿 努力而 开脱, 其实, 世上无 难事, 只怕有 心人, 积极的 思想几 乎能够 战胜世 间的一 切障碍 。 9、如果你希望成功,当以恒心为良友, 以经验 为参谋 ,以当 心为兄 弟,以 希望为 哨兵。 ——爱 迪生
1 知识小结
任何一元一次方程都可以转化为ax+b=0(a,b为常 数,a≠0)的形式,所以解一元一次方程可以转化为当某 个一次函数的函数值为0时,求相应的自变量的值.从图 象上看,相当于已知直线y=ax+b,确定它与x轴的交点 的横坐标.即“形”题用“数”解,“数”题用“形”解, 充分体现了数形结合的思想.
1 【2016·桂林】如图,直线y=ax+b过点A(0,2) 和点B(-3,0),则方程ax+b=0的解是( D ) A.x=2 B.x=0 C.x=-1 D.x=-3
2 【中考·合肥】已知方程 1 x+b=0的解是x=
2 -2,下列可能为直线y=
1 2
x+b的图象的是
( C)
3 如图,若一次函数y=-2x+b的图象交y轴于点
因为任何一个以x为未知数的一 元一次方程都可以变形为ax+b=0(a≠0)的形式,所以解 一元一次方程相当于在某个一次函数y=ax+b的函数值为 0时,求自变量x的值.
一次函数与一元一次方程的联系: 任何一个以x为未知数的一元一次方程都可以变
形为ax+b=0(a≠0,a,b为常数)的形式,所以解一 元一次方程可以转化为:求一次函数y=ax+b(a≠0, a,b为常数)的函数值为0时,自变量x的取值;反映 在图象上,就是直线y=ax+b与x轴的交点的横坐标.
一次函数与一元一次方程、不等式

2
易错小结
-1<x<2
易错点:利用函数图象解不等式时,对函数值和点的坐 标的关系不理解导致出错(数形结合思想).
例1
利用函数图象解出x:3x-2=x+4.
先将方程化为ax+b=0的形式, 再在坐标系中画出函数y=ax+ b的图象,然后观察出直线y= ax+b与x轴的交点坐标,从而 取定所求x的值.
导引:
由3x-2=x+4得2x-6=0画函 数y=2x-6的图象,如图所示, 由图可知,直线y=2x-6与x轴的交点为(3,0), 所以x=3.
3
C
已知一次函数y=2x+n的图象如图所示,则方程2x+n=0的解可能是( ) A.x=1 B.x= C.x=- D.x=-1
4
C
【2017·湘潭】一次函数y=ax+b的图象如图所示,则不等式ax+b≥0的解集是( ) A.x≥2 B.x≤2 C.x≥4 D.x≤4
5
B
【2017·菏泽】如图,函数y1=-2x与y2=ax+3的图象相交于点A(m,2),则关于x的不等式-2x>ax+3的解集是( ) A.x>2 B.x<2 C.x>-1 D.x<-1
D
【中考·合肥】已知方程 x+b=0的解是x= -2,下列可能为直线y= x+b的图象的是 ( )
2
C
如图,若一次函数y=-2x+b的图象交y轴于点A(0,3),则不等式-2x+b>0的解集为( ) A.x> B.x>3 C.x< D.x<3
2
已知小刚从家出发7分钟时与家的距离是1 200米, 从上公交车到他到达学校共用10分钟.下列说法: ①公交车的速度为400米/分钟; ②小刚从家出发5分钟时乘上公交车; ③小刚下公交车后跑向学校的速度是100米/分钟; ④小刚上课迟到了1分钟.其中正确的有( ) A.4个 B.3个 C.2个 D.1个
第6课时 一次函数与一元一次方程、一元一次不等式PPT课件(沪科版)

B.x<-3
C.x>3
D.x<3
11.如图所示,某公司市场营销部的营销人员的个人收入与 其每月的销售量成一次函数关系,由图中给出的信息,营销人 员没有销售量时的收入是( B )
A.310元 B.300元 C.290元 D.280元
12.已知关于x的方程ax-5=7的解为x=1, 则一次函数y=ax
解:(1)设大枣粽子的单价为 x 元/盒,普通粽子的单价为 y 元/盒, 根据题意得x2-x+y=4y1=5,300,解得xy==6405,. 答:大枣粽子的单价为 60 元/盒,普通粽子的单价为 45 元/盒
(2)①设买大枣粽子 x 盒,则购买普通粽子(20-x)盒,买水果共用了 w 元,根据题意得,w=1 240-60x-45(20-x)=1 240-60x-900+45x=- 15x+340,故 w 关于 x 的函数关系式为 w=-15x+340;
-12与x轴交点的坐标为 (1,0)
.
13.已知一次函数y=kx+b(k,b是常数,且k≠0),x与y的部分对 应值如下表所示,那么不等式kx+b<0的解集是____.x>1
x
- 2
- 1
0
1
2
3
y3
2
1
0
-- 12
14.如图,经过点B(-2,0)的直线y=kx+b与直线y=4x+2相
交于点A(-1,-2),则不等式4x+2<kx+b<0的
经过(D )
A.(2,0) B.(0,3) C.(0,4) D.(0,-3)
4.(4 分)如图,一次函数 y=kx+b 的图象经过点(2,0)与(0,3),
则关于 x 的不等式 kx+b>0 的Байду номын сангаас集是( A )
一次函数与一元一次不等式-市级优质课PPT

目录
• 一次函数简介 • 一元一次不等式简介 • 一次函数与一元一次不等式的关系 • 实例解析 • 总结与展望
01 一次函数简介
一次函数的定义
01
一次函数是形如$y = kx + b$的 函数,其中$k$和$b$是常数,且 $k neq 0$。
02
$k$是斜率,决定了函数的增减性 ;$b$是截距,决定了函数与y轴 的交点。
一次函数的图像
一次函数的图像是一条直线,其斜率为$k$,与y轴的交点为 $(0, b)$。
当$k > 0$时,函数图像为增函数;当$k < 0$时,函数图像 为减函数。
一次函数的性质
一次函数的图像是直线,且斜率固定。 一次函数具有唯一解,即对于任意给定的自变量值,都有唯一的因变量值与之对应。
一次函数的值域和定义域都是全体实数集。
分析一次函数与一元一次不等式的重点和难点
重点
理解和掌握一次函数的性质以及一元一次不等式的解法。
难点
如何在实际问题中应用一次函数和一元一次不等式的知识,以及如何解决一些复杂的问 题。
对未来学习的展望
深入学习函数的性质和不等式的解法, 进一步加深对函数和不等式的理解。
学习其他类型的函数和不等式,如二 次函数、一元二次不等式等,以扩展 知识面和增强数学能力。
02 一元一次不等式简介
一元一次不等式的定义
总结词
一元一次不等式是数学中一个基础概 念,它是指只含有一个变量,且该变 量的指数为1的不等式。
详细描述
一元一次不等式的一般形式为 ax + b > c,其中a、b、c是常数,且a≠0。这个 不等式表示一个直线在坐标系上的上半 部分或下半部分。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2、一次函数与二元一次方程组的关系从“形”的角度看: 二元一次方程组的解就是两条相应直线交点的横、纵坐标。
y
y1=k1x+b1
0 y2=k2x+b2
一次函数y1=k1x+b1与y2=k2x+b2的图 象如图所示,观察图象回答以下问题。
1、直线y1=k1x+b1与直线y2=k2x+b2 的交点坐标为_____(2_,;1)
y =x+5
y 的x 解5 为______ y 25
y =0.5x+15
2、观察图象,回答以下问题。
b
(1)a=__5__,b=_1_5__;
(2)直线y=0.5x+15与直线y=x+5
a
的交点坐标为__(_2_0_,2_5_)__。
O
x
1、求两条直线的交点坐标就是求两个一次函数解析式函 数值相等时对应的自变量的值,以及这个函数值是多少。
0时,求自变量的值。
5
一次函数y=kx+b的图象如图所示, 则不等式kx+b>0的解集为_x_>_-_1_。
任何一个一元一次不等式都可以转化为 kx+b>0或kx+b<0(k,b为常数,k≠0)的形式。
解一元一次不等式kx+b>0(k≠0),相当于一次函数 y=kx+b的函数值大于0时,求自变量的取值范围。
解一元一次不等式kx+b<0(k≠0),相当于一次函数 y=kx+b的函数值小于0时,求自变量的取值范围。
6
一次函数y=kx+b的图象如图所示, 则不等式kx+b>2的解集为_x_>__0_。
任何一个一元一次不等式都可以转化为 kx+b>0或kx+b<0(k,b为常数,k≠0)的形式。
解一元一次不等式kx+b>0(k≠0),相当于一次函数 y=kx+b的函数值大于0时,求自变量的取值范围。
xb k
一次函数y=kx+b的图 象与x轴的交点坐标
( b ,0) k
方程kx+b=0的解即为直线y=kx+b与x轴交点的横坐标
解方程kx+b=0(k≠0),相当于一次函数y=kx+b的函数值为
0时,求自变量的值。
3
已知方程mx+n=0的解为x=-3,则直线 y=mx+n与x轴的交点是__(_-3_,_0_)__.
二元一次方程组的关系
10
任何一个二元一次 方程都可以转化为 y=kx+b(k,b为常数, k≠0)的形式。
二元一次方程 y=kx+b的一xy 个mn解 对应着直线y=kx+b
的一个点的(m坐, n)
标。
每个二元一次方程 y=kx+b都对应一个 一次函数y=kx+b。
每个一次函数 y=kx+b对应一条直 线y=kx+b。
任何一个一元一次
方程都可以转化为 kx+b=0(k,b为常数, k≠0)的形式。
xb k
一次函数y=kx+b的图 象与x轴的交点坐标
( b ,0) k
方程kx+b=0的解即为直线y=kx+b与x轴交点的横坐标
解方程kx+b=0(k≠0),相当于一次函数y=kx+b的函数值为
0时,求自变量的值。
11
由含有未知数x和y的 两个二元一次方程组 成的一个二元一次方 程组。
二元一次方程组的解 对应着两条直线 ________________ _。
两个二元一次方程 即一个二元一次方程 组对应两个一次函数。
两个一次函数对应 两条直线。
12
1、二元一次方程组
y
y 0.5x 15
x 20
19.2.3 一次函数与一元一次方程、
一元一次不等式的关系
1
认真阅读课本 P96~P97问题3以上内容
试着完成《百练》 P63.教材训练1、2
2
一次函数y=kx+b的图象如图所示, 则方程kx+b=0的解为__x_=__-_1 ___。
任何一个一元一次
方程都可以转化为 kx+b=0(k,b为常数, k≠0)的形式。
ห้องสมุดไป่ตู้
x<2.5
1
2.5
(4) x取哪些值时,kx+b>3?
-1 0 1 2 3 4 5 6 -1
x
x>4
-2
(5) x取哪些值时,-5<y<0 -3
0<x<2.5
-4
(6) y取哪些值时,2.5<x<4 -5
0<y<3
8
SUCCESS
THANK YOU
2019/8/2
19.2.3 一次函数与二元一次方程、
4
直线y=kx-3与x轴的交点是(-1,0),则kx-3=0 的解是x=-1. √
任何一个一元一次
方程都可以转化为 kx+b=0(k,b为常数, k≠0)的形式。
xb k
一次函数y=kx+b的图 象与x轴的交点坐标
( b ,0) k
方程kx+b=0的解即为直线y=kx+b与x轴交点的横坐标
解方程kx+b=0(k≠0),相当于一次函数y=kx+b的函数值为
解一元一次不等式kx+b<0(k≠0),相当于一次函数 y=kx+b的函数值小于0时,求自变量的取值范围。
7
如图为y=kx+b的图象,观察图象回答下列问题:
(1) x取何值时,kx+b=0?
x=2.5
y
(2) x取哪些值时, y>0?
4
x>2.5
3
y=2x-5
(3) x取哪些值时,kx+b<0? 2
二元一次方程组的解 对应着两条直线 _交__点_的__横__、__纵__坐_标__。_ _。
两个二元一次方程 对应两个一次函数。
两个一次函数对应 两条直线。
15
一次函数与二元一次方程, 二元一次方程组的关系
16
《百练》 P69~P70 中考真题训练
17
SUCCESS
THANK YOU
2019/8/2
2、二元一次方程组
x (2,-1)
的 yy解21 为kk12xx__bb_12_____
x2
y
1
3、当y1=y2时,x=_____2; 4、当y1>y2时,x_____; 2 5、当y1<y2时,x_____; 2
14
由含有未知数x和y的 两个二元一次方程组 成的一个二元一次方 程组。
