2粘性流体动力学基础
合集下载
粘性流体动力学基础
f 1 p = dv dt
ρ
1 p dvx fx = ρ x dt 1 p dv y fy = ρ y dt 1 p dvz fz = ρ z dt
方程中， f ：作用在单位质量流体上的质量力
1
ρ
p ：作用在单位质量流体上的表面力
dv ：作用在单位质量流体上的惯性力 dt
这一方程就是以应力形式表示的运动微分方程。
在这一方程中，通常质量力 f x 、 f y 、 f z 是已知的，对不可压缩流体 ρ
τ 也是已知的。方程组中的未知量有：三个法向应力 pii ，六个切向应力 ij ，
三个速度分量vi 。 运动微分方程加上连续性方程共四个， 无法求解 12 个未 知量，下面寻求补充方程。 三 、 切应力分量之间的关系 切应力分量之间存在着一定的联系， 应用力矩平衡原理可以证明切应 力具有对称性。 τ xy = τ yx τ yz = τ zy
τ yz dz τ zy dz τ yz dxdydz τ zy dxdydz + dxdydz dxdydz = 0 y 2 z 2
略去高阶无穷小，可得：
τ yz = τ zy
同理可得：
τ xy = τ yx
τ xz = τ zx
可见应力分量中的切应力是两两对称的。 四 、 切应力与变形速度的关系 牛顿内摩擦定律（平面流动） dv dα τ = x =
M ，六面体为 ABCD, A 点的应力为：
pxx τ yx τ zx
τ xy
p yy
τ zy
τ xz τ yz
pzz
其方向确定为：法向应力以内法线方向为正，切向应力（正） ，过 A 点 的三个面上切向应力与坐标方向相反，其它三个面则相同。 采用泰勒级数展开并取前二项可写出其它三个面上的应力分量。
ρ
1 p dvx fx = ρ x dt 1 p dv y fy = ρ y dt 1 p dvz fz = ρ z dt
方程中， f ：作用在单位质量流体上的质量力
1
ρ
p ：作用在单位质量流体上的表面力
dv ：作用在单位质量流体上的惯性力 dt
这一方程就是以应力形式表示的运动微分方程。
在这一方程中，通常质量力 f x 、 f y 、 f z 是已知的，对不可压缩流体 ρ
τ 也是已知的。方程组中的未知量有：三个法向应力 pii ，六个切向应力 ij ，
三个速度分量vi 。 运动微分方程加上连续性方程共四个， 无法求解 12 个未 知量，下面寻求补充方程。 三 、 切应力分量之间的关系 切应力分量之间存在着一定的联系， 应用力矩平衡原理可以证明切应 力具有对称性。 τ xy = τ yx τ yz = τ zy
τ yz dz τ zy dz τ yz dxdydz τ zy dxdydz + dxdydz dxdydz = 0 y 2 z 2
略去高阶无穷小，可得：
τ yz = τ zy
同理可得：
τ xy = τ yx
τ xz = τ zx
可见应力分量中的切应力是两两对称的。 四 、 切应力与变形速度的关系 牛顿内摩擦定律（平面流动） dv dα τ = x =
M ，六面体为 ABCD, A 点的应力为：
pxx τ yx τ zx
τ xy
p yy
τ zy
τ xz τ yz
pzz
其方向确定为：法向应力以内法线方向为正，切向应力（正） ，过 A 点 的三个面上切向应力与坐标方向相反，其它三个面则相同。 采用泰勒级数展开并取前二项可写出其它三个面上的应力分量。
第六章粘性流体动力学基础
第六章 粘性流体动力学基础实际流体都是有粘性的，只有当粘性力与惯性力相比很小时，才能忽略粘性力而采用“理想流体”这个简单的理想模型。
支配粘性流体运动的方程比理想流体的基本方程复杂得多，因此粘性流体动力学问题的求解比理想流体动力学问题更加复杂、困难。
本章的目的在于介绍粘性流体动力学的一些基本知识。
§1 雷诺数（Re ）——粘性对于流动的影响的大小的度量粘性流体运动方程为：⎪⎪⎭⎫ ⎝⎛∂∂+∂∂+∂∂+=z y x Dt D z y x p p p f V ρ1 在x 方向的投影为：⎪⎪⎭⎫ ⎝⎛∂∂+∂∂+∂∂+=∂∂+∂∂+∂∂+∂∂z p y p x p f z u w y u v x u u t u zx yx xx x ρ1 这里以xu u ∂∂作为惯性力的代表； y p yx ∂∂ρ1作为粘性力项的代表，其大小为⎪⎪⎭⎫ ⎝⎛∂∂∂∂y u y μρ1。
下面以圆球的粘性流体绕流为例，来估算作用在单位质量流体上的惯性力和粘性力的量阶：（插圆球绕流图）L 为所研究问题的特征长度；∞V 为特征速度；∞ρ为特征密度；∞μ为特征粘性系数。
u 的量阶为∞V ；x u ∂∂的量阶为L V ∞； 22yu ∂∂的量阶为L V 2∞， 则： 作用在单位质量流体上的惯性力的量阶为：LV 2∞ 作用在单位质量流体上的粘性力的量阶为：2L V ∞∞∞ρμ 粘性力惯性力～22L V L V ∞∞∞∞ρμ＝∞∞v L V ＝∞Re Re 称为雷诺数（Reynolds 数），它的物理意义是作用在流体上的惯性力与粘性力的比值的度量。
Re 数是粘性流体动力学中最重要的无量纲参数，它在粘性流体动力学中所占地位与无粘气体动力学的M 数相当。
在不同Re 数范围内的粘性流体运动可以有完全不同的性质，下面以圆柱绕流为例看不同Re 数范围内的圆柱绕流运动。
（插圆柱绕流图）总之：Re 增加，粘性影响变弱，当Re 》1时，对于某些问题，如无分离绕流物体的升力问题，可忽略粘性影响，采用“理想流体”模型。
空气动力学第四章粘性流体动力学基础
v(x x, y y, z z,t) v(x, y, z,t) v x v y v z x y z
v(x, y, z,t) (zx xz) xyx yyy zyz
w(x x, y y, z z,t) w(x, y, z,t) w x w y w z x y z
4.2、流体微团的运动形式与速度分解定理
以x方向速度分量为例，由泰勒级数展开，有
u(x x, y y, z z,t) u(x, y, z,t) u x u y u z
x y z 将上式分别加、减下列两项
1 v y , 1 w z
得到
2 x
2 x
u(x x, y y, z z,t)
1 0 0
0
2
0
0 0 3
I1 1 2 3 I2 1 2 23 13 I3 1 23
4.3、粘性流体的应力状态
1、理想流体和粘性流体作用面受力差别 流体处于静止状态，只能承受压力，几乎不能承受拉力和剪力，不具有 抵抗剪切变形的能力。理想流体在运动状态下，流体质点之间可以存在 相对运动，但不具有抵抗剪切变形的能力。因此，作用于流体内部任意 面上的力只有正向力，无切向力。 粘性流体在运动状态下，流体质点之间可以存在相对运动，流体具有 抵抗剪切变形的能力。因此，作用于流体内部任意面上力既有正向力， 也有切向力。
D ( ps cos )ds 0 2R
4.1、流体的粘性及其对流动的影响
对于粘性流体的绕流，与理想流体绕流存在很大的差别。由于流体 与固壁表面的粘附作用，在物面近区将产生边界层，受流体粘性的 阻滞作用，流体质点在由A点到B点的流程中，将消耗部分动能用之 克服摩擦阻力做功，以至使其无法满足由B点到D点压力升高的要求 ，导致流体质点在BD流程内，流经一段距离就会将全部动能消耗殆 尽（一部分转化为压能，一部分克服摩擦阻力做功），于是在壁面 某点速度变为零（S点），以后流来的流体质点将从这里离开物面进 入主流场中，这一点称为分离点。这种现象称为边界层分离。在分 离点之间的空腔内流体质点发生倒流，由下游高压区流向低压区， 从而在圆柱后面形成了旋涡区。这个旋涡涡区的出现，使得圆柱壁 面压强分布发生了变化，前后不对称（如前驻点的压强要明显大于 后驻点的压强），因此出现了阻力D。
v(x, y, z,t) (zx xz) xyx yyy zyz
w(x x, y y, z z,t) w(x, y, z,t) w x w y w z x y z
4.2、流体微团的运动形式与速度分解定理
以x方向速度分量为例，由泰勒级数展开，有
u(x x, y y, z z,t) u(x, y, z,t) u x u y u z
x y z 将上式分别加、减下列两项
1 v y , 1 w z
得到
2 x
2 x
u(x x, y y, z z,t)
1 0 0
0
2
0
0 0 3
I1 1 2 3 I2 1 2 23 13 I3 1 23
4.3、粘性流体的应力状态
1、理想流体和粘性流体作用面受力差别 流体处于静止状态，只能承受压力，几乎不能承受拉力和剪力，不具有 抵抗剪切变形的能力。理想流体在运动状态下，流体质点之间可以存在 相对运动，但不具有抵抗剪切变形的能力。因此，作用于流体内部任意 面上的力只有正向力，无切向力。 粘性流体在运动状态下，流体质点之间可以存在相对运动，流体具有 抵抗剪切变形的能力。因此，作用于流体内部任意面上力既有正向力， 也有切向力。
D ( ps cos )ds 0 2R
4.1、流体的粘性及其对流动的影响
对于粘性流体的绕流，与理想流体绕流存在很大的差别。由于流体 与固壁表面的粘附作用，在物面近区将产生边界层，受流体粘性的 阻滞作用，流体质点在由A点到B点的流程中，将消耗部分动能用之 克服摩擦阻力做功，以至使其无法满足由B点到D点压力升高的要求 ，导致流体质点在BD流程内，流经一段距离就会将全部动能消耗殆 尽（一部分转化为压能，一部分克服摩擦阻力做功），于是在壁面 某点速度变为零（S点），以后流来的流体质点将从这里离开物面进 入主流场中，这一点称为分离点。这种现象称为边界层分离。在分 离点之间的空腔内流体质点发生倒流，由下游高压区流向低压区， 从而在圆柱后面形成了旋涡区。这个旋涡涡区的出现，使得圆柱壁 面压强分布发生了变化，前后不对称（如前驻点的压强要明显大于 后驻点的压强），因此出现了阻力D。
水力学5.1(2、3)实际流体的动力学基础(N-S方程,能量方程)
能量方程的几何意义:
水力坡度J: 当总水头线为直线时,
J hw l
当总水头线为曲线时, J dhw dH dl dl
5.3.3 实际流体恒定总流能量方程的意义
能量方程的几何意义:
(2)测管水头线可沿程降 低或升高.为什么?
测管水头线坡度JP:
d(z p)
JP
dl
水力学中规定:所有沿 程下降的坡度为正,所 以式中有一负号.
5.3.3 实际流体恒定总流能量方程的意义
能量方程的几何意义:
(3)在流速不变的流段内, 测管水头线与总水头线 平行.为什么?
5.3.4 实际流体恒定总流能量方程的应用
能量方程的应用条件及注意事项: (1)必须是恒定流,且为不可压缩的均质流体.
(2)作用于流体上的质量力只有重力,所研究的流 体边界是静止的.
流速分布越均匀,α越接近于1. 流速分布越不均匀,α的值越大. 一般渐变流, α≈1.05~1.10
为简便，常常取α=1.0
5.3.2 实际流体恒定总流的能量方程
Q (z1i
p1i
)dQi
Q
u12i 2g
dQi
Q (z2i
p2i
)dQi
Q
u22i 2g
dQi
Q hw idQi
(3)第三类积分: Q hw dQ
5 实际(粘性)流体的动力学基础
实际(粘性)流体
仅有连续性方程远远不能解决实际 问题,如:作用力,能量问题等
本章主要任务:
给出实际(粘性)流体的运动微分方程 (N-S方程),在此基础上讨论元流和恒定 总流的伯努利方程(能量方程),动量方程 的推导以及它们的意义和应用
5 实际(粘性)流体的动力学基础
水力坡度J: 当总水头线为直线时,
J hw l
当总水头线为曲线时, J dhw dH dl dl
5.3.3 实际流体恒定总流能量方程的意义
能量方程的几何意义:
(2)测管水头线可沿程降 低或升高.为什么?
测管水头线坡度JP:
d(z p)
JP
dl
水力学中规定:所有沿 程下降的坡度为正,所 以式中有一负号.
5.3.3 实际流体恒定总流能量方程的意义
能量方程的几何意义:
(3)在流速不变的流段内, 测管水头线与总水头线 平行.为什么?
5.3.4 实际流体恒定总流能量方程的应用
能量方程的应用条件及注意事项: (1)必须是恒定流,且为不可压缩的均质流体.
(2)作用于流体上的质量力只有重力,所研究的流 体边界是静止的.
流速分布越均匀,α越接近于1. 流速分布越不均匀,α的值越大. 一般渐变流, α≈1.05~1.10
为简便，常常取α=1.0
5.3.2 实际流体恒定总流的能量方程
Q (z1i
p1i
)dQi
Q
u12i 2g
dQi
Q (z2i
p2i
)dQi
Q
u22i 2g
dQi
Q hw idQi
(3)第三类积分: Q hw dQ
5 实际(粘性)流体的动力学基础
实际(粘性)流体
仅有连续性方程远远不能解决实际 问题,如:作用力,能量问题等
本章主要任务:
给出实际(粘性)流体的运动微分方程 (N-S方程),在此基础上讨论元流和恒定 总流的伯努利方程(能量方程),动量方程 的推导以及它们的意义和应用
5 实际(粘性)流体的动力学基础
第五章 实际(粘性)流体动力学基础
hw----能量损失
能量损失包括：沿程损失和局部损失。
物理意义：总流各过流断面上单位重力流体所具有的平均势
能和平均动能之和，机总机械能平均值沿程减少，部分机械 能转化为热能而损失；同时，各项机械能之间可以相互转化。
2、几何意义 z——位置水头 hw----水头损失
p
——压强水头
v 2
2g
——流速水头
p
p
(5.12)
上式表示总流重力流量（γQ）所具有的势能。
u2 （2）第二类积分 Q dQ A u3dA ，表示总流重力流量 2g 2g
所具有的动能。 总流在同一过流断面上的流速分布一般是不均匀的，即
3 3 u dA v A A
引入修正系数α，即令
3 3 u dA u dA A A 3 v A Qv 2
下降，平均测压管水头线可以上升，
可以下降。
总水头线的坡度叫做水力坡度， 表示单位重力流体在单位长度的 流程上所损失的平均水头。以H 表示总流的平均总水头，则水力
坡度为
dH dhw J ds ds
(5.21)
5.3.3
恒定总流伯努利方程的应用
总流伯努利方程适用条件：
（1）不可压缩流体；
（2）恒定流； （3）作用于流体上的质量力不可压缩流体； （4）所取过流断面1-1，2-2都在渐变流区域，但两断面之
式中，
(5.5)
g
( 2 ux dx 2 u y dy 2 uz dz ) 为单位质量流体粘性
，代入（5.5）式 力所作的微功，记为 dhw
u2 0 d ( gz ) dhw 2g p
对上式沿流线（或元流）由点1到点2积分，得
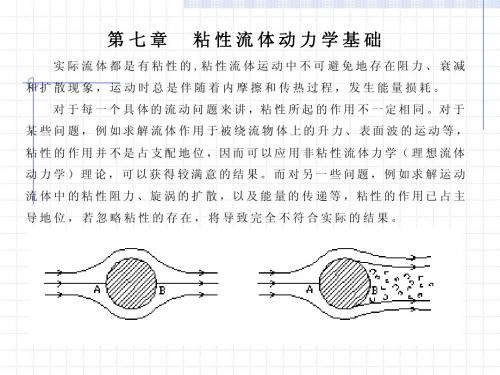
第七章 粘性流体动力学基础
第七章 粘性流体动力学基础实际流体都具有粘性，而在研究粘性较小的流体的某些流动现象时，可将有粘性的实际流体近似地按无粘性的理想流体处理。
例如，粘性小的流体在大雷诺数情况下，其流速和压强分布等均与理想流体理论十分接近。
但在研究粘性小的流体的另一些问题时，与实际情况不符，如按照理想流体理论得到绕流物体的阻力为零。
产生矛盾的主要原因是未考虑实际流体所具有的粘性对流动的影响。
本章，首先建立具有粘性的实际流体运动微分方程，并介绍该方程的在特定条件下的求解。
由于固体边界对流体与固体的相互作用有重要的影响，本章后面主要介绍边界层的一些基本概念、基本原理和基本的分析方法。
§7.1 纳维—斯托克斯方程7.1.1 粘性流体的应力实际流体具有粘性，运动时会产生切应力，它的力学性质不同于理想流体，在作用面上的表面应力既有压应力，也有切应力。
在流场中任取一点M ，过该点作一垂直于z 轴的水平面，如图7-1 所示。
过M 点作用于水平面上的表面应力p n 在x 、y 、z 轴上的分量为一个垂直于水平面的压应力p zz 和两个与水平面相切的切应力τzx 、τzy 。
压应力和切应力的下标中第一个字母表示作用面的法线方向，第二个字母表示应力的作用方向。
显然，通过M 点在三个相互垂直的作用面上的表面应力共有九个分量，其中三个是压应力p xx 、p yy 、p zz ，六个是切应力τxy 、τxz 、τyx 、τyz 、τzx 、τzy ，将应力分量写成矩阵形式：图7-1 作用于水平面的表面应力⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧ττττττzz zyzxyz yy yxxz xy xx p p p (7-1) 九个应力分量中，由于τxy =τyx 、τyz =τzy 、τzx =τxz ，粘性流体中任意一点的应力分量只有6个独立分量，即τxy 、τyz 、τzx 、p xx 、p yy 、p zz 。
7.1.2 应力形式的运动方程在粘性流体的流场中，取一以点M 为中心的微元直角六面体，其边长分别为dx 、dy 、 dz 。
流体第六章 粘性动力学
同理可得切应力与剪切速率的关系式 ：
上式（6—5）称为广义牛顿内摩擦定律。
式（6—6）
3、粘性流体中的压力
式（6—7）
一、纳维—斯托克斯方程的建立（N—S）
不可压缩牛顿流体层流流动的运动微分方程
矢量形式
二、方程的几种解析解
1、平行平板间的纯剪切流
2、平行平板间的泊谡叶流
部分固体边界的长度。 湿周长 ↑→外部阻力Fo↑ （3）绝对粗糙度Δ ：管道内壁上的粗糙突起 高度的平均值。 相对粗糙度：绝对粗糙度与管径的比值
二、有效断面的水力要素
绝对粗糙度Δ ↑→阻力↑
（4）与管路的长度有关
l↑→阻力↑
二、有效断面的水力要素
讨论：有效断面面积A与湿周长 的影响
3、平行平板间的库特流
第四节 圆管中的层流流动
一、圆管中层流的速度分布
一、圆管中层流的速度分布
二、最大流量、流量、平均流速、切应力
1、最大流量
2、流量
层流时管中流量与管径的四次方成比例
3、平均流速
4、切应力
三、沿程水头损失的计算
p 32L D 2 p 32L D2
1/ 1.8 lg[6.8 / Re ( / 3.7d )1.11 ]
（4）紊流粗糙区（f—g以右） 当Re>（665-765lgε）/ε时，λ与Re无关而与
Δ /d有关。 2 1/[21g (3.7d / )] 希夫林松公式1m，管长l=300m的圆管中， 流动着10℃的水，其雷诺数Re=80000，试求绝 对粗糙度为0.15mm时的工业管道的水头损失。
紊流
64 Re
粘性流体动力学基础
染色液线迅速发散的流动状态称之为湍流。湍流也称为紊流。 雷诺的实验告诉我们，当流速较慢(或圆管直径较小)时，流动处于 层流状态，增加流速(或增加雷诺数)到某一临界值以后，染色液线开始 抖动，并随着Re的增加抖动趋剧烈，直至Re大于某一值之后，染色线 迅速发散，进入湍流状态。层流与湍流之间的区域称之为过渡流状态。
其物理意义是惯性力与粘性力的比值。不可压缩粘性流动过程的运 动方程为：
上式是无量纲形式的粘性运动方程，关于无量纲化过程将在讨论相 似理论再论述。由于雷诺数=惯性力/粘性力，可知当Re→∞时，粘性 力的影响趋向于零，方程退化为理想流体的运动方程——欧拉方程。 当Re→0时，惯性力的影响趋向于零，方程退化为关于速度场的拉普 拉斯方程。实际的流动过程，雷诺数总是在大于零而小于无穷的范 围内。那么，雷诺数在由0 →∞变化的过程中，流动现象是不是也在 由粘性流动的图画向理想流动的图画变化呢？
为此我们可以定义一个平均意义上的压力pm，它是球行流体微团 表面所承受的法向应力的平均值的负值：
即平均应力为三个坐标面上的法向应力的算术平均值，这样，应力张 量可以写成：
其中D为偏应力张量。
二、变形速率张量
三、应力张量与变形速率张量之间的关系
为了建立两者之间的关系，斯托克斯根据牛顿粘性公式提出了以 下假定：
一、连续方程 二、运动方程
由第五章得到了运动方程的一般形式：
如果流体满足斯托克斯三假设，应力张量就可以用广义牛顿粘性公式表 示，注意应力张量的梯度运算：
将广义牛顿粘性应力公式代入：
或写成分量形式：
这就是著名的纳维—斯托克斯方程，又称N—S方程。 对于不可压缩流动在μ=const时，有： 而此时有 ＝0，所以N—S方程可简化为：
p
其物理意义是惯性力与粘性力的比值。不可压缩粘性流动过程的运 动方程为：
上式是无量纲形式的粘性运动方程，关于无量纲化过程将在讨论相 似理论再论述。由于雷诺数=惯性力/粘性力，可知当Re→∞时，粘性 力的影响趋向于零，方程退化为理想流体的运动方程——欧拉方程。 当Re→0时，惯性力的影响趋向于零，方程退化为关于速度场的拉普 拉斯方程。实际的流动过程，雷诺数总是在大于零而小于无穷的范 围内。那么，雷诺数在由0 →∞变化的过程中，流动现象是不是也在 由粘性流动的图画向理想流动的图画变化呢？
为此我们可以定义一个平均意义上的压力pm，它是球行流体微团 表面所承受的法向应力的平均值的负值：
即平均应力为三个坐标面上的法向应力的算术平均值，这样，应力张 量可以写成：
其中D为偏应力张量。
二、变形速率张量
三、应力张量与变形速率张量之间的关系
为了建立两者之间的关系，斯托克斯根据牛顿粘性公式提出了以 下假定：
一、连续方程 二、运动方程
由第五章得到了运动方程的一般形式：
如果流体满足斯托克斯三假设，应力张量就可以用广义牛顿粘性公式表 示，注意应力张量的梯度运算：
将广义牛顿粘性应力公式代入：
或写成分量形式：
这就是著名的纳维—斯托克斯方程，又称N—S方程。 对于不可压缩流动在μ=const时，有： 而此时有 ＝0，所以N—S方程可简化为：
p
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
流体力学基础
粘性流体动力学基础
两块相距为b的平行平板，它们之间充满着某种流体，这两块 乎板具有足够的长度。让下板B静止不动，用力F拖动A板，使 A板以速度U作匀速直线运动．从试验可以发现，紧贴A板的一 层流体与A板以同样的速度U运动，而静贴B板的流体则与B板 具有同样的速度，即速度为零。当速度U不是很大时，两板之 间某点y处的流体速度与距离满足线性关系。 粘度单位：Ｎ·s/m2=Pa·s=帕·秒，随温度升高而降低。20。C， 粘度单位 水的粘度约为1.002×10-3Pa·s，空气的粘度1.81×10-5Pa·s 运动粘性系数：动力粘度/密度 m2/s，水1.01×10-6 m2/s 运动粘性系数
流体力学基础
粘性流体动力学基础
层流和紊流
• 雷诺实验
ru2与惯性力成正比，mu/d与粘性力成正比， 由此可见，雷诺准数的物理意义是惯性力与粘性力之比。
流体力学基础
粘性流体动力学基础
层流与紊流
• 湍流 湍流，也称为紊流 紊流，是流体 流体的一种流动状态。当流速很小 紊流 流体 时，流体分层流动，互不混合，称为层流，或称为片流； 逐渐增加流速，流体的流线开始出现波浪状的摆动，摆动 的频率及振幅随流速的增加而增加，此种流况称为过渡流； 当流速增加到很大时，流线不再清楚可辨，流场中有许多 小漩涡，称为湍流，又称为乱流、扰流或紊流。 • 这种变化可以用雷诺数来量化。雷诺数较小时，黏滞力对 流场的影响大于惯性力，流场中流速的扰动会因黏滞力而 衰减，流体流动稳定，为层流；反之，若雷诺数较大时， 惯性力对流场的影响大于黏滞力，流体流动较不稳定，流 速的微小变化容易发展、增强，形成紊乱、不规则的湍流 流场。
流体力学基础
粘性流体动力学基础
流体力学发展简史
• 理论流体力学进一步的发展是从1821年开始，纳维 纳维(Navier， 纳维 1785年～1836年)等人开始考虑将分子问的作用力加人到 欧拉方程中去。1845年斯托克斯 斯托克斯(Stokes，1819年～1903年) 斯托克斯 将这个分子间的作用力用粘性系数miu表示，并正式完成 了纳维—斯托克斯方程，最终建立了粘性流体力学的基本 方程，奠定了近代粘性流体力学的基础。但是，由于方程 式的非线性，解此方程，在数学上碰到了很大的困难。因 此，一直到19世纪末，理论的和实验的流体力学仍然各自 独立地发展。
流体力学基础
粘性流体动力学基础
粘性流体力学
李连侠
水力学与山区河流开发保护国家重点实验室 2009年4月
流体力学基础
粘性流体动力学基础
本课程主要内容
• 粘性流体动力学基础 • 湍流 • 边界层理论
流体力学基础
粘性流体动力学基础
流体力学发展简史
• 人类在上古时代使用的武器从石块和棍棒发展到流线 型的矛和带有羽毛的箭，说明人类对粘性流体的阻力 已经早有认识，并在实践中加以了应用。但是对流体 粘性理性的认识则可以说是从1687年牛顿 牛顿(Isac 牛顿 Newton 1642 Newton，1642年一1727年)著名的粘性流动试验开始。 1727 ) 牛顿发现了几乎所有的普通流体，像水与空气等，其 阻力与流速梯度成线性关系。为了纪念牛顿，这样的 流体称为牛顿流体。
流体力学基础
粘性流体动力学基础
卡门涡街频率
• 卡门涡街起因流体流经阻流体时，流体从阻流体两侧剥离， 形成交替的涡流。这种交替的涡流，使阻流体两侧流体的 瞬间速度不同。流体速度不同，阻流体两侧受到的瞬间压 流体速度不同， 流体速度不同 力也不同，因此使阻流体发生振动。 力也不同，因此使阻流体发生振动。振动频率与流体速度 成正比，与阻流体的正面宽度成反比。卡门涡街频率与流 体速度和阻流体(旋涡发生体)宽度有如下关系： f=SrV/d • 其中：f=卡门涡街频率 – Sr=斯特劳哈尔数 (~0.2) 斯特劳哈尔数 – V=流体速度 – d=阻流体迎面宽度
流体力学基础
粘性流体动力学基础
有关湍流的举例
• 香烟产生的烟。在最初的几厘米,烟的流场 是层流,随着热空气的向上加速,烟就开始变 得不稳定形成了湍流。与此类似，空气中 污染的扩散就是由湍流主宰的。 • F1赛车高速转弯时，前车尾部造成的湍流 使后车前定风翼下压力损失约30%。如果距 离前车太近，会造成转向不足。
流体力学基础ቤተ መጻሕፍቲ ባይዱ
粘性流体动力学基础
达郎贝尔佯谬
• D’ Alembert paradox理想不可压缩流体绕任意剖面的不脱 体绕流问题中物体不遭受任何阻力，这与实际是不符合的， 产生佯谬的根本原因是没有考虑粘性的作用。 • Viscous / ideal • 理想流体与真实流体的区别：是否考虑粘性
流体力学基础
流体力学基础
粘性流体动力学基础
流体力学发展简史
• 历史上，流体力学一直沿着理论的和实验的两个不同的途 径发展。理论流体力学由于17历年欧拉 欧拉(Euler,1707年 欧拉 ~1783年)方程的提出，对于不考虑粘性的理想流体流动已 逐渐达到完美的程度。遗憾的是理想流动的解往往与试验 结果和真实流动相差甚远，以至相反。1752年达朗贝尔 达朗贝尔 ( D’ Lambert,1717年~1783年)发表了他著名的达朗贝尔佯 谬，指出在一个无界、理想不可压缩流体中，物体作匀速 直线运动时的阻力为零。稍后拉普拉斯 拉普拉斯(Laplace，1749年 拉普拉斯 ~1827年)，拉格朗日 拉格朗日(Lagrange,1736年~1813年)等人把理想 拉格朗日 流体运动的研究推向了新的高峰。但是，达朗贝尔佯谬的 结论对从事实际工程的工程师来说是无法接受的，从而工 程师们为了解决生产和技术发展中提出的流体运动问题而 发展了高度经验性的一门流体力学的分支----水力学 水力学 (Hydraulics)。
绕隙，圆板B与一小电动机相连。开始时，A与B盘都处于静止状态。 随后启动小电动机，B盘开始转动，过了一会儿，A盘也会跟着转动 起来，且越转越快，直到A盘转速接近B盘为止。这就表明空气有粘 性，当B盘转动时，带动附近一层空气跟着转动，这层空气又带动相 邻的一层空气转动，这样一层带动一层，最店带动紧贴着A板的一层 空气转动．于是这层空气带动A板跟着转动起来了。
• Karman, Th. von, Uber den Mechanismus des Widerstandes,den ein bewegter Korper in einer Flusigkeit erfarhrt, Gottingen Nachrichten mathematichephysicalische Klasse (1911) 509-517.
流体力学基础
粘性流体动力学基础
流体力学发展简史
• 20世纪初，德国工程师普朗持 普朗持(Prandtl，1875年～1953年) 普朗持 由于提出边界层理论 边界层理论，而对流体力学，持别是粘性流体力 边界层理论 学的发展做出了卓越的贡献。普朗特提出在雷诺数很大的 情况下，粘性的作用主要局限在绕流物体或其他流动边界 的固体壁面附近很薄的一层流动中，这个薄层称为边界层。 边界层外部流动则可按理想流动处理。这一设想克服了粘 性流动求解中数学上的巨大困难。根本上解决了流动阻力 和能量损失这样重大的粘性流动问题。边界层理论的提出 使理论和实验完美地统一起来，从而使流体力学的两个分 支——理想流体力学和水力学逐渐结合和统一，使流体力 学得到划时代的发展。
流体力学基础
粘性流体动力学基础
流体力学基础
粘性流体动力学基础
二元翼型绕流
• 看教材
流体力学基础
粘性流体动力学基础
管内流动
• 粘性流体自水罐中稳定地流入圆管， 由于流体粘性作用，在管壁附近形 成边界层流动。边界层厚度顺流向 逐渐增加、并由层流边界层经过转 捩发展为紊流边界层。当边界层厚 度发展到管道中心．整个管道中均 成为边界层流动。再经过一个短距 离的调整、形成“充分发展紊流” ， 此后管道内的流速分布剖面将不再 变化。由管道进口到充分发展紊流 (或称充分发展管流)这一段称为进口 段。
流体力学基础
粘性流体动力学基础
层流到紊流过渡
• 流态转变时的雷诺数值称为临界雷诺数。临界雷 诺数与流场的参考尺寸有密切关系。一般管道流 雷诺数Re＜2100为层流状态，Re＞4000为湍流状 态，Re＝2100～4000为过渡状态。 • 绝对稳定层流状态，第一临界雷诺数以下 • 过渡状态 • 无条件不稳定及湍流状态 第二临界雷诺数以上 • 有效地描述湍流的性质，至今仍然是物理学中的 一个重大难题。
流体力学基础
粘性流体动力学基础
小结
• 由这个例子可以看出理想流动与粘性流动的明显不同。它 们的流谱、流速分布、壁面压强与切应力均有很大区别。 而且粘性流动表现得更为复杂多佯。同样的流动边界层随 雷诺数的不同而有着不向的流谱、流速分布、压强分布、 阻力规律、层流与紊流边界层的形成及其与绕植物体壁面 的分离、尾流的形成与发展等等。
流体力学基础
粘性流体动力学基础
卡门涡街发现历史
• 1911年，西奥多 冯·卡门 西奥多·冯 卡门 卡门在德国哥廷根大学空气动力学家路德维希 普 路德维希·普 西奥多 路德维希 朗特手下任助教。当时普朗特正研究边界层现象，他命一位攻读博士 朗特 学位的研究生卡尔 希门茨（Karl Hiemenz）设计一个流水槽，以便观 卡尔·希门茨 卡尔 希门茨（ ） 察流水经过一个圆柱体时的边界层，並令希门茨测量圆柱体表面上不 同点的压力。希门茨发现圆柱体表面的压力并非如预期的平稳，而是 剧烈地振动。他将这个情况向普朗特汇报，普朗特说，“你的圆柱体 显然不圆”。希门茨细心将圆柱体磨了又磨，测了又测，不见改进。 冯·卡门走过实验室时不在意地问道：“卡尔，怎么样了”？卡尔答道 “还是振动”，过几天又问：“卡尔，怎么样了？”，“还是振动得 厉害”。这引起冯·卡门注意了，他想“也许振动不是偶然的，而是由 内在原因决定的”。于是冯·卡门从理论上进行思考，起初他设想圆柱 体后的水流形成两道对称排列但反方向的旋涡，但发现这种状态不能 维持，很快不稳定。于是他假设两道旋涡交错排列，计算结果表明这 种状态能够维持。冯·卡门将计算结果向导师普朗特报告。普朗特命 冯·卡门写出论文发表。这是冯·卡门的第一篇论文，也是他的成名之 作。冯·卡门关于卡门涡街的理论被后来的实验证实。“卡门涡街”的 名称，沿用至今。