均匀物质的热力学性质热力学
合集下载
热统3
∂p ∂V C p − CV = T ∂T V ∂T p
C p − CV =
VTα 2
κT
≥0
γ ≥1
例 范氏气体（计入分子体积和相互吸引修正后的气体模型） 范氏气体（计入分子体积和相互吸引修正后的气体模型）
n2a p + 2 (V − nb ) = nRT V
第二章 均匀物质的热力学性质
1. 基本热力学函数 2. 麦氏关系及应用 3. 气体节流和绝热膨胀
§2.1 基本热力学函数
1. 内能
dU = TdS − pdV
∂U ∂U U = U ( S , V ), dU = dS + dV ∂S V ∂V S ∂U ∂U T = = T ( S , V ), p = − = p( S , V ) ∂S V ∂V S
∂ 2G ∂ 2G = ∂p∂T ∂T∂p
∂G H = G + TS = G − T ∂T p
∂S ∂V = − ∂p ∂T p T ∂G ∂G U = H − pV = G − T − p ∂p ∂T p T
∂p dU = CV dT + T − p dV ∂T V CV ∂p dS = dT + dV T ∂T V
∂2 p ∂2S ∂2S ∂CV =T = T 2 =T ∂T ∂V∂T ∂T∂V ∂V T V
4. 吉布斯函数（自由焓） G = H − TS = F + pV 吉布斯函数（自由焓）
dG = − SdT + Vdp
热力学与统计物理—第二章
§2.2 麦氏关系的简单应用
一、以T, V为状态参量
U p T p V T T V U S CV T T V T V
能态方程
CV p dS dT dV T T V
dS dU pdV T
4 d(VT 3 ) 3 4 S VT 3 S 0 3
3.物态方程 ：
1 1 p u (T ) T 4 3 3
1 c J u cu T 4 T 4 4 4
Ju T 4
斯特藩—玻耳兹曼定律
三 . 红外技术及应用
红外探测
dG
V m ( )T , p 0 ( )T ,H H p
磁致伸缩 压磁效应
G G G dT dp dH T p H
G G V , 0 m p T ,H H T , p
§2.4 热辐射的热力学理论
第二章 均匀物质的热力学性质
1. 麦克斯韦关系及应用
2. 热辐射的热力学理论
3. 磁介质热力学
§2.1 麦克斯韦关系
热力学基本微分方程：
dU T dS Yi dyi
i
四个全微分（简单系统）：
dU TdS pdV
H U pV
dH TdS Vdp dF SdT pdV
p dU CV dT T p dV T V
二
、以T, p为状态 dp T T p Tpp T
V dH C p dT V T dp T p
3. 辐射能量密度u：
U= u (T)V
4. 辐射通量密度：
平衡辐射的热力学均匀物质的热力学性质热力学
能量称为辐射通量密度
Ju 。
6. 辐射压强： 电磁波投射到物体上时，它对物体所施加的压强。
电磁场理论：
p 1 3 u
物态方程
平衡辐射特点：窖内电磁辐射的能量密度以及能量密度按频率 的分布只是温度的函数，而与空腔的其他性质无关。即：
u=u(T)
证明：
假设在ω — ω+dω范围内
u1 u 2
则能量将由空窖1流向空窖2，造成
积分得：
u (T ) T
4
3. 辐射场的熵 S ：
p 1 3 u
u (T ) T
4
U ( T , V ) Vu ( T )
dS
dU pdV T
1 1 4 4 d T V T dV T 3
4 T V d T T d V
4 4 2) 与面元dA成θ角的,单位时间内,传播到dA 上的能量为 d u ( cdA cos ) 4 u d u sin d d
3) 辐射的总能量,则对球体的立体角求和. 0 ,0 2 取球面坐标系：
2
J udA
一. 基本微分方程
dU TdS
磁场做功：
Y dy
i i
i
激发磁场的功
磁化功
dW Vd (
0H
2
2
) 0VHdM
当热力学系统界定为介质时：
dW 0VHdM
0 Hdm
( m VM )
中
p 0H , V m
忽略体积变化功时，将 dU TdS pdV
U ( T , V ) Vu ( T )
Ju 。
6. 辐射压强： 电磁波投射到物体上时，它对物体所施加的压强。
电磁场理论：
p 1 3 u
物态方程
平衡辐射特点：窖内电磁辐射的能量密度以及能量密度按频率 的分布只是温度的函数，而与空腔的其他性质无关。即：
u=u(T)
证明：
假设在ω — ω+dω范围内
u1 u 2
则能量将由空窖1流向空窖2，造成
积分得：
u (T ) T
4
3. 辐射场的熵 S ：
p 1 3 u
u (T ) T
4
U ( T , V ) Vu ( T )
dS
dU pdV T
1 1 4 4 d T V T dV T 3
4 T V d T T d V
4 4 2) 与面元dA成θ角的,单位时间内,传播到dA 上的能量为 d u ( cdA cos ) 4 u d u sin d d
3) 辐射的总能量,则对球体的立体角求和. 0 ,0 2 取球面坐标系：
2
J udA
一. 基本微分方程
dU TdS
磁场做功：
Y dy
i i
i
激发磁场的功
磁化功
dW Vd (
0H
2
2
) 0VHdM
当热力学系统界定为介质时：
dW 0VHdM
0 Hdm
( m VM )
中
p 0H , V m
忽略体积变化功时，将 dU TdS pdV
U ( T , V ) Vu ( T )
热力学-统计物理第二章 均匀物质的热力学性质
T H S
P
V H P
S
*
G G dG SdT VdPdG TPdTPTdP
S
G T
P
V
G P
T
* dF SdT PdVdF F TVdT V FTdV
S
F T
V
P F V
T
三、麦氏关系 全微分满足
dff dxf dy x y
(f ) (f ) y x x y
T
U S
V
P U V
s, t (3) s, t 1
(2)
u xy
u, x,
y y
(4)
u, v x, y
1 x,
y
即:
u,v x, y
x, y u,v 1
u, v
u,v u,v x,s
(5)
x,y
x,
s
x,y
u ,v x,s x,y x,s
（5）的 2 个推论：
u,v
∴
V H
p
1 T
V S
p
1 T
T p
S
故： Tp
H
V Cp
T p
S
B、所求偏导数中， S是不变量，可先用下题方法，再 用相关定义或麦氏关系等。
例5、求证 V KTCV
TS T
证明： V •T •S 1
TS SV VT
∴
V TS
S V TVST
CV T
p
C TVT pV
→确定基本热力学函数 →或特性函数 (态式、内能、熵）
→基本目标 把不可测的态函数或物理效应
或方法
与可测量联系，用可测量表达
→基础 1、四个微分式 2、麦氏关系
《热力学与统计物理》第二章 均匀物质的热力学性质
焓判据:绝热等压过程中，系统的焓永不增加（系统无 其他形式的功).系统发生的过程总是向着焓减少的方向 进行，平衡态时，焓最小.
§2.2 内能、焓、自由能、吉布斯函数的全微分
本节要求： ①掌握状态函数的全微分； ②记住热力学偏导数和麦克斯韦关系。
一.状态函数的全微分
dU TdS pdV 看成是U以S,V为变量的全微分 U (S,V )
1
,得:
T V
U
T U
V
U V
T
U V
T
U
T
V
利用方法1可求出 U
V T
，连同
CV
的定义便得到
T V
U
1 CV
T
p T
V
p
CV
U T
V
U V
T
T
p T
V
p
由此可见，已知 CV 和状态方程便可求得气体的焦耳系数。
方法4.链式关系法
条件：若所求偏导数包含S，且已在分子或分母上，但 不能用热容量的定义或麦氏关系消除时，可用此法。
说明：本章在定义新的态函数和导出普遍热力学关 系时，都以P、V、T 系统为例进行。
§2.1 自由能和吉布斯函数
本节要求：①理解自由能和吉布斯函数的概念； ②理解自由能判据和吉布斯判据
一.自由能
1.定义:
对于等温条件:
引入新的热力学函数: 自由能 F U TS
有: 2.最大功原理：系统自由能的减少是在等温过程中
热力学基本方程
dU TdS pdV dH TdS Vdp dF SdT pdV dG SdT Vdp
热力学偏导数
T
U S
V
p
U V
S
§2.2 内能、焓、自由能、吉布斯函数的全微分
本节要求： ①掌握状态函数的全微分； ②记住热力学偏导数和麦克斯韦关系。
一.状态函数的全微分
dU TdS pdV 看成是U以S,V为变量的全微分 U (S,V )
1
,得:
T V
U
T U
V
U V
T
U V
T
U
T
V
利用方法1可求出 U
V T
，连同
CV
的定义便得到
T V
U
1 CV
T
p T
V
p
CV
U T
V
U V
T
T
p T
V
p
由此可见，已知 CV 和状态方程便可求得气体的焦耳系数。
方法4.链式关系法
条件：若所求偏导数包含S，且已在分子或分母上，但 不能用热容量的定义或麦氏关系消除时，可用此法。
说明：本章在定义新的态函数和导出普遍热力学关 系时，都以P、V、T 系统为例进行。
§2.1 自由能和吉布斯函数
本节要求：①理解自由能和吉布斯函数的概念； ②理解自由能判据和吉布斯判据
一.自由能
1.定义:
对于等温条件:
引入新的热力学函数: 自由能 F U TS
有: 2.最大功原理：系统自由能的减少是在等温过程中
热力学基本方程
dU TdS pdV dH TdS Vdp dF SdT pdV dG SdT Vdp
热力学偏导数
T
U S
V
p
U V
S
第二章均匀物质的热力学性质
第二章 均匀物质的热力学性质1.18．麦克斯韦关系在第一章中，我们根据热力学的基本规律引进了三个基本的热力学函数物态方程、内能和熵，并得到在两个邻近的平蘅状态之间内能、熵和体积之差的关系dU=TdS-pdV (18．1)(18．1)式是热力学的基本微分方程。
在本章中我们将从这基本微分方程出发，通过数学推演得出系统各种平衡性质的相互关系。
这是热力学应用的一个重要方面。
我们将会看到所得到的热力学关系是非常普遍的，可以应用于处在平衡状态的任何热力学系统。
将U 看作变量S,V 的函数U=(S,V)，其全微分为dV V U dS S U dU S V ⎟⎠⎞⎜⎝⎛∂∂+⎟⎠⎞⎜⎝⎛∂∂= 上式和(18．1)式对于任意的dS 和dV 都相等，故有P V U T S U S V−=⎟⎠⎞⎜⎝⎛∂∂=⎟⎠⎞⎜⎝⎛∂∂, (18.2) 考虑到求偏导数的次序可以交换,即SV U V S U ∂∂∂=∂∂∂22，还可以得到以下关系 V SS p V T ⎟⎠⎞⎜⎝⎛∂∂−=⎟⎠⎞⎜⎝⎛∂∂ (18.3) 在上面的推导中我们取S,V 为自变量。
我们可以通过勒让德(Legendre),将自变量换为其它变量。
这里先对勒让德变换作一简单的介绍。
设L 是变量x,y 的因数，L=L(x,y)．函数L 的全微分为(18.4)Ydy Xdx dL +=其中yL Y X L X ∂∂=∂∂=,一般来说也是X, y 的函数。
作变换 Xx L L −= (18.5)求(18．5)式的微分,有xdX Xx dL L d −−=将(18．4)式代入，得函数L 的全微分为Ydy xdX L d +−= (18.6)根据(18．6)式，可以把L 看作是以X 和y 为自变量的函数。
其偏导数为Y yL X X L =∂∂−=∂∂, (18.7) 变换(18.5)称为勒让德变换。
·如果作勒让德变换H=U+Pv (18.8)H 就是在1.6所引进的焓。
热力学与统计物理学-第二章
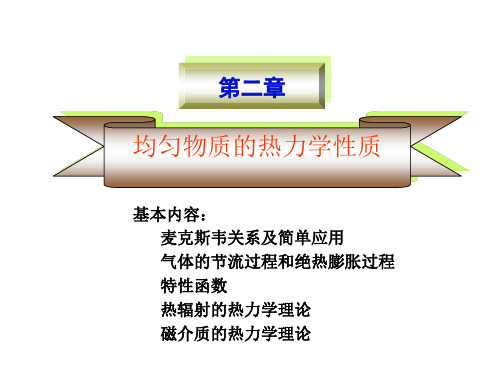
dG=-SdT+VdP
S V
P T
T P
Good Physicists Have Studied Under Very Fine Teachers
太阳照在小树上
(
S V
)T
(
p T
)V
（河流）由山峰流向山谷
照向和流向方向一致取正号，否则取负号。看对 方的分母，取自己的脚标。
T
p
T
V
( V
)S
( S
)V
;
( p )S ( S ) p
( S V
)T
(
p T
)V
;
( V T
)p
(
S p
)T
——麦克斯韦关系
Sun
太阳 peak
山峰
Tree
小树 Valley
山谷
§2-2 麦克斯韦关系的简单应用
麦克斯韦关系的应用有：
⑴用实验可测量的量（如状态方程，热容量
Summary
dU=TdS-PdV dH=TdS+VdP
P T S V V S
T V
P S
S P
G
T
P
F
H
V
S
U
dF=-SdT -PdV
S P
V T
T V
一.能态方程和定容热容量
U T p p V T T V
CV
T S T
V
第一式给出了温度不变时, 系统内能随体积的变化率与物态方程的关系，称 为能态方程；第二式是定容热容量。
热力学统计物理均匀物质的热力学性质
scT VdTRlnVbs0
作业: 2.2, 2.4, 2.6, 2.8, 2.9
热统
30
§2. 5 特性函数
定义：在适当选取独立变量的条件下，只要知道一个热力学函数，就可
以求得其余全部热力学函数，从而把均匀系统的平衡性质完全确定，这个 函数称为特性函数。
例如 UU(S,V) 独立参量 S ,V
(V ,T ) ( p,S )
( p,T )
T
T
S
T S
T
V P
CV . Cp
例二 求证
p
2
C p CV
T
T V p
V T
Cp
TS Tp
T(S,p) (T,p)
利用麦氏关系：S V
T
P T
V
(S,p) S p S p
T(T,V) TTVVT VTTV
(T,p) (T,V)
p VT
虚线－范德瓦耳斯气体 的反转温度。
实线－氮气反转温度。
热统
24
第二位力系数随温度的变化关系
C 1p(T V TpV)C np[Td dT BB ]
30
B/(cm3/mol)
20 10
He
N2
H2
Ne
He
100 200 300 400 500 600 700 0
T/K Ar
-10 N2
-20
-30
*
S
F T
V
P F V
T
V(S)TV( F TV)T
T(P)V
T( V FT)V
S V
T
P T
V
热统
9
在函数关系 GG(T,P) 中得到：
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
p
S T
V
由于熵可写成 S ( T, p ) = S ( T, V( T, p ) )，并利用
复合函数求微商的法则，可得：
S S S V T p T V V T T p
所以
Cp
CV
T S V
V T T
p
(2.2.5)
利用麦氏关系(2.2.3)，最后可得
T
(
S T
)
p
(
V p
)T
(
S p
)T
(
V T
)p
(T ,V ) (T , p)
(
V p
)T
作2.2业，：2.23.，1，2.4
T ( S ) T
Cp T
p
(
T
V T
(
S p
)T
(
( V
)
2 p
p
V T
)T
)
p
(
V p
)T
Cp
Cp
CV
T
(
V T
)
p
(
V T
(
V p
)T
)p
（ V T T)2ps源自1 VV pS
所以
T
1 V
V p
T
s
1 V
V p
S
T
1 V
V p
T
(V , S )
( p, S) (V ,T )
( p,T )
(V , S )
(V ,T ) ( p, S)
( p,T )
CV Cp
三. 简单系统的 Cp 和CV 的关系
2. (a) Cp －CV：
Cp
CV
T
S T
V T
（
V p
)T
T
2
13
附录1：几个重要的数学关系式
给定四个态变量x、y、z 和 w，且 f (x, y, z) = 0，w 是变量x, y, z 中任意两个的函数，则有
x y
z
1 y
x z
x y
z
y z
x
z x y
1
x w z
x y
z
y w z
x y
z
x y
w
x w
y
dT
( S V
)T
dV
dU TdS pdV
S
S
T
( T
)V
dT
T
( V
)T
dV
pdV
S
S
T (T )V
dT
[T ( V
)T
p]dV
T
(
S T
)V
dT
[T
(
p T
)V
p]dV
比较，得定容热容量： CV
(
U T
)V
T
(
S T
)V
能态方程：
( U V
)T
T ( S V
)T
p
T
(
p T
)V
p
7
理想气体和范氏气体能态方程的推导：
(2.1.1)
由 H = U + pV、 F = U – TS 和 G = H – TS 易得：
dH = TdS + Vdp
(2.1.4)
dF = – SdT – pdV
(2.1.7)
dG = – SdT + Vdp
(2.1.10)
二. 麦克斯韦( Maxwell )关系
由于U, H, F, G均为状态函数，它们的微分必定满足 全微分条件，即:
理想气体：
pV nRT
范氏气体：
( U V
)T
T
(
p T
)V
p
T
nR V
p
0
(
p
an2 V2
)(V
nb)
nRT
p
nRT V nb
an2 V2
p (T )V
nR V nb
( U V
)T
nRT V b
p
an2 V2
8
二. 焓态方程
H p
T
V
T V T
p
Cp
T
S T
p
(2.2.10) (2.2.8)
T
(
S T
)
p
dT
T
(
S p
)T
dp
Vdp
T ( S T
) p dT
[T
(
S p
)T
V ]dp
S
V
T (T ) p dT [T ( T ) p V ]dp
比较，得定压热容量：
Cp
( H T
)p
T ( S T
)p
焓态方程：
( H p
)T
T
(
S p
)T
V
T (V T
)p
V
10
三. 简单系统的 Cp 和CV 的关系 1. CV /Cp： s / T CV / C p
U 0 V T
这正是焦耳定律。
(2)
对于范氏气体（1
mol），
p
a v2
v
b
RT
U V
T
a v2
实际气体的内能不仅与温度 有关，而且与体积有关。
能态方程的推导，选T,V为参量：
U U (T,V )
dU
( U T
)V
dT
( U V
)T
dV
S S(T ,V )
dS
( S T
)V
第二章 均匀物质的热力学性质
本章介绍均匀物质系统的热力学性质。 主要内容有：
麦克斯韦关系及简单应用； 气体的节流过程和绝热膨胀过程； 特性函数； 辐射热力学； 磁介质热力学
§2.1 内能、焓、自由能和吉布斯函数的全微分
一. 热力学函数U, H, F, G 的全微分
热力学基本微分方程：
dU = TdS – pdV
Cp
CV
T p T
V V T
p
VT 2 T
对于理想气体，C p
CV
T（
p T
)V（
V T
)
p
T
nR nR Vp
nR
2. (b) Cp －CV： 用雅可比行列式证明
证明：
S
(S,V )
CV T (T )V T (T ,V )
Cp
CV
（ V T（ VT
p
)
2 p
)T
T
(S,V ) (T , p)
S V V S
比较 dU = TdS – pdV
可得： U T S V
U p V S
(2.1.2)
同理：
H T S p F S T V G S T p
H p
S
V
F p V T
G p
T
V
(2.1.5) (2.1.8) (2.1.11)
§2.2 麦氏关系的简单应用
T V
S
p S
V
(2.2.1)
T p
S
V S
p
(2.2.2)
S V
T
p T
V
(2.2.3)
S p
T
V T
p
(2.2.4)
以上四式就是著名的麦克斯韦关系（简称为麦
氏关系）。它们在热力学中应用极其广泛。
三. 麦克斯韦( Maxwell )关系数学推导：
由U=U(S, V)，得： dU U dS U dV
一. 能态方程
U T p p V T T V
CV
T S T
V
(2.2.7) (2.2.5)
第一式给出了温度不变时, 系统内能随体积的变化 率与物态方程的关系，称为能态方程。
第二式是定容热容量。
温度不变时内能随体积的变化率与物态方程的关系。
讨论：
(1) 对于理想气体, pV = nRT，显然有：
第一式给出了温度不变时, 系统焓随压强的变化率 与物态方程的关系，称为焓态方程。
第二式是定压热容量。
温度不变时焓随压强的变化率与物态方程的关系。
焓态方程的推导，选T,P为参量
H H (T, p)
dH
( H T
)p
dT
( H p
)T
dp
S S(T, p)
dS
( S T
)
p
dT
( S p
)T
dp
dH TdS Vdp
w y
z
(2.2.A1) (2.2.A2) (2.2.A3) (2.2.A4)
附录2：运用雅可比行列式进行导数变换
设： u u(x, y),v v(x, y)